Self-Consumption and Self-Sufficiency in Photovoltaic Systems: Effect of Grid Limitation and Storage Installation
Abstract
1. Introduction
2. Review of the Most Common Strategies to Maximize Self-Consumption and Self-Sufficiency
2.1. Definition of Self-Consumption and Self-Sufficiency
2.2. Main Strategies to Maximize the Self-Consumption and the Self-Sufficiency
2.3. Description of Peak Shaving Techniques without Energy Storage
2.4. Review of Methodologies Maximizing Self-Consumption or Self-Sufficiency
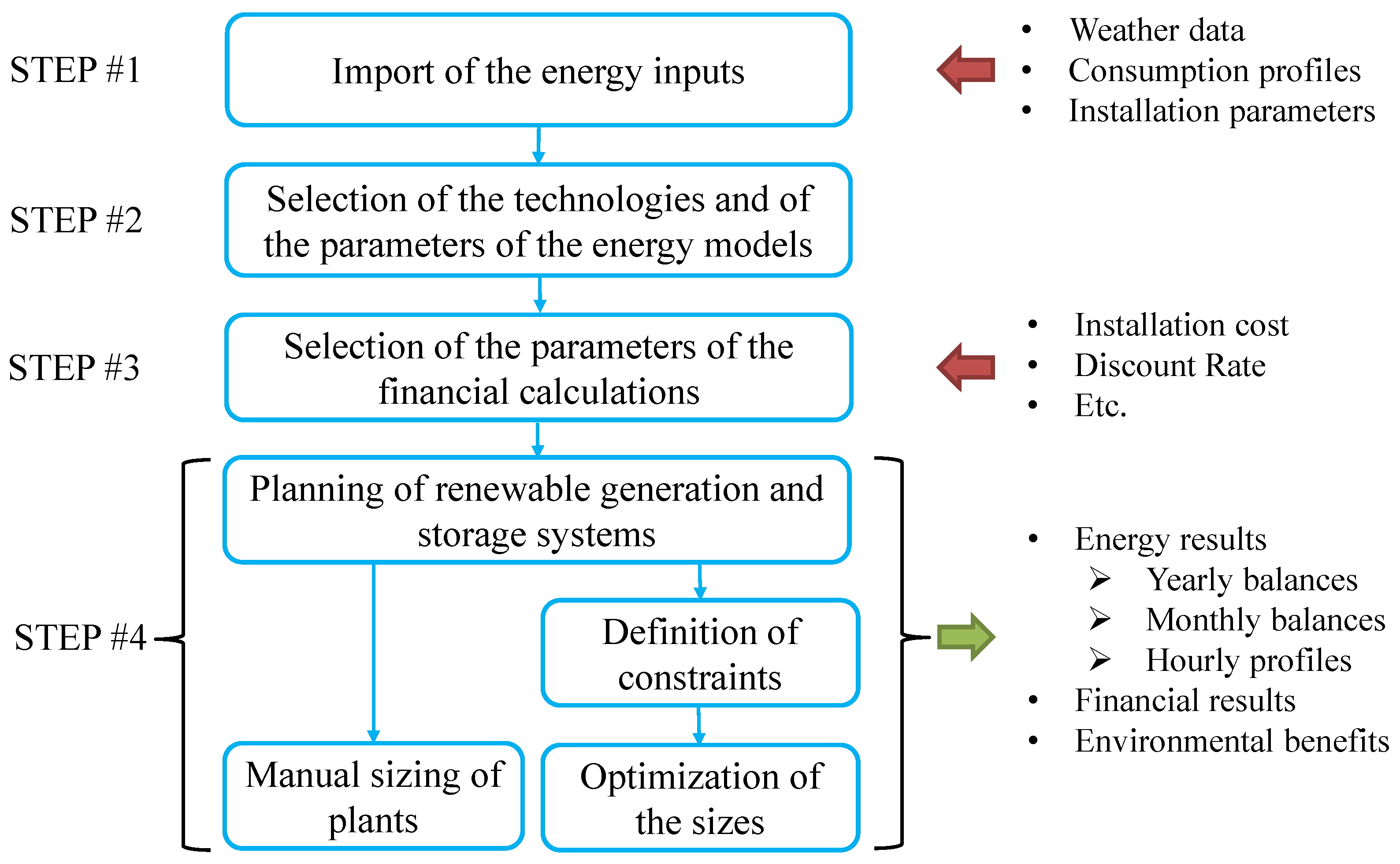
3. A Methodology for the Optimal Sizing of PV and Batteries
3.1. STEP #1—Import of the Energy Inputs
3.2. STEP #2—Selection of the Technologies and of the Parameters of the Energy Models
3.3. STEP #3—Selection of the Parameters for the Financial Calculation
3.4. STEP #4—Planning of Renewable Generation and Storage Systems
3.5. Considerations Related to the Optimization Criterion
3.6. Application of the Procedure in a Software Program for Research and Remote Teaching
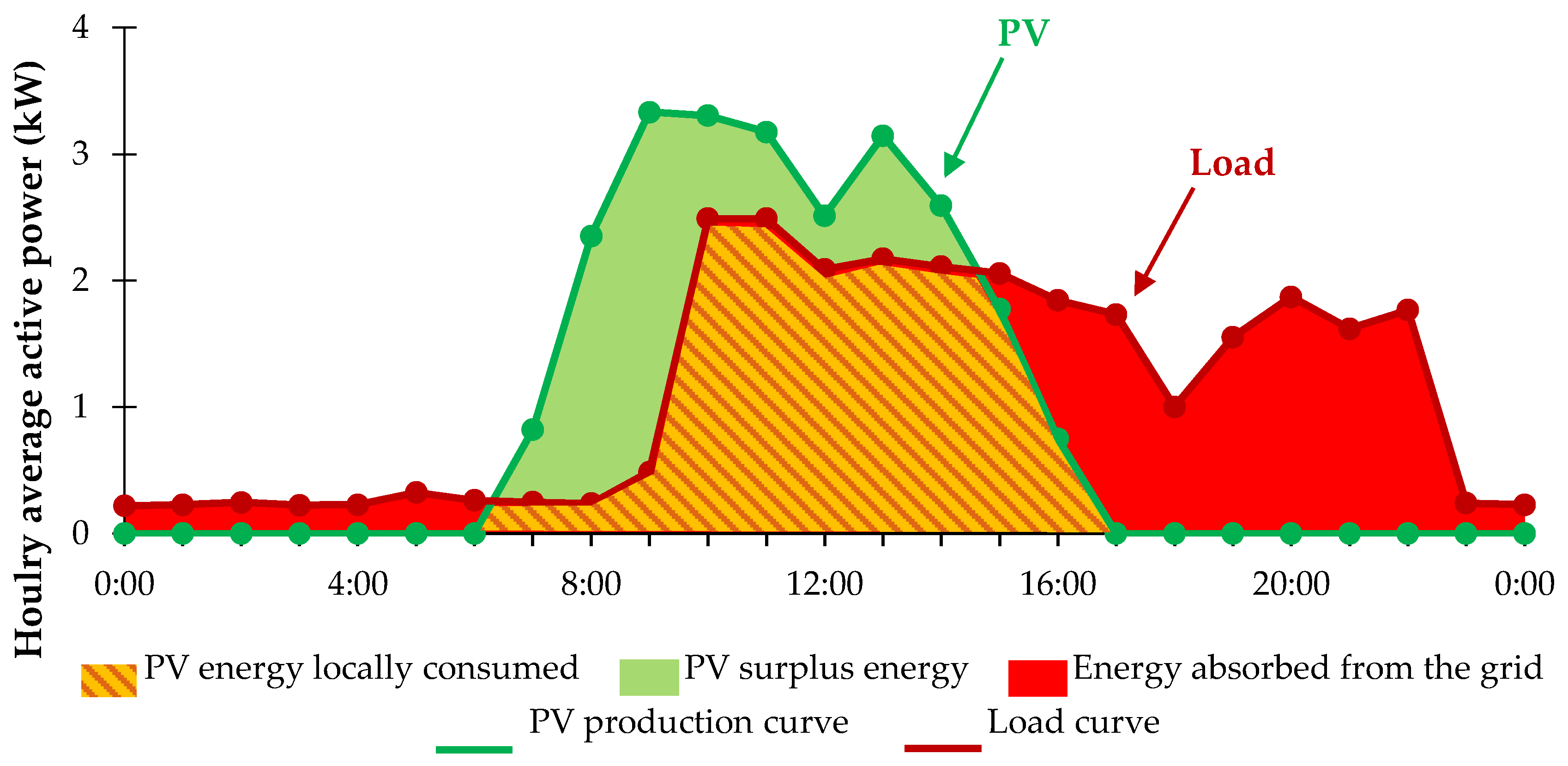
4. Case Study for the Calculation of Self-Consumption and Self-Sufficiency
4.1. Calculation Inputs
4.2. Financial Parameters
4.3. Reference Case
4.4. PV Plant Coupled to BESS
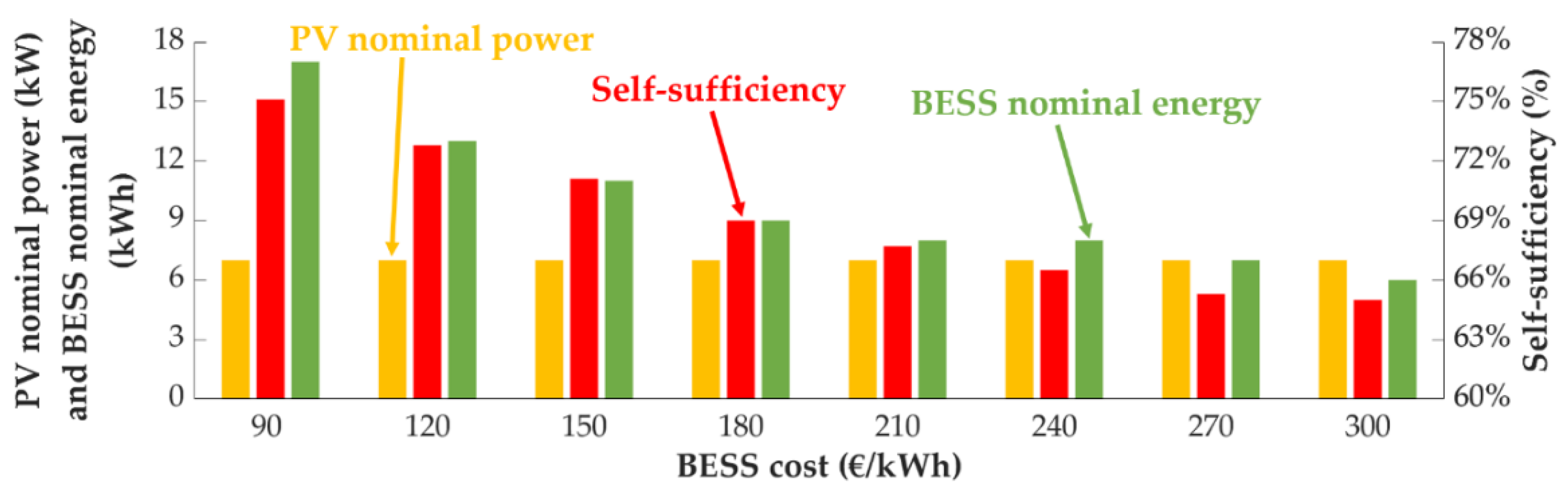
4.5. Variation in BESS Investment Cost
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Acronym | Definition |
| BESS | Battery energy storage system |
| DHW | Domestic hot water |
| MPP | Maximum power point |
| O&M | Operation and maintenance |
| OS | Operating system |
| PV | Photovoltaic |
| RES | Renewable energy sources |
| STC | Standard test conditions |
| WT | Wind turbine |
| Symbol | Description |
| APV | PV surface (m2) |
| CE,bat | Storage energy capacity (kWh) |
| CI | Investment cost (EUR) |
| C | Negative cash flow (EUR) |
| Ebat | Energy from batteries (kWh) |
| Egen | Local energy generation (kWh) |
| Egrid | Energy exchanged with the grid (kWh) |
| Elgc | Locally generated and consumed energy (kWh) |
| Eload | Total energy consumption (kWh) |
| EPV | PV energy (kWh) |
| Esurplus | PV energy injected into the grid (kWh) |
| Γ1 | Objective function maximizing self-sufficiency |
| Γ2 | Objective function maximizing economic return |
| G | Solar irradiance (W/m2) |
| G0 | Threshold irradiance (W/m2) |
| GSTC | Solar irradiance at STC (W/m2) |
| i | Discount rate (%) |
| I.L. | Injection limit (kW) |
| IRR | Internal rate of return (%) |
| n | Number of years (-) |
| N | Expected lifetime of the system (years) |
| NPV | Net present value (EUR) |
| Pbat | Exchanged power of battery during charge/discharge (kW) |
| PSTC | PV power at STC (kW) |
| PPV | Size of PV system (kW) |
| R | Positive cash flow (EUR) |
| SC | Self-consumption (%) |
| SOC | State of charge (%) |
| SOH | State of health (%) |
| SS | Self-sufficiency (%) |
| t | Time instant (s) |
| Tc | PV module temperature (°C) |
| TSTC | PV module temperature at STC (°C) |
| γ | PV thermal coefficient for power (%/°C) |
| Δt | Time step (s) |
| ηbat | Battery efficiency (%) |
| ηDC/AC | DC/AC conversion efficiency (%) |
| ηmix | PV miscellaneous efficiency (%) |
| ηPV | PV efficiency (%) |
| ηSTC | PV efficiency at STC (%) |
| ηth | PV thermal efficiency (%) |
| PV equivalent efficiency (%) |
References
- EUR-Lex. Access to European Union Law. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?qid=1588752259111&uri=CELEX:52015SC0141#document1 (accessed on 6 May 2020).
- Bahramara, S.; Mazza, A.; Chicco, G.; Shafie-khah, M.; Catalão, J.P.S. Comprehensive review on the decision-making frameworks referring to the distribution network operation problem in the presence of distributed energy resources and microgrids. Int. J. Electr. Power Energy Syst. 2020, 115, 105466. [Google Scholar] [CrossRef]
- Rubino, S.; Mazza, A.; Chicco, G.; Pastorelli, M.; Sandro, R. Advanced control of inverter-interfaced generation behaving as a virtual synchronous generator. In Proceedings of the 2015 IEEE Eindhoven PowerTech, Eindhoven, The Netherlands, 29 June–2 July 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Chicco, G.; Cocina, V.; Mazza, A. Data pre-processing and representation for energy calculations in net metering conditions. In Proceedings of the 2014 IEEE International Energy Conference (ENERGYCON), Dubrovnik, Croatia, 13–16 May 2014; pp. 413–419. [Google Scholar]
- Senato della Repubblica. Available online: http://www.senato.it/application/xmanager/projects/leg18/attachments/documento_evento_procedura_commissione/files/000/000/945/2018_12_21_-_RSE.pdf (accessed on 6 May 2020).
- Hasheminamin, M.; Agelidis, V.G.; Salehi, V.; Teodorescu, R.; Hredzak, B. Index-Based Assessment of Voltage Rise and Reverse Power Flow Phenomena in a Distribution Feeder Under High PV Penetration. IEEE J. Photovolt. 2015, 5, 1158–1168. [Google Scholar] [CrossRef]
- Gabash, A.; Li, P. On Variable Reverse Power Flow-Part I: Active-Reactive Optimal Power Flow with Reactive Power of Wind Stations. Energies 2016, 9, 121. [Google Scholar] [CrossRef]
- Téllez Molina, M.B.; Prodanovic, M. Profitability assessment for self-sufficiency improvement in grid-connected non-residential buildings with on-site PV installations. In Proceedings of the 2013 International Conference on Clean Electrical Power (ICCEP), Alghero, Italy, 11–13 June 2013; pp. 353–360. [Google Scholar]
- Mahatkar, T.K.; Bachawad, M.R. An Overview of Energy Storage Devices for Distribution Network. In Proceedings of the 2017 International Conference on Computation of Power, Energy Information and Communication (ICCPEIC), Melmaruvathur, India, 22–23 March 2017; pp. 536–541. [Google Scholar]
- Zhou, X.; Lin, Y.; Ma, Y. The overview of energy storage technology. In Proceedings of the 2015 IEEE International Conference on Mechatronics and Automation, Beijing, China, 2–5 August 2015; pp. 43–48. [Google Scholar]
- Giordano, F.; Ciocia, A.; Di Leo, P.; Mazza, A.; Spertino, F.; Tenconi, A.; Vaschetto, S. Vehicle-to-Home Usage Scenarios for Self-Consumption Improvement of a Residential Prosumer With Photovoltaic Roof. IEEE Trans. Ind. Appl. 2020, 56, 2945–2956. [Google Scholar] [CrossRef]
- Ould Amrouche, S.; Rekioua, D.; Rekioua, T.; Bacha, S. Overview of energy storage in renewable energy systems. Int. J. Hydrog. Energ. 2016, 41, 20914–20927. [Google Scholar] [CrossRef]
- Liang, X. Emerging Power Quality Challenges Due to Integration of Renewable Energy Sources. IEEE Trans. Ind. Appl. 2017, 53, 855–866. [Google Scholar] [CrossRef]
- Bereczki, B.; Hartmann, B.; Kertész, S. Industrial Application of Battery Energy Storage Systems: Peak shaving. In Proceedings of the 7th International Youth Conference on Energy (IYCE), Bled, Slovenia, 3–6 July 2019; pp. 1–5. [Google Scholar]
- Oudalov, A.; Cherkaoui, R.; Beguin, A. Sizing and Optimal Operation of Battery Energy Storage System for Peak Shaving Application. In Proceedings of the 2007 IEEE Lausanne Power Tech, Lausanne, Switzerland, 1–5 July 2007; pp. 621–625. [Google Scholar]
- Leadbetter, J.; Swan, L. Battery storage system for residential electricity peak demand shaving. Energ. Build. 2012, 55, 685–692. [Google Scholar] [CrossRef]
- Aziz, M.; Oda, T.; Mitani, T.; Watanabe, Y.; Kashiwagi, T. Utilization of Electric Vehicles and Their Used Batteries for Peak-Load Shifting. Energies 2015, 8, 3720–3738. [Google Scholar] [CrossRef]
- Rossi, M.; Viganò, G.; Moneta, D.; Clerici, D.; Carlini, C. Analysis of active power curtailment strategies for renewable distributed generation. In Proceeding of the 2016 AEIT International Annual Conference (AEIT), Capri, Italy, 5–7 October 2016; pp. 1–6. [Google Scholar]
- Liew, S.N.; Strbac, G. Maximising penetration of wind generation in existing distribution networks. IEE Proc. Gener. Transm. Distrib. 2002, 149, 256–262. [Google Scholar] [CrossRef]
- Siano, P.; Chen, P.; Chen, Z.; Piccolo, A. Evaluating maximum wind energy exploitation in active distribution networks. IET Gener. Transm. Distrib. 2010, 4, 598–608. [Google Scholar] [CrossRef]
- Mutale, J. Benefits of Active Management of Distribution Networks with Distributed Generation. In Proceedings of the 2006 IEEE PES Power Systems Conference and Exposition, Atlanta, GA, USA, 29 October–1 November 2006; pp. 601–606. [Google Scholar]
- Ahmad, J.; Spertino, F.; Ciocia, A.; Di Leo, P. A maximum power point tracker for module integrated PV systems under rapidly changing irradiance conditions. In Proceedings of the 2015 International Conference on Smart Grid and Clean Energy Technologies (ICSGCE), Offenburg, Germany, 20–23 October 2015; pp. 7–11. [Google Scholar]
- Benetti, G.; Caprino, D.; Della Vedova, M.L.; Facchinetti, T. Electric load management approaches for peak load reduction: A systematic literature review and state of the art. Sustain. Cities Soc. 2016, 20, 124–141. [Google Scholar] [CrossRef]
- Shen, J.; Jiang, C.; Liu, Y.; Qian, J. A Microgrid Energy Management System with Demand Response for Providing Grid Peak Shaving. Electr. Power Components Syst. 2016, 44, 843–852. [Google Scholar] [CrossRef]
- Dlamini, N.G.; Cromieres, F. Implementing Peak Load Reduction Algorithms for Household Electrical Appliances. Energ. Policy 2012, 44, 280–290. [Google Scholar] [CrossRef]
- Wanitschke, A.; Pieniak, N.; Schaller, F. Economic and environmental cost of self-sufficiency—Analysis of an urban micro grid. Energy Procedia 2017, 135, 445–451. [Google Scholar] [CrossRef]
- Hernández, J.C.; Sanchez-Sutil, F.; Muñoz-Rodríguez, F.J.; Baier, C.R. Optimal sizing and management strategy for PV household-prosumers with self-consumption/sufficiency enhancement and provision of frequency containment reserve. Appl. Energy 2020, 277, 115529. [Google Scholar] [CrossRef]
- Thebault, M.; Gaillard, L. Optimization of the integration of photovoltaic systems on buildings for self-consumption—Case study in France. City Environ. Interact. 2021, 100057. [Google Scholar] [CrossRef]
- Merei, G.; Moshövel, J.; Magnor, D.; Uwe Sauer, D. Optimization of self-consumption and techno-economic analysis of PV-battery systems in commercial applications. Appl. Energy 2016, 168, 171–178. [Google Scholar] [CrossRef]
- Hernández, J.C.; Sanchez-Sutil, F.; Muñoz-Rodríguez, F.J. Design criteria for the optimal sizing of a hybrid energy storage system in PV household-prosumers to maximize self-consumption and self-sufficiency. Energy 2019, 186, 115827. [Google Scholar] [CrossRef]
- More of a Good Thing—Is Surplus Renewable Electricity an Opportunity for Early Decarbonisation? Available online: https://www.iea.org/commentaries/more-of-a-good-thing-is-surplus-renewable-electricity-an-opportunity-for-early-decarbonisation (accessed on 27 February 2021).
- Schulz, J.; Scharmer, V.M.; Zaeh, M.F. Energy self-sufficient manufacturing systems—Integration of renewable and decentralized energy generation systems. Procedia Manuf. 2020, 43, 40–47. [Google Scholar] [CrossRef]
- Jurasz, J.K.; Dąbek, P.B.; Campana, P.E. Can a city reach energy self-sufficiency by means of rooftop photovoltaics? Case study from Poland. J. Clean. Prod. 2020, 245, 118813. [Google Scholar] [CrossRef]
- Photovoltaic Geographical Information System (PVGIS). Available online: https://ec.europa.eu/jrc/en/pvgis (accessed on 15 January 2021).
- SODA Solar Radiation Data. Available online: http://www.soda-pro.com (accessed on 15 January 2021).
- US Department of Energy. Open EI. Commercial and Residential Hourly Load Profiles in USA. Available online: https://openei.org/doe-opendata/dataset/commercial-and-residential-hourly-load-profiles-for-all-tmy3-locations-in-the-united-states (accessed on 2 July 2020).
- Ollas, P.; Persson, J.; Markusson, C.; Alfadel, U. Impact of Battery Sizing on Self-Consumption, Self-Sufficiency and Peak Power Demand for a Low Energy Single-Family House With PV Production in Sweden. In Proceedings of the 2018 IEEE 7th World Conference on Photovoltaic Energy Conversion (WCPEC), Waikoloa Village, HI, USA, 10–15 June 2018; pp. 0618–0623. [Google Scholar]
- Tutkun, N.; Çelebi, N.; Bozok, N. Optimum unit sizing of wind-PV-battery system components in a typical residential home. In Proceedings of the 2016 International Renewable and Sustainable Energy Conference (IRSEC), Marrakech, Morocco, 14–17 November 2016; pp. 432–436. [Google Scholar]
- Burgio, A.; Menniti, D.; Sorrentino, N.; Pinnarelli, A.; Leonowicz, Z. Influence and Impact of Data Averaging and Temporal Resolution on the Assessment of Energetic, Economic and Technical Issues of Hybrid Photovoltaic-Battery Systems. Energies 2020, 13, 354. [Google Scholar] [CrossRef]
- Beck, T.; Kondziella, H.; Huard, G.; Bruckner, T. Assessing the influence of the temporal resolution of electrical load and PV generation profiles on self-consumption and sizing of PV-battery systems. Appl. Energy 2016, 173, 331–342. [Google Scholar] [CrossRef]
- Sun, S.I.; Smith, B.D.; Wills, R.G.A.; Crossland, A.F. Effects of time resolution on finances and self-consumption when modeling domestic PV-battery systems. Energy Rep. 2020, 6, 157–165. [Google Scholar] [CrossRef]
- European Commission. Regulation 2017/2195 of 23 November 2017 Establishing a Guideline on Electricity Balancing C/2017/7774. Available online: http://data.europa.eu/eli/reg/2017/2195/oj (accessed on 20 January 2021).
- Ciocia, A.; Ahmad, J.; Chicco, G.; Di Leo, P.; Spertino, F. Optimal size of photovoltaic systems with storage for office and residential loads in the Italian net-billing scheme. In Proceedings of the 51st International Universities Power Engineering Conference (UPEC), Coimbra, Portugal, 6–9 September 2016; pp. 1–6. [Google Scholar]
- Schujman, S.B.; Mann, J.R.; Dufresne, G.; LaQue, L.M.; Rice, C.; Wax, J.; Metacarpa, D.J.; Haldar, P. Evaluation of protocols for temperature coefficient determination. In Proceedings of the 2015 IEEE 42nd Photovoltaic Specialist Conference (PVSC), New Orleans, LA, USA, 14–19 June 2015; pp. 1–4. [Google Scholar]
- Liu, S.; Dong, M. Quantitative research on impact of ambient temperature and module temperature on short-term photovoltaic power forecasting. In Proceedings of the 2016 International Conference on Smart Grid and Clean Energy Technologies (ICSGCE), Chengdu, China, 19–22 October 2016; pp. 262–266. [Google Scholar]
- National Renewable Energy Laboratory of U.S.A. Photovoltaic Degradation Rates—An Analytical Review. Available online: https://www.nrel.gov/docs/fy12osti/51664.pdf (accessed on 2 July 2020).
- Carullo, A.; Castellana, A.; Vallan, A.; Ciocia, A.; Spertino, F. In-field monitoring of eight photovoltaic plants: Degradation rate over seven years of continuous operation. Acta IMEKO 2018, 7, 75–81. [Google Scholar] [CrossRef]
- Spertino, F.; Ciocia, A.; Cocina, V.; Di Leo, P. Renewable sources with storage for cost-effective solutions to supply commercial loads. In Proceedings of the 2016 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Anacapri, Italy, 22–24 June 2016; pp. 242–247. [Google Scholar]
- Di Leo, P.; Spertino, F.; Fichera, S.; Malgaroli, G.; Ratclif, A. Improvement of Self-Sufficiency for an Innovative Nearly Zero Energy Building by Photovoltaic Generators. In Proceedings of the 2019 IEEE Milan PowerTech, Milan, Italy, 23–27 June 2019; pp. 1–6. [Google Scholar]
- A Closer Look at State of Charge (SOC) and State of Health (SOH) Estimation Techniques for Batteries. Available online: https://www.analog.com/media/en/technical-documentation/technical-articles/A-Closer-Look-at-State-Of-Charge-and-State-Health-Estimation-Techniques-....pdf (accessed on 15 January 2021).
- Laajimi, M.; Go, Y.I. Energy storage system design for large-scale solar PV in Malaysia: Technical and environmental assessments. J. Energ. Storage 2019, 26, 100984. [Google Scholar] [CrossRef]
- Zeh, A.; Müller, M.; Naumann, M.; Hesse, H.C.; Jossen, A.; Witzmann, R. Fundamentals of Using Battery Energy Storage Systems to Provide Primary Control Reserves in Germany. Batteries 2016, 2, 29. [Google Scholar] [CrossRef]
- Carullo, A.; Ciocia, A.; Di Leo, P.; Giordano, F.; Malgaroli, G.; Peraga, L.; Spertino, F.; Vallan, A. Comparison of correction methods of wind speed for performance evaluation of wind turbines. In Proceedings of the 24th IMEKO TC4 International Symposium and 22nd International Workshop on ADC and DAC Modelling and Testing, Palermo, Italy, 14–16 September 2020; pp. 291–296. [Google Scholar]
- Lin, C.; Hsieh, W.; Chen, C.; Hsu, C.; Ku, T. Optimization of Photovoltaic Penetration in Distribution Systems Considering Annual Duration Curve of Solar Irradiation. IEEE Trans. Power Syst. 2012, 27, 1090–1097. [Google Scholar] [CrossRef]
- U.S. Energy Information Administration. Levelized Cost and Levelized Avoided Cost of New Generation Resources in the Annual Energy Outlook. 2016. Available online: http://www.eia.gov/outlooks/aeo/pdf/electricity_generation.pdf (accessed on 20 January 2021).
- Rajput, P.; Malvoni, M.; Manoj Kumar, N.; Sastry, O.S.; Jayakumar, A. Operational Performance and Degradation Influenced Life Cycle Environmental–Economic Metrics of mc-Si, a-Si and HIT Photovoltaic Arrays in Hot Semi-arid Climates. Sustainability 2020, 12, 1075. [Google Scholar] [CrossRef]
- Spertino, F.; Ahmad, J.; Chicco, G.; Ciocia, A.; Di Leo, P. Matching between electric generation and load: Hybrid PV-wind system and tertiary-sector users. In Proceedings of the 2015 50th International Universities Power Engineering Conference (UPEC), Stoke on Trent, UK, 1–4 September 2015; pp. 1–6. [Google Scholar]
- Ullah, A.; Imran, H.; Maqsood, Z.; Zafar Butt, N. Investigation of optimal tilt angles and effects of soiling on PV energy production in Pakistan. Renew. Energy 2019, 139, 830–843. [Google Scholar] [CrossRef]
- Spertino, F.; Ahmad, J.; Ciocia, A.; Di Leo, P. How much is the advisable self-sufficiency of aggregated prosumers with photovoltaic-wind power and storage to avoid grid upgrades? In Proceedings of the 2017 IEEE Industry Applications Society Annual Meeting, Cincinnati, OH, USA, 1–4 October 2017; pp. 1–8. [Google Scholar]
- ElSayed, S.K.; Elattar, E.E. Hybrid Harris hawks optimization with sequential quadratic programming for optimal coordination of directional overcurrent relays incorporating distributed generation. Alex. Eng. J. 2021, 60, 2421–2433. [Google Scholar] [CrossRef]
- Euro-Mongolian Cooperation for Modernization of Engineering Education (EU MONG). Available online: http://eu-mong.eu/ (accessed on 28 May 2020).
- Tzanova, S. Work in Progress: Competence Building in Engineering Education in Mongolia. In Proceedings of the EDUCON 2020, Porto, Portugal, 27–30 April 2020; pp. 33–36. [Google Scholar]
- Gestore dei Servizi Energetici (GSE). Available online: https://www.gse.it/documenti_site/Documenti%20GSE/Rapporti%20statistici/Relazione_annuale_situazione_energetica_nazionale_dati_2018.pdf (accessed on 14 May 2020).
- Italian Law, DM 04/07/2019. Accesso agli Incentivi. Available online: https://www.gse.it/servizi-per-te/fonti-rinnovabili/fer-elettriche/incentivi-dm-04-07-2019 (accessed on 4 July 2020).
- Gestore dei Servizi Energetici (GSE). Available online: https://www.gse.it/servizi-per-te/fotovoltaico/scambio-sul-posto (accessed on 18 May 2020).
- GSE. Servizio di Scambio sul posto: Regole Tecniche. Available online: https://www.gse.it/documenti_site/Documenti%20GSE/Servizi%20per%20te/SCAMBIO%20SUL%20POSTO/Regole%20e%20procedure/Regole%20Tecniche%20Scambio%20sul%20Posto_2019.pdf. (accessed on 15 June 2020).
- ARERA. Valori del Corrispettivo Unitario di Scambio Forfetario per l’anno. 2019. Available online: https://www.arera.it/allegati/comunicati/CorrispettiviCUsf2019.pdf (accessed on 15 June 2020).
- Ciocia, A.; Di Leo, P.; Malgaroli, G.; Spertino, F. Subhour Simulation of a Microgrid of All-Electric nZEBs Based on Italian Market Rules. In Proceedings of the 2020 IEEE International Conference on Environment and Electrical Engineering and 2020 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Madrid, Spain, 9–12 June 2020; pp. 1–6. [Google Scholar] [CrossRef]
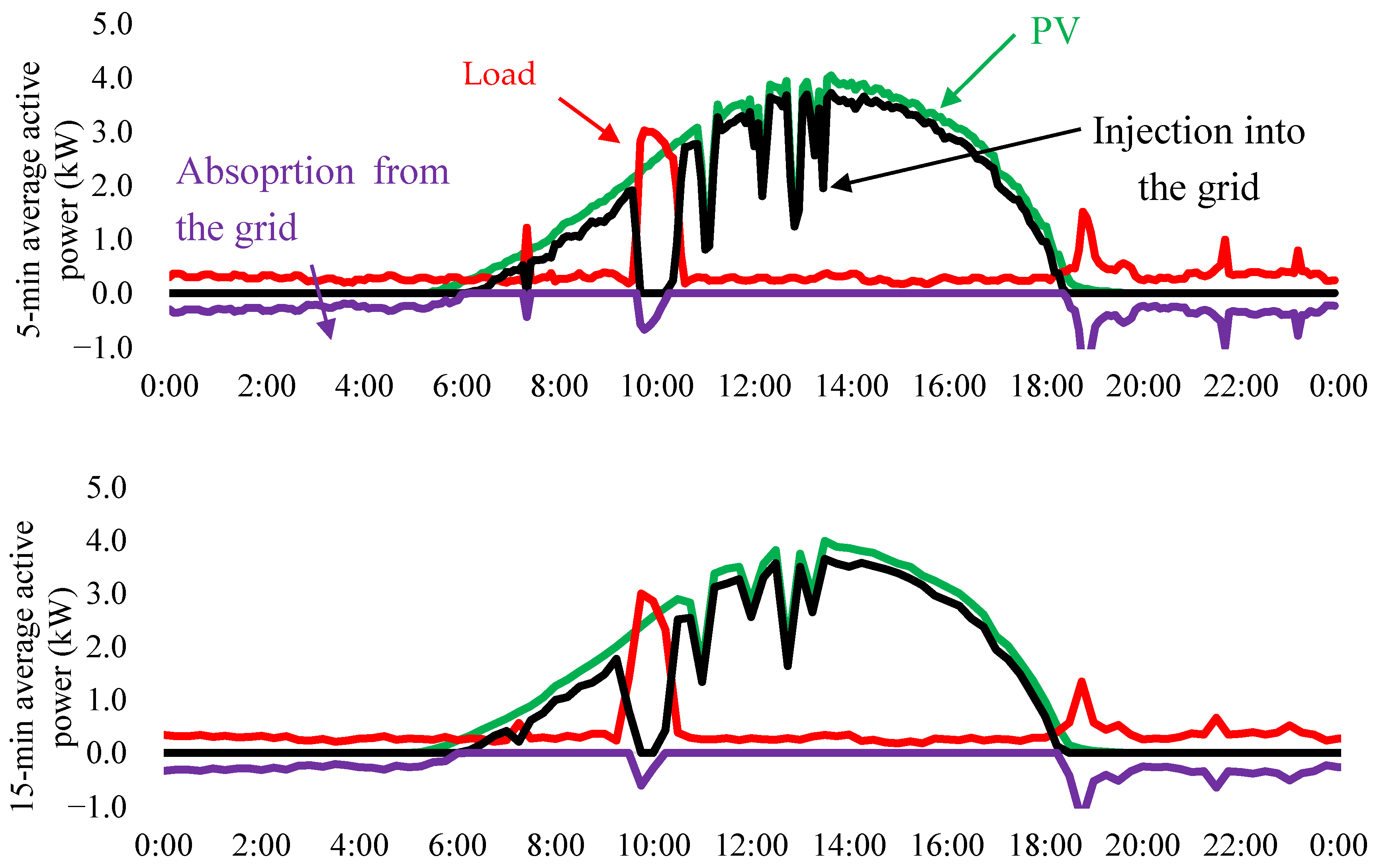
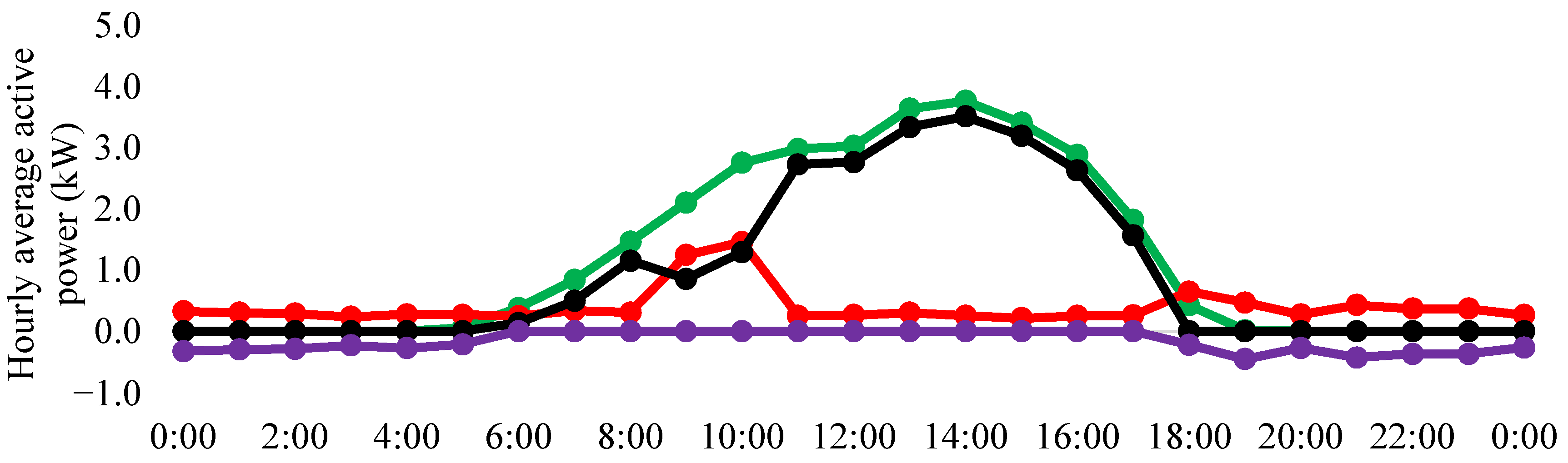
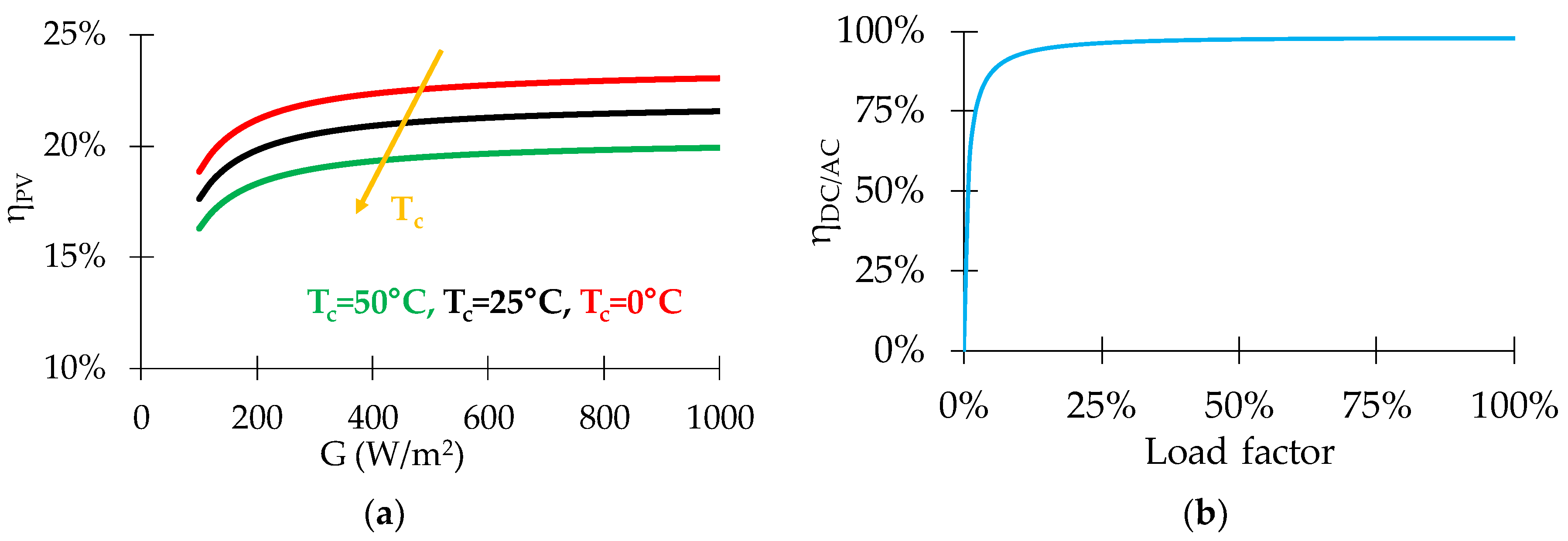
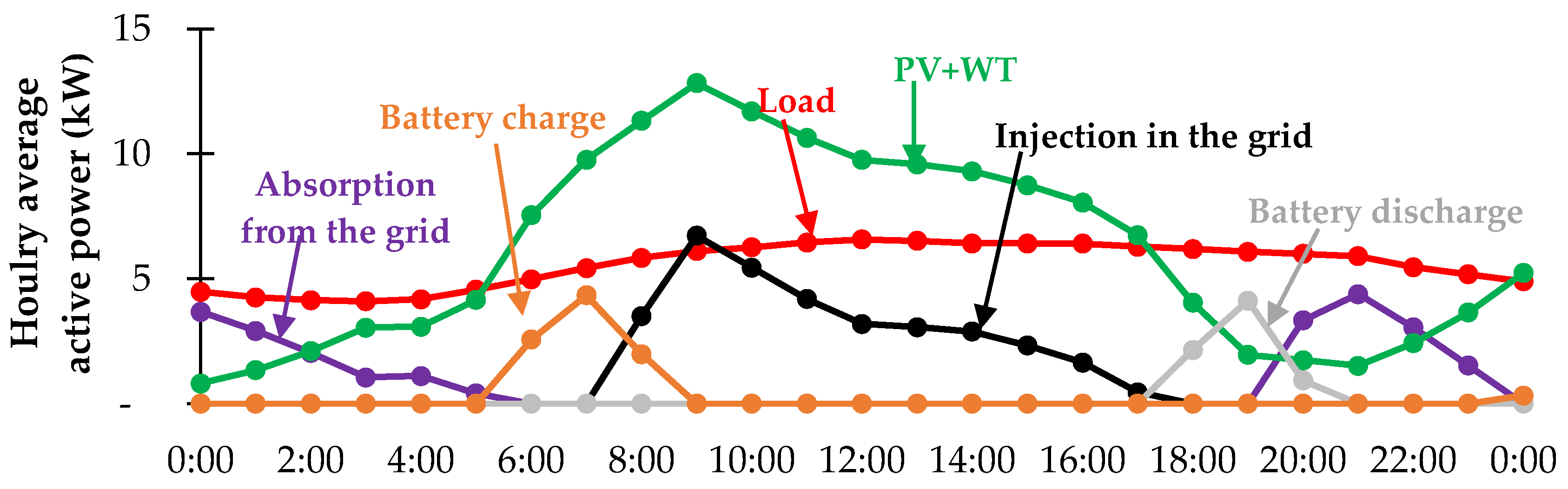
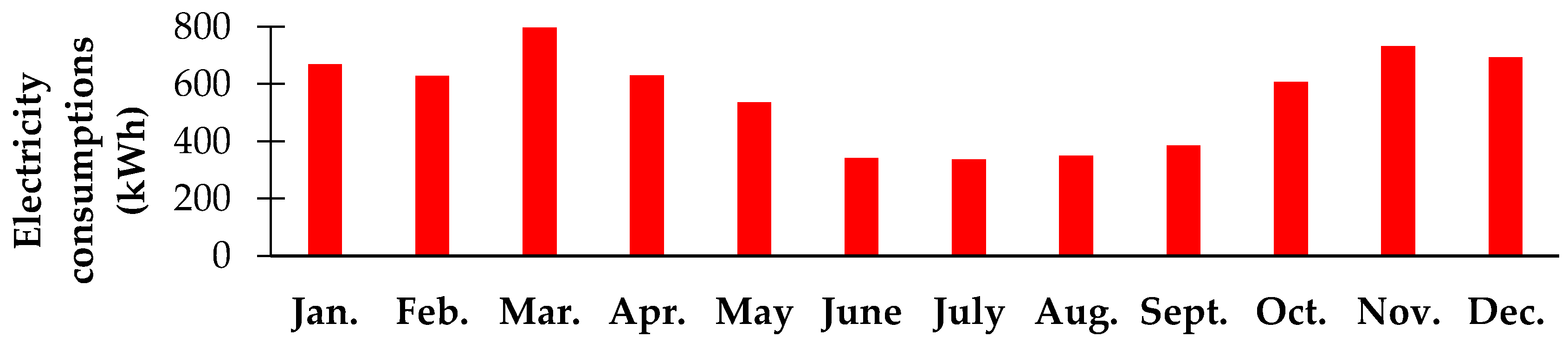
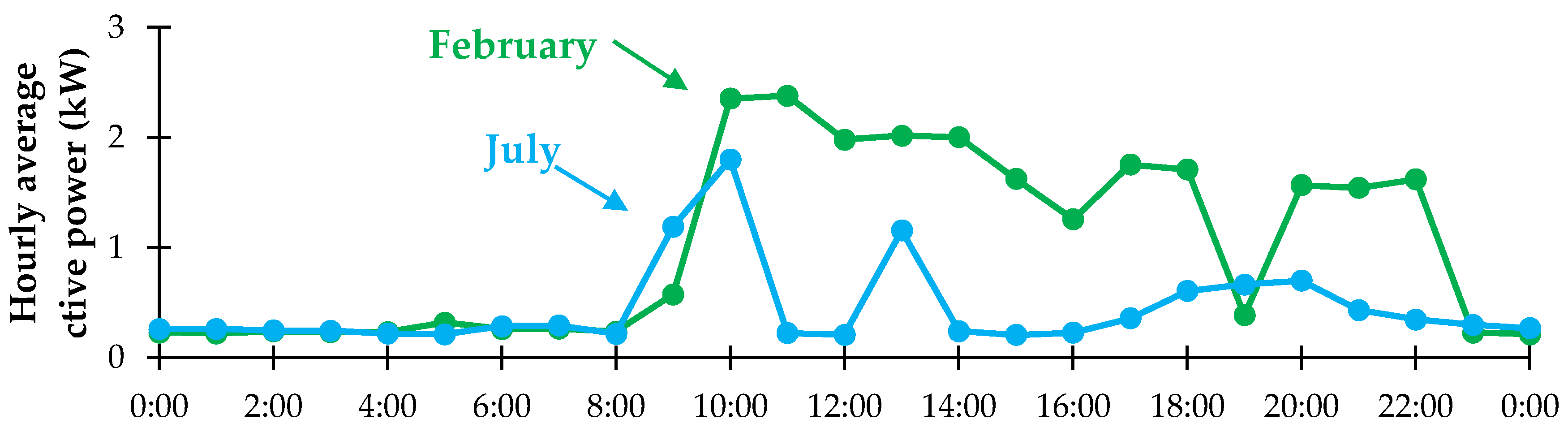
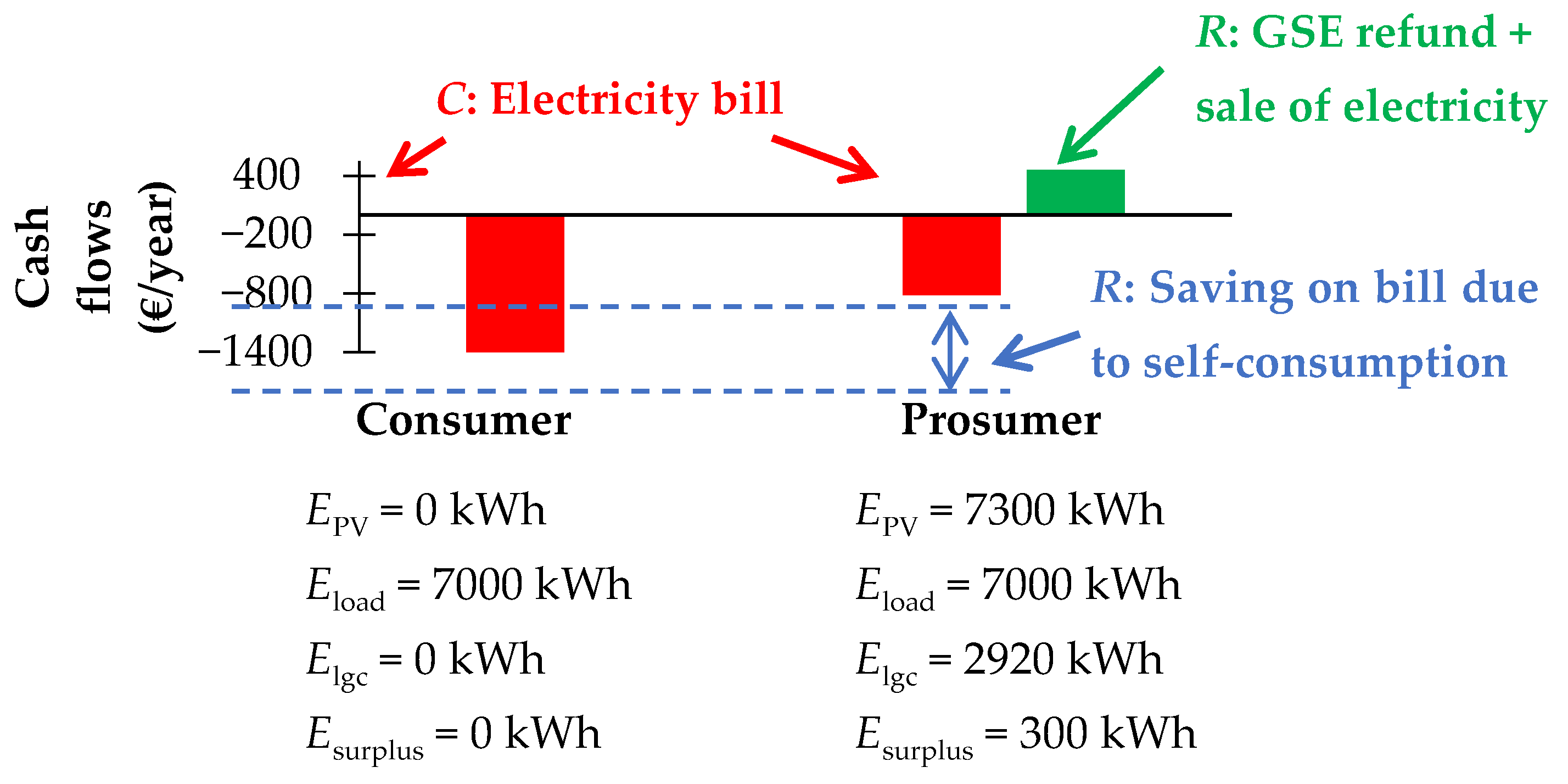


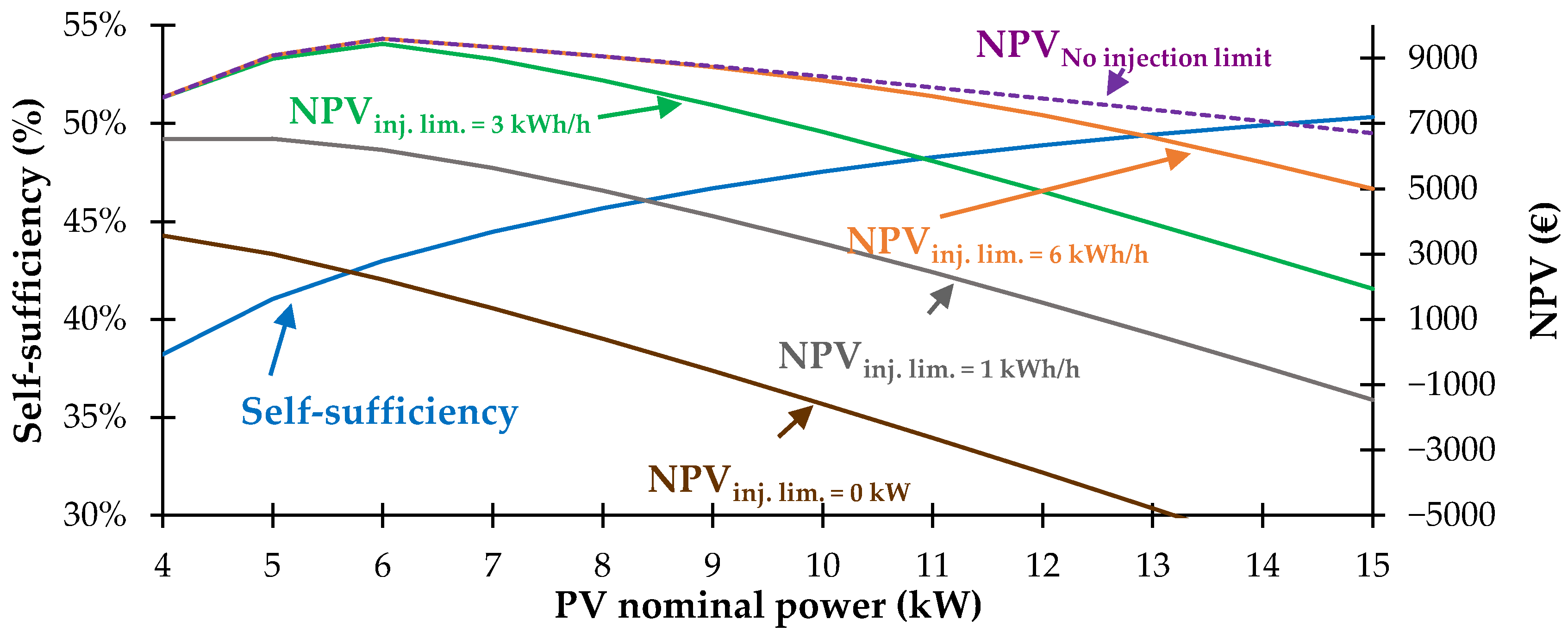
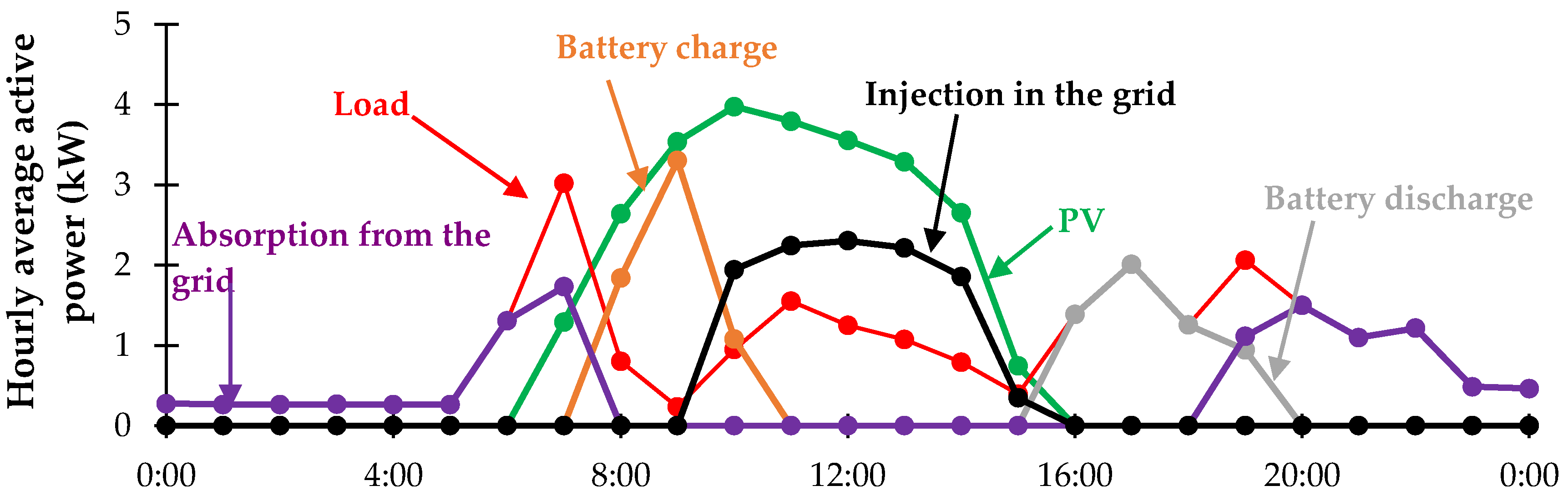
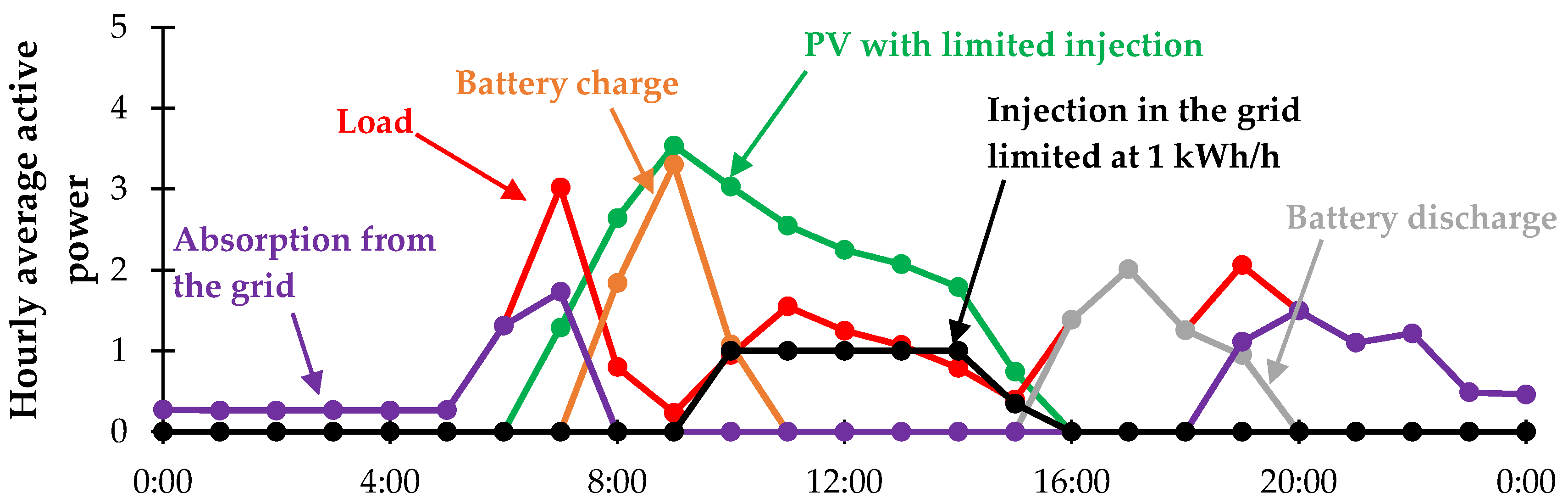
| Energy Quantities | Measurement Unit | Time Step | ||
|---|---|---|---|---|
| 5 min | 15 min | 1 h | ||
| Consumption | kWh | 9.6 | 9.6 | 9.6 |
| PV generation | kWh | 29.6 | 29.6 | 29.6 |
| Injection in the grid | kWh | 24.2 | 24.1 | 23.7 |
| Absorption from the grid | kWh | −4.3 | −4.2 | −3.8 |
| Self-sufficiency | - | 55.6% | 56.6% | 61.1% |
| Self-consumption | - | 18.1% | 18.5% | 19.9% |
| Energy Quantities | Measurement Unit | Time Step | ||
|---|---|---|---|---|
| 5 min | 15 min | 1 h | ||
| Consumption | kWh | 6700 | 6700 | 6700 |
| PV generation | kWh | 5715 | 5715 | 5715 |
| Injection in the grid | kWh | 3318 | 3254 | 3102 |
| Absorption from the grid | kWh | −4303 | −4238 | −4087 |
| Self-sufficiency | - | 35.8% | 36.7% | 39.0% |
| Self-consumption | - | 41.9% | 43.1% | 45.7% |
| Energy and Economic Quantities | Maximization of Self-Sufficiency | Maximization of NPV | ||||
|---|---|---|---|---|---|---|
| No I.L. | I.L. = 2 kWh/h | I.L. = 0 kWh/h | No I.L. | I.L. = 2 kWh/h | I.L. = 0 kWh/h | |
| PV nominal power | 13 kW | 10 kW | 5 kW | 6 kW | 6 kW | 4 kW |
| SS | 49% | 48% | 41% | 43% | 43% | 38% |
| SC | 21% | 40% | 100% | 40% | 45% | 100% |
| IRR | 6.4% | 6.3% | 6.5% | 11.2% | 10.5% | 8.0% |
| NPV | EUR 7423 | EUR 5657 | EUR 2996 | EUR 9594 | EUR 8663 | EUR 3571 |
| Energy and Economic Quantities | Maximization of Self-Sufficiency | ||||
|---|---|---|---|---|---|
| No I.L. | I.L. = 3 kWh/h | I.L. = 2 kWh/h | I.L. = 1 kWh/h | I.L. = 0 kWh/h | |
| PV nominal power | 7 kW | 7 kW | 7 kW | 6 kW | 4 kW |
| BESS nominal energy | 6 kWh | 6 kWh | 5 kWh | 4 kWh | 4 kWh |
| SS | 65% | 65% | 62% | 58% | 52% |
| SC | 51% | 54% | 59% | 71% | 98% |
| IRR | 6.4% | 6.1% | 6.4% | 6.4% | 6.2% |
| NPV | EUR 4364 | EUR 4028 | EUR 4278 | EUR 3654 | EUR 2367 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ciocia, A.; Amato, A.; Di Leo, P.; Fichera, S.; Malgaroli, G.; Spertino, F.; Tzanova, S. Self-Consumption and Self-Sufficiency in Photovoltaic Systems: Effect of Grid Limitation and Storage Installation. Energies 2021, 14, 1591. https://doi.org/10.3390/en14061591
Ciocia A, Amato A, Di Leo P, Fichera S, Malgaroli G, Spertino F, Tzanova S. Self-Consumption and Self-Sufficiency in Photovoltaic Systems: Effect of Grid Limitation and Storage Installation. Energies. 2021; 14(6):1591. https://doi.org/10.3390/en14061591
Chicago/Turabian StyleCiocia, Alessandro, Angela Amato, Paolo Di Leo, Stefania Fichera, Gabriele Malgaroli, Filippo Spertino, and Slavka Tzanova. 2021. "Self-Consumption and Self-Sufficiency in Photovoltaic Systems: Effect of Grid Limitation and Storage Installation" Energies 14, no. 6: 1591. https://doi.org/10.3390/en14061591
APA StyleCiocia, A., Amato, A., Di Leo, P., Fichera, S., Malgaroli, G., Spertino, F., & Tzanova, S. (2021). Self-Consumption and Self-Sufficiency in Photovoltaic Systems: Effect of Grid Limitation and Storage Installation. Energies, 14(6), 1591. https://doi.org/10.3390/en14061591










