Comparison of Heat Demand Prediction Using Wavelet Analysis and Neural Network for a District Heating Network
Abstract
1. Introduction
2. Related Work and Theoretical Basis
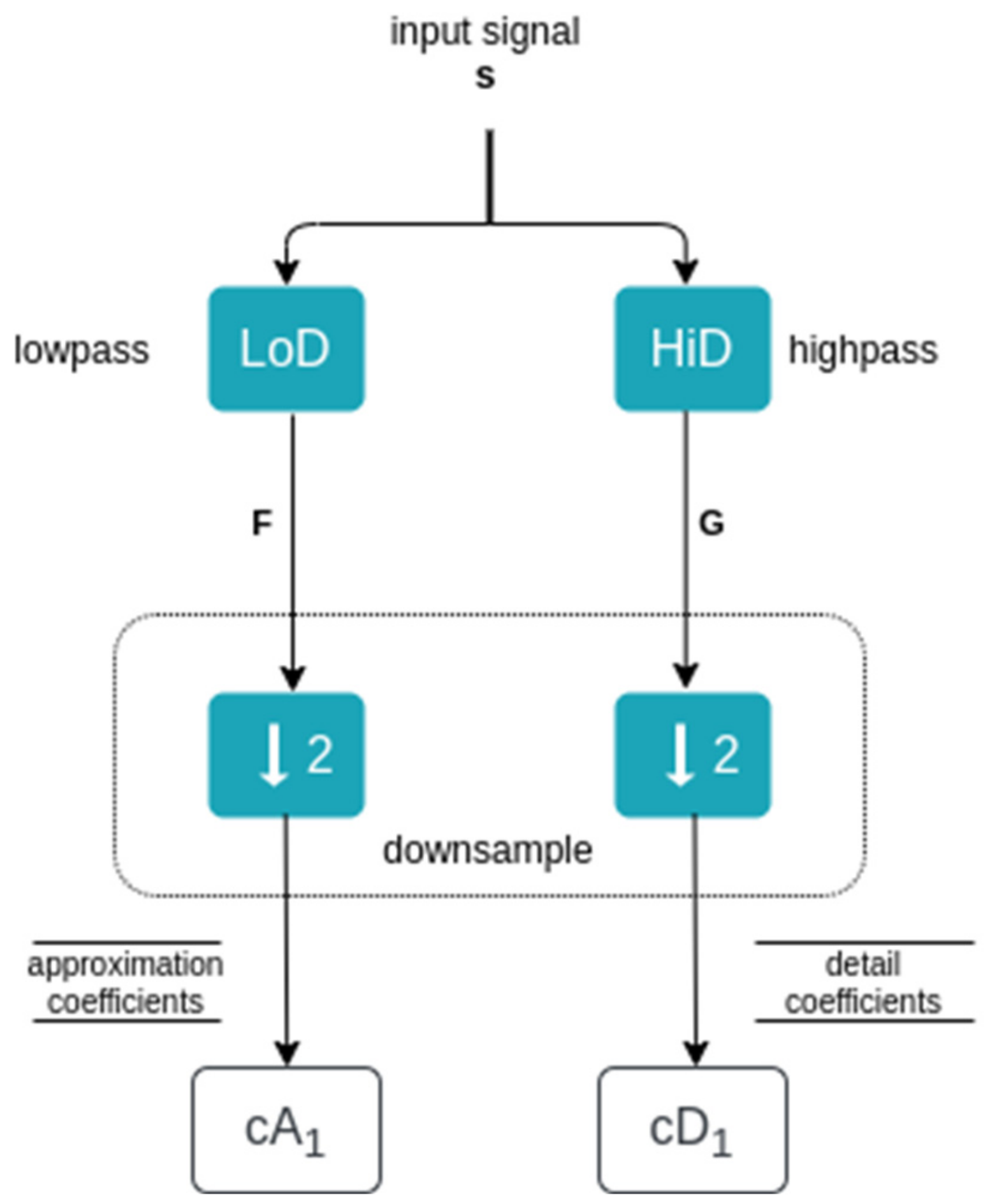
2.1. Wavelet Theory and Multiresolution Analysis
2.2. Artificial Neural Networks
2.2.1. Scaled Conjugate Gradient
2.2.2. Levenberg‒Marquardt
2.2.3. BFGS Quasi-Newton Backpropagation
3. Dataset Overview
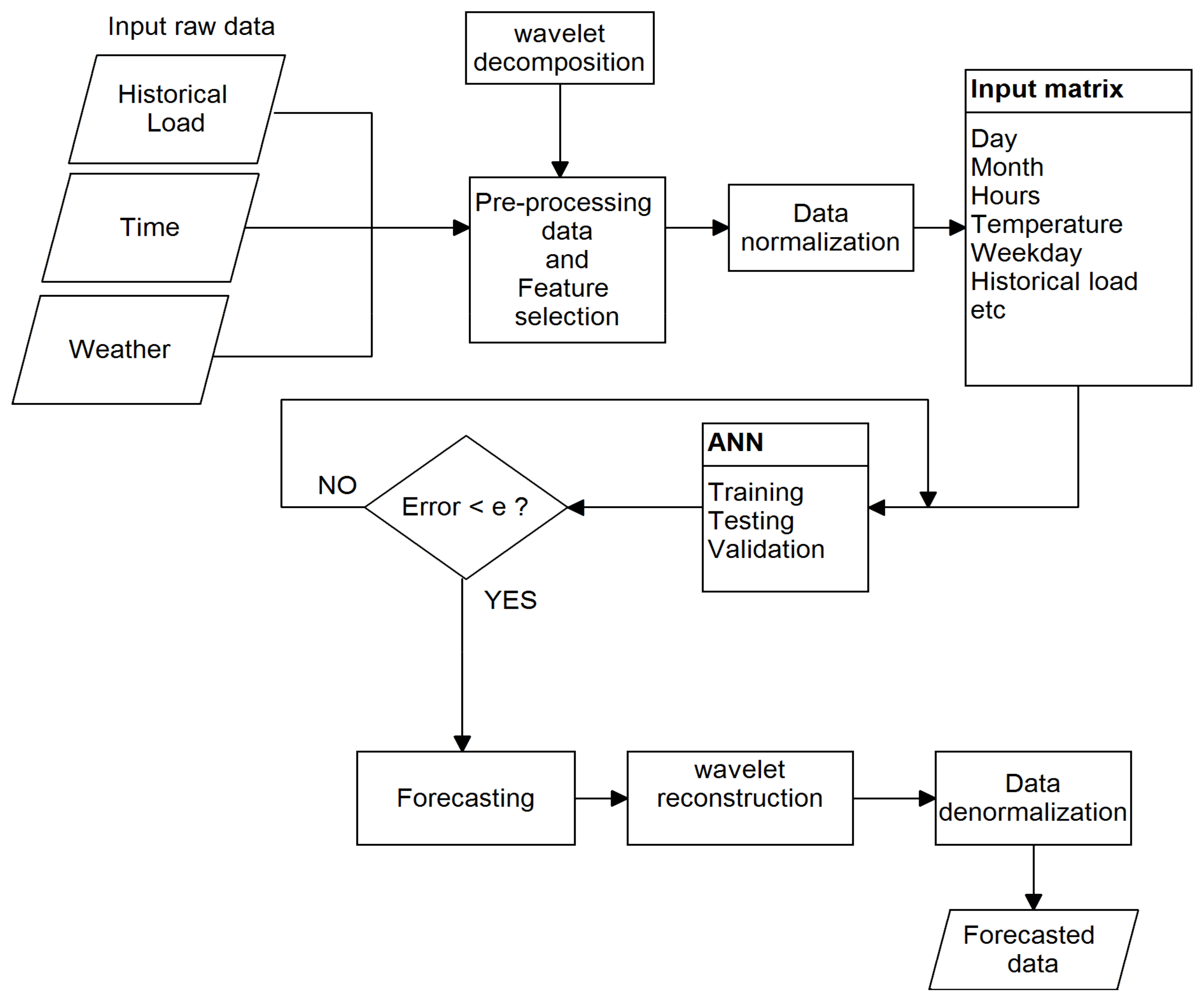
4. ANN and WANN Modeling
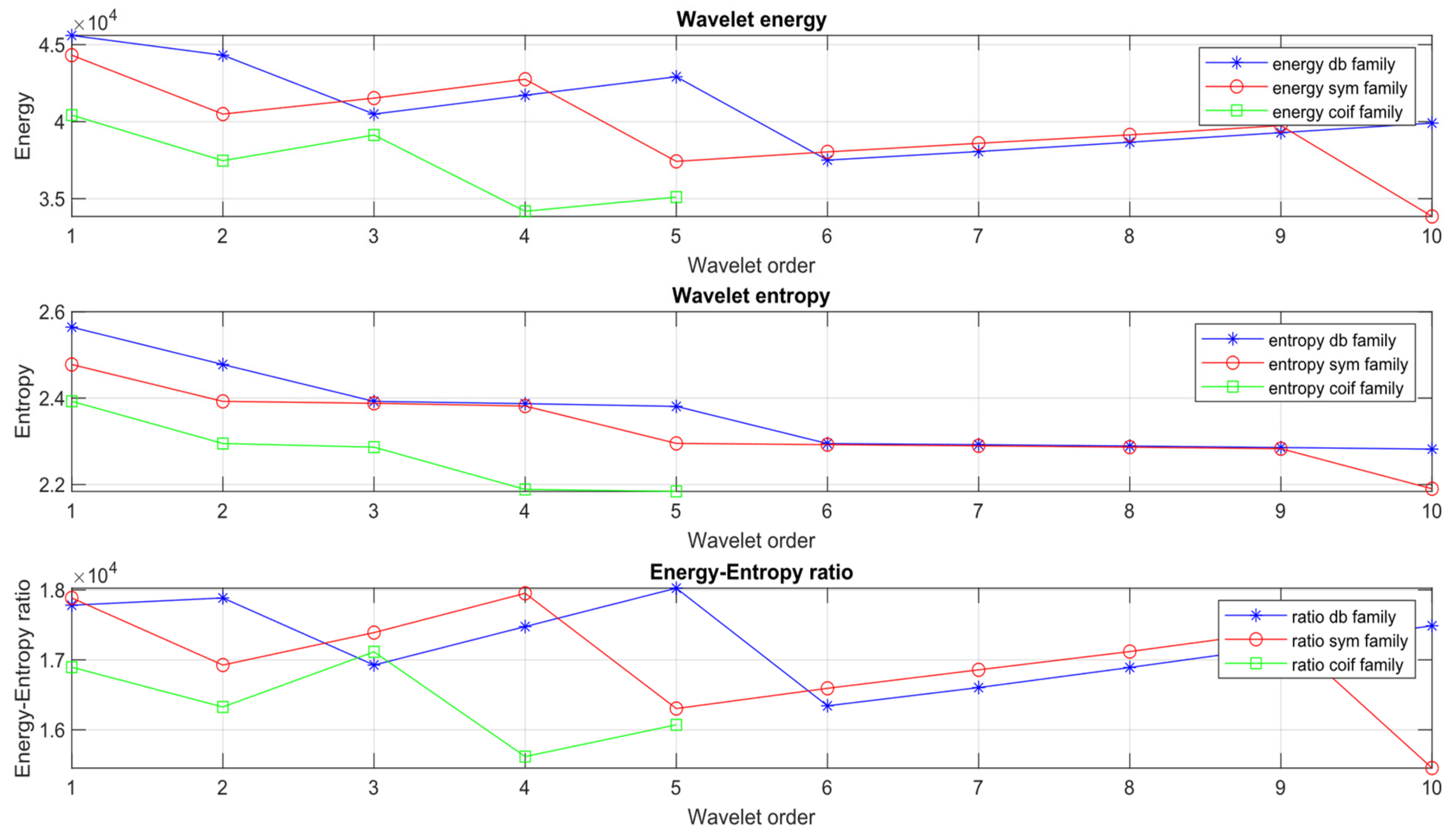
4.1. Mother Wavelet Selection Criteria
- Maximum Energy Criteria
- 2.
- Minimum Shannon Entropy
- 3.
- Energy-to-Shannon Entropy ratio
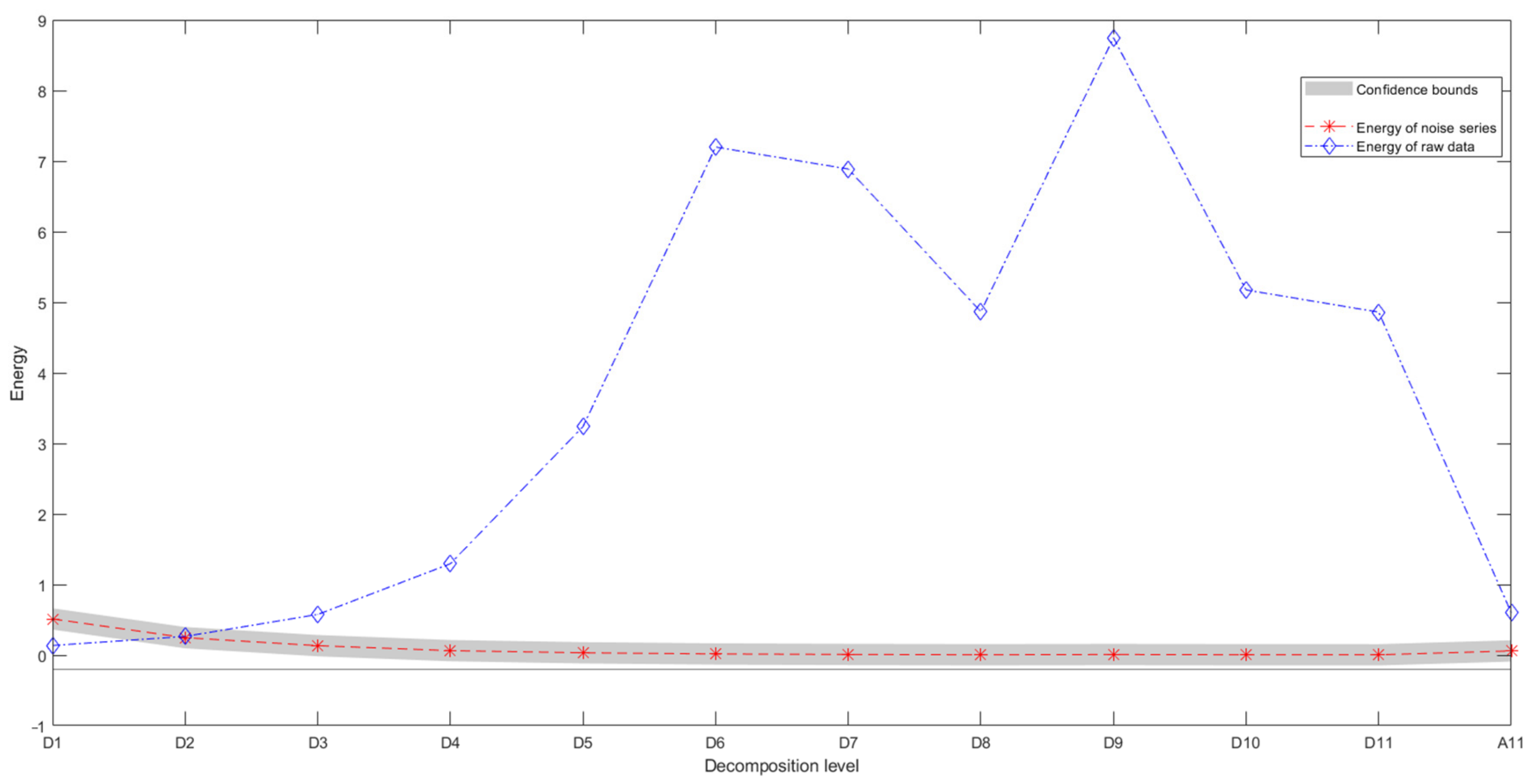
4.2. Decomposition Level Selection
4.3. Building WANN and ANN Models
- Hour—To capture the cyclical behavior of the series, the hour variable was encoded via sine and cosine transform:
- Load input raw data;
- Decompose load data using DWT into N subseries of details and approximations;
- Perform feature selection—autocorrelation, correlation analysis;
- Normalize data using mapstd function;
- Create an input matrix from selected features;
- Divide the processed data into training and testing sets;
- Create WANN models
- Compute the number of hidden neurons (2/3 of inputs)
- Train and test until error starts to increase, then stop training;
- Reconstruct predicted outputs and reconstruct signal Xrec = D1+,…,+ Dn + An;
- Denormalize outputs using reverse mapstd function;
- Validate proposed models on a new dataset.
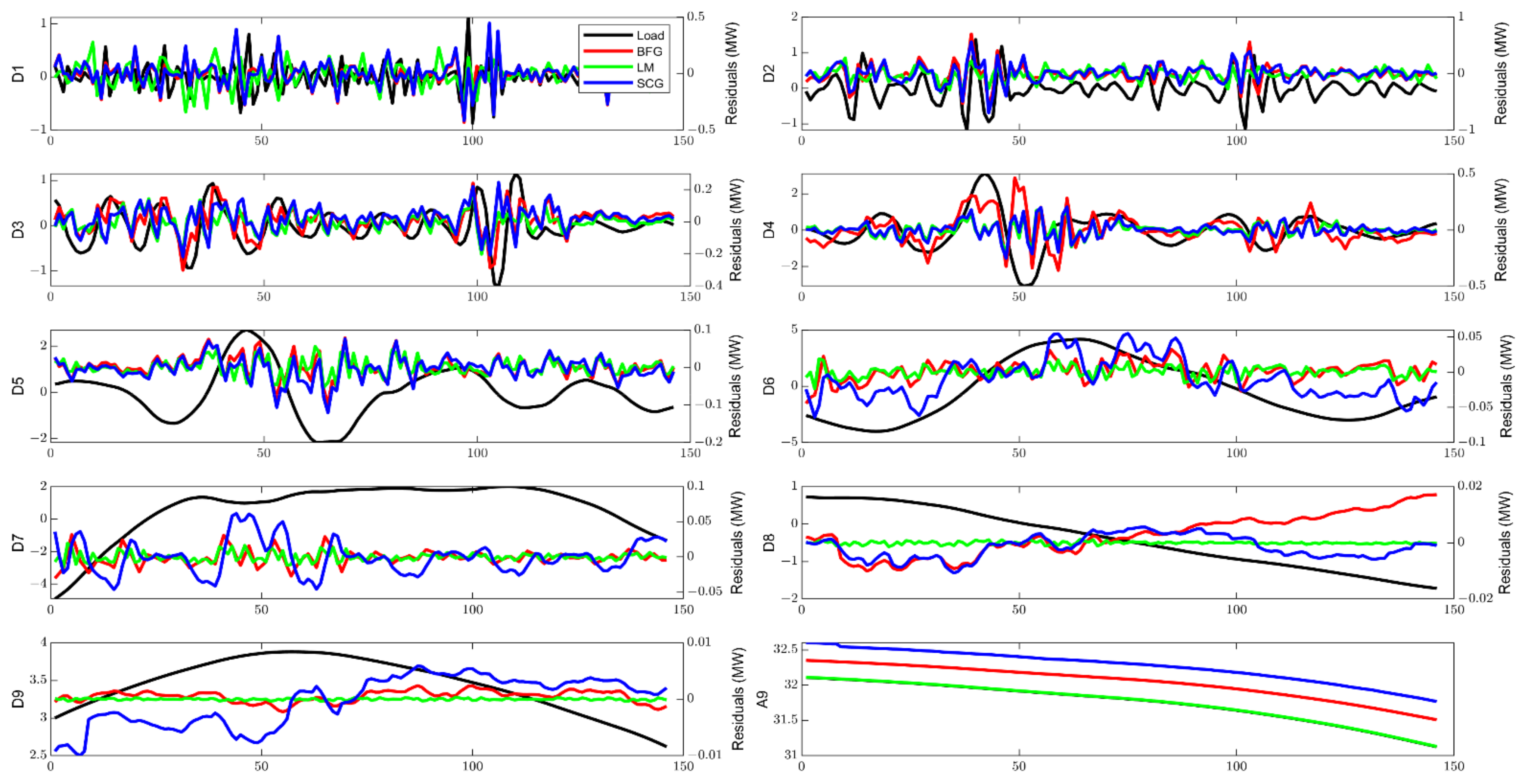
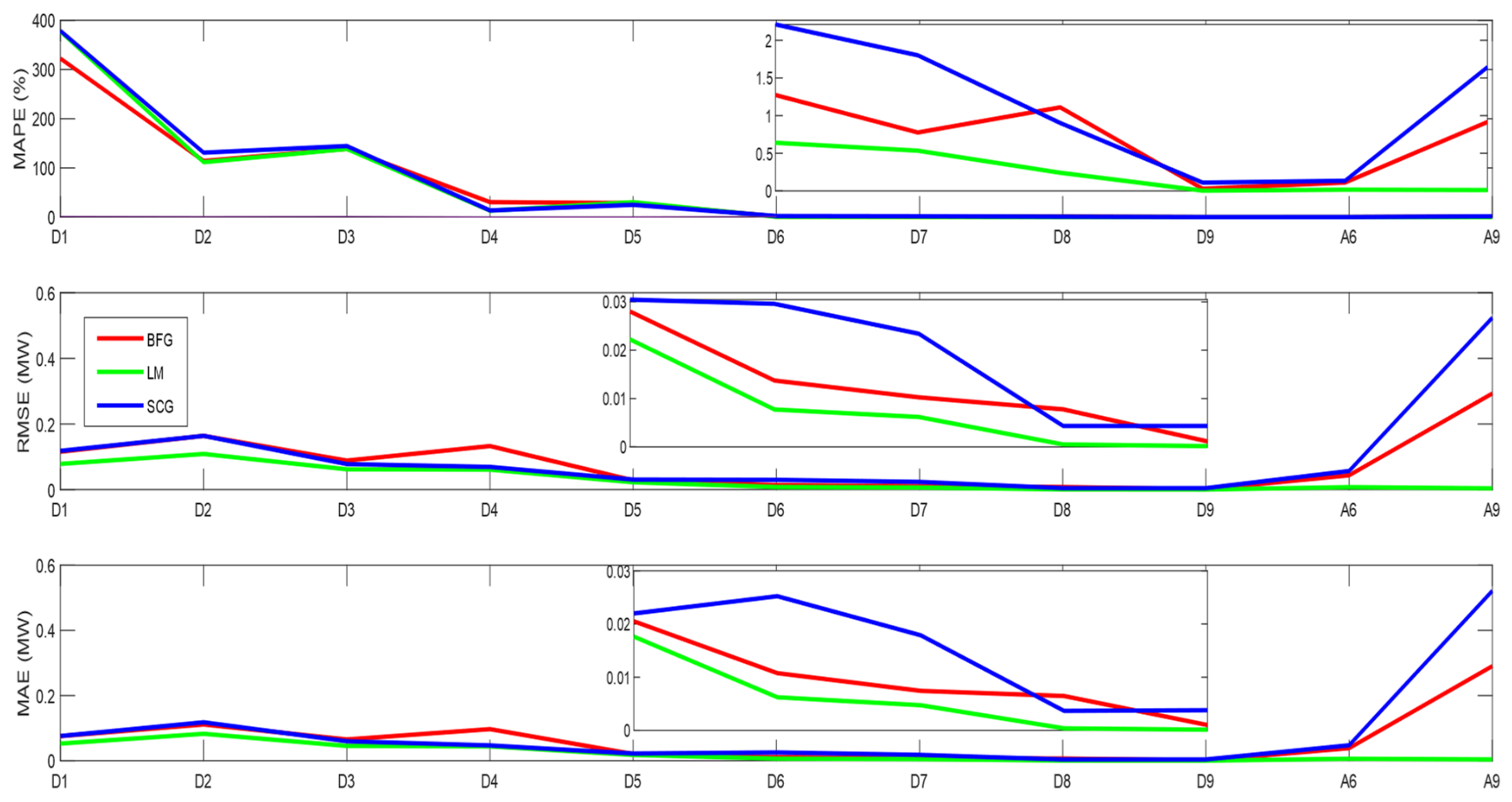
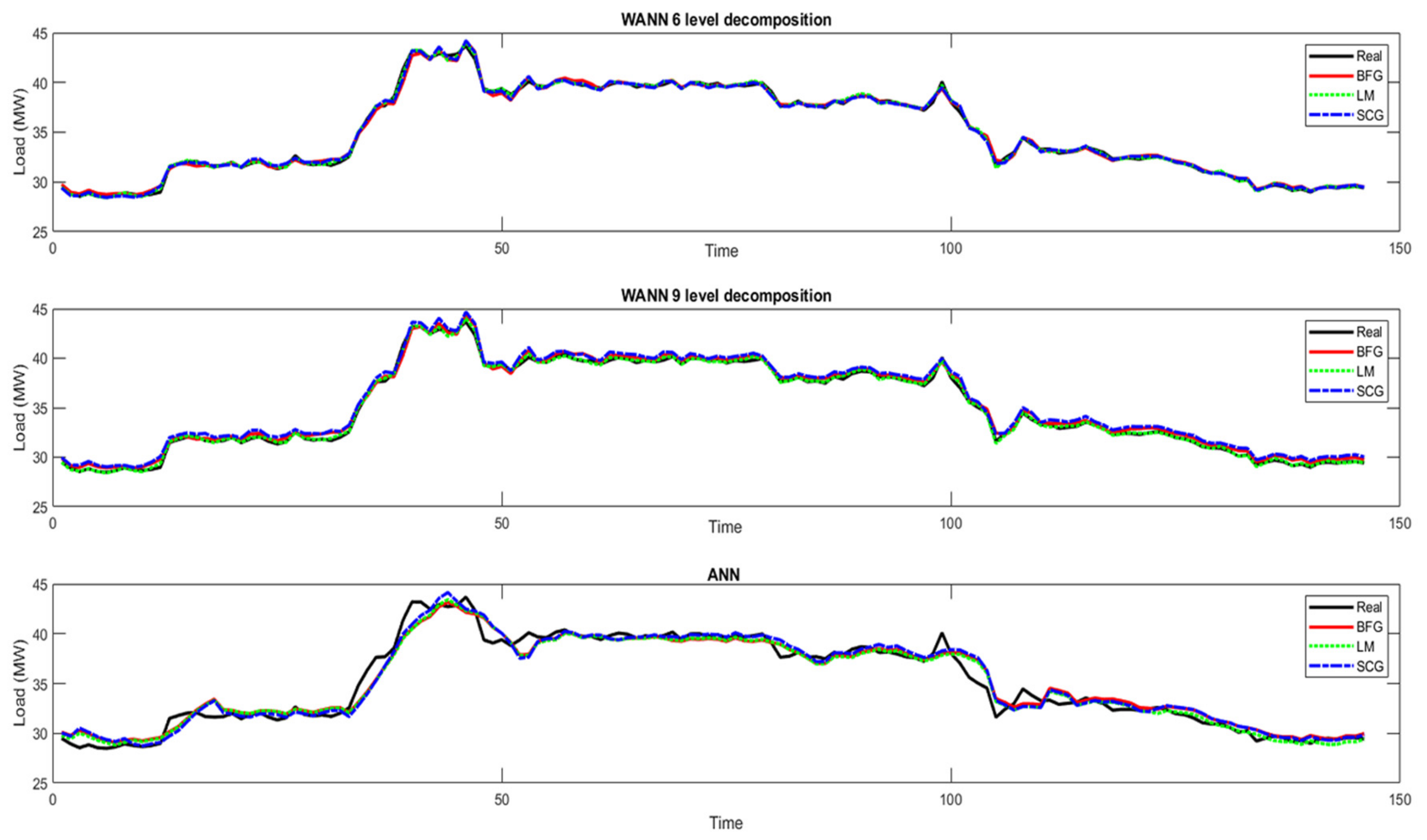
5. Results and Discussion
5.1. Evaluation Metrics
5.2. WANN and ANN Prediction Comparison
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gabriska, D. Evaluation of the Level of Reliability in Hazardous Technological Processes. Appl. Sci. 2021, 11, 134. [Google Scholar] [CrossRef]
- Kurek, T.; Bielecki, A.; Świrski, K.; Wojdan, K.; Guzek, M.; Białek, J.; Brzozowski, R.; Serafin, R. Heat Demand forecasting algorithm for a Warsaw district heating network. Energy 2021, 217. [Google Scholar] [CrossRef]
- Guo, B.; Cheng, L.; Xu, J.; Chen, L. Prediction of the Heat Load in Central Heating Systems Using GA-BP Algorithm. In Proceedings of the International Conference on Computer Network, Electronic and Automation (ICCNEA 2017), Xi’an, China, 23–25 September 2017; pp. 441–445. [Google Scholar] [CrossRef]
- GRANRYD Eric. Refrigerating engineering; Royal Institute of Technology: Stockholm, Sweden, 2009; ISBN 978-91-7415-415-3. [Google Scholar]
- Panapakidis, I.P.; Dagoumas, A.S. Day-ahead natural gas demand forecasting based on the combination of wavelet transform and ANFIS/genetic algorithm/neural network model. Energy 2017, 118, 231–245. [Google Scholar] [CrossRef]
- Yan, K.; Li, W.; Ji, Z.; Du, Y.; Qi, M. A Hybrid LSTM Neural Network for Energy Consumption Forecasting of Individual Households. IEEE Access 2019, 7, 157633–157642. [Google Scholar] [CrossRef]
- Nemeth, M.; Borkin, D.; Michalconok, G. The comparison of machine-learning methods XGBoost and LightGBM to predict energy development. In Proceedings of the Computational Statistics and Mathematical Modeling Methods in Intelligent Systems: Proceedings of 3rd Computational Methods in Systems and Software, Zlín, Czech Republic, 10–12 September 2019; Silhavy, R., Silhavy, P., Prokopova, Z., Eds.; Springer: Cham/Basel Switzerland, 2019; Volume 2, pp. 208–215. [Google Scholar] [CrossRef]
- Nemetova, A.; Borkin, D.; Michalconok, G. Comparison of methods for time series data analysis for further use of machine learning algorithms. In Proceedings of the Computational Statistics and Mathematical Modeling Methods in Intelligent Systems: Proceedings of 3rd Computational Methods in Systems and Software, Zlín, Czech Republic, 10–12 September 2019; Silhavy, R., Silhavy, P., Prokopova, Z., Eds.; Springer: Cham/Basel Switzerland, 2019; Volume 2, pp. 90–99. [Google Scholar] [CrossRef]
- Lang, X.; Rehman, N.; Zhang, Y.; Xie, L.; Su, H. Median ensemble empirical mode decomposition. Signal Process. 2020, 176. [Google Scholar] [CrossRef]
- Zuo, G.; Luo, J.; Wang, N.; Lian, Y.; He, X. Decomposition ensemble model based on variational mode decomposition and long short-term memory for streamflow forecasting. J. Hydrol. 2020, 585. [Google Scholar] [CrossRef]
- Yesilli, M.C.; Khasawneh, F.A.; Otto, A. On transfer learning for chatter detection in turning using wavelet packet transform and ensemble empirical mode decomposition. Cirp J. Manuf. Sci. Technol. 2020, 28, 118–135. [Google Scholar] [CrossRef]
- Mallat, S.G. A Theory for Multiresolution Signal Decomposition: The Wavelet Representation; Technical Report; University of Pennsylvania: Philadelphia, PA, USA, 1987. [Google Scholar]
- Meyer, Y. Wavelets, Algorithms & Applications, 1st ed.; SIAM: Philadelphia, PA, USA, 1993. [Google Scholar]
- Sui, K.; Kim, H.G. Research on application of multimedia image processing technology based on wavelet transform. J. Image Video Process. 2019, 24. [Google Scholar] [CrossRef]
- Mahesh, M.; Kumar, T.R.R.; Shoban Babu, B.; Saikrishna, J. Image Enhancement using Wavelet Fusion for Medical Image Processing. Int. J. Eng. Adv. Technol. 2019, 9. [Google Scholar] [CrossRef]
- Shanmugapriya, K.; Priya, D.J.; Priya, N. Image Enhancement Techniques in Digital Image Processing. Int. J. Innov. Technol. Explor. Eng. 2019, 8. [Google Scholar] [CrossRef]
- Kumar, K.; Mustafa, N.; Li, J.; Shaikh, R.A.; Khan, S.A.; Khan, A. Image edge detection scheme using wavelet transform. In Proceedings of the International Computer Conference on Wavelet Active Media Technology and Information Processing (ICCWAMTIP 2014), Chengdu, China, 19–21 December 2014; pp. 261–265. [Google Scholar] [CrossRef]
- Hashim, M.A.; Nasef, M.H.; Kabeel, A.E.; Ghazaly, N.M. Combustion fault detection technique of sparkignition engine based on wavelet packet transform and artificial neural network. Alex. Eng. J. 2020. [Google Scholar] [CrossRef]
- Gharesi, N.; Mehdi Arefi, M.; Razavi-Farb, R.; Zarei, J.; Yin, S. A neuro-wavelet based approach for diagnosing bearing defects. Adv. Eng. Inform. 2020, 46. [Google Scholar] [CrossRef]
- Kou, L.; Liu, C.; Cai, G.; Zhang, Z. Fault Diagnosis for Power Electronics Converters based on Deep Feedforward Network and Wavelet Compression. Electr. Power Syst. Res. 2020, 185. [Google Scholar] [CrossRef]
- Valizadeh, M.; Sohrabi, M.R.; Motiee, F. The application of continuous wavelet transform based on spectrophotometric method and high-performance liquid chromatography for simultaneous determination ofanti-glaucoma drugs in eye drop. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2020, 242. [Google Scholar] [CrossRef]
- Győrfi, Á.; Szilágyi, L.; Kovács, L. A Fully Automatic Procedure for Brain Tumor Segmentation from Multi-Spectral MRI Records Using Ensemble Learning and Atlas-Based Data Enhancement. Appl. Sci. 2021, 11, 564. [Google Scholar] [CrossRef]
- Akansu, A.N.; Serdijn, W.A.; Selesnick, W.I. Emerging applications of wavelets: A review. Phys. Commun. 2010, 3. [Google Scholar] [CrossRef]
- Zuo, H.; Chen, Y.; Jia, F. A new C0 layer wise wavelet finite element formulation for the static and free vibration analysis of composite plates. Compos. Struct. 2020, 254. [Google Scholar] [CrossRef]
- Qin, Y.; Mao, Y.; Tang, B.; Wang, Y.; Chen, H. M-band flexible wavelet transform and its application to thefault diagnosis of planetary gear transmission systems. Mech. Syst. Signal Process. 2019, 134. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, X.; Zhang, Y.; Gou, H.; Yang, F. Wind speed prediction based on wavelet analysis and time series method. In Proceedings of the International Conference on Wavelet Analysis and Pattern Recognition (ICWAPR 2017), Ningbo, China, 9–12 July 2017; pp. 23–27. [Google Scholar] [CrossRef]
- Ren, P.; Xiang, Z.; Shangguan, R. Design and Simulation of a prediction algorithm based on wavelet support vector machine. In Proceedings of the Seventh International Conference on Natural Computation, Shanghai, China, 26–28 July 2011; pp. 208–211. [Google Scholar] [CrossRef]
- Barthel, K.U.; Brandau, S.; Hermesmeier, W.; Heising, G. Zerotree wavelet coding using fractal prediction. In Proceedings of the International Conference on Image Processing (ICIP 1997), Santa Barbara, CA, USA, 26–29 October 1997; Volume 2, pp. 314–317. [Google Scholar] [CrossRef]
- Yin, J.; Gao, C.; Wang, Y.; Wang, Y. Hyperspectral image classification using wavelet packet analysis and gray prediction model. In Proceedings of the International Conference on Image Analysis and Signal Processing (IASP 2010), Zhejiang, China, 9–11 April 2010; pp. 322–326. [Google Scholar] [CrossRef]
- Elarabi, T.; Sammoud, A.; Abdelgawad, A.; Li, X.; Bayoumi, M. Hybrid wavelet—DCT intra prediction for H.264/AVC interactive encoder. In Proceedings of the IEEE China Summit & International Conference on Signal and Information Processing (ChinaSIP 2014), Xi’an, China, 9–13 July 2014; pp. 281–285. [Google Scholar] [CrossRef]
- Li, H.; Guo, C.; Yang, S.X.; Jin, H. Hybrid Model of WT and ANFIS and Its Application on Time Series Prediction of Ship Roll Motion. In Proceedings of the Multiconference on Computational Engineering in Systems Applications (CESA 2006), Beijing, China, 4–6 October 2006; pp. 333–337. [Google Scholar] [CrossRef]
- Stefenon, S.F.; Ribeiro, M.H.D.M.; Nied, A.; Mariani, V.C.; Coelho, L.D.S.; da Rocha, D.F.M.; Grebogi, R.B.; Ruano, A.E.D.B. Wavelet group method of data handling for fault prediction in electrical power insulators. Int. J. Electr. Power Energy Syst. 2020, 123. [Google Scholar] [CrossRef]
- Prabhakar, D.V.N.; Kumar, M.S.; Krishna, A.G. A Novel Hybrid Transform approach with integration of Fast Fourier, Discrete Wavelet and Discrete Shearlet Transforms for prediction of surface roughness on machined surfaces. Measurement 2020, 164. [Google Scholar] [CrossRef]
- Zhang, T.; Chaofeng, L.; Fumin, M.; Zhao, K.; Wang, H.; O’Hare, G.M. A photovoltaic power forecasting model based on dendritic neuron networks with the aid of wavelet transform. Neurocomputing 2020, 397, 438–446. [Google Scholar] [CrossRef]
- Chang, Z.; Zhang, Y.; Chen, W. Electricity price prediction based on hybrid model of Adam optimized LSTM neural network and wavelet transform. Energy 2019, 187. [Google Scholar] [CrossRef]
- El-Hendawi, M.; Wang, Z. An ensemble method of full wavelet packet transform and neural network for short term electrical load forecasting. Electr. Power Syst. Res. 2020, 182. [Google Scholar] [CrossRef]
- Liu, H.; Mi, X.; Li, Y. Smart deep learning based wind speed prediction model using wavelet packet decomposition, convolutional neural network and convolutional long short term memory network. Energy Convers. Manag. 2018, 166, 120–131. [Google Scholar] [CrossRef]
- Xia, C.; Zhang, M.; Cao, J. A hybrid application of soft computing methods with wavelet SVM and neural network to electric power load forecasting. J. Electr. Syst. Inf. Technol. 2018, 5, 681–696. [Google Scholar] [CrossRef]
- Bashir Tayab, U.; Zia, A.; Yang, F.; Lu, J.; Kashif, M. Short-term load forecasting for microgrid energy management system using hybrid HHO-FNN model with best-basis stationary wavelet packet transform. Energy 2020, 203. [Google Scholar] [CrossRef]
- Farhadi, M.; Abbaspour-Gilandeh, Y.; Mahmoudi, A.; Mari Maja, J. An Integrated System of Artificial Intelligence and Signal Processing Techniques for the Sorting and Grading of Nuts. Appl. Sci. 2020, 10, 3315. [Google Scholar] [CrossRef]
- Feng, X.; Feng, Q.; Li, S.; Hou, X.; Zhang, M.; Liu, S. Wavelet-Based Kalman Smoothing Method for Uncertain Parameters Processing: Applications in Oil Well-Testing Data Denoising and Prediction. Sensors 2020, 20, 4541. [Google Scholar] [CrossRef]
- Obidin, M.V.; Serebrovski, A.P. Signal denoising with the use of the wavelet transform and the Kalman filter. J. Commun. Technol. Electron. 2014, 59, 1440–1445. [Google Scholar] [CrossRef]
- Li, Y.J.; Kokkinaki, A.; Darve, E.T.; Kitanidis, P.K. Smoothing-based compressed state Kalman filter for joint state-parameter estimation: Applications in reservoir characterization and CO2 storage monitoring. Water Resour. Res. 2017, 53, 7190–7207. [Google Scholar] [CrossRef]
- Zhang, X.; Ni, W.; Liao, H.; Pohl, E.; Xu, P.; Zhang, W. Fusing moving average model and stationary wavelet decomposition for automatic incident detection: Case study of Tokyo Expressway. J. Traffic Transp. Eng. 2014, 1, 404–414. [Google Scholar] [CrossRef]
- Szi-Wen, C.; Hsiao-Chen, C.; Hsiao-Lung, C. A real-time QRS detection method based on moving-averaging incorporating with wavelet denoising. Comput. Methods Programs Biomed. 2006, 82, 187–195. [Google Scholar]
- Akansu, A.N.; Haddad, R.A. Multiresolution Signal Decomposition: Transforms, Subbands, and Wavelets, 2nd ed.; Academic Press: San Diego, CA, USA, 2000. [Google Scholar]
- Tan, L.; Jiang, J. Discrete Wavelet Transform. In Digital Signal Processing—Fundamentals and Applications, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 623–632. [Google Scholar]
- Boashash, B. The Discrete Wavelet Transform. In Time-Frequency Signal Analysis and Processing—A Comprehensive Reference; Elsevier: Amsterdam, The Netherlands, 2016; pp. 141–142. [Google Scholar]
- Loizou, C.P.; Pattichis, C.S.; D’hooge, J. Discrete Wavelet Transform. In Handbook of Speckle Filtering and Tracking in Cardiovascular Ultrasound Imaging and Video; Institution of Engineering and Technology: London, UK, 2018; pp. 174–177. [Google Scholar]
- Bankman, I.N. Three-Dimensional Image Compression with Wavelet Transforms. In Handbook of Medical Image Processing and Analysis, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2009; pp. 963–964. [Google Scholar]
- MathWorks Wavedec. Available online: https://www.mathworks.com/help/wavelet/ref/wavedec.html (accessed on 1 November 2020).
- Freire, P.K.D.M.M.; Santos, C.A.G.; da Silva, G.B.L. Analysis of the use of discrete wavelet transforms coupled with ANN for short-term streamflow forecasting. Appl. Soft Comput. 2019, 80, 494–505. [Google Scholar] [CrossRef]
- Junior, L.A.; Souza, R.M.; Menezes, M.L.; Cassiano, K.M.; Pessanha, J.F.; Souza, R. Artificial Neural Network and Wavelet Decomposition in the Forecast of Global Horizontal Solar Radiation. Pesqui. Oper. 2015, 35, 73–90. [Google Scholar] [CrossRef]
- Moller, M.F. A scaled conjugate gradient algorithm for fast supervised learning. Neural Netw. 1993, 6, 525–533. [Google Scholar] [CrossRef]
- Rodrigues, F.; Cardeira, C.; Calado, J.M.F. The Daily and Hourly Energy Consumption and Load Forecasting Using Artificial Neural Network Method: A case Study Using a Set of 93 Households in Portugal. Energy Procedia 2014, 62, 220–229. [Google Scholar] [CrossRef]
- Perera, A.; Azamathulla, H.; Rathnayake, U. Comparison of different Artificial Neural Network (ANN) training algorithm to predict atmospheric temperature in Tabuk, Saudi Arabia. Mausam 2020, 25, 1–11. [Google Scholar]
- Gong, M.; Wang, J.; Bai, Y.; Li, B.; Zhang, L. Heat load prediction of residential buildings based on discrete wavelet transform and tree-based ensemble learning. J. Build. Eng. 2020, 32. [Google Scholar] [CrossRef]
- Wang, M.; Qi, T. Application of wavelet neural network on thermal load forecasting. Int. J. Wirel. Mob. Comput. 2013, 6, 608–614. [Google Scholar] [CrossRef]
- Amjady, N.; Keynia, F. Short-term load forecasting of power systems by com- bination of wavelet transform and neuro-evolutionary algorithm. Energy 2009, 34, 46–57. [Google Scholar] [CrossRef]
- Bashir, Z.A.; El-Hawary, M.E. Applying wavelets to short-term load forecasting using PSO-based neural networks. IEEE Trans. Power Syst. 2009, 24, 20–27. [Google Scholar] [CrossRef]
- Gao, R.X.; Yan, R. Wavelets: Theory and applications for manufacturing. Wavelets Theory Appl. Manuf. 2011, 165–187. [Google Scholar] [CrossRef]
- Tascikaraoglu, A.; Sanandaji, B.M.; Poolla, K.; Varaiya, P. Exploiting sparsity of interconnections in spatio-temporal wind speed forecasting using Wavelet Transform. Appl. Energy 2016, 165, 735–747. [Google Scholar] [CrossRef]
- Daubechies, I. Ten Lectures on Wavelets, CBMS-NSF Regional Conference Series in Applied Mathematics; SIAM: Philadelphia, PA, USA, 1992. [Google Scholar]
- Freire, P.K.D.M.; Santos, C.A.G. Optimal level of wavelet decomposition for daily inflow forecasting. Earth Sci. Inf. 2020, 13, 1163–1173. [Google Scholar] [CrossRef]
- Sang, Y. A Practical Guide to Discrete Wavelet Decomposition of Hydrologic Time Series. Water Resour. Manag. 2012, 26, 3345–3365. [Google Scholar] [CrossRef]
- Yang, H.; Jin, S.; Feng, S.; Wang, B.; Zhang, F.; Che, J. Heat Load Forecasting of District Heating System Based on Numerical Weather Prediction Model. In Proceedings of the 2nd International Forum on electrical Engineering and Automation (IFEEA 2015), Guangzhou, China, 26–27 December 2015; pp. 1–5. [Google Scholar] [CrossRef][Green Version]
- Karsoliya, S.; Azad, M. Approximating Number of Hidden layer neurons in Multiple Hidden Layer BPNN Architecture. Int. J. Eng. Trends Technol. 2012, 3, 714–717. [Google Scholar]


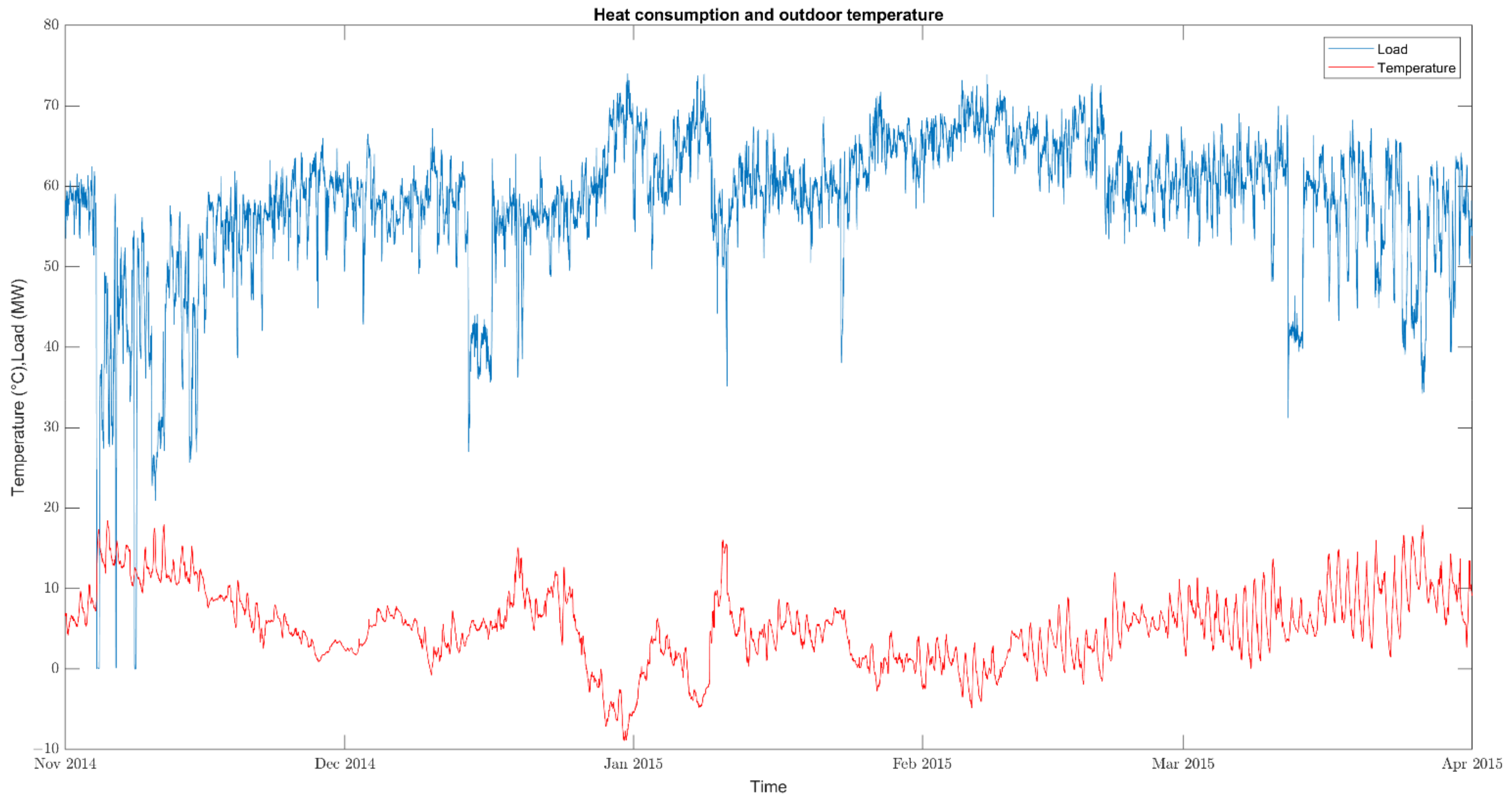

| Parameter | Min | Max | Mean | Std |
|---|---|---|---|---|
| Temperature (°C) | −8.93 | 18.47 | 5.27 | 4.52 |
| Load (MW) | 0 | 74.04 | 32.34 | 8.92 |
| Input Number | Input Name | Value | Calculation |
|---|---|---|---|
| 1. | Hour | 0–23 | Timestamp |
| 2. | Weekend | 0–1 | |
| 3. | Day of the week | 1–7 | |
| 4. | Temperature | Various | Exogenous |
| 5. | Lagged load | Various | Endogenous + timestamp |
| Number | Selected Lags | Model Structure (I × h × o) | ||
|---|---|---|---|---|
| L(t) | T(t) | |||
| D1 | 1–5 | – | 10 × h × 1 | |
| D2 | 1–4, 6 | – | 10 ×h × 1 | |
| D3 | 1,2,4,5,6 | – | 10 × h × 1 | |
| D4 | 1–3,10–12 | – | 11 × h × 1 | |
| D5 | 1–4,20–24 | – | 14 × h × 1 | |
| D6 | 1–5, 39–42 | ✓ | 18 × h × 1 | |
| D7 | 1–5, 79–81 | – | 13 × h × 1 | |
| D8 | 1–5, 172–174 | – | 13 × h × 1 | |
| D9 | 1–5, 319–321 | ✓ | 17 × h × 1 | |
| A9 | 1–5 | ✓ | 14 × h × 1 | |
| A6 | 1–5 | ✓ | 14 × h × 1 | |
| Model | Parameter | Value |
|---|---|---|
| BPNN and WANN | Number of hidden layers | 1 |
| Number of neurons in hidden layer | 21 for ANN models Various for WANN; see Table 3 | |
| Number of output neurons | 1 | |
| Hidden layer activation function | tansig | |
| Output layer activation function | purelin | |
| Data set division train/test | random 80/20 (%) | |
| Epochs | 1000 | |
| Data normalization | mapstd; see (Equation (7)) | |
| Training algorithms | trainlm, trainscg, trainbfg | |
| Learning rate | 0.001 | |
| WANN | Decomposition level | 6 and 9 |
| Mother wavelet | db5 |
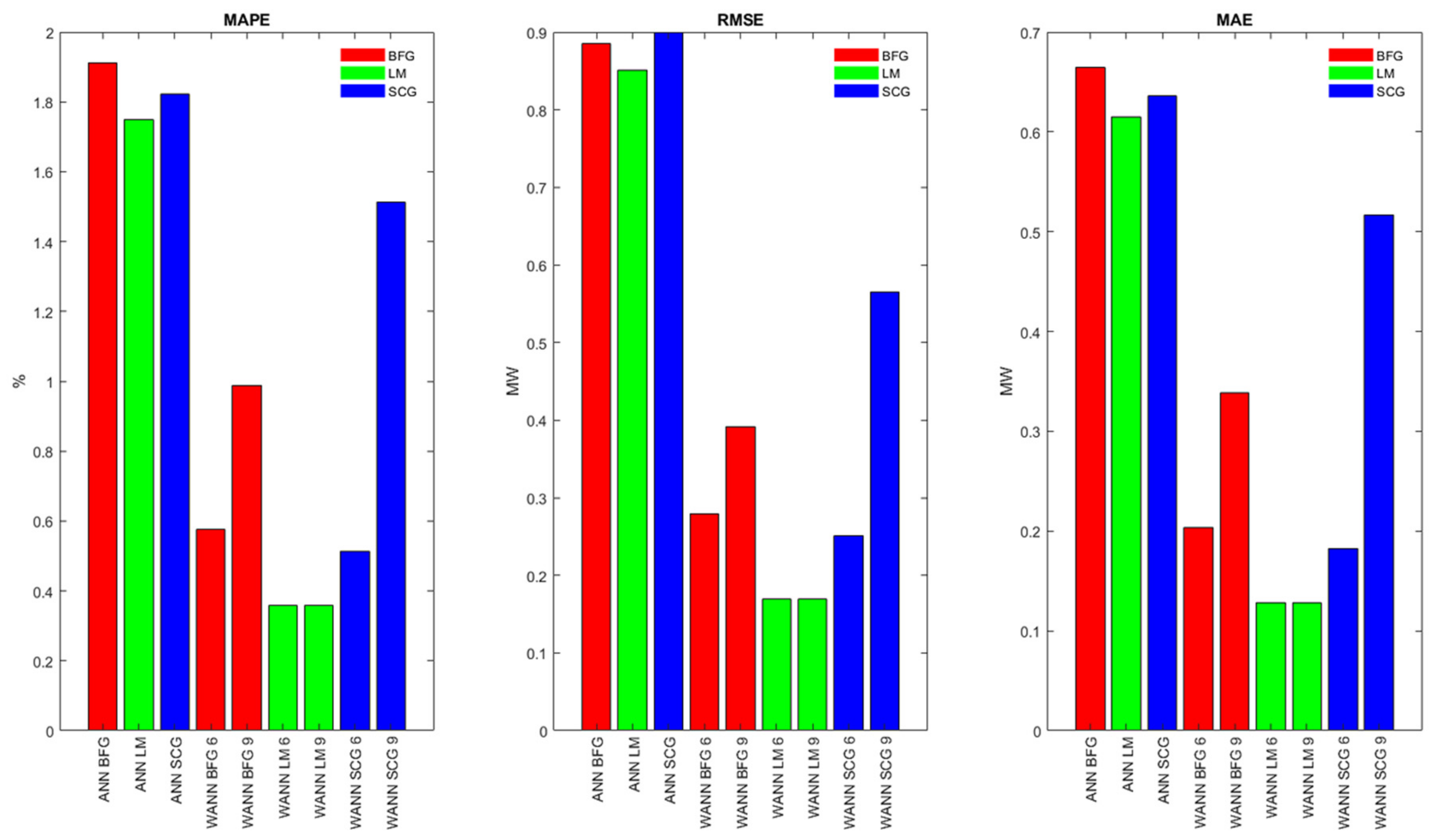
| Models | ANN | WANN | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Parameters | Dec. Level 6 | Dec. Level 9 | |||||||
| BFG | LM | SCG | BFG | LM | SCG | BFG | LM | SCG | |
| MAPE (%) | 1.91 | 1.75 | 1.83 | 0.58 | 0.36 | 0.51 | 0.98 | 0.36 | 1.51 |
| RMSE (MW) | 0.88 | 0.85 | 0.89 | 0.28 | 0.16 | 0.25 | 0.39 | 0.16 | 0.56 |
| MAE (MW) | 0.66 | 0.61 | 0.64 | 0.20 | 0.12 | 0.18 | 0.33 | 0.12 | 0.51 |
| Improvement percentage | WANN | |||||
|---|---|---|---|---|---|---|
| Dec. level 6 | Dec. level 9 | |||||
| BFG | LM | SCG | BFG | LM | SCG | |
| MAPE | 69% | 79% | 72% | 48% | 79% | 17% |
| RMSE | 68% | 81% | 71% | 55% | 81% | 37% |
| MAE | 81% | 80% | 71% | 50% | 80% | 20% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kováč, S.; Micha’čonok, G.; Halenár, I.; Važan, P. Comparison of Heat Demand Prediction Using Wavelet Analysis and Neural Network for a District Heating Network. Energies 2021, 14, 1545. https://doi.org/10.3390/en14061545
Kováč S, Micha’čonok G, Halenár I, Važan P. Comparison of Heat Demand Prediction Using Wavelet Analysis and Neural Network for a District Heating Network. Energies. 2021; 14(6):1545. https://doi.org/10.3390/en14061545
Chicago/Turabian StyleKováč, Szabolcs, German Micha’čonok, Igor Halenár, and Pavel Važan. 2021. "Comparison of Heat Demand Prediction Using Wavelet Analysis and Neural Network for a District Heating Network" Energies 14, no. 6: 1545. https://doi.org/10.3390/en14061545
APA StyleKováč, S., Micha’čonok, G., Halenár, I., & Važan, P. (2021). Comparison of Heat Demand Prediction Using Wavelet Analysis and Neural Network for a District Heating Network. Energies, 14(6), 1545. https://doi.org/10.3390/en14061545






