Mathematical Analysis of Line Intersection and Shortest Distance Algorithms †
Abstract
1. Introduction
2. Issues for TOA Trilateration Method
3. Enhanced TOA Trilateration Algorithms
3.1. Shortest Distance Algorithm
3.2. Line Intersection Algorithm
4. Mathematical Analysis of Enhanced TOA Trilateration Algorithms
4.1. Mathematical Verification for Line Intersection Algorithm
4.2. Mathematical Relations between Two Algorithms
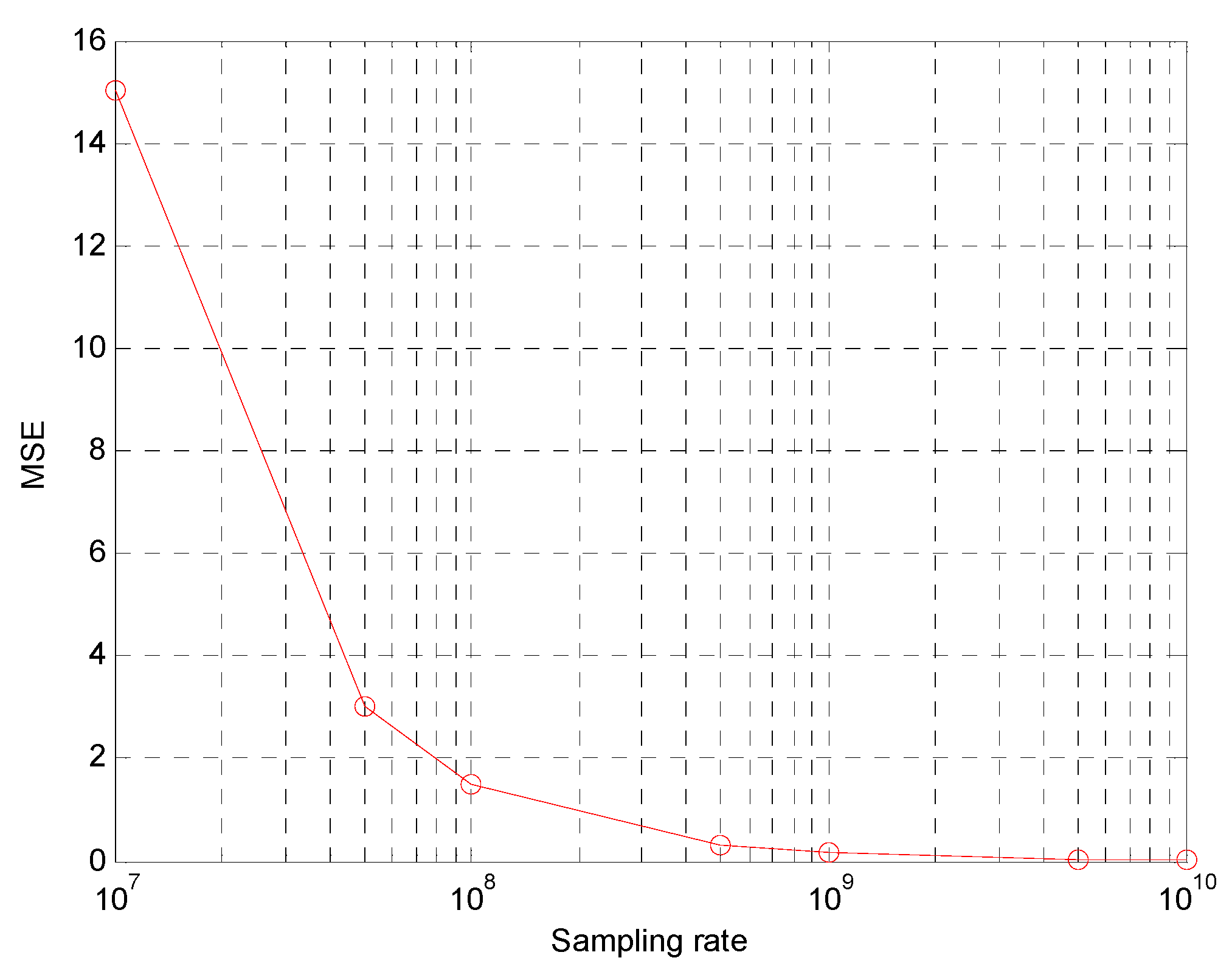
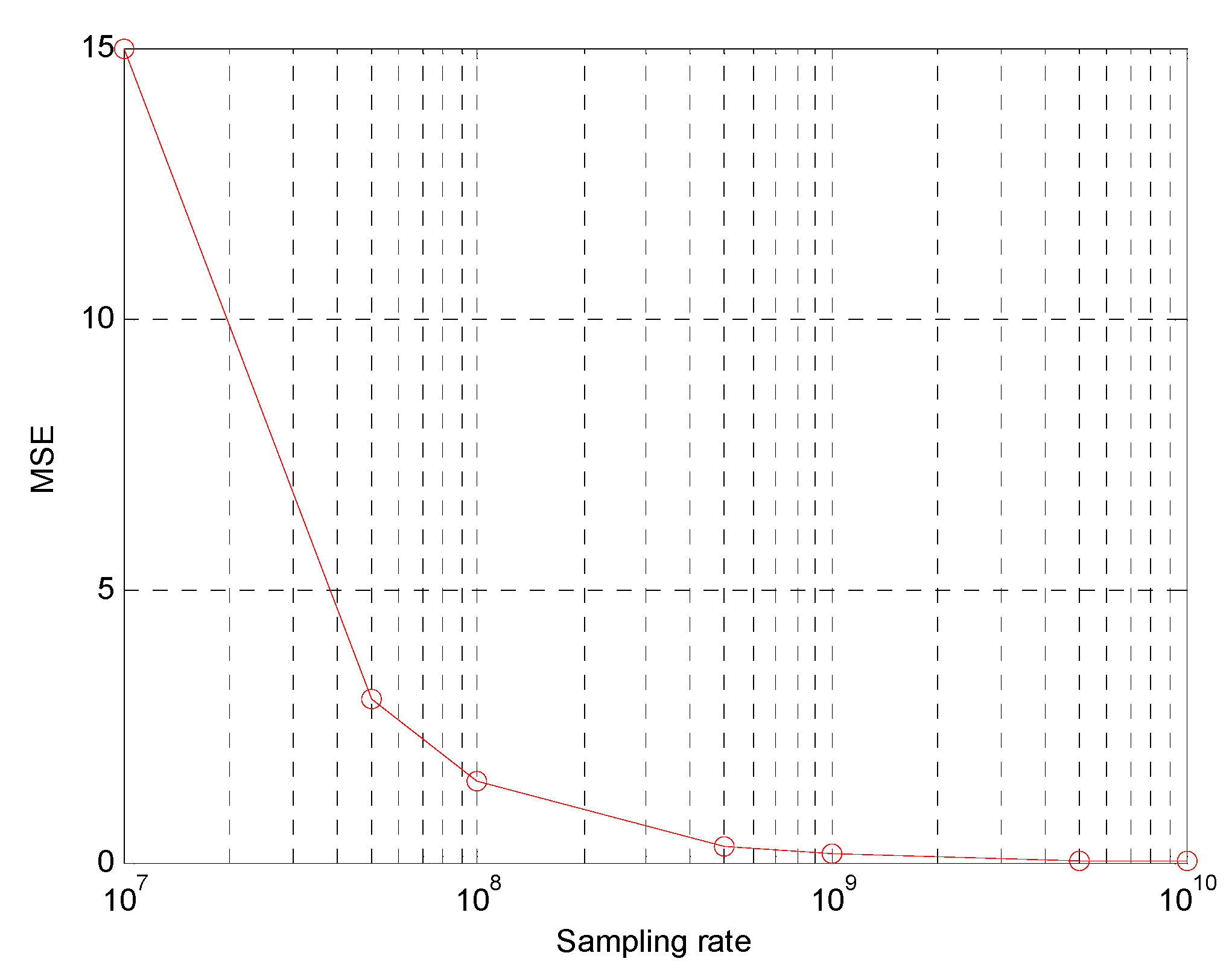
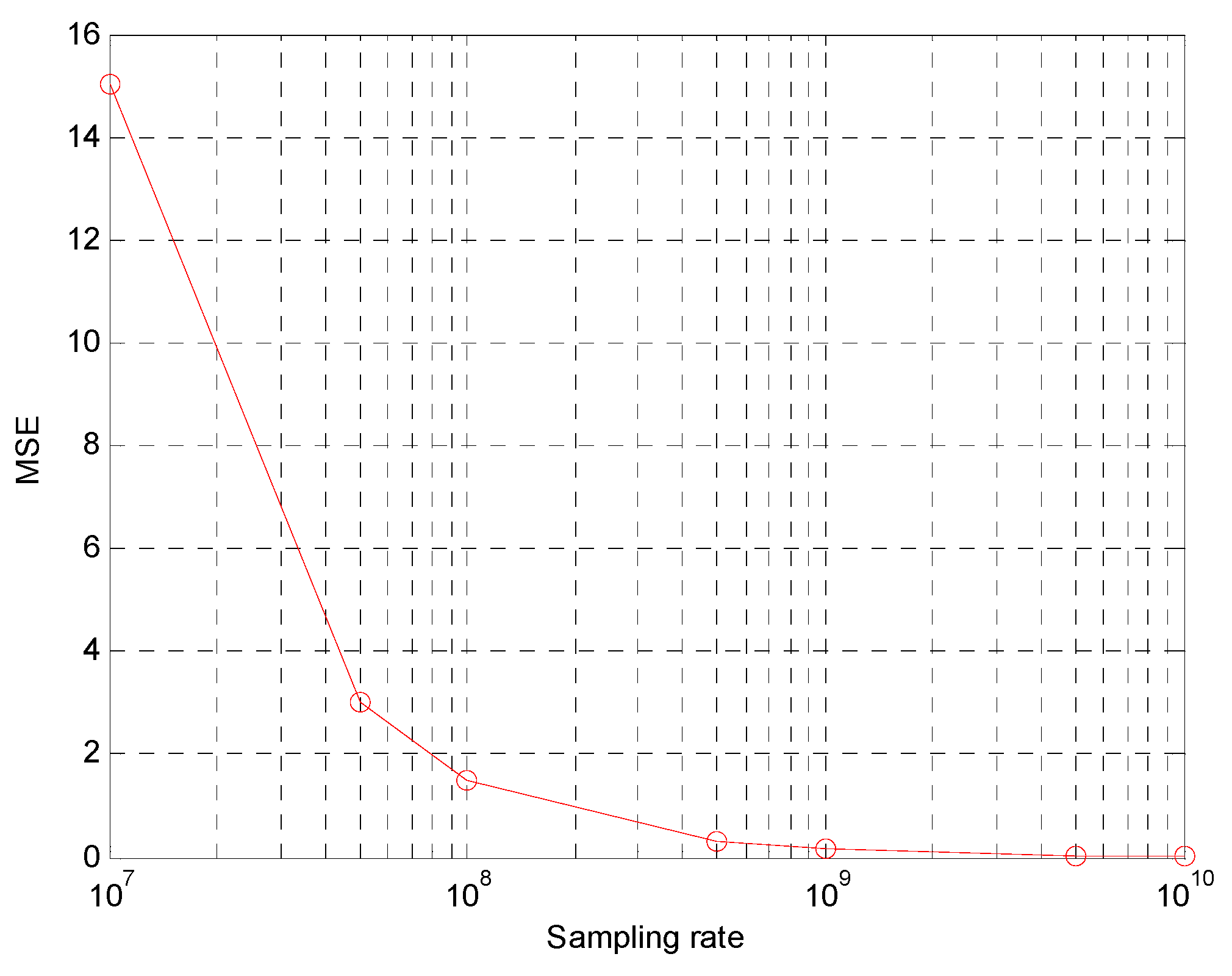
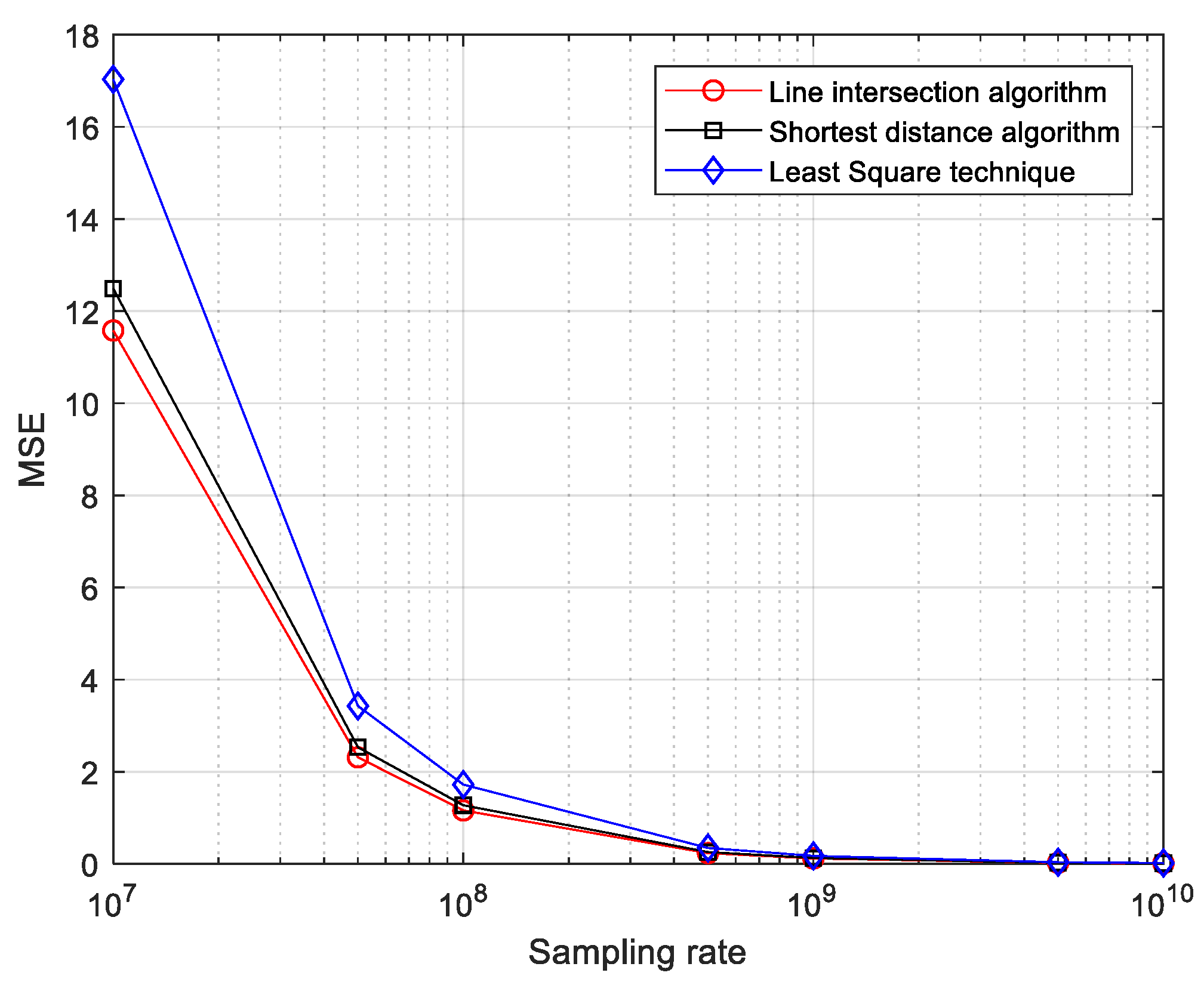
5. Computer Simulations
5.1. Error Model
5.2. Simulation Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Abu-Shaban, Z.; Zhou, X.; Abhayapala, T.D. A Novel TOA-Based Mobile Localization Technique Under Mixed LOS/NLOS Conditions for Cellular Networks. IEEE Trans. Veh. Technol. 2016, 65, 8841–8853. [Google Scholar] [CrossRef]
- Khan, U.F.; Lazaridis, P.I.; Mohamed, H.; Albarracín, R.; Zaharis, Z.D.; Atkinson, R.C.; Tachtatzis, C.; Glover, I.A. An Efficient Algorithm for Partial Discharge Localization in High-Voltage Systems Using Received Signal Strength. Sensors 2018, 18, 4000. [Google Scholar] [CrossRef] [PubMed]
- Federal Communications Commission (Ed.) Revision of the Commission’s Rules to Insure Compatibility with Enhanced 911 Emergency Calling Systems; FCC Docket No. 94-102; July 1996. Available online: https://www.fcc.gov/document/revision-commissions-rules-ensure-compatibility-enhanced-30 (accessed on 15 December 2020).
- Reed, J.; Krizman, K.; Woerner, B.; Rappaport, T. An overview of the challenges and progress in meeting the E-911 requirement for location service. IEEE Commun. Mag. 1998, 36, 30–37. [Google Scholar] [CrossRef]
- Rappaport, T.; Reed, J.; Woerner, B. Position location using wireless communications on highways of the future. IEEE Commun. Mag. 1996, 34, 33–41. [Google Scholar] [CrossRef]
- Adusei, I.; Kyamakya, K.; Erbas, F. Location-based services: Advances and challenges. In Proceedings of the Canadian Conference on Electrical and Computer Engineering 2004 (IEEE Cat. No.04CH37513), Niagara Falls, ON, Canada, 2–5 May 2004; Volume 1, pp. 1–7. [Google Scholar]
- Küpper, A. Location-based Services: Fundamentals and Operation; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Mohapatra, D.; Suma, S.B. Survey of location based wireless services. In Proceedings of the 2005 IEEE International Conference on Personal Wireless Communications (ICPWC 2005), New Delhi, India, 23–25 January 2005; pp. 358–362. [Google Scholar]
- Zhang, Y.; Fu, W.; Wei, D.; Jiang, J.; Yang, B. Moving target localization in indoor wireless sensor networks mixed with LOS/NLOS situations. EURASIP J. Wirel. Commun. Netw. 2013, 2013, 291. [Google Scholar] [CrossRef]
- Wang, Y. Linear least squares localization in sensor networks. EURASIP J. Wirel. Commun. Netw. 2015, 2015, 51. [Google Scholar] [CrossRef]
- Koh, J.Y.; Nevat, I.; Leong, D.; Wong, W.-C. Geo-Spatial Location Spoofing Detection for Internet of Things. IEEE Internet Things J. 2016, 3, 971–978. [Google Scholar] [CrossRef]
- Kim, P.; Chang, S. Intelligent positioning and optimal diversity schemes for mobile agents in ubiquitous networks. Int. J. Softw. Eng. Knowl. Eng. 2008, 18, 637–650. [Google Scholar] [CrossRef]
- Caffery, J.; Stuber, G. Overview of radiolocation in CDMA cellular systems. IEEE Commun. Mag. 1998, 36, 38–45. [Google Scholar] [CrossRef]
- Drane, C.; Macnaughtan, M.; Scott, C. Positioning GSM telephones. IEEE Commun. Mag. 1998, 36, 46–54. [Google Scholar] [CrossRef]
- Jami, I.; Ali, M.; Ormondroyd, R. Comparison of methods of locating and tracking cellular mobiles. In Proceedings of the IEEE Colloquium on Novel Methods of Location and Tracking of Cellular Mobiles and Their System Applications, London, UK, 17 May 1999. [Google Scholar]
- Spirito, M.A.; Pöykkö, S.; Knuuttila, O. Experimental performance of methods to estimate the location of legacy handsets in GSM. In Proceedings of the IEEE 54th Vehicular Technology Conference, Atlantic City, NJ, USA, 7–11 October 2001; pp. 2716–2720. [Google Scholar]
- Wann, C.-D.; Chen, Y.-M. Position tracking and velocity estimation for mobile positioning systems. In Proceedings of the 5th International Symposium on Wireless Personal Multimedia Communications, Honolulu, HI, USA, 27–30 October 2002; pp. 310–314. [Google Scholar]
- Yilin, Z.H. Standardization of mobile phone positioning for 3G systems. IEEE Commun. Mag. 2002, 40, 108–116. [Google Scholar] [CrossRef]
- Chen, C.-S.; Su, S.-L.; Lu, C.-D. Geometrical positioning approached for mobile location estimation. In Proceedings of the 2010 2nd IEEE International Conference on Information Management and Engineering, Chengdu, China, 16–18 April 2010; pp. 268–272. [Google Scholar]
- Shen, J.; Molisch, A.F.; Salmi, J. Accurate Passive Location Estimation Using TOA Measurements. IEEE Trans. Wirel. Commun. 2012, 11, 2182–2192. [Google Scholar] [CrossRef]
- Chan, S.K.C.; Kan, K.K.H.; Ng, J.K.-Y. A Dual-Channel System for Providing Location Estimation in Mobile Computing. J. Interconnect. Netw. 2003, 4, 271–290. [Google Scholar] [CrossRef]
- Caffery, J. A new approach to the geometry of TOA location. In Proceedings of the 52nd IEEE Vehicular Technology Conference (Cat. No.00CH37152), Boston, MA, USA, 24–28 September 2000; Volume 1944, pp. 1943–1949. [Google Scholar]
- Sayed, A.H.; Tarighat, A.; Khajehnouri, N. Network-based wireless location: Challenges faced in developing techniques for accurate wireless location information. IEEE Signal. Process. Mag. 2005, 22, 24–40. [Google Scholar] [CrossRef]
- Chen, J.C.; Wang, Y.C.; Maa, C.S.; Chen, J.T. Network-Side Mobile Position Location Using Factor Graphs. IEEE Trans. Wirel. Commun. 2006, 5, 2696–2704. [Google Scholar] [CrossRef]
- Go, S.; Chong, J. Improved TOA-based localization method with BS selection scheme for wireless sensor networks. ETRI J. 2015, 37, 707–716. [Google Scholar] [CrossRef]
- Pradhan, S.; Khadka, G.; Hwang, S.S. Mobile Location Estimation Based on the TOA Geometry. In Proceedings of the Conference of the Korean Institute of Communications and Information Sciences, Naju, Korea, 10 May 2013; pp. 40–43. [Google Scholar]
- Pradhan, S.; Hwang, S.-S.; Cha, H.-R.; Bae, Y.-C. Line Intersection Algorithm for the Enhanced TOA Trilateration Technique. Int. J. Hum. Robot. 2014, 11, 1442003. [Google Scholar] [CrossRef]
- Caffery, J.J. Wireless Location in CDMA Cellular Radio Systems; Kluwer Academic: Boston, MA, USA, 2000. [Google Scholar]
- Ying, L.; Liang, Y.-C.; Wang, S.-X. Location parameters estimation in mobile communication systems. In Proceedings of the 2000 International Conference on Communication Technology Proceedings (Cat. No.00EX420), Beijing, China, 21–25 August 2002; pp. 261–268. [Google Scholar]
- McGuire, M.; Plataniotis, K.N.; Venetsanopoulos, A.N. Location of mobile terminals using time measurements and survey points. IEEE Trans. Veh. Technol. 2003, 52, 999–1011. [Google Scholar] [CrossRef]
- Cheung, K.; So, H. A multidimensional scaling framework for mobile location using time-of-arrival measurements. IEEE Trans. Signal. Process. 2005, 53, 460–470. [Google Scholar] [CrossRef]
- Gustafsson, F.; Gunnarsson, F. Mobile positioning using wireless networks: Possibilities and fundamental limitations based on available wireless network measurements. IEEE Signal. Process. Mag. 2005, 22, 41–53. [Google Scholar] [CrossRef]
- Kbar, G.; Mansoor, W. Mobile Station Location Based on Hybrid of Signal Strength and Time of Arrival. In Proceedings of the International Conference on Mobile Business (ICMB’05), Sydney, NSW, Australia, 11–13 July 2005; pp. 585–591. [Google Scholar]
- Sun, G.; Chen, J.; Guo, W.; Liu, K.R. Signal processing techniques in network-aided positioning: A survey of state-of-the-art positioning designs. IEEE Signal. Process. Mag. 2005, 22, 12–23. [Google Scholar] [CrossRef]
- Porretta, M.; Nepa, P.; Manara, G.; Giannetti, F. Location, location, location. IEEE Veh. Technol. Mag. 2008, 3, 20–29. [Google Scholar] [CrossRef]
- Enge, P.P.K. The Global Positioning System: Signals, measurements, and performance. Int. J. Wirel. Inf. Netw. 1994, 1, 83–105. [Google Scholar] [CrossRef]
- Patwari, N.; Ash, J.N.; Kyperountas, S.; Hero, A.; Moses, R.; Correal, N.S. Locating the nodes: Cooperative localization in wireless sensor networks. IEEE Signal. Process. Mag. 2005, 22, 54–69. [Google Scholar] [CrossRef]
- Thomas, F.; Ros, L. Revisiting trilateration for robot localization. IEEE Trans. Robot. 2005, 21, 93–101. [Google Scholar] [CrossRef]
- Liu, H.; Darabi, H.; Banerjee, P.; Liu, J. Survey of Wireless Indoor Positioning Techniques and Systems. IEEE Trans. Syst. Man Cybern. Part. C Appl. Rev. 2007, 37, 1067–1080. [Google Scholar] [CrossRef]
- Gezici, S. A Survey on Wireless Position Estimation. Wirel. Pers. Commun. 2008, 44, 263–282. [Google Scholar] [CrossRef]
- Sand, S.; Dammann, A.; Mensing, C. Position estimation. In Positioning in Wireless Communications Systems; Wiley: Hoboken, NJ, USA, 2014; pp. 69–99. [Google Scholar]
- Ahonen, S.; Eskelinen, P. Mobile terminal location for UMTS. IEEE Aerosp. Electron. Syst. Mag. 2003, 18, 23–27. [Google Scholar] [CrossRef]
- Vossiek, M.; Wiebking, L.; Gulden, P.; Wieghardt, J.; Hoffmann, C.; Heide, P. Wireless local positioning. IEEE Microw. Mag. 2003, 4, 77–86. [Google Scholar] [CrossRef]
- Guvenc, I.; Chong, C.-C. A Survey on TOA Based Wireless Localization and NLOS Mitigation Techniques. IEEE Commun. Surv. Tutor. 2009, 11, 107–124. [Google Scholar] [CrossRef]
- Hussain, S.A.; Emran, M.; Salman, M.; Shakeel, U.; Naeem, M.; Ahmed, S.; Azeem, M. Positioning a mobile subscriber in a cellular network system based on signal strength. IAENG Int. J. Comput. Sci. 2007, 34, 245–250. [Google Scholar]
- Pradhan, S.; Hwang, S.-S. Mathematical analysis of line intersection algorithm for TOA trilateration method. In Proceedings of the 2014 Joint 7th International Conference on Soft Computing and Intelligent Systems (SCIS) and 15th International Symposium on Advanced Intelligent Systems (ISIS), Kitakyushu, Japan, 3–6 December 2014; pp. 1219–1223. [Google Scholar]
- Pradhan, S.; Pyun, J.-Y.; Kwon, G.-R.; Shin, S.; Hwang, S.-S. Enhanced location detection algorithms based on time of arrival trilateration. In Proceedings of the 2014 48th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 2–5 November 2014; pp. 1179–1183. [Google Scholar]
- Cheung, K.; So, H.; Ma, W.-K.; Chan, Y. Least Squares Algorithms for Time-of-Arrival-Based Mobile Location. IEEE Trans. Signal. Process. 2004, 52, 1121–1128. [Google Scholar] [CrossRef]
- Abramovich, Y.I.; Spencer, N.K. DOA estimation performance breakdown: A new approach to prediction and cure. In Proceedings of the 2002 11th European Signal Processing Conference, Toulouse, France, 3–6 September 2002; pp. 1–4. [Google Scholar]
- Van Trees, H.L. Optimum Array Processing: Part IV of Detection, Estimation, and Modulation Theory; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- Xu, W.; Baggeroer, A.; Richmond, C. Bayesian Bounds for Matched-Field Parameter Estimation. IEEE Trans. Signal. Process. 2004, 52, 3293–3305. [Google Scholar] [CrossRef]
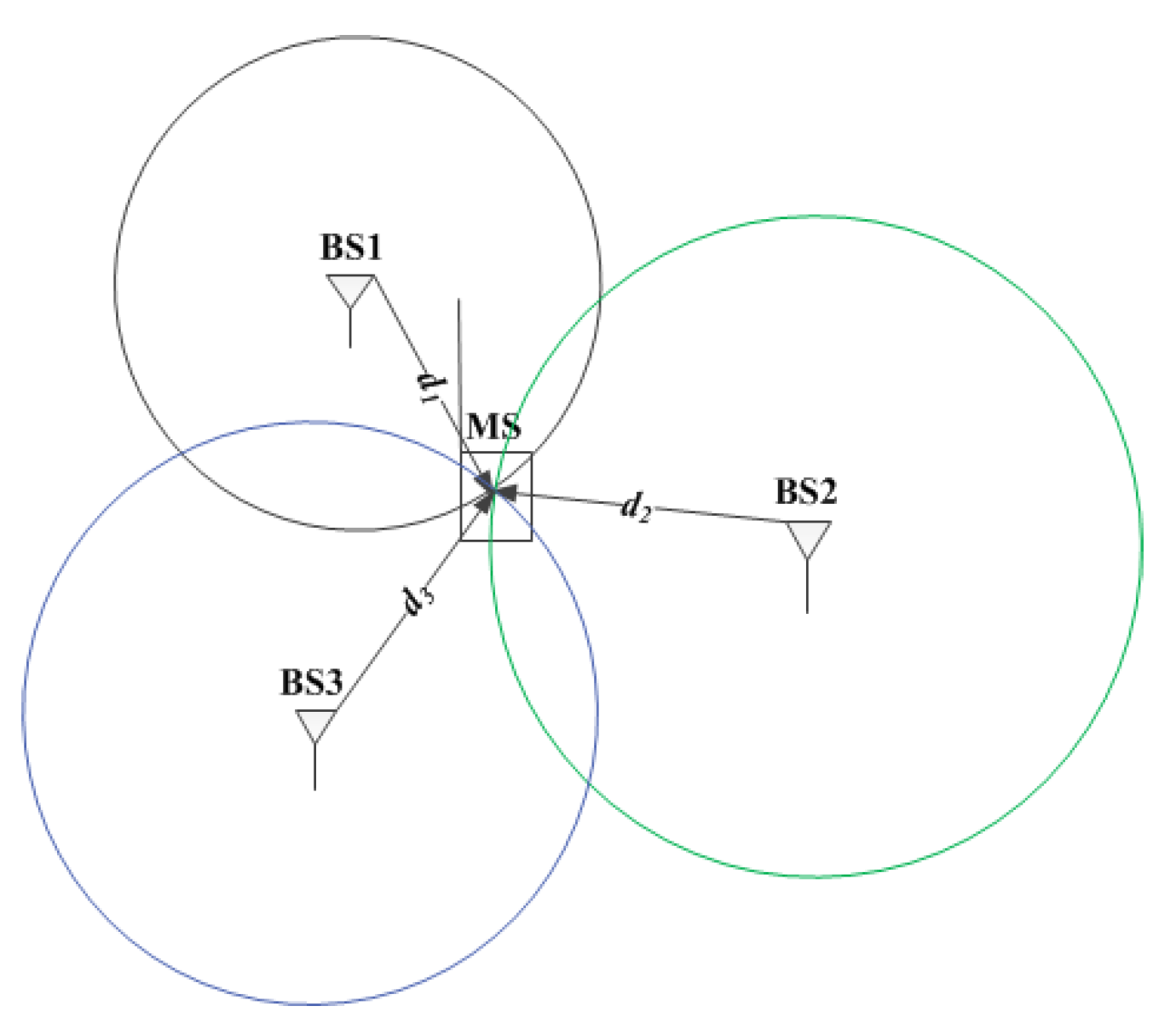
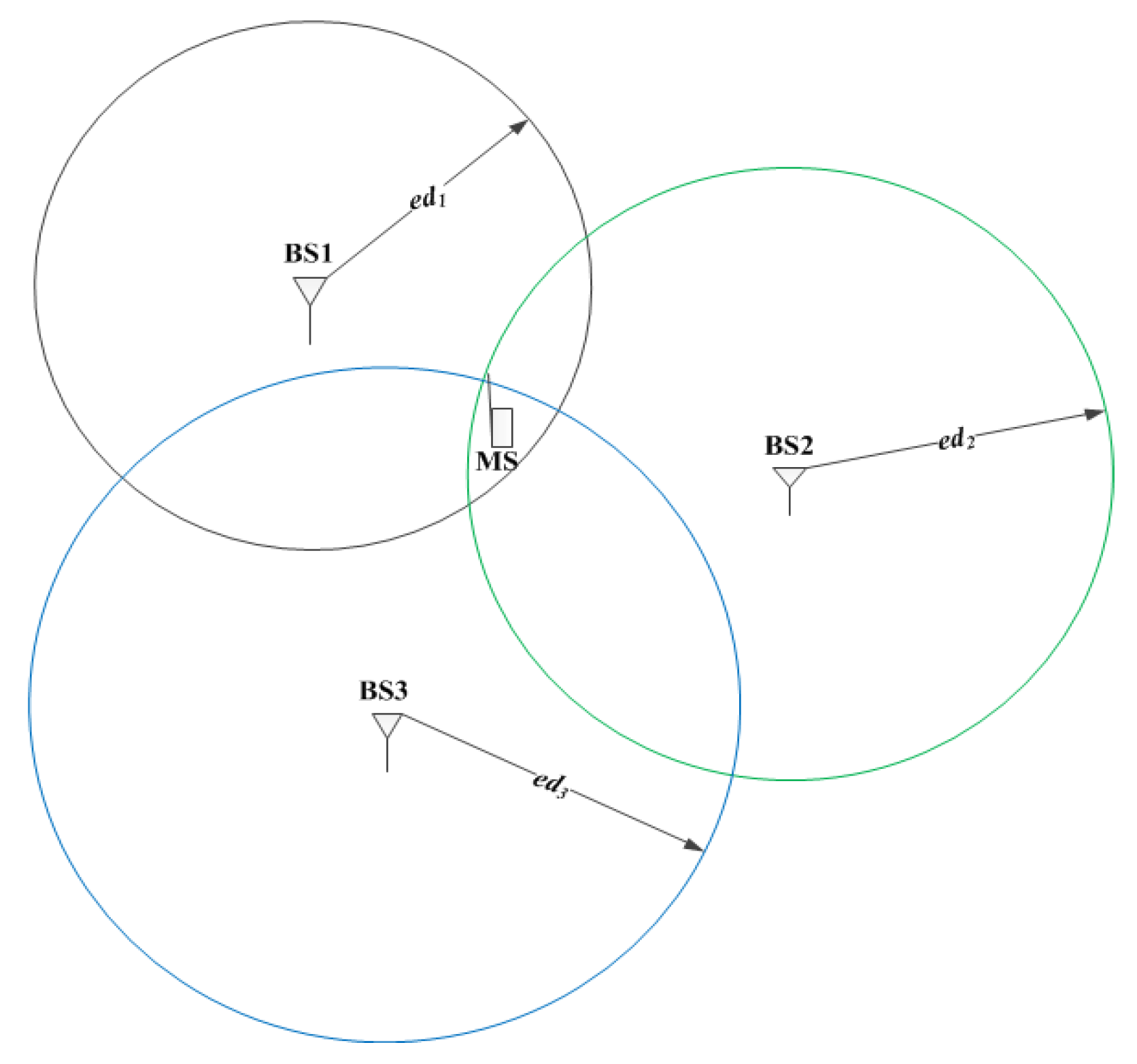
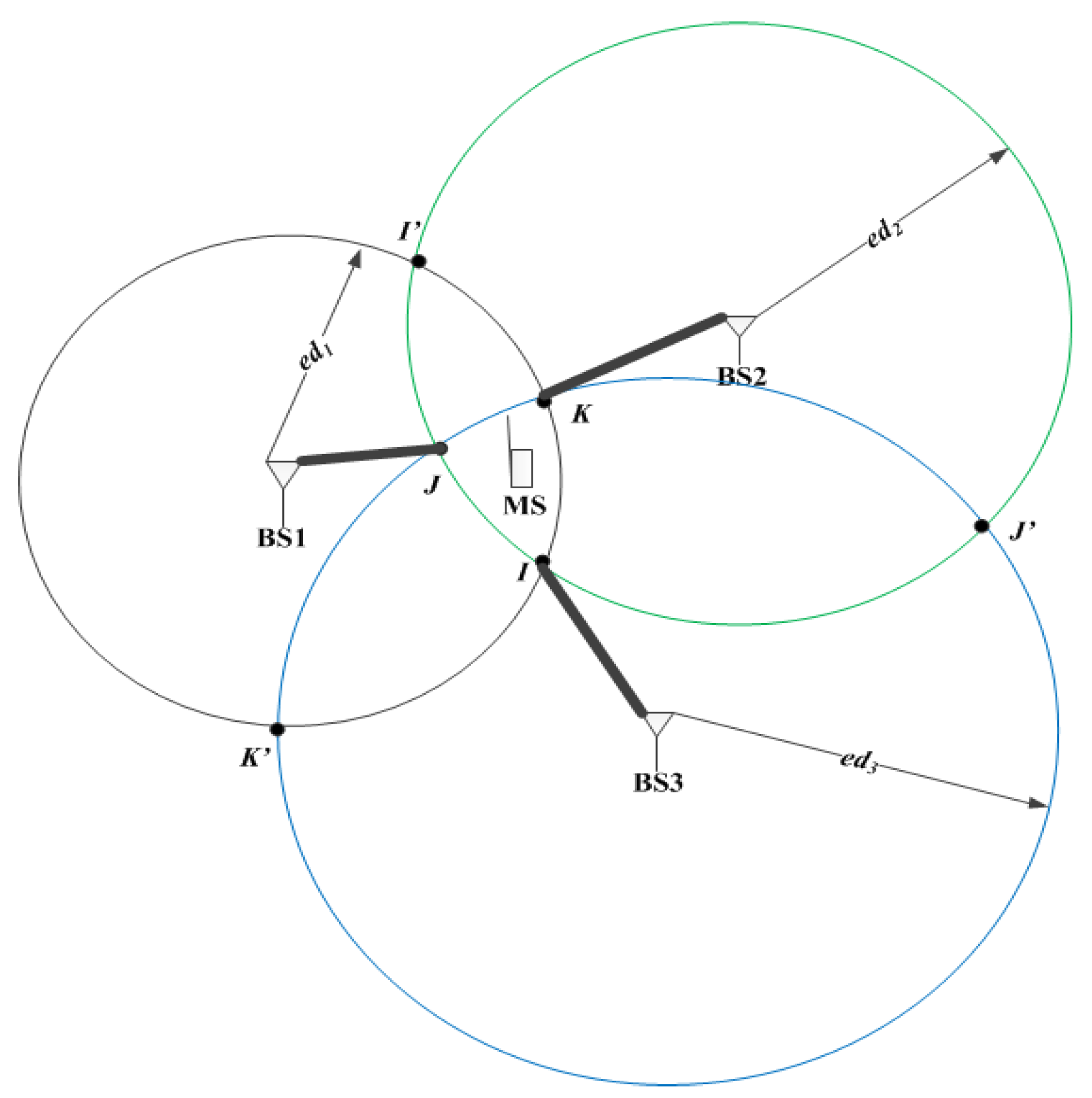
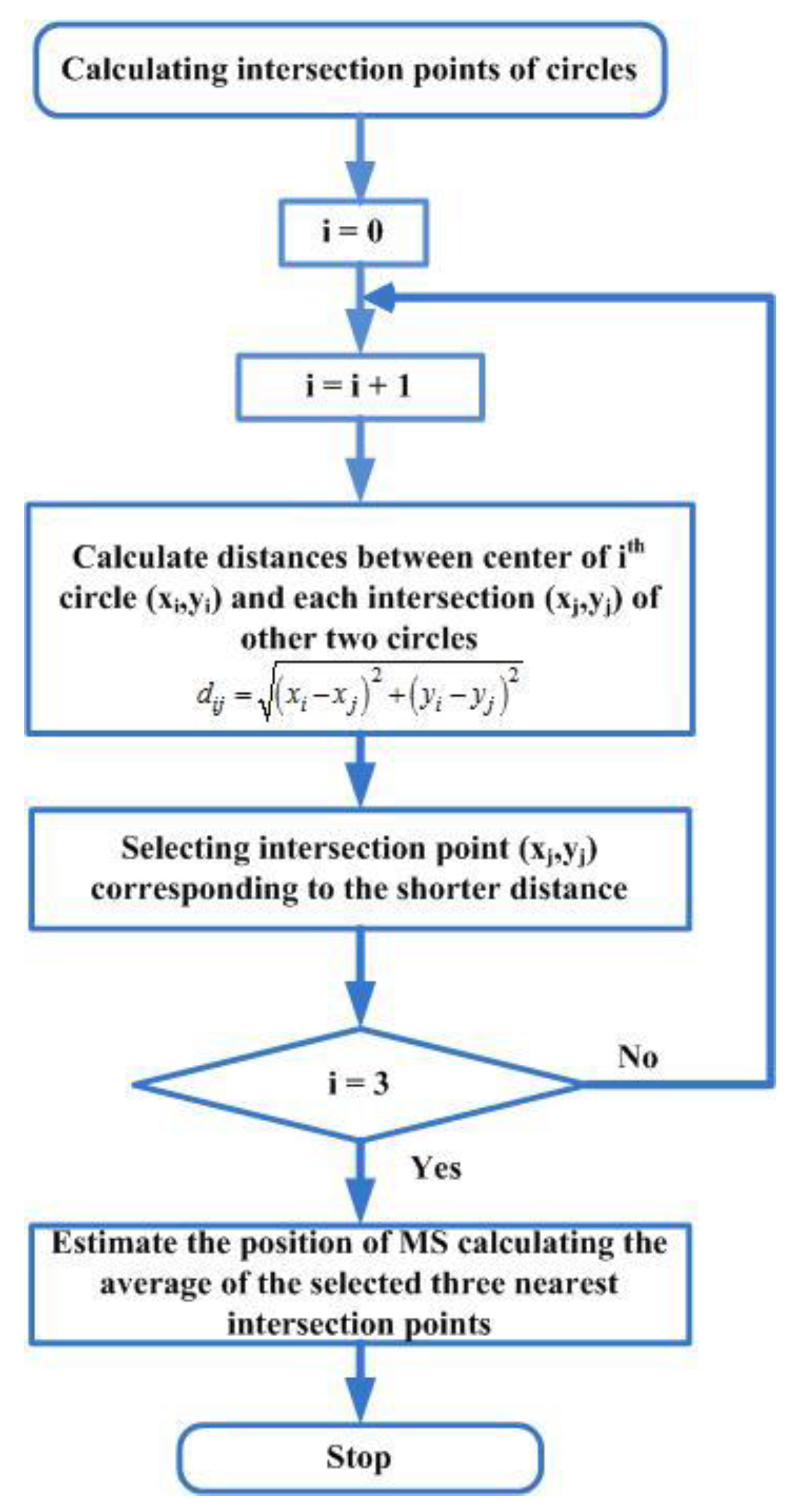


| 1. Initialize the circles c1, c2, and c3 of BSs with radii corresponding to the estimated distances , , and . The three estimated distances between BSs and MS are calculated by . 2. Find all six intersection coordinate points (I, I′, J, J′, K, and K′) formed by three circles of BS. 3. Calculate the distances between the center of the circle, c1 , and each intersection point formed by other circles of BSs (c2 and c3): . 4. Select the intersection point corresponding to the shorter distance from step 3. 5. Repeat step 3 and 4 for the center of circles, c2 and c3. 6. Decide the position of the MS by taking the average of the selected three points. 7. |
| 1. Calculate three estimated distances between each BS and MS using . 2. Generate three circle equations using the three estimated distances and center coordinates of BSs: , where , , and . 3. Determine the location of the MS, , using and . |
| Cases | Specific Sampling Rates | Specific MSE Values (m) | ||
|---|---|---|---|---|
| Line Intersection Algorithm | Shortest Distance Algorithm | Least Square Algorithm | ||
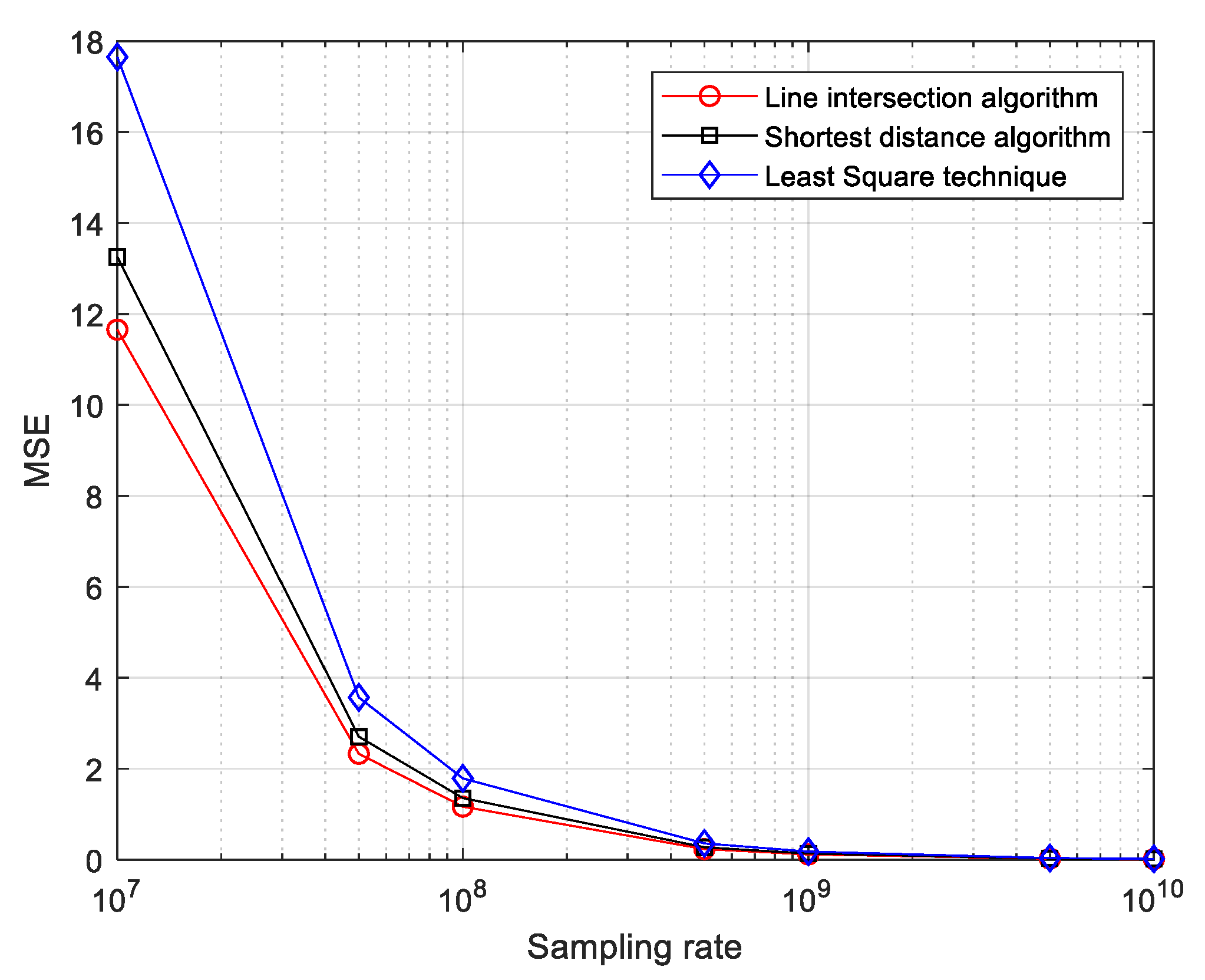
| First case | 10 MHz | 11.5800 | 12.4906 | 17.0327 |
| 100 MHz | 1.1587 | 1.2717 | 1.7204 | |
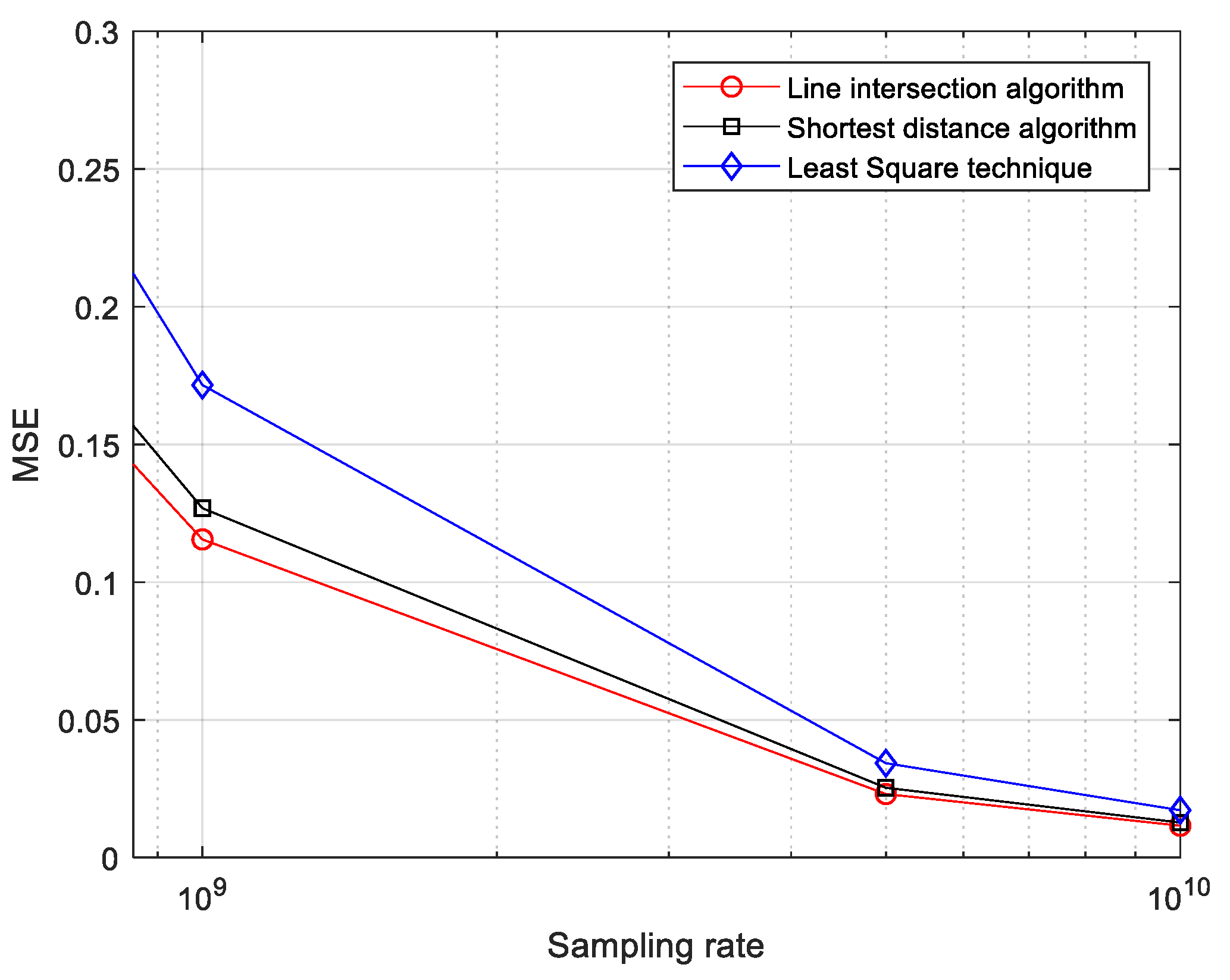
| 1 GHz | 0.1155 | 0.1268 | 0.1716 | |
| 10 GHz | 0.0116 | 0.0127 | 0.0172 | |
| Second case | 10 MHz | 11.6557 | 13.2552 | 17.6510 |
| 100 MHz | 1.1662 | 1.3548 | 1.7876 | |
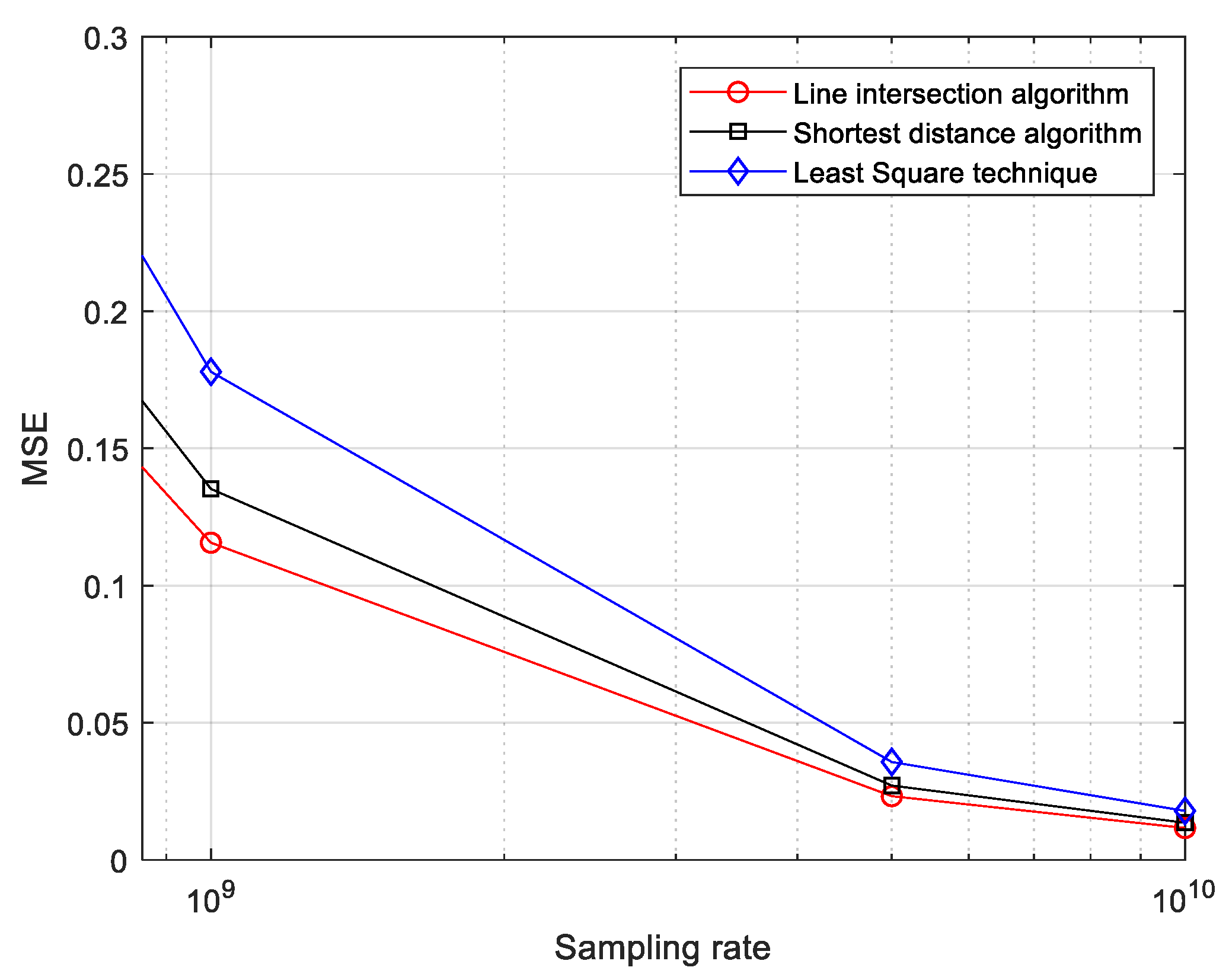
| 1 GHz | 0.1156 | 0.1352 | 0.1779 | |
| 10 GHz | 0.0116 | 0.0135 | 0.0179 | |
| Third case | 10 MHz | 11.8168 | 15.0384 | 19.1257 |
| 100 MHz | 1.1772 | 1.5658 | 1.9590 | |
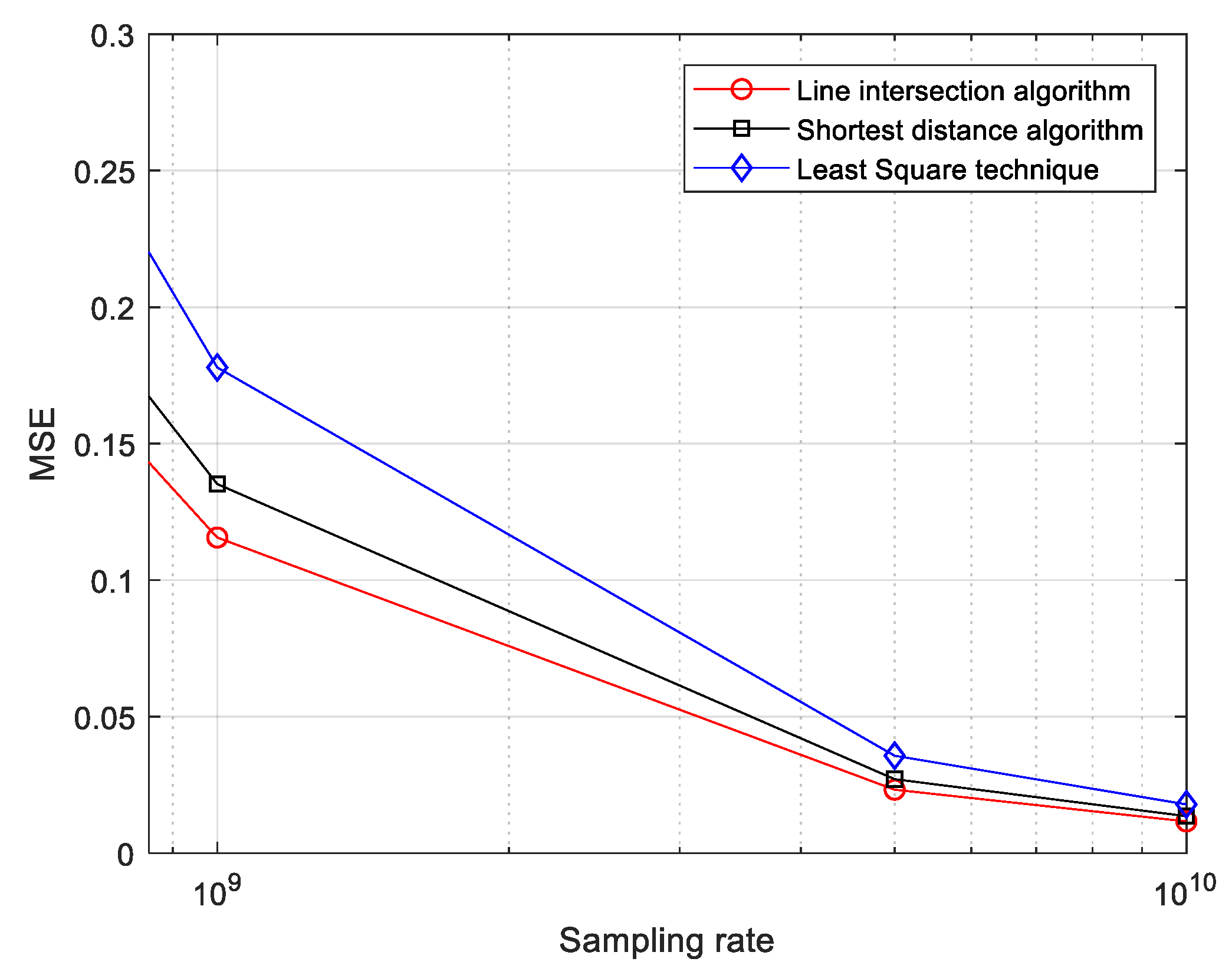
| 1 GHz | 0.1175 | 0.1562 | 0.1955 | |
| 10 GHz | 0.0118 | 0.0157 | 0.0196 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pradhan, S.; Hwang, S.-s.; Lee, D. Mathematical Analysis of Line Intersection and Shortest Distance Algorithms. Energies 2021, 14, 1492. https://doi.org/10.3390/en14051492
Pradhan S, Hwang S-s, Lee D. Mathematical Analysis of Line Intersection and Shortest Distance Algorithms. Energies. 2021; 14(5):1492. https://doi.org/10.3390/en14051492
Chicago/Turabian StylePradhan, Sajina, Suk-seung Hwang, and Dongbin Lee. 2021. "Mathematical Analysis of Line Intersection and Shortest Distance Algorithms" Energies 14, no. 5: 1492. https://doi.org/10.3390/en14051492
APA StylePradhan, S., Hwang, S.-s., & Lee, D. (2021). Mathematical Analysis of Line Intersection and Shortest Distance Algorithms. Energies, 14(5), 1492. https://doi.org/10.3390/en14051492







