Simplified Transition and Turbulence Modeling for Oscillatory Pipe Flows
Abstract
1. Introduction
2. Modeling Methods and Rationale
2.1. Mass Conservation
2.2. Turbulence Modeling
2.3. Transition and Relaminarization Modeling
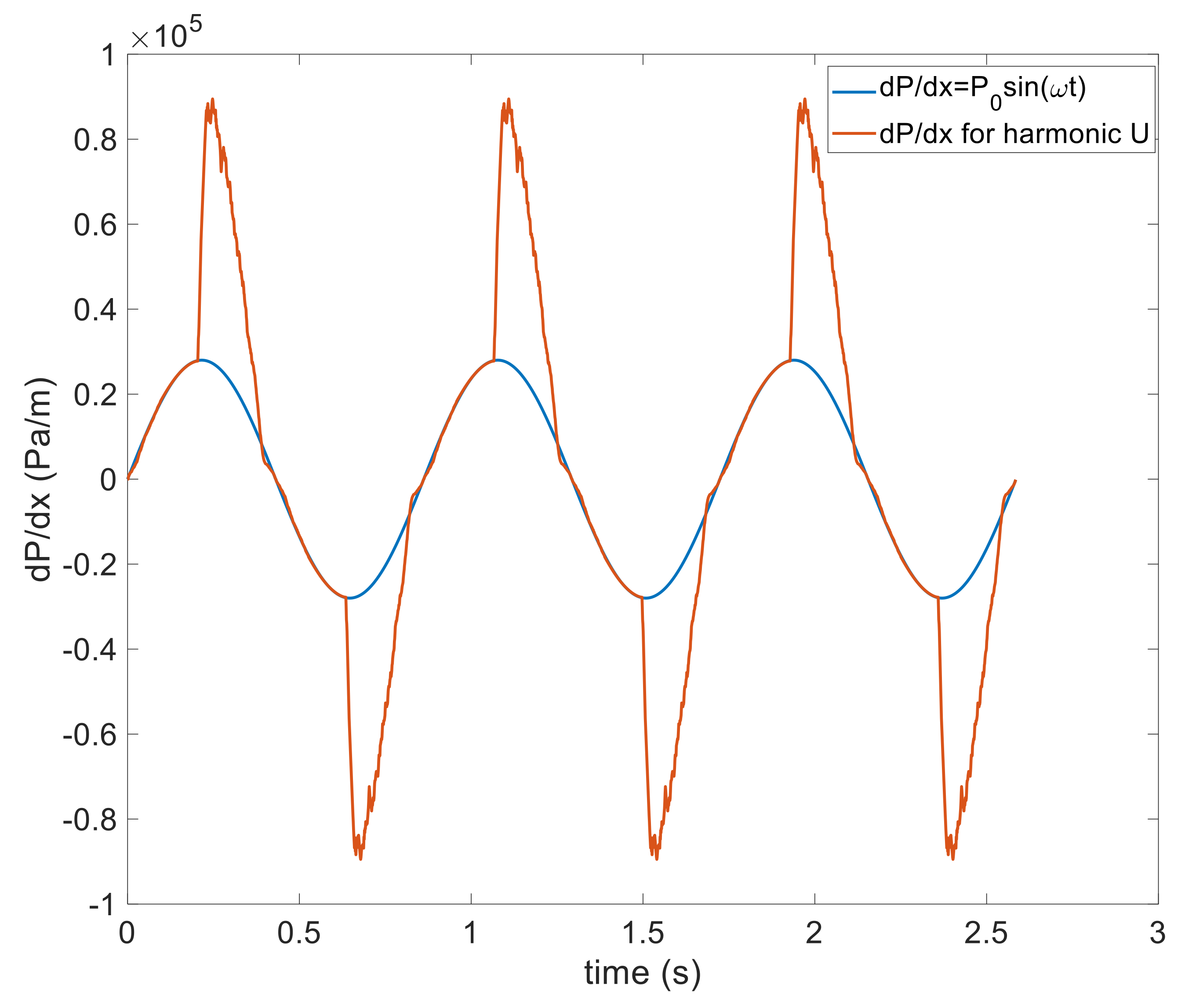
2.4. Enforcing Harmonic Average Bulk Flow
2.5. Two-Dimensional Unsteady Computations
3. Computational Results
3.1. Conditionally and Critically Turbulent Regime
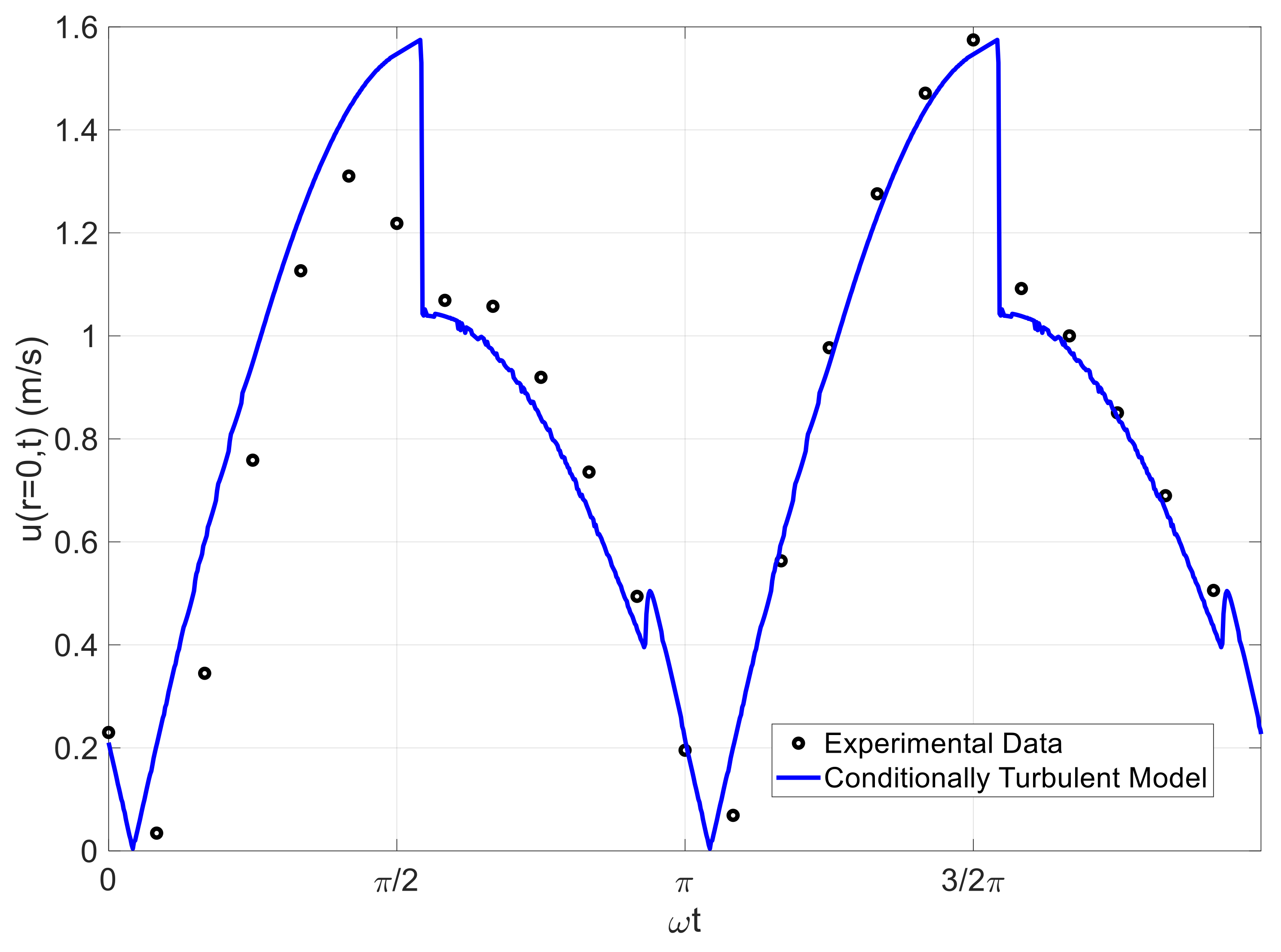
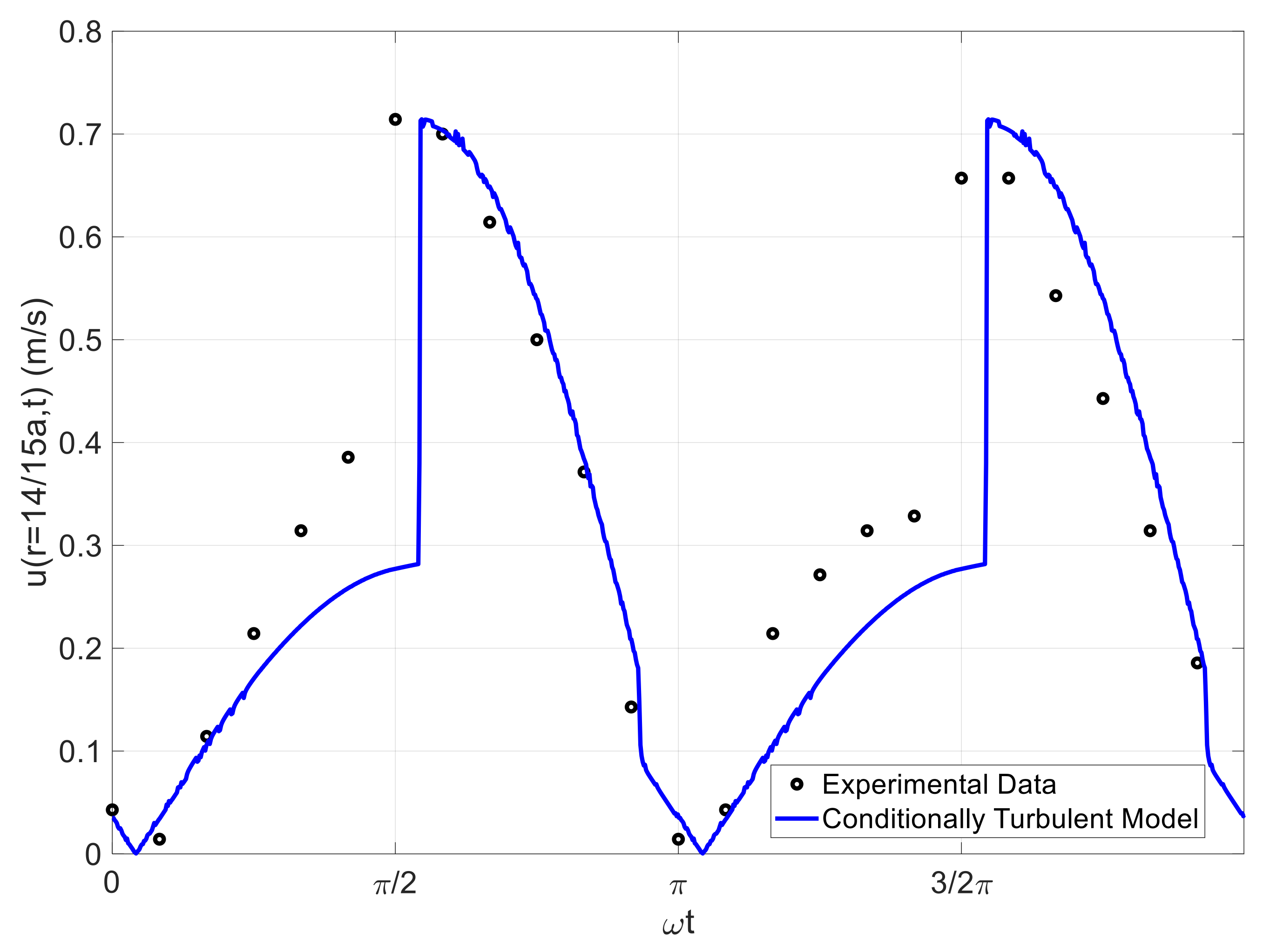
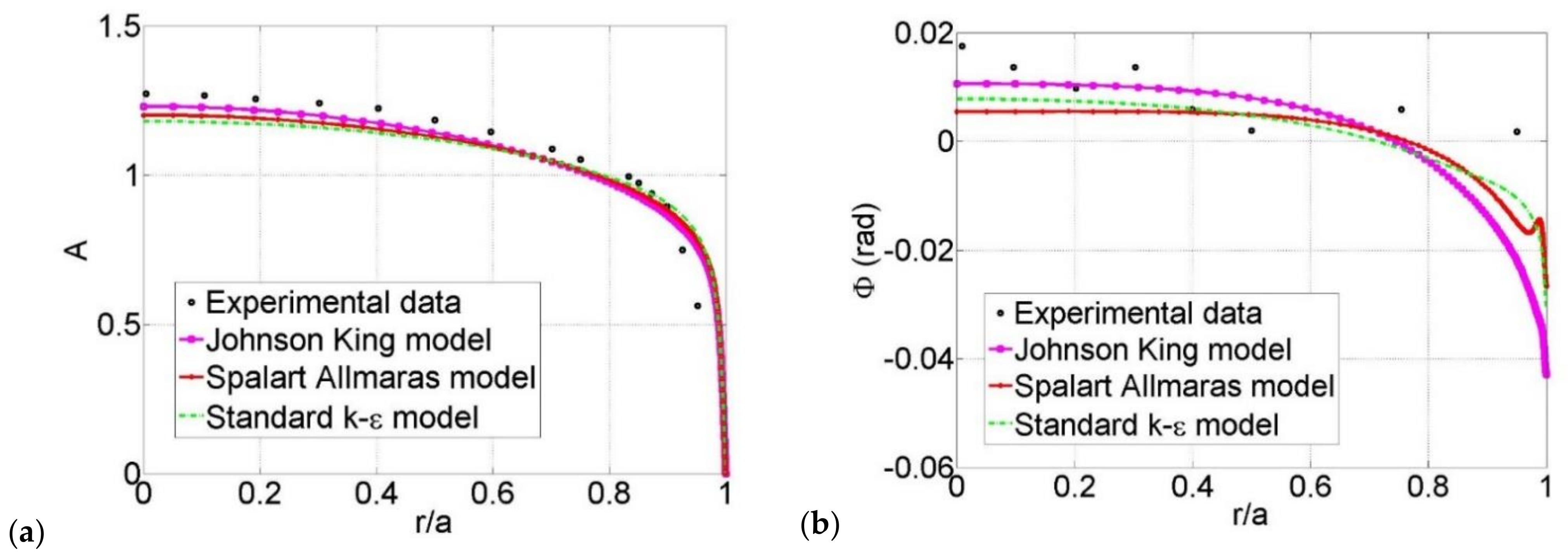
3.2. Comparisons to Phase-Averaged Data
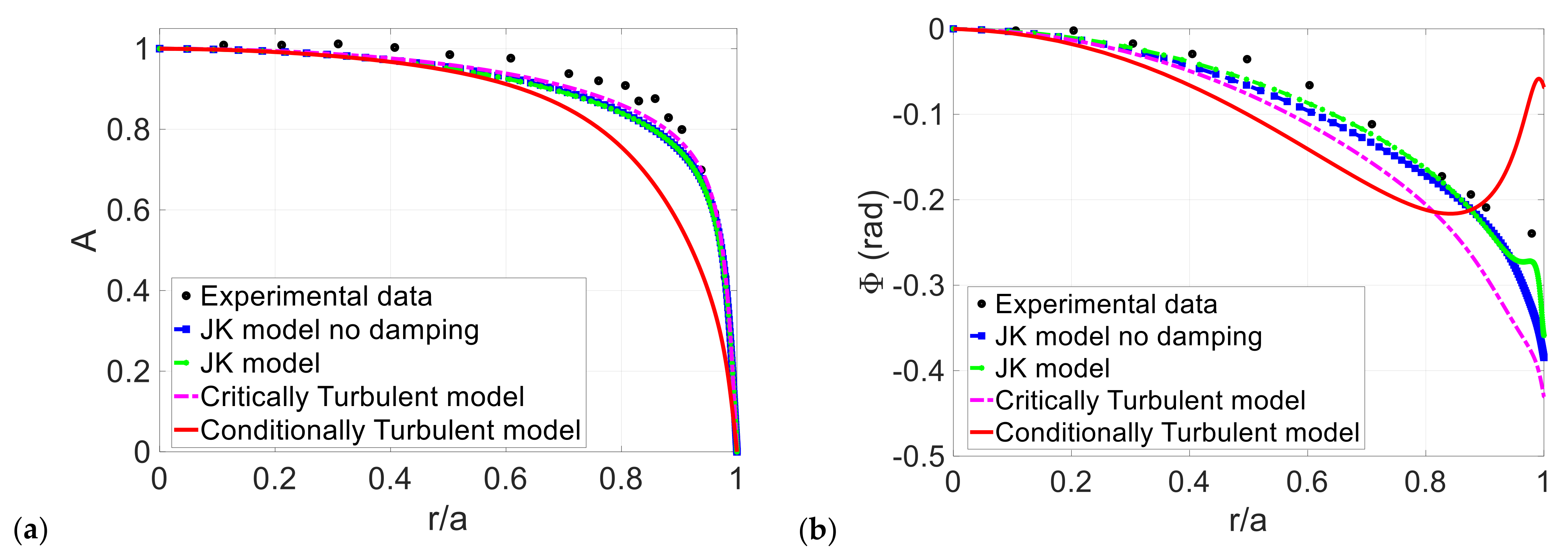
3.3. The Turbulent Womersley Number
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| A(r) | velocity cross-sectional amplitude ratio |
| A+ | van Driest damping parameter |
| a | pipe radius |
| D | near-wall damping term, |
| d | pipe diameter |
| k | constant in relation between Reos and α. |
| L | pipe length |
| lm | turbulent mixing length |
| P | pressure |
| ∆P | pressure difference |
| P0 | amplitude of the oscillating pressure gradient |
| p+ | non-dimensional pressure gradient |
| normalized pressure gradient, defined in Equation (14) | |
| Q(t) | Time-dependent bulk volumetric flowrate |
| Reos | peak oscillatory Reynolds number |
| r | radial coordinate |
| t | time |
| t+ | non-dimensional time |
| phase-averaged bulk velocity | |
| Uos | phase-averaged bulk velocity amplitude |
| u(r,t) | local phase-averaged axial velocity |
| uos | local phase-averaged velocity amplitude |
| uτ | friction velocity |
| u+ | non-dimensional velocity |
| phase-averaged Reynolds stress | |
| x | axial coordinate |
| y | distance from the wall |
| y+ | dimensionless distance from the wall |
| α | Womersley number |
| β | outer-layer empirical constant, 0.08 |
| Stokes parameter | |
| Φ | velocity cross-sectional phase-shift relative to |
| κ | von Kármán constant, 0.4 |
| ρ | fluid density |
| ν | kinematic viscosity |
| νt | turbulent kinematic viscosity |
| τw | wall shear stress |
| ω | circular oscillation frequency |
References
- Radebaugh, R. Pulse tube cryocoolers. In Low Temperature and Cryogenic Refrigeration; Springer: Dordrecht, The Netherlands, 2003; Volume 99, pp. 415–434. [Google Scholar]
- McMahon, H.O.; Gifford, W.E. A new low-temperature gas expansion cycle—Part I. Adv. Cryog. Eng. 1960, 5, 354–366. [Google Scholar]
- Chan, C.K.; Nguyen, T.; Colbert, R.; Raab, J.; Ross, R.G., Jr.; Johnson, D.L. IMAS Pulse tube cooler development and testing. Cryocoolers 1999, 10, 139–147. [Google Scholar]
- Wollan, J.J.; Swift, G.W.; Backhaus, S.; Gardner, D.L. Development of a thermoacoustic natural gas liquefier. In Proceedings of the Conference 2002 AIChE New Orleans Meeting, New Orleans, LA, USA, 11–14 May 2002. [Google Scholar]
- Hino, M.; Sawamoto, M.; Takasu, S. Experiments on transition to turbulence in an oscillatory pipe flow. J. Fluid Mech. 1976, 75, 193–207. [Google Scholar] [CrossRef]
- Narasimha, R.; Sreenivasan, K.R. Relaminarization of fluid flows. Adv. Appl. Mech. 1979, 19, 221–309. [Google Scholar]
- Çarpınlıoğlu, M.Ö.; Özahi, E. An updated portrait of transition to turbulence in laminar pipe flows with periodic time dependence (a correlation study). Flow Turbul. Combust. 2012, 89, 691–711. [Google Scholar] [CrossRef]
- Sergeev, S.I. Fluid oscillations in pipes at moderate Reynolds numbers. Fluid Dyn. 1966, 1, 121–122. [Google Scholar] [CrossRef]
- Ohmi, M.; Iguchi, M.; Kakehashi, K.; Masuda, T. Transition to turbulence and velocity distributions in an oscillating pipe flow. Bull. JSME 1982, 25, 365–371. [Google Scholar] [CrossRef]
- Ohmi, M.; Iguchi, M. Critical Reynolds number in an oscillating pipe flow. Bull. JSME 1982, 25, 165–172. [Google Scholar] [CrossRef]
- Eckmann, D.M.; Grotberg, J.B. Experiments on transition to turbulence in oscillatory pipe flow. J. Fluid Mech. 1991, 222, 329–350. [Google Scholar] [CrossRef]
- Akhavan, R.; Kamm, R.D.; Shapiro, A.H. An investigation of transition to turbulence in bounded oscillatory Stokes flows—Part 1: Experiments. J. Fluid Mech. 1991, 225, 395–422. [Google Scholar] [CrossRef]
- Das, D.; Arakeri, J.H. Transition of unsteady velocity profiles with reverse flow. J. Fluid Mech. 1998, 374, 251–283. [Google Scholar] [CrossRef]
- Merkli, P.; Thomann, H. Transition to turbulence in oscillating pipe flow. J. Fluid Mech. 1975, 68, 567–575. [Google Scholar] [CrossRef]
- Zhao, T.S.; Cheng, P. Experimental studies of the onset of turbulence and frictional losses in an oscillatory pipe flow. Heat Fluid Flow 1996, 17, 356–362. [Google Scholar] [CrossRef]
- Lodahl, C.R.; Sumer, B.M.; Fredsøe, J. Turbulent combined oscillatory flow and current in a pipe. J. Fluid Mech. 1998, 373, 313–348. [Google Scholar] [CrossRef]
- Ahn, K.H.; Ibrahim, M.B. Laminar/turbulent oscillating flow in circular pipes. Int. J. Heat Fluid Flow 1992, 13, 340–346. [Google Scholar] [CrossRef]
- Walther, C.; Kuhl, H.-D.; Schulz, S. Numerical investigation on the heat transfer in turbulent oscillating pipe flow. Heat Mass Transf. 2000, 36, 135–141. [Google Scholar] [CrossRef]
- Feldmann, D.; Wagner, C. Direct numerical simulation of fully developed turbulent and oscillatory pipe flows at Reτ = 1440. J. Turbul. 2012, 13, 1–28. [Google Scholar] [CrossRef]
- Feldmann, D.; Wagner, C. On phase asymmetries in oscillatory pipe flow. In New Results in Numerical and Experimental Fluid Mechanics X; Dillmann, A., Heller, G., Krämer, E., Wagner, C., Breitsamter, C., Eds.; Notes on Numerical Fluid Mechanics and Multidisciplinary Design 132; Springer: Cham, Switzerland, 2018; pp. 113–122. [Google Scholar]
- Hanjalić, K.; Jakirlić, S.; Hadžić, I. Computation of oscillating turbulent flows at transitional re-numbers. In Turbulent Shear Flows 9; Springer: Berlin, Heidelberg, 1995; pp. 323–342. [Google Scholar]
- Spalart, P.R.; Baldwin, B.S. Direct simulation of a turbulent oscillating boundary layer. In Turbulent Shear Flows 6, Proceedings of the Selected Papers from the Sixth International Symposium on Turbulent Shear Flows, Université Paul Sabatier, Toulouse, France, 7–9 September 1987; Andre, J.-C., Cousteix, J., Durst, F., Launder, B.E., Schmidt, F.W., Whitelaw, J.H., Eds.; Springer: Berlin, Germany, 1989. [Google Scholar]
- Hino, M.; Kashiwayanagi, M.; Nakayama, A.; Hara, T. Experiments on the turbulence statistics and the structure of a reciprocating oscillatory flow. J. Fluid Mech. 1983, 131, 363–399. [Google Scholar] [CrossRef]
- Sumer, B.M.; Jensen, B.L.; Fredsøe, J. Turbulence in oscillatory boundary layers. In Advances in Turbulence; Comte-Bellot, G., Mathieu, J., Eds.; Springer: Berlin/Heidelberg, Germany, 1987; pp. 556–567. [Google Scholar]
- Ghodke, C.; Apte, S. DNS study of particle-bed-turbulence interactions in an oscillatory wall-bounded flow. J. Fluid Mech. 2016, 792, 232–251. [Google Scholar] [CrossRef]
- Ghodke, C.D.; Apte, S.V. Roughness effects on the second-order turbulence statistics in oscillatory flows. Comput. Fluids 2018, 162, 160–170. [Google Scholar] [CrossRef]
- Greenblatt, D. Hybrid turbulence model for unsteady boundary layers. AIAA J. 1998, 36, 481–484. [Google Scholar] [CrossRef]
- Johnson, D.; King, L. A mathematically simple turbulence closure model for attached and separated turbulence boundary layers. AIAA J. 1985, 23, 1684–1692. [Google Scholar] [CrossRef]
- Mao, Z.X.; Hanratty, T.J. Studies of the wall shear stress in a turbulent pulsating pipe flow. J. Fluid Mech. 1986, 170, 545–564. [Google Scholar] [CrossRef]
- Spalart, P.R.; Allmaras, S.R. A one-equation turbulence model for aerodynamic flows. In Proceedings of the 30th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1992. [Google Scholar]
- Sexl, T. Über den von E. G. Richardson entdeckten Annulareffekt. Z. Physik 1930, 61, 349–362. [Google Scholar]
- Duan, Z.; Yovanovich, M.M.; Muzychka, Y.S. Pressure drop for fully developed turbulent flow in circular and non-circular ducts. J. Fluid Eng. 2012, 134, 6. [Google Scholar] [CrossRef]
- Schlichting, H. Boundary Layer Theory; McGraw-Hill: New York, NY, USA, 1979. [Google Scholar]
- Greenblatt, D.; Moss, E.A. Rapid temporal acceleration of a turbulent pipe flow. J. Fluid Mech. 2004, 514, 65–75. [Google Scholar] [CrossRef]
- Greenblatt, D.; Moss, E.A. Pipe-flow relaminarization by temporal acceleration. Phys. Fluids 1999, 11, 3478–3481. [Google Scholar] [CrossRef]
- Akhavan, R.; Kamm, R.D.; Shapiro, A.H. An investigation of transition to turbulence in bounded oscillatory Stokes flows—Part 2: Numerical simulations. J. Fluid Mech. 1991, 225, 423–444. [Google Scholar] [CrossRef]
- Womersley, J.R. Method for the calculation of velocity, rate of flow and viscous drag in arteries when the pressure gradient is known. J. Physiol. 1955, 127, 553–563. [Google Scholar] [CrossRef] [PubMed]
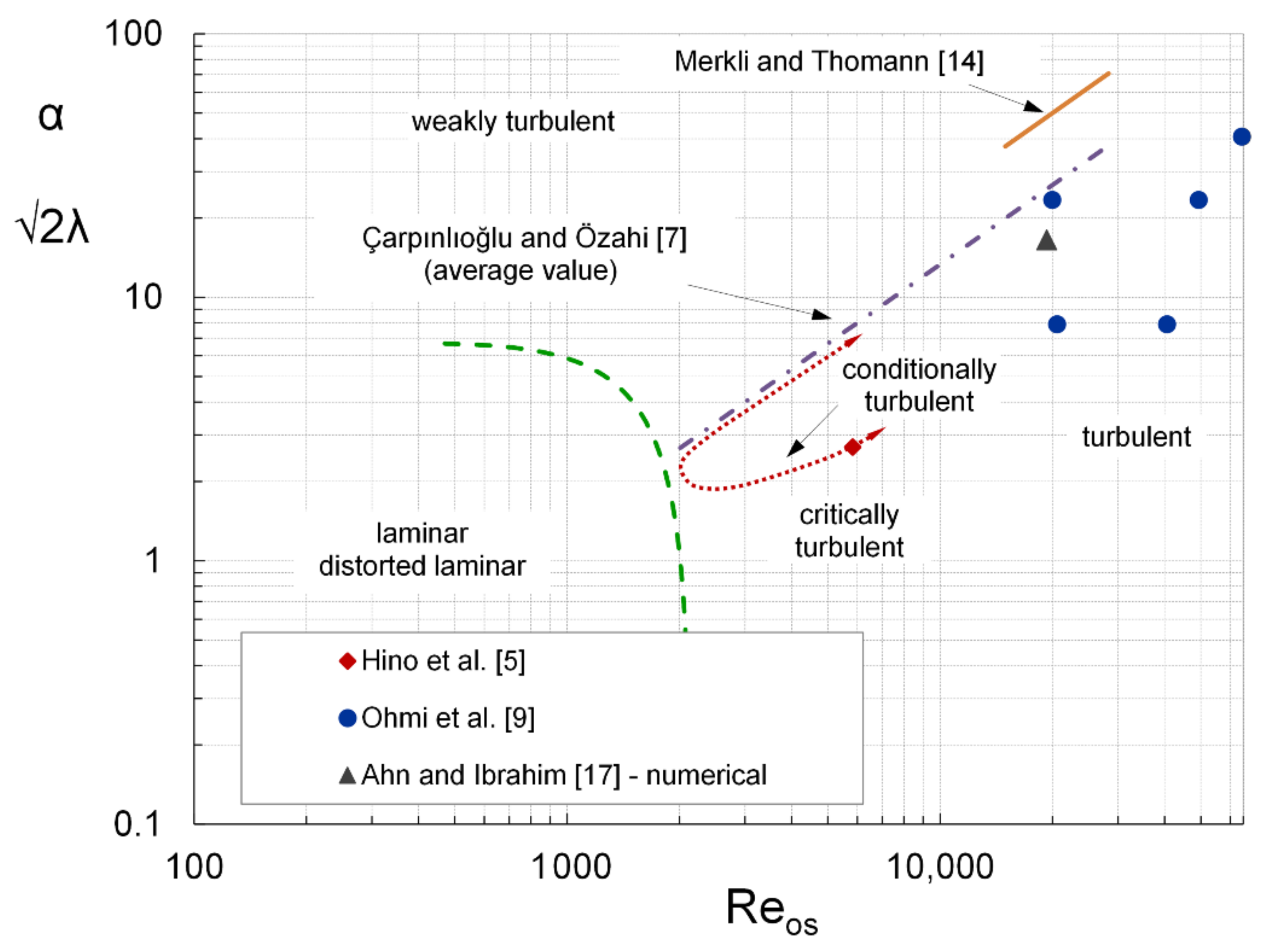
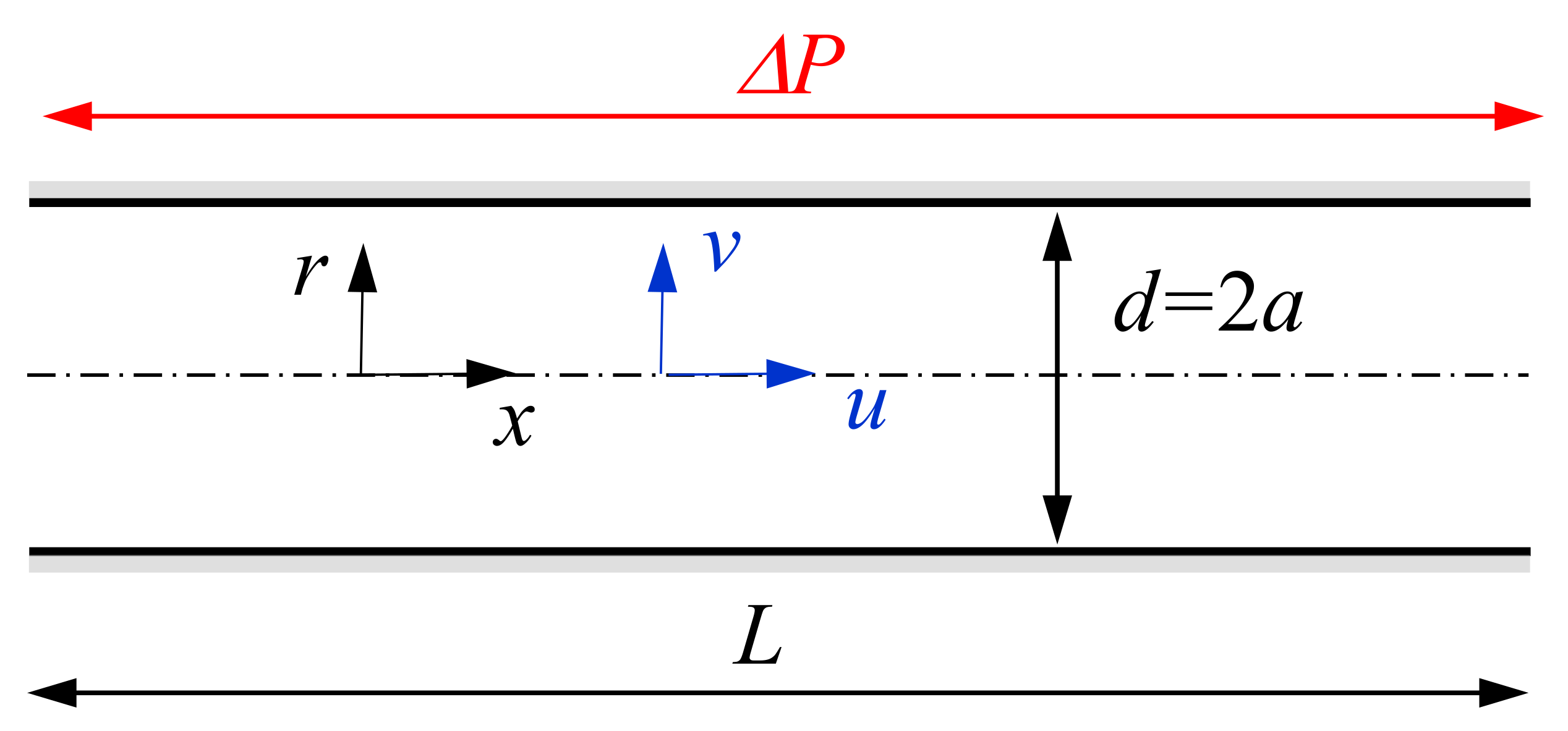
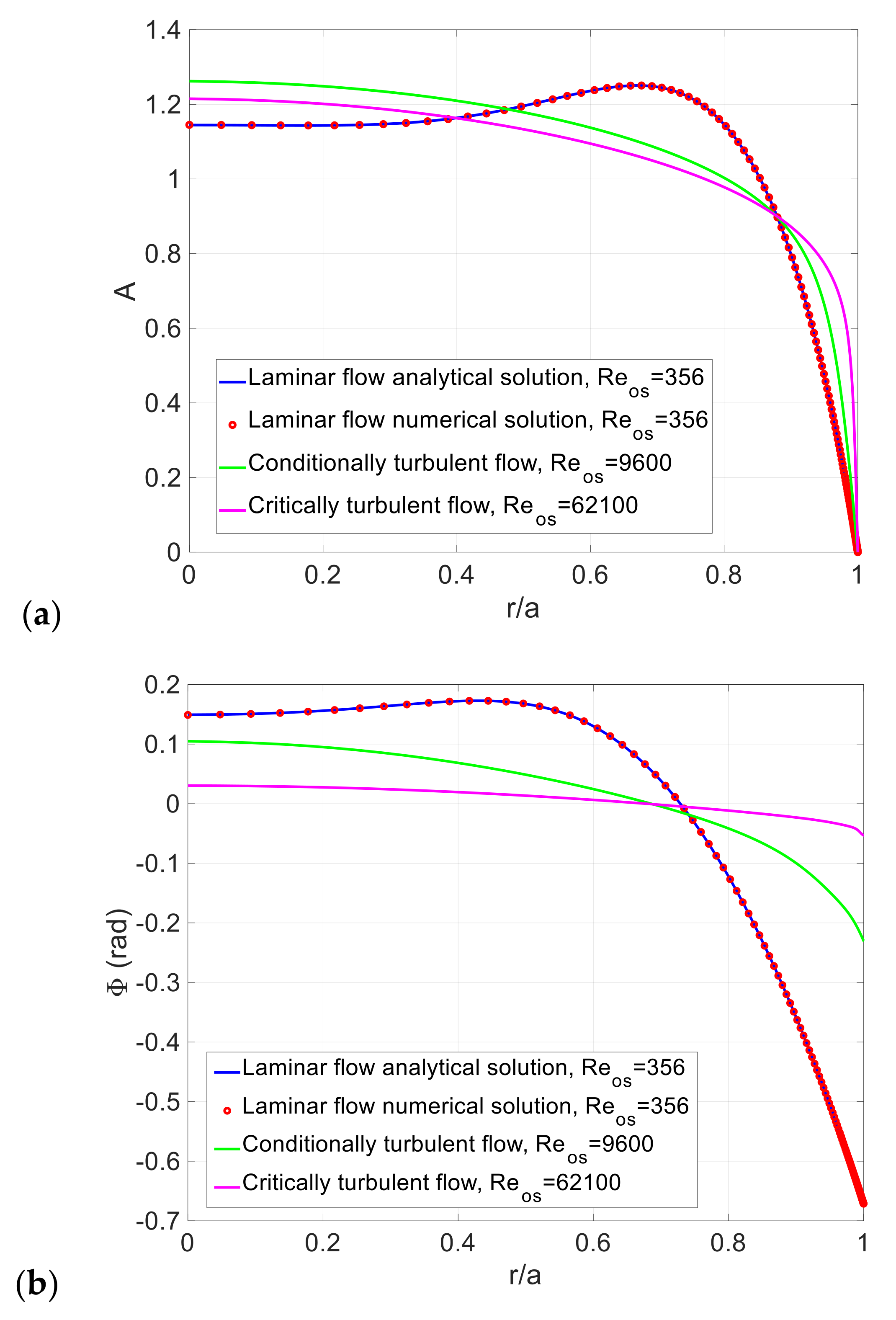
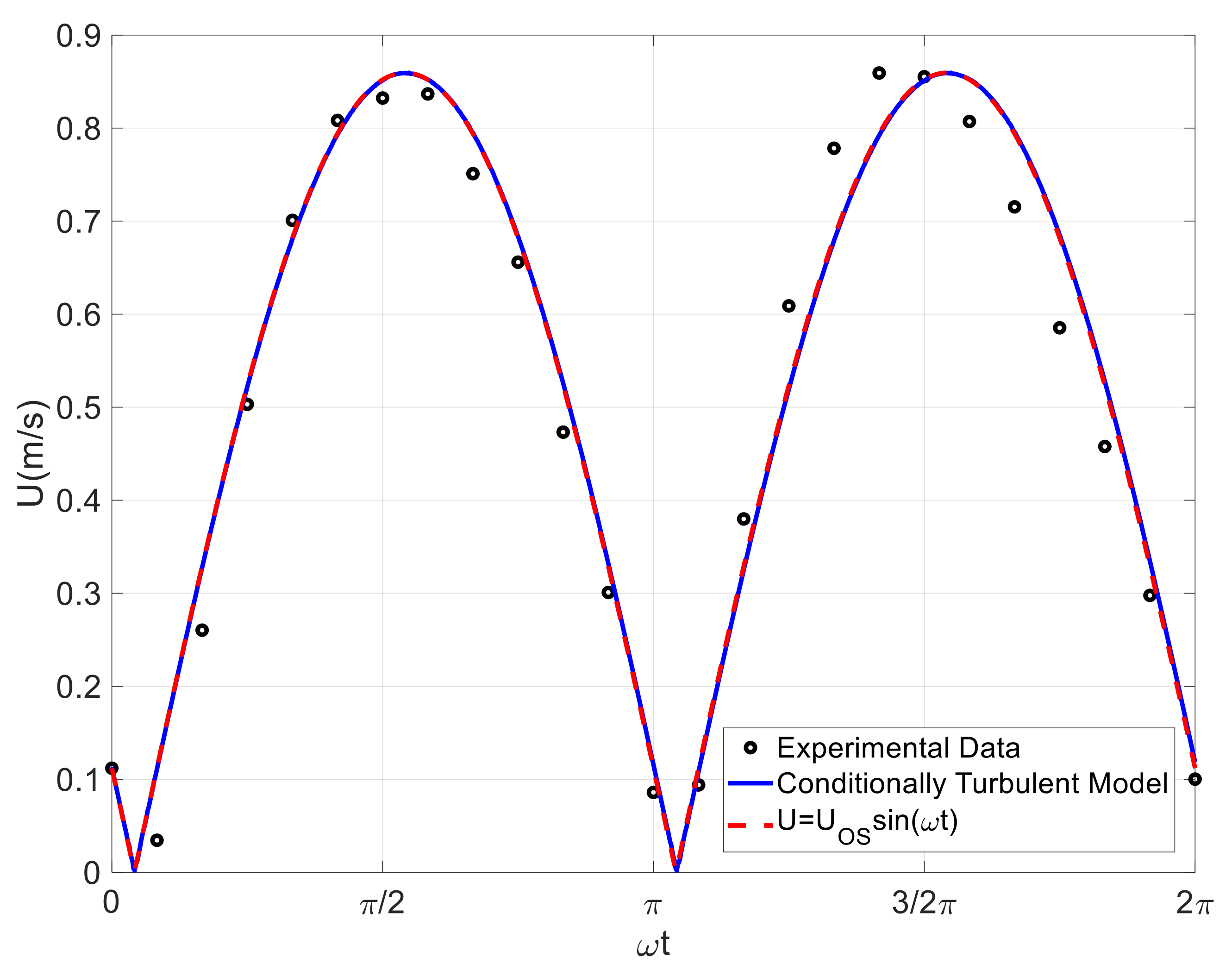
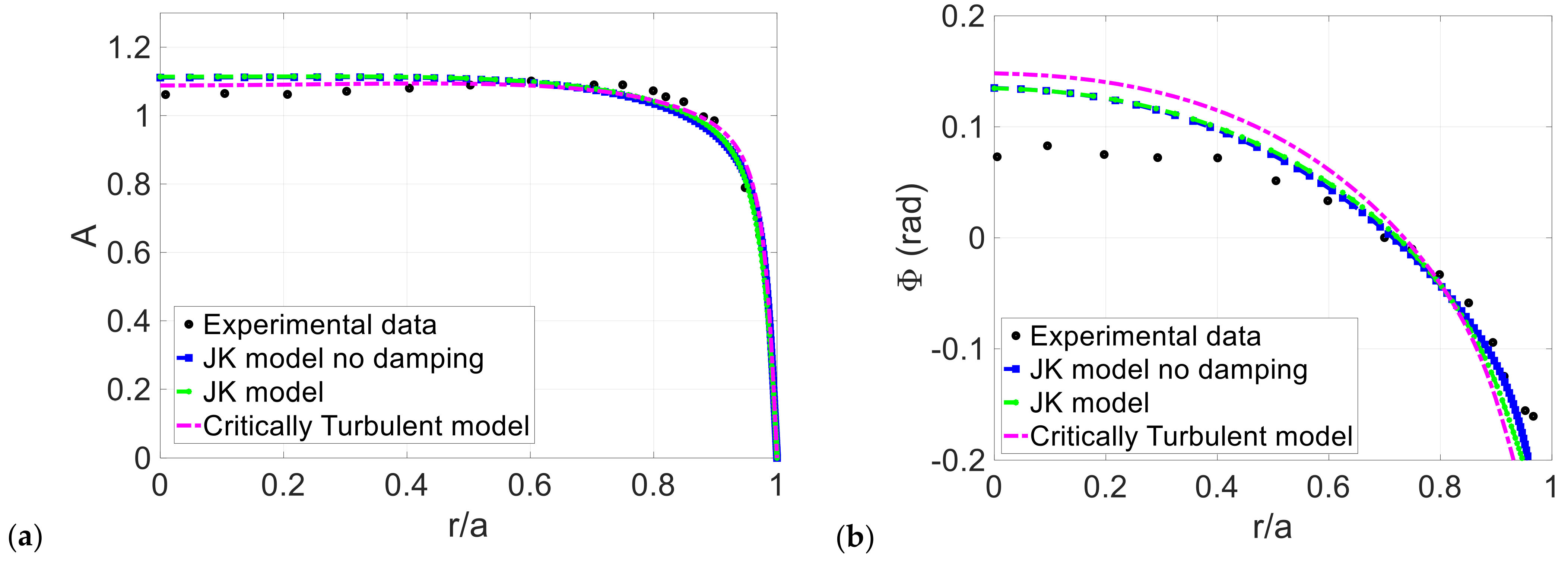
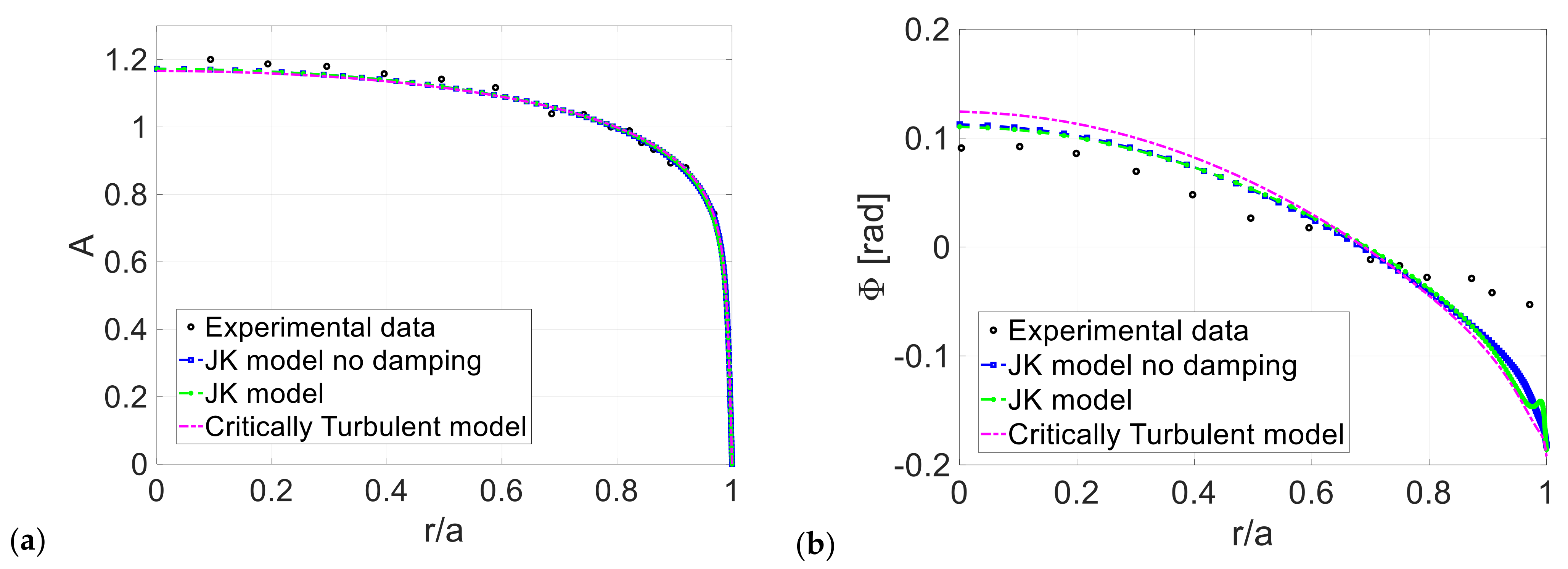
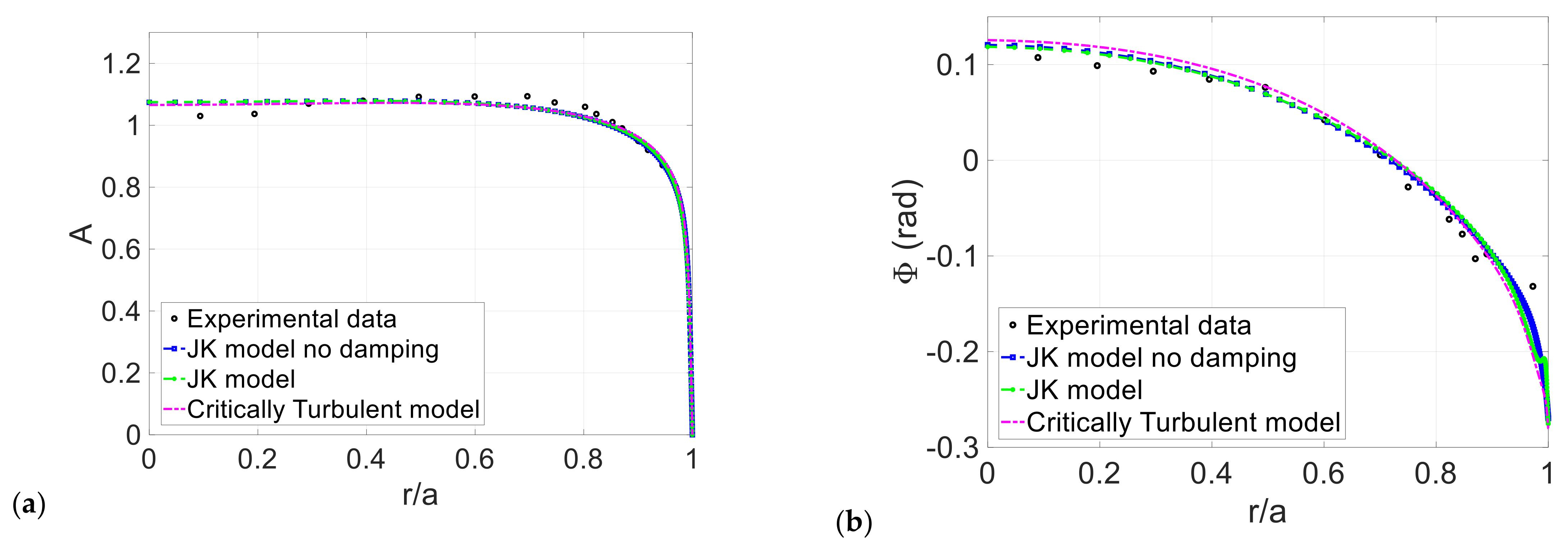
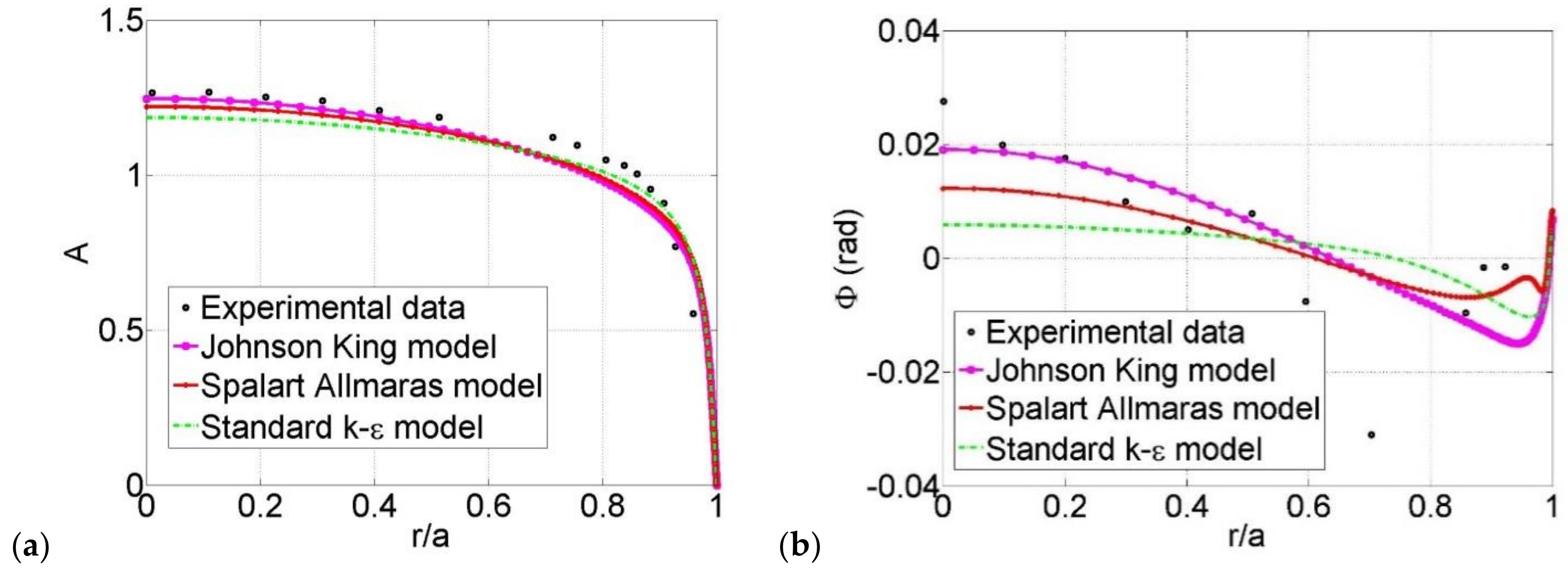
| Case | Reference | Reos | |
|---|---|---|---|
| 1 | Hino et al. [5] | 5830 | 2.70 |
| 2 | Ahn and Ibrahim [17] | 19,300 | 16.5 |
| 3 | Ohmi et al. [9] | 20,000 | 23.4 |
| 4 | Ohmi et al. [9] | 49,400 | 23.4 |
| 5 | Ohmi et al. [9] | 64,500 | 40.7 |
| 6 | Ohmi et al. [9] | 20,600 | 7.9 |
| 7 | Ohmi et al. [9] | 40,600 | 7.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shapiro, A.; Grossman, G.; Greenblatt, D. Simplified Transition and Turbulence Modeling for Oscillatory Pipe Flows. Energies 2021, 14, 1410. https://doi.org/10.3390/en14051410
Shapiro A, Grossman G, Greenblatt D. Simplified Transition and Turbulence Modeling for Oscillatory Pipe Flows. Energies. 2021; 14(5):1410. https://doi.org/10.3390/en14051410
Chicago/Turabian StyleShapiro, Alexander, Gershon Grossman, and David Greenblatt. 2021. "Simplified Transition and Turbulence Modeling for Oscillatory Pipe Flows" Energies 14, no. 5: 1410. https://doi.org/10.3390/en14051410
APA StyleShapiro, A., Grossman, G., & Greenblatt, D. (2021). Simplified Transition and Turbulence Modeling for Oscillatory Pipe Flows. Energies, 14(5), 1410. https://doi.org/10.3390/en14051410






