A Fully Meshless Approach to the Numerical Simulation of Heat Conduction Problems over Arbitrary 3D Geometries

Abstract

One of the goals of new CAE (Computer Aided Engineering) software is to reduce both time and costs of the design process without compromising accuracy. This result can be achieved, for instance, by promoting a “plug and play” philosophy, based on the adoption of automatic mesh generation algorithms. This in turn brings about some drawbacks, among others an unavoidable loss of accuracy due to the lack of specificity of the produced discretization. Alternatively it is possible to rely on the so called “meshless” methods, which skip the mesh generation process altogether. The purpose of this paper is to present a fully meshless approach, based on Radial Basis Function generated Finite Differences (RBF-FD), for the numerical solution of generic elliptic PDEs, with particular reference to time-dependent and steady 3D heat conduction problems. The absence of connectivity information, which is a peculiar feature of this meshless approach, is leveraged in order to develop an efficient procedure that accepts as input any given geometry defined by a stereolithography surface (.stl file format). In order to assess its performance, the aforementioned strategy is tested over multiple geometries, selected for their complexity and engineering relevance, highlighting excellent results both in terms of accuracy and computational efficiency. In order to account for future extensibility and performance, both node generation and domain discretization routines are entirely developed using Julia, an emerging programming language that is rapidly establishing itself as the new standard for scientific computing.

1. Introduction

Engineering design often involve the solution of some boundary value problem, e.g., heat conduction problems, with the aid of numerical approaches. Well-known Finite Volume (FVM) [1] and Finite Element (FEM) [2] methods are usually employed to discretize the governing equations, i.e., partial differential equations (PDEs), in order to obtain a finite dimensional problem that can be solved numerically.

The solution attained in the end is indeed bound to be just an approximation, due to an unavoidable loss of information that takes place already at this stage, and the quality of the discretization determines how much information is lost and how much is preserved.

Usually the discretization process begins with the creation of a mesh, i.e., a subdivision of the domain in many discrete cells, which is often generated by some computer algorithm under the supervision of a specialist. Sometimes, due to time and/or budget constraints, the mesh is automatically generated, and the designer is left free to focus on other topics. In both cases the key point is the introduction of a mesh in the formulation stage; therefore, any numerical method applied afterwards relies on the related connectivity information.

This procedure presents some important weaknesses [3], two of them are:

• the cost of the mesh creation and the size of the consequent data structure,
• the inability to allow large (geometric) deformations of the domain.

The first one refers to both computational and economical costs; indeed operator costs now outweigh the cost of CPU time for the computer [3], and if the operator intervention is avoided it becomes mandatory to use a finer automated mesh generation algorithm. This in turn gives as output a greater data structure and thus slows down successive numerical manipulations.

The second weakness becomes of interest in many practical cases, for example when the solver is paired with some optimization algorithm and the geometry is changed many times. At each step the mesh is degraded in quality, and even when morphing algorithms are employed, the solution becomes less reliable at every iteration. In some cases a periodic complete re-meshing of the domain becomes necessary.

These facts led to the development of various meshless or meshfree methods for the solution of partial differential equations over complex shaped domains encountered in practical problems [4,5,6,7]. Some authors have successfully experimented with the use of meshfree methods in order to enforce specific boundary conditions, for example Absorbing Boundary Conditions (ABCs), while the state equation is solved using the more traditional Finite Element Method (FEM) [8]. Meshfree methods are also destined to play a key role in the development of new implementations of peridynamic (PD) models, as shown in [9]. Numerical methods belonging to this class allow to skip the mesh generation procedure altogether and, therefore, overcome its inherent shortcomings.

Most meshless methods (also called meshfree methods) can be classified according to three different criteria [3]:

• according to the formulation procedure,
• according to the function approximation schemes, and
• according to the domain representation.

The common characteristic is the use of the so-called field nodes: at first a set of nodes is scattered over the domain (and/or over the boundaries). Then, shape functions are constructed for each node of interest and are based on selected local nodes; the shape functions can change when the node of interest changes [3].

This paper discusses the implementation of one such method and its integration with a novel node generation procedure. In order to reach maximum compatibility with commercial software, the domain is assumed as defined by a generic stereolithography (.stl) file, like those used in the fields of computer graphics and 3D printing. Furthermore the obtained data structure is more efficient than that of a traditional mesh, since it carries no information about the connectivity between nodes. To the best of the authors’ knowledge, this is the first time a fully meshless approach, based on the RBF-FD method, is employed for the accurate solution of heat conduction problems over arbitrary 3D domains defined by a generic stereolithography CAD file.

The greater geometric flexibility of truly meshless approaches is therefore fully leveraged, with the aim of making them more accessible and user-friendly in the future. More precisely, the RBF-generated Finite Differences (RBF-FD) method is employed [10,11], similar to the one described in [5]. This method has been successfully employed for solving various heat transfer problems [12,13,14,15]. Interested readers might also refer to [16] for further details and comparisons between the performance attained with different RBF schemes.

This method belongs to the following classes, according to the aforementioned classification criteria:

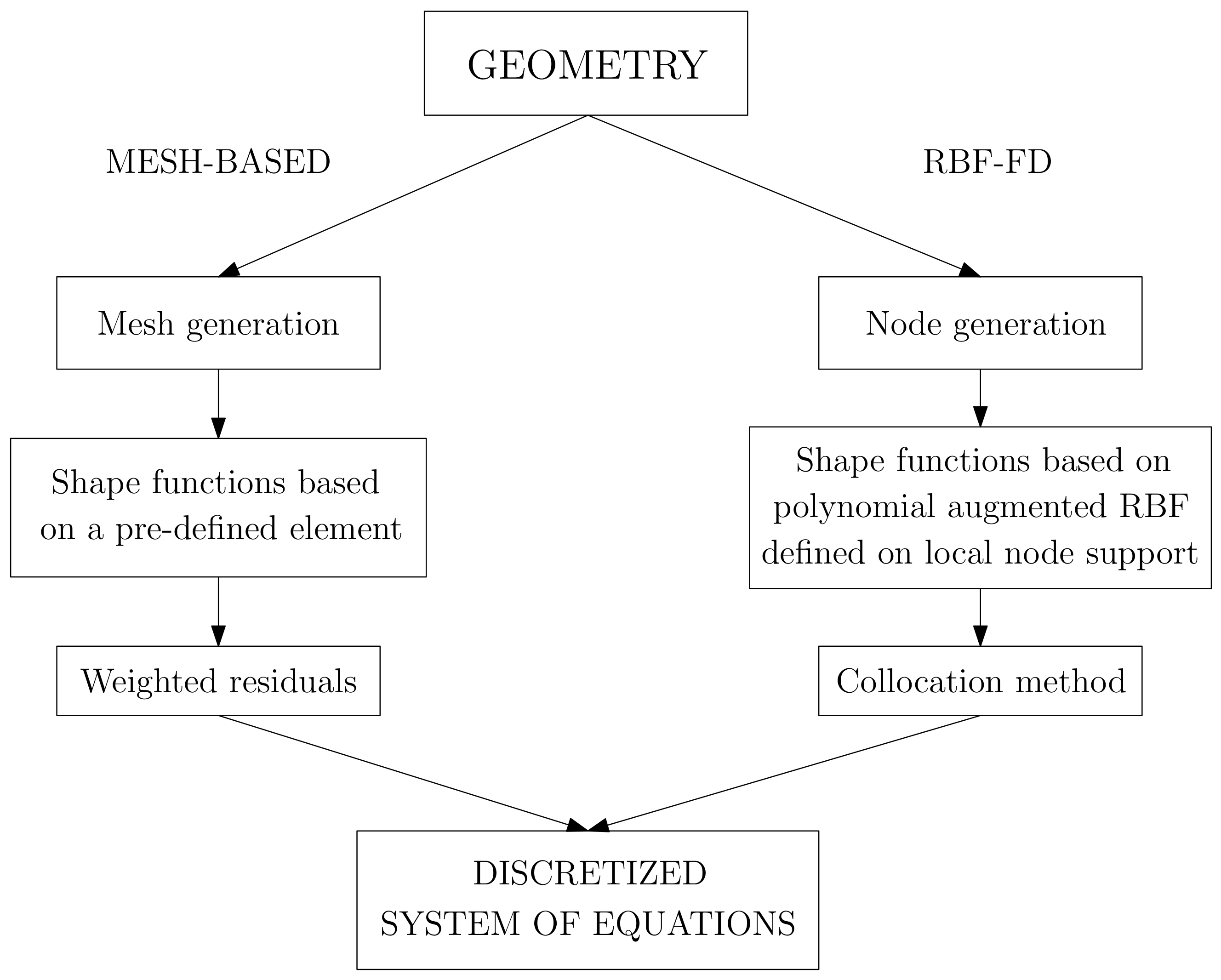
• formulation procedure: collocation technique. The problem to be solved is formulated in the strong form, i.e., strong forms of governing equations and boundary conditions are directly discretized at the field nodes.
• function approximation scheme: point interpolation (PIM). All functions are approximated at a certain node using RBFs defined on a compact support around the field nodes. In order to achieve greater accuracy and stability the RBF scheme is augmented with a polynomial term [17,18].
• domain representation: both domain and boundaries are represented by field nodes.

See Figure 1 for a schematic representation of the differences between the RBF-FD meshless method and traditional mesh-based methods. It must be remarked that the solution procedure is totally independent of the particular shape of such domain.

The whole code is developed using Julia programming language [19] and can be executed in parallel on multiple cores, allowing extensive code reuse and excellent computational performances already at the development stage.

Several tests over different 3D geometries with different boundary conditions will be presented in order to illustrate the numerical properties of the proposed truly meshless approach. Excellent results in terms of both accuracy and computational efficiency have been obtained in each of the presented cases, confirming the ability of RBF-FD method to easily deal with problems of engineering relevance.

2. Materials and Methods

2.1. Governing Equation

The generic heat equation with internal heat generation (see [20]) can be written in the form

$$\frac{\partial u}{\partial t}-△u=f$$

(1)

In this paper the steady-state version of Equation (1) will be considered; therefore, the governing equations are given by the following boundary value problem:

$$\left\{\begin{array}{cc}-△u=f\hfill & in\Omega \hfill \\ au+b\frac{\partial u}{\partial n}=g\hfill & on\partial \Omega \hfill \end{array}\right.$$

(2)

where $\Omega$ is an open subset of ${\mathbb{R}}^3$ and $\partial \Omega$ its boundary; f, a, b, and g are known functions; and n is the unit normal vector of $\partial \Omega$. The second equation in (2) represents, therefore, a boundary condition (b.c.).

The presented method can also be employed to solve transient heat conduction problems, as well as generic heat transfer problems with time-dependent behavior, allowing the implementation of standard explicit or implicit time integration schemes as shown in [7,13,21].

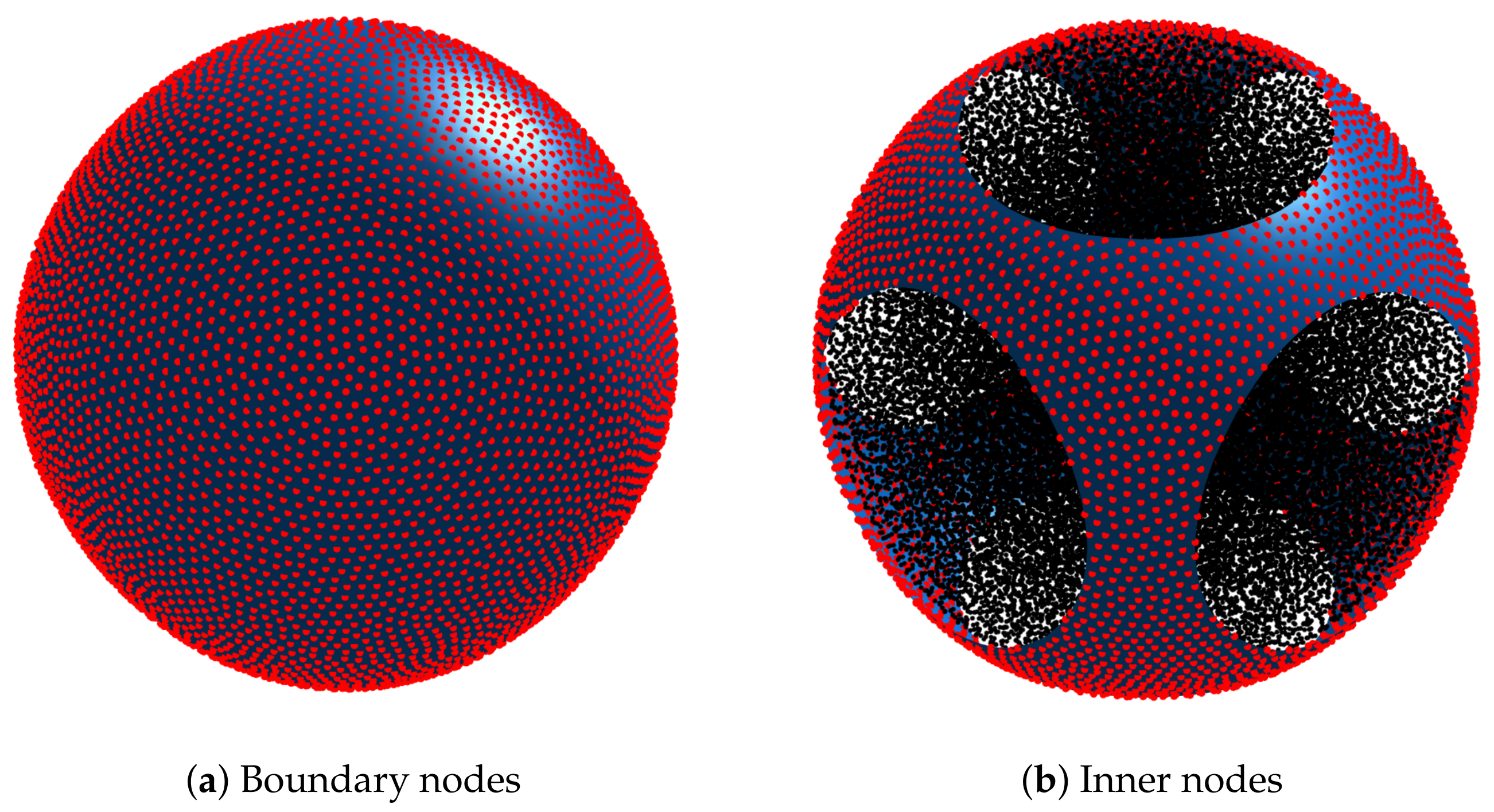
2.2. Node Generation

The first step of the employed meshless approach is to generate a 3D node distribution in $\Omega$ and on $\partial \Omega$, i.e., nodes are placed both inside the domain $\Omega$ and on the boundary $\partial \Omega$ according to a prescribed spacing function s. Although traditional mesh generation software could be employed, it is obvious that truly meshless node generation could bring great benefits in the whole meshless simulation chain. Different meshless-based node generation algorithms have been proposed [22,23,24,25], with particular reference to the ones based on the node-repel approach [26,27,28], which is employed in this work. The latter approach consists of two sequential steps:

• generation of a volumetric node distribution in $\Omega$ that satisfies the spacing function s on average;
• refinement of the initial node distribution through a node-repel approach that provides a suitable node distribution also on $\partial \Omega$.

In the last step, i.e., the refinement step, nodes are moved according to the mutual repulsion forces of the nearest neighbor nodes in order to obtain isotropic node arrangements, i.e., the spacing between the nodes is independent of the direction and matches the prescribed spacing function s. This node-repel approach can be viewed as an iterative process that minimizes the total potential energy U of the node distribution by moving one node at a time. In this work 50 refinement iterations and a constant spacing function s have been considered [27,28].

The nodes leaving the domain due to the repulsion forces during the refinement step are projected onto the nearest boundary point, resulting in a boundary-conforming node distribution. This projection operation is efficiently performed by exploiting an octree data structure [29,30] for the boundary triangles of the stereolitography surface (.stl file), which is used to determine the distance between a given node and the nearest boundary triangle, i.e., the minimum distance between the node and the boundary.

The triangle-based octree partitioning of the space around the object is performed by recursive subdivision of the space into octants while fulfilling the following rules:

• each leaf-box, i.e., box with no children, can not contain more than $T_M=5$ triangles;
• the minimum size of each leaf-box is $h_m=5\times {10}^{-3}$ (the domain is assumed to lie in the unit cube);
• the first constraint can be ignored if a box and its parent-box both contain exactly one vertex of the triangulated surface, which is also the same vertex;

where the last rule avoids infinite octree subdivisions around nodes connected to more than $T_M$ triangles. Graphical representations of generated node distributions are shown in Figure 2 and Figure 3 for the employed models.

2.3. Function Approximation

The value of a function at a generic point is approximated applying the Radial Point Interpolation Method (RPIM) using Radial Basis Functions (RBFs) augmented with polynomial terms [3]. Given a boundary-conforming node distribution as outlined in Section 2.2, this method is based on the assumption that the value $u\left(x\right)$ taken by the function u at the generic point $x\in \Omega$ can be locally approximated by the quantity $u^h\left(x\right)$ defined as follows:

$$u\left(x\right)\approx u^h\left(x\right):=\sum _{i=1}^{\overline{n}}{\alpha }_i\phi (\parallel x-x_i{\parallel }_2)+\sum _{j=1}^m{\beta }_j{p}_j\left(x\right)$$

(3)

where

• $\left\{\phi \right(\parallel x-x_i{\parallel }_2):i=1,\dots ,\overline{n}\}$ is a set of $\overline{n}$ RBFs, each of which is associated to the corresponding node $x_i$. The set of the considered nodes is local, i.e., $x_1,\dots ,x_{\overline{n}}$ are the $\overline{n}$ nearest nodes to x. For brevity of notation, $\phi (x,x_i)$ will be used instead of $\phi (\parallel x-x_i{\parallel }_2)$.
• $\{p_j:j=1,\dots ,m\}$ is a complete polynomial basis of degree P.

The adoption of the polynomial is motivated by the need to solve those accuracy and stability issues affecting pure RBF schemes [17].

In this implementation of the method, multiquadric functions [31] have been used:

$$\phi \left(r\right):=\sqrt{1+{\left(\epsilon r\right)}^2}$$

(4)

where the actual shape factor $\epsilon :=\overline{\epsilon }/s\left(x\right)$ is obtained by normalizing the shape factor parameter $\overline{\epsilon }$ with the local nodal spacing defined by the spacing function $s\left(x\right)$.

Since the number of nodes is finite, $u^h$ is a finite-dimensional approximation of u; therefore, great care must be taken in the choice of such number in order to balance efficiency and accuracy. From now on we will assume that a small number of neighbors $\overline{n}\ll N$ located within a neighborhood of the point x is used, where N is the total number of nodes generated. From this assumption it is implicitly understood that the RBFs have compact support, i.e., they are zero for $\parallel x-x_i\parallel >\delta$ for a certain $\delta$. The employment of compactly supported RBFs was made compulsory by two closely related reasons: the great number of nodes required to properly describe complex shaped domains, such as those presented in the following sections, and the consequent necessity to deal with large-scale matrices. Local RBF expansions lead to sparse linear systems that can be efficiently solved, in contrast to global approaches that lead to dense and ill-conditioned matrices, which preclude any application to large scale problems [14,32,33,34]. Accuracy and stability issues affecting global methods are clearly addressed in [35,36], where further possible solutions are discussed.

This in turn means that the value assumed by $u^h$ at a certain point x only depends on $u^h\left(x_i\right)$ estimated at the closest nodes $\{x_1,\dots ,x_{\overline{n}}\}$, from now on called the stencil:

$$u\left(x\right)\approx u^h\left(x\right):=\sum _{i=1}^{\overline{n}}{\alpha }_i\phi (x,x_i)+\sum _{j=1}^m{\beta }_j{p}_j\left(x\right)$$

(5)

The calculation of the weights $\{{\alpha }_1,\dots ,{\alpha }_{\overline{n}}\}$ and $\{{\beta }_1,\dots ,{\beta }_m\}$ depends on the position of the stencil. Therefore, if some nodes of the stencil belongs to the boundary $\partial \Omega$, then boundary conditions must be taken into account.

2.3.1. Stencil Contained within $\Omega$

In this case none of the nodes belonging to the stencil lies on the boundary $\partial \Omega$. Assuming the values of the function u at the nodes of the stencil $\{x_1,\dots ,x_{\overline{n}}\}$ are known, then a linear system of equations can be solved by imposing the exactness of the approximation $u^h$ at each of those nodes:

$$u^h\left(x_i\right)=u\left(x_i\right),i=1,\dots ,\overline{n}$$

(6)

Substituting the definition of $u^h\left(x\right)$ given in Equation (5) and evaluating at the $\overline{n}$ points $\{x_1,\dots ,x_{\overline{n}}\}$ leads to the following linear system of equations:

$$\mathsf{\Phi }\mathit{\alpha }+\mathit{P}\mathbf{\beta }=\overline{\mathit{u}}$$

(7)

where $\mathsf{\Phi }$ is a $(\overline{n}\times \overline{n})$ square matrix with entries ${\mathsf{\Phi }}_{i,j}=\phi (x_i,x_j)$ as defined in Equation (4), $\mathit{P}$ is the $(\overline{n}\times m)$ matrix of the polynomial coefficients, $\mathit{\alpha }\in {\mathbb{R}}^{\overline{n}}$ and $\mathbf{\beta }\in {\mathbb{R}}^m$ are the vectors with a total of $(\overline{n}+m)$ unknowns. $\overline{\mathit{u}}$ is instead the $(\overline{n}\times 1)$ column vector with entries $u\left(x_i\right)$ for each $x_i$ node of the stencil.

In order to make the system solvable, m more rows are needed, this is why the following additional orthogonality conditions are imposed:

$$\sum _{i=1}^{\overline{n}}{\alpha }_i{p}_j\left(x_i\right)=0,j=1,\dots ,m$$

(8)

The final linear system can thus be written using block matrices notation in the following form:

$$\left[\begin{array}{cc}\mathsf{\Phi }& \mathit{P}\\ {\mathit{P}}^T& \mathbf{0}\end{array}\right]\left\{\begin{array}{c}\mathit{\alpha }\\ \mathit{\beta }\end{array}\right\}=\left\{\begin{array}{c}\overline{\mathit{u}}\\ \mathbf{0}\end{array}\right\}$$

(9)

which has a unique solution in the set of weights $\{{\alpha }_1\dots {\alpha }_{\overline{n}},{\beta }_1,\dots {\beta }_m\}$ if the $\overline{n}$ nodes $x_1,\dots ,x_{\overline{n}}$ are distinct.

2.3.2. Stencil with Boundary Nodes

When some boundary nodes are included in the stencil, then instead of assuming the true value of the function u, the appropriate condition must be imposed. In the attempt of providing a general description we shall assume that a Robin b.c., as defined in Equation (2), is applied to such nodes:

$$a\left(x_i\right)u^h\left(x_i\right)+b\left(x_i\right)\frac{\partial u^h}{\partial n}\left(x_i\right)=g\left(x_i\right),x_i\in \partial \Omega$$

(10)

where a, b, g are all known functions defined on the boundary.

Now suppose the nodes are listed in the following order: the first ${\overline{n}}_I$ indices correspond to the nodes lying within the domain $\Omega$, the following ${\overline{n}}_B$ indices correspond instead to the nodes lying on $\partial \Omega$, and ${\overline{n}}_I+{\overline{n}}_B=\overline{n}$. More formally:

$$\left\{\begin{array}{cc}{x}_i\in \Omega \hfill & \iff i\in \mathcal{I}:=\{1,\dots ,{\overline{n}}_I\}\hfill \\ x_i\in \partial \Omega \hfill & \iff i\in \mathcal{B}:=\{{\overline{n}}_I+1,\dots ,{\overline{n}}_I+{\overline{n}}_B\}\hfill \end{array}\right.$$

(11)

Building on what was done when dealing with inner nodes, the problem to be solved is the following:

$$\left\{\begin{array}{cc}{u}^h\left(x_i\right)=u\left(x_i\right),\hfill & i\in \mathcal{I}\hfill \\ a\left(x_i\right)u^h\left(x_i\right)+b\left(x_i\right)\frac{\partial u^h}{\partial n}\left(x_i\right)=g\left(x_i\right),\hfill & i\in \mathcal{B}\hfill \end{array}\right.$$

(12)

By substituting once again the definition of $u^h$ given in Equation (5) we get

$$\sum _{k=1}^{\overline{n}}{\alpha }_i\phi (x_i,x_k)+\sum _{j=1}^m{\beta }_j{p}_j\left(x_i\right)=u\left(x_i\right),i\in \mathcal{I}$$

(13)

$$\begin{array}{cc}\hfill a\left(x_i\right)& \left[\sum _{k=1}^{\overline{n}}{\alpha }_k\phi (x_i,x_k)+\sum _{j=1}^m{\beta }_j{p}_j\left(x_i\right)\right]+\hfill \\ \hfill +& b\left(x_i\right)\left[\sum _{k=1}^{\overline{n}}{\alpha }_k\frac{\partial \phi }{\partial n}(x_i,x_k)+\sum _{j=1}^b\frac{\partial p_j}{\partial n}\left(x_i\right)\right]=g\left(x_i\right),i\in \mathcal{B}\hfill \end{array}$$

(14)

By reordering the terms for case $i\in \mathcal{B}$ of Equation (14) in order to isolate unknown coefficients ($\alpha$’s and $\beta$’s), we obtain the following linear system:

$$\begin{array}{cc}\hfill \sum _{k=1}^{\overline{n}}{\alpha }_k& \left(a\left(x_i\right)\phi (x_i,x_k)+b\left(x_i\right)\frac{\partial \phi }{\partial n}(x_i,x_k)\right)+\hfill \\ \hfill & +\sum _{j=1}^m{\beta }_j\left(a\left(x_i\right)p_j\left(x_i\right)+b\left(x_i\right)\frac{\partial p_j}{\partial n}\left(x_i\right)\right)=g\left(x_i\right),i\in \mathcal{B}\hfill \end{array}$$

(15)

Once again we can now impose the orthogonality conditions of Equation (8) and obtain a linear system of the following form:

$$\underset{{\displaystyle \mathit{M}}}{\underbrace{\left[\begin{array}{cc}{\mathsf{\Phi }}^{\prime }& {\mathit{P}}^{\prime }\\ {\mathit{P}}^{\mathit{T}}& \mathbf{0}\end{array}\right]}}\left\{\begin{array}{c}\mathit{\alpha }\\ \mathit{\beta }\end{array}\right\}=\left\{\begin{array}{c}\overline{\mathit{u}}\\ \overline{\mathit{g}}\\ \mathbf{0}\end{array}\right\}$$

(16)

where the block matrix ${\mathit{P}}^T$ and the vector of unknowns $\{{\alpha }_1,\dots ,{\alpha }_{\overline{n}}\}$ are the only unchanged terms inherited from the previous system (9). The other terms in Equation (16) are fully expanded below for clarity.

$$\left[\begin{array}{c}{\mathsf{\Phi }}^{\prime }\end{array}\right]=\left[\begin{array}{ccc}\phi (x_1,x_1)& \dots & \phi (x_1,x_{\overline{n}})\\ ⋮& \ddots & ⋮\\ \phi (x_{{\overline{n}}_I},x_1)& \dots & \phi (x_{{\overline{n}}_I},x_{\overline{n}})\\ a\phi (x_{{\overline{n}}_I+1},x_1)+b\frac{\partial \phi }{\partial n}(x_{{\overline{n}}_I+1},x_1)& \dots & a\phi (x_{{\overline{n}}_I+1},x_{\overline{n}})+b\frac{\partial \phi }{\partial n}(x_{{\overline{n}}_I+1},x_{\overline{n}})\\ ⋮& \ddots & ⋮\\ a\phi (x_{\overline{n}},x_1)+b\frac{\partial \phi }{\partial n}(x_{\overline{n}},x_1)& \dots & a\phi (x_{\overline{n}},x_{\overline{n}})+b\frac{\partial \phi }{\partial n}(x_{\overline{n}},x_{\overline{n}})\end{array}\right]$$

$$\left[\begin{array}{c}{\mathit{P}}^{\prime }\end{array}\right]=\left[\begin{array}{ccc}{p}_1\left(x_1\right)& \dots & p_m\left(x_1\right)\\ ⋮& \ddots & ⋮\\ p_1\left(x_{{\overline{n}}_I}\right)& \dots & p_m\left(x_{{\overline{n}}_I}\right)\\ a{p}_1\left(x_{{\overline{n}}_I+1}\right)+b\frac{\partial p_1}{\partial n}\left(x_{{\overline{n}}_I+1}\right)& \dots & a{p}_m\left(x_{{\overline{n}}_I+1}\right)+b\frac{\partial p_m}{\partial n}\left(x_{{\overline{n}}_I+1}\right)\\ ⋮& \ddots & ⋮\\ a{p}_1\left(x_{\overline{n}}\right)+b\frac{\partial p_1}{\partial n}\left(x_{\overline{n}}\right)& \dots & a{p}_m\left(x_{\overline{n}}\right)+b\frac{\partial p_m}{\partial n}\left(x_{\overline{n}}\right)\end{array}\right]$$

$$\left[\begin{array}{c}\overline{\mathit{u}}\\ \overline{\mathit{g}}\\ \mathbf{0}\end{array}\right]=\left\{\begin{array}{c}u\left(x_1\right)\\ ⋮\\ u\left(x_{{\overline{n}}_I}\right)\\ g\left(x_{{\overline{n}}_I+1}\right)\\ ⋮\\ g\left(x_{\overline{n}}\right)\\ 0_1\\ ⋮\\ 0_m\end{array}\right\}$$

Please note that a and b are two known functions; therefore, they may have different values in different rows. Finally we remark that Equation (9) can be considered as a special case of Equation (16) with no boundary nodes, i.e., where none of the neighbors lie on the boundary.

2.4. Collocation Technique

Considering the boundary value problem in (2), an approximation of the solution u with a finite dimensional function $u^h$ leads to a certain error. $u^h$ is now defined over the whole domain $\Omega$, and its value at each point is interpolated using local information, as explained in Equation (5). The numerical procedure adopted in order to solve the linear problem in (2) aims at finding a “good” finite dimensional representation of the solution u. The Weighted Residual Method in combination with the Collocation Technique is employed, here follows a brief discussion of such procedure, see [3] for further details.

The linear PDE in (2) is applied to the approximate solution $u^h$ given by Equation (5) instead of u. Therefore, the initial PDE will not be solved exactly, in general, and a nonzero residual function $R_s$ will appear:

$$R_s\left(x\right):=△u^h\left(x\right)+f\left(x\right)\ne 0,x\in \Omega$$

(17)

The Weighted Residual Method now consists in forcing to zero the following integrals, where $N_I$ is the total number of nodes generated inside the domain $\Omega$:

$${\int }_{\Omega }{W}_i{R}_{s}d\Omega =0,i=1,\dots ,N_I$$

(18)

Substituting the definition of the residual functions leads to the following system of equations:

$${\int }_{\Omega }{W}_i(△u^h+f)d\Omega =0,i=1,\dots ,N_I$$

(19)

In order to get rid of the integrals in the above equations, many techniques are proposed, among others the Collocation Method has been chosen. The main advantage is its ability to discretize the Boundary Value problem expressed in strong form, thus leading to a real fully meshless approach (see again [3,28]).

The basic idea behind the Collocation Method is to choose the solution with vanishing residuals at the nodes only. Formally, this is achieved by defining the weight functions $W_i$ as Dirac Delta Functions as follows:

$$W_i\left(x\right)=\delta (x-x_i),i=1,\dots ,N_I$$

(20)

As a result, $u^h$ is required to send the residual function $R_s$ to zero at the nodes $x_i$:

$${\int }_{\Omega }\delta (x-x_i)(△u^h+f)d\Omega ={\left.△u^h\phantom{|}\right|}_{x=x_i}+f\left(x_i\right)=0,i=1,\dots ,N_I$$

(21)

At this point we are allowed to substitute the definition of $u^h$, as defined in Equation (5), into Equation (21). From now on let us focus our attention on a specific node $x_i\in \Omega$:

$${\left.△\left(\sum _{k=1}^{\overline{n}}{\alpha }_k\phi (x,x_k)+\sum _{j=1}^m{\beta }_j{p}_j\left(x\right)\right)\phantom{|}\right|}_{x=x_i}+f\left(x_i\right)=0$$

(22)

Finally, because of the linearity of the Laplace differential operator, it can be distributed over the basis functions (radial and polynomial), thus yielding the following equation:

$$\sum _{k=1}^{\overline{n}}{\alpha }_k△{\left.\phi (x,x_k)\phantom{|}\right|}_{x=x_i}+\sum _{j=1}^m{\beta }_j△{\left.p_j\left(x\right)\phantom{|}\right|}_{x=x_i}+f\left(x_i\right)=0$$

(23)

Equation (23) can be recast into the following compact form:

$${\left\{\begin{array}{c}\mathsf{\Psi }\left(x_i\right)\\ \mathsf{\Pi }\left(x_i\right)\end{array}\right\}}^T\left\{\begin{array}{c}\mathit{\alpha }\\ \mathit{\beta }\end{array}\right\}+f\left(x_i\right)=0$$

(24)

where $\mathsf{\Psi }\left(x_i\right)$ and $\mathsf{\Pi }\left(x_i\right)$ are defined as follows:

$$\mathsf{\Psi }\left(x\right):=\left\{\begin{array}{c}△\phi (x,x_1)\\ ⋮\\ △\phi (x,x_{\overline{n}})\end{array}\right\},\mathsf{\Pi }\left(x\right):=\left\{\begin{array}{c}△p_1\left(x\right)\\ ⋮\\ △p_m\left(x\right)\end{array}\right\}$$

(25)

whereas $\mathit{\alpha }=\{{\alpha }_1,\dots ,{\alpha }_{\overline{n}}\}$ and $\mathit{\beta }=\{{\beta }_1,\dots ,{\beta }_m\}$ are unknown vectors of the expansion coefficients. Then, Equation (16) can be formally solved for $\mathit{\alpha }$ and $\mathit{\beta }$, assuming the value of $u^h$ to be formally known at the nodes belonging to the stencil:

$$\left\{\begin{array}{c}\mathit{\alpha }\\ \mathit{\beta }\end{array}\right\}={\left[\begin{array}{c}\mathit{M}\end{array}\right]}^{-1}\left\{\begin{array}{c}{\overline{\mathit{u}}}^h\\ \overline{\mathit{g}}\\ \mathbf{0}\end{array}\right\}$$

(26)

This result can then be substituted back into Equation (24), thus yielding the following equation:

$${\left\{\begin{array}{c}\mathsf{\Psi }\left(x_i\right)\\ \mathsf{\Pi }\left(x_i\right)\end{array}\right\}}^T{\left[\begin{array}{c}\mathit{M}\end{array}\right]}^{-1}\left\{\begin{array}{c}{\overline{\mathit{u}}}^h\\ \overline{\mathit{g}}\\ \mathbf{0}\end{array}\right\}+f\left(x_i\right)=0$$

(27)

We might now observe that the first two factors of Equation (27) are known and their product yields to a row vector ${\mathit{c}}^T$. Therefore, instead of performing the inversion of matrix $\mathit{M}$, we can therefore solve the following adjoint linear system for $\mathit{c}$, where the right-hand side is known:

$${\left[\begin{array}{c}\mathit{M}\end{array}\right]}^T\left\{\begin{array}{c}\mathit{c}\end{array}\right\}=\left\{\begin{array}{c}\mathsf{\Psi }\left(x_i\right)\\ \mathsf{\Pi }\left(x_i\right)\end{array}\right\}$$

(28)

The scalar Equation (27) written in terms of the known vector $\mathit{c}$ reads as follows:

$$\left\{\begin{array}{c}\mathit{c}\end{array}\right\}\left\{\begin{array}{c}{\overline{\mathit{u}}}^h\\ \overline{\mathit{g}}\\ \mathbf{0}\end{array}\right\}+f\left(x_i\right)=0$$

(29)

which represents the ith scalar equation of the following sparse linear system:

$$\left[\begin{array}{c}\mathit{C}\end{array}\right]\left\{\begin{array}{c}{\mathit{u}}^h\end{array}\right\}=\mathit{q}-\mathit{f}$$

(30)

where ${\mathit{u}}^h=\{u^h\left(x_1\right),\dots ,u^h\left(x_{N_I}\right)\}$, $\mathit{f}=\{f\left(x_1\right),\dots ,f\left(x_{N_I}\right)\}$ and $\mathit{q}=\{q_1,\dots ,q_{N_I}\}$ are referred to all the $N_I$ internal nodes, i.e., those contained in $\Omega$, while vector $\mathit{q}$ comes from the imposition of the boundary conditions at the interpolant level.

2.5. Solution Procedure

The final sparse system of Equation (30) can now be solved using an iterative method, thus obtaining the value of unknowns ${\mathit{u}}^h=\{u^h\left(x_1\right),\dots ,u^h\left(x_{N_I}\right)\}$ at all internal nodes.

In the current implementation, a LU decomposition is performed for the solution of the small linear systems (28) associated to each inner node $x_i$, while the final sparse system (30) is solved instead by performing an Incomplete LU Factorization (ILU) [37] (package IncompleteLU in Julia) of the sparse matrix $\mathit{C}$ followed by the application of the Biconjugate Gradient Stabilized Method [38] (package IterativeSolvers in Julia) employing a relative norm $tol={10}^{-14}$ on the residuals.

2.6. Julia Programming Language

The Julia Programming Language [19] was announced as an open source project in February 2012, in the attempt of taking advantage of modern techniques for executing dynamic languages effectively and providing a single solution, capable of being both fast and dynamic at the same time.

High-level dynamic languages on one side provide great advantages in terms of convenience and productivity and are often preferred even in the fields of data analysis, applied math, engineering, and other sciences. On the other hand, lower-level languages like C and Fortran remain the gold standard for computationally intensive problems, since high-level dynamic languages tend to lack sufficient performance [39].

C and Fortran, however, tend to be harder to work with and require more specific skills; therefore, they might become less productive and sometimes slow down the whole development process.

If a compromise between convenience and performance is desired, then one of the following two approaches were available at the time Julia came out.

• Two-tiered architecture solutions: programmers express high-level logic in a dynamic language (like MATLAB, Octave, R, or SciPi), while heavy lifting is done in C and Fortran [39].
• Enhanced versions of existing dynamic languages: specific libraries need to be used for this purpose; however, the same programmer is given the possibility to contribute to the whole process without completely loosing understanding.

Julia was therefore designed from the ground up and succeeded in providing a new and radically different alternative for the aforementioned compromise. It has indeed the performance of a statically compiled language while providing interactive dynamic behavior and productivity comparable to those of Python, LISP, or Ruby [39]. On top of that, a large community rapidly grew around the initial project, and many open source packages and excellent integration with text editors have become available to date.

For these reasons, Julia was chosen for the development of all the components of the RBF-FD solver presented in this paper, allowing optimal management of data structures and also taking into account future extensibility and high performance.

2.7. MATLAB PDE Toolbox

In order to compare the results of the presented approach with other numerical methods, MATLAB Partial Differential Equation Toolbox was employed [40]. This toolbox offers the user a complete package (including both discretization and solution routines) based on FEM with tetrahedral elements in 3D.

Quadratic elements, i.e., 10-node tetrahedrals, have been used. The aforementioned toolbox was chosen in order to allow a comparison with the FEM, which is one of the most employed methods for the numerical simulation of engineering problems. It is important to point out that the tetrahedral mesh that was generated is patch-conforming, i.e., the dimension of the elements adapts to the size of the features of the geometry. On the other side, the meshless node distributions are obtained with constant spacing functions for simplicity. Therefore, FEM results are expected to be truly optimal since they are attained using a fully developed adaptive meshing, while meshless results, on the other side, are expected to improve substantially in the case of the engine domain. The accuracy of the meshless method would indeed be improved significantly with the adoption of an advanced node generation routine, capable of performing some local reduction in the nodal spacing in proximity to complex geometrical features.

3. Results

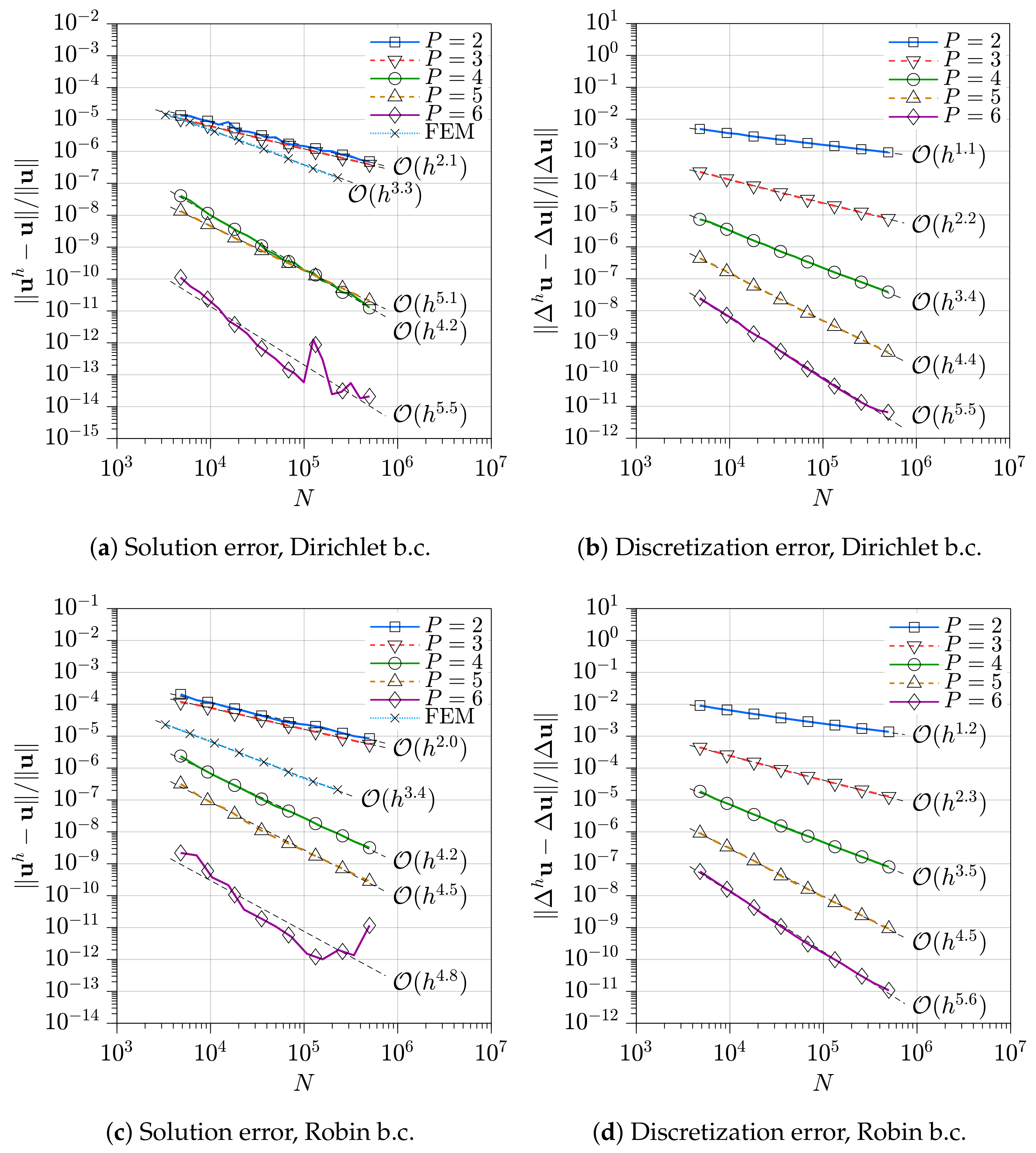
3.1. Code Verification

In order to assess correctness, accuracy, and efficiency of the presented meshless implementation, the Method of Manufactured Solution (MMS) [41] is applied:

• a sufficiently smooth function $u\left(x\right)$ is chosen,
• the boundary conditions and the internal heat generation f are analytically computed in order to ensure $u\left(x\right)$ to be the exact solution of the Boundary Value Problem (2),
• the RBF-FD method is employed to solve the Boundary Value Problem, thus leading to an approximated solution $u^h\left(x\right)$. Much information concerning order of accuracy and efficiency is collected during the calculations,
• $u^h\left(x\right)$ is finally compared to $u\left(x\right)$ according to various metrics, and the performance of the method is assessed.

3.2. Analytical Solution

The analytical solution chosen for the verification of the correctness of the code is simply any polynomial $u\left(x\right)$ of degree $\overline{P}$. For simplicity, the following polynomial has been chosen:

$$u\left(x\right)=x_1^{\overline{P}}+x_2^{\overline{P}}+x_3^{\overline{P}}$$

(31)

with $\overline{P}=1,\dots ,6$ and which can be exactly solved by the RBF-FD method as long as the degree P of the augmented polynomial fulfills the condition $P\ge \overline{P}$.

The analytical solution chosen for the assessment of the accuracy of the presented implementation of the RBF-FD method is the following function, defined for every $x\in {\mathbb{R}}^3$ and continuously differentiable infinitely many times:

$$u\left(x\right)=exp(x_1+x_2+x_3)$$

(32)

3.3. Choice of the Domain

By taking into account the final accuracy alone, one might underestimate the importance of the node generation routine, since the performances of the solver strongly depend on the quality of this previous step. In our case both elements, i.e., node generator and solver, are written using Julia and developed from the very beginning to be seamlessly integrated. For this reason two very different domains are selected: one is very regular and the other is complex and can be considered to be a good representative for the class of problems usually met in engineering design. Both domains are described by standard stereolitography surfaces encoded in the .stl format:

• The first is given by the 3D sphere highlighted in Figure 2. This surface is chosen for its regularity, and the absence of any sharp edge is an especially forgiving feature when the stencil around each node is chosen. The accuracy and the robustness of the whole approach are therefore expected to be very high: the final accuracy depends almost exclusively on the solver.
• The second is given by a 3D model of the crankcase of a $V8$ ICE (Internal Combustion Engine). This surface, shown in Figure 3, is chosen for its complexity since it presents different features: there are both regular surfaces (cylindrical and flat) as well as sharp and rounded edges. If the integration between node generator and solver is capable of providing reliable results on this scenario, then it is safe to conclude its applicability to many other shapes of engineering relevance.

The quality of the generated node distributions can be assessed visually, for , by carefully inspecting the plotted result. For instance, one might check whether the normal vectors associated to the surface nodes are correctly oriented, especially in correspondence with the edges or vertices at the intersection between different triangles of the stereolithography.

Another visual test is to check whether there are inner nodes too close to the surface since such nodes repel those belonging to the boundary, thus leading to a suboptimal enforcement of the boundary conditions.

We also point out that, for simplicity, the spacing function s is always set to be uniform for all the results presented in this paper. This is not an issue for regular domains, like the sphere, but might harm the accuracy when the geometry presents some strong 3D curvature localized at certain spots, for example in the case of the crankcase domain.

3.4. RBF-FD Parameters

The achieved performances mainly depend on four parameters:

• $\tilde{n}$, number of nodes included in each stencil, see Equation (5),
• $\overline{\epsilon }$, shape parameter of the Radial Basis Function, see Equation (4),
• N, total number of nodes generated on both $\Omega$ and $\partial \Omega$,
• P, degree of the polynomial term in the definition of $u^h$, see Equation (5).

The number of nodes included in each stencil $\tilde{n}$ is linked to P in the sense that a minimum number of nodes is required for any given order of the polynomial term. It has been shown that the choice of larger stencils, like $\overline{n}=2m$ given in Equation (33), overcomes stability and accuracy problems due to Runge’s phenomenon [17]:

$$\overline{n}=2m=2\left(\genfrac{}{}{0pt}{}{P+d}{P}\right)$$

(33)

where m is the number of terms in the polynomial basis function, and d is the number of dimensions ($d=3$ in 3D problem).

The shape parameter $\overline{\epsilon }$ defines the flatness of the Radial Basis Function (RBF) reported in Equation (4); its value must be selected carefully due to the following trade-off:

• in the limit $\overline{\epsilon }⟶0$ the RBF becomes increasingly flat, until some typical oscillations appears due to the Runge’s phenomenon [28], on top of that, too little values of $\overline{\epsilon }$ might also lead to numerical issues, due to an ill-conditioning of the interpolation matrix,
• as $\overline{\epsilon }$ increases, on the other side, the solution becomes more stable but less accurate.

A reasonable choice based on previous numerical studies [21,28,42] is $\overline{\epsilon }=0.3$, while the influence of parameters N and P is instead discussed in succeeding paragraphs, since they are strongly related to the order of accuracy.

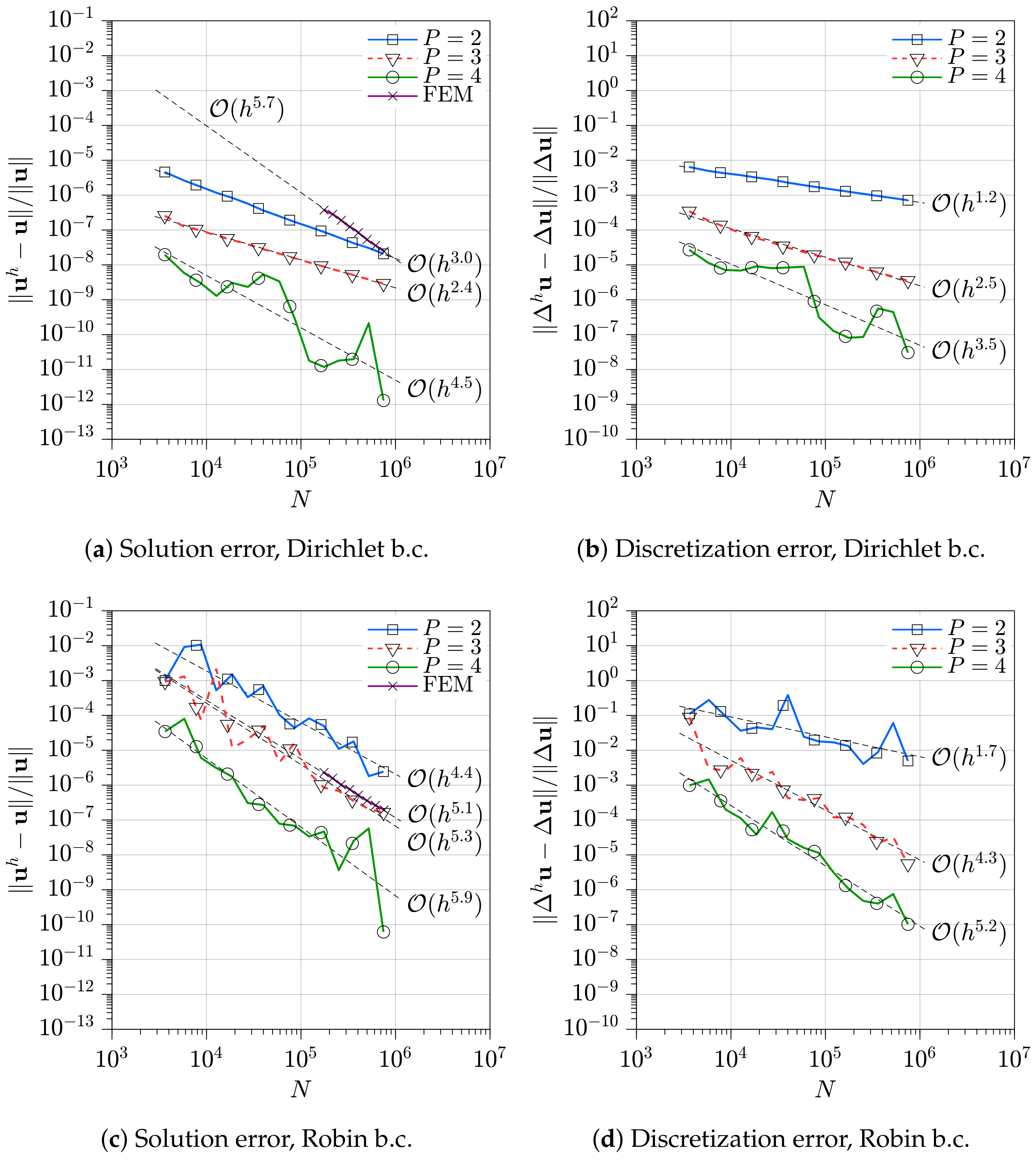
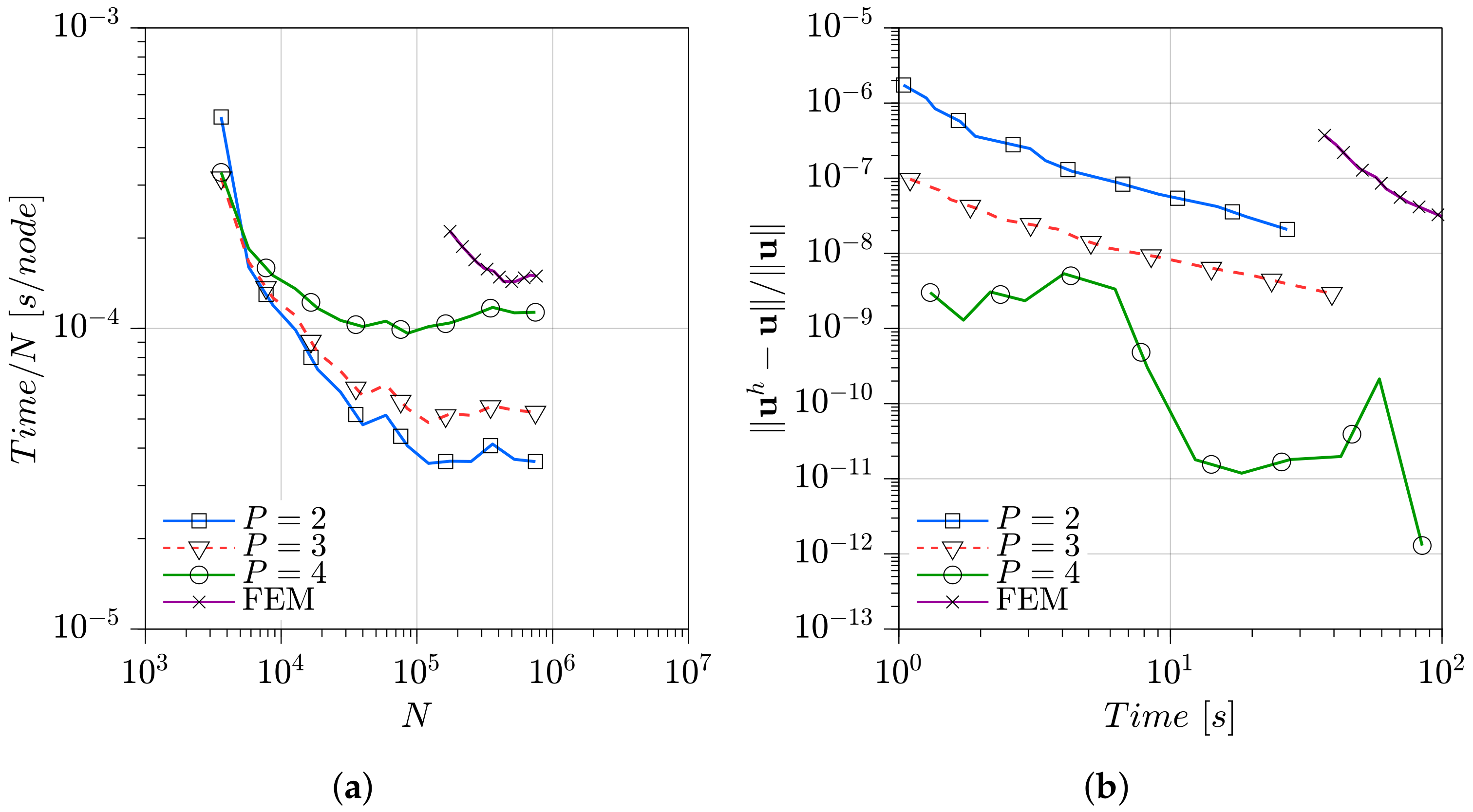
3.5. Sphere

In Figure 4 the convergence curves for the solution (Figure 4a,c) and for the Laplacian (Figure 4b,d) are shown for polynomial degrees $P=2,\dots ,6$ on the spherical domain, where the total number of nodes ranges from $N=5$k to $N=500$k nodes. Dirichlet b.c., i.e., $a=1$ and $b=0$ in Equation (2), and Robin b.c., i.e., $a=1$ and $b=1$, have been considered. Errors are normalized with respect to the norm of analytical values.

Errors in the approximation of the Laplacian operator, presented in Figure 4b,d , are simply attained as the result of the matrix-vector product reported in Equation (34), where $\mathbf{C}$ is the sparse matrix from (30) and $\mathbf{u}$ is the analytical solution evaluated at the inner nodes. Therefore Figure 4b,d represents an estimation of the mean discretization error, calculated as

$$\left\{\begin{array}{c}{△}^h\mathit{u}\end{array}\right\}:=\left[\begin{array}{c}\mathit{C}\end{array}\right]\left\{\begin{array}{c}\mathit{u}\end{array}\right\}-\left\{\begin{array}{c}\mathit{q}\end{array}\right\}$$

(34)

Figure 4a shows an increase in the order of accuracy, which ranges from $\sigma =2.2$ to $\sigma =5.5$, when the polynomial degree P is increased from $P=2$ to $P=6$. The order of accuracy $\sigma$ is defined by the following equation:

$$error\propto h^{\sigma }$$

(35)

where $h\propto N^{-1/3}$ is a reference value for the nodal spacing in 3D.

Figure 4c shows slightly lower $\sigma$’s when Robin b.c. are enforced, even if present, the degradation in performance with these boundary conditions can still be considered more than acceptable. We believe that the apparent lack of convergence appearing in the case $P=6$ for $N>300$k nodes is due to numerical instabilities caused by the large size of the local stencils when Robin boundary nodes are included. Indeed, with $P=6$ quite a large local stencil is employed, i.e., $\overline{n}=168$ nodes, leading to an ill-conditioned dense local matrix $\mathit{M}$. However, this is not a problem since $P=6$ is a limit case in 3D, and such instabilities seem to only play a non-negligible role once the method has come to convergence near machine epsilon in the global error.

From Figure 4a,c it can also be observed that it is always convenient to choose a polynomial basis of even degree P in order to solve a Poisson equation, which is a second-order PDE: odd degrees not only provide negligible improvements in terms of solution errors, but even lead to worse orders of accuracy. Furthermore, we point out that, in the case $P=6$ and $N>200$k nodes, the normalized error becomes quite close to machine epsilon in double precision, and any further increase in N will not reduce the error. FEM convergence curves are also displayed in Figure 4a,c for comparison; it can be observed that the FEM curve is very similar to the ones for the cases $P=2,3$ for Dirichlet b.c., while for Robin b.c. the FEM curve lies between the cases $P=3$ and $P=4$.

The convergence curves represented in Figure 4b,d show a continuous improvement in both the order of accuracy $\sigma$ and absolute value of the discretization error when P is increased, and they seem to follow the rule of thumb $\sigma \approx 1.1\times (P-1)$.

Figure 5 can instead be used to compare the different choices of P under the aspect of time efficiency. Figure 5a gives a rough idea of the actual computational time required for the calculation of the solution $u^h$. The values are referred to a portable computer equipped with Intel i7-6700 HQ CPU (4 cores) and 16 GB of RAM. The total computational time accounts for the time required for node generation, calculation of RBF-FD stencil, Equation (28), and final sparse linear system solution, Equation (30). Both node generation and RBF-FD stencils calculations are explicitly parallelized in Julia using Distributed package and Base.Threads module for multithreaded computations distributed over multiple cores.

Figure 5b shows instead the specific total times in terms of seconds per node, where it can be seen that, whatever the value of P, the specific time tends to constant values for sufficiently large N, where the total time is dominated by node generation, and RBF-FD stencils calculations which are perfectly linear in N. As N increases further, the specific time shows a slight increase due to the asymptotic cost of the ILU-preconditioned BiCGStabl algorithm, which scales more than linearly. The total and specific computational times required for the FEM solution are also displayed in Figure 5, showing a significant increase beyond $N=100$k nodes.

Figure 6 shows an analysis of the time efficiency allowed by each choice of the polynomial degree P. For better visualization only the results attained with more than 20k nodes are included. It is possible to see that, when the geometry is sufficiently smooth as the spherical one, choosing a higher even polynomial degree is always advisable for the solution of a Poisson equation. Figure 6 also shows that the time efficiency of the FEM approach is very similar to the cases $P=2,3$.

The estimation of the condition number $\kappa \left(\mathbf{C}\right)$ of the final sparse matrix $\mathbf{C}$ is shown in Figure 7 for both Dirichlet and Robin b.c., where $\kappa \left(\mathbf{C}\right)$ is defined as $\kappa \left(\mathbf{C}\right)={\parallel \mathbf{C}\parallel }_2{\parallel {\mathbf{C}}^{-1}\parallel }_2$ using the 2-norm. The condition number grows approximately with order $\mathcal{O}\left(N^{0.7}\right)$ in both cases, regardless of P, thus very much comparable with the order $\mathcal{O}\left(N^{2/3}\right)$ of classic finite difference schemes for the 3D Laplacian operator on uniform grids [43]. The condition number for Robin b.c. ($a=b=1$ in Equation (2)), Figure 7b, is approximately 7 times larger than the condition number for Dirichlet b.c., Figure 7a, which is again comparable to the value 5.78 of classic finite difference schemes with the same b.c.

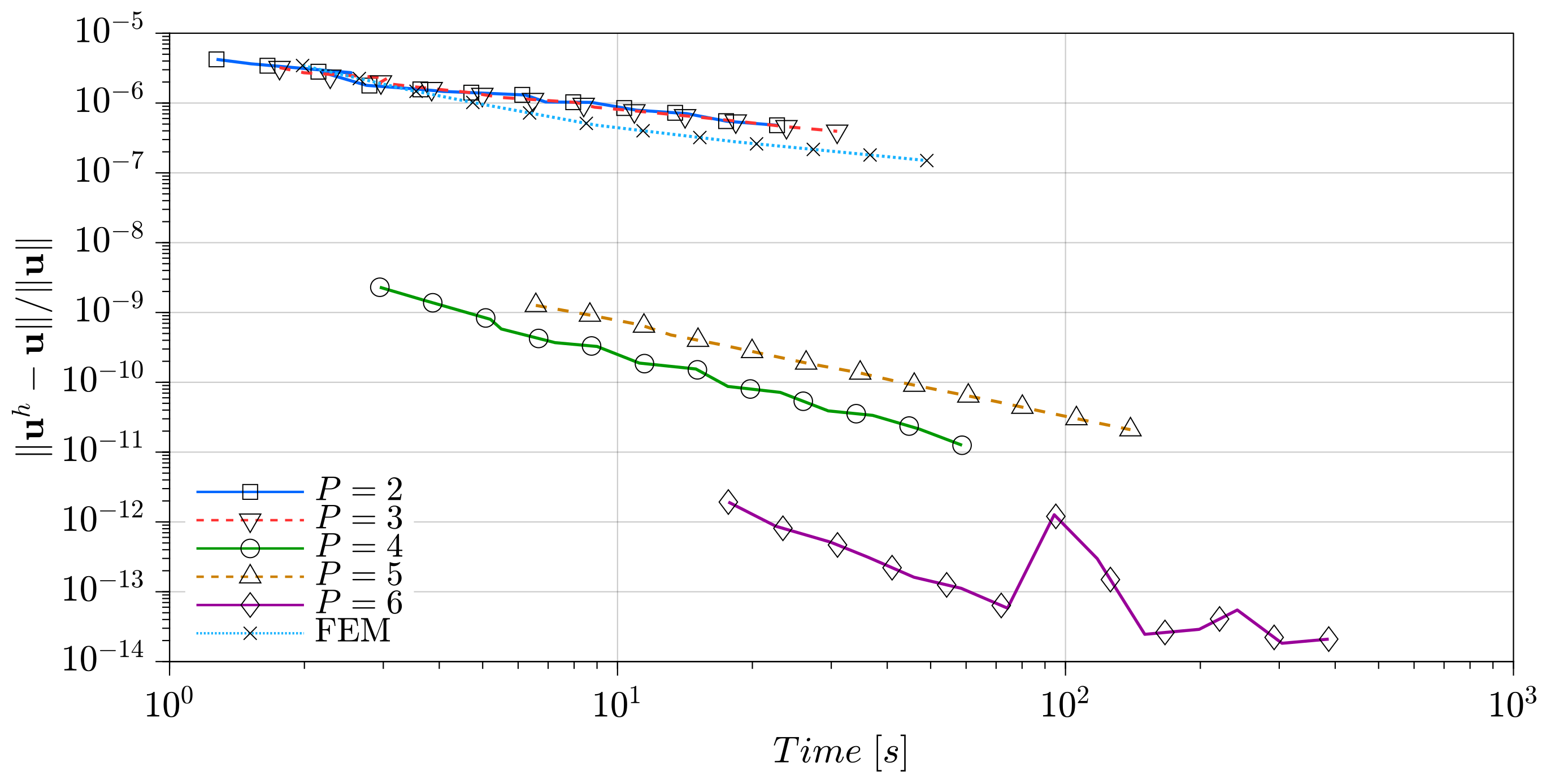
3.6. Engine

Convergence curves for the solution and for the Laplacian are shown in Figure 8, again for both Dirichlet b.c., i.e., $a=1$ and $b=0$ in Equation (2), and Robin b.c., i.e., $a=1$ and $b=1$. The chosen values for the polynomial degree are $P=2,3,4$, and the total number of nodes ranges from $N=5$k to $N=750$k nodes.

In the case of Dirichlet b.c., the order of accuracy for the solution, Figure 8a, varies from $\sigma =3.0$ to $\sigma =4.5$ when the polynomial degree is increased from $P=2$ to $P=4$. Similarly to the sphere, passing from $P=2$ (even) to $P=3$ (odd) does not increase the order of accuracy, which instead decreases from $\sigma =3.0$ to $\sigma =2.4$, while an improvement in absolute terms appears. A further increase to $P=4$ (odd) results in both increased order of accuracy, i.e., $\sigma =4.5$, and reduced errors in absolute terms. FEM convergence curves are also shown in Figure 8a, revealing an order of accuracy $\sigma =5.7$, which is significantly higher than the ones for $P=2,3,4$, but the FEM error has larger absolute value than $P=2$ below $N=1$M nodes.

The convergence curves for the Laplacian, Figure 8b, show instead a continuous increase in the order of accuracy when P grows, analogously to the corresponding results on the spherical domain. Unlike the case of the sphere, the convergence curves for $P=4$ in both the previous figures exhibit some irregularities compared to the curves for $P=2,3$. This is probably due to the fact that the large stencil, required by the condition of Equation (33) in the case $P=4$, i.e., $\overline{n}=70$ nodes, leads to very distorted 3D nodal arrangements in the proximity of particular features of the complex surface, giving rise to unstable RBF interpolants. This problem, which is mainly due to the employment of a constant spacing function, can be alleviated through some proper refinement of the node distribution, for instance some reduction in the nodal spacing in proximity to such geometrical features.

In the case of Robin b.c., it has been necessary to impose three additional requirements for the inclusion of boundary nodes in the stencil:

• Angle rule:

  $$\frac{x_b-x_i}{\parallel x_b-x_i\parallel }·n\left(x_b\right)>0.6$$

  (36)

  where $x_b$ is a boundary node and $x_i$ is an inner node where the Laplacian is required to be approximated. Equation (36) states that a boundary node $x_b$ can be included in the stencil only if the angle $\gamma$ between the outer normal $n\left(x_b\right)$ associated to the boundary node $x_b$ and the line connecting $x_b$ to $x_i$ satisfies $\gamma <arccos\left(0.6\right)\approx {53}^{\circ }$.
• Distance rule: $\parallel x_b-x_i\parallel <2s$, i.e., only boundary nodes closer to the center $x_i$ than twice the spacing function can be included in the stencil.
• Number rule: no more than 10 boundary nodes can be included in the stencil.

The resulting convergence curves for the solution and for the Laplacian are shown in Figure 8c,d, respectively. The comparison with the corresponding curves for Dirichlet b.c., Figure 8a, shows a general loss in accuracy in absolute terms due to the effects of Robin b.c., i.e., the curves are shifted upwards, while the apparent order of accuracy for the solution ranges from $\sigma =4.4$ to $\sigma =5.9$ when the polynomial degree is increased from $P=2$ to $P=4$. FEM results are very much comparable to the case $P=3$ in terms of both absolute error and order of accuracy. The convergence curves for the Laplacian highlight a similar behavior, with a continuous improvement in the order of accuracy when P is increased. The graphical comparison between the convergence curves of Dirichlet b.c. and Robin b.c. also reveals a higher sensitivity to boundary node arrangements for the latter case, as expected. Again, local node refinement in the neighborhood of particular geometrical features of the boundary should mitigate this problem.

Figure 9 shows the analysis of computational times. The curves for the specific time, i.e., time per node, depicted in Figure 9a, are very similar to the ones obtained for the spherical domain, depicted in Figure 5b. The presented approach is thus almost perfectly linear in the range N = 100k–1M nodes; the specific times for the FEM solution are instead always slightly larger than the case $P=4$.

Figure 9b shows the curves of the solution error versus computational time in the case of Dirichlet b.c. These curves reveal that it is always convenient to employ high-degree polynomials, e.g., $P=4$, also in this case where a very complex-shaped domain is subjected to analysis. Figure 9b shows that the FEM approach appears to be the less efficient. Indeed it required longer times than $P=4$, as can be seen in Figure 9a, still not being able to further reduce the corresponding errors, see Figure 8a.

4. Conclusions

In this work a fully meshless approach is applied to the simulation of heat conduction problems. The code is verified according to the Method of Manufactured Solutions, and it is proven to be reliable and suitable for practical applications, even with convective boundary conditions. Indeed, the results presented in this paper exceeded the most optimistic expectations, especially on complex domains.

The potential of the RBF-FD meshless method lies both in its geometrical flexibility and its inclination towards parallelization: the root of its advantages can be found in the lack of connectivity information between the nodes.

As many simulations were carried over it became apparent that a key role was played by the node generation algorithm and the nearest-neighbors search algorithm. Different implementations of these routines yielded very different results when the code was verified over the engine domain. The proposed node generator allowed to properly leverage the great flexibility of the RBF-FD method, favoring performances over complex domains very much comparable to the ones attained on the spherical domain, both in terms of accuracy and consistency. Very interestingly such improvements were reached without any measurable increase in the computational cost of the whole solution procedure.

Speaking of computational cost, from the comparison between different polynomial basis it emerged an advantage of the ones with higher degrees when error vs. time was considered. We remark that most mesh-based commercial CFD CAE software only allow second-order accuracy and therefore cannot take advantage of the gain in performance permitted by higher orders. Such an advantage seems somehow reduced when Robin b.c. are applied to complex geometries; however, the results exposed above were attained with uniform spacing between nodes. Great improvements in the results are expected by the application of some local refinement algorithm, as usually employed also in mesh-based solvers. Such a refinement routine would be required to generate more inner nodes in close proximity to those geometrical features where the available space is otherwise insufficient, thus providing better RBF interpolants. Nonetheless, the presented meshless approach allowed better performances in terms of both absolute errors and computational efficiency when compared with patch-conforming quadratic FEM, highlighting the great advantages of the employed RBF-FD approach.

Julia language proved to be very convenient and highly efficient at the same time, allowing extensive code reuse and making parallelization fairly easy. Furthermore, the use of a single programming language ensured better integration between the node generator and the solver and made it possible to measure the total computational times reported in the results.

Future developments in the short term are the implementation of an autonomous node-refinement algorithm and an algebraic multilevel solver. Finally, the simulation of problems based on Navier–Stokes equations is planned for the near future.

Overcoming the need to generate a mesh constitute a great advantage over traditional CAE software, potentially making the design process far more convenient and democratic. This is why, also encouraged by the promising results reported in the present work, we believe that RBF-FD method will rapidly grow in popularity and become a major resource in the years to come.