Pore-Scale Simulation of Confined Phase Behavior with Pore Size Distribution and Its Effects on Shale Oil Production
Abstract
1. Introduction
2. Methodologies
2.1. Pseudopotential Lattice Boltzmann Method
2.2. Thermodynamic Modeling of Vapor-Liquid Equilibrium
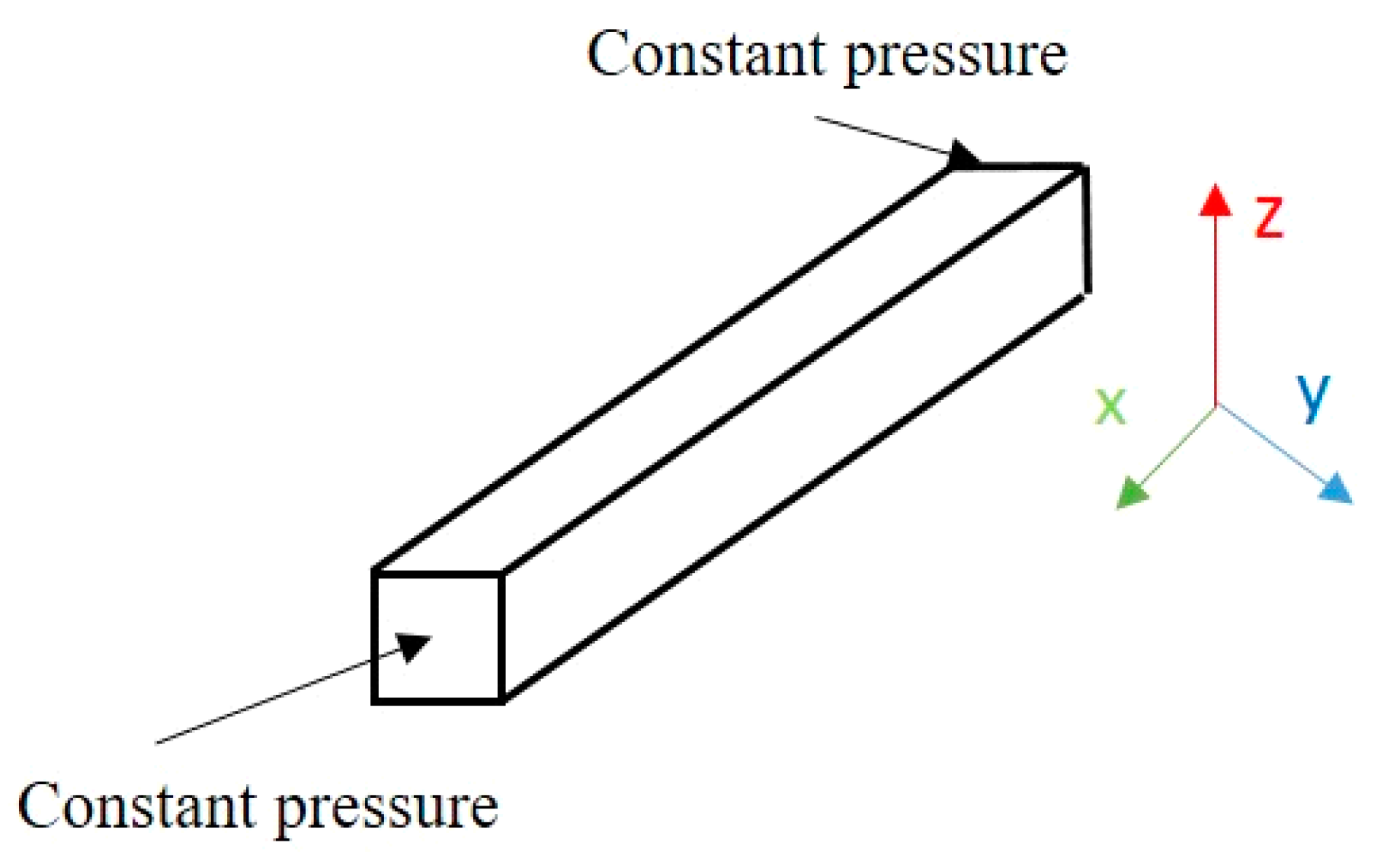
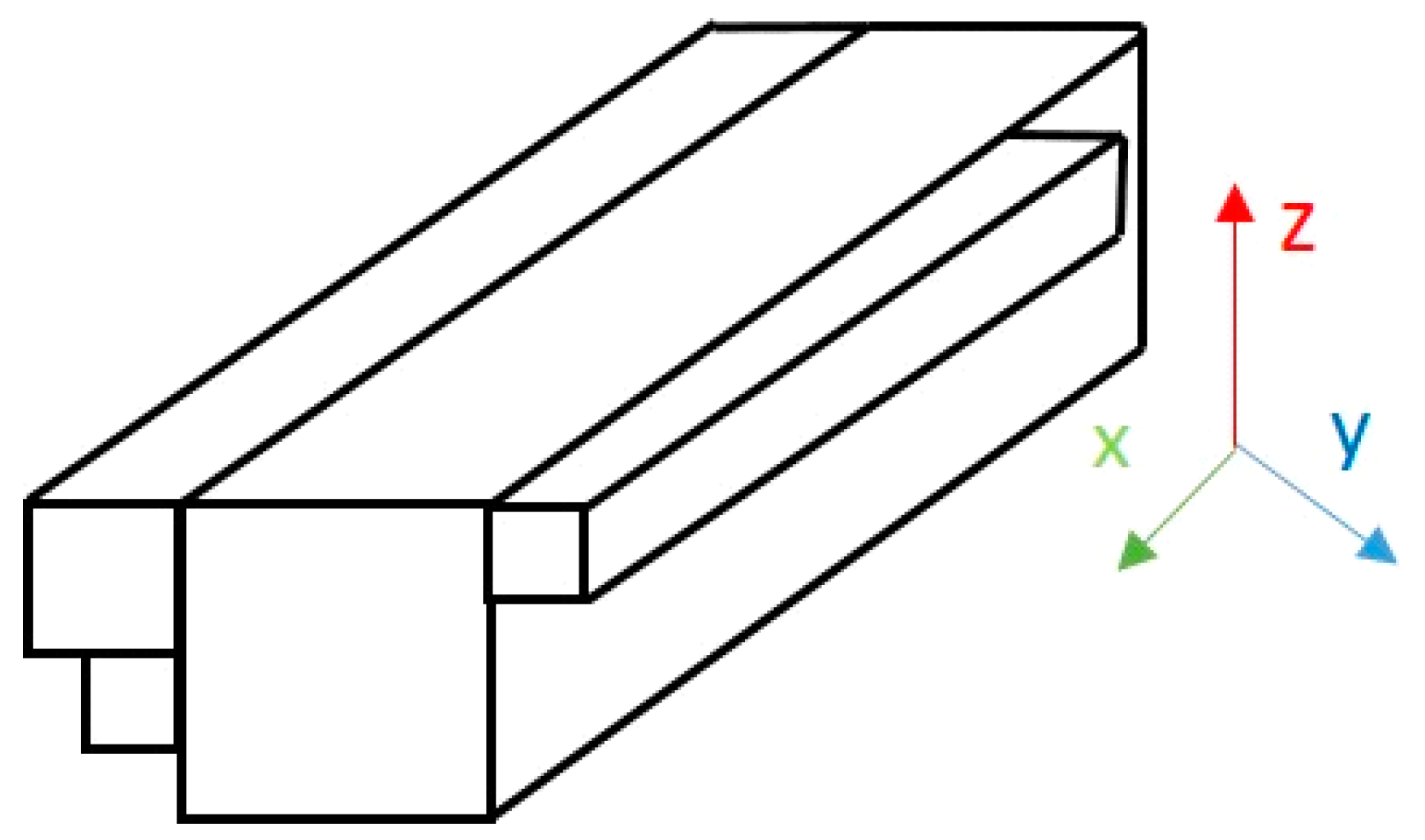
2.3. Simulation of Production from Shale Reservoir
3. Results and Discussion
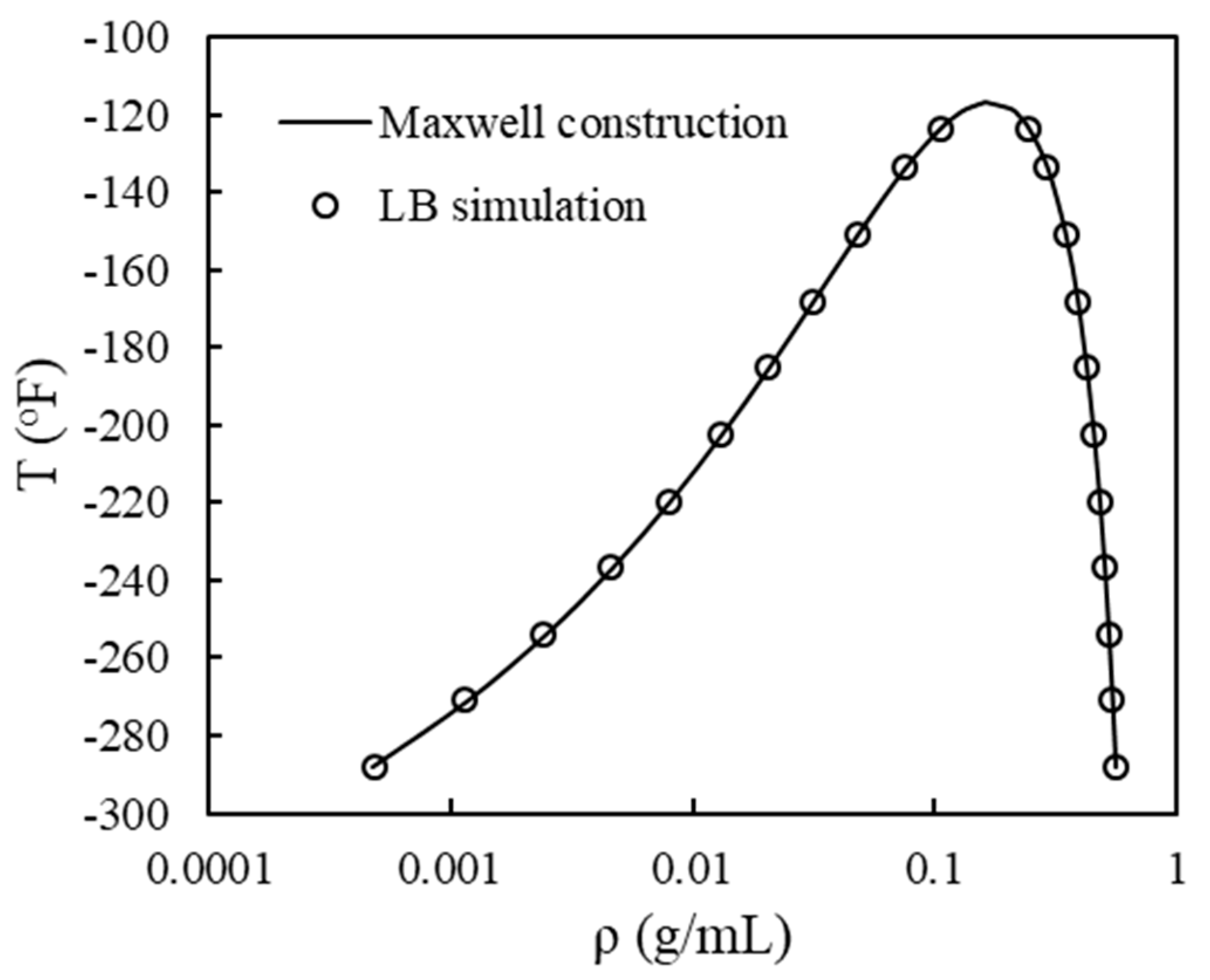
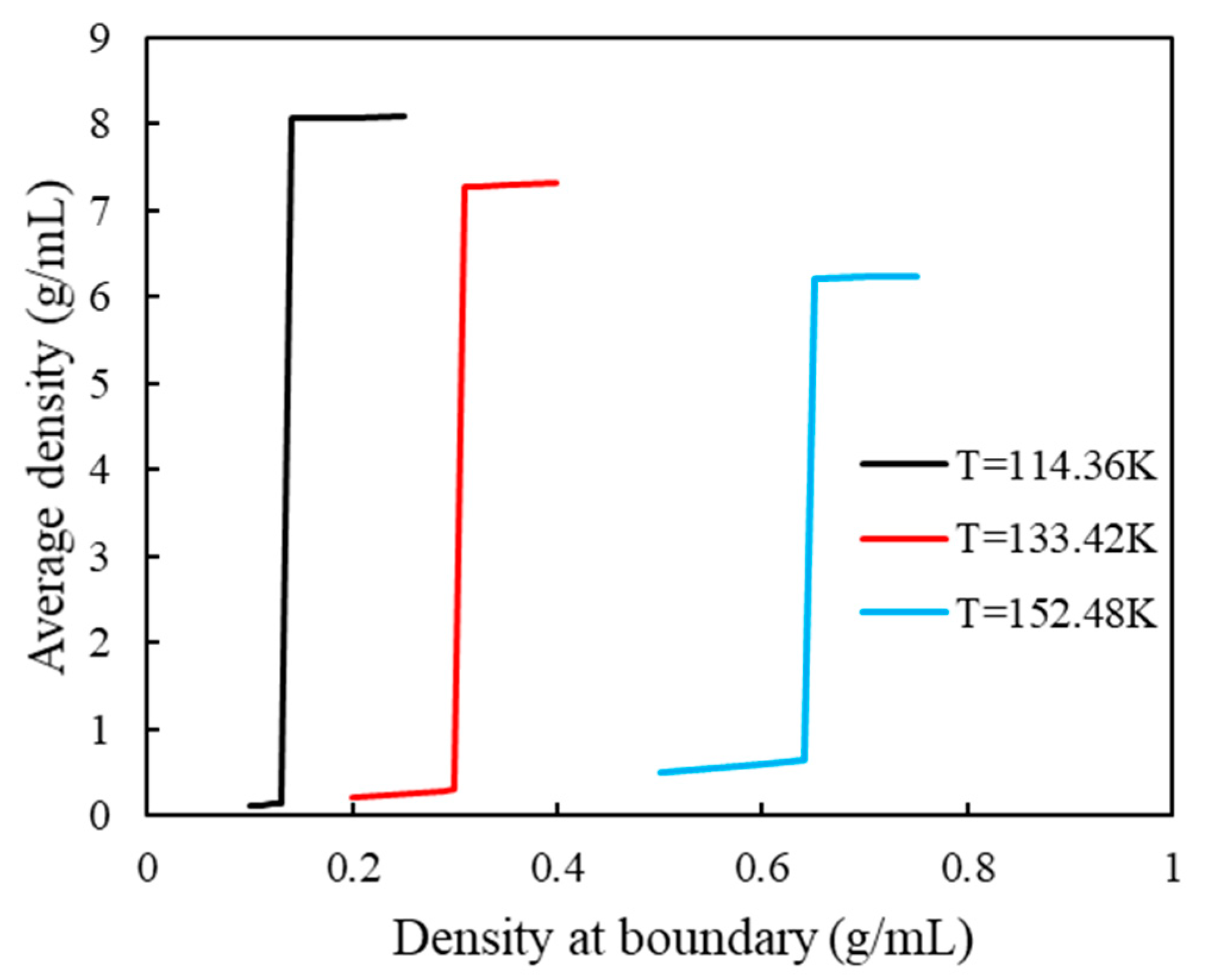
3.1. Phase Equilibrium in a Single Pore
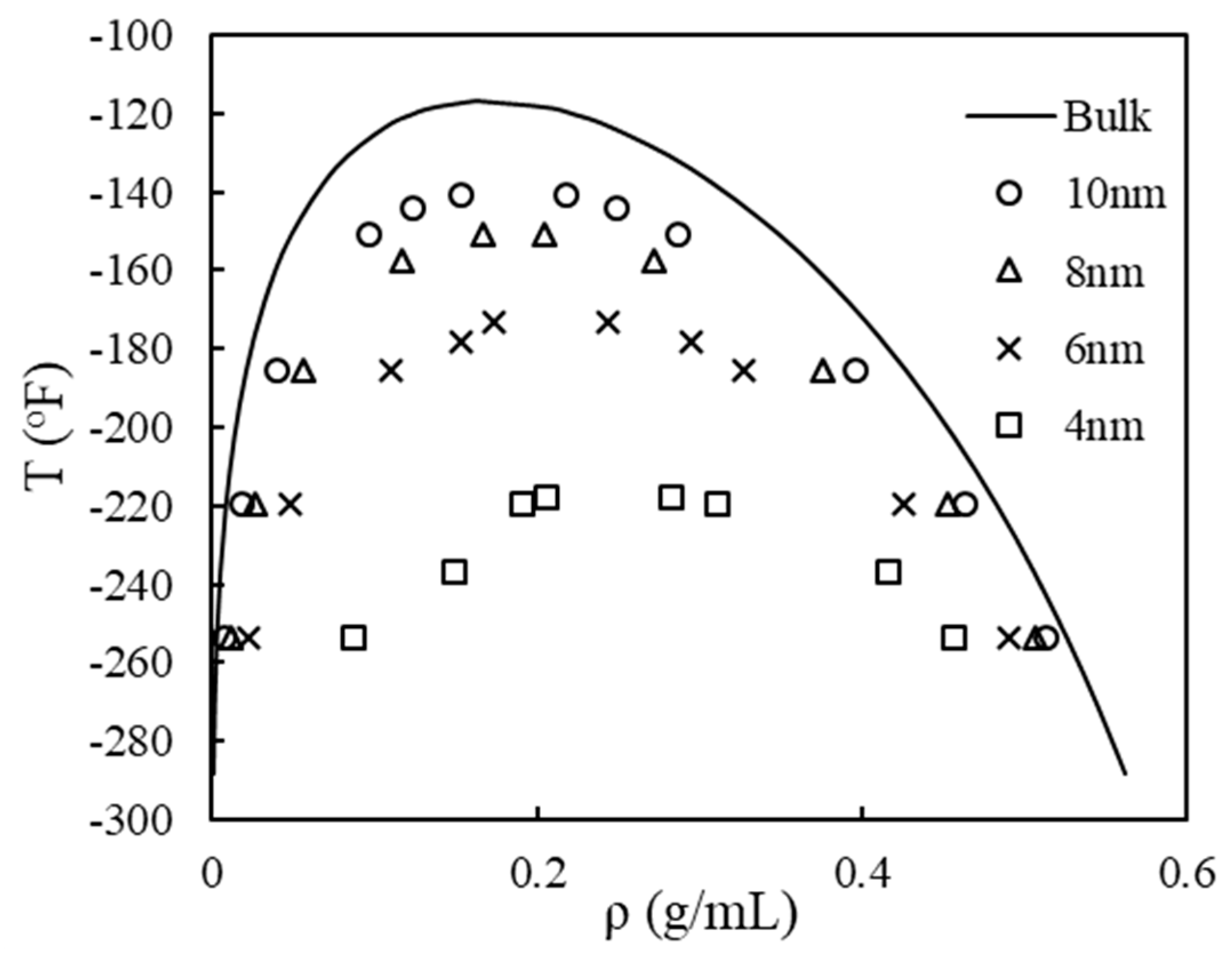
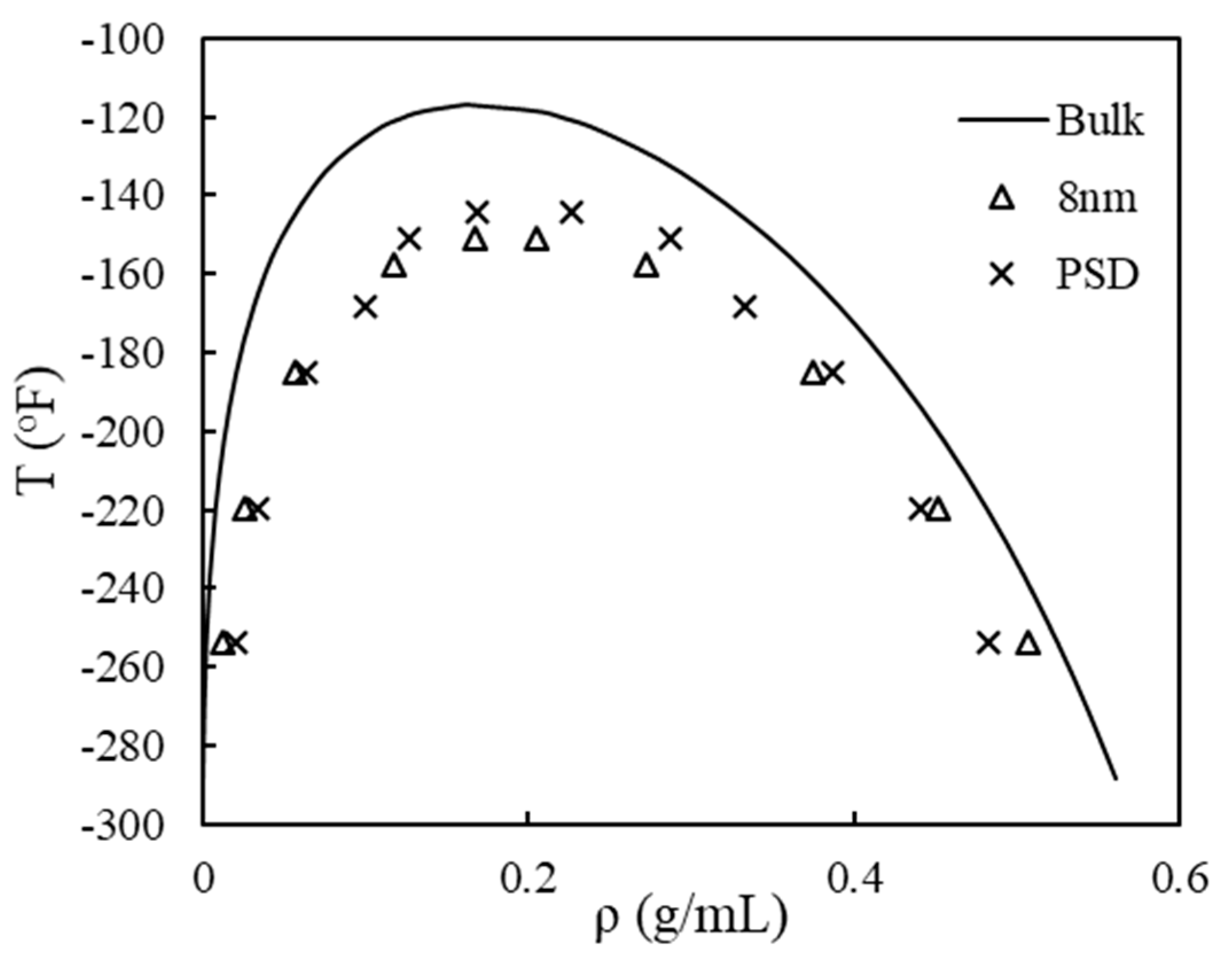
3.2. Phase Equilibrium with the Pore Size Distribution
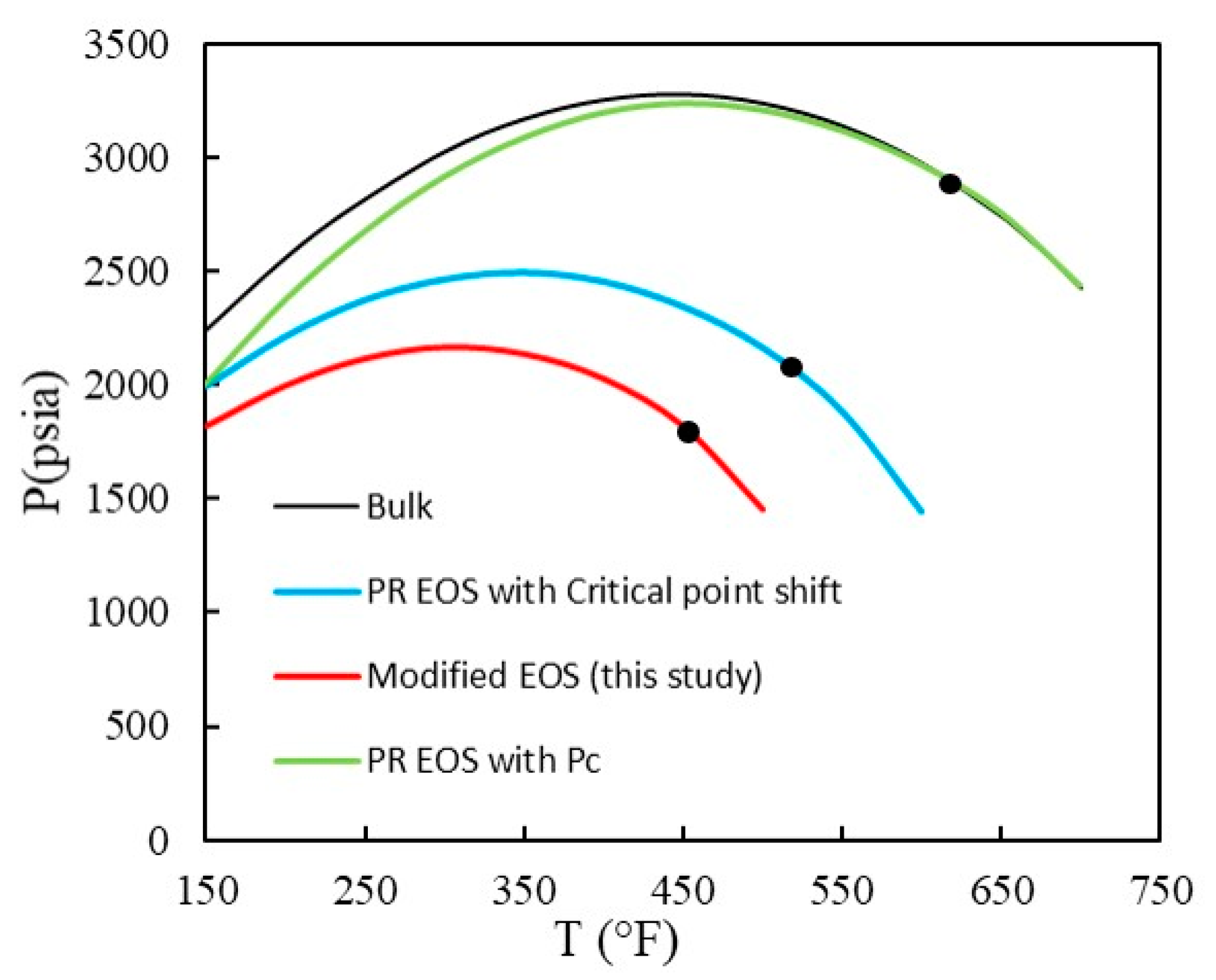
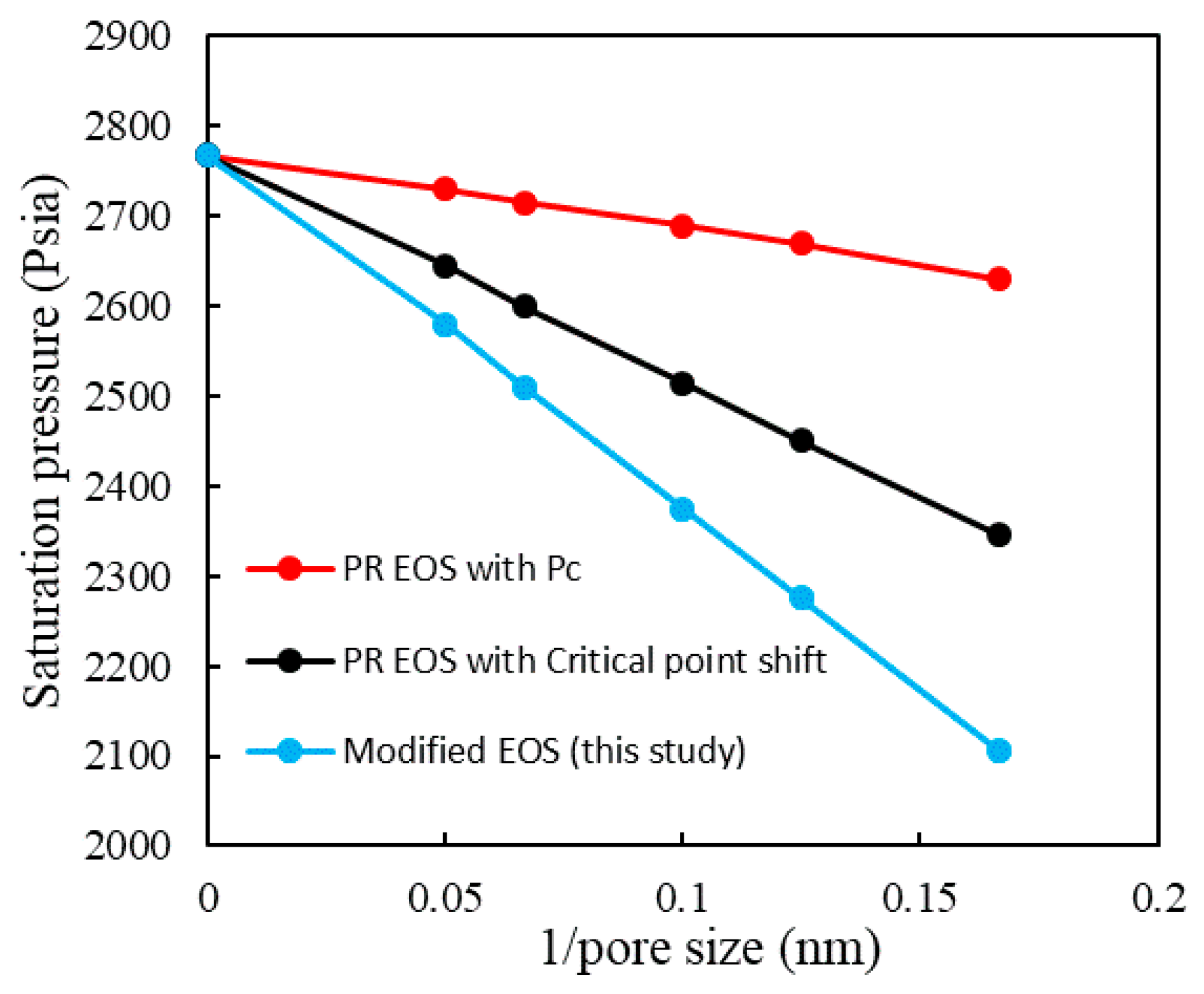
3.3. Modified EOS from Pore-Scale Simulation
3.4. Compositional Simulation of Shale Reservoir Considering Confined Phase Bahavior
4. Conclusions
- By comparing constructed coexistence curves, we propose that an effective pore size can be used to represent a real rock sample with distributed nanopores.
- Shifted critical properties and suppressed bubble points were observed when using the modified EOS.
- Compared to methods using capillary pressure and critical shift, the phase diagram using modified EOS shrinks more significantly.
- Compositional simulation indicated that both oil and gas production will increase if modified EOS is implemented. Considering capillary pressure or shifted critical point only will underestimate oil and gas production and ultimate recovery from shale reservoir.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| discrete set of velocity vectors | |
| fugacity of component i in liquid phase | |
| fugacity of component i in vapor phase | |
| velocity distribution function of particles | |
| distribution function at equilibrium state | |
| fluid pressure, Psi | |
| critical pressure, Psi | |
| capillary pressure, Psi | |
| pore radius, nm | |
| universal gas constant | |
| switch function, 0 or 1 | |
| oil saturation | |
| gas saturation | |
| critical temperature, °F | |
| initial width of interface | |
| position of particles | |
| fluid density, g/mL | |
| liquid density, g/mL | |
| vapor density, g/mL | |
| fluid viscosity | |
| pseudopotential | |
| weighting parameter | |
| interfacial tension in real unit [N/m] | |
| contact angle | |
| porosity |
References
- Yu, W.; Lashgari, H.R.; Wu, K.; Sepehrnoori, K. CO2 injection for enhanced oil recovery in Bakken tight oil reservoirs. Fuel 2015, 159, 354–363. [Google Scholar] [CrossRef]
- Hu, X.; Li, M.; Peng, C.; Davarpanah, A. Hybrid thermal-chemical enhanced oil recovery methods; an experimental study for tight reservoirs. Symmetry 2020, 12, 947. [Google Scholar] [CrossRef]
- Hu, X.; Xie, J.; Cai, W.; Wang, R.; Davarpanah, A. Thermodynamic effects of cycling carbon dioxide injectivity in shale reservoirs. J. Pet. Sci. Eng. 2020, V195, 107717. [Google Scholar] [CrossRef]
- Yang, G.; Fan, Z.; Li, X. Determination of confined fluid phase behavior using extended Peng-Robinson equation of state. Chem. Eng. J. 2019, 378, 122032. [Google Scholar] [CrossRef]
- Pommer, M.; Milliken, K. Pore types and pore-size distributions across thermal maturity, Eagle Ford Formation, southern Texas. AAPG Bull. 2015, 99, 1713–1744. [Google Scholar] [CrossRef]
- Nojabaei, B.; Johns, R.T.; Chu, L. Effect of capillary pressure on phase behavior in tight rocks and shales. SPE Reserv. Eval. Eng. 2013, 16, 281–289. [Google Scholar] [CrossRef]
- Davarpanah, A.; Mirshekari, B. Experimental Investigation and Mathematical Modeling of Gas Diffusivity by Carbon Dioxide and Methane Kinetic Adsorption. Ind. Eng. Chem. Res. 2019, 58, 12392–12400. [Google Scholar] [CrossRef]
- Sanaei, A.; Ma, Y.; Jamili, A. Nanopore Confinement and Pore Connectivity Considerations in Modeling Unconventional Resources. J. Energy Resour. Technol. 2019, 141, 012904. [Google Scholar] [CrossRef]
- Qiao, S.Z.; Bhatia, S.K.; Nicholson, D. Study of hexane adsorption in nanoporous MCM-41 silica. Langmuir 2004, 20, 389–395. [Google Scholar] [CrossRef]
- Russo, P.A.; Carrott, M.M.L.R.; Carrott, P.J.M. Hydrocarbons adsorption on templated mesoporous materials: Effect of the pore size, geometry and surface chemistry. New J. Chem. 2011, 35, 407–416. [Google Scholar] [CrossRef]
- Morishige, K.; Fujii, H.; Uga, M.; Kinukawa, D. Capillary critical point of argon, nitrogen, oxygen, ethylene, and carbon dioxide in MCM-41. Langmuir 1997, 13, 3494–3498. [Google Scholar] [CrossRef]
- Wang, L.; Parsa, E.; Gao, Y.; Ok, J.T.; Neeves, K.; Yin, X.; Ozkan, E. Experimental study and modeling of the effect of nanoconfinement on hydrocarbon phase behavior in unconventional reservoirs. In Proceedings of the SPE Western North American and Rocky Mountain Joint Meeting, Denver, CO, USA, 17–18 April 2014. [Google Scholar]
- Parsa, E.; Yin, X.; Ozkan, E. Direct observation of the impact of nanopore confinement on petroleum gas condensation. In Proceedings of the SPE Annual Technical Conference and Exhibition, Society of Petroleum Engineers, Houston, TX, USA, 27–30 September 2015. [Google Scholar]
- Alfi, M.; Nasrabadi, H.; Banerjee, D. Experimental investigation of confinement effect on phase behavior of hexane, heptane and octane using lab-on-a-chip technology. Fluid Phase Equilib. 2016, 423, 25–33. [Google Scholar] [CrossRef]
- Alfi, M.; Nasrabadi, H.; Banerjee, D. Effect of confinement on bubble point temperature shift of hydrocarbon mixtures: Experimental investigation using nanofluidic devices. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 9–11 October 2017. [Google Scholar]
- Yang, Q.; Jin, B.; Banerjee, D.; Nasrabadi, H. Direct visualization and molecular simulation of dew point pressure of a confined fluid in sub-10nm slit pores. Fuel 2019, 235, 1216–1223. [Google Scholar] [CrossRef]
- Sedghi, M.; Piri, M. Capillary condensation and capillary pressure of methane in carbon nanopores: Molecular Dynamics simulations of nanoconfinement effects. Fluid Phase Equilib. 2018, 459, 196–207. [Google Scholar] [CrossRef]
- Ambrose, R.J.; Hartman, R.C.; Diaz-Campos, M.; Akkutlu, I.Y.; Sondergeld, C.H. Shale gas-in-place calculations part I: New pore-scale considerations. SPE J. 2012, 17, 219–229. [Google Scholar] [CrossRef]
- Peterson, B.K.; Gubbins, K.E. Phase transitions in a cylindrical pore. Mol. Phys. 1987, 62, 215–226. [Google Scholar] [CrossRef]
- Hamada, Y.; Koga, K.; Tanaka, H. Phase equilibria and interfacial tension of fluids confined in narrow pores. J. Chem. Phys. 2007, 127, 084908. [Google Scholar] [CrossRef] [PubMed]
- Singh, S.K.; Sinha, A.; Deo, G.; Singh, J.K. Vapor−liquid phase coexistence, critical properties, and surface tension of confined alkanes. J. Phys. Chem. C 2009, 113, 7170–7180. [Google Scholar] [CrossRef]
- Singh, S.K.; Singh, J.K. Effect of pore morphology on vapor–liquid phase transition and crossover behavior of critical properties from 3D to 2D. Fluid Phase Equilib. 2011, 300, 182–187. [Google Scholar] [CrossRef]
- Vishnyakov, A.; Piotrovskaya, E.M.; Brodskaya, E.N.; Tovbin, Y.K. Critical properties of Lennard-Jones fluids in narrow slit-shaped pores. Langmuir 2001, 17, 4451–4458. [Google Scholar] [CrossRef]
- Huang, J.; Yin, X.; Killough, J. Thermodynamic consistency of a pseudopotential lattice Boltzmann fluid with interface curvature. Phys. Rev. E 2019, 100, 053304. [Google Scholar] [CrossRef]
- Huang, J.; Yin, X.; Barrufet, M.; Killough, J. Lattice Boltzmann Simulation of Phase Behavior of Hydrocarbons in Nanopores: Role of Capillary Pressure and Fluid-Solid Interaction. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 26–29 October 2020. SPE-201458-MS. [Google Scholar]
- Li, Z.; Firoozabadi, A. Interfacial tension of nonassociating pure substances and binary mixtures by density functional theory combined with Peng–Robinson equation of state. J. Chem. Phys. 2009, 130, 154108. [Google Scholar] [CrossRef]
- Jin, Z.; Firoozabadi, A. Thermodynamic Modeling of Phase Behavior in Shale Media. SPE J. 2016, 21, 190–207. [Google Scholar] [CrossRef]
- Li, Z.; Jin, Z.; Firoozabadi, A. Phase behavior and adsorption of pure substances and mixtures and characterization in nanopore structures by density functional theory. SPE J. 2014, 19, 1096–1109. [Google Scholar] [CrossRef]
- Stimpson, B.C.; Barrufet, M.A. Thermodynamic Modeling of Pure Components Including the Effects of Capillarity. J. Chem. Eng. Data 2016, 61, 2844–2850. [Google Scholar] [CrossRef]
- Du, F.; Nojabaei, B. A black-oil approach to model produced gas injection in both conventional and tight oil-rich reservoirs to enhance oil recovery. Fuel 2020, V263, 116680. [Google Scholar] [CrossRef]
- Huang, J.; Jin, T.; Chai, Z.; Barrufet, M.; Killough, J. Compositional simulation of fractured shale reservoir with distribution of nanopores using coupled multi-porosity and EDFM method. J. Pet. Sci. Eng. 2019, 179, 1078–1089. [Google Scholar] [CrossRef]
- Zarragoicoechea, G.J.; Kuz, V.A. Critical shift of a confined fluid in a nanopore. Fluid Phase Equilib. 2004, 220, 7–9. [Google Scholar] [CrossRef]
- Alharthy, N.S.; Nguyen, T.; Teklu, T.; Kazemi, H.; Graves, R. Multiphase compositional modeling in small-scale pores of unconventional shale reservoirs. In Proceedings of the SPE Annual Technical Conference and Exhibition, Society of Petroleum Engineers, New Orleans, LA, USA, 30 September–2 October 2013. [Google Scholar]
- Du, F.; Huang, J.; Chai, Z.; Killough, J. Effect of vertical heterogeneity and nano-confinement on the recovery performance of oil-rich shale reservoir. Fuel 2020, 267, 117199. [Google Scholar] [CrossRef]
- Luo, S.; Jin, B.; Lutkenhaus, J.L.; Nasrabadi, H. A novel pore-size-dependent equation of state for modeling fluid phase behavior in nanopores. Fluid Phase Equilib. 2019, 498, 72–85. [Google Scholar] [CrossRef]
- Travalloni, L.; Castier, M.; Tavares, F.W. Phase equilibrium of fluids confined in porous media from an extended Peng-Robinson equation of state, Fluid Phase Equilib. 2014, 362, 335–341. Fluid Phase Equilib. 2014, 362, 335–341. [Google Scholar] [CrossRef]
- Wang, Y.; Aryana, S.A. Coupled confined phase behavior and transport of methane in slit nanopores. Chem. Eng. J. 2021, 404, 126502. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, W.; Sepehrnoori, K.; Di, Y. Investigation of nanopore confinement on fluid flow in tight reservoirs. J. Petrol. Sci. Eng. 2017, 150, 265–271. [Google Scholar] [CrossRef]
- Haider, B.A.; Aziz, K. Impact of Capillary Pressure and Critical Property Shift due to Confinement on Hydrocarbon Production in Shale Reservoirs. In Proceedings of the SPE Reservoir Simulation Conference, Montgomery, TX, USA, 20–22 February 2017. Paper Number: SPE-182603-MS. [Google Scholar]
- Song, Z.; Song, Y.; Guo, J.; Feng, D.; Dong, J. Effect of Nanopore Confinement on Fluid Phase Behavior and Production Performance in Shale Oil Reservoir. Ind. Eng. Chem. Res. 2021, 60, 1463–1472. [Google Scholar] [CrossRef]
- d’Humières, D. Multiple–relaxation–time lattice Boltzmann models in three dimensions. Philosophical Transactions of the Royal Society of London. Ser. A Math. Phys. Eng. Sci. 2002, 360, 437–451. [Google Scholar]
- Gong, S.; Cheng, P. Numerical investigation of droplet motion and coalescence by an improved lattice Boltzmann model for phase transitions and multiphase flows, Comput. Fluids 2012, 53, 93–104. [Google Scholar]
- Yuan, P.; Schaefer, L. Equations of state in a lattice Boltzmann model. Phys. Fluids 2006, 18, 042101. [Google Scholar] [CrossRef]
- Li, Q.; Luo, K.H.; Kang, Q.J.; Chen, Q. Contact angles in the pseudopotential lattice Boltzmann modeling of wetting. Phys. Rev. E. 2014, 2014, 053301. [Google Scholar] [CrossRef]
- Kupershtokh, A.L.; Medvedev, D.A.; Karpov, D.I. On equations of state in a lattice Boltzmann method. Comput. Math. Appl. 2009, 58, 965–974. [Google Scholar] [CrossRef]
- Yan, B.; Wang, Y.; Killough, J.E. A fully compositional model considering the effect of nanopores in tight oil reservoirs. J. Pet. Sci. Eng. 2017, 152, 675–682. [Google Scholar] [CrossRef]
- Chai, Z.; Yan, B.; Killough, J.E.; Wang, Y. An efficient method for fractured shale reservoir history matching: The embedded discrete fracture multi-continuum approach. J. Pet. Sci. Eng. 2018, 160, 170–181. [Google Scholar] [CrossRef]
- Chai, Z.; Tang, H.; He, Y.; Killough, J.E.; Wang, Y. Uncertainty Quantification of the Fracture Network with a Novel Fractured Reservoir Forward Model. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 24–26 September 2018. SPE-191395-MS. [Google Scholar]
- Clarkson, C.R.; Solano, N.; Bustin, R.M.; Bustin, A.M.M.; Chalmers, G.R.L.; He, L.; Melnichenko, Y.B.; RadliÅski, A.P.; Blach, T.P. Pore structure characterization of north american shale gas reservoirs using usans/sans, gas adsorption, and mercury intrusion. Fuel 2013, 103, 606–616. [Google Scholar] [CrossRef]
- Jin, B.; Bi, R.; Nasrabadi, H. Molecular simulation of the pore size distribution effect on phase behavior of methane confined in nanopores. Fluid Phase Equilib. 2017, V452, 94–102. [Google Scholar] [CrossRef]




| Component | Mole Fraction | Critical Pressure (Psia) | Critical Temperature (°F) | Acentric Factor | Mole Weight | Parachor |
|---|---|---|---|---|---|---|
| C1 | 0.36736 | 655.02 | −124.33 | 0.01020 | 16.54 | 74.8 |
| C2–C3 | 0.24219 | 681.05 | 135.01 | 0.12176 | 35.70 | 124.7 |
| C4–C6 | 0.12157 | 501.58 | 360.81 | 0.23103 | 68.75 | 221.5 |
| C7–C12 | 0.15854 | 363.34 | 593.58 | 0.42910 | 120.56 | 350.2 |
| C13–C80 | 0.11034 | 229.64 | 1044.43 | 0.81953 | 295.51 | 800.4 |
| C1 | C2–C3 | C4–C6 | C7–C12 | C13–C80 | |
|---|---|---|---|---|---|
| C1 | 0 | ||||
| C2–C3 | 0.0044 | 0 | |||
| C4–C6 | 0.0036 | 0.0019 | 0 | ||
| C7–C12 | 0.0033 | 0.0016 | 0 | 0 | |
| C13–C80 | 0.0033 | 0.0016 | 0 | 0 | 0 |
| Properties of Reservior | |
|---|---|
| Reservoir pressure (Psia) | 3700 |
| Reservoir temperature (°F) | 240 |
| Bottom-hole pressure (Psia) | 1000 |
| Porosity | 0.08 |
| Reservior dimension | 45 × 21 × 1 |
| Grid size (ft) | 50 × 50 × 50 |
| Pore diameter (nm) | 8 |
| Permeability (nd) | 300 |
| Water saturation | 0.10 |
| Properties of Fracture | |
| Number of hydraulic fractures | 17 |
| Conductivity of hydraulic fractures (mD.ft) | 200 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, J.; Wang, H. Pore-Scale Simulation of Confined Phase Behavior with Pore Size Distribution and Its Effects on Shale Oil Production. Energies 2021, 14, 1315. https://doi.org/10.3390/en14051315
Huang J, Wang H. Pore-Scale Simulation of Confined Phase Behavior with Pore Size Distribution and Its Effects on Shale Oil Production. Energies. 2021; 14(5):1315. https://doi.org/10.3390/en14051315
Chicago/Turabian StyleHuang, Jingwei, and Hongsheng Wang. 2021. "Pore-Scale Simulation of Confined Phase Behavior with Pore Size Distribution and Its Effects on Shale Oil Production" Energies 14, no. 5: 1315. https://doi.org/10.3390/en14051315
APA StyleHuang, J., & Wang, H. (2021). Pore-Scale Simulation of Confined Phase Behavior with Pore Size Distribution and Its Effects on Shale Oil Production. Energies, 14(5), 1315. https://doi.org/10.3390/en14051315




