On the Experimental, Numerical and Data-Driven Methods to Study Urban Flows
Abstract
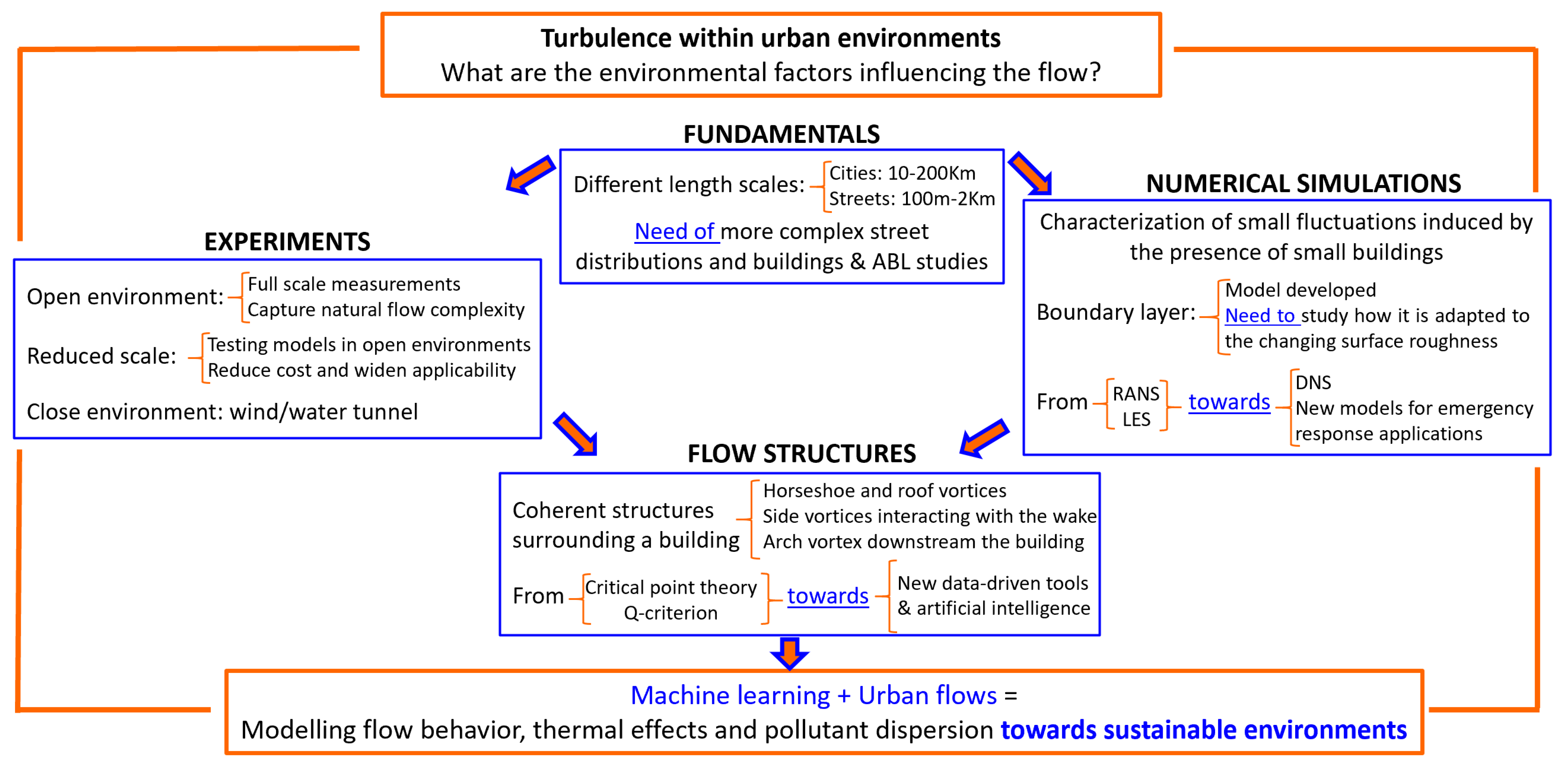
1. Motivation
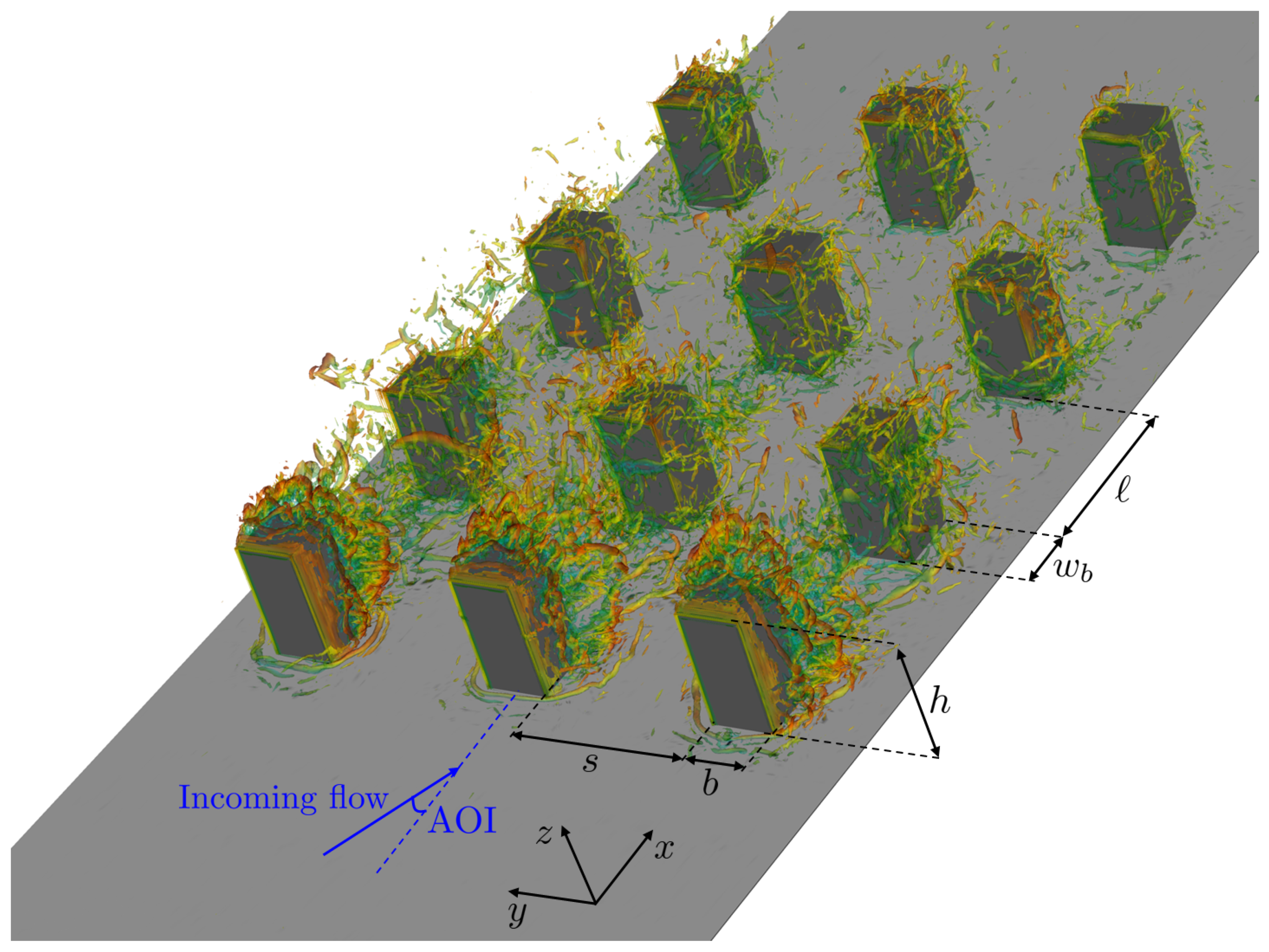
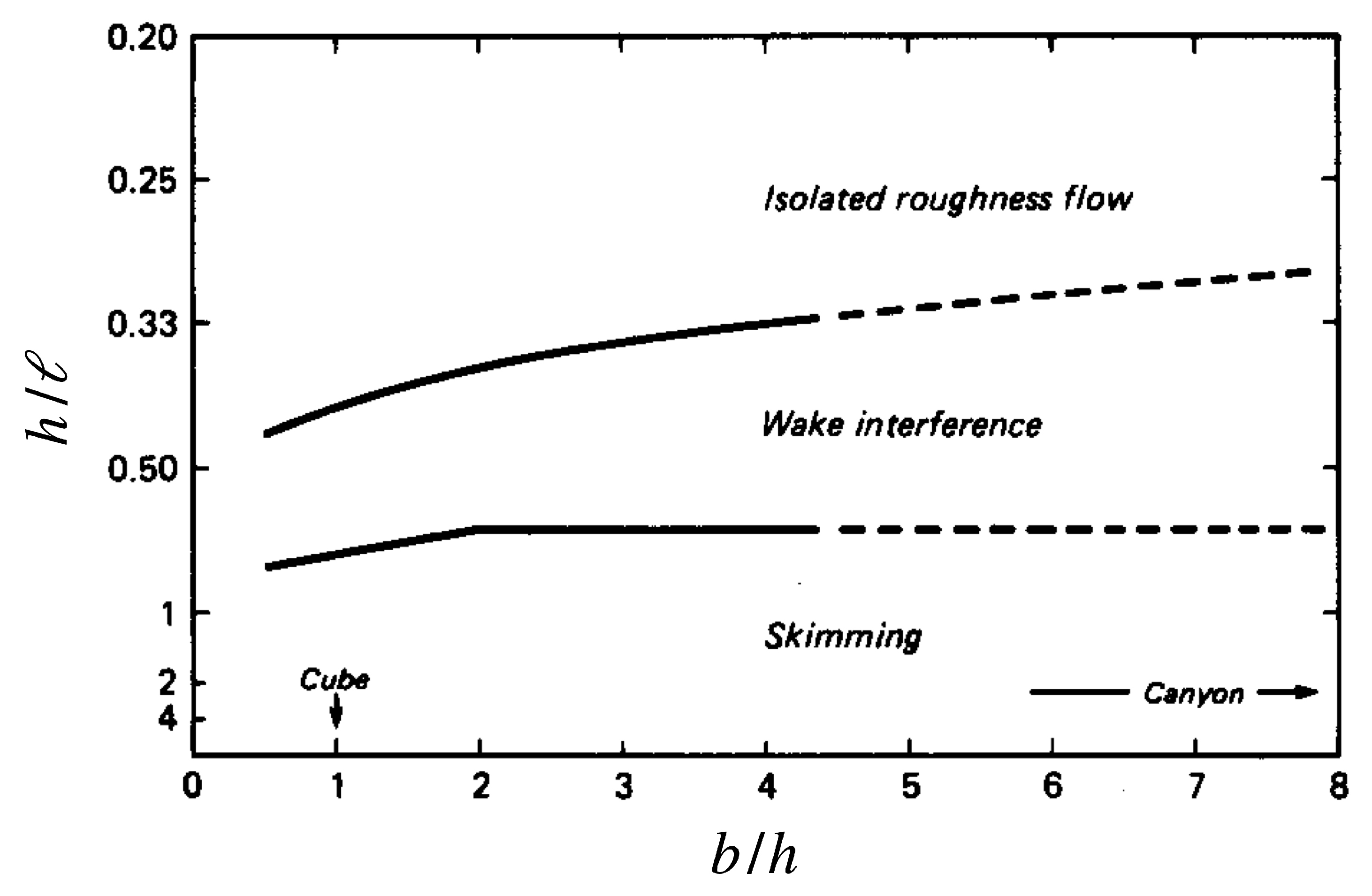
2. Fundamentals of Urban Flows
3. Experimental Studies
3.1. Open-Environment Experiments
3.1.1. Full-Scale Measurements
3.1.2. Reduced-Scale Measurements
3.2. Closed-Environment Experiments
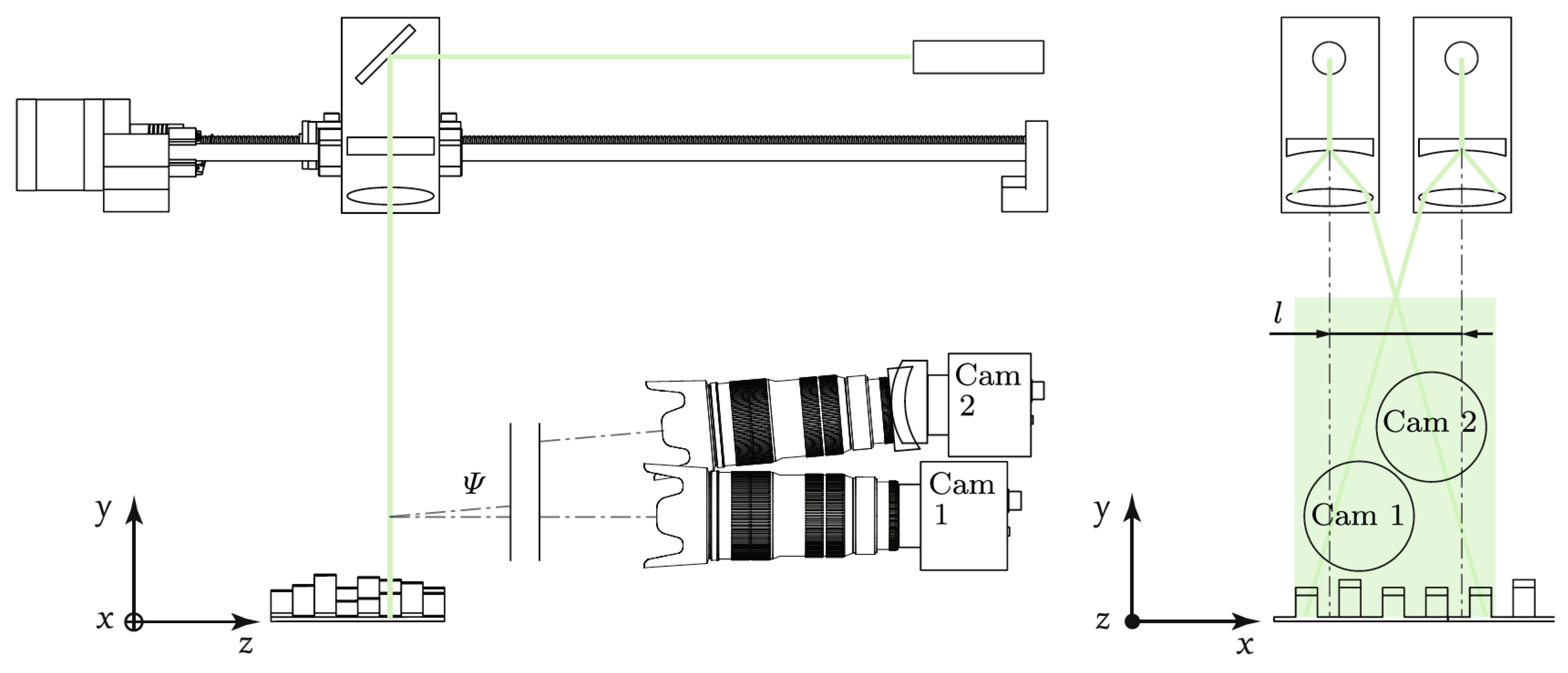
Closed-Environment Experiments with Particle Image Velocimetry
3.3. Experiments Combining Various Techniques
4. Numerical Studies
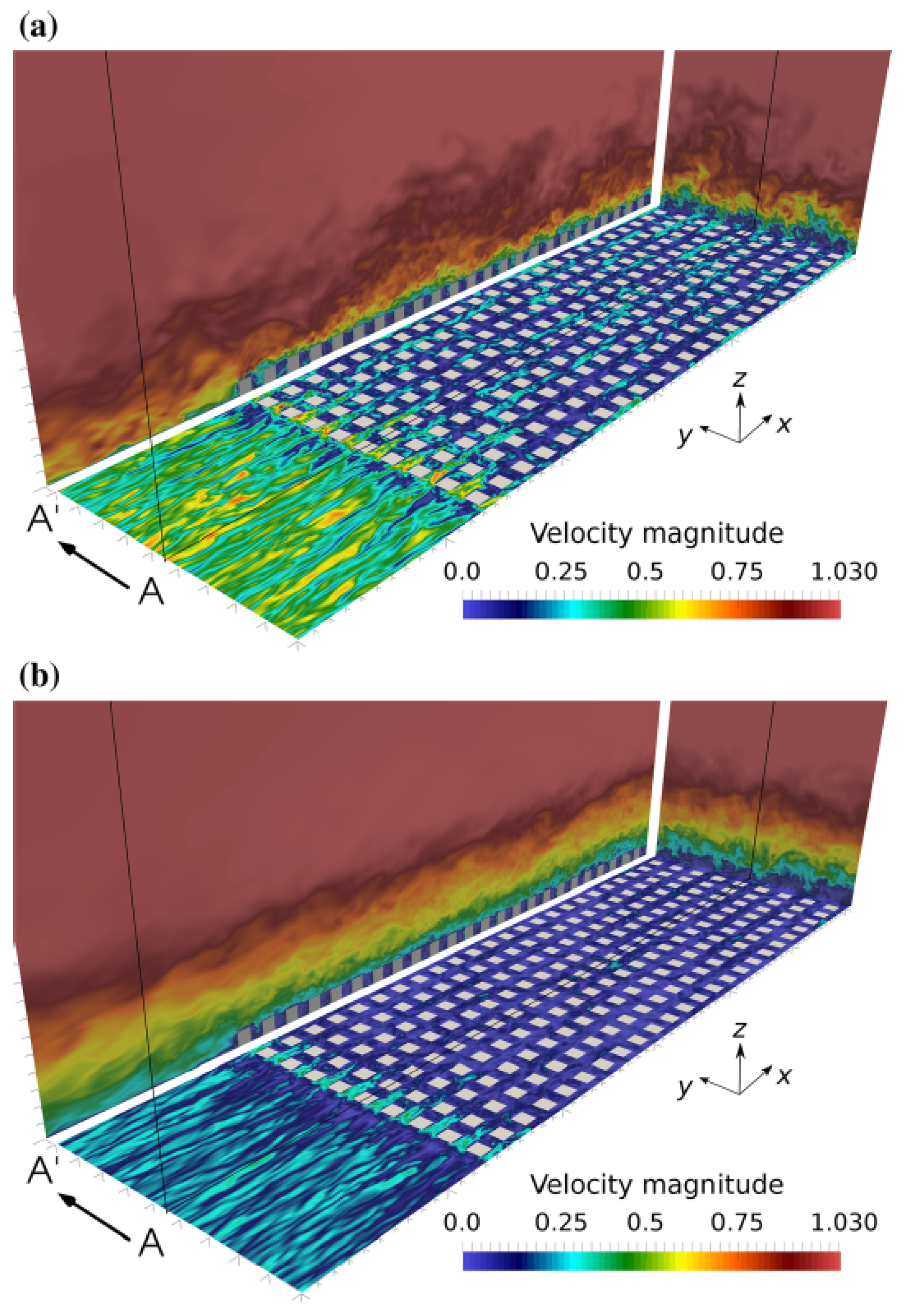
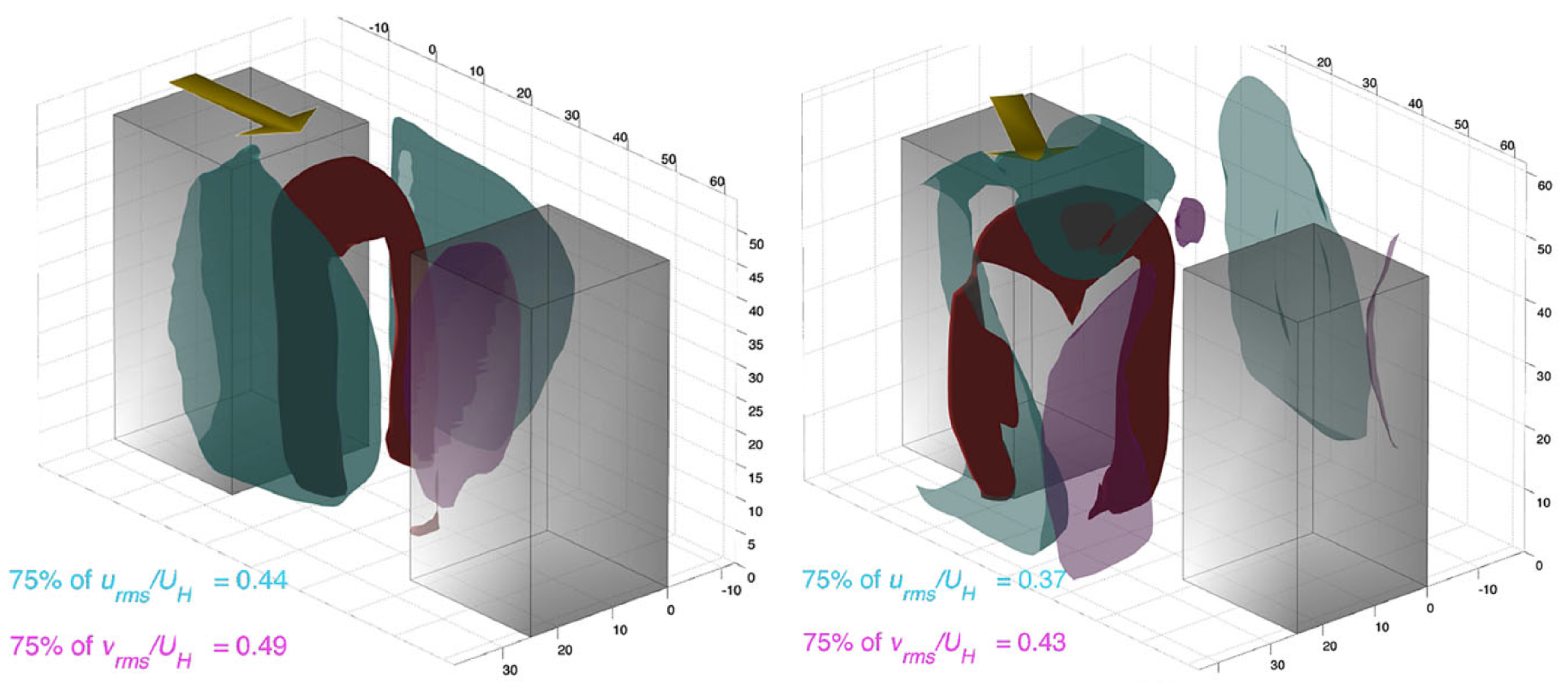
5. Flow Structures and Data-Driven Methods
6. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Summary of Modal Decompositions
Appendix A.1. Singular Value Decomposition and Proper Orthogonal Decomposition
Appendix A.2. Spectral Proper Orthogonal Decomposition
Appendix A.3. Dynamic Mode Decomposition and Higher-Order Dynamic Mode Decomposition
- Step 1: dimension reduction. Applying truncated singular value decomposition (SVD) to the snapshot matrix yields:The matrix is the dimension-reduced snapshot matrix. The number of SVD modes retained in this approximation N is defined as the spatial complexity. These modes are selected as in the SVD algorithm presented in Appendix A.1. A (tunable) tolerance estimates the standard SVD error, as described in Equation (A6).
- Step 2: the DMD-d algorithm for the dimension-reduced snapshots. The high-order Koopman assumption is applied to the reduced snapshot matrix, resulting in:After some calculations, the several Koopman operators are grouped into a single matrix, the eigenvalue problem of which provides the DMD modes, frequencies and growth rates that define the DMD expansion (A7). This expansion is sorted in decreasing order of the mode amplitudes and it is further truncated by eliminating the modes such that:for some tunable parameter . The number of modes retained in this expansion, M, is called as the spectral complexity.
Appendix A.4. Some Variants of DMD Not Related to Time-Lagged Snapshots
- Sparsity-promoting DMD [187]. This method uses convex optimization techniques to identify a smaller set of important modes.
- Extended DMD [188]. This algorithm includes more basis functions in the standard DMD approximation, a fact that allows the method to retain more modes, thus enabling the description of more complex dynamical systems.
- Optimized DMD [189]. An optimization problem is solved to compute the DMD expansion (A7). Both DMD and HODMD are purely linear-algebra-driven approaches compared to optimized DMD. Furthermore, other authors [190] have developed other linear-algebra-oriented algorithms which treat separable nonlinear least-squares problems.
- DMD variants to treat noisy data. Several authors have put an effort on identifying and removing noise from the analysed data. Among other techniques it is important to mention the method by Dawson et al. [191], which characterizes the noise properties; the total least-squares DMD by Hemati et al. [192], which combines standard DMD with total least squares; and the method by Takeishi et al. [193], which combines standard DMD with a Bayesian formulation.
- Multi-resolution DMD (mrDMD) [194]. The main idea behind mrDMD is to separate the high- and low-frequency events which generally occur in complex flows. The algorithm divides the snapshot matrix (A1) into several segments to identify high- and low-frequency modes depending on the segment length. The resulting DMD expansion (A7) is then represented by the various sub-expansions of DMD modes with different frequency ranges. A similar idea is behind the multi-resolution POD algorithm [173].
References
- European Commission Urbanisation worldwide. Available online: https://ec.europa.eu/knowledge4policy/foresight/topic/continuing-urbanisation/urbanisation-worldwide_en (accessed on 10 September 2020).
- United Nations Climate Action. Cities and Pollution Contribute to Climate Change. Available online: https://www.un.org/en/climatechange/cities-pollution.shtml (accessed on 10 September 2020).
- United Nations Paris Agreement on Climate Change. 2015. Available online: https://unfccc.int/process-and-meetings/the-paris-agreement/the-paris-agreement (accessed on 10 September 2020).
- European Environment Agency. Air Quality in Europe—2019 Report; European Environment Agency: København, Denmark, 2019. [Google Scholar]
- Lelieveld, J.; Klingmüller, K.; Pozzer, A.; Pöschl, U.; Fnais, M.; Daiber, A.; Münzel, T. Cardiovascular disease burden from ambient air pollution in Europe reassessed using novel hazard ratio functions. Eur. Heart J. 2019, 40, 1590–1596. [Google Scholar] [CrossRef]
- Manoli, G.; Fatichi, S.; Schläpfer, M.; Yu, K.; Crowther, T.W.; Meili, N.; Burlando, P.; Katul, G.G.; Bou-Zeid, E. Magnitude of urban heat islands largely explained by climate and population. Nature 2019, 573, 55–60. [Google Scholar] [CrossRef] [PubMed]
- Heaviside, C.; Vardoulakis, S.; Cai, X.M. Attribution of mortality to the urban heat island during heatwaves in the West Midlands, UK. Environ. Healt 2016, 15, S27. [Google Scholar] [CrossRef] [PubMed]
- EC Air Quality Framework Directive. European Commission, ambient air quality assessment and management. In Council Directive 96/62/EC; European Environment Agency: København, Denmark, 1996. [Google Scholar]
- Carpentieri, M. Pollutant dispersion in the urban environment. Rev. Environ. Sci. Biotechnol. 2013, 12, 5–8. [Google Scholar] [CrossRef]
- Weng, Q. Thermal infrared remote sensing for urban climate and environmental studies: Methods, applications, and trends. ISPRS J. Photogramm. 2009, 64, 335–344. [Google Scholar] [CrossRef]
- UN General Assembly (UNGA). Transforming Our World: The 2030 Agenda for Sustainable Development; Resolut: London, UK, 2015; pp. 1–35. [Google Scholar]
- Vinuesa, R.; Azizpour, H.; Leite, I.; Balaam, M.; Dignum, V.; Domisch, S.; Domisch, S.; Felländer, A.; Langhans, S.D.; Tegmark, M.; et al. The role of artificial intelligence in achieving the Sustainable Development Goals. Nat. Commun. 2020, 11, 233. [Google Scholar] [CrossRef]
- Lumley, J.L. The Structure of Inhomogeneous Turbulent Flows. In Proceedings of the International Colloquium on the Fine Scale Structure of the Atmosphere and Its Influence on Radio Wave Propagation; Yaglam, A.M., Tatarsky, V.I., Eds.; Doklady Akademii Nauk SSSR: Nauka, Moscow, 1967. [Google Scholar]
- Schmid, P. Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 2010, 656, 5–28. [Google Scholar] [CrossRef]
- Luchini, P.; Bottaro, A. Adjoint equations in Stability Analysis. Annu. Rev. Fluid Mech. 2014, 46, 493–517. [Google Scholar] [CrossRef]
- Britter, R.E.; Hanna, S.R. Flow and dispersion in urban areas. Annu. Rev. Fluid Mech. 2003, 35, 469–496. [Google Scholar] [CrossRef]
- Grimmond, S.B.; Oke, T.R. Turbulent heat fluxes in urban areas: Observations and a local-scale urban meteorological parameterization schemes. J. Appl. Meteorol. 2002, 41, 792–810. [Google Scholar] [CrossRef]
- Oke, T.R. Street design and urban canopy layer climate. Energ. Build. 1988, 11, 103–112. [Google Scholar] [CrossRef]
- Sini, J.F.; Anquetin, S.; Mestayer, P.G. Pollutant dispersion and thermal effects in urban street canyons. Atmos. Environ. 1996, 30, 2659–2677. [Google Scholar] [CrossRef]
- Fisher, P.; Kruse, J.; Mullen, J.; Tufo, H.; Lottes, J.; Kerkemeier, S. Nek5000: Open Source Spectral Element CFD Solver. Available online: http://nek5000.mcs.anl.gov/ (accessed on 21 September 2020).
- Vinuesa, R.; Negi, P.S.; Atzori, M.; Hanifi, A.; Henningson, D.S.; Schlatter, P. Turbulent boundary layers around wing sections up to Rec=1,000,000. Int. J. Heat Fluid Flow 2018, 72, 86–99. [Google Scholar] [CrossRef]
- Jeong, J.; Hussain, F. On the identification of a vortex. J. Fluid Mech. 1995, 285, 69–94. [Google Scholar] [CrossRef]
- Torres, P. High-Order Spectral Simulations of the Flow in a Simplified Urban Environment. Bachelor’s Thesis, Polytechnic University of Valencia, Valencia, Spain, 2020. [Google Scholar]
- Zajic, D.; Fernando, H.J.S.; Calhoun, R.; Princevac, M.; Brown, M.J.; Pardyjak, E.R. Flow and Turbulence in an Urban Canyon. J. Appl. Meteorol. Climatol. 2011, 50, 203–223. [Google Scholar] [CrossRef]
- Britter, R.E.; Hunt, J.C.R. Velocity measurements and order of magnitude estimates of the flow between two buildings in a simulated atmospheric boundary layer. J. Ind. Aerodyn. 1975, 4, 165–182. [Google Scholar] [CrossRef]
- Penwarden, A.D.; Wise, A.F.E. Wind environments between buildings. In Building Research Establishment Report. Dept. of the Environment; H.M.S.O.: London, UK, 1975. [Google Scholar]
- Isyumov, N.; Davenport, A.G. The ground level wind environment in built-up area. Int. Conf. Wind. Eff. Build. Struct. 1977, 4, 165–182. [Google Scholar]
- Hlevca, D.; Degeratu, M. Atmospheric boundary layer modeling in a short wind tunnel. Eur. J. Mech. B/Fluids 2020, 79, 367–375. [Google Scholar] [CrossRef]
- Counihan, J. Adiabatic Atmospheric Boundary Layer: A Review of the Analysis of Data from the Period 1880–1972. Atmos. Environ. 1975, 9, 871–905. [Google Scholar] [CrossRef]
- Blocken, P.; Stathopoulos, T.; Carmeliet, J. CFD Simulation of the atmospheric boundary layer: Wall function problems. Atmos. Environ. 2007, 41, 238–252. [Google Scholar] [CrossRef]
- Martinuzzi, R.J.; Tropea, C. The flow around surface-mounted, prismatic obstacles placed in a fully developed channel flow. J. Fluids Eng. 1993, 115, 85–92. [Google Scholar] [CrossRef]
- Cheng, H.; Castro, I.P. Near wall flow over urban-like roughness. Boundary-Layer Meteorol. 2002, 104, 229–259. [Google Scholar] [CrossRef]
- Castro, I.P.; Cheng, H.; Reynolds, R.T. Turbulence over urban-type roughness: Deductions from wind-tunnel measurements. Boundary-Layer Meteorol. 2006, 118, 109–131. [Google Scholar] [CrossRef]
- Reynolds, R.T.; Castro, I.P. Measurements in an urban-type boundary layer. Exp. Fluids 2008, 45, 141–156. [Google Scholar] [CrossRef]
- MacDonald, R.; Schofield, S.C.; Slawson, P. Physical modelling of urban roughness using arrays of regular roughness elements. Water Air Soil Pollut. 2002, 2, 541–554. [Google Scholar] [CrossRef]
- Wang, Z.; Plate, E.; Rau, M.; Keiser, R. Scale effects in wind tunnel modelling. J. Wind Eng. Ind. Aerodyn. 1996, 61, 113–130. [Google Scholar] [CrossRef]
- Xing, F.; Mohotti, D.; Chauhan, K.A. Experimental and numerical study on mean pressure distributions around an isolated gable roof building with and without openings. Build. Environ. 2018, 132, 30–44. [Google Scholar] [CrossRef]
- Martinuzzi, R.; Havel, B. Vortex shedding from two surface-mounted cubes in tandem. Int. J. Heat Fluid Flow 2004, 25, 364–372. [Google Scholar] [CrossRef]
- Hussein, H.; Martinuzzi, R. Energy balance for turbulent flow around a surface mounted cube placed in a channel. Phys. Fluids 1996, 8, 764–780. [Google Scholar] [CrossRef]
- Nagib, H.M.; Corke, T.C. Wind microclimate around buildings: Characteristics and control. J. Wind Eng. Ind. Aerodyn. 1984, 16, 1–15. [Google Scholar] [CrossRef]
- Vinuesa, R.; Schlatter, P.; Malm, J.; Mavriplis, C.; Henningson, D.S. Direct numerical simulation of the flow around a wall-mounted square cylinder under various inflow conditions. J. Turbul. 2015, 16, 555–587. [Google Scholar] [CrossRef]
- Rotach, M.W.; Fisher, B.; Piringer, M. COST 715 workshop on urban boundary layer parameterizations. B. Am. Meteorol. Soc. 2002, 83, 1501–1504. [Google Scholar] [CrossRef]
- Coceal, O.; Belcher, S. A canopy model of mean winds through urban areas. Q. J. R. Meteorol. Soc. 2004, 130, 1349–1372. [Google Scholar] [CrossRef]
- Rafailidis, S. Influence of building areal density and roof shape on the wind characteristics above a town. Boundary-Layer Meteorol. 1997, 85, 255–271. [Google Scholar] [CrossRef]
- Kastner-Klein, P.; Rotach, M. Mean flow and turbulence characteristics in an urban roughness sublayer. Boundary-Layer Meteorol. 2004, 111, 55–84. [Google Scholar] [CrossRef]
- Li, X.; Leung, D.; Liu, C.; Lam, K. Physical modeling of flow field inside urban street canyons. J. Appl. Meteorol. 2008, 47, 2058–2067. [Google Scholar] [CrossRef]
- Princevac, M.; Baik, J.; Li, X.; Pan, H.; Park, S. Lateral channeling within rectangular arrays of cubical obstacles. J. Wind Eng. Ind. Aerodyn. 2010, 98, 377–385. [Google Scholar] [CrossRef]
- Richards, P.; Hoxey, R.; Short, L. Wind pressures on a 6 m cube. J. Wind Eng. Ind. Aerodyn. 2001, 89, 1553–1564. [Google Scholar] [CrossRef]
- Richards, P.; Hoxey, R.; Connell, B.; Lander, D. Wind-tunnel modelling of the Silsoe Cube. J. Wind Eng. Ind. Aerodyn. 2007, 95, 1384–1399. [Google Scholar] [CrossRef]
- Takimoto, H.; Sato, A.; Onomaura, S.; Barlow, J.; Moriwaki, R.; Inagaki, A.; Kanda, M. Particle image velocimetry measurements of turbulent flow within outdoor and indoor urban scale models and flushing motions in urban canopy layers. Boundary-Layer Meteorol. 2011, 140, 295–314. [Google Scholar] [CrossRef]
- Hagishima, A.; Tanimoto, J.; Nagayama, K. Aerodynamic parameters of regular arrays of rectangular blocks with various geometries. Boundary-Layer Meteorol. 2009, 132, 315–337. [Google Scholar] [CrossRef]
- Kovar-Panskus, A.; Louka, P.; Sini, J.; Savory, E.; Czech, M.; Abdelqari, A.; Mestayer, P.; Toy, N. Influence of geometry on the mean flow within urban street canyons—A comparison of wind tunnel experiments and numerical simulations. Water Air Soil Pollut. 2002, 2, 365–380. [Google Scholar] [CrossRef]
- Kovar-Panskus, A.; Moulinneuf, L.; Savory, E.; Abdelqari, A.; Sini, J.F.; Rosant, J.M.; Robins, A.; Toy, N. A wind tunnel investigation of the influence of solar-induced wall-heating on the flow regime within a simulated urban street canyon. Water Air Soil Pollut. 2002, 2, 555–571. [Google Scholar] [CrossRef]
- Gromke, C.; Ruck, B. Influence of trees on the dispersion of pollutants in an urban street canyon – Experimental investigation of the flow and concentration field. Atmos. Environ. 2007, 41, 3287–3302. [Google Scholar] [CrossRef]
- Gromke, C.; Ruck, B. On the impact of trees on dispersion processes of traffic emissions in street canyons. Boundary-Layer Meteorol. 2009, 131, 19–34. [Google Scholar] [CrossRef]
- Gromke, C.; Buccolieri, R.; Sabatino, S.D.; Ruck, B. Dispersion study in a street canyon with tree planting by means of wind tunnel and numerical investigations – Evaluation of CFD data with experimental data. Atmos. Environ. 2008, 42, 8640–8650. [Google Scholar] [CrossRef]
- Wang, C.; Li, Q.; Wang, Z. Quantifying the impact of urban trees on passive pollutant dispersion using a coupled large-eddy simulation–Lagrangian stochastic model. Build. Environm. 2018, 145, 33–49. [Google Scholar] [CrossRef]
- Gayev, Y.; Savory, E. Influence of street obstructions on flow processes within urban canyons. J. Wind Eng. Ind. Aerodyn. 1999, 82, 89–103. [Google Scholar] [CrossRef]
- Kellnerova, R.; Kukacka, J.; Jurcakova, K.; Uruba, V.; Janur, Z. PIV measurement of turbulent flow within a street canyon: Detection of coherent motion. J. Wind Eng. Ind. Aerodyn. 2012, 104–106, 302–313. [Google Scholar]
- Fernando, H.J.S.; Zajic, D.; Di Sabatino, S.; Dimitrova, R.; Hedquist, B.; Dallman, A. Flow, turbulence, and pollutant dispersion in urban environments. Phys. Fluids 2010, 22, 051301. [Google Scholar] [CrossRef]
- Biltoft, C.A. Customer report for Mock Urban Setting Test. In DPG Document No WDTC-FR-01-121, West Desert Test Center, US Army Dugway Proving Ground, Dugway, Utah; Defense Threat Reduction Agency: Alexandria, VA, USA, 2001. [Google Scholar]
- Sharma, A.; Fernando, H.J.S.; Hellmann, J.; Chen, F. Sensitivity of WRF model to urban parametrizations, with applications to Chicago metropolitan urban heat island. In Proceedings of the 4th Joint US-European Fluids Engineering Summer Meeting FEDSM14, Chicago, IL, USA, 3–7 August 2014. [Google Scholar]
- Di Sabatino, S.; Leo, L.S.; Hedquist, B.C.; Carter, W.; Fernando, H.J.S. Results from the Phoenix Urban Heat Island (UHI) experiment: Effects at the local, neighbourhood and urban scales. In Proceedings of the Eighth Symposium on the Urban Environment, Phoenix, AZ, USA, 12–15 January 2009. [Google Scholar]
- Gadilhe, A.; Janvier, L.; Barnaud, G. Numerical and experimental modelling of the three-dimensional turbulent wind flow through an urban square. J. Wind. Eng. Ind. Aerodyn. 1993, 46–47, 755–766. [Google Scholar] [CrossRef]
- Vita, G.; Shu, Z.; Jesson, M.; Quinn, A.; Hemida, H.; Sterling, M.; Baker, C. On the assessment of pedestrian distress in urban winds. J. Wind. Eng. Ind. Aerodyn. 2020, 203, 1–18. [Google Scholar] [CrossRef]
- Hirose, C.; Ikegaya, N.; Hagishima, A.; Tanimoto, J. Outdoor measurement of wall pressure on cubical scale model affected by atmospheric turbulent flow. Build. Environ. 2019, 160, 1–11. [Google Scholar]
- Vinuesa, R.; Nagib, H.M. Enhancing the accuracy of measurement techniques in high Reynolds number turbulent boundary layers for more representative comparison to their canonical representations. Eur. J. Mech.-B/Fluids 2016, 55, 300–312. [Google Scholar] [CrossRef]
- Vinuesa, R.; Schlatter, P.; Nagib, H.M. Role of data uncertainties in identifying the logarithmic region of turbulent boundary layers. Exp. Fluids 2014, 55, 1751. [Google Scholar] [CrossRef]
- Vinuesa, R. Synergetic Computational and Experimental Studies of Wall-Bounded Turbulent Flows and Their Two-Dimensionality. Ph.D. Thesis, Illinois Institute of Technology, Chicago, IL, USA, 2013. [Google Scholar]
- Örlü, R.; Vinuesa, R. Thermal anemometry. In Experimental Aerodynamics; Discetti, S., Ianiro, A., Eds.; CRC Press Taylor & Francis Group: Boca Raton, FL, USA, 2017. [Google Scholar]
- Weerasuriya, A.U.; Tse, K.T.; Zhang, X.; Li, S.W. A wind tunnel study of effects of twisted wind flows on the pedestrian-level wind field in an urban environment. Build. Environ. 2018, 128, 225–235. [Google Scholar] [CrossRef] [PubMed]
- Chauhan, K.A.; Monkewitz, P.A.; Nagib, H.M. Criteria for assessing experiments in zero pressure gradient boundary layers. Fluid Dyn. Res. 2009, 41, 021404. [Google Scholar] [CrossRef]
- Sanmiguel Vila, C.; Vinuesa, R.; Discetti, S.; Ianiro, A.; Schlatter, P.; Örlü, R. On the identification of well-behaved turbulent boundary layers. J. Fluid Mech. 2017, 822, 109–138. [Google Scholar] [CrossRef]
- Mo, Z.; Liu, C.H. Wind tunnel measurements of pollutant plume dispersion over hypothetical urban areas. Build. Environ. 2018, 132, 357–366. [Google Scholar] [CrossRef]
- Talluru, K.M.; Philip, J.; Chauhan, K.A. Self-similar spectra of point-source scalar plumes in a turbulent boundary layer. J. Fluid Mech. 2019, 870, 698–717. [Google Scholar] [CrossRef]
- Hertwig, D.; Grimmond, S.; Kotthaus, S.; Vanderwel, C.; Gough, H.; Haeffelin, M.; Robins, A. Variability of physical meteorology in urban areas at different scales: Implications for air quality. Faraday Discuss. R. Soc. Chem. 2020, 00, 2–11. [Google Scholar] [CrossRef] [PubMed]
- Monnier, B.; Neiswander, B.; Wark, C. Stereoscopic particle image velocimetry measurements in an urban-type boundary layer: Insight into flow regimes and incidence angle effect. Boundary-Layer Meteorol. 2010, 135, 243–268. [Google Scholar] [CrossRef]
- Nagib, H.; Morkovin, M.; Yung, J.; Tan-Atichat, J. On modeling of atmospheric surface layers by the counter-jet technique. AIAA J. 1974, 14, 185–190. [Google Scholar] [CrossRef]
- Ferreira, M.; Ganapathisubramani, B. PIV-based pressure estimation in the canopy of urban-like roughness. Exp. Fluids 2020, 61, 70. [Google Scholar] [CrossRef]
- Michioka, T.; Takimoto, H.; Sato, A. Large-Eddy Simulation of pollutant removal from a three-dimensional street canyon. Boundary-Layer Meteorol. 2014, 150, 259–275. [Google Scholar] [CrossRef]
- Boppana, V.B.L.; Xie, Z.T.; Castro, I.P. Thermal stratification effects on flow over a generic urban canopy. Boundary-Layer Meteorol. 2014, 130, 141–162. [Google Scholar] [CrossRef]
- Tong, H.; Walton, A.; Sang, J.; Chan, J. Numerical simulation of the urban boundary layer over the complex terrain of Hong Kong. Atmos. Environ. 2005, 39, 3549–3563. [Google Scholar] [CrossRef]
- Santiago, J.; Dejoan, A.; Martilli, A.; Martin, F.; Pinelli, A. Comparison Between Large-Eddy Simulation and Reynolds-Averaged Navier–Stokes Computations for the MUST Field Experiment. Part I: Study of the Flow for an Incident Wind Directed Perpendicularly to the Front Array of Containers. Boundary-Layer Meteorol. 2010, 135, 109–132. [Google Scholar] [CrossRef]
- Jacob, J.; Sagaut, P. Wind comfort assessment by means of large eddy simulation with lattice Boltzmann method in full scale city area. Building Environ. 2019, 139, 110–124. [Google Scholar] [CrossRef]
- Sullivan, P.; Weil, J.C.; Patton, E.; Jonker, H.; Mironov, D. Turbulent Winds and Temperature Fronts in Large-Eddy Simulations of the Stable Atmospheric Boundary Layer. J. Atmos. Sci. 2016, 73, 1815–1840. [Google Scholar] [CrossRef]
- Dejoan, A.; Santiago, J.; Martilli, A.; Martin, F.; Pinelli, A. Comparison Between Large-Eddy Simulation and Reynolds-Averaged Navier–Stokes Computations for the MUST Field Experiment. Part II: Effects of Incident Wind Angle Deviation on the Mean Flow and Plume Dispersion. Boundary-Layer Meteorol. 2010, 133, 135–150. [Google Scholar] [CrossRef]
- Monnier, B.; Goudarzi, S.A.; Vinuesa, R.; Wark, C. Turbulent structure of a simplified urban fluid flow studied through stereoscopic particle image velocimetry. Boundary-Layer Meteorol. 2018, 166, 239–268. [Google Scholar] [CrossRef]
- Nakayama, H.; Takemi, T.; Nagai, H. LES Analysis of the Aerodynamic Surface Properties for Turbulent Flows over Building Arrays with Various Geometries. J. Appl. Meteorol. Clim. 2011, 50, 1692–1712. [Google Scholar] [CrossRef]
- Nakayama, H.; Takemi, T.; Nagai, H. Large-eddy simulation of urban boundary-layer flows by generating turbulent inflows from mesoscale meteorological simulations. Atmos. Sci. Let. 2012, 13, 180–186. [Google Scholar] [CrossRef]
- Smagorinsky, J. General circulation experiments with the primitive equations. Mon. Wea. Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Kataoka, H.; Mizuno, M. Numerical flow computation around aeroelastic 3D square cylinder using inflow turbulence. Wind Struct. 2002, 5, 379–392. [Google Scholar] [CrossRef]
- Giometto, M.G.; Christen, A.; Meneveau, C.; Fang, J.; Krafczyk, M.; Parlange, M.B. Spatial characteristics of roughness sublayer mean flow and turbulence over a realistic urban surface. Boundary-Layer Meteorol. 2016, 160, 425–452. [Google Scholar] [CrossRef]
- Mason, P.; Thomson, D. Stochastic backscatter in large-eddy simulations of boundary layers. J. Fluid Mech. 1992, 242, 51–78. [Google Scholar] [CrossRef]
- Bou-Zeid, E.; Meneveau, C.; Parlange, M. A scale-dependent Lagrangian dynamic model for large eddy simulation of complex turbulent flows. Phys. Fluids 2005, 17, 25–105. [Google Scholar] [CrossRef]
- Inagaki, A.; Kanda, M.; Ahmad, N.; Yaki, A.; Onodera, N.; Aoki, T. A Numerical Study of Turbulence Statistics and the Structure of a Spatially-Developing Boundary Layer Over a Realistic Urban Geometry. Boundary-Layer Meteorol. 2017, 164, 161–181. [Google Scholar] [CrossRef]
- Crylls, T.; Suter, I.; van Reeuwijk, M. Steady-State Large-Eddy Simulations of Convective and Stable Urban Boundary Layers. Boundary-Layer Meteorol. 2020, 175, 309–341. [Google Scholar]
- Belcher, S. Mixing and transport in urban areas. Philos. Trans. R Soc. 2005, 363, 3583–3597. [Google Scholar] [CrossRef] [PubMed]
- Theurer, W.; Plate, E.; Hoeschele, K. Semi-empirical models as a combination of wind tunnel and numerical dispersion modelling. Atmos. Environ. 1996, 30, 3583–3597. [Google Scholar] [CrossRef]
- Davidson, M.; Snyder, W.; Lawson, R.; Hunt, J. Wind tunnel simulations of plume dispersion through groups of obstacles. Atmos. Environ. 1996, 30, 3715–3725. [Google Scholar] [CrossRef]
- Macdonald, R.; Griffiths, R.; Cheah, S. Field experiments of dispersion through regular arrays of cubic structures. Atmos. Environ. 1997, 31, 783–795. [Google Scholar] [CrossRef]
- Coceal, O.; Thomas, T.G.; Castro, I.; Belcher, S. Mean flow and turbulence statistics over groups of urban-like cubical obstacles. Boundary-Layer Meteorol. 2006, 121, 491–519. [Google Scholar] [CrossRef]
- Coceal, O.; Dobre, A.; Thomas, T.; Belcher, S. Structure of turbulent flow over regular arrays of cubical roughness. J. Fluid Mech. 2007, 589, 375–409. [Google Scholar] [CrossRef]
- Brandford, S.; Coceal, O.; Thomas, T.; Belcher, S. Dispersion of a Point-Source Release of a Passive Scalar Through an Urban-Like Array for Different Wind Directions. Boundary-Layer Meteorol. 2011, 139, 367–394. [Google Scholar] [CrossRef]
- Germano, M.; Piomelli, U.; Moin, P.; Cabot, W. A dynamic subgrid-scale eddy viscosity model. Phys. Fluids 1991, A3, 1760–1766. [Google Scholar] [CrossRef]
- Lilly, D. A proposed modification of the Germano subgrid-scale closure method. Phys. Fluids 1992, A4, 633–636. [Google Scholar] [CrossRef]
- Lee, J.; Sung, H.; Krogstad, P. Direct numerical simulation of the turbulent boundary layer over a cube-roughened wall. J. Fluid Mech. 2011, 669, 397–431. [Google Scholar] [CrossRef]
- Cheng, W.C.; Porté-Agel, F. Adjustment of turbulent boundary-layer flow to idealized urban surfaces: A large-eddy simulation study. Boundary-Layer Meteorol. 2015, 155, 249–270. [Google Scholar] [CrossRef]
- Tomas, J.M.; Pourquie, M.J.B.M.; Jonker, H.J.J. Stable stratification effects on flow and pollutant dispersion in boundary layers entering a generic urban environment. Boundary-Layer Meteorol. 2016, 159, 221–239. [Google Scholar] [CrossRef]
- Vreman, A.W. An eddy-viscosity subgrid-scale model for turbulent shear flow: Algebraic theory and applications. Phys. Fluis 2004, 16, 3670. [Google Scholar] [CrossRef]
- Tomas, J.M.; Eisma, H.E.; Pourquie, M.J.B.M.; Elsinga, G.E.; Jonker, H.J.J.; Westerweel, J. Pollutant dispersion in boundary layers exposed to rural-to-urban transitions: Varying the spanwise length scale of the roughness. Boundary-Layer Meteorol. 2017, 163, 225–251. [Google Scholar] [CrossRef]
- Eisma, H.E.; Tomas, J.M.; Pourquie, M.J.B.M.; Elsinga, G.E.; Jonker, H.J.J.; Westerweel, J. Effects of a fence on pollutant dispersion in a boundary layer exposed to a rural-to-urban transition. Boundary-Layer Meteorol. 2018, 169, 185–208. [Google Scholar] [CrossRef] [PubMed]
- Vinçont, J.; Simoëns, S.; Ayrault, M.; Wallace, J.M. Passive scalar dispersion in a turbulent boundary layer from a line source at the wall and downstream of an obstacle. J. Fluid Mech. 2000, 424, 127–167. [Google Scholar] [CrossRef]
- Soulhac, L. Modelisation de la Dispersion Atmospheric a l’interieur de la Canopee Urbaine. Ph.D. Thesis, Ecole Centrale de Lyon, Lyon, France, 2000. [Google Scholar]
- Soulhac, L.; Salizzoni, P.; Cierco, F.; Perkins, R. The model SIRANE for atmospheric urban pollution dispersion: Part I, presentation of the model. Atmos. Environ. 2011, 45, 7379–7395. [Google Scholar] [CrossRef]
- Hamlyn, D.; Hilderman, T.; Britter, R. A simple network approach to modelling dispersion among large groups of obstacle. Atmos. Environ. 2007, 41, 5848–5862. [Google Scholar] [CrossRef]
- Belcher, S.; Coceal, O.; Goulart, E.; Rudd, A.; Robins, A. Processes controlling atmospheric dispersion through city centres. J. Fluid Mech. 2015, 763, 51–81. [Google Scholar] [CrossRef][Green Version]
- Goulart, E.; Coceal, O.; Belcher, S. Dispersion of a passive scalar within and above an urban street network. Boundary-Layer Meteorol. 2018, 166, 351–366. [Google Scholar] [CrossRef]
- Hutchins, N.; Chauhan, K.; Marusic, I.; Monty, J.; Klewicki, J. Towards reconciling the large-scale structure of turbulent boundary layers in the atmosphere and laboratory. Boundary-Layer Meteorol. 2012, 145, 273–306. [Google Scholar] [CrossRef]
- Choi, H.; Moin, P. Grid-point requirements for large eddy simulation: Chapman’s estimates revisited. Phys. Fluids 2012, 24, 011702. [Google Scholar] [CrossRef]
- Businger, J.A.; Wyngaard, J.C.; Izumi, Y.; Bradley, E.F. Flux-profile relationships in the atmospheric surface layer. J. Atmos. Sci. 1971, 28, 181–189. [Google Scholar] [CrossRef]
- Rotach, M.W.; Vogt, R.; Bernhofer, C.; Batchvarova, E.; Christen, A.; Clappier, A.; Feddersen, B.; Gryning, S.E.; Martucci, G.; Mayer, H.; et al. BUBBLE—An urban boundary layer meteorology project. Theor. Appl. Climatol. 2005, 81, 231–261. [Google Scholar] [CrossRef]
- Moeng, C. A large-eddy-simulation model for the study of planetary boundary-layer turbulence. J. Atmos. Sci. 1984, 13, 2052–2062. [Google Scholar] [CrossRef]
- Launder, B.E.; Spalding, D.B. Lectures in Mathematical Models of Turbulence; Academic Press: London, UK, 1972. [Google Scholar]
- Chen, S.; Doolen, G.D. Lattice Boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- Dogan, E.; Örlü, R.; Gatti, D.; Vinuesa, R.; Schlatter, P. Quantification of amplitude modulation in wall-bounded turbulence. Fluid Dyn. Res. 2019, 51, 011408. [Google Scholar] [CrossRef]
- Schenk, F.; Vinuesa, R. Enhanced large-scale atmospheric flow interaction with ice sheets at high model resolution. Results Eng. 2019, 3, 100030. [Google Scholar] [CrossRef]
- Schenk, F.; Väliranta, M.; Muschitiello, F.; Tarasov, L.; Heikkilä, M.; Björck, S.; Brandefelt, J.; Johannson, A.; Näslund, J.O.; Wohlfarth, B. Warm summers during the Younger Dryas cold reversal. Nat. Commun. 2018, 9, 1634. [Google Scholar] [CrossRef]
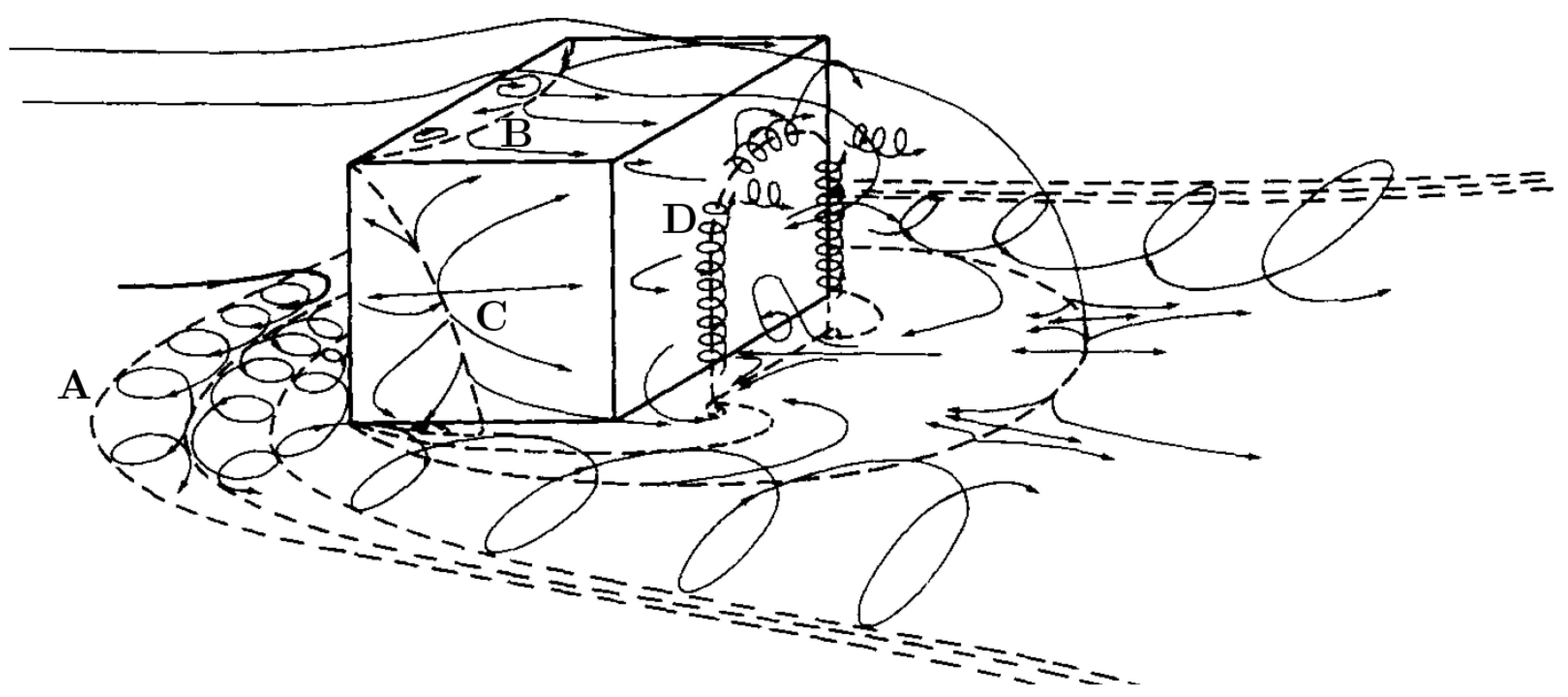
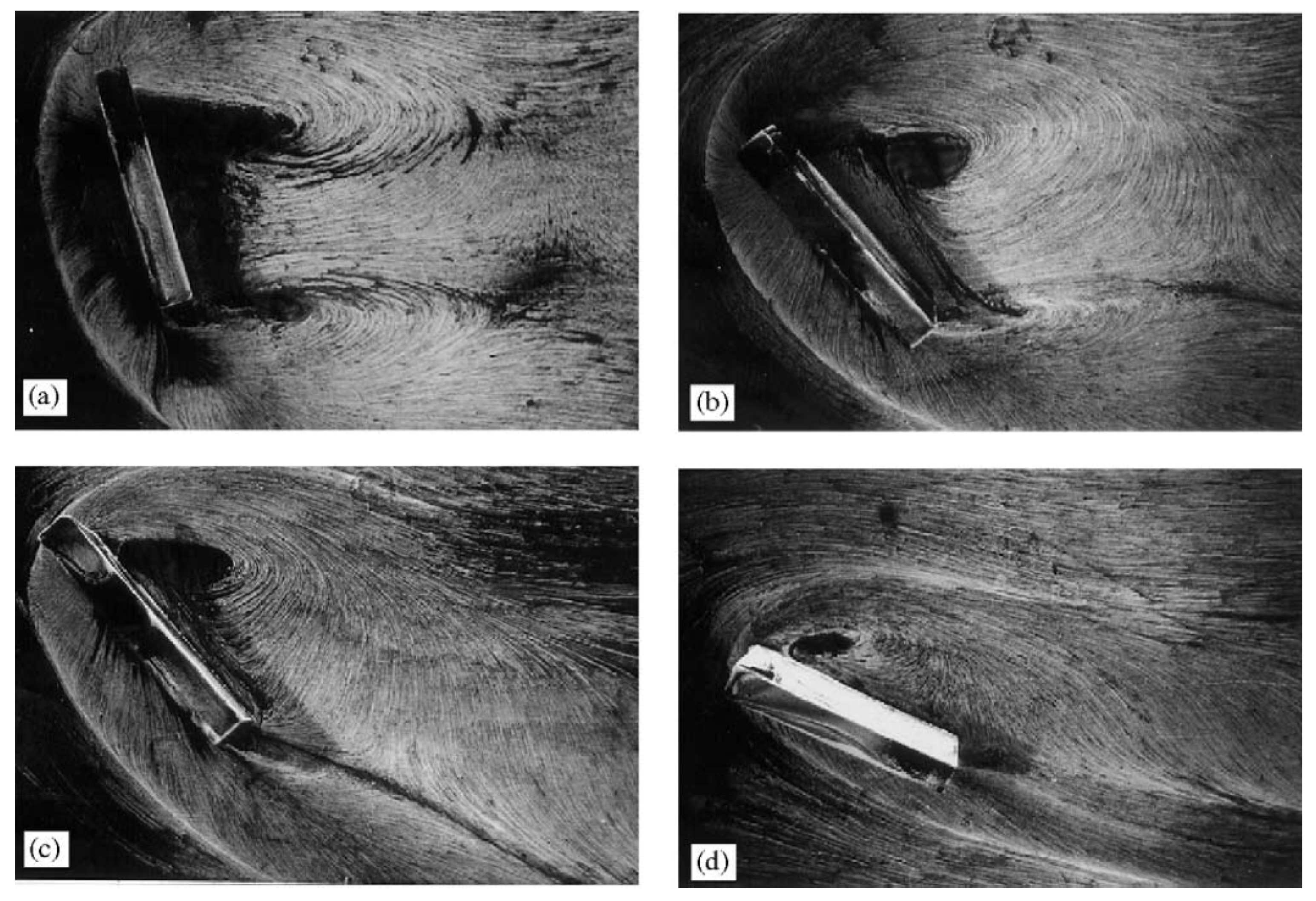
- Hunt, J.C.R.; Abell, C.J.; Peterka, J.A.; Woo, H. Kinematical studies of the flows around free or surface-mounted obstacles: Applying topology to flow visualization. J. Fluid Mech. 1978, 86, 179–200. [Google Scholar] [CrossRef]
- Vinuesa, R.; Prus, C.; Schlatter, P.; Nagib, H.M. Convergence of numerical simulations of turbulent wall-bounded flows and mean cross-flow structure of rectangular ducts. Meccanica 2016, 51, 3025–3042. [Google Scholar] [CrossRef]
- Sousa, J. Turbulent flow around a surface-mounted obstacle using 2D-3C DPIV. Exp. Fluids 2002, 33, 854–862. [Google Scholar] [CrossRef]
- Zhou, J.; Adrian, R.J.; Balachandar, S.; Kendali, T.M. Mechanisms for generating coherent packets of hairpin vortices. J. Fluid Mech. 1990, 387, 353–396. [Google Scholar] [CrossRef]
- Becker, S.; Lienhart, H.; Durst, F. Flow around three-dimensional obstacles in boundary layers. J. Wind Eng. Ind. Aerodyn. 2002, 90, 265–279. [Google Scholar] [CrossRef]
- Martinuzzi, R. Experimentelle Untersuchungen der Umströmung Wandgebundener, Rechteckiger, Prismatischer Hindernisses. Ph.D. Thesis, Universität Erlangen-Nürnberg, Erlangen, Germany, 1982. [Google Scholar]
- Kim, J.; Baik, J. A numerical study of the effects of ambient wind direction on flow and dispersion in urban street canyons using the RNG k–ε turbulence model. Atmos. Environ. 2004, 38, 3039–3048. [Google Scholar] [CrossRef]
- Kawai, H.; Okuda, Y.; Ohashi, M. Near wake structure behind a 3D square prism with the aspect ratio of 2.7 in a shallow boundary layer flow. J. Wind Eng. Ind. Aerodyn. 2012, 104–106, 196–202. [Google Scholar] [CrossRef]
- Del Álamo, J.C.; Jiménez, J.; Zandonade, P.; Moser, R.D. Self-similar vortex clusters in the turbulent logarithmic region. J. Fluid Mech. 2006, 561, 329–358. [Google Scholar] [CrossRef]
- Lozano-Durán, A.; Flores, O.; Jiménez, J. The three-dimensional structure of momentum transfer in turbulent channels. J. Fluid Mech. 2012, 694, 100–130. [Google Scholar] [CrossRef]
- Atzori, M.; Vinuesa, R.; Lozano-Durán, A.; Schlatter, P. Characterization of turbulent coherent structures in square duct flow. J. Phys. Conf. Ser. 2018, 1001, 012008. [Google Scholar] [CrossRef]
- Atzori, M.; Vinuesa, R.; Lozano-Durán, A.; Schlatter, P. Coherent structures in turbulent boundary layers over an airfoil. J. Phys. Conf. Ser. 2020, 1522, 012020. [Google Scholar] [CrossRef]
- Hunt, J.C.R.; Wray, A.A.; Moin, P. Eddies, Streams, and Convergence Zones in Turbulent Flows; Center for Turbulence Research (CTR) Proceedings of Summer Program: Standford, CA, USA, 1998. [Google Scholar]
- Krajnovic, S.; Davidson, L. Flow around a three-dimensional bluff body. In 9th International Symposium on Flow Visualization; Heriot-Watt Univeristy: Edinburgh, Scotland, 2000. [Google Scholar]
- Chong, M.S.; Perry, A.E.; Cantwell, B.J. A general classification of three-dimensional flow fields. Phys. Fluids 1990, 5, 765. [Google Scholar] [CrossRef]
- Kida, S.; Miura, H. Identification and analysis of vortical structures. Eur. J. Mech. B Fluids 1998, 17, 471–488. [Google Scholar] [CrossRef]
- Graftieaux, L.; Michard, M.; Grosjean, N. Combining PIV, POD and vortex identification algorithms for the study of unsteady turbulent swirling flows. Meas. Sci. Technol. 2001, 12, 1422–1429. [Google Scholar] [CrossRef]
- Rempfer, D.; Wark, C.; Monnier, B.; Kandala, S. Characterization and Low-Dimensional Modeling of Urban Fluid Flow; AFOSR Final Report, Contract Number FA9550-11-1-0056; Air Force Reasearch Laboratory: Arlington, VA, USA, 2014. [Google Scholar]
- Amor, C.; Pérez, J.M.; Schlatter, P.; Vinuesa, R.; Le Clainche, S. Soft computing techniques to analyse the turbulent wake of a wall-mounted square cylinder. Adv. Intell. Syst. Comput. 2019, 950, 577–586. [Google Scholar]
- Guastoni, L.; Güemes, A.; Ianiro, A.; Discetti, S.; Schlatter, P.; Azizpour, H.; Vinuesa, R. Convolutional-network models to predict wall-bounded turbulence from wall quantities. arXiv 2020, arXiv:2006.12483. [Google Scholar]
- Guastoni, L.; Encinar, M.P.; Schlatter, P.; Azizpour, H.; Vinuesa, R. CPrediction of wall-bounded turbulence from wall quantities using convolutional neural networks. J. Phys. Conf. Ser. 2020, 1522, 012022. [Google Scholar] [CrossRef]
- Encinar, M.P.; Jiménez, J. Logarithmic-layer turbulence: A view from the wall. Phys. Rev. Fluids 2019, 4, 114603. [Google Scholar] [CrossRef]
- Sasaki, K.; Vinuesa, R.; Cavalieri, A.V.G.; Schlatter, P.; Henningson, D.S. Transfer functions for flow predictions in wall-bounded turbulence. J. Fluid Mech. 2019, 864, 708–745. [Google Scholar] [CrossRef]
- Murata, T.; Fukami, K.; Fukagata, K. Nonlinear mode decomposition with convolutional neural networks for fluid dynamics. J. Fluid Mech. 2020, 882, A13. [Google Scholar] [CrossRef]
- Eivazi, H.; Guastoni, L.; Schlatter, P.; Azizpour, H.; Vinuesa, R. Recurrent neural networks and Koopman-based frameworks for temporal predictions in turbulence. arXiv 2020, arXiv:2005.02762. [Google Scholar]
- Srinivasan, P.A.; Guastoni, L.; Azizpour, H.; Schlatter, P.; Vinuesa, R. Predictions of turbulent shear flows using deep neural networks. Phys. Rev. Fluids 2019, 4, 054603. [Google Scholar] [CrossRef]
- Haller, G. An objective definition of a vortex. J. Fluid Mech. 2005, 525, 1–26. [Google Scholar] [CrossRef]
- Le Clainche, S. An Introduction to Some Methods for Soft Computing in Fluid Dynamics. In International Workshop on Soft Computing Models in Industrial and Environmental Applications; Springer: Berlin/Heidelberg, Germany, 2019; pp. 557–566. [Google Scholar]
- Sirovich, L. Turbulence and the dynamics of coherent structures. Parts I–III. Q. Appl. Math. 1987, 45, 561–571. [Google Scholar] [CrossRef]
- Schmid, P. Application of the dynamic mode decomposition to experimental data. Exp. in Fluids 2011, 50, 1123–1130. [Google Scholar] [CrossRef]
- Tu, J.; Rowley, C.; Luchtemburg, D.; Brunton, S.; Kutz, J. On dynamic mode decomposition: Theory and applications. J. Comp. Dyn. 2014, 1, 391–421. [Google Scholar] [CrossRef]
- Rowley, C.; Dawson, S. Model reduction for flow analysis and control. Annual Rev. Fluid Mech. 2017, 49, 387–417. [Google Scholar] [CrossRef]
- Schmidt, O.; Towne, A.; Colonius, T.; Cavalieri, A.; Jordan, P.; Bres, G. Wavepackets and Trapped Acoustic Modes in a Mach 0.9 Turbulent Jet: A Global Stability Analysis. In International Workshop on Soft Computing Models in Industrial and Environmental Applications; Springer: Berlin/Heidelberg, Germany, 2017; Volume 825, pp. 1153–1181. [Google Scholar]
- Le Clainche, S.; Vega, J.M. Higher order dynamic mode decomposition. SIAM J. Appl. Dyn. Sys. 2017, 16, 882–925. [Google Scholar] [CrossRef]
- Geoga, C.; Haley, C.; Siegel, A.; Anitescu, M. Frequency-wavenumber Spectral analysis of spatio-temporal flows. J. Fluid Mech. 2018, 848, 545–559. [Google Scholar] [CrossRef]
- Le Clainche, S.; Izvassarov, D.; Rosti, M.; Brandt, L.; Tammisola, O. Coherent structures in the turbulent flow of an elastoviscoplastic fluid. J. Fluid Mech. 2020, 888, A5. [Google Scholar] [CrossRef]
- Le Clainche, S.; Vega, J.M.; Soria, J. Higher order dynamic mode decomposition of noisy experimental data: The flow structure of a zero-net-mass-flux jet. Exp. Therm. Fluid Sci. 2017, 88, 336–353. [Google Scholar] [CrossRef]
- Le Clainche, S.; Mao, X.; Vega, J.M. New method to capture traveling waves in flow passing a wind turbine. Wind Energy 2019, 22, 1095–4244. [Google Scholar] [CrossRef]
- Le Clainche, S.; Rosti, M.; Brandt, L. Flow structures and shear-stress predictions in the turbulent channel flow over an anisotropic porous wall. J. Phys. Conf. Series 2020, 1522, 012016. [Google Scholar] [CrossRef]
- Le Clainche, S.; Vega, J. Analyzing Nonlinear Dynamics via Data-Driven Dynamic Mode Decomposition-Like Methods. Complexity 2018, 6920783, 1–21. [Google Scholar] [CrossRef]
- Rowley, C.; Dawson, S. Modal analysis of fluid flows: An overview. AIAA J. 2017, 55, 4013–4041. [Google Scholar]
- Noack, B.R.; Morzynski, M.; Tadmor, G. Reduced-Order Modelling for Flow Control; Springer: New York, NY, USA, 2011. [Google Scholar]
- Tammisola, O.; Juniper, M.P. Coherent structures in a swirl injector at Re=4800 by nonlinear simulations and linear global modes. J. Fluid Mech. 2016, 792, 620–657. [Google Scholar] [CrossRef]
- Le Clainche, S.; Li, I.; Theofilis, V.; Soria, J. Flow around a hemisphere-cylinder at high angle of attack and low Reynolds number. Part I: Experimental and numerical investigation. Aerosp. Sci. Tech. 2015, 44, 77–87. [Google Scholar] [CrossRef]
- Parente, A. Experimental and Numerical Investigation of Advanced Systems for Hydrogen-Based Fuel Compustion. Ph.D. Thesis, University of Pisa, Pizza, Italy, 2008. [Google Scholar]
- Mendez, M.A.; Balabane, M.; Buchlin, J. Multi-scale proper orthogonal decomposition of complex fluid flows. J. Fluid Mech. 2019, 870, 988–1036. [Google Scholar] [CrossRef]
- Willcox, K.; Peraire, J. Balanced model reduction via theproper orthogonal decomposition. AIAA J. 2002, 40, 2323–2330. [Google Scholar] [CrossRef]
- Rowley, C. Model reduction for fluids, using balanced proper orthogonal decomposition. Int. J. Bifurcation Chaos 2005, 15, 997. [Google Scholar] [CrossRef]
- Phillips, J.; Silveira, L. Computer-Aided Design of Integrated Circuits andSystems. IEEE Trans. 2005, 24, 43–55. [Google Scholar]
- Karami, S.; Soria, J. Analysis of coherent structures in an under-expanded supersonic impinging jet using spectral proper orthogonal decomposition (SPOD). Aerospace 2018, 5, 73. [Google Scholar] [CrossRef]
- Abreu, L.I.; Cavalieri, A.V.G.; Schlatter, P.; Vinuesa, R.; Henningson, D.S. SPOD and resolvent analysis of near-wall coherent structures in turbulent pipe flows. J. Fluid Mech. 2020, 900, A11. [Google Scholar] [CrossRef]
- Abreu, L.I.; Cavalieri, A.V.G.; Schlatter, P.; Vinuesa, R.; Henningson, D.S. Resolvent modelling of near-wall coherent structures in turbulent channel flow. Int. J. Heat Fluid Flow 2020, 85, 108662. [Google Scholar] [CrossRef]
- Takens, F. Detecting strange attractors in turbulence. In Lecture Notes in Mathematics; Rand, D.A., Young, L.-S., Eds.; Springer: Berlin/Heidelberg, Germany, 1981; pp. 366–381. [Google Scholar]
- Le Clainche, S.; Vega, J.M. Higher order dynamic mode decomposition to identify and extrapolate flow patterns. Phys. Fluids 2017, 29, 084102. [Google Scholar] [CrossRef]
- Le Clainche, S.; Ferrer, E. A reduced order model to predict transient flows around straight bladed vertical axis wind turbines. Energies 2018, 11, 566. [Google Scholar] [CrossRef]
- Le Clainche, S.; Moreno-Ramos, R.; Taylor, P.; Vega, J.M. A new robust method to study flight flutter testing. J. Aircraft 2018, 56, 336–343. [Google Scholar] [CrossRef]
- Le Clainche, S.; Vega, J.M. Spatio-temporal Koopman decomposition. J. Nonlin. Sci. 2018, 28, 1–50. [Google Scholar] [CrossRef]
- Rowley, C.; Mezić, I.; Bagheri, S.; Schlatter, P.; Henningson, D. Spectral analysis of nonlinear flows. J. Fluid Mech. 2009, 641, 115–127. [Google Scholar] [CrossRef]
- Gómez, F.; Clainche, S.L.; Paredes, P.; Hermanns, M.; Theofilis, V. Four decades of studying global linear instability. AIAA J. 2012, 50, 2731–2743. [Google Scholar] [CrossRef]
- Jovanovic, M.; Schmid, P.; Nichols, J. Sparsity-promoting dynamic mode decomposition. Phys. Fluids 2014, 26, 024103. [Google Scholar] [CrossRef]
- Williams, M.; Kevrekidis, I.; Rowley, C. A data driven approximation of the Koopman operator: Extending dynamic mode decomposition. J. Nonlin. Sci. 2015, 25, 1307–1346. [Google Scholar] [CrossRef]
- Chen, K.; Tu, J.; Rowley, C. Variants of dynamic mode decomposition: Boundary condition, Koopman and Fourier analyses. J. Nonlin. Sci. 2012, 22, 8871–8875. [Google Scholar] [CrossRef]
- Askham, T.; Kutz, J.N. Variable projection methods for an optimized dynamic mode decomposition. SIAM J. Appl. Dyn. Systems 2018, 17, 380–416. [Google Scholar] [CrossRef]
- Dawson, S.; Hemati, M.; Williams, M.; Rowley, C. Characterizing and correcting for the effect of sensor noise in the dynamic mode decomposition. Exp. Fluids 2016, 17, 42–57. [Google Scholar] [CrossRef]
- Hemati, M.; Rowley, C.; Deem, E.; Cattafesta, L. De-Biasing the dynamic mode decomposition for applied Koopman spectral analysis of noisy datasets. In Theoretical and Computational Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 2017; pp. 349–368. [Google Scholar]
- Takeishi, N.; Kawahara, Y.; Tabei, Y.; Yairi, T. Bayesian dynamic mode decomposition. In Proceedings of the 26th Intl Joint Conf. on Artificial Intelligence (IJCAI), Melbourne, Australia, 19–25 August 2017; pp. 2814–2821. [Google Scholar]
- Kutz, J.; Fu, X.; Brunton, S. Multiresolution Dynamic Mode Decomposition. SIAM J. Appl. Dyn. Sys. 2016, 15, 713–735. [Google Scholar] [CrossRef]

| Studies | DNS | LES | RANS | Other |
|---|---|---|---|---|
| Vinuesa et al. [41], Coceal et al. [101,102], | ✓ | |||
| Brandford et al. [103] and Lee et al. [106] | ||||
| Belcher et al. [97] and Goulart et al. [117] | ✓ | Analytical models | ||
| Michioka et al. [80], Boppana et al. [81], | ||||
| Sullivan et al. [85], Nakayama et al. [88,89], | ||||
| Kataoka and Mizuno [91], Giometto et al. [92], | ✓ | |||
| Crylls et al. [96], Cheng and Porté-Agel [107], | ||||
| Tomas et al. [108,110] and Eisma et al. [111] | ||||
| Santiago et al. [83] and Dejoan et al. [86] | ✓ | [123] | ||
| Inagaki et al. [95] | ✓ | Lattice-Boltzmann method [124] | ||
| Sini et al. [19] | [123] | |||
| Jacob and Sagaut [84] | Lattice-Boltzmann method [124] | |||
| Tong et al. [82] | Momentum and energy balances | |||
| Theurer et al. [98] and Davidson et al. [99] | Gaussian plume models | |||
| Soulhac et al. [114] | SIRANE model [113] | |||
| Hamlyn et al. [115] | Network models |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Torres, P.; Le Clainche, S.; Vinuesa, R. On the Experimental, Numerical and Data-Driven Methods to Study Urban Flows. Energies 2021, 14, 1310. https://doi.org/10.3390/en14051310
Torres P, Le Clainche S, Vinuesa R. On the Experimental, Numerical and Data-Driven Methods to Study Urban Flows. Energies. 2021; 14(5):1310. https://doi.org/10.3390/en14051310
Chicago/Turabian StyleTorres, Pablo, Soledad Le Clainche, and Ricardo Vinuesa. 2021. "On the Experimental, Numerical and Data-Driven Methods to Study Urban Flows" Energies 14, no. 5: 1310. https://doi.org/10.3390/en14051310
APA StyleTorres, P., Le Clainche, S., & Vinuesa, R. (2021). On the Experimental, Numerical and Data-Driven Methods to Study Urban Flows. Energies, 14(5), 1310. https://doi.org/10.3390/en14051310








