1. Introduction
In recent years, electrical systems for distributed generation have experienced increased expansion and importance owing to the increase in the integration of different renewable energy sources, such as photovoltaics and wind energy. As a consequence, a multidirectional energy flow is present in the point of common coupling (PCC), which is simultaneously shared by loads and generators. Voltage-source converter high-voltage direct current (VSC–HVDC) systems allow us to exploit the feature of a multidirectional power flow, as they can be used to interconnect several AC grids by means of DC networks [
1]. Since HVDC systems offer some superior advantages to those of high-voltage alternating current (HVAC) schemes—such as the asynchronous connection of two or more independent AC networks, the lack of reactive power in the DC link, lower power losses [
2]—they can contribute to provide a more reliable power network and to the development of smart grids [
3,
4].
From the first commercial HVDC system, i.e., the HVDC Gotland [
5], to the present day, power electronics has undergone great advances. Several commercial HVDC systems can be found involving various technologies, such as HVDCs based on current-source converters (CSC), in addition to the current VSC–HVDCs. The main different converter technologies have been explained in [
6].
In accordance with [
7,
8], VSC–HVDC systems exhibit some advantages with regard to CSC-HVDCs, such as their four-quadrant operation, their use in the connection to both strong and weak grids, high dynamic performance and multiterminal possibility, and greater controllability [
9]. Furthermore, multilevel topologies for VSC can be used in HVDCs in order to synthesize an output voltage with a low harmonic distortion. The most well-known multilevel configurations are the neutral-point clamped (NPC) converter [
10], the flying-capacitor (FC) converter [
11], and the modular multilevel converter (MMC) [
12].
Among all the flexible transmission systems (FTS), HVDCs are the devices that offer the broadest range of functionalities, such as voltage control, active and reactive power control, frequency control, and the interconnection of AC systems [
7]. Besides, HVDCs also feature some power quality (PQ) functionalities in order to ameliorate the PQ of the AC grids to which they are connected [
13].
Several works have dealt with some PQ issues related to HVDC systems. In [
14], a strategy to extend the operation region of MMC-based HVDCs by means of the current injection of a second harmonic was presented; this second component must be carefully injected in order to obtain proper behavior of the converter. As a result, a wider range of active and reactive powers could be controlled with a sinusoidal current injected by the HVDC into the grid. Nevertheless, this work did not study the compensation of current harmonics caused by loads connected to AC networks. A proposal to improve the PQ using multiterminal VSC–HVDC systems was presented in [
15], where a total solution to the PQ issue was described. Nonetheless, the control structure was reduced to the use of conventional proportional–integral (PI) regulators to achieve decoupled control of the active and reactive powers, while the use of passive high-pass filters was proposed to reduce the output voltage distortion of the VSC–HVDC, which is an expensive solution. On the other hand, the use of a modified active filter to improve the PQ in a HVDC link was proposed in [
16]; this solution is very expensive, as it requires an additional converter for the amelioration of PQ. A PQ comparison between HVAC and HVDC systems was studied in [
17]; the study concluded that HVDCs are a better option than HVAC systems, but no solutions to improve the PQ were proposed. A power compensation scheme to remove the double frequency ripples in active and reactive powers for a VSC–HVDC system was proposed in [
18]; this control scheme is able to compensate the active and reactive powers exchanged between the HVDC and the grids when the grid voltages are unbalanced. This compensation was carried out without ripple, however, the proposed strategy was not able to compensate the imbalances in the grid voltages. An overview of a PQ analysis was studied in [
19]; the work analyzed several PQ compensators as well as the most common control techniques applied to VSC to improve the PQ. The paper concluded that VSC–HVDCs offer a wide range of functionalities, particularly applied to the PQ improvements of smart grids, and still require in-depth research.
Main Contributions
Several references have been analyzed in the literature review, concluding that HVDC systems are not usually employed to compensate PQ disturbances that can affect AC grids. This paper proposes a multiterminal multilevel VSC–HVDC system that is able to ameliorate the PQ of the AC grids connected to the VSC terminals. To be precise, the HVDC is able not only to compensate for active power, but also to cancel out sags in the grid voltages and harmonics in the currents that flow through the different AC grids. Balanced and unbalanced voltage sag compensation in a specific AC grid is carried out through the injection of reactive power by the terminal of the HVDC associated with that grid, and by the use of a resonant controller to cancel out the second harmonic component, which is present in the case of imbalances. Moreover, each terminal of the HVDC offers active-power filter functionality to remove harmonics from the current of each AC grid; this compensation is performed by using several resonant controllers implemented in a synchronous reference frame (SRF). The result is that the currents that flow through each AC grid are balanced and sinusoidal, yielding balanced and sinusoidal voltages at the PCC. Simulation results show that the control scheme performs effectively in terms of stability, transient response, error in steady-state, and total-harmonic distortion (THD).
The paper is organized as follows: The description of the dynamic model of the multiterminal multilevel VSC–HVDC is presented in
Section 2. The topology of the control scheme with PQ capabilities is thoroughly explained in
Section 3. Simulation results obtained by using PSCAD
TM/EMTDC
TM (Power System Computer-Aided Design; Electromagnetic Transients including Direct Current) are presented in
Section 4. Finally, the main conclusions are provided in
Section 5.
2. Model of the Multiterminal VSC–HVDC
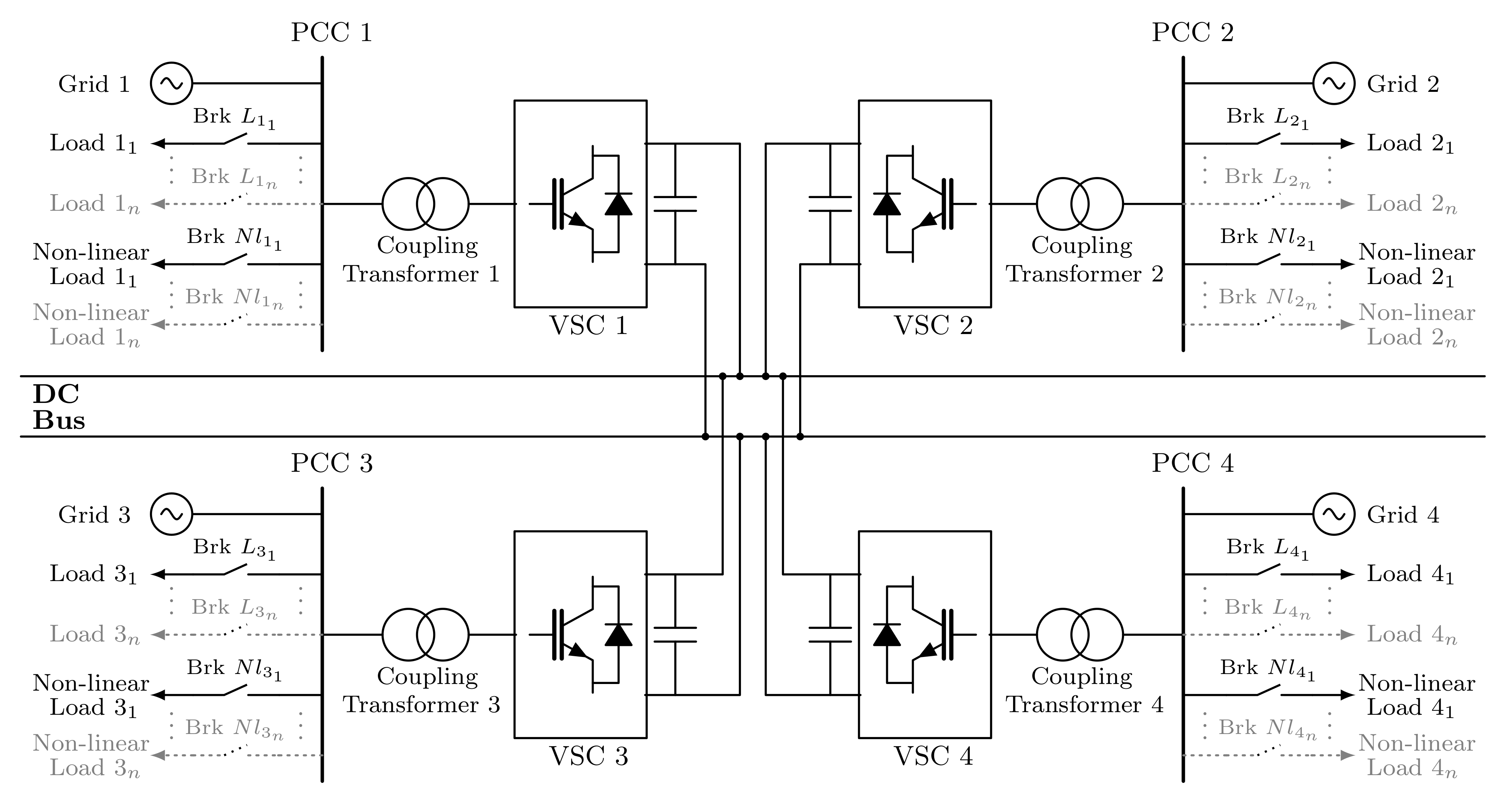
The scheme of a multiterminal HVDC system is plotted in
Figure 1. In this case, four terminals are connected to their respective AC grids and share the same DC link. Several load types can be connected to the various PCCs by means of breakers (Brk), i.e., linear loads, both balanced and unbalanced loads, and nonlinear loads. Each VSC is connected to its respective AC network by means of a coupling transformer that is modeled by a resistance
and an inductance
, where the subscript
m denotes the number of the terminal, i.e.,
.
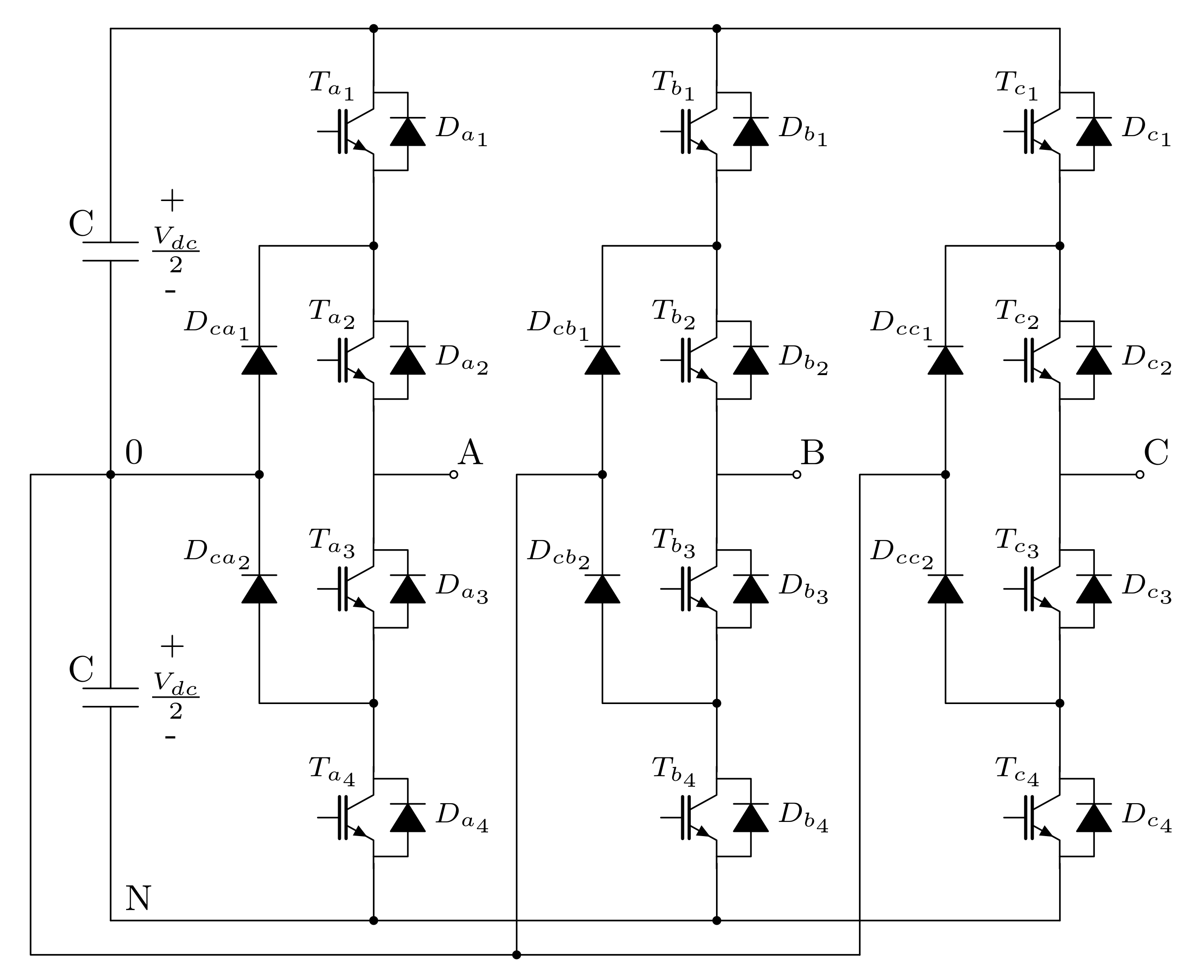
An NPC multilevel topology is employed for each VSC. Particularly, a three-level NPC converter was chosen (see
Figure 2 for more details) owing to its ease of implementation and to the fact that it is a well-established commercial solution compared to other multilevel topologies. The advantages of this configuration can be found in [
20], while a comparison between several multilevel topologies can be seen in [
21].
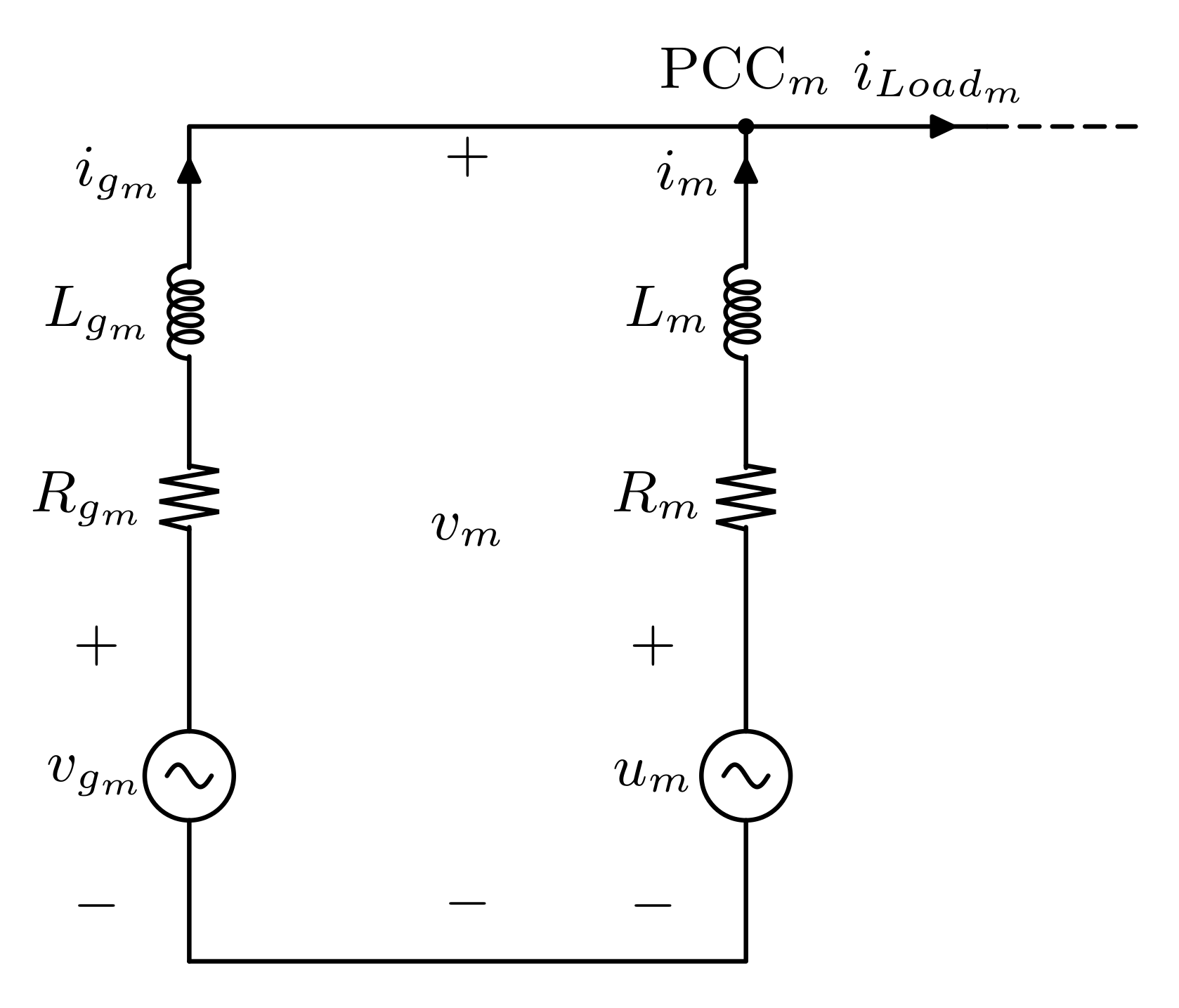
The single-phase diagram of the
m-th terminal of the HVDC system connected to its respective AC grid is shown in
Figure 3, where
is the output voltage of the VSC,
is the current exchanged between the VSC and the grid, and
is the voltage at the PCC. The current
stands for the sum of all the currents drawn by the various loads connected to the PCC, while
is the AC grid voltage and
is the grid current. Finally, the parameters
and
are the resistance and the inductance, respectively, employed to model the line of the grid.
A state-space model can be obtained for the current
by using an SRF together with Park’s transformation [
22] and under the assumption that a three-wire system is employed, yielding
where
and
are the
d and
q components of the current
, respectively;
and
are the
d an
q components of the output voltage of the VSC, which will be used as control input to regulate the current
; and
is the
d component of the grid voltage
that can be seen as a disturbance. The parameter
is the angular frequency of the grid voltage.
The dynamic system (
1) is coupled and must be decoupled in order to implement independent control laws for
and
. This can achieved by rewriting the system (
1) as
where the
d and
q components of the VSC output voltage can be obtained using the following decoupling equations:
It should be noticed that the
q component of
is zero in the SRF, as explained in [
23], which implies that, under balanced conditions, the instantaneous active and reactive powers exchanged between the VSC and the grid at the PCC can be written as
The active power
and the reactive power
can therefore be controlled by regulating the
d and
q components, respectively, of the current
. Similarly, the active and reactive powers at the VSC output are
Under the assumption of an ideal VSC, the power at the input of the VSC,
, must be equal to the power stored in the DC-link capacitor of the VSC,
, plus the output power of the VSC:
Moreover, the term
can be calculated using the following dynamic model:
where
is the equivalent capacitor of the DC side of the VSC associated with the
m-th terminal,
is the voltage across the capacitor
, and
is the current through the capacitor
. The output power of the VSC can be written as
where the term
is the power dissipated in the coupling transformer used to connect the VSC to the AC grid. If this power is neglected [
24], then
, and the combination of Equations (
4), (
6), (
8) and (
9) yield
Equation (
11) reveals that if the voltage
remains constant, all the power at the input of the VSC will be equal to the active power at the PCC, which can be used to inject power to the AC grid or, on the contrary, absorb power from the AC network.
3. Proposed Control Topology
Multiterminal VSC–HVDC systems allow the energy to flow between the different AC grids to fulfill the requirements of power demanded by the energy consumption. Moreover, a reactive power compensation can be carried out by the VSC–HVDC in order to correct the drop voltage at the PCC owing to the line impedance of the grid and the current through it.
Owing to the various types of loads connected to each PCC, the grid current can contain imbalances and harmonics and, thus, the voltages at each PCC will be polluted. In order to cancel out these disturbances, each VSC in the multiterminal VSC–HVDC system was employed to inject the unbalanced current and the harmonics components necessary for the correct operation of the various loads connected to the PCCs, while maintaining the grid current with a low distortion, thus, yielding a more sinusoidal waveform for the voltages at the PCCs.
In this work, one of the VSCs is in charge of maintaining a regulated DC voltage across the DC bus, thus providing a power slack to guarantee that the power balance is fulfilled. Nevertheless, an additional VSC can be designed to provide a backup of the control of the DC voltage [
15].
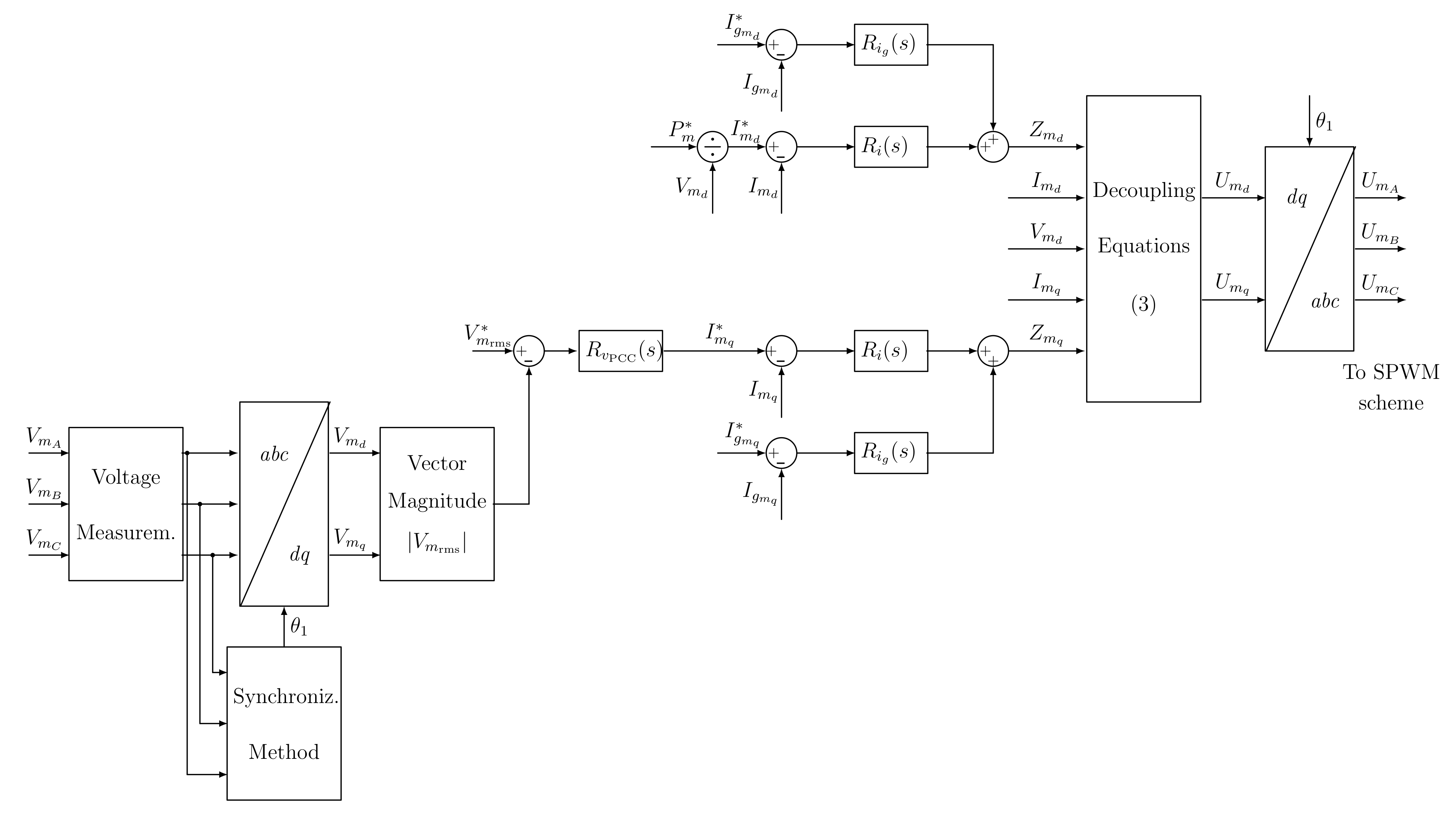
Figure 4 shows the proposed control topology based on the control scheme of the STATCOM reported in [
25].
As the scheme is implemented in the SRF [
26], a synchronization method is employed to obtain the angle
necessary to carry out the Park transformation. Several alternatives can be used, although the synchronization scheme chosen in this work is the open-loop estimator explained in [
27], owing to its capabilities to operate in the presence of harmonics.
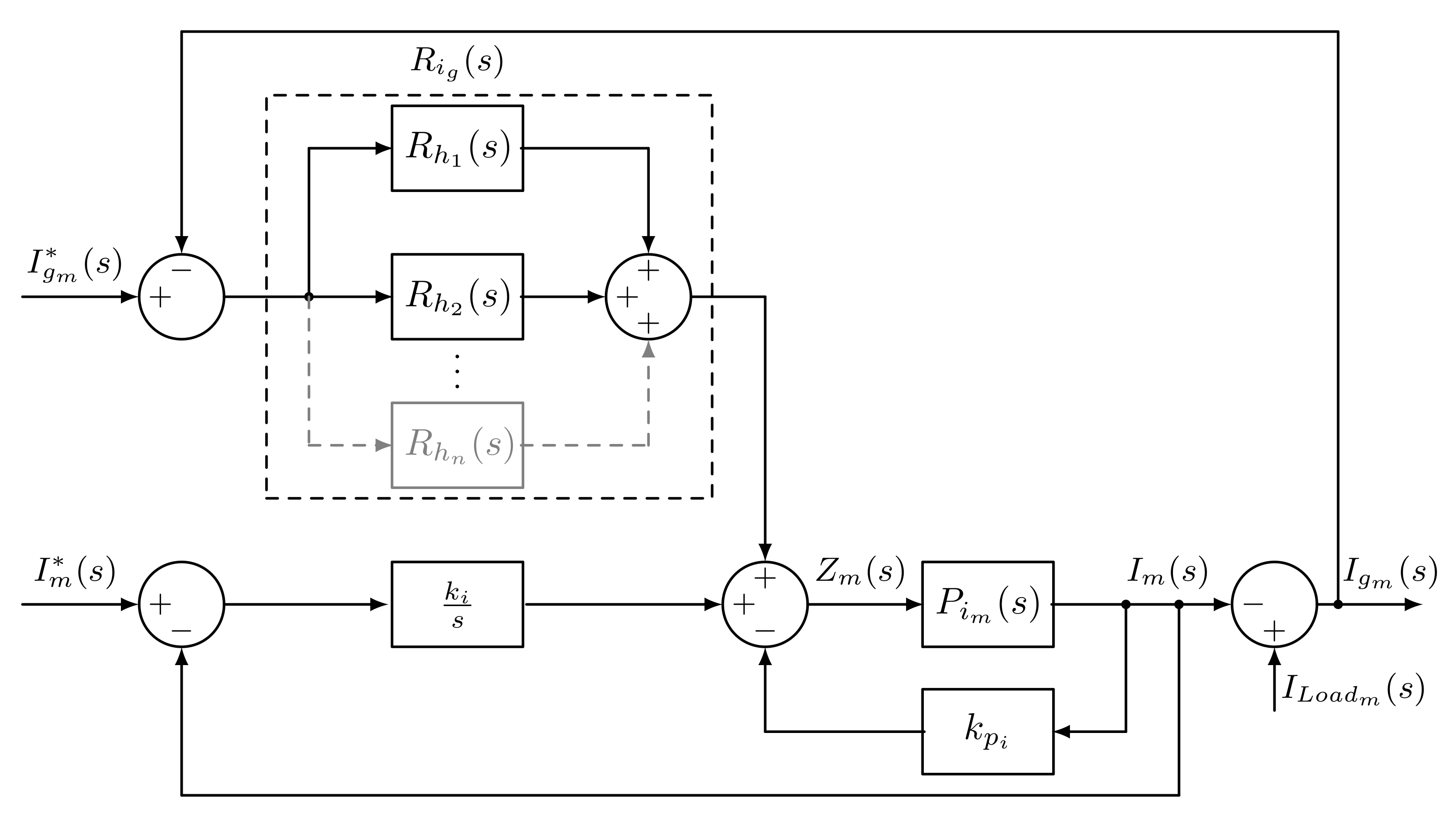
The structure contains several nested control loops to regulate a number of variables compared to their set-point values, denoted by an asterisk: controller
is in charge of regulating the DC voltage of the complete DC bus, while controller
maintains the voltage at the PCC constant; the two controllers
are designed to regulate the DC component of the current injected into the AC grid by the VSC in both
d and
q axes, whereas the two regulators
are tailored to compensate the harmonics and imbalances of the grid current in both
d and
q axes. The sum of the control actions provided by
and
yields the variables
and
, which are used together with the currents
and
and the voltage
in the decoupling Equation (
3) to obtain the
d and
q components of the output voltage of the VSC. These components are transformed into three-phase voltages by means of the inverse Park Transformation and are driven to a sinusoidal pulse-width modulation (SPWM) scheme to implement the firing signals of the switches in the VSC [
28].
The complete control scheme to operate a VSC that will not regulate the DC voltage across the DC bus is very similar and is plotted in
Figure 5. The difference with the scheme shown in
Figure 4 is that the controller
is not present and the reference of active power can be generated in accordance with a power dispatcher.
3.1. Regulation of the DC Voltage across the DC Bus
The DC voltage of the HVDC system is controlled by using a multiloop scheme with two PI controller loops: the inner control loop,
, regulates the
d component of the current
using one of the most well-known scheme to operate with grid-connected VSCs [
29]; the outer control loop,
, is in charge of regulating the DC voltage. The output of
is the reference for the active power,
, which, divided by the
d component of the voltage at the PCC
, yields the reference for the current,
, of the inner control loop.
Let
be the output of the controller
for the
d axis. This output can be calculated in accordance with the following PI control law:
where
and
are the proportional gain and the integral gain of the PI controller, respectively, and are tailored to control the dynamic system (
13) for the
d axis, which can be easily obtained from the decoupled plant (
2):
Furthermore, the proposed PI control law for the regulator
is
where
and
are the proportional gain and the integral gain of the controller
, respectively. These gains are designed using the dynamic model (
15) in the Laplace domain obtained from (
11):
where
is a disturbance input that cannot be controlled and
is the control input that will be modified to vary
and, therefore, the value of the voltage
.
3.2. Regulation of the Voltage at the PCC
A similar structure to the one employed in
Section 3.1 based on a multiloop control scheme is used to regulate the voltage at the PCC. In this case, the inner control loop,
, controls the
q component of the current
, while the outer control loop,
, is the responsible for regulating the root-mean square (RMS) value of the voltage at the PCC. The output of
is the reference for the
q component of the current injected by the VSC,
.
The control law for
in the
q axis is the same as the one obtained for the
d axis:
where
is the output of the controller
for the
q axis and the gains
and
are calculated to control the dynamic system (
17) for the
q axis, which are obtained from the decoupled plant (
2):
It should be noticed that Equations (
13) and (
17) contain the same parameters and, under the assumption that the same design specifications hold for the regulator
, the gains of
will, therefore, be equal in both axes.
The controller
is designed under the assumption of a balanced three-phase system, which yields a constant RMS value for the voltage. For that reason, a PI controller is also proposed with the following control law:
where
and
are the proportional and integral gains, respectively, of the controller
. These parameters must be carefully calculated as the dynamic model of the grid and loads is unknown and an arbitrary design might render the system unstable.
3.3. Compensation of Imbalances and Harmonics of the Grid Current
When unbalanced loads or nonlinear loads are connected to the AC grid, imbalances and harmonics appear in the current that flows through the grid, which cause a distorted and unbalanced voltage at the PCC in weak grids owing to the line impedance. The HVDC system can be used to compensate these disturbances and improve the power quality at the various PCCs, resembling the behavior of an active power filter. This section proposes a control scheme based on proportional-resonant (PR) controllers to cancel out the imbalances and harmonics in the grid current. Usually, the most frequent harmonics present in the voltage at the PCC are uneven components [
30]. These components are transformed into even harmonics in the SRF [
27]. Moreover, imbalances in the fundamental component are transformed into second harmonic components in the SRF. For that reason, the use of several resonant regulators tuned at even harmonics, based on the scheme reported in [
31], is proposed to remove the harmonics and the imbalances from the grid current. The general transfer function of these resonant controllers is
where the transfer function
is a phase-lead or phase-lag compensator designed to fulfill the specifications of the controller, and the term
is the resonant regulator tuned at the frequency
.
exhibits a band-pass behavior that is useful to design the regulator without considering the remaining resonant controllers [
32].
Figure 6 shows the control scheme that employs several resonant regulators to compensate the imbalances and the harmonics in the grid current. The scheme also plots the implementation of the inner control loop for the regulation of the current injected by the VSC. The scheme is implemented in both
d and
q axes. As the grid current should not contain either imbalances or harmonics, the reference of the grid current,
, must be set to zero. In accordance with
Figure 6, the resulting regulator
that is present in
Figure 4 and
Figure 5 is the sum of the various resonant controllers tuned at different frequencies:
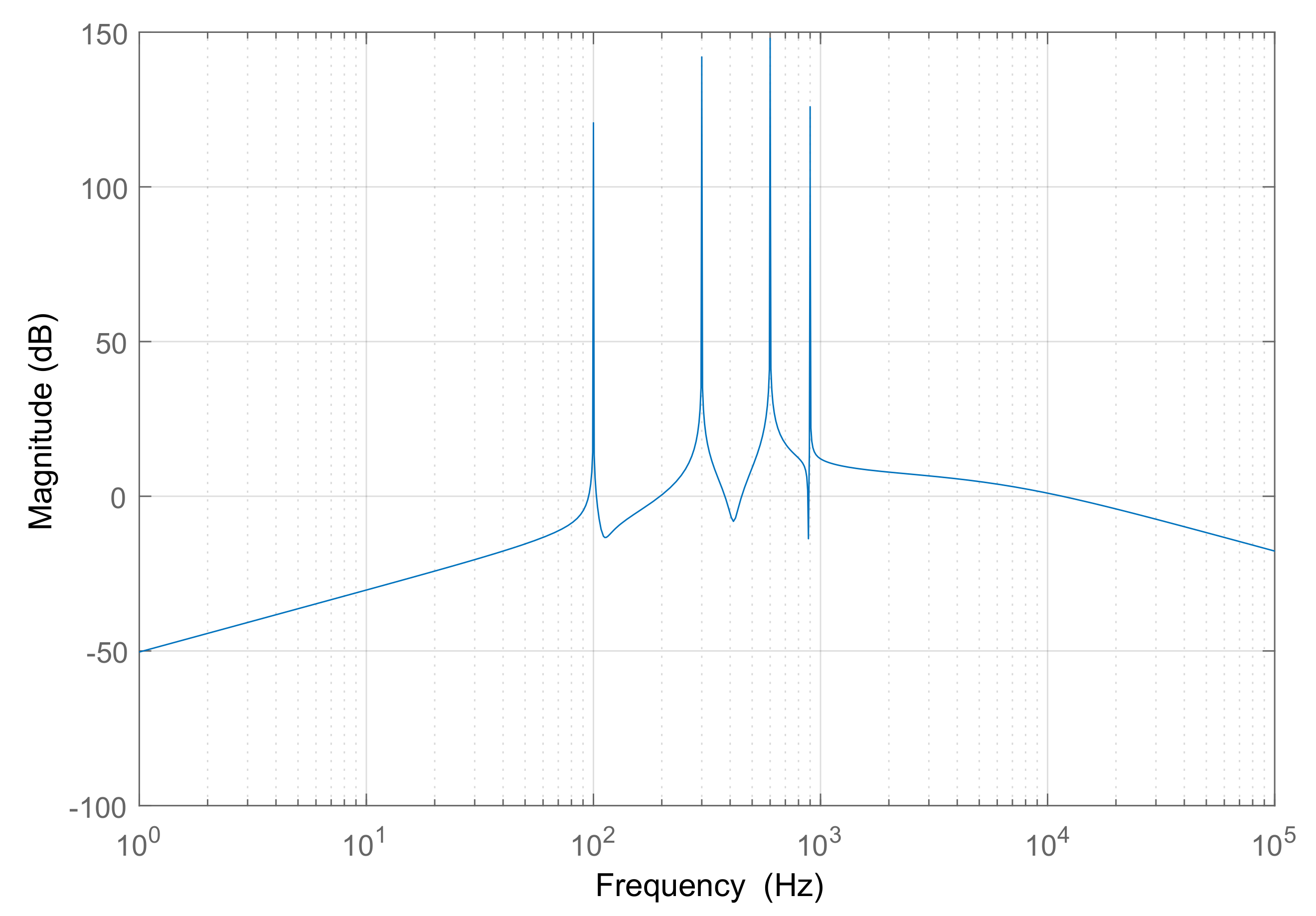
As an example,
Figure 7 shows the magnitude of the frequency response for a regulator
designed to compensate the 2nd, 6th, 12th, and 18th harmonic components in the SRF. It can be seen that
exhibits infinite gain at the selected frequencies with band-pass behavior, which implies that
is suitable for compensating harmonics at these frequencies.
4. Case Study
A four-terminal HVDC system such as the one depicted in
Figure 1 has been simulated using PSCAD
TM/EMTDC
TM. Four AC grids are interconnected by means of the HVDC system. The main features of these networks are as follows:
AC Grid 1: 11 kV and 50 Hz, inductance of the line mH.
AC Grid 2: 13.8 kV and 50 Hz, inductance of the line mH.
AC Grid 3: 13.8 kV and 50 Hz, inductance of the line mH.
AC Grid 4: 11 kV and 50 Hz, inductance of the line mH.
The HVDC system employs four three-level three-phase NPC VSCs, which are connected to their respective AC grids by means of four coupling transformers with a winding ratio of 20 KV/60 KV and star/star connection. These transformers have been considered ideal, and additional inductive-resistive elements have, therefore, been added to model the resistances and the inductances of the transformers, which are summarized in
Table 1 in reference to the 20 KV, primary side of the coupling transformers.
Each VSC employs two series-connected capacitors of
, and the DC bus line has been modeled as ideal, therefore, yielding a DC bus capacitor of 1320
. The switching frequency of each VSC is equal to 5950 Hz, and ideal insulated-gate bipolar transistors (IGBTs) are used as switches in each VSC. The voltage across the DC bus is set to 80 kV. Several linear loads and one nonlinear load are connected to the PCC of each AC grid by means of circuit breakers. In all cases, the same nonlinear load is used, which is composed of a three-phase full-bridge uncontrolled rectifier that feeds an inductive DC load with a constant current of 2 kA. This nonlinear load causes odd harmonics in the AC side current of the rectifier [
33]. The main features of the linear loads are the following:
AC grid 1.
Balanced load 1: active power 20 MW and reactive power 11 MVAr; connected at instant s.
Balanced load 2: active power 30 MW and reactive power 15 MVAr; connected at instant s.
Unbalanced load 1 (resistive load): consumption of 8 MW in phase A, consumption of 8 MW in phase B, and consumption of 1.6 MW in phase C; connected at instant s.
AC grid 2.
Balanced load 1: active power 25 MW and reactive power 12 MVAr; connected at instant s.
Balanced load 2: active power 35 MW and reactive power 15 MVAr; connected at instant s.
Unbalanced load 1 (resistive load): consumption of 1.6 MW in phase A, consumption of 20 MW in phase B, and consumption of 20 MW in phase C; connected at instant s.
AC grid 3.
Balanced load 1: active power 15 MW and reactive power 8 MVAr; connected at instant s.
Balanced load 2: active power 25 MW and reactive power 16 MVAr; connected at instant s.
Unbalanced load 1 (resistive load): consumption of 2 MW in phase A, consumption of 8 MW in phase B, and consumption of 2 MW in phase C; connected at instant s.
AC grid 4.
Balanced load 1: active power 25 MW and reactive power 15 MVAr; connected at instant s.
Balanced load 2: active power 35 MW and reactive power 10 MVAr; connected at instant s.
Unbalanced load 1 (resistive load): consumption of 1.4 MW in phase A, consumption of 10 MW in phase B, and consumption of 1.4 MW in phase C; connected at instant s.
The four nonlinear loads are connected, simultaneously, at instant s. Terminal 1 is in charge of maintaining the voltage across the DC bus at 80 kV, while the other terminals operate as power dispatchers: Terminal 2 injects 20 MW into AC grid 2 at instant s, whereas, at s, it absorbs 10 MW from AC grid 2; terminal 3 injects 25 MW and 15 MW at instants s and s, respectively, into AC grid 3. Finally, terminal 4 injects 10 MW into AC grid 4 at instant s, and it absorbs 30 MW from AC grid 4 at instant s.
The regulators
and
have been calculated using the pole placement technique [
34]. The design specification for the controller
is to choose real poles in order to avoid overshoots in the time response. With this criterion, the location of the two closed-loop poles is chosen to be −1200 rad/s, and the resulting parameters are shown in
Table 2. The poles of the outer closed-loop system obtained with
are chosen to be slower than the poles of the inner control loop; in this case, the poles are placed at
rad/s and
rad/s, yielding the following parameters:
and
.
The parameters of the regulator are chosen after following a trial–error procedure, as the plant contains uncertainties. In this case study, the chosen parameters for the four regulators are and . The controller is activated at instant s.
The controller
is designed to compensate the imbalances in the grid current and the harmonics caused by the nonlinear loads. Recalling that these harmonics are uneven components, they are transformed into the components
in the SRF. Hence, the regulator
is composed of five resonant controllers in parallel, tailored to compensate the 2nd, 6th, 12th, 18th, and 24th harmonics in the SRF. The parameters of the various regulators
are obtained using the frequency response method [
35] with the design specifications of a phase margin of 60 at the following crossover gain frequencies:
, with
, i.e., the 2nd harmonic;
, with
, i.e., the 6th harmonic;
, with
, i.e., the 12th harmonic;
, with
, i.e., the 18th harmonic; and
, with
, i.e., the 24th harmonic. The resulting parameters of the regulators
are shown in
Table 3. The controller
is activated at instant
s. The total simulation time is 3 s.
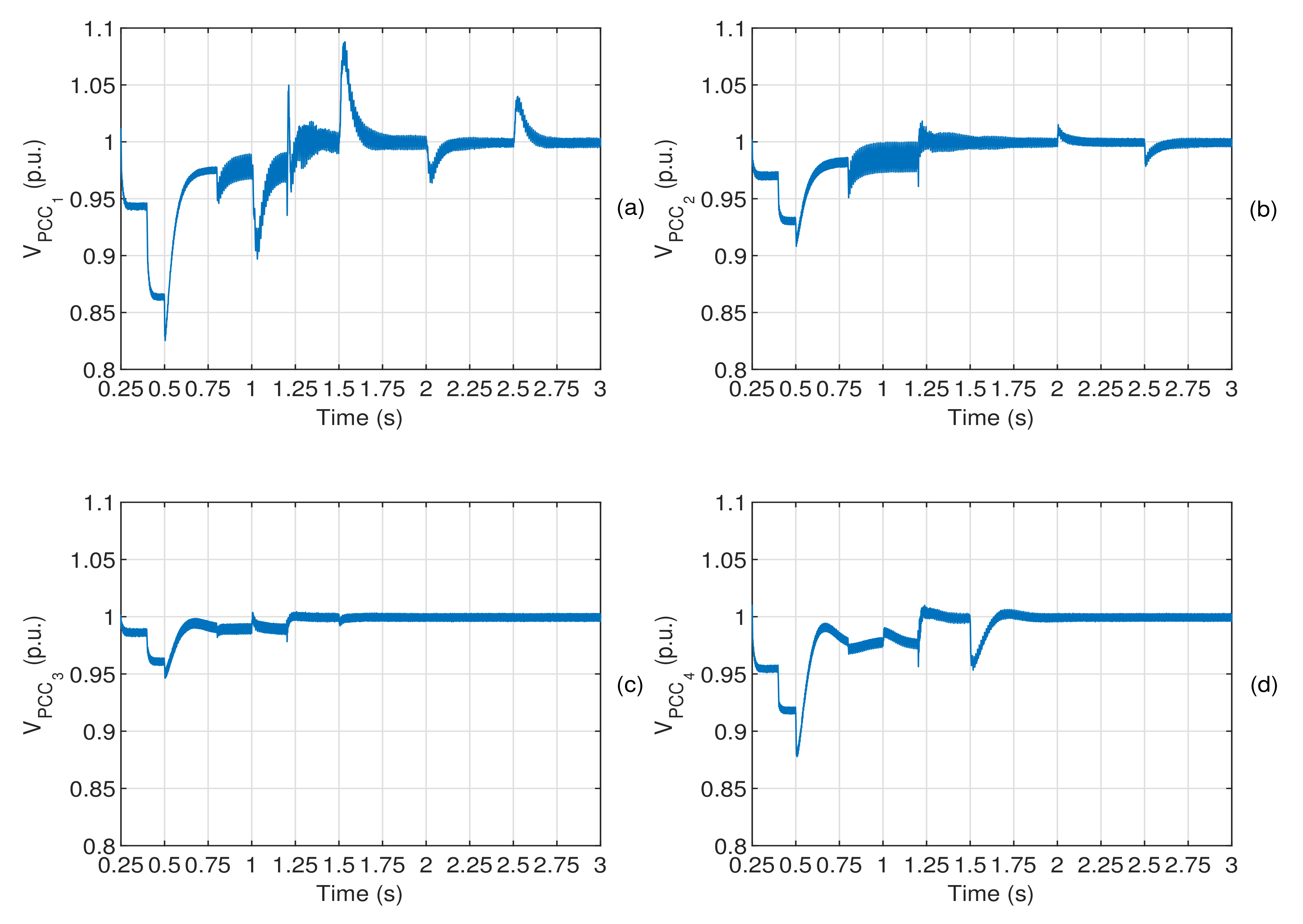
Figure 8 shows the time response of the voltage of each of the four PCCs to which the HVDC system is connected: Before instant
s, voltage sags with different amplitudes are present in all PCCs owing to the connections of the linear and nonlinear loads to their respective AC grids. The greatest voltage sag takes place at PCC
with an amplitude around 13%. Once the regulators
are activated in the terminals of the HVDC systems at
s, all voltages at the PCCs increase their amplitudes until the steady-state value of 1 p.u is reached. Although there are changes in these voltages when the references of the active powers of the terminal power dispatchers are modified, the steady-state error in the voltage is zero owing to the integral action of the controller
.
The voltage across the DC bus is plotted in
Figure 9: A double frequency ripple is present when imbalances begin to be compensated [
18]. Moreover, even voltage harmonics are present in the voltage waveform when the harmonics of the grid currents are compensated by each terminal of the HVDC system. However, the DC value of the voltage across the DC bus remains around 80 kV, despite the disturbances caused by changes in the references of the active powers of the terminal power dispatchers.
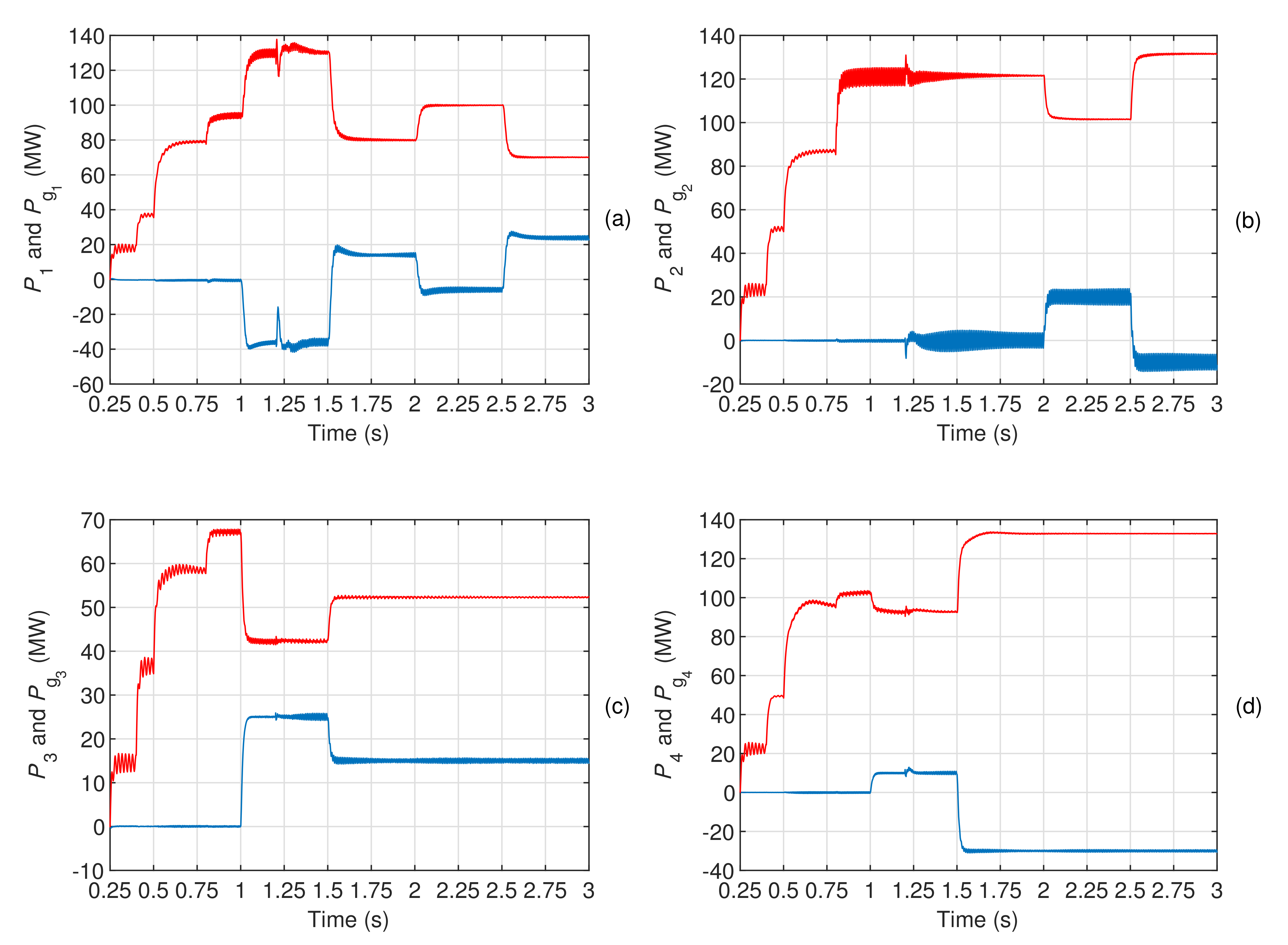
The process of the transmission of active power in the HVDC from one terminal to another is shown in
Figure 10, which plots in blue color the injected/absorbed active powers by the four terminals into/from their respective AC grids (if the active power is positive, it is considered that the terminal injects active power into the grid, in accordance with [
7]). It should be noticed that the VSC connected to terminal 1 keeps the power balanced owing to the control of the voltage across the DC bus; e.g., at instant
s, the active powers of the three dispatcher terminals are
= −10 MW,
= 15 MW, and
= −25 MW, respectively, yielding a power balance at terminal 1 equal to
MW; the actual active power injected by the terminal 1 is, however, slightly higher owing to the losses in the coupling transformers, as shown in
Figure 10a.
In addition,
Figure 10 also shows, in red color, the active powers extracted (positive value) or absorbed (negative value) from each AC grid: these active powers contain not only the components exchanged with the HVDC system, but also the active power consumed by the various loads connected to the AC grids.
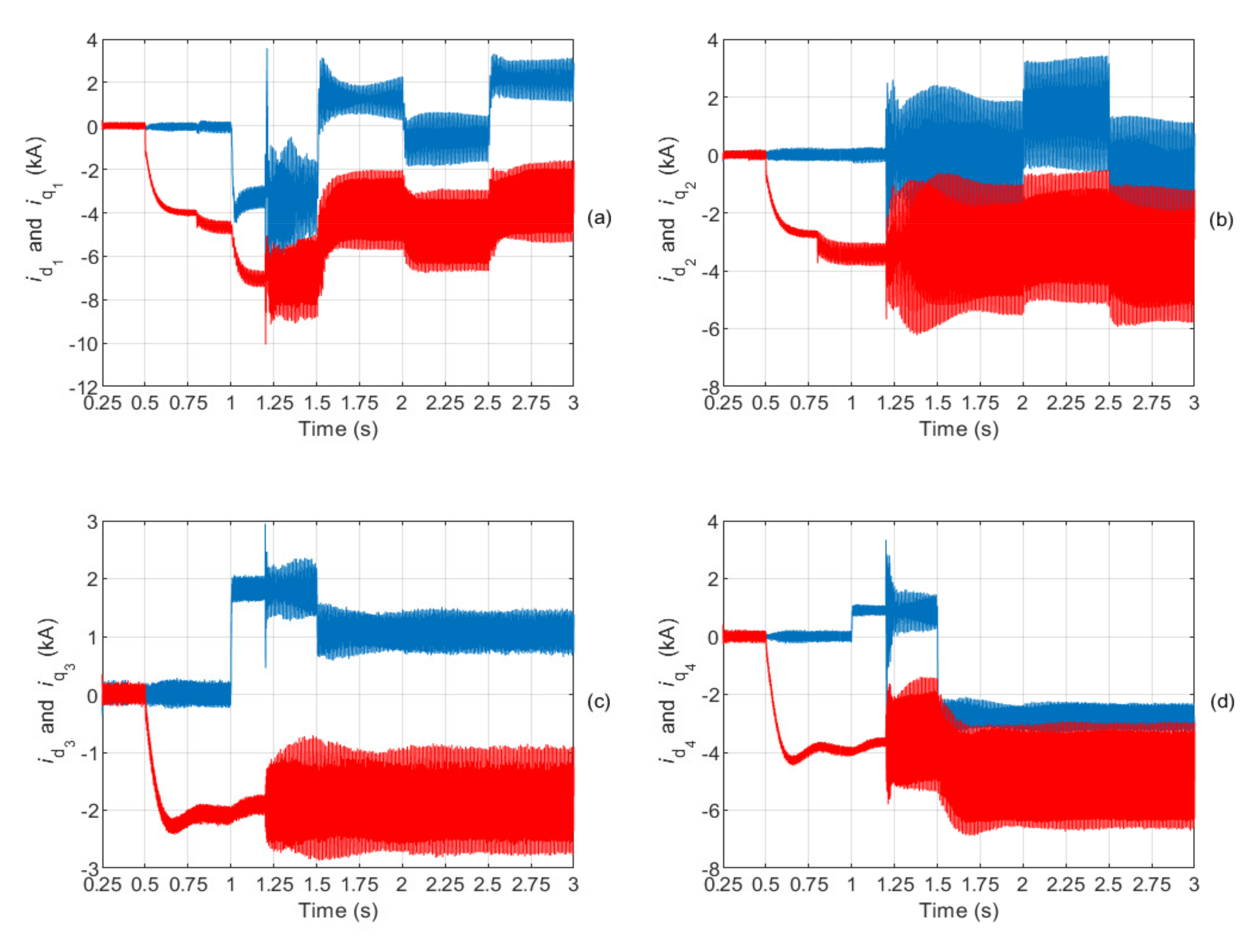
The
d and
q components of the current injected by each terminal into its AC grid are plotted in blue and red colors, respectively, in
Figure 11. Both
d and
q components contain even harmonics, which are the result of the transformation of the odd harmonics into the SRF. Furthermore, the mean value of the
d component of the current is proportional to its respective active power, as shown in
Figure 10, while the mean value of the
q component of the current is proportional to the RMS value of the voltage at the PCC to which the terminal is connected (see
Figure 8 for more details).
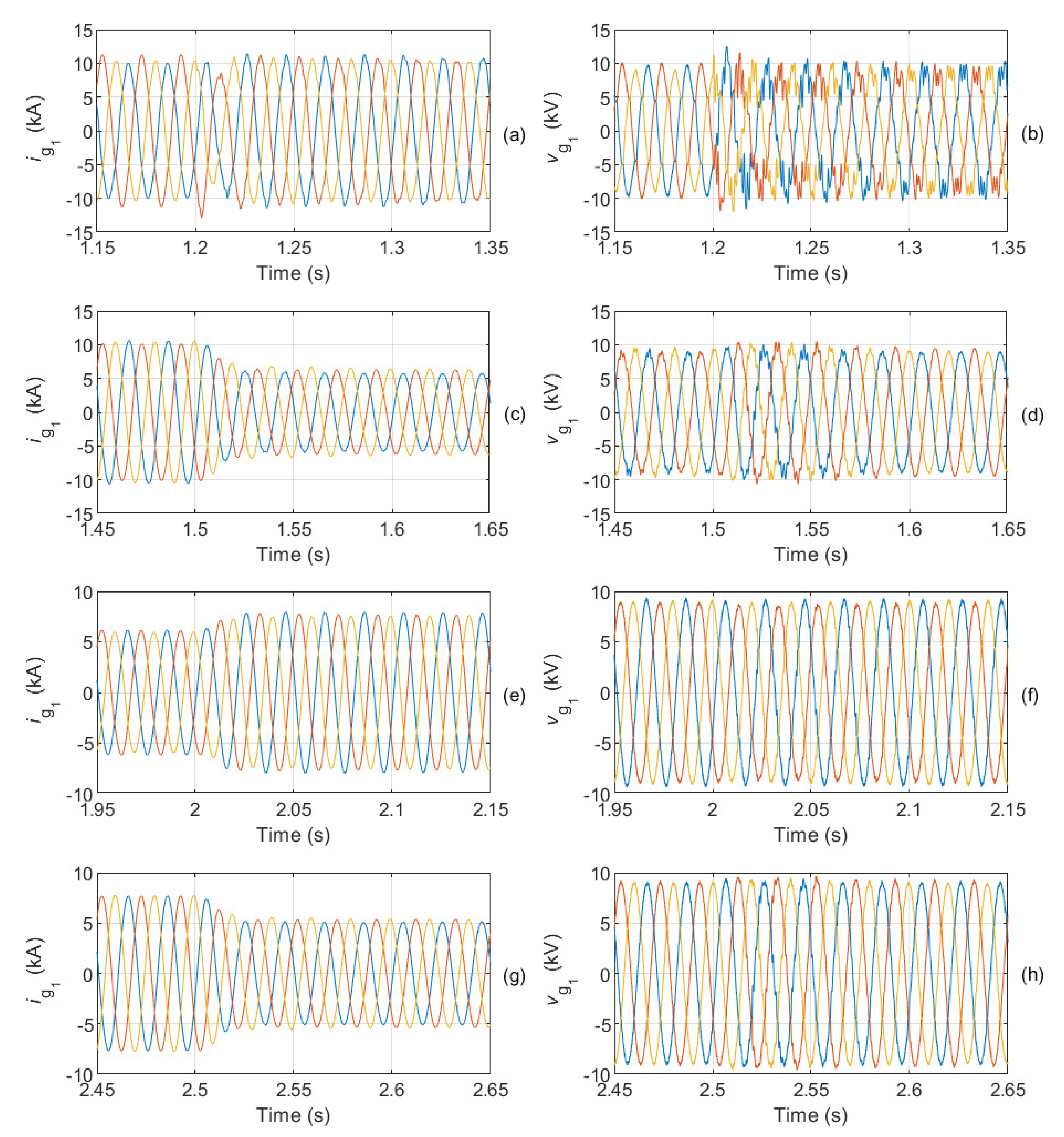
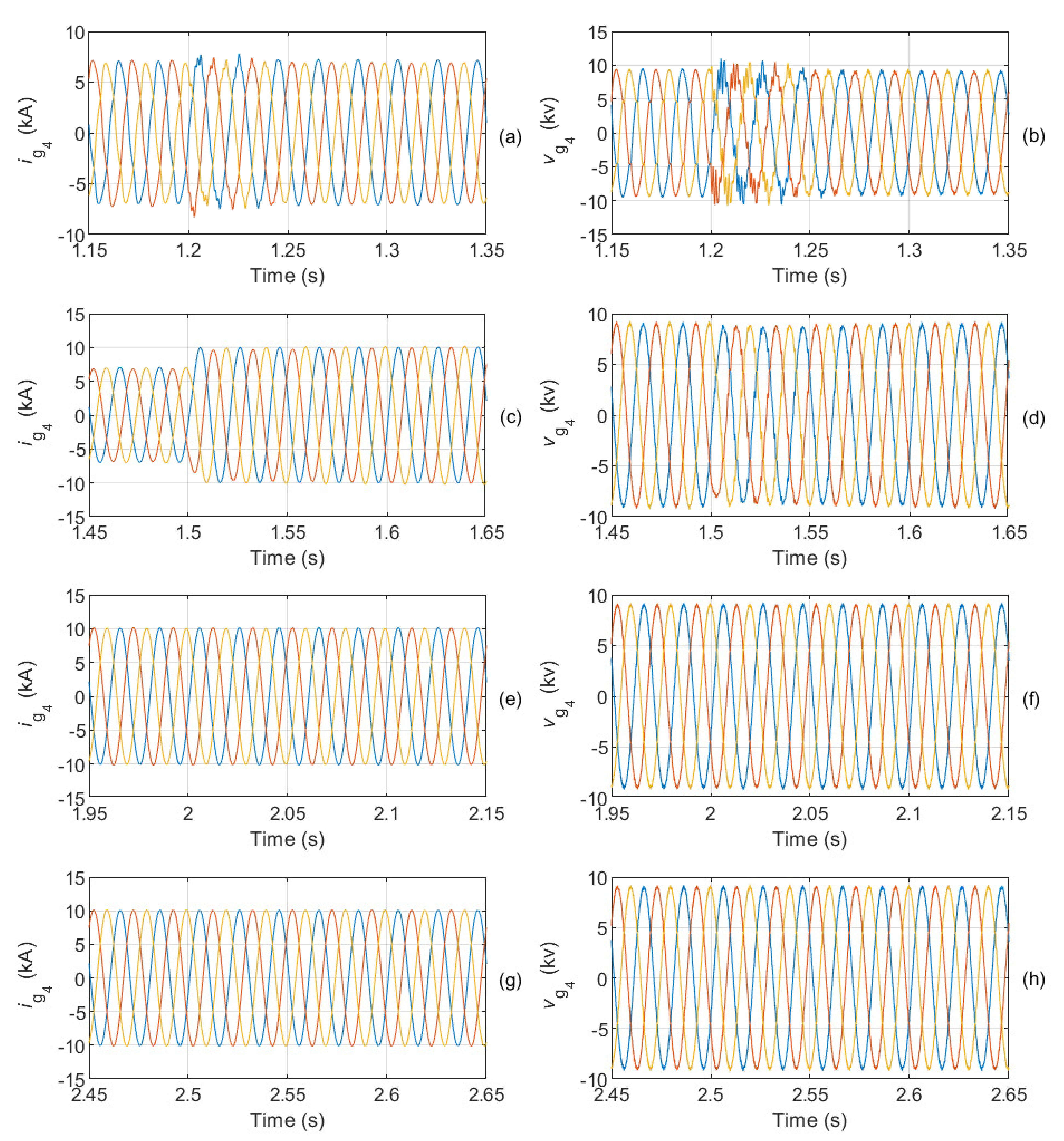
Figure 12 show the waveforms obtained from the current through AC grid 1 and the voltage at PCC
for different time intervals. At instant
s, the resonant regulators
are activated;
Figure 12a,b show how the grid current and the voltage at PCC
are unbalanced and contain harmonics before the activation of
. Once
is in operation, the voltage at PCC
is initially more distorted. At instants
s and
s, changes in the active powers of the dispatcher terminal occur, and they cause disturbances in the grid current and the voltage at the PCC that were previously balanced and had low distortion, as shown in
Figure 12c–f. Finally, the last change in the active power of terminal 2 occurs at
s, as shown in
Figure 12g,h; after this change, the current total harmonic distortion is
, while the voltage total harmonic distortion is
. In the same way,
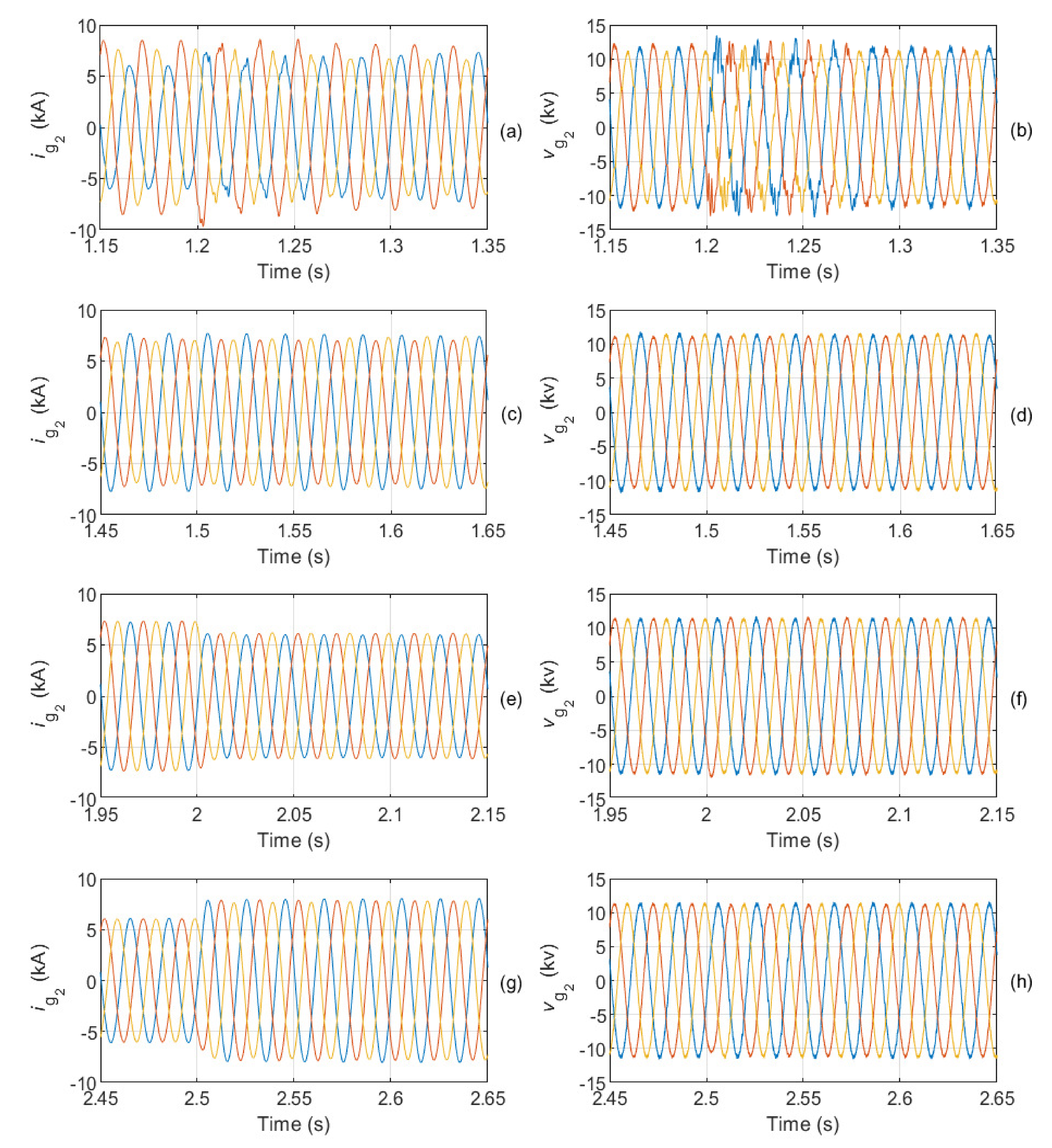
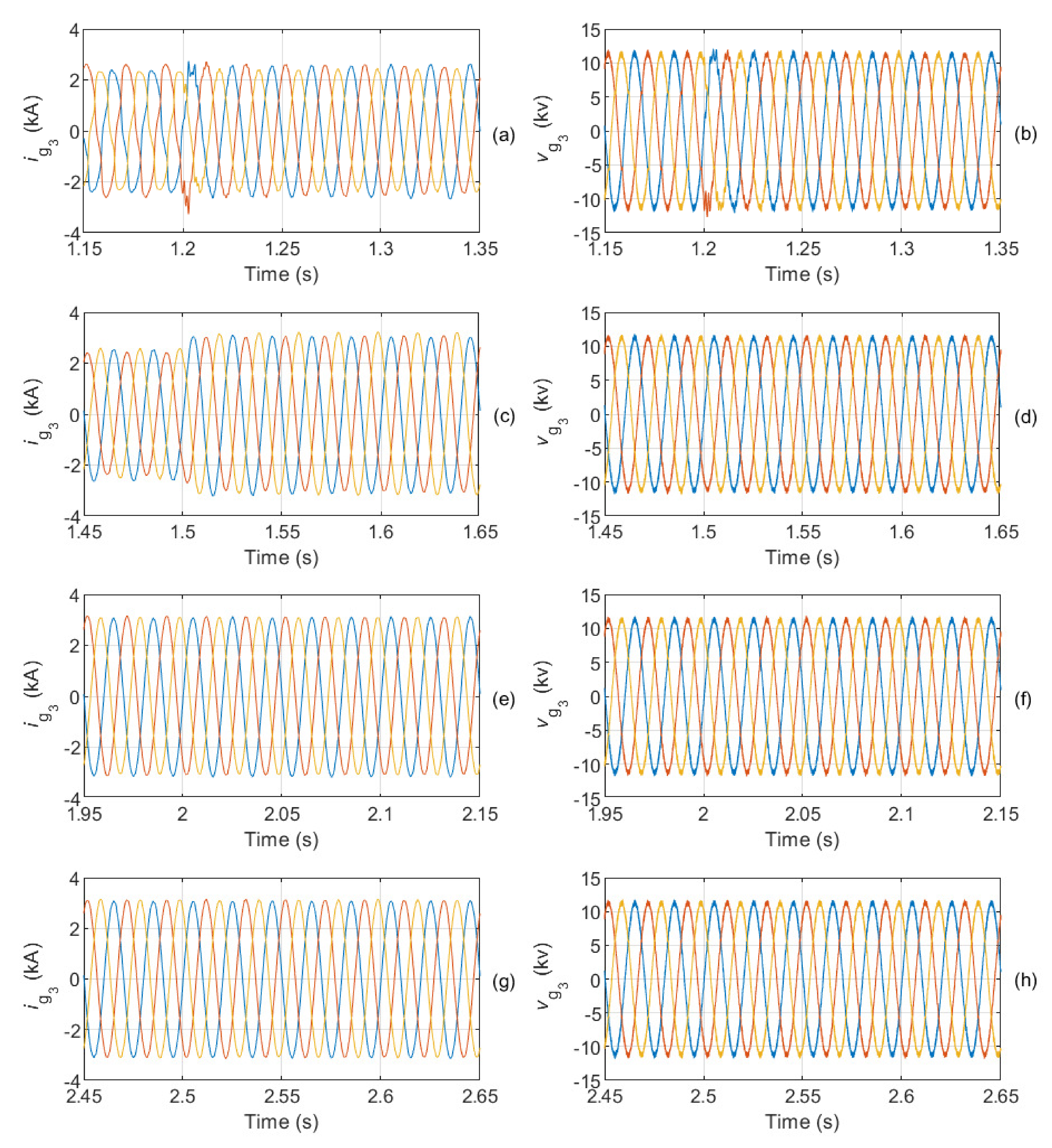
Figure 13,
Figure 14 and
Figure 15 show the waveforms of the current through AC grids 2–4 and the voltages at PCCs
for the same time intervals considered in
Figure 12. Similar results are obtained with reduced distortions and balanced current as well as balanced voltages. The values of the total harmonic distortion for the currents and the voltages of the four AC grids are summarized in
Table 4.