Temperature, Ageing and Thermal Management of Lithium-Ion Batteries
Abstract
1. Introduction
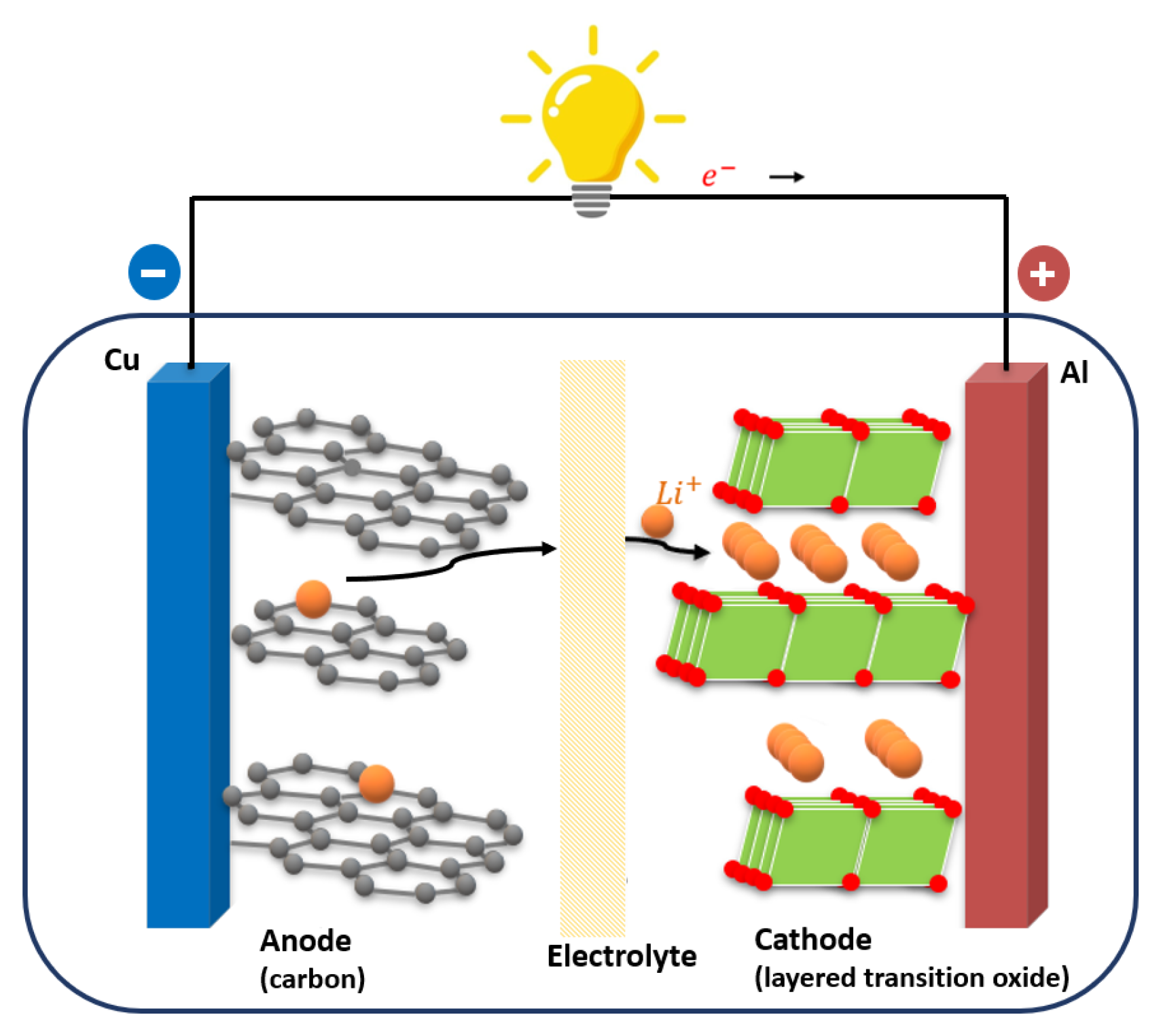
1.1. Working Principle and Geometries
1.2. Currently Used Chemistries and Development Trends
1.3. Thermal Modelling
1.4. Thermal Management
2. Comparing Ageing and Degradation Studies
2.1. Ageing Mechanism
2.2. Definitions and Calculations
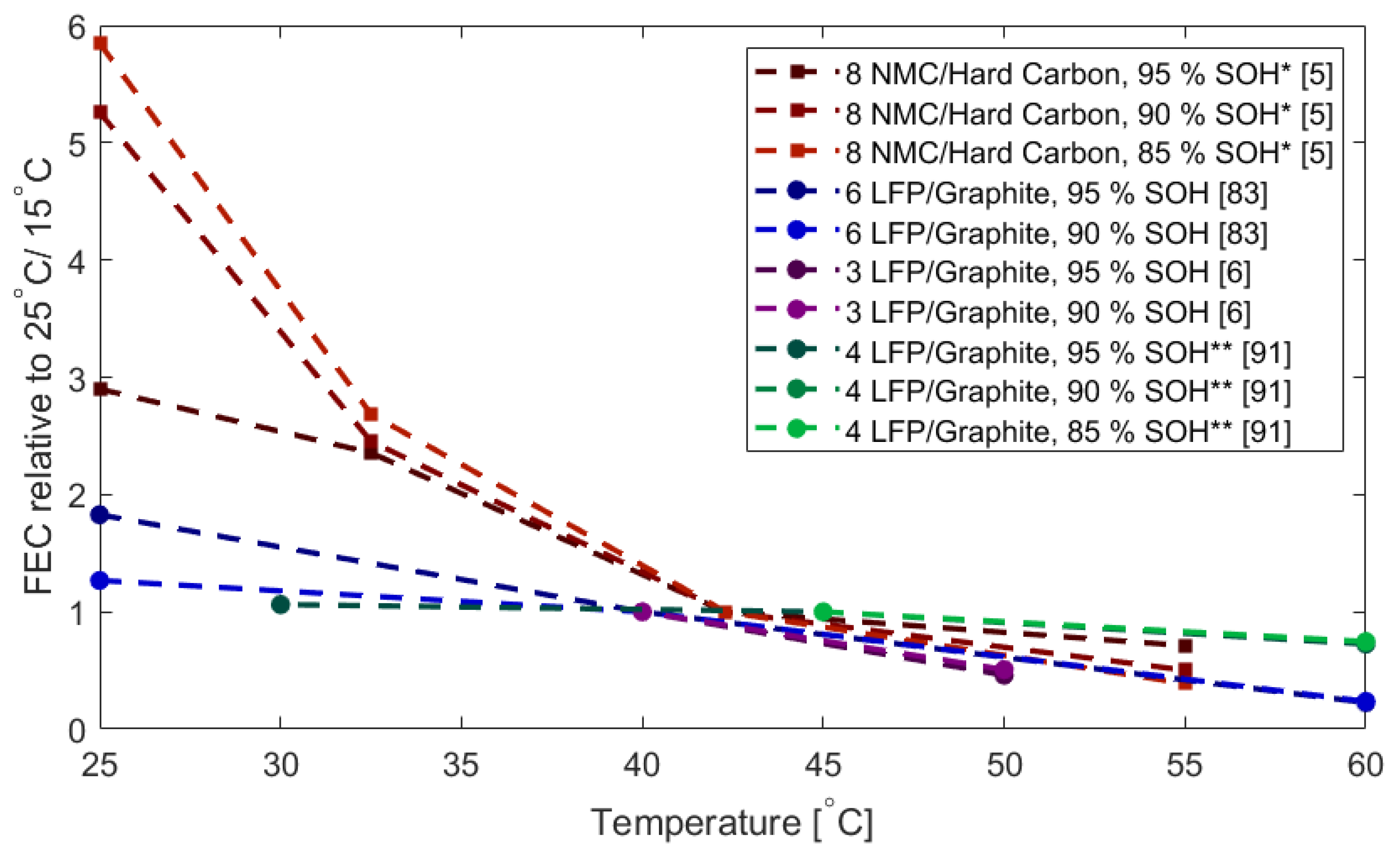
2.3. Cycling: Capacity Fade and Resistance Increase as a Function of Temperature, C Rate and SOC Window
2.3.1. Capacity Fade
2.3.2. Resistance Increase from Cycling Rate
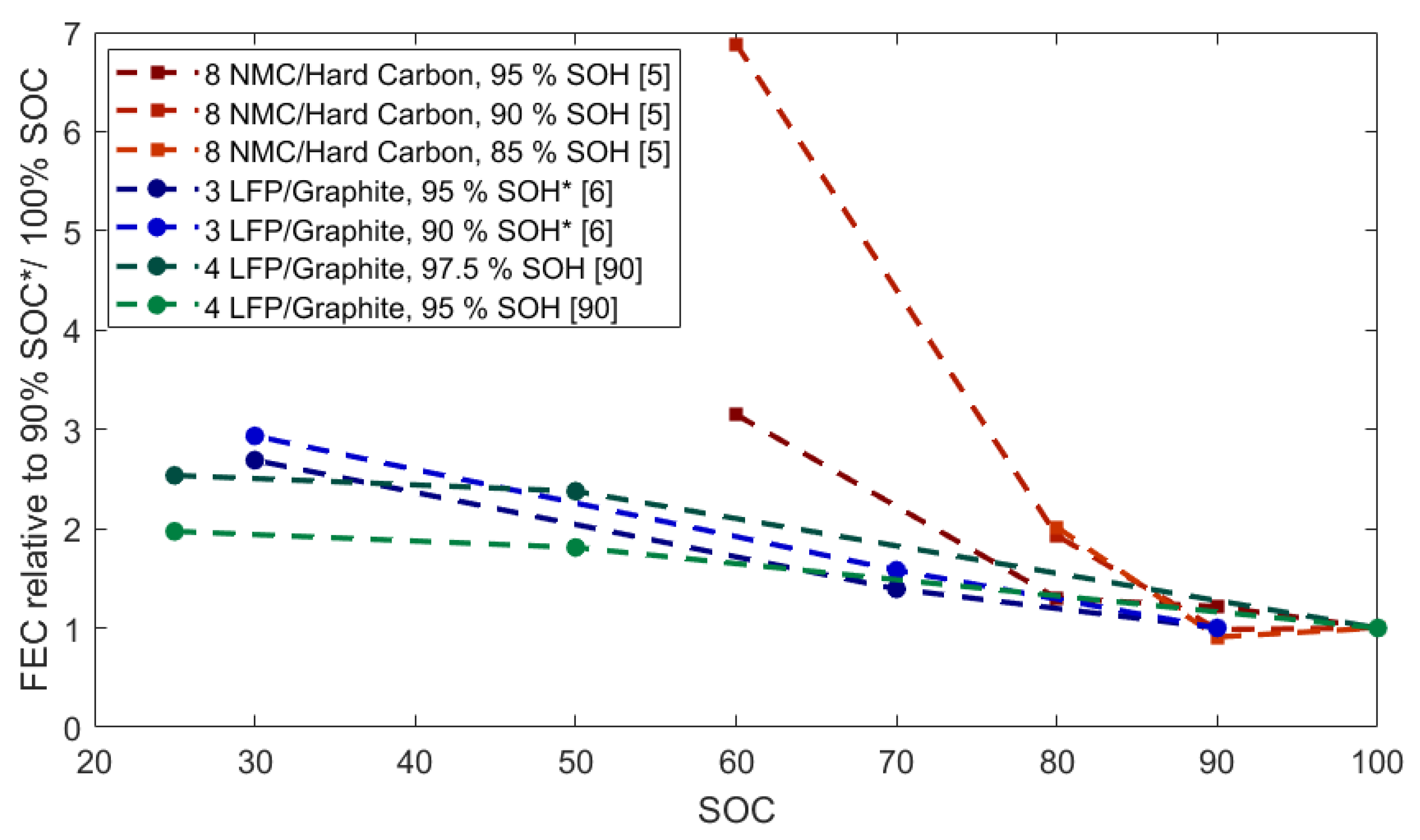
2.4. Calendar Ageing: Capacity Fade as a Function of SOC and Temperature
2.4.1. Capacity Fade
2.4.2. Resistance Increase during Storage
2.5. Discussion
3. Modelling Battery Temperature
3.1. Thermal Model
- heat due to the resistances to the electrochemical reactions, expressed in the overpotential, ,
- the ohmic heat, , due to the paths of the charge carrier (the ion transport in the electrolyte, and the electron transport in the solid-state materials and metals.
- heat due to rearrangement in the electrode, expressed as entropy change, , which is reversible and acts as a heat source during discharge and heat sink during charge.
3.2. Modelling Cases and Parameterisation
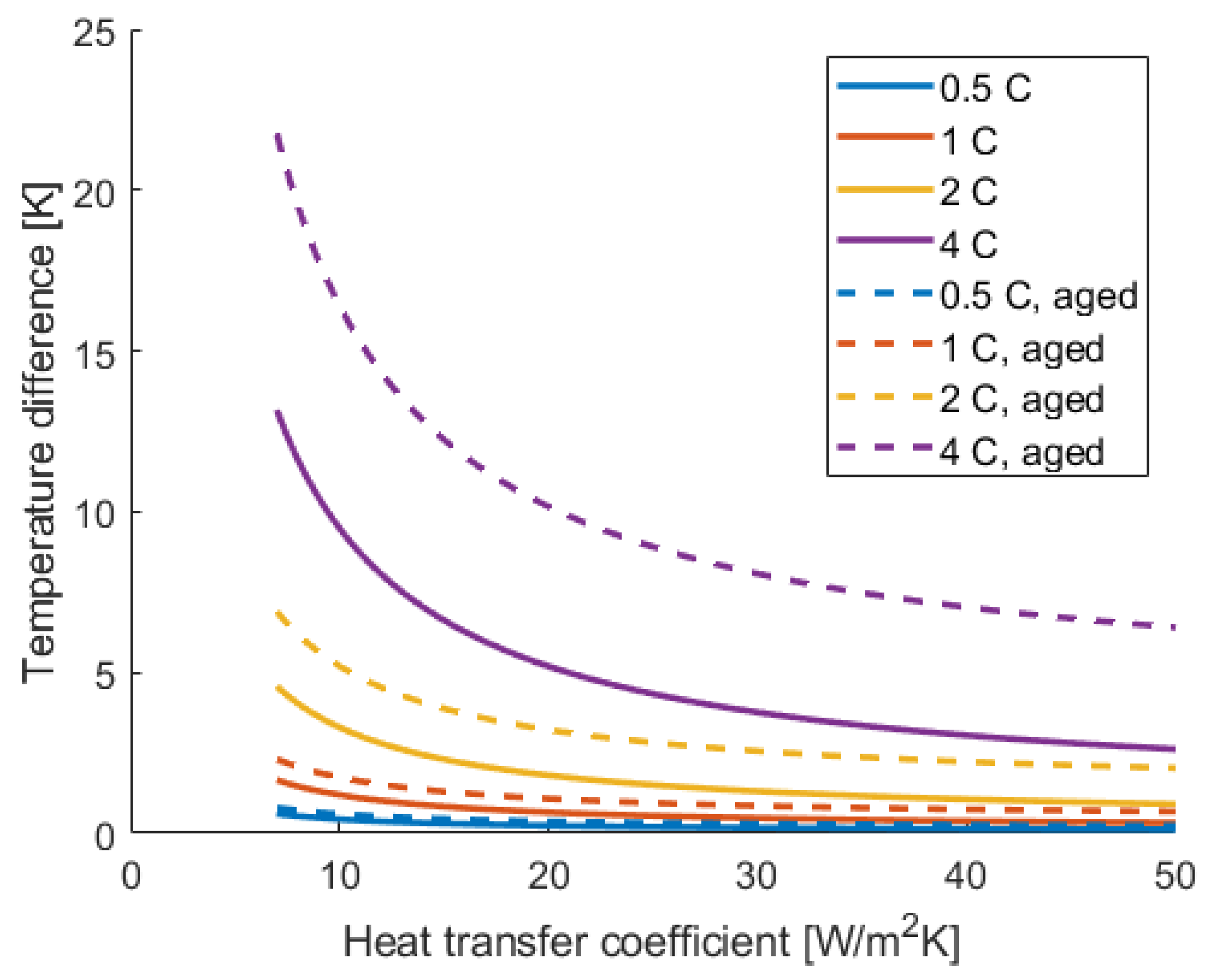
4. Results and Discussion
5. Conclusions
- In general, it appeared that the size of the nominal capacity and geometry does not impact the degradation behavior during cycling as much as electrode material composition, with the cathode material being more important than the anode material for all anodes without silicon.
- Considering the operation conditions, it was found that temperature has the largest comparative impact on battery ageing above room temperature. It accelerates both capacity degradation and resistance increase.
- LIB utilizing LFP as cathode and carbon-based anodes appear to be less affected by higher cycling rates (up to 2 C) and SOC window changes, then other chemistries.
- The resistance generally increases between 30% and 100% from beginning of life (BOL) with 100% SOH to end of life (EOL) (80% SOH).
- Both increased SOC window and temperature were shown to accelerate capacity degradation during storage with the temperature being more damaging.
- LIB utilizing LFP cathode and carbon based anodes are less have a longer storage life and are less effected by storage temperature and storage SOC then LIB with NMC cathode and carbon-based anodes.
- During storage, an approximately linear increase (after an initial decrease) of internal resistance with storage time was observed.
- For cells stored without cycling, the frequency of cell characterisation tests appears to affect the results, indicating that this type of studies has to be evaluated and compared carefully.
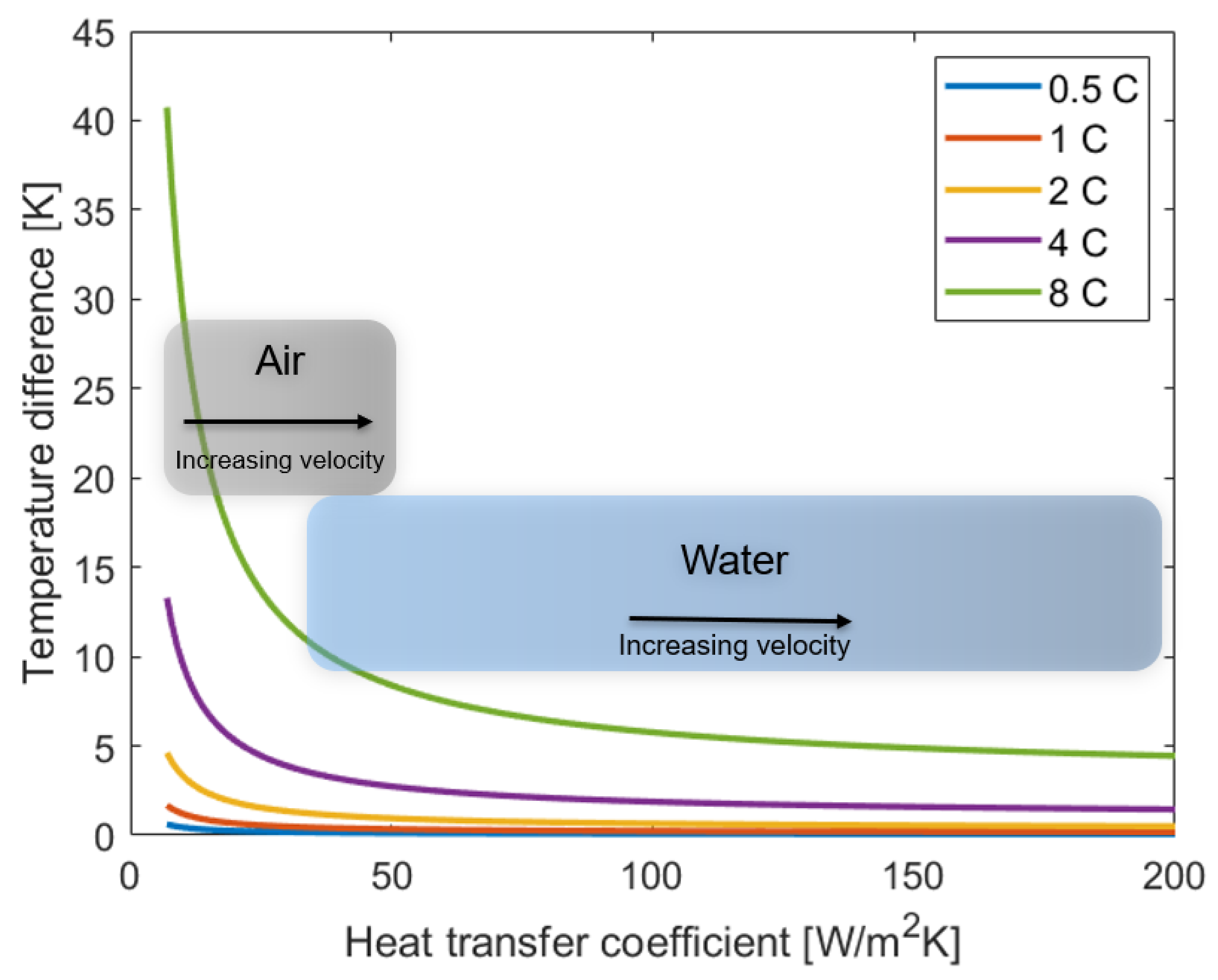
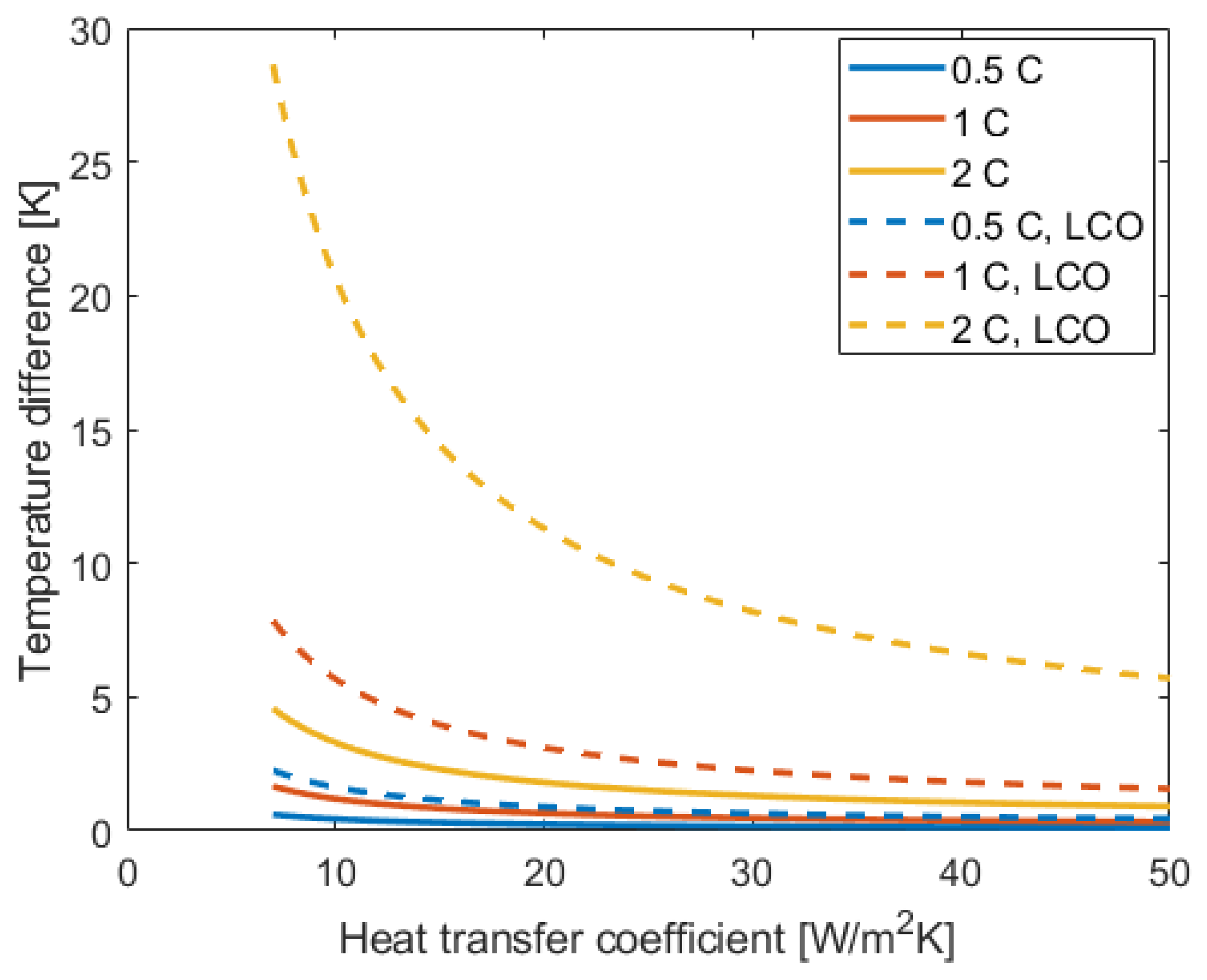
- When testing cells, the actual cell temperature can deviate severely from the reported ambient temperature. Depending on the cooling strategy and C rate, the difference between cell and ambient temperature can range between only a fraction of a degree, up to 40 °C.
- The battery lifetime reduction at high C rates can be for large parts (Table 3) due to an increase in temperature, especially for high energy cells and poor cooling during cycling studies.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BOL | Beginning of life |
| BTMS | Battery thermal management system |
| Thickness of component i | |
| DEC | Diethyl carbonate |
| DMC | Dimethyl carbonate |
| DOD | Depth of discharge |
| Entropy change | |
| EC | Ethylene carbonate |
| EIS | Electrochemical impedance spectroscopy |
| EMC | Ethyl methyl carbonate |
| EOL | End of life |
| Overpotential | |
| EV | Electrical vehicle |
| FEC | Fully equivalent cycle |
| j | Current density |
| Exchange current density | |
| LAM | Loss of active materials |
| Thermal conductivity in the through-plane direction | |
| LCO | Lithium cobalt oxide |
| LFP | Lithium iron phosphate |
| LFP | Lithium iron phosphate |
| LIB | Lithium ion battery |
| LLI | Loss of Li inventory |
| LMO | Lithium manganese oxide |
| n | Number of unit cells |
| NCA | Lithium nickel cobalt aluminium oxide |
| NMC | Lithium nickel cobalt manganese oxide |
| PC | Propylene carbonate |
| PCM | Phase change material |
| PE | Polyethylene |
| PP | Polypropylene |
| q | Area specific heat generation |
| Q | Volumetric heat generation |
| Ohmic resistance | |
| Ambient temperature | |
| SEI | Solid electrolyte interphase |
| SOC | State of charge |
| SOH | State of health |
| SSE | Solid-state electrolytes |
References
- Marom, R.; Amalraj, S.F.; Leifer, N.; Jacob, D.; Aurbach, D. A review of advanced and practical lithium battery materials. J. Mater. Chem. 2011, 21, 9938. [Google Scholar] [CrossRef]
- Bloomberg NEF. Electric Vehicle Outlook 2020. Available online: bnef.turtl.co/story/evo-2020 (accessed on 15 October 2020).
- Zubi, G.; Dufo-López, R.; Carvalho, M.; Pasaoglu, G. The lithium-ion battery: State of the art and future perspectives. Renew. Sustain. Energy Rev. 2018, 89, 292–308. [Google Scholar] [CrossRef]
- Dubarry, M.; Qin, N.; Brooker, P. Calendar aging of commercial Li-ion cells of different chemistries—A review. Curr. Opin. Electrochem. 2018, 9, 106–113. [Google Scholar] [CrossRef]
- Richter, F.; Kjelstrup, S.; Vie, P.J.; Burheim, O.S. Thermal conductivity and internal temperature profiles of Li-ion secondary batteries. J. Power Sources 2017, 359, 592–600. [Google Scholar] [CrossRef]
- Sarasketa-Zabala, E.; Gandiaga, I.; Rodriguez-Martinez, L.M.; Villarreal, I. Calendar ageing analysis of a LiFePO4/graphite cell with dynamic model validations: Towards realistic lifetime predictions. J. Power Sources 2014, 272, 45–57. [Google Scholar] [CrossRef]
- Sarasketa-Zabala, E.; Gandiaga, I.; Martinez-Laserna, E.; Rodriguez-Martinez, L.M.; Villarreal, I. Cycle ageing analysis of a LiFePO4/graphite cell with dynamic model validations: Towards realistic lifetime predictions. J. Power Sources 2015, 275, 573–587. [Google Scholar] [CrossRef]
- Wang, J.; Liu, P.; Hicks-Garner, J.; Sherman, E.; Soukiazian, S.; Verbrugge, M.; Tataria, H.; Musser, J.; Finamore, P. Cycle-life model for graphite-LiFePO4 cells. J. Power Sources 2011, 196, 3942–3948. [Google Scholar] [CrossRef]
- Saw, L.H.; Poon, H.M.; Thiam, H.S.; Cai, Z.; Chong, W.T.; Pambudi, N.A.; King, Y.J. Novel thermal management system using mist cooling for lithium-ion battery packs. Appl. Energy 2018, 223, 146–158. [Google Scholar] [CrossRef]
- Fang, G.; Huang, Y.; Yuan, W.; Yang, Y.; Tang, Y.; Ju, W.; Chu, F.; Zhao, Z. Thermal management for a tube–shell Li-ion battery pack using water evaporation coupled with forced air cooling. RSC Adv. 2019, 9, 9951–9961. [Google Scholar] [CrossRef]
- Mohammadian, S.K.; He, Y.L.; Zhang, Y. Internal cooling of a lithium-ion battery using electrolyte as coolant through microchannels embedded inside the electrodes. J. Power Sources 2015, 293, 458–466. [Google Scholar] [CrossRef]
- Shah, K.; McKee, C.; Chalise, D.; Jain, A. Experimental and numerical investigation of core cooling of Li-ion cells using heat pipes. Energy 2016, 113, 852–860. [Google Scholar] [CrossRef]
- Julien, C.; Mauger, A.; Vijh, A.; Zaghib, K. Lithium Batteries; Springer: Cham, Swizerland, 2016. [Google Scholar]
- Rahn, C.D.; Wang, C.Y. Battery Systems Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Besenhard, J.O. Handbook of Battery Materials; Wiley-VCH: Weinheim, Germany, 2018. [Google Scholar]
- Nitta, N.; Wu, F.; Lee, J.T.; Yushin, G. Li-ion battery materials: Present and future. Mater. Today 2015, 18, 252–264. [Google Scholar] [CrossRef]
- Zhang, J.; Terrones, M.; Park, C.R.; Mukherjee, R.; Monthioux, M.; Koratkar, N.; Kim, Y.S.; Hurt, R.; Frackowiak, E.; Enoki, T.; et al. Carbon science in 2016: Status, challenges and perspectives. Carbon 2016, 98, 708–732. [Google Scholar] [CrossRef]
- Li, W.; Song, B.; Manthiram, A. High-voltage positive electrode materials for lithium-ion batteries. Chem. Soc. Rev. 2017, 46, 3006–3059. [Google Scholar] [CrossRef] [PubMed]
- Placke, T.; Kloepsch, R.; Dühnen, S.; Winter, M. Lithium ion, lithium metal, and alternative rechargeable battery technologies: The odyssey for high energy density. J. Solid State Electrochem. 2017, 21, 1939–1964. [Google Scholar] [CrossRef]
- Zheng, F.; Kotobuki, M.; Song, S.; Lai, M.O.; Lu, L. Review on solid electrolytes for all-solid-state lithium-ion batteries. J. Power Sources 2018, 389, 198–213. [Google Scholar] [CrossRef]
- Mizushima, K.; Jones, P.; Wiseman, P.; Goodenough, J.B. LixCoO2 (0 < x < −1): A new cathode material for batteries of high energy density. Mater. Res. Bull. 1980, 15, 783–789. [Google Scholar]
- Liu, F.; Mukherjee, P.P. Materials for positive electrodes in rechargeable lithium-ion batteries. In Rechargeable Lithium Batteries; Elsevier: Amsterdam, The Netherlands, 2015; pp. 21–39. [Google Scholar]
- Fergus, J.W. Recent developments in cathode materials for lithium ion batteries. J. Power Sources 2010, 195, 939–954. [Google Scholar] [CrossRef]
- Thackeray, M.; Kock, A.; David, W. Synthesis and structural characterization of defect spinels in the lithium-manganese-oxide system. Mater. Res. Bull. 1993, 28, 1041–1049. [Google Scholar] [CrossRef]
- Whittingham, M.S. Lithium Batteries and Cathode Materials. Chem. Rev. 2004, 104, 4271–4302. [Google Scholar] [CrossRef]
- Noh, H.J.; Youn, S.; Yoon, C.S.; Sun, Y.K. Comparison of the structural and electrochemical properties of layered Li[NixCoyMnz]O2 (x = 1/3, 0.5, 0.6, 0.7, 0.8 and 0.85) cathode material for lithium-ion batteries. J. Power Sources 2013, 233, 121–130. [Google Scholar] [CrossRef]
- Li, X.; Colclasure, A.M.; Finegan, D.P.; Ren, D.; Shi, Y.; Feng, X.; Cao, L.; Yang, Y.; Smith, K. Degradation mechanisms of high capacity 18650 cells containing Si-graphite anode and nickel-rich NMC cathode. Electrochim. Acta 2019, 297, 1109–1120. [Google Scholar] [CrossRef]
- Manthiram, A.; Song, B.; Li, W. A perspective on nickel-rich layered oxide cathodes for lithium-ion batteries. Energy Storage Mater. 2017, 6, 125–139. [Google Scholar] [CrossRef]
- Schipper, F.; Erickson, E.M.; Erk, C.; Shin, J.Y.; Chesneau, F.F.; Aurbach, D. Review—Recent Advances and Remaining Challenges for Lithium Ion Battery Cathodes: I. Nickel-Rich, LiNixCoyMnzO2. J. Electrochem. Soc. 2017, 164, 6220–6228. [Google Scholar] [CrossRef]
- Song, H.J.; Jang, S.H.; Ahn, J.; Oh, S.H.; Yim, T. Artificial cathode-electrolyte interphases on nickel-rich cathode materials modified by silyl functional group. J. Power Sources 2019, 416, 1–8. [Google Scholar] [CrossRef]
- Xia, Y.; Zheng, J.; Wang, C.; Gu, M. Designing principle for Ni-rich cathode materials with high energy density for practical applications. Nano Energy 2018, 49, 434–452. [Google Scholar] [CrossRef]
- Zhao, W.; Zheng, G.; Lin, M.; Zhao, W.; Li, D.; Guan, X.; Ji, Y.; Ortiz, G.F.; Yang, Y. Toward a stable solid-electrolyte-interfaces on nickel-rich cathodes: LiPO2F2 salt-type additive and its working mechanism for LiNi0.5Mn0.25Co0.25O2 cathodes. J. Power Sources 2018, 380, 149–157. [Google Scholar] [CrossRef]
- Julien, C.M.; Mauger, A. NCA, NCM811, and the Route to Ni-Richer Lithium-Ion Batteries. Energies 2020, 13, 6363. [Google Scholar] [CrossRef]
- Structural changes and thermal stability of charged LiNixMnyCozO2 cathode materials studied by combined in situ time-resolved XRD and mass spectroscopy. ACS Appl. Mater. Interfaces 2014, 6, 22594–22601. [CrossRef]
- Li, T.; Yuan, X.Z.; Zhang, L.; Song, D.; Shi, K.; Bock, C. Degradation Mechanisms and Mitigation Strategies of Nickel-Rich NMC-Based Lithium-Ion Batteries. Electrochem. Energy Rev. 2020, 3, 43–80. [Google Scholar] [CrossRef]
- Xu, G.L.; Liu, Q.; Lau, K.K.S.; Liu, Y.; Liu, X.; Gao, H.; Zhou, X.; Zhuang, M.; Ren, Y.; Li, J.; et al. Building ultraconformal protective layers on both secondary and primary particles of layered lithium transition metal oxide cathodes. Nat. Energy 2019, 4, 484–494. [Google Scholar] [CrossRef]
- Goriparti, S.; Miele, E.; de Angelis, F.; Di Fabrizio, E.; Proietti Zaccaria, R.; Capiglia, C. Review on recent progress of nanostructured anode materials for Li-ion batteries. J. Power Sources 2014, 257, 421–443. [Google Scholar] [CrossRef]
- Azuma, H.; Imoto, H.; Yamada, S.; Sekai, K. Advanced carbon anode materials for lithium ion cells. J. Power Sources 1999, 81-82, 1–7. [Google Scholar] [CrossRef]
- Peled, E.; Golodnitsky, D.; Ulus, A.; Yufit, V. Effect of carbon substrate on SEI composition and morphology. Electrochim. Acta 2004, 50, 391–395. [Google Scholar] [CrossRef]
- An, S.J.; Li, J.; Daniel, C.; Mohanty, D.; Nagpure, S.; Wood, D.L. The state of understanding of the lithium-ion-battery graphite solid electrolyte interphase (SEI) and its relationship to formation cycling. Carbon 2016, 105, 52–76. [Google Scholar] [CrossRef]
- Qi, Y.; Gou, H.; Hector, L.; Timmons, A. Threefold Increase in the Young’s Modulus of Graphite Negative Electrode during Lithium Intercalation. J. Electrochem. Soc. 2010, 157, A558–A566. [Google Scholar] [CrossRef]
- Zuo, X.; Zhu, J.; Müller-Buschbaum, P.; Cheng, Y.J. Silicon based lithium-ion battery anodes: A chronicle perspective review. Nano Energy 2017, 31, 113–143. [Google Scholar] [CrossRef]
- Liu, X.H.; Zhong, L.; Huang, S.; Mao, S.X.; Zhu, T.; Huang, J.Y. Size-dependent fracture of silicon nanoparticles during lithiation. ACS Nano 2012, 6, 1522–1531. [Google Scholar] [CrossRef] [PubMed]
- Chan, C.K.; Peng, H.; Liu, G.; McIlwrath, K.; Zhang, X.F.; Huggins, R.A.; Cui, Y. High-performance lithium battery anodes using silicon nanowires. Nat. Nanotechnol. 2008, 3, 31. [Google Scholar] [CrossRef] [PubMed]
- Yao, Y.; Huo, K.; Hu, L.; Liu, N.; Cha, J.J.; McDowell, M.T.; Chu, P.K.; Cui, Y. Highly conductive, mechanically robust, and electrochemically inactive TiC/C nanofiber scaffold for high-performance silicon anode batteries. ACS Nano 2011, 5, 8346–8351. [Google Scholar] [CrossRef]
- Wen, Z.; Lu, G.; Mao, S.; Kim, H.; Cui, S.; Yu, K.; Huang, X.; Hurley, P.T.; Mao, O.; Chen, J. Silicon nanotube anode for lithium-ion batteries. Electrochem. Commun. 2013, 29, 67–70. [Google Scholar] [CrossRef]
- Szczech, J.R.; Jin, S. Nanostructured silicon for high capacity lithium battery anodes. Energy Environ. Sci. 2011, 4, 56–72. [Google Scholar] [CrossRef]
- Burrell, A.; Cunningham, B. Silicon Electrolyte Interface Stabilization (SEISta): Second Quarter Progress Report 2018; SEISta Project; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2018.
- Wang, C.; Wu, H.; Chen, Z.; McDowell, M.T.; Cui, Y.; Bao, Z. Self-healing chemistry enables the stable operation of silicon microparticle anodes for high-energy lithium-ion batteries. Nat. Chem. 2013, 5, 1042. [Google Scholar] [CrossRef]
- Chen, X.; Li, X.; Mei, D.; Feng, J.; Hu, M.Y.; Hu, J.; Engelhard, M.; Zheng, J.; Xu, W.; Xiao, J.; et al. Reduction mechanism of fluoroethylene carbonate for stable solid–electrolyte interphase film on silicon anode. ChemSusChem 2014, 7, 549–554. [Google Scholar] [CrossRef]
- Zong, L.; Jin, Y.; Liu, C.; Zhu, B.; Hu, X.; Lu, Z.; Zhu, J. Precise perforation and scalable production of Si particles from low-grade sources for high-performance lithium ion battery anodes. Nano Lett. 2016, 16, 7210–7215. [Google Scholar] [CrossRef]
- Dash, R.; Pannala, S. The potential of silicon anode based lithium ion batteries. Mater. Today 2016, 19, 483–484. [Google Scholar] [CrossRef]
- Chae, S.; Ko, M.; Park, S.; Kim, N.; Ma, J.; Cho, J. Micron-sized Fe–Cu–Si ternary composite anodes for high energy Li-ion batteries. Energy Environ. Sci. 2016, 9, 1251–1257. [Google Scholar] [CrossRef]
- Yoon, T.; Nguyen, C.C.; Seo, D.; Lucht, B. Capacity Fading Mechanisms of Silicon Nanoparticle Negative Electrodes for Lithium Ion Batteries. J. Electrochem. Soc. 2015, 162, A2325–A2330. [Google Scholar] [CrossRef]
- Philippe, B.; Dedryvère, R.; Gorgoi, M.; Rensmo, H.; Gonbeau, D.; Edström, K. Role of the LiPF6 salt for the long-term stability of silicon electrodes in Li-ion batteries—A photoelectron spectroscopy study. Chem. Mater. 2013, 25, 394–404. [Google Scholar] [CrossRef]
- Jin, Y.; Zhu, B.; Lu, Z.; Liu, N.; Zhu, J. Challenges and recent progress in the development of Si anodes for lithium-ion battery. Adv. Energy Mater. 2017, 7, 1700715. [Google Scholar] [CrossRef]
- Kim, H.J.; Choi, S.; Lee, S.J.; Seo, M.W.; Lee, J.G.; Deniz, E.; Lee, Y.J.; Kim, E.K.; Choi, J.W. Controlled prelithiation of silicon monoxide for high performance lithium-ion rechargeable full cells. Nano Lett. 2016, 16, 282–288. [Google Scholar] [CrossRef]
- Forney, M.W.; Ganter, M.J.; Staub, J.W.; Ridgley, R.D.; Landi, B.J. Prelithiation of silicon—Carbon nanotube anodes for lithium ion batteries by stabilized lithium metal powder (SLMP). Nano Lett. 2013, 13, 4158–4163. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Lu, Z.; Liu, N.; Lee, H.W.; McDowell, M.T.; Cui, Y. Dry-air-stable lithium silicide—Lithium oxide core—Shell nanoparticles as high-capacity prelithiation reagents. Nat. Commun. 2014, 5, 5088. [Google Scholar] [CrossRef]
- Liu, J.; Liu, Y.; Yang, W.; Ren, Q.; Li, F.; Huang, Z. Lithium ion battery separator with high performance and high safety enabled by tri-layered SiO2@PI/m-PE/SiO2@PI nanofiber composite membrane. J. Power Sources 2018, 396, 265–275. [Google Scholar] [CrossRef]
- Man, C.; Jiang, P.; Wong, K.W.; Zhao, Y.; Tang, C.; Fan, M.; Lau, W.M.; Mei, J.; Li, S.; Liu, H.; et al. Enhanced wetting properties of a polypropylene separator for a lithium-ion battery by hyperthermal hydrogen induced cross-linking of poly(ethylene oxide). J. Mater. Chem. A 2014, 2, 11980–11986. [Google Scholar] [CrossRef]
- Liu, Y.; Xie, K.; Pan, Y.; Wang, H.; Li, Y.; Zheng, C. Simplified modeling and parameter estimation to predict calendar life of Li-ion batteries. Solid State Ionics 2018, 320, 126–131. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, S.; Fang, J.; Ding, L.X.; Wang, H. A nano-silica modified polyimide nanofiber separator with enhanced thermal and wetting properties for high safety lithium-ion batteries. J. Membr. Sci. 2017, 537, 248–254. [Google Scholar] [CrossRef]
- Chen, W.; Liu, Y.; Ma, Y.; Yang, W. Improved performance of lithium ion battery separator enabled by co-electrospinnig polyimide/poly(vinylidene fluoride-co-hexafluoropropylene) and the incorporation of TiO2-(2-hydroxyethyl methacrylate). J. Power Sources 2015, 273, 1127–1135. [Google Scholar] [CrossRef]
- Li, X.; Jiang, J.; Le Wang, Y.; Chen, D.; Zhang, Y.; Zhang, C. A capacity model based on charging process for state of health estimation of lithium ion batteries. Appl. Energy 2016, 177, 537–543. [Google Scholar] [CrossRef]
- Zhang, S.S. A review on electrolyte additives for lithium-ion batteries. J. Power Sources 2006, 162, 1379–1394. [Google Scholar] [CrossRef]
- Famprikis, T.; Canepa, P.; Dawson, J.A.; Islam, M.S.; Masquelier, C. Fundamentals of inorganic solid-state electrolytes for batteries. Nat. Mater. 2019, 18, 1278–1291. [Google Scholar] [CrossRef]
- Damay, N.; Forgez, C.; Bichat, M.P.; Friedrich, G. Thermal modeling of large prismatic LiFePO 4 /graphite battery. Coupled thermal and heat generation models for characterization and simulation. J. Power Sources 2015, 283, 37–45. [Google Scholar] [CrossRef]
- Cheng, X.; Shi, N.; Li, Y.; Wang, S. Engineering-Oriented Modeling for Thermal Behaviors of 18650 Li-ion Batteries. Energy Procedia 2017, 105, 4757–4762. [Google Scholar] [CrossRef]
- Mastali, M.; Foreman, E.; Modjtahedi, A.; Samadani, E.; Amirfazli, A.; Farhad, S.; Fraser, R.A.; Fowler, M. Electrochemical-thermal modeling and experimental validation of commercial graphite/LiFePO4 pouch lithium-ion batteries. Int. J. Therm. Sci. 2018, 129, 218–230. [Google Scholar] [CrossRef]
- An, Z.; Jia, L.; Wei, L.; Yang, C. Numerical modeling and analysis of thermal behavior and Li+ transport characteristic in lithium-ion battery. Int. J. Heat Mass Transf. 2018, 127, 1351–1366. [Google Scholar] [CrossRef]
- Bernardi, D.; Pawlikowski, E.; Newman, J. A general energy balance for battery systems. J. Electrochem. Soc. 1985, 132, 5. [Google Scholar] [CrossRef]
- Cavalheiro, G.M.; Iriyama, T.; Nelson, G.J.; Huang, S.; Zhang, G. Effects of nonuniform temperature distribution on degradation of lithium-ion batteries. J. Electrochem. Energy Convers. Storage 2020, 17, 021101. [Google Scholar] [CrossRef]
- Wang, X.; Li, S.; Wang, L.; Sun, Y.; Wang, Z. Degradation and Dependence Analysis of a Lithium-Ion Battery Pack in the Unbalanced State. Energies 2020, 13, 5934. [Google Scholar] [CrossRef]
- Bhattacharjee, A.; Mohanty, R.K.; Ghosh, A. Design of an Optimized Thermal Management System for Li-Ion Batteries under Different Discharging Conditions. Energies 2020, 13, 5695. [Google Scholar] [CrossRef]
- Zhao, C.; Zhang, B.; Zheng, Y.; Huang, S.; Yan, T.; Liu, X. Hybrid Battery Thermal Management System in Electrical Vehicles: A Review. Energies 2020, 13, 6257. [Google Scholar] [CrossRef]
- Huber, C.; Kuhn, R. Thermal management of batteries for electric vehicles. In Advances in Battery Technologies for Electric Vehicles; Elsevier: Amsterdam, The Netherlands, 2015; pp. 327–358. [Google Scholar]
- Huang, Y.H.; Cheng, W.L.; Zhao, R. Thermal management of Li-ion battery pack with the application of flexible form-stable composite phase change materials. Energy Convers. Manag. 2019, 182, 9–20. [Google Scholar] [CrossRef]
- Liu, H.; Wei, Z.; He, W.; Zhao, J. Thermal issues about Li-ion batteries and recent progress in battery thermal management systems: A review. Energy Convers. Manag. 2017, 150, 304–330. [Google Scholar] [CrossRef]
- Chen, D.; Jiang, J.; Kim, G.H.; Yang, C.; Pesaran, A. Comparison of different cooling methods for lithium ion battery cells. Appl. Therm. Eng. 2016, 94, 846–854. [Google Scholar] [CrossRef]
- Gao, Y.; Jiang, J.; Zhang, C.; Zhang, W.; Jiang, Y. Aging mechanisms under different state-of-charge ranges and the multi-indicators system of state-of-health for lithium-ion battery with Li(NiMnCo)O2 cathode. J. Power Sources 2018, 400, 641–651. [Google Scholar] [CrossRef]
- Waldmann, T.; Wilka, M.; Kasper, M.; Fleischhammer, M.; Wohlfahrt-Mehrens, M. Temperature dependent ageing mechanisms in Lithium-ion batteries—A Post-Mortem study. J. Power Sources 2014, 262, 129–135. [Google Scholar] [CrossRef]
- Naumann, M.; Schimpe, M.; Keil, P.; Hesse, H.C.; Jossen, A. Analysis and modeling of calendar aging of a commercial LiFePO4/graphite cell. J. Energy Storage 2018, 17, 153–169. [Google Scholar] [CrossRef]
- Schmitt, J.; Maheshwari, A.; Heck, M.; Lux, S.; Vetter, M. Impedance change and capacity fade of lithium nickel manganese cobalt oxide-based batteries during calendar aging. J. Power Sources 2017, 353, 183–194. [Google Scholar] [CrossRef]
- Gao, Y.; Jiang, J.; Zhang, C.; Zhang, W.; Ma, Z.; Jiang, Y. Lithium-ion battery aging mechanisms and life model under different charging stresses. J. Power Sources 2017, 356, 103–114. [Google Scholar] [CrossRef]
- Leng, F.; Tan, C.M.; Pecht, M. Effect of Temperature on the Aging rate of Li Ion Battery Operating above Room Temperature. Sci. Rep. 2015, 5, 12967. [Google Scholar] [CrossRef]
- Wikner, E. Lithium Ion Battery Aging: Battery Lifetime Testing and Physics-Based Modeling for Electric Vehicle Applications. Ph.D. Thesis, Department of Electrical Engineering, Chalmers University of Technology, Göteborg, Sweden, 2017. [Google Scholar]
- Keil, P.; Jossen, A. Calendar Aging of NCA Lithium-Ion Batteries Investigated by Differential Voltage Analaysis and Coulomb Tracking. J. Electrochem. Soc. 2017, 164. [Google Scholar] [CrossRef]
- Berecibar, M.; Dubarry, M.; Omar, N.; Villarreal, I.; Van Mierlo, J. Degradation mechanism detection for NMC batteries based on Incremental Capacity curves. World Electr. Veh. J. 2016, 8, 350. [Google Scholar] [CrossRef]
- Yang, F.; Wang, D.; Zhao, Y.; Tsui, K.L.; Bae, S.J. A study of the relationship between coulombic efficiency and capacity degradation of commercial lithium-ion batteries. Energy 2018, 145, 486–495. [Google Scholar] [CrossRef]
- Keil, P.; Schuster, S.; Wilhelm, J.; Travi, J.; Hauser, A.; Karl, R.C.; Jossen, A. Calendar Aging of Lithium-Ion Batteries. J. Electrochem. Soc. 2016, 163, A1872–A1880. [Google Scholar] [CrossRef]
- Grolleau, S.; Delaille, A.; Gualous, H.; Gyan, P.; Revel, R.; Bernard, J.; Redondo-Iglesias, E.; Peter, J. Calendar aging of commercial graphite/LiFePO4 cell – Predicting capacity fade under time dependent storage conditions. J. Power Sources 2014, 255, 450–458. [Google Scholar] [CrossRef]
- Richter, F.; Vie, P.J.; Kjelstrup, S.; Burheim, O.S. Measurements of ageing and thermal conductivity in a secondary NMC-hard carbon Li-ion battery and the impact on internal temperature profiles. Electrochim. Acta 2017, 250, 228–237. [Google Scholar] [CrossRef]
- Aurbach, D.; Markovsky, B.; Salitra, G.; Markevich, E.; Talyossef, Y.; Koltypin, M.; Nazar, L.; Ellis, B.; Kovacheva, D. Review on electrode—Electrolyte solution interactions, related to cathode materials for Li-ion batteries. J. Power Sources 2007, 165, 491–499. [Google Scholar] [CrossRef]
- Barré, A.; Deguilhem, B.; Grolleau, S.; Gérard, M.; Suard, F.; Riu, D. A review on lithium-ion battery ageing mechanisms and estimations for automotive applications. J. Power Sources 2013, 241, 680–689. [Google Scholar] [CrossRef]
- Galvez-Aranda, D.E.; Verma, A.; Hankins, K.; Seminario, J.M.; Mukherjee, P.P.; Balbuena, P.B. Chemical and mechanical degradation and mitigation strategies for Si anodes. J. Power Sources 2019, 419, 208–218. [Google Scholar] [CrossRef]
- Yu, B.Z.; Liu, X.L.; Zhang, H.G.; Jing, G.Y.; Ma, P.; Luo, Y.; Xue, W.M.; Ren, Z.Y.; Fan, H.M. Fabrication and structural optimization of porous single-crystal α-Fe2O3 microrices for high-performance lithium-ion battery anodes. J. Mater. Chem. A 2015, 3, 16544–16550. [Google Scholar] [CrossRef]
- Rucci, A.; Ngandjong, A.C.; Primo, E.N.; Maiza, M.; Franco, A.A. Tracking variabilities in the simulation of Lithium Ion Battery electrode fabrication and its impact on electrochemical performance. Electrochim. Acta 2019, 312, 168–178. [Google Scholar] [CrossRef]
- Lenze, G.; Röder, F.; Bockholt, H.; Haselrieder, W.; Kwade, A.; Krewer, U. Simulation-supported analysis of calendering impacts on the performance of lithium-ion-batteries. J. Electrochem. Soc. 2017, 164, A1223. [Google Scholar] [CrossRef]
- Ming, J.; Cao, Z.; Wu, Y.; Wahyudi, W.; Wang, W.; Guo, X.; Cavallo, L.; Hwang, J.Y.; Shamim, A.; Li, L.J.; et al. New insight on the role of electrolyte additives in rechargeable lithium ion batteries. ACS Energy Lett. 2019, 4, 2613–2622. [Google Scholar] [CrossRef]
- Zhao, H.; Yu, X.; Li, J.; Li, B.; Shao, H.; Li, L.; Deng, Y. Film-forming electrolyte additives for rechargeable lithium-ion batteries: Progress and outlook. J. Mater. Chem. A 2019, 7, 8700–8722. [Google Scholar] [CrossRef]
- Haregewoin, A.M.; Wotango, A.S.; Hwang, B.J. Electrolyte additives for lithium ion battery electrodes: Progress and perspectives. Energy Environ. Sci. 2016, 9, 1955–1988. [Google Scholar] [CrossRef]
- Burheim, O.; Vie, P.; Pharoah, J.G.; Kjelstrup, S. Ex situ measurements of through-plane thermal conductivities in a polymer electrolyte fuel cell. J. Power Sources 2010, 195, 249–256. [Google Scholar] [CrossRef]
- Murashko, K.A.; Mityakov, A.V.; Mityakov, V.Y.; Sapozhnikov, S.Z.; Jokiniemi, J.; Pyrhönen, J. Determination of the entropy change profile of a cylindrical lithium-ion battery by heat flux measurements. J. Power Sources 2016, 330, 61–69. [Google Scholar] [CrossRef]
- Viswanathan, V.V.; Choi, D.; Wang, D.; Xu, W.; Towne, S.; Williford, R.E.; Zhang, J.G.; Liu, J.; Yang, Z. Effect of entropy change of lithium intercalation in cathodes and anodes on Li-ion battery thermal management. J. Power Sources 2010, 195, 3720–3729. [Google Scholar] [CrossRef]
- Burheim, O.S.; Onsrud, M.A.; Pharoah, J.G.; Vullum-Bruer, F.; Vie, P.J.S. Thermal Conductivity, Heat Sources and Temperature Profiles of Li-Ion Batteries. ECS Trans. 2014, 58, 145–171. [Google Scholar] [CrossRef]
- Lee, K.J.; Smith, K.; Pesaran, A.; Kim, G.H. Three dimensional thermal-, electrical-, and electrochemical-coupled model for cylindrical wound large format lithium-ion batteries. J. Power Sources 2013, 241, 20–32. [Google Scholar] [CrossRef]
- Chen, Y.; Evans, J. Thermal Analysis of Lithium-Ion Batteries. J. Electrochem. Soc. 1996, 143, 2708–2712. [Google Scholar] [CrossRef]
- Lasance, C.J.; Simons, R.E. Advances in high-performance cooling for electronics. Electron. Cool. 2005, 11, 22–39. [Google Scholar]
- Lee, J.J.; Kim, J.S.; Chang, H.K.; Lee, D.C.; Kim, C.W. The Effect of Tab Attachment Positions and Cell Aspect Ratio on Temperature Difference in Large-Format LIBs Using Design of Experiments. Energies 2021, 14, 116. [Google Scholar] [CrossRef]
- Du, S.; Jia, M.; Cheng, Y.; Tang, Y.; Zhang, H.; Ai, L.; Zhang, K.; Lai, Y. Study on the thermal behaviors of power lithium iron phosphate (LFP) aluminum-laminated battery with different tab configurations. Int. J. Therm. Sci. 2015, 89, 327–336. [Google Scholar] [CrossRef]
- Li, H.; Wang, Y.; He, X.; Li, Q.; Lian, C.; Wang, Z. Effects of structure parameters on the thermal performance of a ternary lithium-ion battery under fast charging conditions. Energy Fuels 2020, 34, 8891–8904. [Google Scholar] [CrossRef]
- Waldmann, T.; Bisle, G.; Hogg, B.I.; Stumpp, S.; Danzer, M.A.; Kasper, M.; Axmann, P.; Wohlfahrt-Mehrens, M. Influence of cell design on temperatures and temperature gradients in lithium-ion cells: An in operando study. J. Electrochem. Soc. 2015, 162, A921. [Google Scholar] [CrossRef]
- Surya, S.; Marcis, V.; Williamson, S. Core Temperature Estimation for a Lithium ion 18650 Cell. Energies 2021, 14, 87. [Google Scholar] [CrossRef]

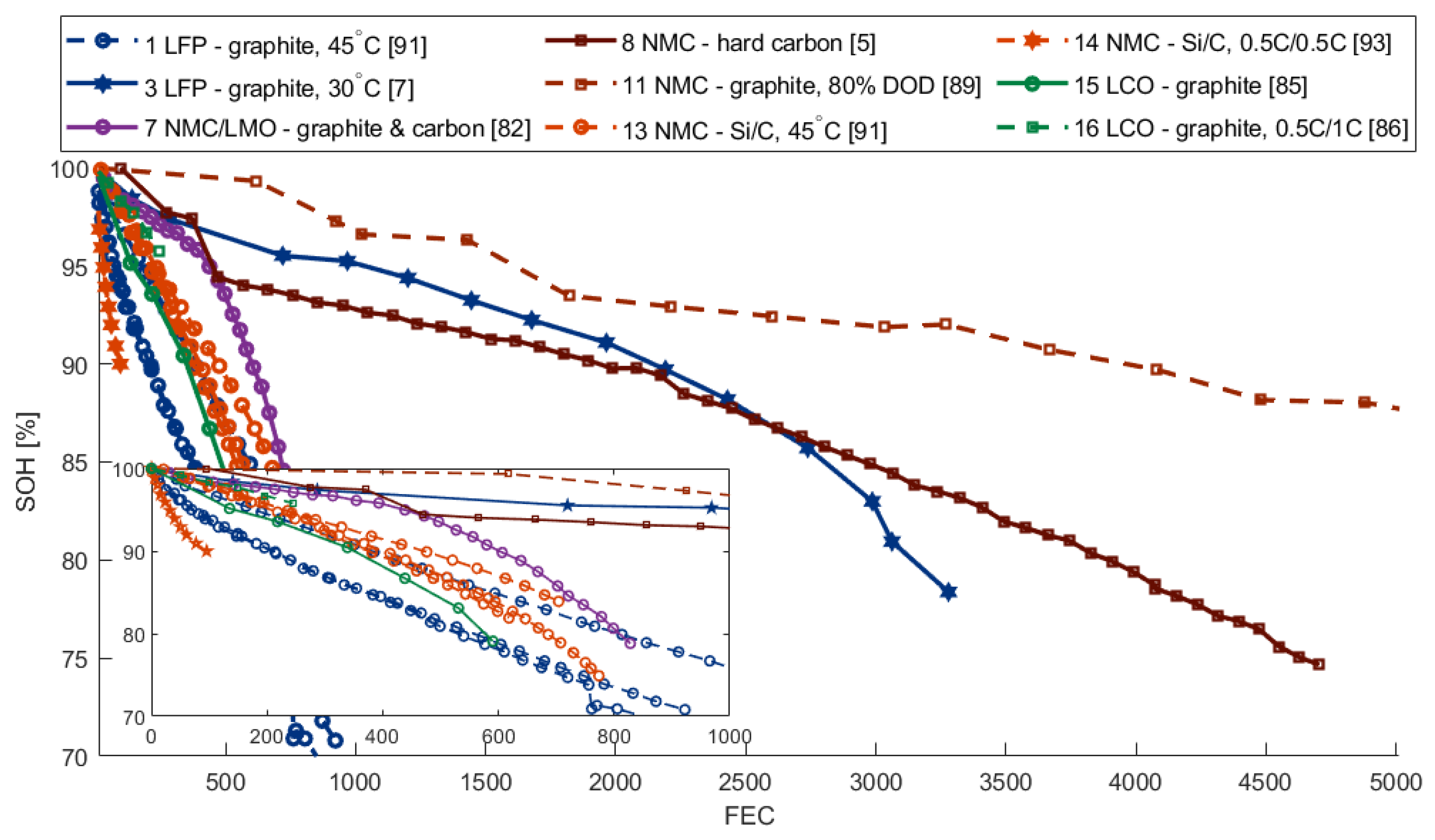
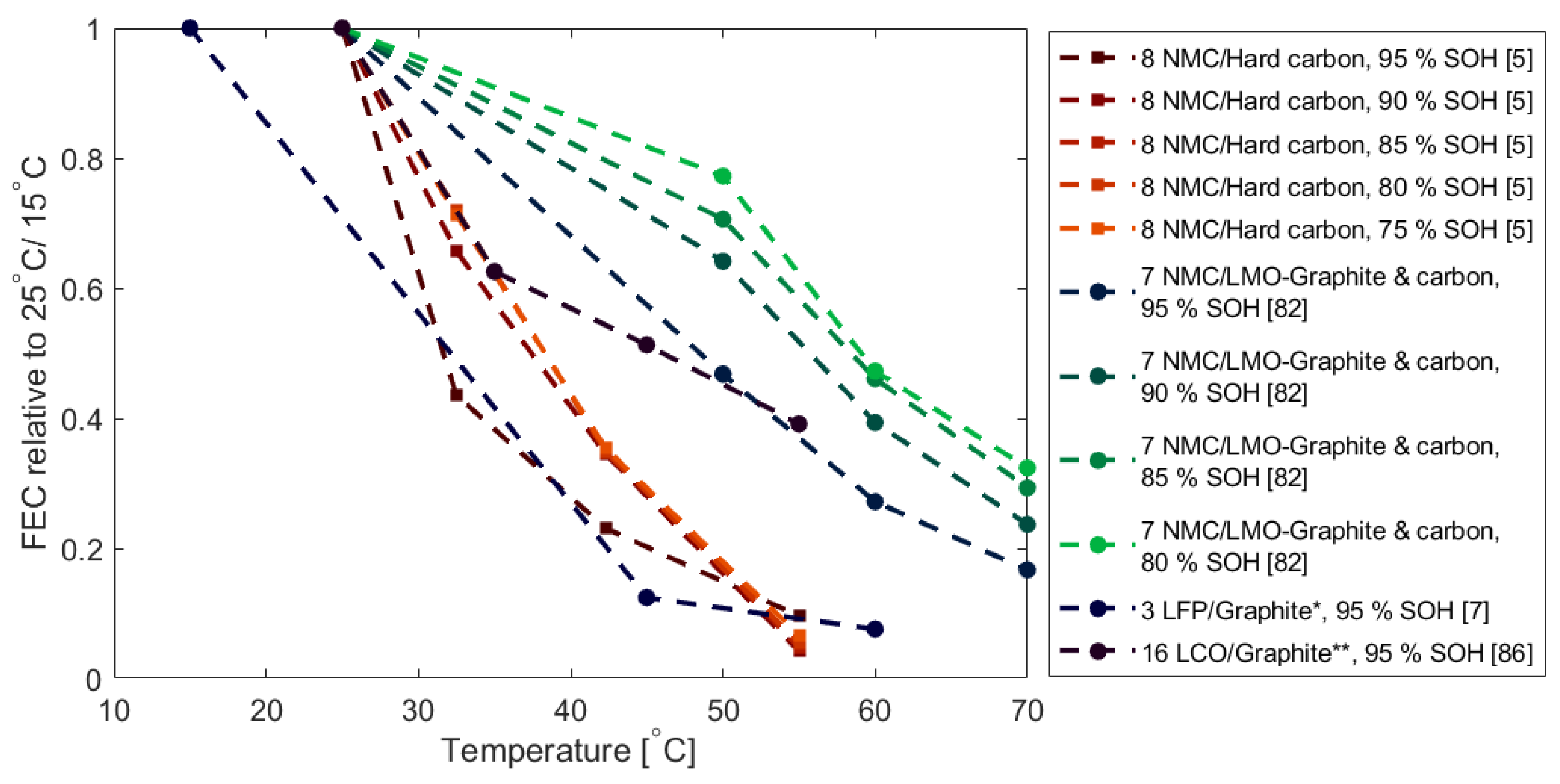
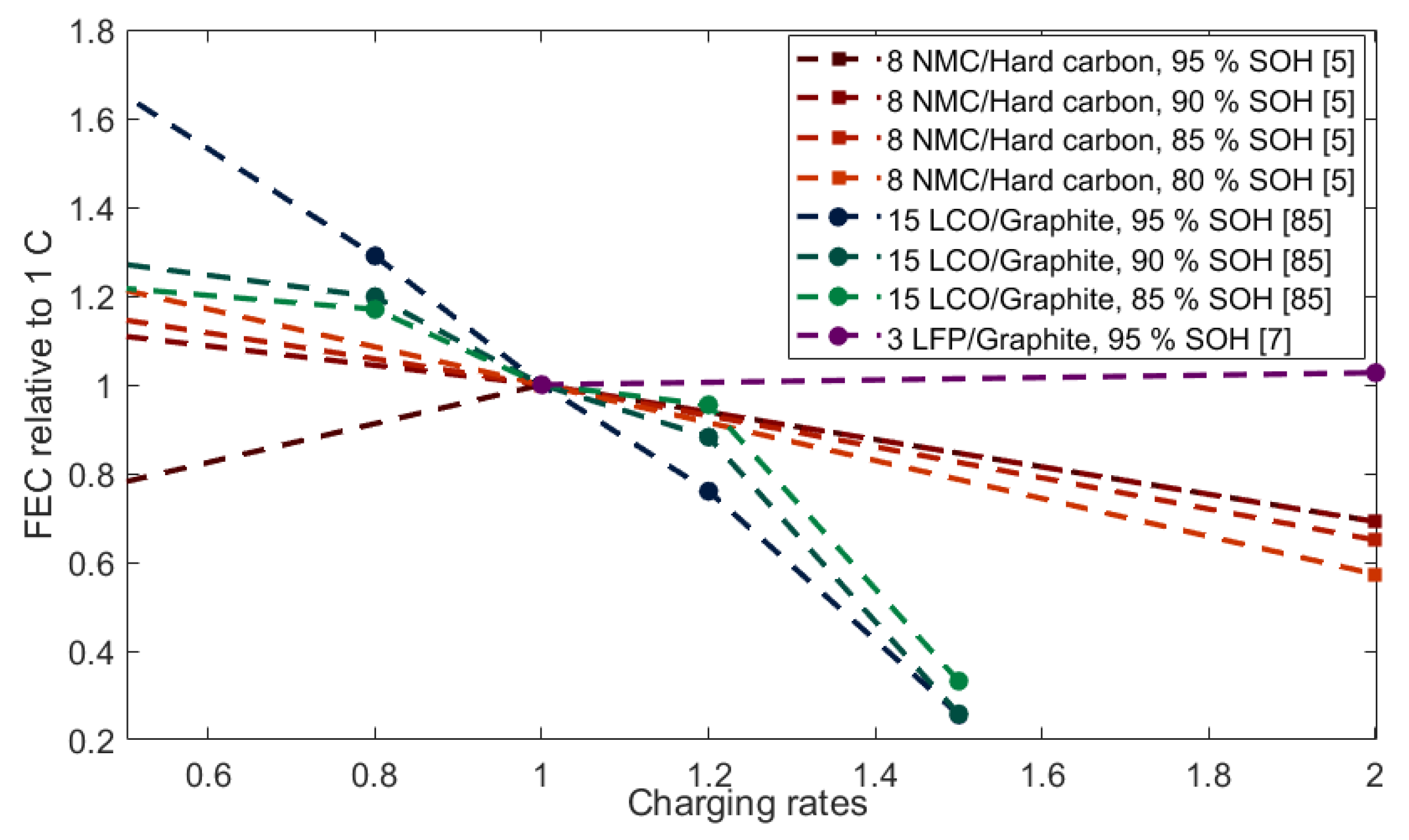

| Nr. | Cathode | Anode | Nominal Capacity | Geometry | Study Type | Ref. |
|---|---|---|---|---|---|---|
| 1 | LFP | graphite | 1 Ah | cylindrical (18,650) | cycling | [90] |
| 2 | LFP | graphite | 1.1 Ah | cylindrical (18,650) | storage | [91] |
| 3 | LFP | graphite | 2.3 Ah | cylindrical (26,650) | cycling, storage | [6,7] |
| 4 | LFP | graphite | 15 Ah | cylindrical (N/S) | storage | [92] |
| 5 | LFP | carbon | 2.2 Ah | cylindrical (26,650) | cycling | [8] |
| 6 | LFP | carbon | 3 Ah | cylindrical (26,650) | storage | [83] |
| 7 | NMC/LMO | graphite and carbon particle | 1.5 Ah | cylindrical (18,650) | cycling | [82] |
| 8 | NMC | hard carbon | 17.5 Ah | pouch (23 × 15 × 0.5 cm) | cycling and storage | [5] |
| 9 | NMC | graphite | 2.05 Ah | cylindrical (18,650) | storage | [91] |
| 10 | NMC | graphite | 2.15 Ah | cylindrical (18,650) | storage | [84] |
| 11 | NMC | graphite | 40 Ah | (N/S) | cycling | [89] |
| 12 | NMC | graphite | 8 Ah | pouch (N/S) | cycling | [81] |
| 13 | NMC | Si/C | 1.3 Ah | cylindrical (18,650) | cycling | [90] |
| 14 | NMC (Ni rich) | Si/C | 3.45 Ah | cylindrical (18,650) | cycling | [27] |
| 15 | LCO | graphite | 2.4 Ah | cylindrical (18,650) | cycling | [85] |
| 16 | LCO | graphite | 1.35 Ah | prismatic (6.6 × 33.8 × 50 mm) | cycling | [86] |
| Parameter | Value | Ref. |
|---|---|---|
| Number of single cells | 24 | |
| Ambient temperature | 290 K | |
| 1 C rate | 35 | |
| Anode thickness | 74 μm | |
| Separator thickness | 12.1 μm | |
| Cathode thickness | 67 μm | |
| Current collector thickness | 20 μm | |
| Thermal conductivity, anode, new and soaked | 1.11 WK m | [5] |
| Thermal conductivity, separator, new and soaked | 0.31 WK m | [5] |
| Thermal conductivity, cathode, new and soaked | 0.33 WK m | [5] |
| Thermal conductivity, anode, aged and dry | 0.32 WK m | [5] |
| Thermal conductivity, separator, aged and dry | 0.10 WK m | [5] |
| Thermal conductivity, cathode, aged and dry | 0.13 WK m | [5] |
| Average entropy change over 0–100% SOC range, LFP-G | 12.5 J mol K | [105] |
| Average entropy change over 0–100% SOC range, NMC-G | 10 J mol K | [105] |
| Average entropy change over 0–100% SOC range, LCO-G | 37 J mol K | [105] |
| Internal resistance, NMC | 2 m | [93] |
| Internal resistance, LCO | 33 m | [85] |
| Tafel parameter a | −0.039 V | [106] |
| Tafel parameter b | 0.068 V decade | [106] |
| LCO | NMC | |
|---|---|---|
| Temperature increase | 14.5 K | 2.3 K |
| Temperature induced FEC reduction (Figure 4) | 43% | 11 ± 1.2% |
| “C rate induced” FEC reduction (Figure 5) | 79.5 ± 0.6% | 30 ± 6% |
| Revised C rate induced FEC reduction | 36% | 19% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Spitthoff, L.; Shearing, P.R.; Burheim, O.S. Temperature, Ageing and Thermal Management of Lithium-Ion Batteries. Energies 2021, 14, 1248. https://doi.org/10.3390/en14051248
Spitthoff L, Shearing PR, Burheim OS. Temperature, Ageing and Thermal Management of Lithium-Ion Batteries. Energies. 2021; 14(5):1248. https://doi.org/10.3390/en14051248
Chicago/Turabian StyleSpitthoff, Lena, Paul R. Shearing, and Odne Stokke Burheim. 2021. "Temperature, Ageing and Thermal Management of Lithium-Ion Batteries" Energies 14, no. 5: 1248. https://doi.org/10.3390/en14051248
APA StyleSpitthoff, L., Shearing, P. R., & Burheim, O. S. (2021). Temperature, Ageing and Thermal Management of Lithium-Ion Batteries. Energies, 14(5), 1248. https://doi.org/10.3390/en14051248







