A Stochastic Planning Model for Battery Energy Storage Systems Coupled with Utility-Scale Solar Photovoltaics
Abstract
:1. Introduction
- A stochastic utility-scale BESS capacity planning model for solar PV systems considering uncertainty and chronology is introduced.
- Uncertain factors, solar DNI, wind power availability, electric load, are modeled as stochastic processes capturing uncertainty and time order of the factors, and the random sample paths for scenarios in the stochastic optimization problem are generated using the stochastic process.
- The presented model is applied to a transmission-level 300-bus power system, and an optimal solution is obtained.
- The impact of inclusion uncertainty in the BESS capacity planning model is investigated using the idea, “Value of Stochastic Solution” (VSS) [14].
2. Methodology
2.1. Sample Path Generation
- The desired process is not stationary in general; therefore, the intermediate process satisfying is defined here, which is stationary. The autocorrelation structure and marginal distribution of the intermediate process, and F, are known, where , and p indicates lag.
- With the autocorrelation structure in Step (1), the AR parameters and the variance are obtained. The ARTA process with is implemented throughout the simulation, therefore, and are obtained.
- A base AR(2) process is formed, where and .
- Generate for 24 h using the initial values .
- The intermediate value can be derived with . Finally, the desired process is obtained from .
- Repeat Steps (1)–(5) for .
2.2. Mathematical Model
3. Simulation
3.1. Building and Operating Costs
3.2. Power System Model
3.3. Hourly Random Sample Paths
4. Simulation Results
4.1. Optimal Capacity and Costs for BESSs
4.2. Charging and Discharging Operations of BESSs
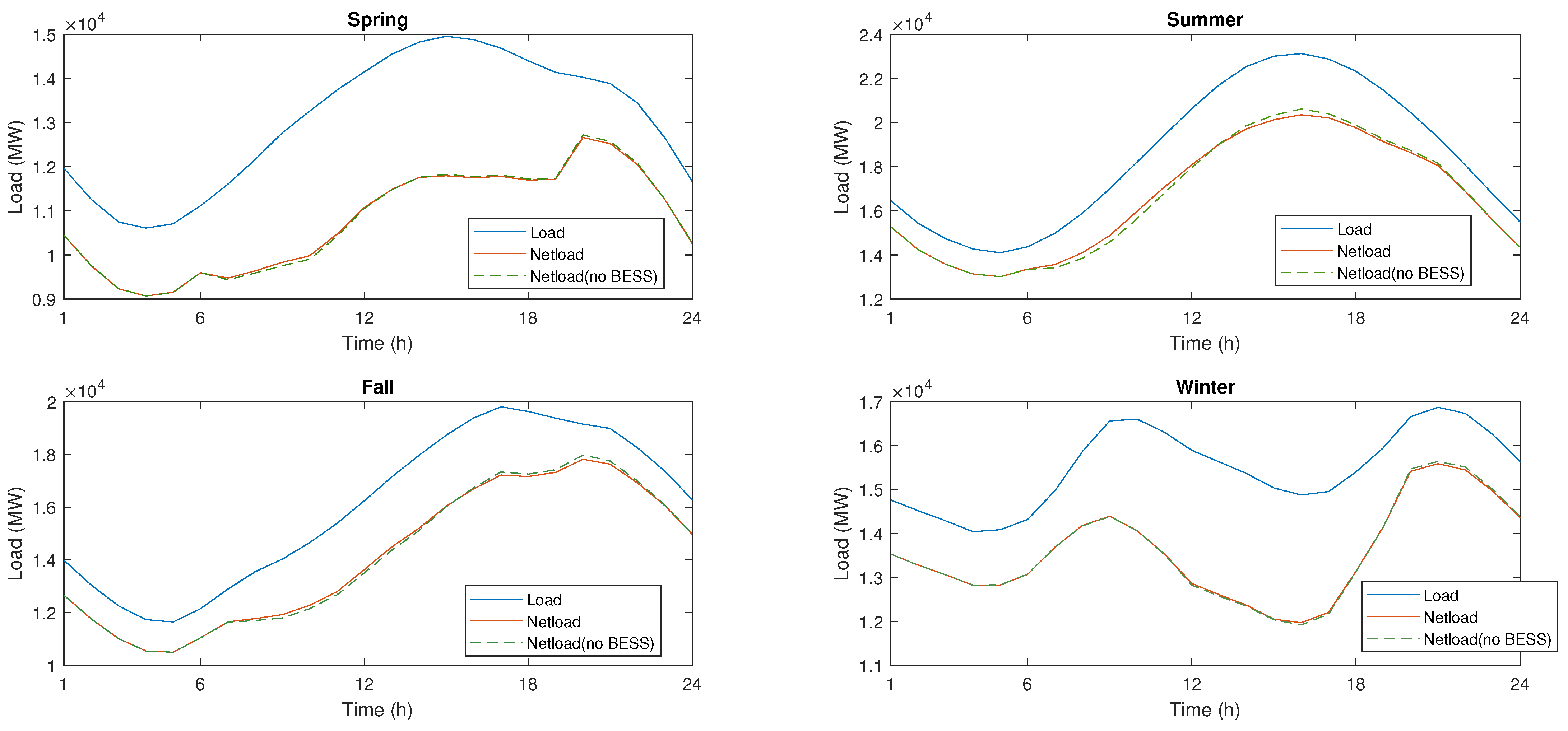
4.3. Load Profile
4.4. Impacts of Stochastic Parameters
5. Discussion
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Energy Storage Technology and Cost Characterization Report. Available online: https://www.energy.gov/sites/prod/files/2019/07/f65/StorageCostandPerformanceCharacterizationReport_Final.pdf (accessed on 11 January 2021).
- Oudalov, A.; Cherkaoui, R.; Beguin, A. Sizing and optimal operation of battery energy storage system for peak shaving application. In Proceedings of the 2007 IEEE Lausanne Power Tech, Lausanne, Switzerland, 1–5 July 2007. [Google Scholar] [CrossRef]
- Lu, B.; Shahidehpour, M. Short-term scheduling of battery in a grid-connected PV/battery system. IEEE Trans. Power Syst. 2005, 20, 1053–1061. [Google Scholar] [CrossRef]
- Hosseinalizadeh, R.; Shakouri, H.; Amalnick, M.S.; Taghipour, P. Economic sizing of a hybrid (PV–WT–FC) renewable energy system (HRES) for stand-alone usages by an optimization-simulation model: Case study of Iran. Renew. Sustain. Energy Rev. 2016, 54, 139–150. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Lundblad, A.; Campana, P.E.; Benavente, F.; Yan, J. Battery sizing and rule-based operation of grid-connected photovoltaic-battery system: A case study in Sweden. Energy Convers. Manag. 2017, 133, 249–263. [Google Scholar] [CrossRef]
- Xia, S.; Chan, K.; Luo, X.; Bu, S.; Ding, Z.; Zhou, B. Optimal sizing of energy storage system and its cost-benefit anlaysis for power grid planning with intermittent wind generation. Renew. Energy 2018, 122, 472–486. [Google Scholar] [CrossRef]
- Talent, O.; Du, H. Optimal sizing and energy scheduling of photovoltaic-battery systems under different tariff structures. Renew. Energy 2018, 129, 513–526. [Google Scholar] [CrossRef]
- Zebarjadi, M.; Askarzadeh, A. Optimization of a reliable grid-connected PV-based power plant with/without energy storage system by a heuristic approach. Sol. Energy 2016, 125, 12–21. [Google Scholar] [CrossRef]
- Xu, L.; Ruan, X.; Mao, C.; Zhang, B.; Luo, Y. An improved optimal sizing method for wind-solar-battery hybrid power system. IEEE Trans. Sustain. Energy 2013, 4, 774–785. [Google Scholar] [CrossRef]
- Hemmati, R.; Saboori, H. Stochastic optimal battery storage sizing and scheduling in home energy management systems equipped with solar photovoltaic panels. Energy Build. 2017, 152, 290–300. [Google Scholar] [CrossRef]
- Jabr, R.A.; Džafić, I.; Pal, B.C. Robust optimization of storage investment on transmission networks. IEEE Trans. Power Syst. 2015, 30, 531–539. [Google Scholar] [CrossRef] [Green Version]
- Chowdhury, N.; Pilo, F.; Pisano, G. Optimal energy storage system positioning and sizing with robust optimization. Energies 2020, 13, 512. [Google Scholar] [CrossRef] [Green Version]
- U.S Energy Information Administration. Short-Term Energy Outlook. Available online: https://www.eia.gov/outlooks/steo/pdf/steo_full.pdf (accessed on 11 January 2021).
- Birge, J.R.; Louveaux, F. Introduction to Stochastic Programming; Springer: New York, NY, USA, 1997. [Google Scholar]
- Cario, M.C.; Nelson, B.L. Autoregressive to anything: Time-series input processes for simulation. Oper. Res. Lett. 1996, 19, 51–58. [Google Scholar] [CrossRef]
- Cario, M.C.; Nelson, B.L. Numerical methods for fitting and simulating Autoregressive-to-Anything processes. Informs J. Comput. 1998, 10, 72–81. [Google Scholar] [CrossRef] [Green Version]
- Park, H. Generation capacity expansion planning considering hourly dynamics of renewable resources. Energies 2020, 13, 5626. [Google Scholar] [CrossRef]
- Shapiro, A.; Dentcheva, D.; Ruszczynski, A. Lectures on Stochastic Programming; MPS-SIAM: Philadelphia, PA, USA, 2009. [Google Scholar]
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes; Wiley: New York, NY, USA, 2013. [Google Scholar]
- Park, H.; Baldick, R. Optimal capacity planning of generation system integrating uncertain solar and wind energy with seasonal variability. Electr. Power Syst. Res. 2020, 180, 106072. [Google Scholar] [CrossRef]
- North American Electric Reliability Corporation. M-1 Reserve Margin. Available online: https://www.nerc.com/pa/RAPA/ri/Pages/PlanningReserveMargin.aspx (accessed on 11 January 2021).
- Ran Fu and Timothy Remo and Robert Margolis. 2018 U.S. Utility-Scale Photovoltaics-Plus-Energy Storage System Costs Benchmark. 2018. Available online: https://www.nrel.gov/docs/fy19osti/71714.pdf (accessed on 11 January 2021).
- Cole, Wesley and Frazier, Allister. Cost Projections for Utility-Scale Battery Storage. 2019. Available online: https://www.nrel.gov/docs/fy19osti/73222.pdf (accessed on 11 January 2021).
- U.S. Energy Information Administration. Annual Energy Outlook 2019. 2020. Available online: https://www.eia.gov/outlooks/archive/aeo19/ (accessed on 11 January 2021).
- Illinois Center for a Smarter Electric Grid. IEEE 300-Bus System. Available online: http://icseg.iti.illinois.edu/ieee-300-bus-system/ (accessed on 11 January 2021).
- University of Washington. Power Aystems Test Case Archive. Available online: https://www2.ee.washington.edu/research/pstca/pf300/pg_tca300bus.htm (accessed on 11 January 2021).
- SolarAnywhere. Available online: https://www.solaranywhere.com/ (accessed on 11 January 2021).
- GAMS Documentation 33. Available online: https://www.gams.com/latest/docs/S_CPLEX.html (accessed on 11 January 2021).
- Park, H.; Baldick, R.; Morton, D.P. A stochastic transmission planning model with dependent load and wind forecasts. IEEE Trans. Power Syst. 2015, 30, 3003–3011. [Google Scholar] [CrossRef]


| Technology Type | Equivalent Annual Installation Cost ($/kW.Year) | Operating Cost ($/MWh) |
|---|---|---|
| Coal | - | 28.93 |
| Conv. CT | - | 45.05 |
| Avd. CT | - | 52.30 |
| CCGT | - | 39.03 |
| Nuclear | - | 9.47 |
| BESS (1-h) | 45.74 | 0.3 |
| BESS (2-h) | 69.11 | 0.3 |
| BESS (4-h) | 115.69 | 0.3 |
| Types of Generation | # of Units | Capacity (MW) | Percents (%) |
|---|---|---|---|
| Coal | 6 | 3900 | 14.55 |
| Conv. CT | 8 | 2400 | 8.96 |
| Avd. CT | 10 | 2100 | 7.84 |
| CCGT | 15 | 9000 | 33.58 |
| Nuclear | 1 | 2000 | 7.46 |
| Wind | 35 | 3500 | 13.06 |
| Solar | 39 | 3900 | 14.55 |
| Total | 114 | 26,800 | 100 |
| Duration | Number of Samples | ||
|---|---|---|---|
| 10 | 20 | 30 | |
| 1-h | 3.25 | 4.24 | 53.97 |
| 2-h | 885.86 | 19.49 | 202.88 |
| 3-h | 3.82 | 1337.21 | 1466.55 |
| Total | 892.94 | 1360.94 | 1723.4 |
| Duration | Number of Samples | ||
|---|---|---|---|
| 10 | 20 | 30 | |
| 1-h | 0.0116 | 0.0152 | 0.1930 |
| 2-h | 4.7856 | 0.1053 | 1.0960 |
| 3-h | 0.0346 | 12.0928 | 13.2626 |
| Total | 4.8318 | 12.2133 | 14.5515 |
| Number of Samples | EEV | RP | VSS |
|---|---|---|---|
| 10 | 3674.294 | 2358.81 | 1315.484 |
| 20 | 8397.132 | 5701.641 | 2695.491 |
| 30 | 8071.124 | 5079.642 | 2991.482 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, H. A Stochastic Planning Model for Battery Energy Storage Systems Coupled with Utility-Scale Solar Photovoltaics. Energies 2021, 14, 1244. https://doi.org/10.3390/en14051244
Park H. A Stochastic Planning Model for Battery Energy Storage Systems Coupled with Utility-Scale Solar Photovoltaics. Energies. 2021; 14(5):1244. https://doi.org/10.3390/en14051244
Chicago/Turabian StylePark, Heejung. 2021. "A Stochastic Planning Model for Battery Energy Storage Systems Coupled with Utility-Scale Solar Photovoltaics" Energies 14, no. 5: 1244. https://doi.org/10.3390/en14051244
APA StylePark, H. (2021). A Stochastic Planning Model for Battery Energy Storage Systems Coupled with Utility-Scale Solar Photovoltaics. Energies, 14(5), 1244. https://doi.org/10.3390/en14051244






