1. Introduction
It is a well-known fact that machines and technical systems are affected by aging [
1,
2,
3,
4,
5,
6], but it is difficult to theoretically estimate this kind of effect.
In particular, the power production of a wind turbine has a very complex dependence on ambient conditions [
7,
8,
9,
10], on the stochastic nature of the source [
11,
12], on the working parameters [
13,
14], on the wake interactions [
15,
16], and on the health status and on the efficiency [
17,
18] of the sub-components. On these grounds, it is a common sense expectation that the efficiency of wind turbines declines with age, but there are no standards about how much and in how much time the performance should decline.
Therefore, a uniquely conceivable approach to the analysis of wind turbine aging consists of learning from experience, which is feasible because a vast number of industrial wind turbines of different sizes and technologies are reaching the end-of-life expectancy. For example, in [
19], it was reported that in 2020, 28% of wind turbines installed in Europe were older than 15 years of age, with peaks in the order of 50% in Spain, Germany, and Denmark.
The analysis of wind turbine aging results in being a very complex problem because a vast number of wind turbines should be considered, in order to obtain statistically robust results: from this point of view, the only possibility is considering cumulative data, as for example average yearly capacity, yearly production, and so on. Unfortunately, due to the fact that wind turbines operate under non-stationary conditions and that failure rates are not irrelevant [
20], the use of cumulative data is equivalent to losing the control details of the behavior of the wind turbines under consideration. It should also be noticed that in wind energy practice, it has become common to refurbish wind turbines by adopting aerodynamic and/or control technology innovations [
21]; therefore, in general, it should be concluded that without knowing in detail the history of the analyzed wind farms, it is likely that the effects of aging are incorrectly estimated.
Despite the above summarized critical points, some remarkable analyses have been conducted. In [
22], two-hundred-eighty-two wind farms in the U.K. were considered, and the mismatch between the theoretical and measured load factor was analyzed by attempting a linear regression between the age and the measured load. In [
22], it was estimated that the output of the considered test cases diminished by
per year: this implies a 9% increase of the levelized cost of electricity over twenty years. An important point of [
22] was that the hypothesis was formulated that wind turbine performance decline with age should be mitigated by innovation in wind turbine technology. In [
23], a similar methodology was proposed based on the analysis of wind farms in Sweden: a linear regression between the capacity factor of wind turbines and their age. The methods in [
22,
23] contain some hints about the fact that a linear trend might be too simple for taking into account the complexity given by the fact that the source (the wind) is stochastic and the response of the machine (i.e., the measured load) depends on several factors; for this reason, some corrections in the linear regression were included, which were an adjustment for the on-site conditions in [
22] and sine-cosine fluctuations of the dependency on the age in [
23].
The critical points of the approaches based on cumulative data can be overcome through an in-depth analysis of wind turbines’ operation data and operation curves [
24,
25], which allows disentangling the aging effects from reliability degradation or ambient effects. In a nutshell, aging can be distinguished with respect to reliability by considering the behavior of operation curves when the wind turbines are running. Aging can be distinguished with respect to ambient effects by analyzing operation curves such as the generator speed-power, rotor speed-power, and blade pitch-power curves [
25]. The drawback of this approach is that it is costly from the point of view of data analysis: for example, the studies in [
24,
25,
26], which constitute the premise of this work, dealt with a unique wind turbine.
In particular, the results in [
24,
25] constitute the motivation of the present work: in those studies, a Vestas V52 wind turbine was studied, which is sited at the Dundalk Institute of Technology in Ireland. The wind turbine has been operating since 2005, and operation data from 2008 to 2019 were analyzed. The generator speed-power curve was analyzed when the wind intensity was between 5 and 9 m/s (indicated as Region 2), because in that regime, the wind turbine control is based on variable rotor and generator speed and fixed pitch. When the wind speed was between 9 and 13 m/s (indicated as Region 2
), the blade pitch-power curve was studied, because the wind turbine operates at rated rotational speed and the blade pitch varies with the wind intensity. The earliest data set available was employed for training a support vector regression for the curves of interest, and the aging was quantified through the analysis of how the residuals between measurements and model estimates evolve as years pass by. The main result of [
25] was that the performance decline with the age of the test case wind turbine can be ascribed mainly to the decline of generator performance: in Region 2, it is observed that progressively, the wind turbine extracts less power for a given generator rotational speed. Comparing the average performance after ten years of operation (2008 vs. 2018), a worsening in the order of 8% is observed. It is further observed that in Region 2
in general, the gearbox efficiency decline contributes almost negligibly to the aging, but in the proximity of the gearbox end of life, it is possible to detect an average performance decline of the order of 1.3%.
The aging estimate obtained in [
24,
25] was lower with respect to the results in [
22], but is in general a non-negligible amount. On these grounds and given the ubiquitous deployment of the Vestas V52 wind turbine model, in [
24,
25], the importance of analyzing how general the obtained results were was noticed. This involves analyzing further test cases of the same wind turbine model, and the present work deals with this objective: four Vestas V52 wind turbines are studied, which are sited in southern Italy in a complex terrain. Data from 2013 to 2020 are analyzed, courtesy of the Lucky Wind company. The objective of this study is twofold:
Analyzing the rate of performance decline with age for the wind turbines sited in Italy and comparing against the results in [
24];
Inquiring if the operation curves, and therefore the aging, of the four Italian wind turbines are comparable to those of the test case in [
24] when the wind turbines have the same age.
The points of strength of the present work are therefore several:
Four test case wind turbines of the same model as [
24] (Vestas V52) are added to the literature;
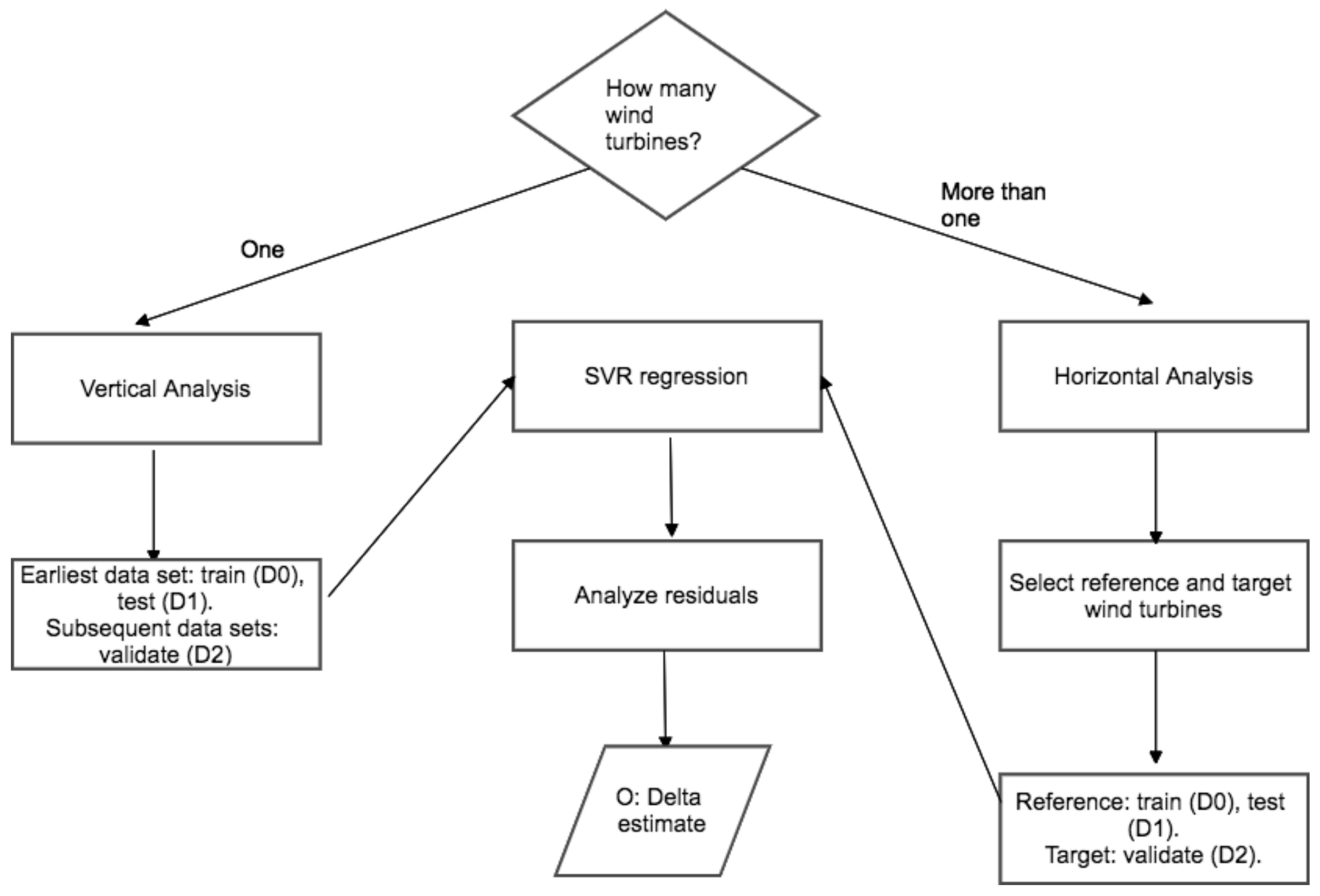
The four wind turbines sited in Italy can be compared among themselves and against the reference of [
24]: the analysis is therefore vertical (each turbine against itself) and horizontal (each wind turbine against the others in the farm and against the reference in [
24]). This investigation provides additional information, with respect to the existing literature, about the extent to which it is possible to individuate recurring patterns in the aging of wind turbines of a certain model.
The generator of one wind turbine sited in Italy reached its end of life in 2018. Therefore, a devoted analysis is performed in this study in order to understand how the performance of the wind turbine changes after the replacement of the generator with respect to the yearly data set immediately before. This analysis, on the one hand, represents a crosscheck of the proposed methodologies and, on the other hand, provides an estimate of the amount of performance recovery that can be expected by replacing an aged main component, as the generator of a wind turbine.
It is possible to inquire at least qualitatively if there is a connection between the wind turbine site and aging: the wind turbine in [
24] is placed in a peri-urban site (in proximity to the Dundalk Institute of Technology in Ireland), while the other four wind turbines considered in this study are placed in an industrial wind farm in a mountainous area.
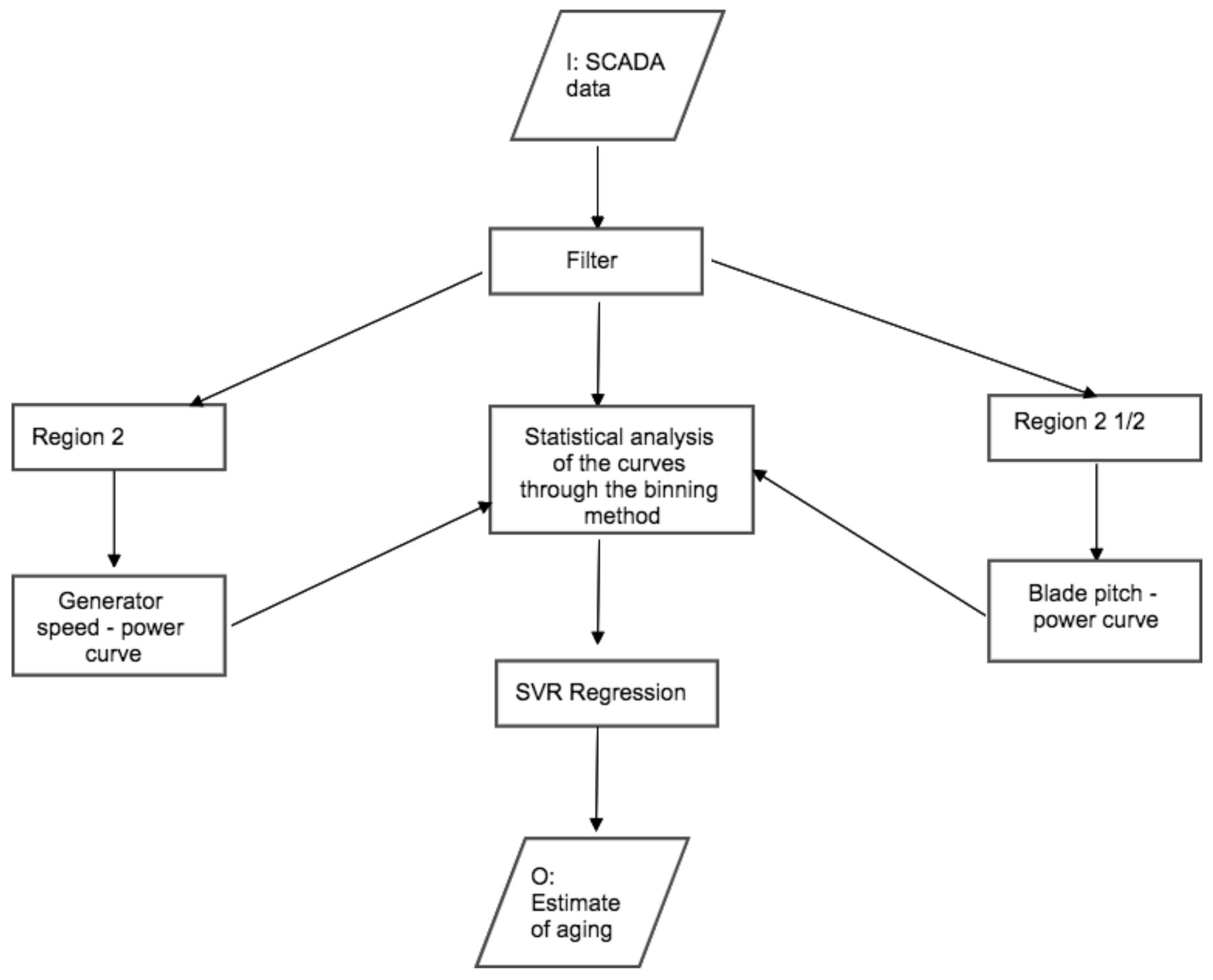
The methodologies employed in this study are similar to those in [
24,
25], but were adapted to the case of multiple wind turbines from two different sites. In particular, the operation curves are analyzed qualitatively, through the generalization of the binning method, which is recommended for power curve analysis [
27], and quantitatively, through support vector regression with a Gaussian kernel. The analysis is conducted in parallel for the two sites, by considering the age of the wind turbines.
It should be noticed that the above summarized methodologies, and in particular the horizontal analysis of the operation curves of the two test cases, represent also a contribution to the more general problem of wind turbine performance analysis and to the problem of comparing the performance of wind turbines of the same model that are sited in different environments: it is known from the literature, and widely discussed in
Section 3, that environmental factors (shear, turbulence, atmospheric stability) have an impact on the wind turbine nacelle transfer function and on the measured power curve [
28,
29]. Therefore, it is more reliable to compare operation curves that do not depend on nacelle wind speed measurements, as is done in the present work and in [
14], where several operation curves were analyzed in detail through a data-driven regression.
The manuscript is organized as follows:
Section 2 is devoted to the description of the test case wind farms and the materials at our disposal for the study; in
Section 3, the methods are described; the results are reported in
Section 4; and finally, in
Section 5, the conclusions are summarized.
2. The Test Cases and the Data Sets
The former test case is the same as in the previous studies [
24,
25]: it is a Vestas V52 installed in 2005 at the Dundalk Institute of Technology, indicated as Test Case 1 (or IREwind turbine) and shown in
Figure 1.
The latter test case is constituted by four Vestas V52 wind turbines, from a wind farm sited in southern Italy in a mountainous area, which were installed in 2007: these are indicated as Test Case 2 (or ITA1, ITA2, ITA3, ITA4 wind turbines).
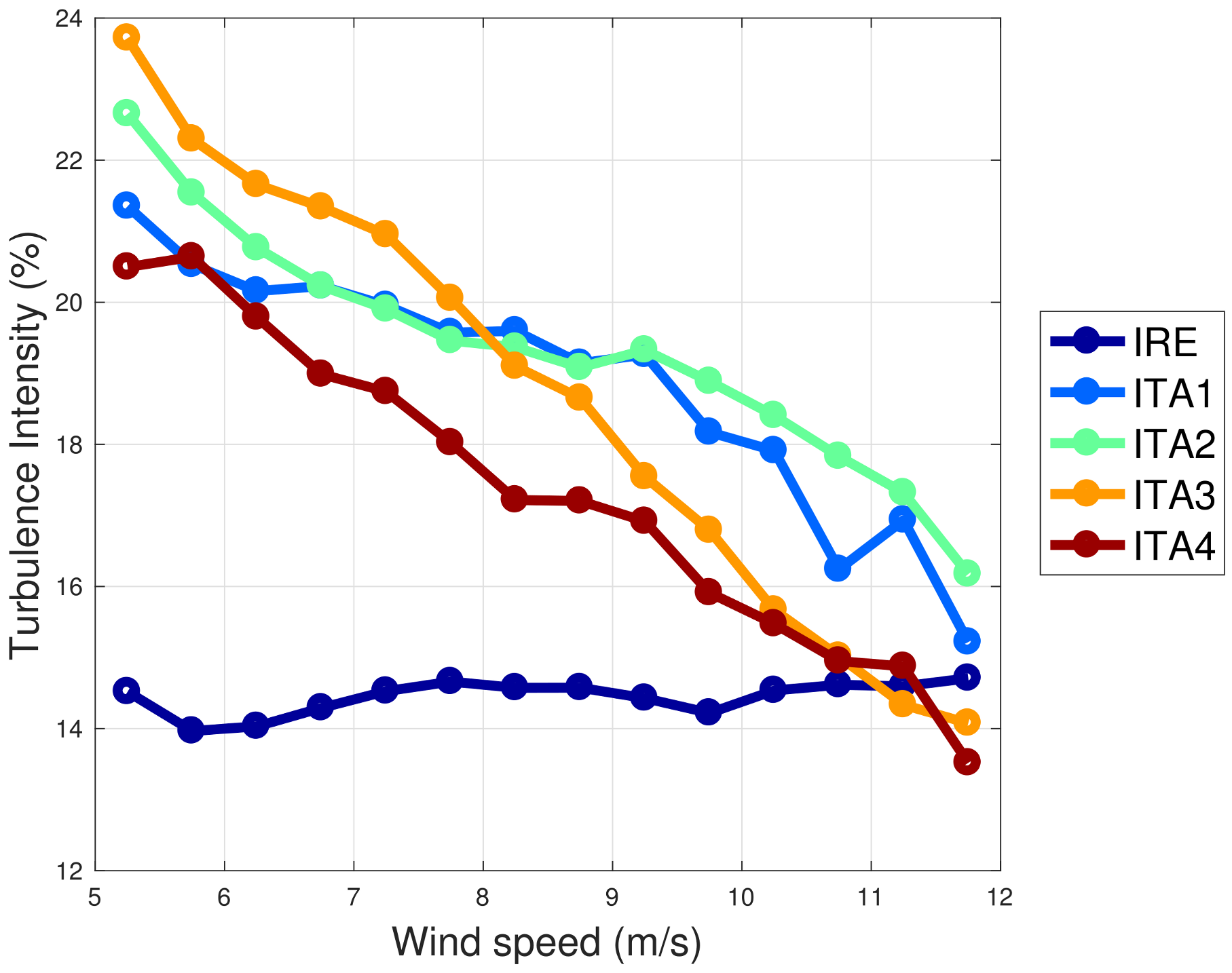
The different climatologies at the two sites are summarized by
Figure 2, where the average yearly turbulence intensity (per wind speed interval of 0.5 m/s) is reported. There were no meteorological mast data at our disposal for the present study, and therefore,
Figure 2 was constructed using the nacelle anemometer data of each wind turbine. The critical points as regards the use of nacelle anemometers for estimating turbulence intensity are well known, but the intention of
Figure 2 is mainly qualitative and aimed at indicating that both environments can be considered complex; the mountainous area of the ITA wind turbines is very complex, with an impressively high level of turbulence. As regards the wind intensity distributions, the same sample year as in
Figure 2 was considered, and the average wind intensities are respectively 6.2 m/s (IRE), 6.4 m/s (ITA1), 6.7 m/s (ITA2), 6.3 m/s (ITA3), and 6.3 m/s (ITA4).
For the purposes of this study, it is sufficient to indicate that the average yearly intensities are similar (order of 6 m/s), with a slightly higher average for the ITA site.
The gearbox and the generator models are the same for all the test case wind turbines. The model of the generator in this case is a Weier 850 kW, shown in
Figure 3, and the main features are reported in
Table 1. It should be noted that the generator of wind turbine ITA4 reached its end of life in February 2018; this represents an interesting test case, because the performance before and after the generator replacement can be analyzed. For this reason, a devoted analysis is performed for ITA4.
The gearbox of the wind turbines is Metso PLH-400V52; it is shown in
Figure 4, and the principal specifications are reported in
Table 2. This information was reported in [
24].
The data sets at our disposal are from 2008 to 2019 for Test Case 1 (except 2016) and from 2013 to 2020 for Test Case 2; these were organized in yearly packets to be analyzed in parallel, which are characterized by the wind turbines having the same age. This is represented in
Table 3.
On the grounds of the above considerations about the ITA4 wind turbine and the generator replacement, a separate analysis was conducted using the data sets , , and . The data set started since the replacement date of the generator at ITA4 (in March).
The measurements at our disposal are reported in
Table 4.
In order to correctly interpret the performance of the wind turbines, it is fundamental to filter the operation data appropriately. The first filter that was applied to the data of both test cases was based on the run time counter. For Test Case 2, where the wind turbines operate under possible limitations dictated by the grid, the measurements corresponding to curtailment were filtered out through the analysis of the outliers with respect to the average wind speed-blade pitch curve.
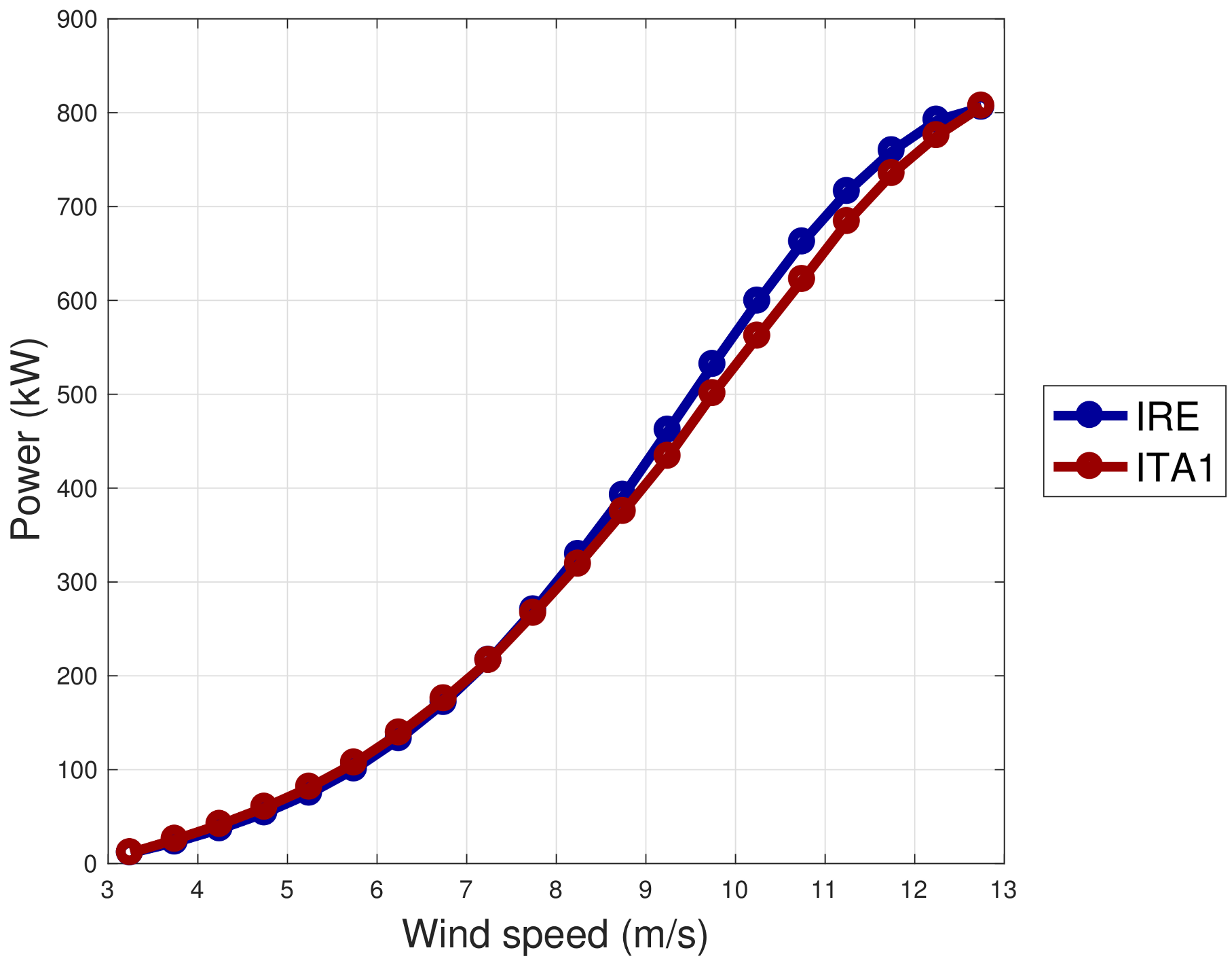
For the objectives of the present study, it is important to distinguish the data sets on the basis of the operation regions, which respectively are fixed pitch-variable rotational speed and vice versa. In order to do this, on the grounds of the qualitative analysis of the wind speed-generator speed and wind speed-blade pitch curves, it was decided to employ the nacelle wind intensity
v to discriminate the two working regions, as indicated in
Table 5 and shown in
Figure 5 on a sample power curve (IRE wind turbine). The same notation as in [
25] was adopted: the regime when the wind turbine operates at full aerodynamic load, with variable rotational speed and fixed pitch, is indicated as Region 2; instead, the regime characterized by rated rotational speed and variable pitch is indicated as Region 2
.
5. Conclusions
The present work deals with the analysis of wind turbine performance decline with age. Motivated by previous findings in [
24,
25] about a Vestas V52 wind turbine sited at the Dundalk Institute of Technology in Ireland, in this study, four Vestas V52 sited in a mountainous area in southern Italy are selected as further test cases. The objective of the study was addressing if wind turbines of the same model present similar aging trends.
The employed methodologies consisted of the analysis of appropriate operation curves depending on the working region of the wind turbines and in a support vector regression for constructing digital twins of the curves of interest and for validating them against target data sets. The selected curves are the generator speed-power curve and blade pitch-power curve, and each is analyzed in the working region where it is of most interest: the former curve is analyzed for moderate wind speed, when the wind turbines operate at fixed pitch and variable rotational speed; the latter curve is analyzed for higher wind speed, when the wind turbines operate at rated rotational speed and variable pitch.
The methodologies were employed vertically and horizontally: in other words, for each wind turbine, its history was studied (vertical analysis), and the horizontal analysis consisted of the comparison between the IRE and ITA wind turbines when they had the same age. This approach goes beyond the scope of the present work because it contributes to the general problem of comparing the performance of the same model of wind turbine, installed in different environments: the power curve analysis is not reliable, because the environmental conditions affect the nacelle transfer function differently at each site. Therefore, it is more appropriate to analyze the operation curves, which do not depend on the nacelle wind speed measurements, as the ones selected in this study.
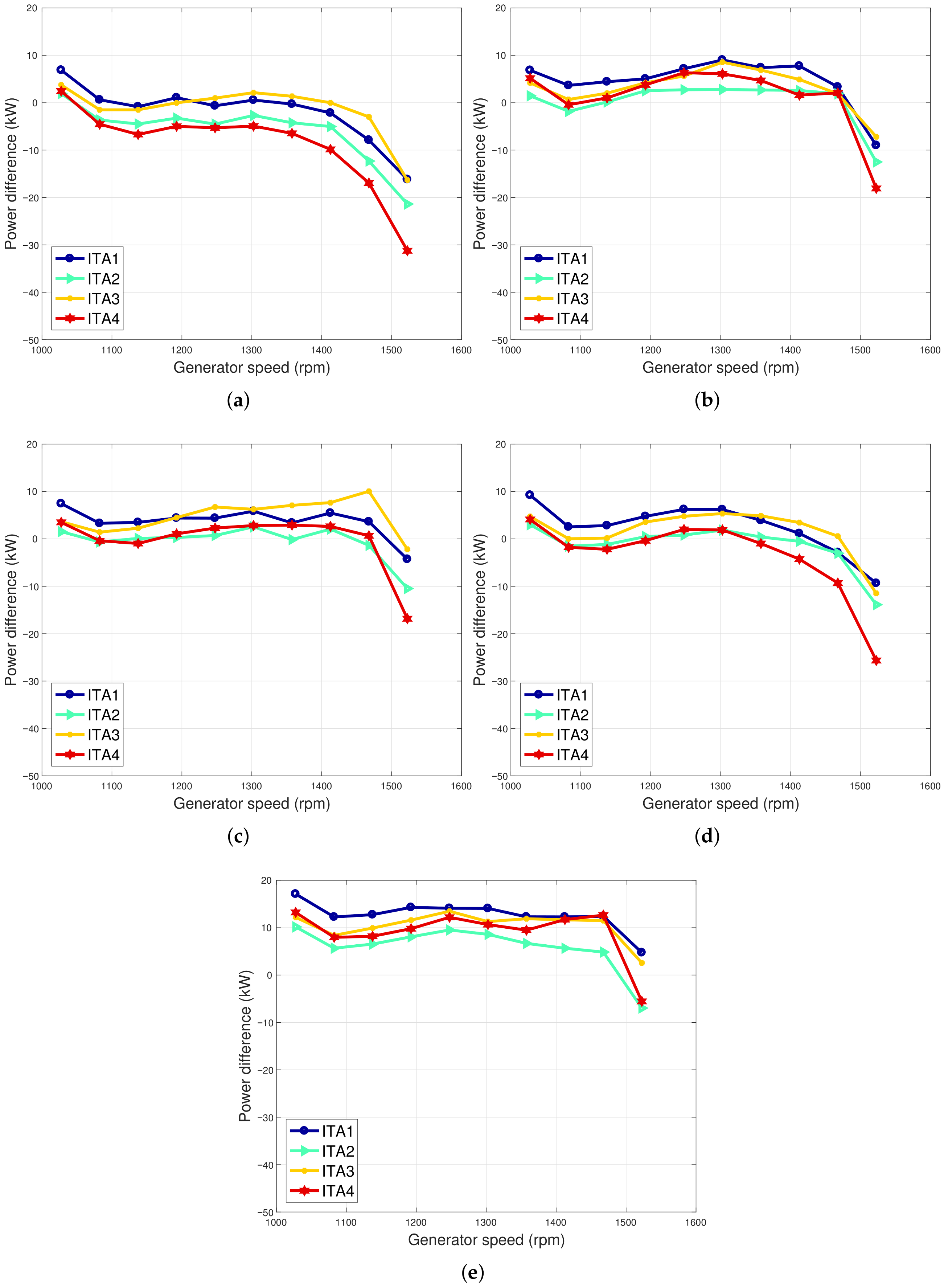
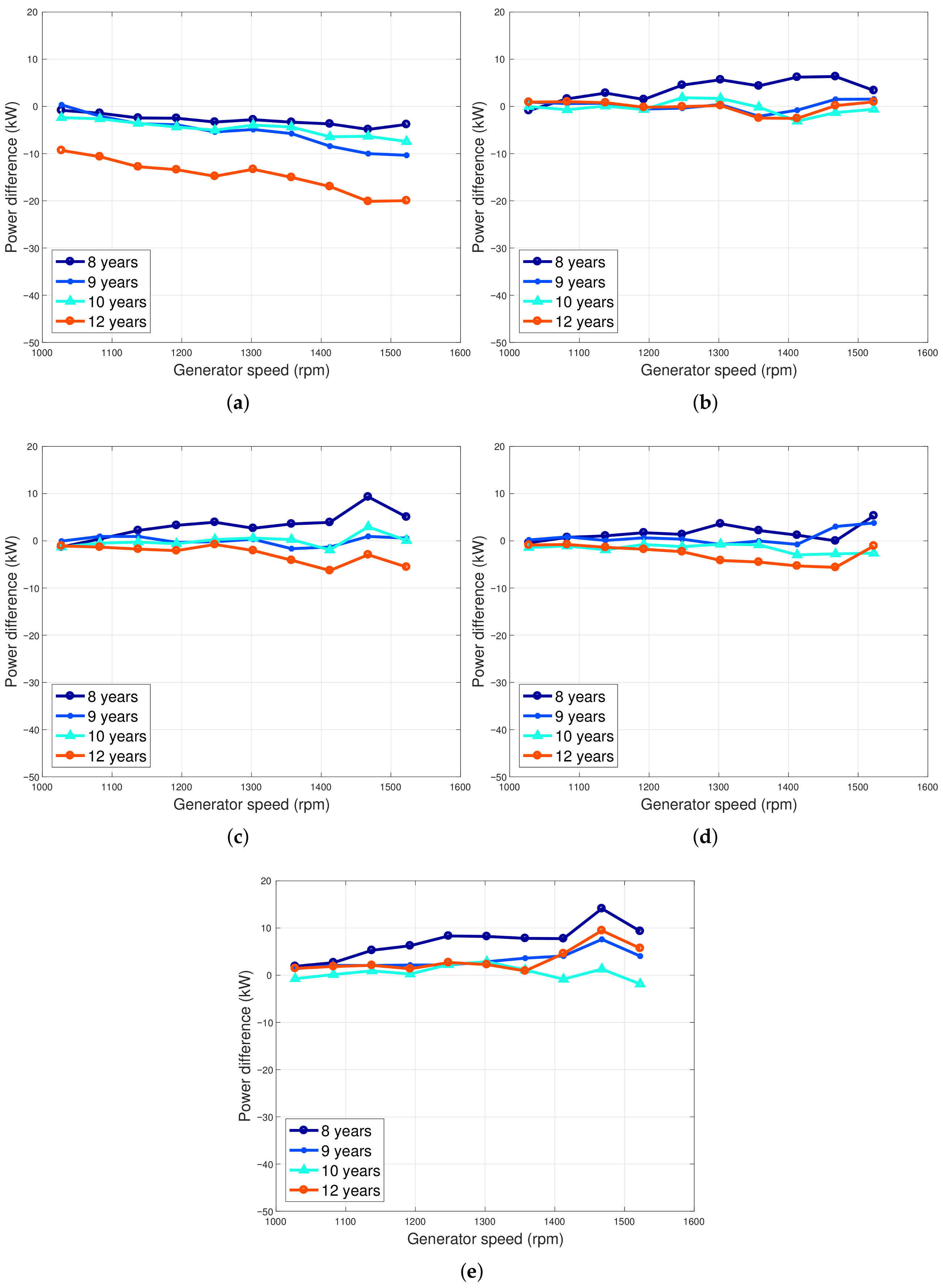
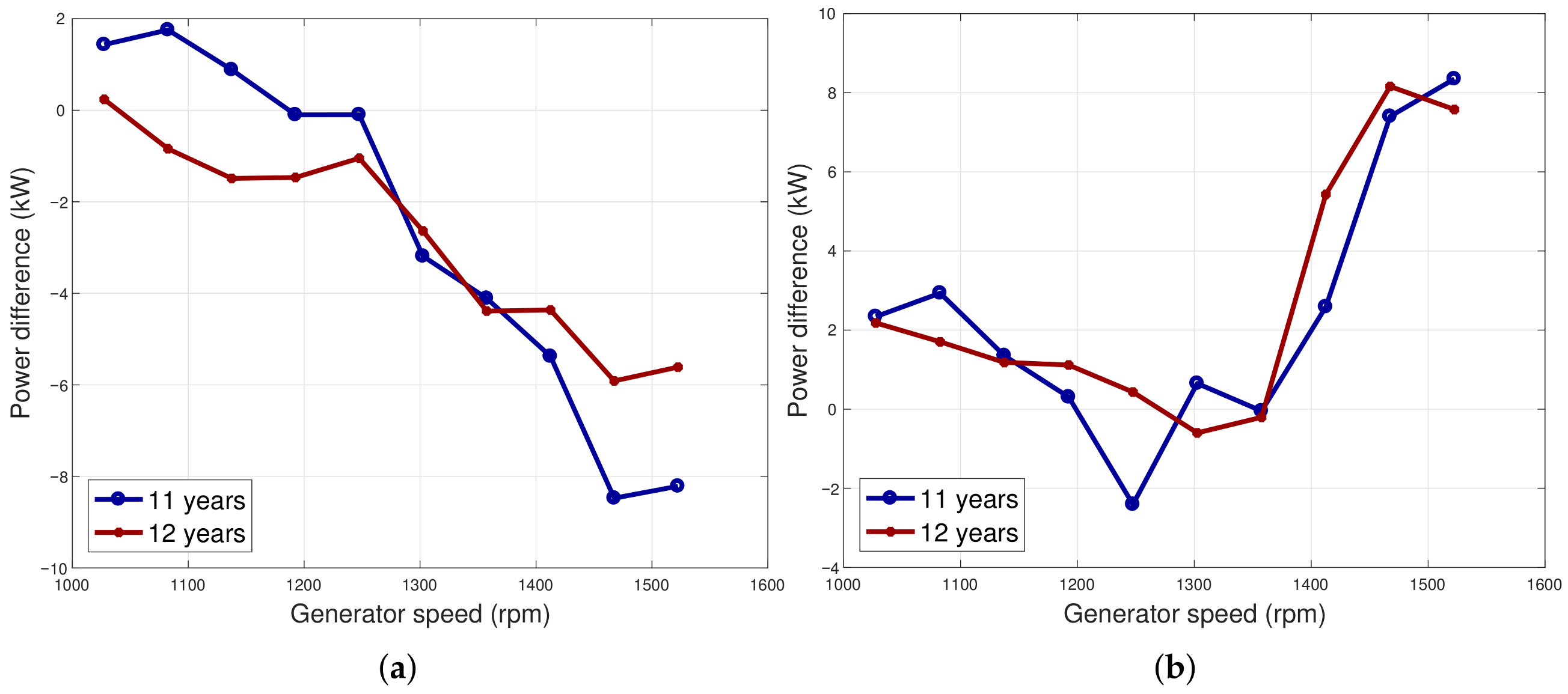
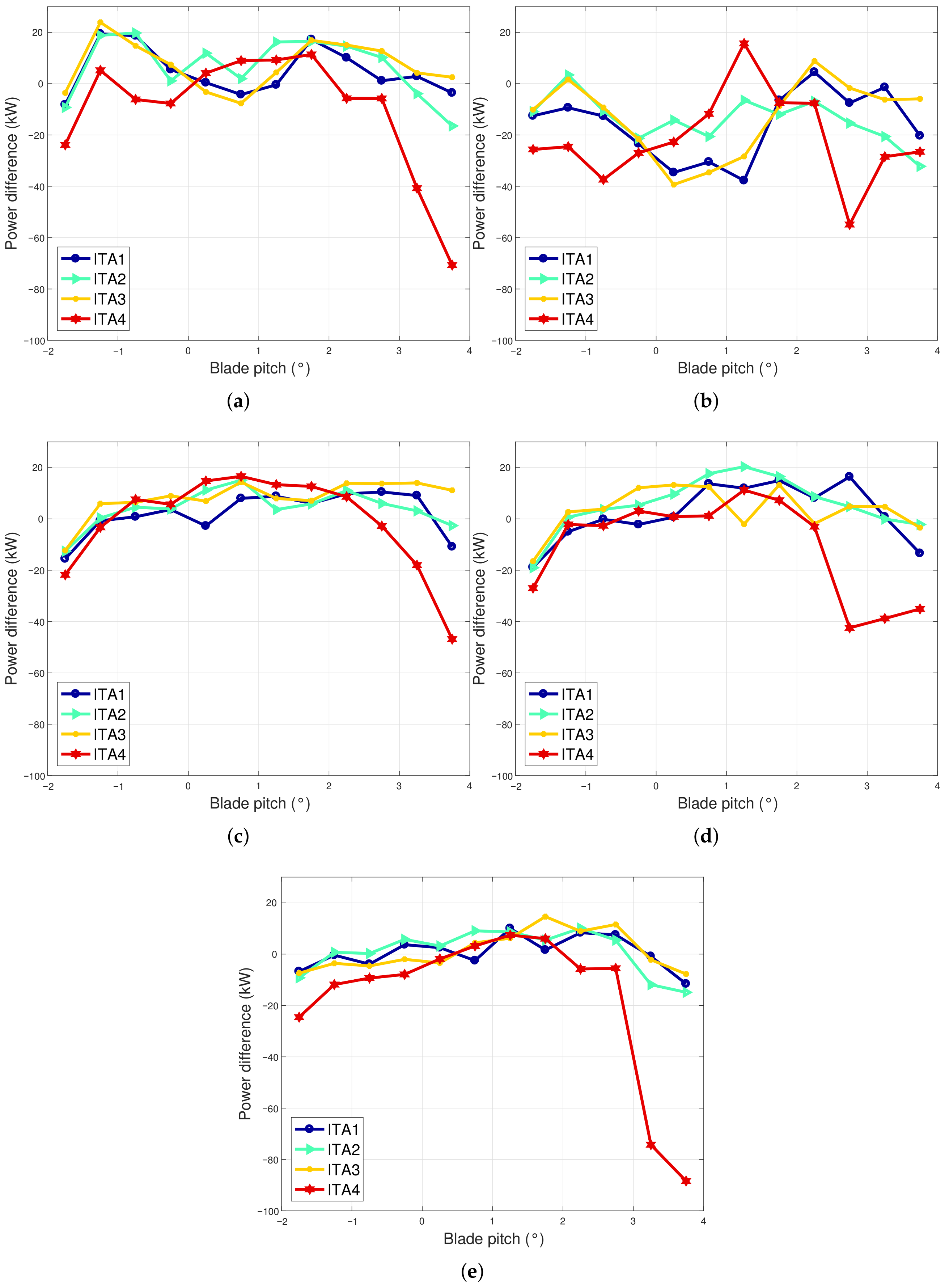
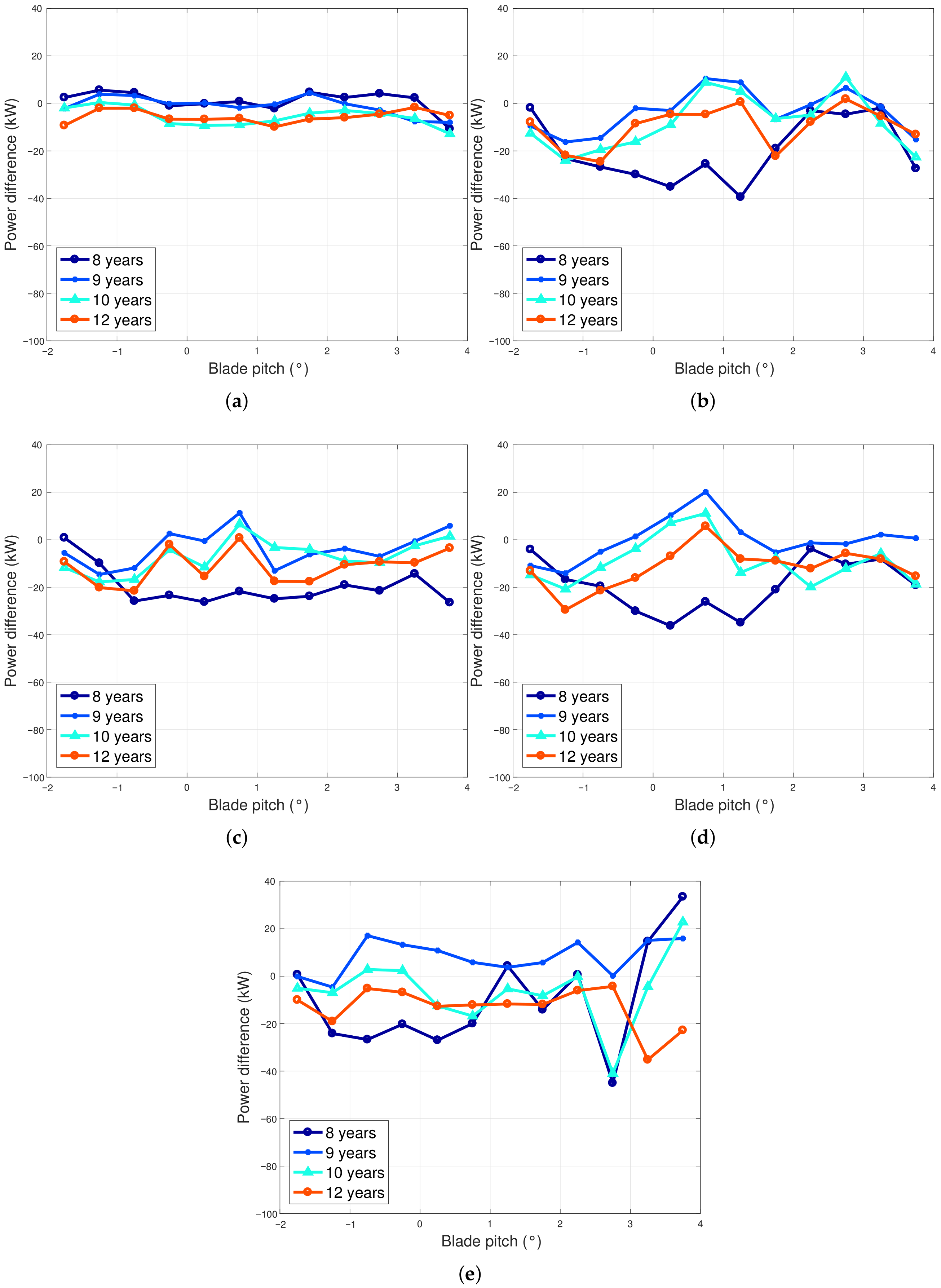
It results that the aging of the generator affects non-negligibly the performance of the wind turbines, and this is highlighted as diminished power extraction for a given generator speed; however, this happens to different extents in the test case wind turbines: from seven to 12 years of age, in Region 2, two wind turbines sited in Italy underwent a performance worsening of the order of 1–2%, while the average performance decrease was −8.8% in the same period for the wind turbine in Ireland. An interesting test case is given by the fact that the generator of one wind turbine sited in Italy reached its end of life in 2018 and was substituted: by comparing the data sets immediately before the ones immediately after the replacement, it can be estimated that the replacement provided a performance improvement of the order of 2%. This provides a consistency check of the proposed methodologies and indicates an estimate of the profitability of substituting aged wind turbine components. In Region 2
, the behavior of all the test case wind turbines was similar, and a performance decline of the order of 2% was observed. Overall, it can be summarized that after five years of operation (which is the span of the data sets at out disposal for this study), the performance of the IRE wind turbine declined below the rated power of the order of 7.7%, while three ITA wind turbines had slightly worsened performance (from 0.2% to 1.4%) and one (ITA4) improved. Another important aspect is given by the fact that the performance worsening with age seems not to be linear in time: the selected data sets go from seven to twelve years of age of the wind turbines, and in particular for the IRE test case, an evident decline occurs at twelve years of age. Referring to the results in [
25] for the IRE wind turbine, if one considers a span of ten years (two years of age against twelve), the estimated worsening is in the order of 8.8%: by comparison, it can be argued that the aging from two to seven years of age is quite low. This ex post supports the rationale of the horizontal and vertical analysis, which were combined in this work: by comparing several test cases, it is possible to analyze the level of performance at a certain age of the wind turbines.
Therefore, on the grounds of what is observed for the four wind turbines in Italy in comparison with the test case in Ireland, it is concluded that it is likely that the effect of aging for the Vestas V52 wind turbines can be in general lower with respect to the estimates provided in [
24,
25], but it cannot be excluded that a similar decline in the generator efficiency would occur as well for the other test case wind turbines in the future. This motivates that an interesting further direction of this work is the analysis of the electrical parameters of wind turbine generators in order to formulate prognostic models. In addition, the operating condition and response of the hydraulic station that controls the blade pitching system deserves further examination, e.g., if oil pressures in the hydraulic station are not well maintained, the blade pitch response may deviate from the optimum and affect the power performance.
Furthermore, the case of the ITA4 wind turbine, which has undergone a replacement of the generator, inspires further developments as regards a detailed analysis of the economic balance: this could give meaningful indications in general as regards the management of wind turbines.
Another interesting further line of research regards the interpretation of the aging performance in terms of the overall maintenance level of the wind turbines: from this point of view, we expect that a large number of test cases should be analyzed, in order to possibly highlight the dependence on this factor, which can be expected to be relevant, but can not be expected to be the only or the main determinant.
A valuable further development of the present work is investigating in more detail the hypothesis formulated in [
22] about the fact that the evolution of wind turbine technology should mitigate the impact of aging: the results reported in [
24,
25] and in the present work indicate that the hypothesis should be confirmed because the observed decline rate is lower with respect to the estimates reported in [
22] for wind turbines installed in the 1990s. At present, further studies are being conducted by the authors on wind turbines of higher size (the order of a 100 m rotor diameter), which were installed in the late 2000s, and the preliminary results indicate that the aging decline is lower with respect to the results of this study.