The Efficiency of a Fence of Tidal Turbines in the Alderney Race: Comparison between Analytical and Numerical Models
Abstract
1. Introduction
2. Materials and Methods
2.1. Site Description—Scenarios of Tidal Stream Energy Extraction
2.2. Analytical Models
2.3. Numerical Model
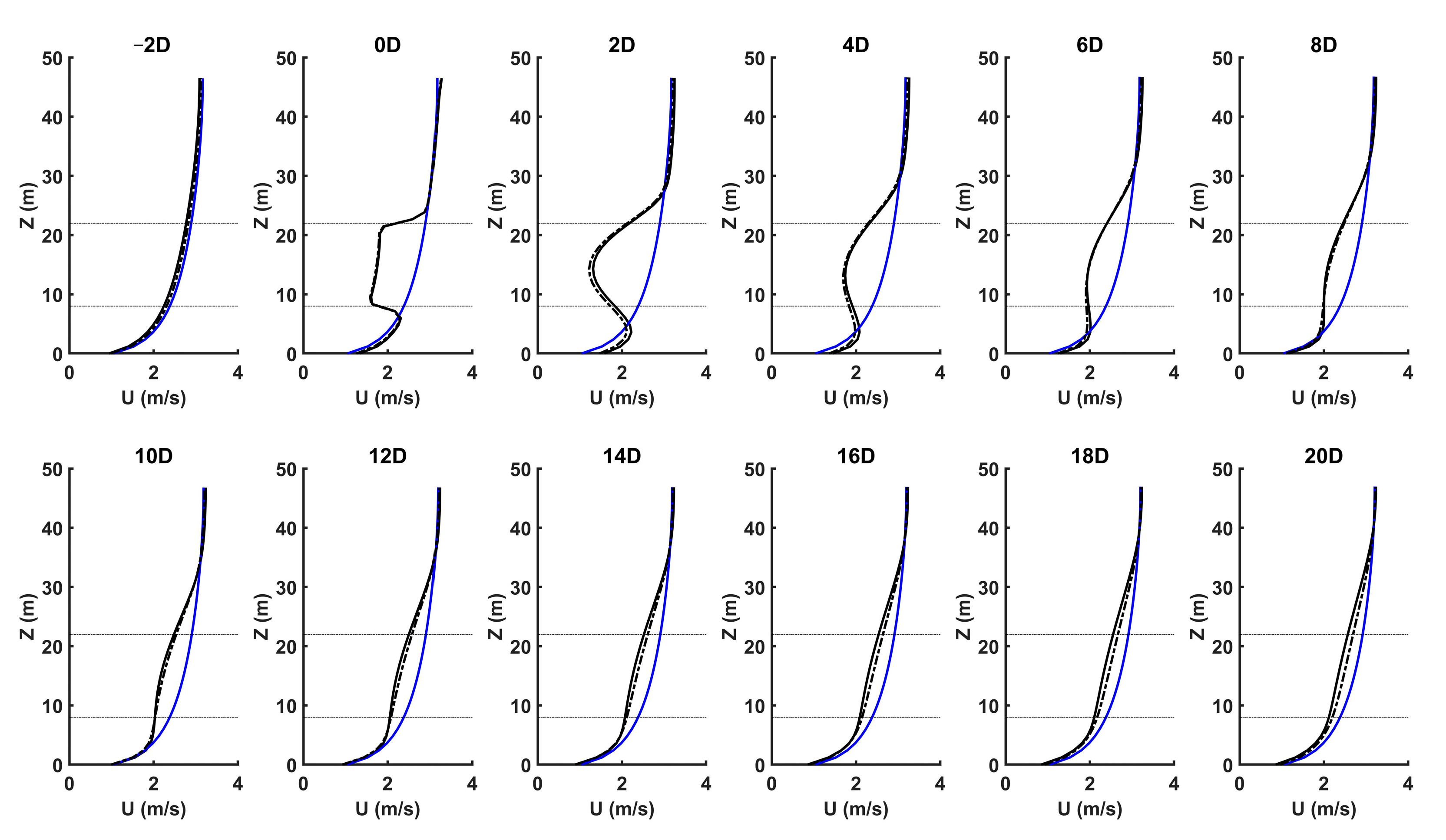
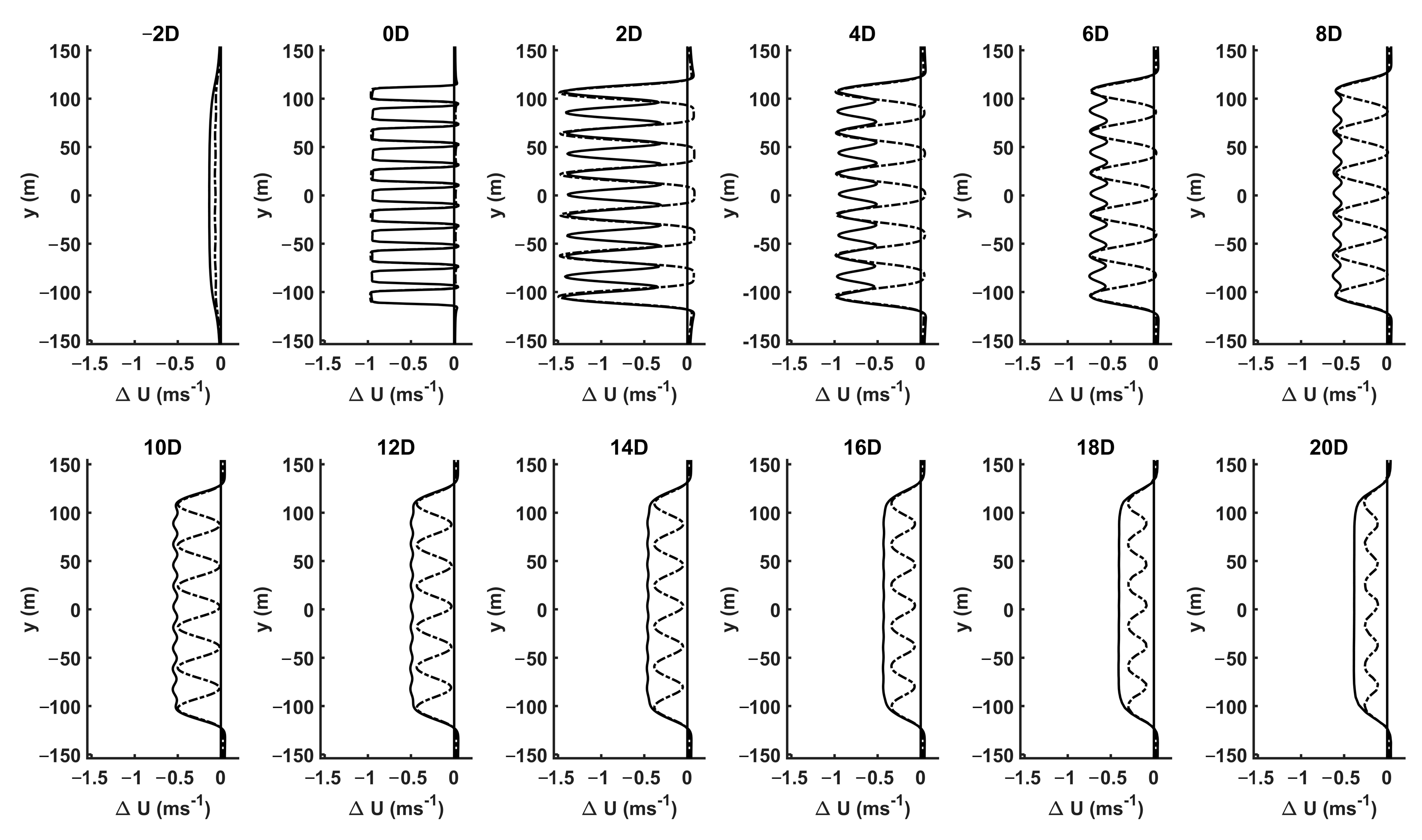
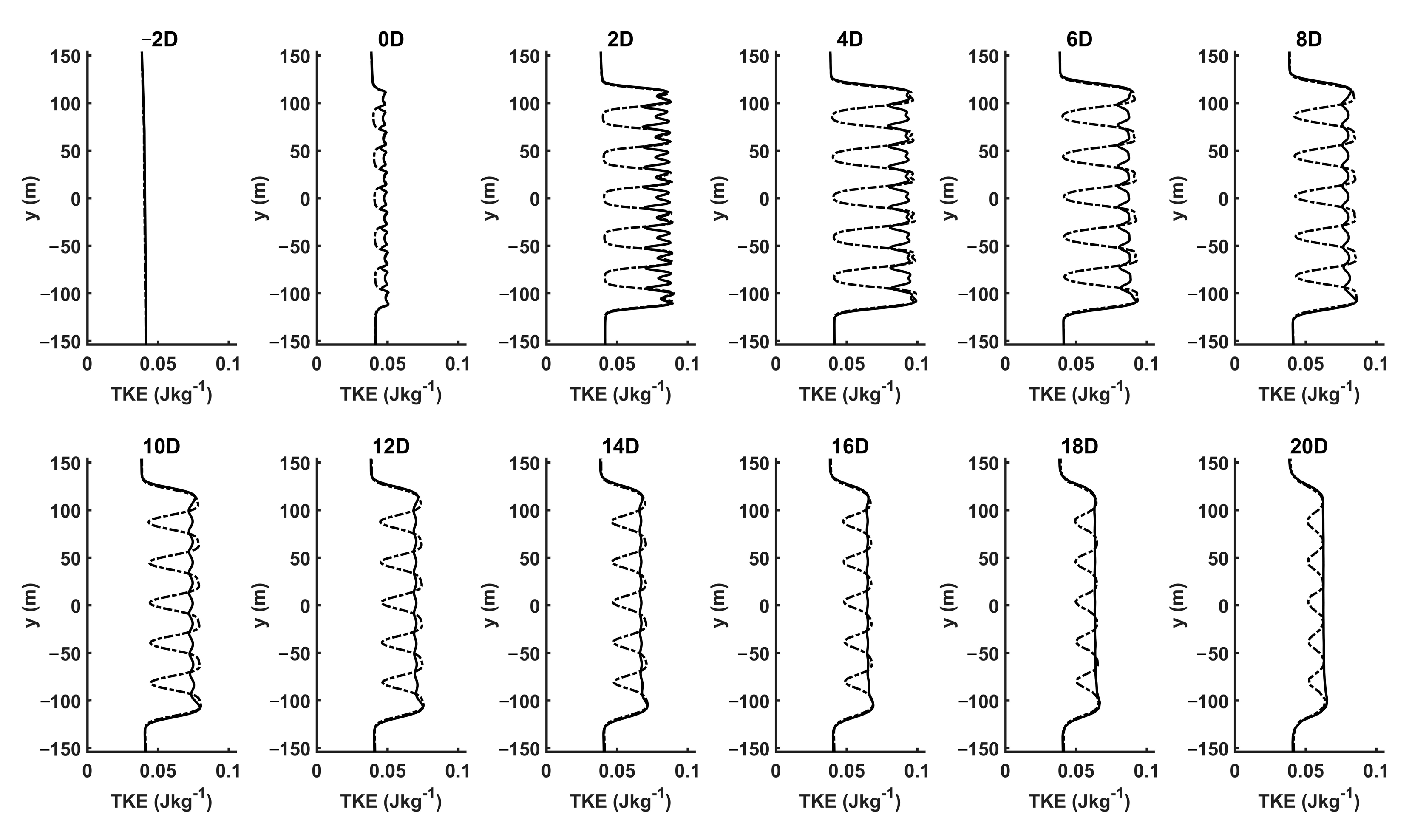
3. Results and Discussion
3.1. Results Overview
3.2. Inter-Comparison of Analytical Models
3.3. Comparison between Analytical and Numerical Models
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Magagna, D.; Uihlein, A. Ocean energy development in Europe: Current status and future perspectives. Int. J. Mar. Energy 2015, 11, 84–104. [Google Scholar] [CrossRef]
- Sentchev, A.; Thiébot, J.; Bennis, A.-C.; Piggott, M. New insights on tidal dynamics and tidal energy harvesting in the Alderney Race. Phil. Trans. R. Soc. A 2020, 378, 20190490. [Google Scholar] [CrossRef]
- De Dominicis, M.; O’Hara Murray, R.; Wolf, J. Multi-scale ocean response to a large tidal stream turbine array. Renew. Energy 2017, 114 B, 1160–1179. [Google Scholar] [CrossRef]
- Guillou, N.; Neill, S.P.; Thiébot, J. Spatio-temporal variability of tidal-stream energy in north-western Europe. Phil. Trans. R. Soc. A 2020, 378, 20190493. [Google Scholar] [CrossRef]
- Garrett, C.; Cummins, P. The efficiency of a turbine in a tidal channel. J. Fluid Mech. 2007, 588, 243–251. [Google Scholar] [CrossRef]
- Whelan, J.I.; Graham, J.M.R.; Peiro, J. A free-surface and blockage correction for tidal turbines. J. Fluid Mech. 2009, 624, 281–291. [Google Scholar] [CrossRef]
- Nishino, T.; Willden, R.H.J. The efficiency of an array of tidal turbines partially blocking a wide channel. J. Fluid Mech. 2012, 708, 596–606. [Google Scholar] [CrossRef]
- Grondeau, M.; Poirier, J.-C.; Guillou, S.; Méar, Y.; Mercier, P.; Poizot, E. Modelling the wake of a tidal turbine with upstream turbulence: LBM-LES versus Navier-Stokes LES. Int. Mar. Energy J. 2020, 3, 83–89. [Google Scholar] [CrossRef]
- Grondeau, M.; Guillou, S.S.; Mercier, P.; Poizot, E. Wake of a ducted vertical axis tidal turbine in turbulent flows, LBM actuator-line approach. Energies 2019, 12, 4273. [Google Scholar] [CrossRef]
- Pinon, G.; Mycek, P.; Germain, G.; Rivoalen, E. Numerical simulation of the wake of marine current turbines with a particle method. Renew. Energy 2012, 46, 111–126. [Google Scholar] [CrossRef]
- Batten, W.M.J.; Harrison, M.E.; Bahaj, A.S. Accuracy of the actuator disc-RANS approach for predicting the performance and wake of tidal turbines. Phil. Trans. R. Soc. A. 2013, 371, 20120293. [Google Scholar] [CrossRef]
- Michelet, N.; Guillou, N.; Chapalain, G.; Thiébot, J.; Guillou, S.; Goward Brown, A.J.; Neill, S.P. Three-dimensional modelling of turbine wake interactions at a tidal stream energy site. Appl. Ocean Res. 2020, 95, 102009. [Google Scholar]
- Shschepetkin, A.F.; Mc Williams, J.C. The regional oceanic modelling system (ROMS): A split-explicit, free-surface, topography-following-coordinate oceanic model. Ocean Model. 2005, 9, 347–404. [Google Scholar] [CrossRef]
- Nguyen, V.T.; Santa Cruz, A.; Guillou, S.S.; Shiekh Elsouk, M.N.; Thiébot, J. Effects of the Current Direction on the Energy Production of a Tidal Farm: The Case of Raz Blanchard (France). Energies 2019, 12, 2478. [Google Scholar] [CrossRef]
- Thiébot, J.; Guillou, N.; Guillou, S.; Good, A.; Lewis, M. Wake field study of tidal turbines under realistic flow conditions. Renew. Energy 2020, 151, 1196–1208. [Google Scholar] [CrossRef]
- Coles, D.S.; Blunden, L.S.; Bahaj, A.S. Assessment of the energy extraction potential at tidal sites around the Channel Islands. Energy 2017, 124, 171–186. [Google Scholar] [CrossRef]
- Campbell, R.; Martinez, A.; Letetrel, C.; Rio, A. Methodology for estimating the French tidal current energy resource. Int. J. Mar. Energy 2017, 19, 256–271. [Google Scholar] [CrossRef]
- Thiébot, J.; Coles, D.S.; Bennis, A.-C.; Guillou, N.; Neill, S.P.; Guillou, S.; Piggott, M. Numerical modelling of hydrodynamics and tidal energy extraction in the Alderney Race: A review. Phil. Trans. R. Soc. A 2020, 378, 20190498. [Google Scholar]
- Hervouet, J.-M. Hydrodynamics of Free Surface Flows, Modelling with the Finite Element Method; Wiley: New York, NY, USA, 2007. [Google Scholar]
- Thiébot, J.; Guillou, S.; Nguyen, V.T. Modelling the effect of large arrays of tidal turbines with depth-averaged Actuator Disks. Ocean Eng. 2016, 126, 265–275. [Google Scholar] [CrossRef]
- Nguyen, V.T.; Guillou, S.S.; Thiébot, J.; Santa Cruz, A. Modelling turbulence with an Actuator Disk representing a tidal turbine. Renew. Energy 2016, 97, 625–635. [Google Scholar] [CrossRef]
- Nishino, T.; Willden, R.H.J. Effects of 3-D channel blockage and turbulent wake mixing on the limit extrcation by tidal turbines. Int. J. Heat Fluid Flow 2012, 37, 123–135. [Google Scholar] [CrossRef]
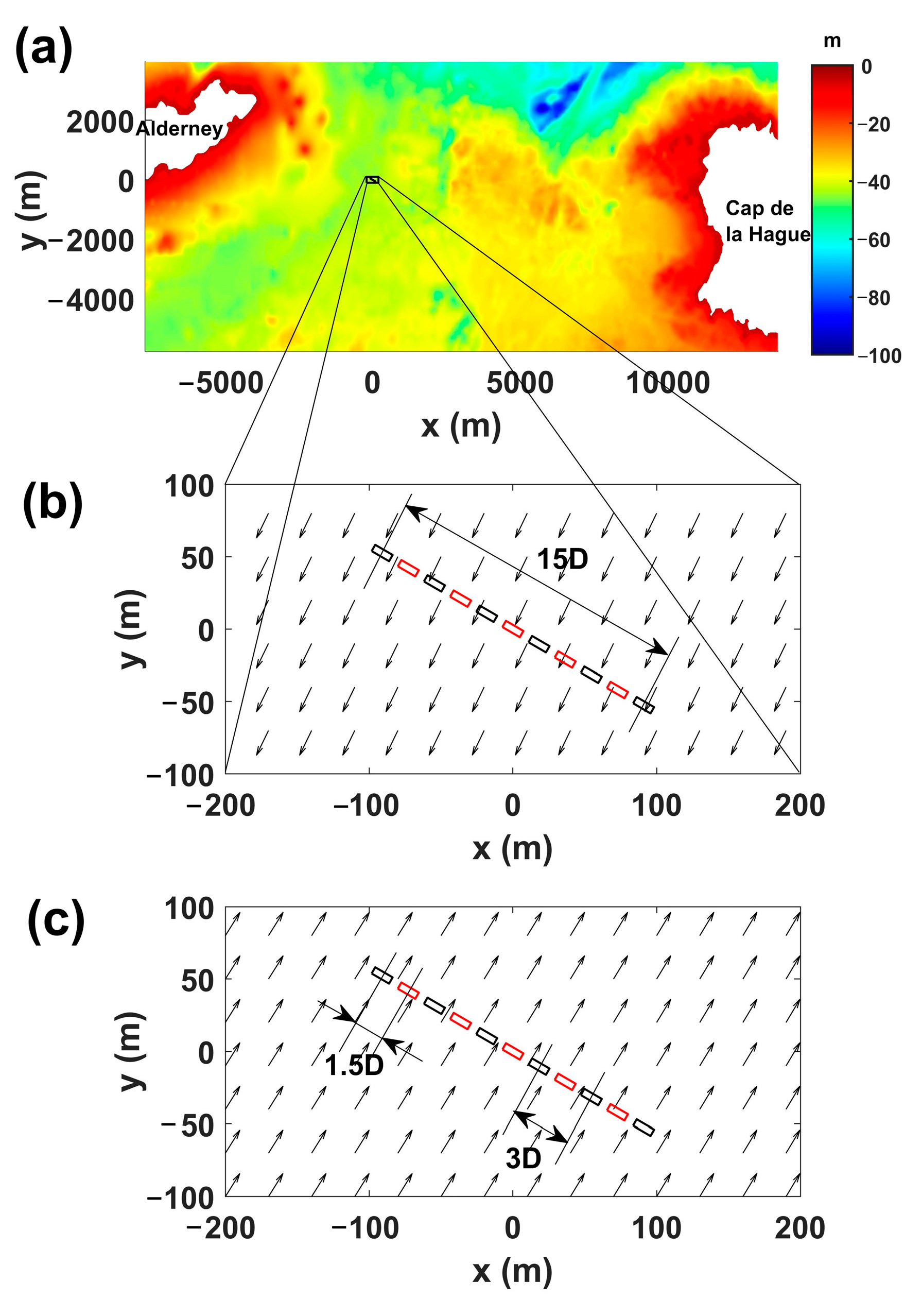
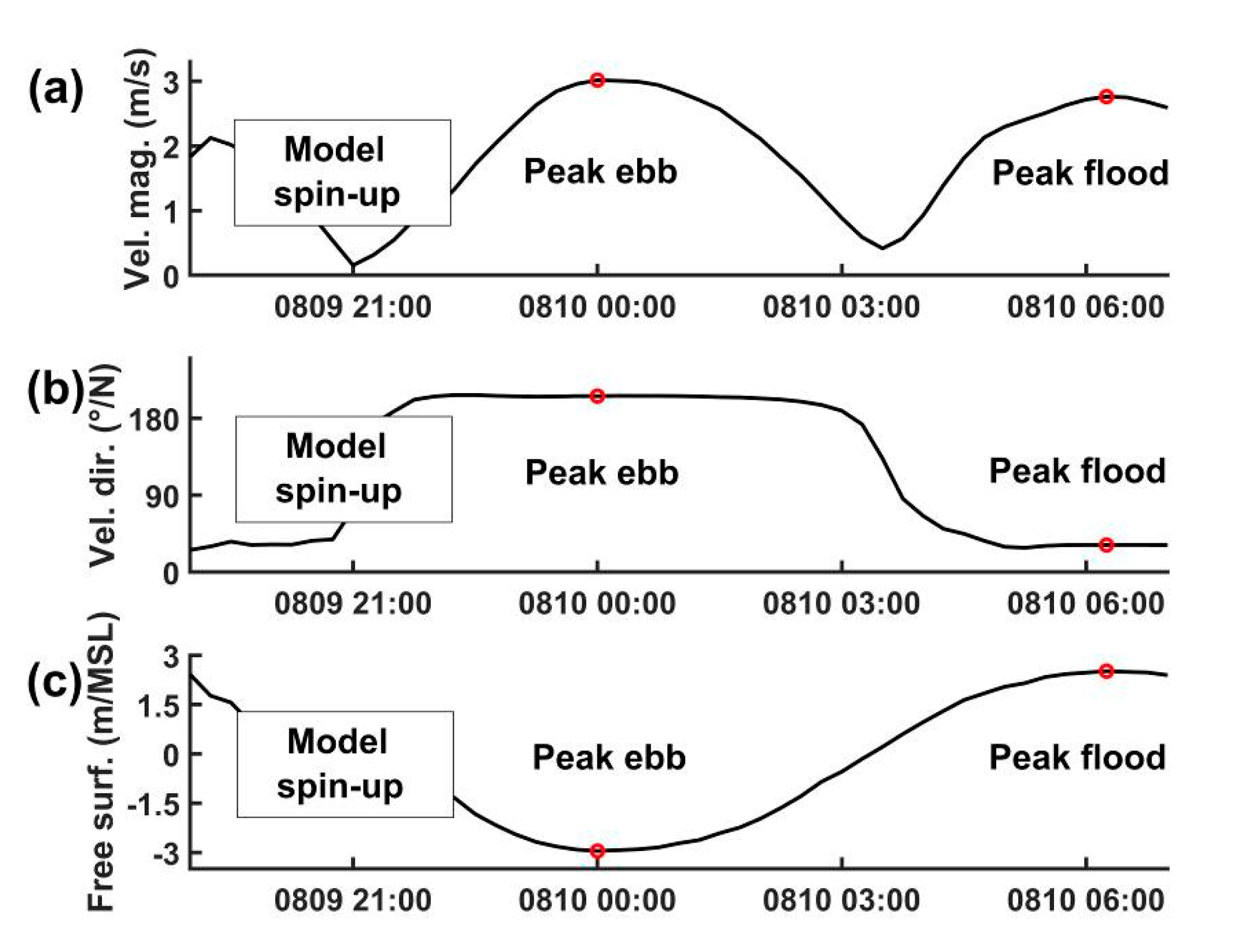
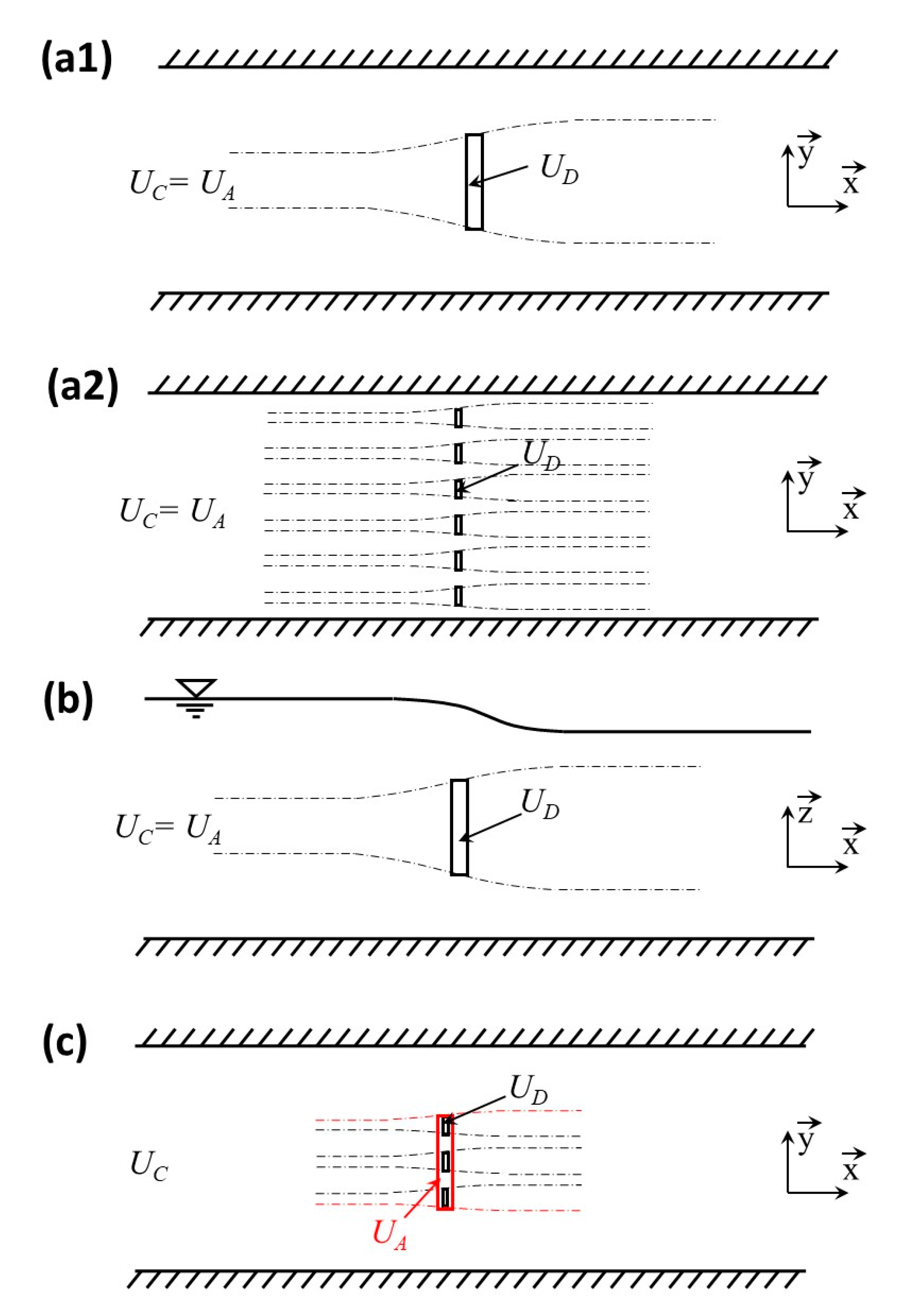
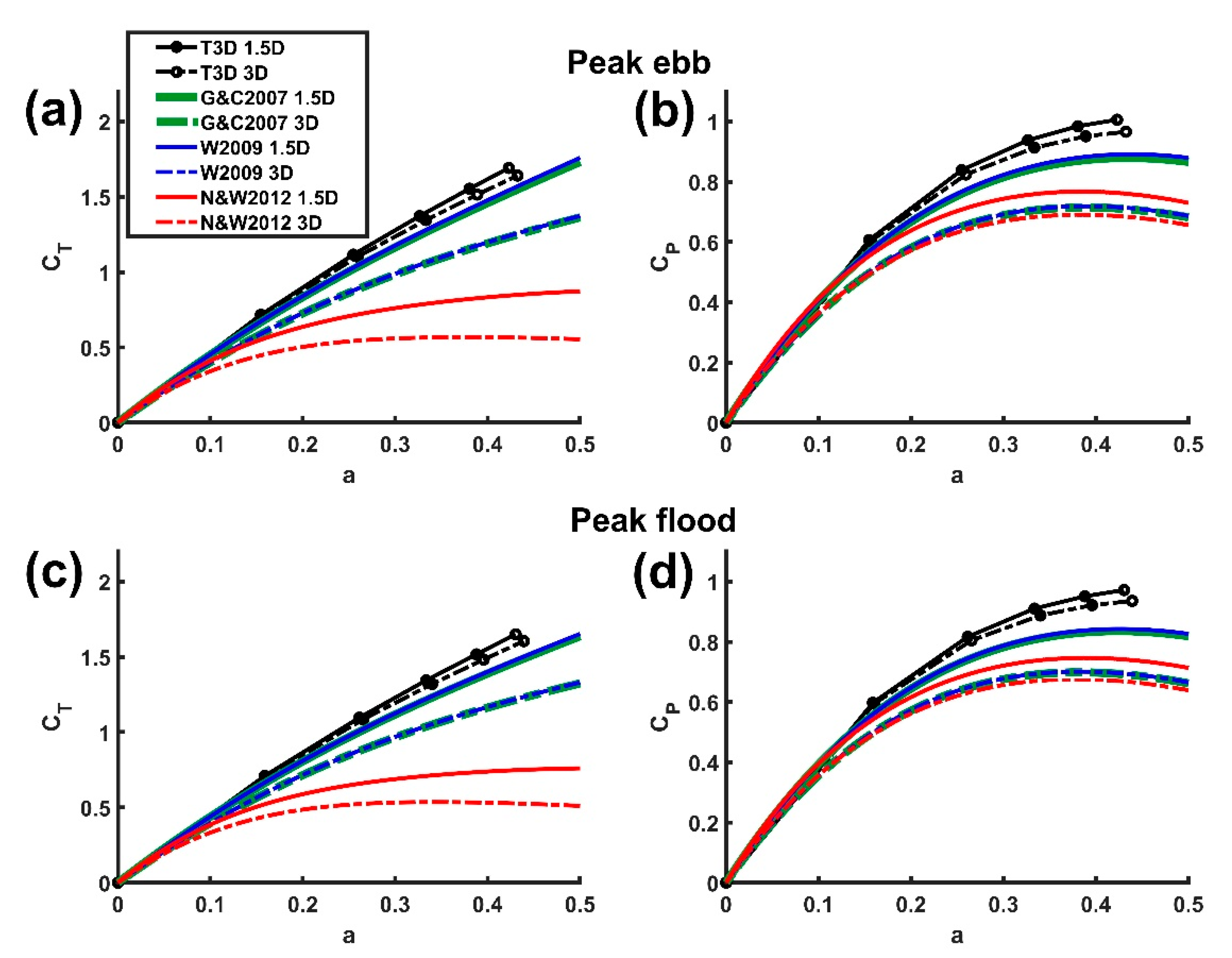
| Peak Ebb | Peak Flood | |
|---|---|---|
| Water depth (m) | 41.05 | 46.52 |
| Depth-averaged velocity magnitude (m/s) | 3.02 | 2.76 |
| Depth-averaged current direction (°/North) | 206 | 32 |
| Blockage ratio (%) Δ = 1.5D/3D | 17.86/8.93 | 15.76/7.88 |
| Froude number (dimensionless) | 0.150 | 0.129 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thiébot, J.; Djama Dirieh, N.; Guillou, S.; Guillou, N. The Efficiency of a Fence of Tidal Turbines in the Alderney Race: Comparison between Analytical and Numerical Models. Energies 2021, 14, 892. https://doi.org/10.3390/en14040892
Thiébot J, Djama Dirieh N, Guillou S, Guillou N. The Efficiency of a Fence of Tidal Turbines in the Alderney Race: Comparison between Analytical and Numerical Models. Energies. 2021; 14(4):892. https://doi.org/10.3390/en14040892
Chicago/Turabian StyleThiébot, Jérôme, Nasteho Djama Dirieh, Sylvain Guillou, and Nicolas Guillou. 2021. "The Efficiency of a Fence of Tidal Turbines in the Alderney Race: Comparison between Analytical and Numerical Models" Energies 14, no. 4: 892. https://doi.org/10.3390/en14040892
APA StyleThiébot, J., Djama Dirieh, N., Guillou, S., & Guillou, N. (2021). The Efficiency of a Fence of Tidal Turbines in the Alderney Race: Comparison between Analytical and Numerical Models. Energies, 14(4), 892. https://doi.org/10.3390/en14040892









