Improving PV Resilience by Dynamic Reconfiguration in Distribution Grids: Problem Complexity and Computation Requirements
Abstract
1. Introduction
- A new formulation of the optimal dynamic reconfiguration problem for losses minimization;
- A quantification of problem complexity and how this complexity scales with the number of switching operations and with the number of time steps (i.e., time span of reconfiguration schedule multiplied by time resolution);
- An illustration of the benefits of finding the optimal dynamic reconfiguration solution over a real network model;
- A discussion of the prospective use of quantum computing to address the complexity of the full dynamic reconfiguration problem in the future.
2. Problem Formulation
2.1. Unrestricted Optimal Reconfiguration
2.2. Optimal Static Configuration
2.3. Time-Bounded Linear Dynamic Reconfiguration
2.4. Time-Unbounded Cyclic Dynamic Reconfiguration
2.5. Open Cyclic Dynamic Reconfiguration
3. Solution Illustration
3.1. PV Generation Profile
3.2. Impact of PV Generation on Net Load Profile
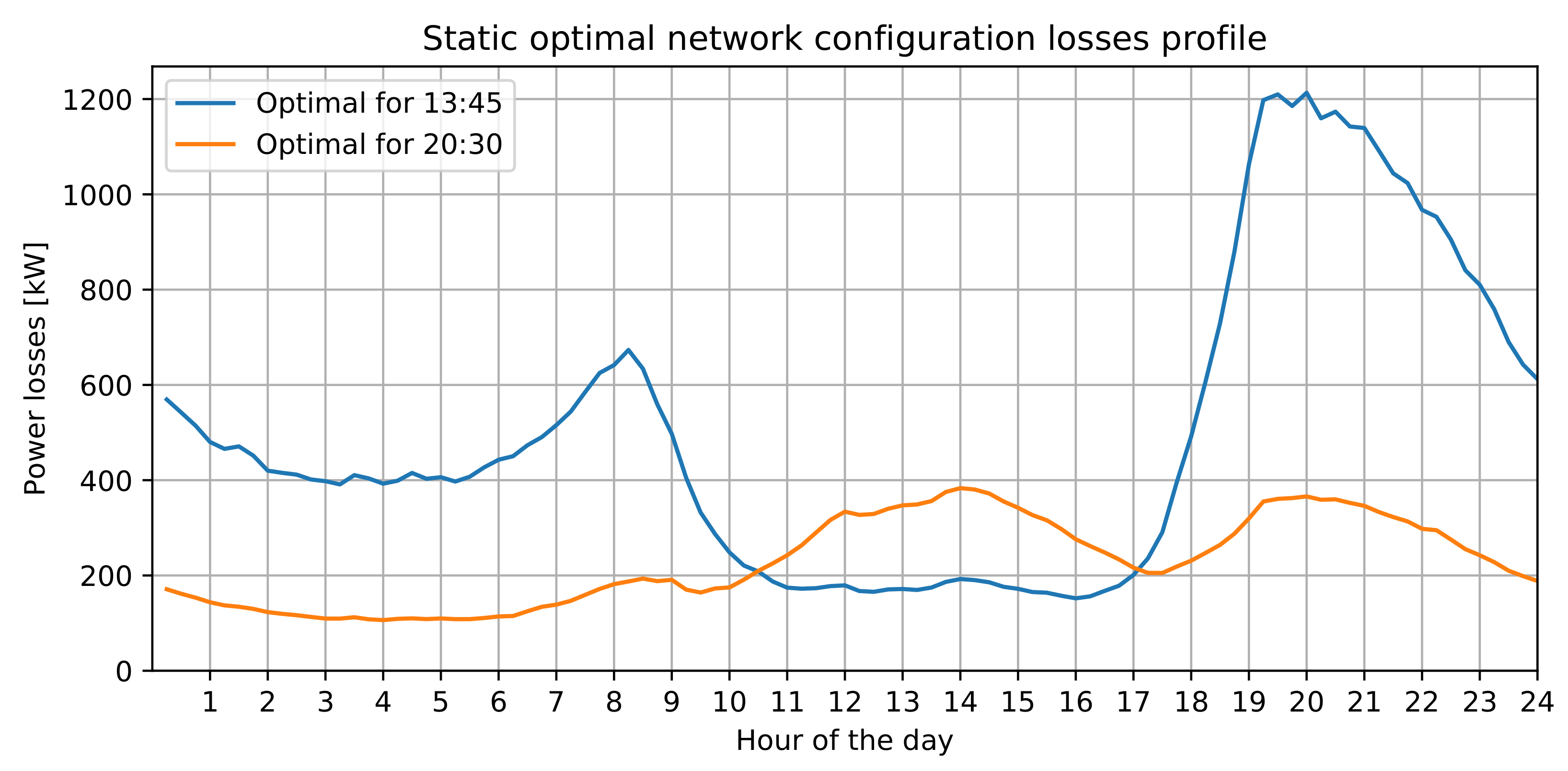
3.3. Static Optimal Network Configuration
3.4. Dynamic Reconfiguration
3.5. Energy Losses Dependence on Reconfiguration Schedule

4. Problem Complexity and New Computation Paradigms
New Perspectives to Handle Problem Complexity
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Network configuration at time t with a linear schedule starting at configuration | |
| Network configuration at time t with a cyclic schedule starting at configuration | |
| G | Network graph |
| Electric current magnitude in operating arc | |
| Time instant of x, | |
| Time instant of the k-element of O in a linear schedule, | |
| Time instant for applying the k-element of O in a cyclic schedule | |
| Time instant for reverting the k-element of O in a cyclic schedule | |
| Optimal time instants for all switching operations in O | |
| L | Total network active power losses |
| m | Maximum number of daily switching operations |
| Normalized PV generation profile | |
| O | Minimum set of switching operations needed to transform the initial configuration into the final configuration |
| Linear reconfiguration schedule defined by the set of switching operations O and their time instants inst | |
| Cyclic reconfiguration schedule defined by the set of switching operations O and their time instants and for applying and reverting the operations, respectively | |
| p | Number of time steps in the discretization of TI |
| PV generation injected on node n (a negative value) at time t | |
| Resistance of arc m | |
| Roof area of the buildings selected for PV generation connected to node n | |
| Net load of node n at time t | |
| Consumers load of node n at time t | |
| Set of all possible spanning trees of G | |
| T | Set of arcs belonging to a spanning tree, |
| Optimal network configuration for time t (a spanning tree) | |
| TI | Time interval considered for an optimization problem |
| x | A network switching operation (a pair of an opening and a closing branch) |
References
- Ilic, M.; Joo, J.; Carvalho, P.M.S.; Ferreira, L.A.F.M.; Almeida, B. Dynamic monitoring and decision systems (DYMONDS) framework for reliable and efficient congestion management in smart distribution grids. In Proceedings of the 2013 IREP Symposium Bulk Power System Dynamics and Control—IX Optimization, Security and Control of the Emerging Power Grid, Rethymno, Greece, 25–30 August 2013; pp. 1–9. [Google Scholar] [CrossRef]
- Lueken, C.; Carvalho, P.M.; Apt, J. Distribution grid reconfiguration reduces power losses and helps integrate renewables. Energy Policy 2012, 48, 260–273, Special Section: Frontiers of Sustainability. [Google Scholar] [CrossRef]
- Nižetić, S.; Papadopoulos, A.; Tina, G.; Rosa-Clot, M. Hybrid energy scenarios for residential applications based on the heat pump split air-conditioning units for operation in the Mediterranean climate conditions. Energy Build. 2017, 140, 110–120. [Google Scholar] [CrossRef]
- Carvalho, P.M.S.; Ferreira, L.A.F.M. Large-Scale Network Optimization with Evolutionary Hybrid Algorithms: Ten Years’ Experience with the Electric Power Distribution Industry. In Computational Intelligence in Expensive Optimization Problems; Springer: Berlin/Heidelberg, Germany, 2010; pp. 325–343. [Google Scholar] [CrossRef]
- Meng, X.; Zhang, L.; Cong, P.; Tang, W.; Zhang, X.; Yang, D. Dynamic reconfiguration of distribution network considering scheduling of DG active power outputs. In Proceedings of the 2014 International Conference on Power System Technology, Chengdu, China, 20–22 October 2014; pp. 1433–1439. [Google Scholar] [CrossRef]
- Capitanescu, F.; Ochoa, L.F.; Margossian, H.; Hatziargyriou, N.D. Assessing the Potential of Network Reconfiguration to Improve Distributed Generation Hosting Capacity in Active Distribution Systems. IEEE Trans. Power Syst. 2015, 30, 346–356. [Google Scholar] [CrossRef]
- Jakus, D.; Čađenović, R.; Vasilj, J.; Sarajčev, P. Optimal Reconfiguration of Distribution Networks Using Hybrid Heuristic-Genetic Algorithm. Energies 2020, 13, 1544. [Google Scholar] [CrossRef]
- Čađenović, R.; Jakus, D.; Sarajčev, P.; Vasilj, J. Optimal Distribution Network Reconfiguration through Integration of Cycle-Break and Genetic Algorithms. Energies 2018, 11, 1278. [Google Scholar] [CrossRef]
- Huang, W.T.; Chen, T.H.; Chen, H.T.; Yang, J.S.; Lian, K.L.; Chang, Y.R.; Lee, Y.D.; Ho, Y.H. A Two-stage Optimal Network Reconfiguration Approach for Minimizing Energy Loss of Distribution Networks Using Particle Swarm Optimization Algorithm. Energies 2015, 8, 13894–13910. [Google Scholar] [CrossRef]
- Kaur, M.; Ghosh, S. Effective Loss Minimization and Allocation of Unbalanced Distribution Network. Energies 2017, 10, 1931. [Google Scholar] [CrossRef]
- Mishra, S.; Das, D.; Paul, S. A comprehensive review on power distribution network reconfiguration. Energy Syst. 2017, 8, 227–284. [Google Scholar] [CrossRef]
- Carvalho, P.; Ferreira, L.; Barruncho, L. Optimization approach to dynamic restoration of distribution systems. Int. J. Electr. Power Energy Syst. 2007, 29, 222–229. [Google Scholar] [CrossRef]
- Xu, L.; Cheng, R.; He, Z.; Xiao, J.; Luo, H. Dynamic Reconfiguration of Distribution Network Containing Distributed Generation. In Proceedings of the 2016 9th International Symposium on Computational Intelligence and Design (ISCID), Hangzhou, China, 10–11 December 2016; Volume 1, pp. 3–7. [Google Scholar] [CrossRef]
- Guimarães, I.G.; Bernardon, D.P.; Garcia, V.J.; Schmitz, M.; Pfitscher, L.L. A decomposition heuristic algorithm for dynamic reconfiguration after contingency situations in distribution systems considering island operations. Electr. Power Syst. Res. 2020, 2020, 106969. [Google Scholar] [CrossRef]
- Košt’álová, A.; Carvalho, P.M. Towards self-healing in distribution networks operation: Bipartite graph modelling for automated switching. Electr. Power Syst. Res. 2011, 81, 51–56. [Google Scholar] [CrossRef]
- Łukaszewski, A.; Nogal, Ł.; Robak, S. Weight Calculation Alternative Methods in Prime’s Algorithm Dedicated for Power System Restoration Strategies. Energies 2020, 13, 6063. [Google Scholar] [CrossRef]
- QGIS Project. Available online: https://qgis.org (accessed on 30 December 2020).
- OpenStreetMap. Available online: https://www.openstreetmap.org (accessed on 30 December 2020).
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information: 10th Anniversary Edition; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar] [CrossRef]
- Biswas, R.; Jiang, Z.; Kechezhi, K.; Knysh, S.; Mandrà, S.; O’Gorman, B.; Perdomo-Ortiz, A.; Petukhov, A.; Realpe-Gómez, J.; Rieffel, E.; et al. A NASA perspective on quantum computing: Opportunities and challenges. Parallel Comput. 2017, 64, 81–98, High-End Computing for Next-Generation Scientific Discovery. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, S.T.; Choi, S.; Pichler, H.; Lukin, M.D. Quantum Approximate Optimization Algorithm: Performance, Mechanism, and Implementation on Near-Term Devices. Phys. Rev. X 2020, 10, 021067. [Google Scholar] [CrossRef]
- Preskill, J. Quantum Computing in the NISQ era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
- D-Wave Advantage™ Quantum Annealer. Available online: https://www.dwavesys.com/d-wave-two%E2%84%A2-system (accessed on 26 January 2021).
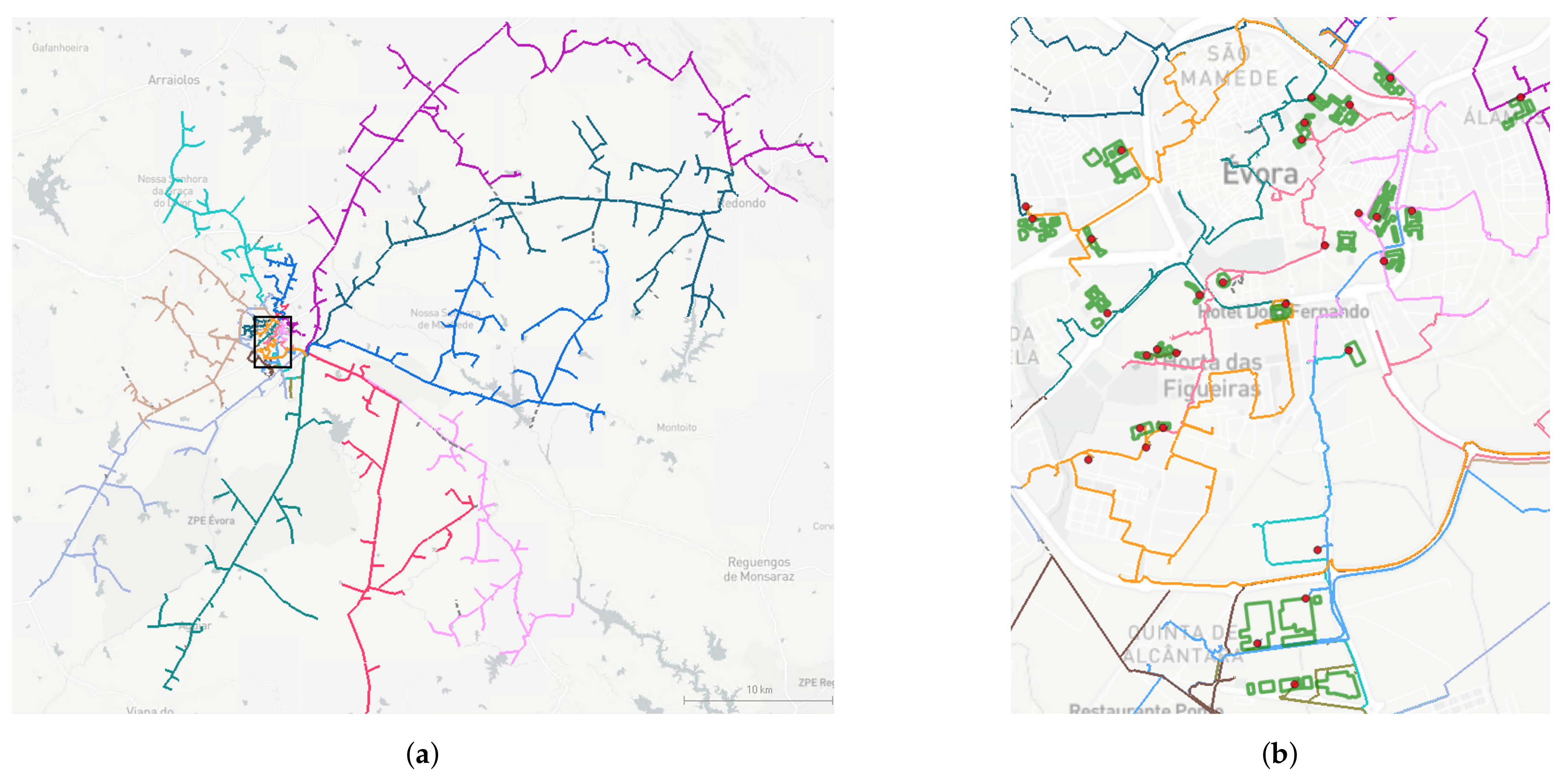
| Feeder Circuit | PV Alone Peak | Load Alone Peak | Net Load + PV Peak | ||
|---|---|---|---|---|---|
| kW | kW | Time | kW | Time | |
| 1 | −1014 | 2952 | 20:30 | same as load alone | |
| 2 | −2310 | 3071 | 19:15 | same as load alone | |
| 3 | −4460 | 3693 | 21:00 | same as load alone | |
| 4 | −986 | 2457 | 20:45 | same as load alone | |
| 5 | −5065 | 2089 | 12:00 | −3099 | 13:45 |
| 6 | −1134 | 1875 | 20:15 | same as load alone | |
| 7 | −9997 | 3406 | 01:00 | −6682 | 13:45 |
| 8 | −4660 | 2530 | 20:30 | −2676 | 13:30 |
| 9 | −803 | 2410 | 19:45 | same as load alone | |
| 10 | −928 | 1920 | 09:15 | 1804 | 20:00 |
| 11 | −4908 | 1889 | 19:30 | −3217 | 13:45 |
| Reconfiguration Schedule | Energy Losses Reduction [%] |
|---|---|
| Base PV peak optimal Base | 16.33 |
| Optimal schedule with switching operations 1,2,3 | 12.54 |
| Base Base + 23 Base + 123 Base + 23 Base | 12.52 |
| Base Base + 3 Base + 123 Base + 3 Base | 12.18 |
| Base Base + 123 Base | 12.02 |
| Problem | Time Complexity | |
|---|---|---|
| Number of Operations | Operation | |
| Unrestricted optimal reconfiguration | p | optimization |
| Optimal static configuration | 1 | optimization |
| Time-bounded linear dynamic reconfiguration | power-flow | |
| Time-unbounded cyclic dynamic reconfiguration | power-flow | |
| Open cyclic dynamic reconfiguration | optimization | |
| Switching Operations | Time Steps | Time Complexity | |
|---|---|---|---|
| m | p | Optimizations | Computation Time |
| 1 | 96 | 4561 | 13 h |
| 1 | 48 | 1129 | 3 h |
| 1 | 24 | 277 | 46 min |
| 1 | 12 | 67 | 11 min |
| 2 | 96 | 20.8 M | 6 years |
| 2 | 48 | 1.3 M | 5 months |
| 2 | 24 | 76,729 | 9 days |
| 2 | 12 | 4489 | 12 h |
| 3 | 12 | 300,763 | 35 days |
| 3 | 6 | 4096 | 11 h |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silva, F.F.C.; Carvalho, P.M.S.; Ferreira, L.A.F.M. Improving PV Resilience by Dynamic Reconfiguration in Distribution Grids: Problem Complexity and Computation Requirements. Energies 2021, 14, 830. https://doi.org/10.3390/en14040830
Silva FFC, Carvalho PMS, Ferreira LAFM. Improving PV Resilience by Dynamic Reconfiguration in Distribution Grids: Problem Complexity and Computation Requirements. Energies. 2021; 14(4):830. https://doi.org/10.3390/en14040830
Chicago/Turabian StyleSilva, Filipe F. C., Pedro M. S. Carvalho, and Luís A. F. M. Ferreira. 2021. "Improving PV Resilience by Dynamic Reconfiguration in Distribution Grids: Problem Complexity and Computation Requirements" Energies 14, no. 4: 830. https://doi.org/10.3390/en14040830
APA StyleSilva, F. F. C., Carvalho, P. M. S., & Ferreira, L. A. F. M. (2021). Improving PV Resilience by Dynamic Reconfiguration in Distribution Grids: Problem Complexity and Computation Requirements. Energies, 14(4), 830. https://doi.org/10.3390/en14040830







