Day-Ahead MPC Energy Management System for an Island Wind/Storage Hybrid Power Plant
Abstract
1. Introduction
1.1. Literature Review
1.2. Contribution
- A comprehensive island microgrid multi-objective energy management problem is established, taking into account the day-ahead dispatch schedule commitment.
- The EMS proposed is able to manage the battery’s charge/discharge cycles and state-of-charge (SoC) efficiently. This is possible due to the development of a Battery Energy Storage System (BESS) model to find optimal solutions that bring the system’s predicted output close to a trajectory of defined future power injections.
- Through a model predictive control strategy, the EMS proposed allows the BESS to be optimized and, thereby, the power injection into the utility grid, while considering the battery’s lifespan.
- An evaluation of the proposed Multi-objective EMS by analyzing and comparing the simulation results from several study cases.
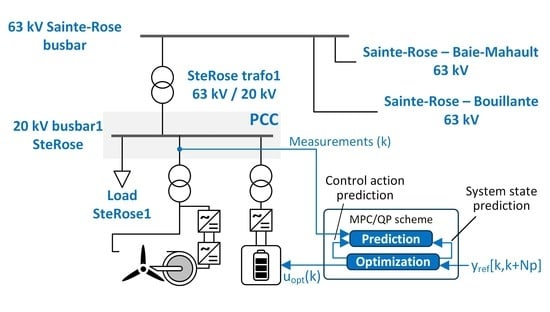
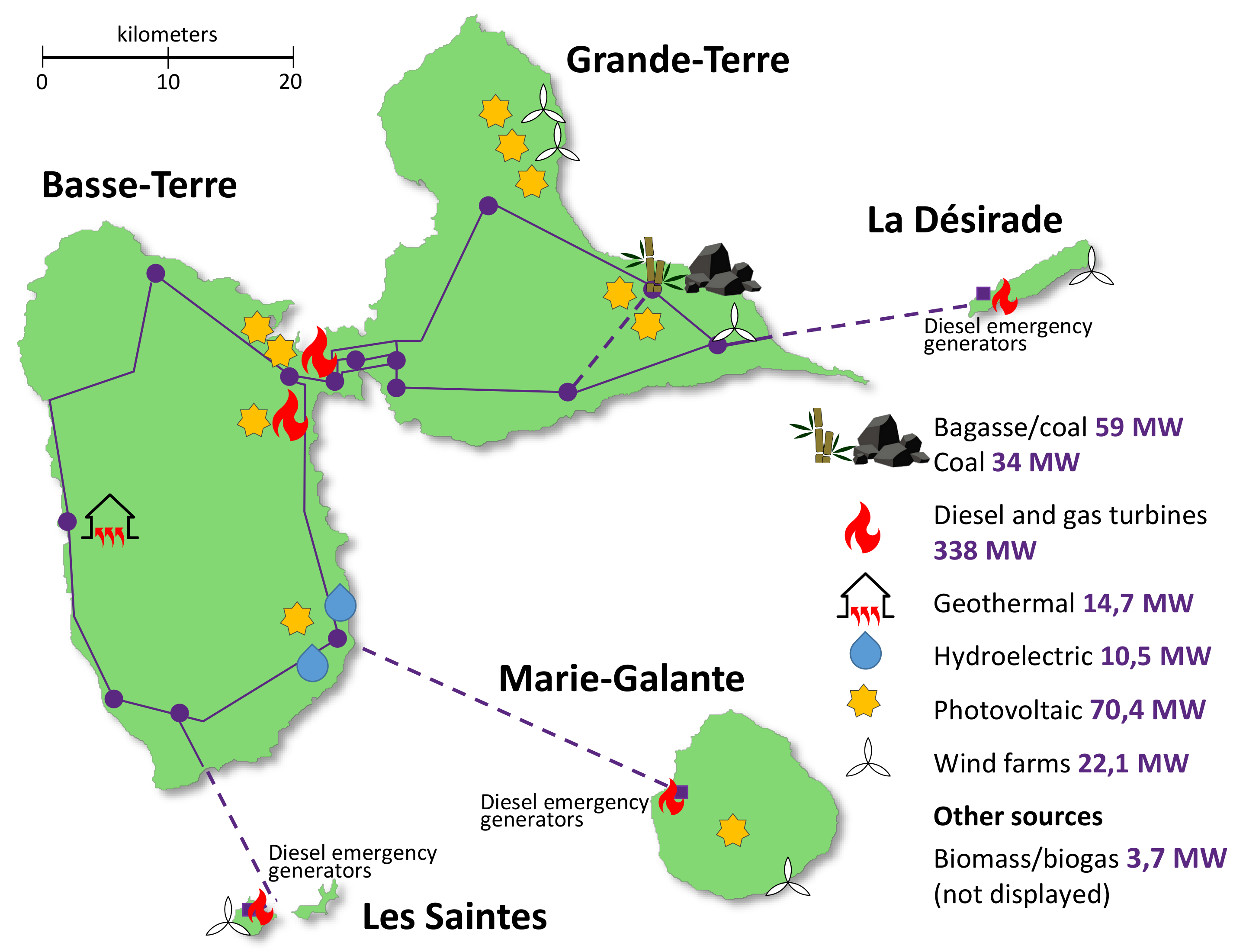
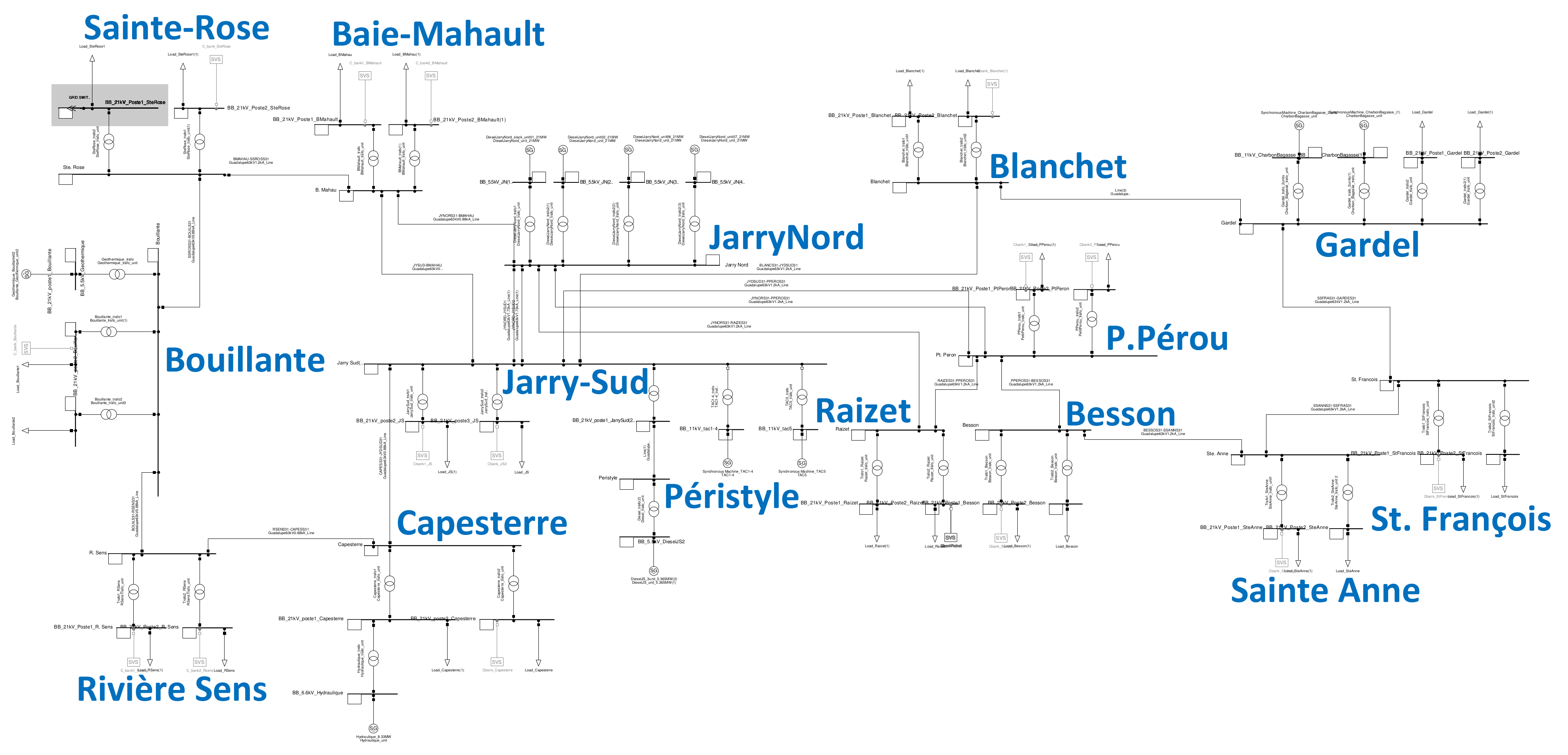
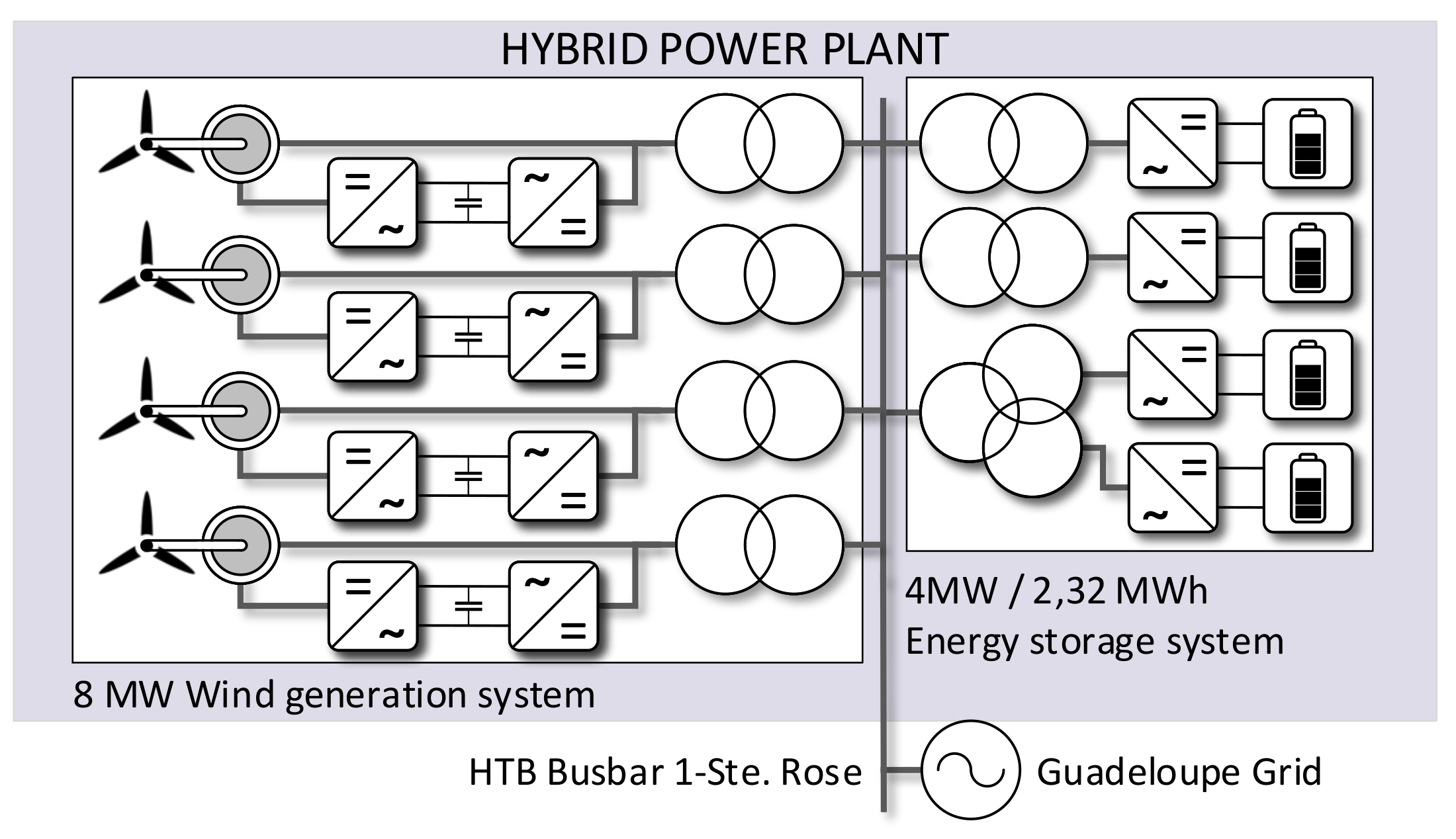
2. Island Grid-Connected Hybrid Power Plant
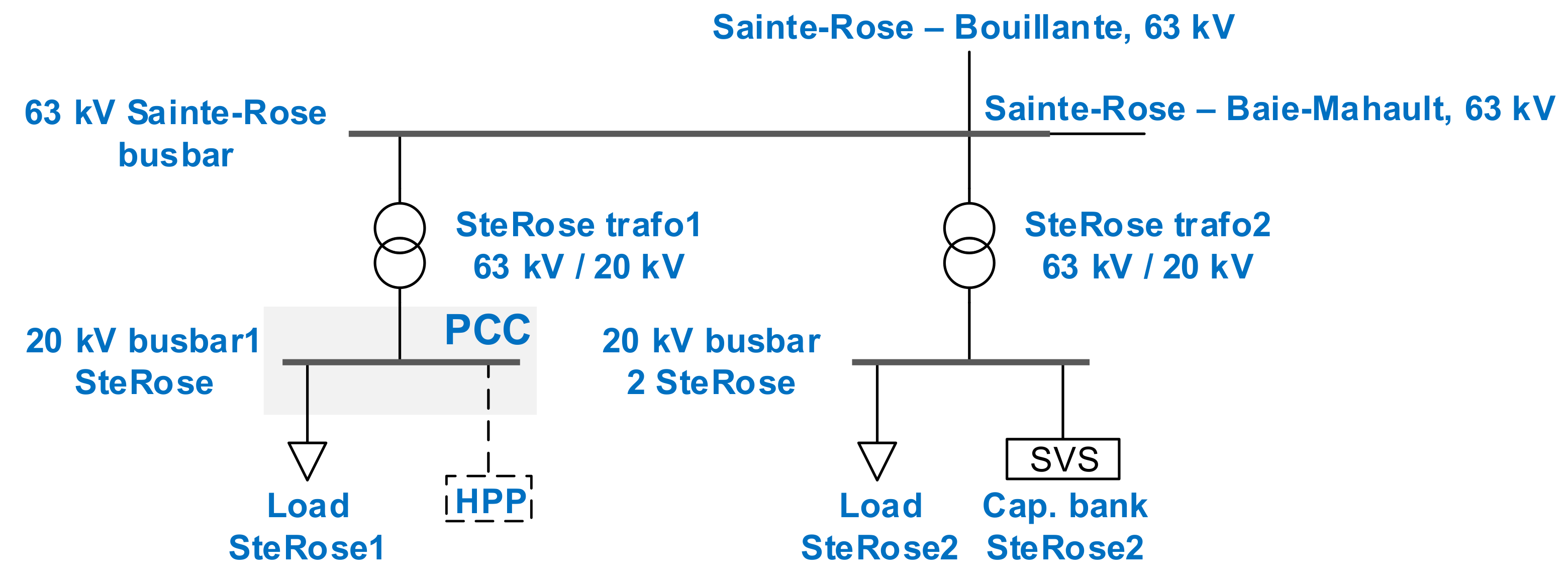
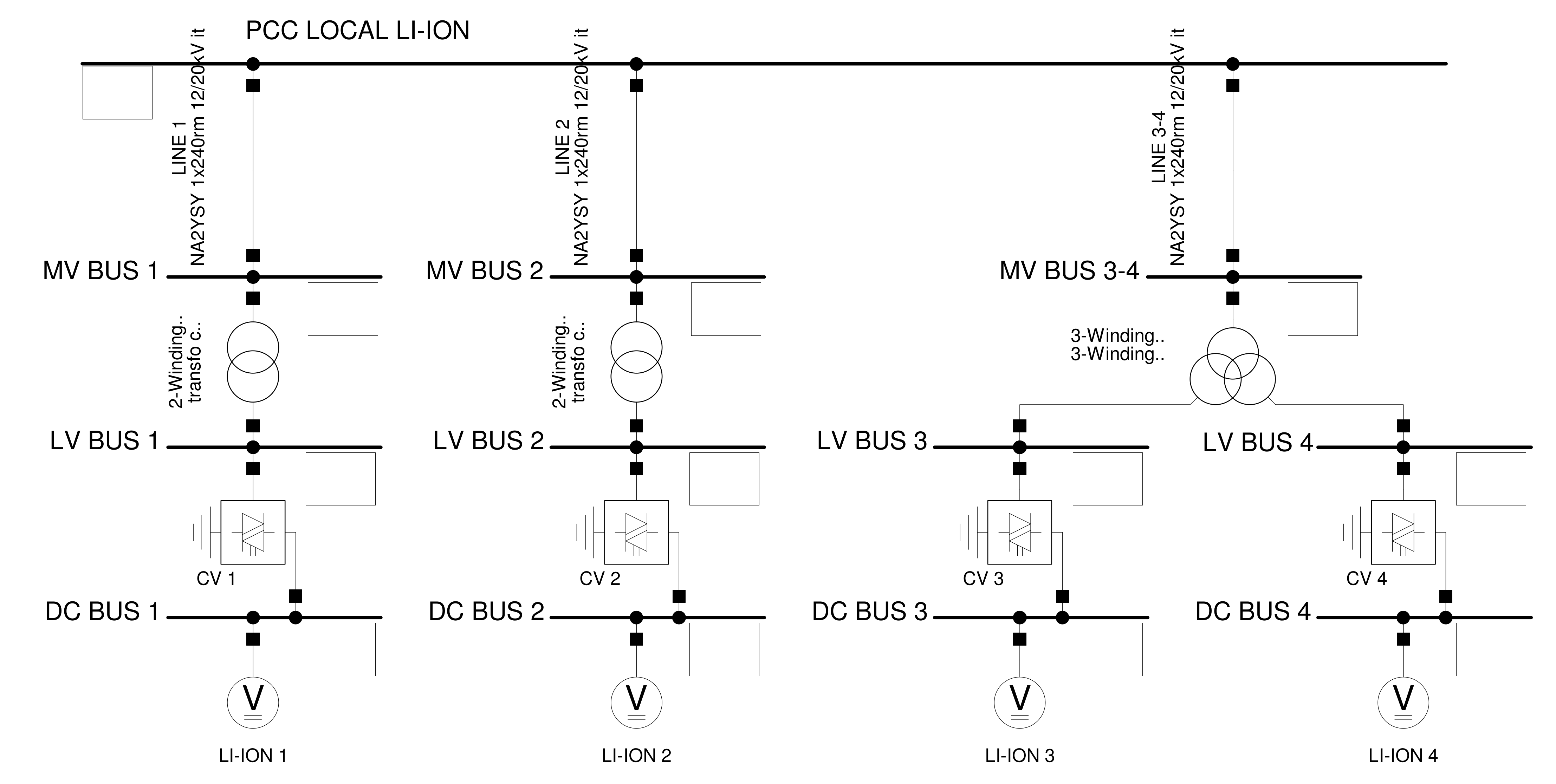
Guadeloupe’s Electrical Grid Model
3. Formulation of the Problem
3.1. Power Dispatch Optimization
3.1.1. Objectives
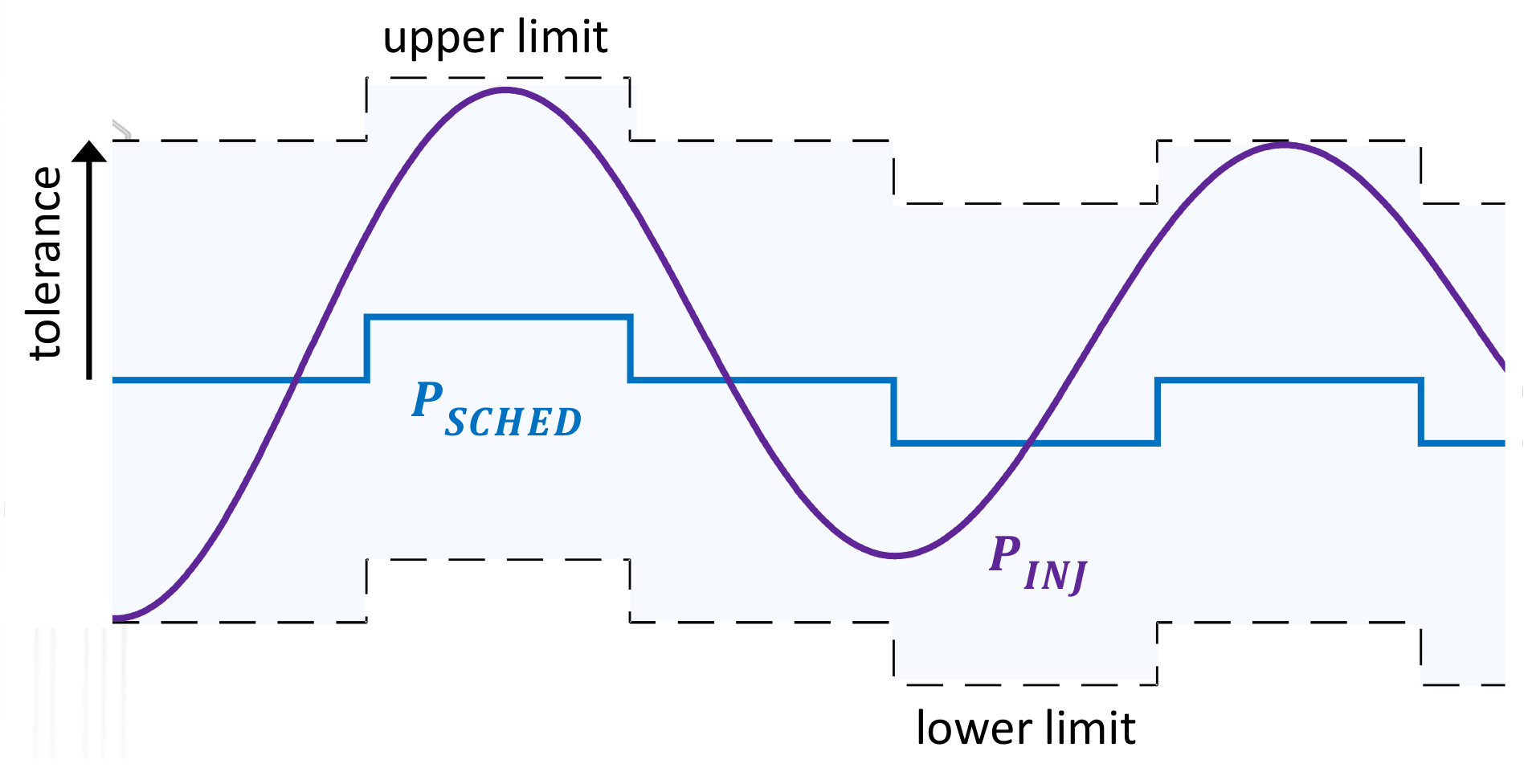
- Power injection band respect: a tolerance region (injection band) is established on the basis of the injection schedule. This objective consists of minimizing the error difference between the power injected () and scheduled (), which is similar to attracting towards the center of the tolerance region.
- Favoring the BESS availability: this objective consists of seeking to reduce the occurrence of BESS unavailable conditions, so, during strong wind periods, it can be used to store power, and it can be discharged during weak wind periods.
3.1.2. Constraints
- Maximal power injection: an upper bound is defined for to reduce the overtakes of the band’s threshold.
- Rate of change of power injected: the speed of change of is limited in order to avoid abrupt changes in the power transferred towards the grid.
- State-of-charge: the BESS must be operated in accordance with the recommendations of the manufacturer in terms of depth-of-discharge and charging rates in order to optimize its lifespan.
- BESS maximum charge/discharge current: Considering the manufacturer’s recommendations, the BESS maximum continuous charge and discharge currents should be respected.
4. Mathematical Modeling of the HPP Subsystems
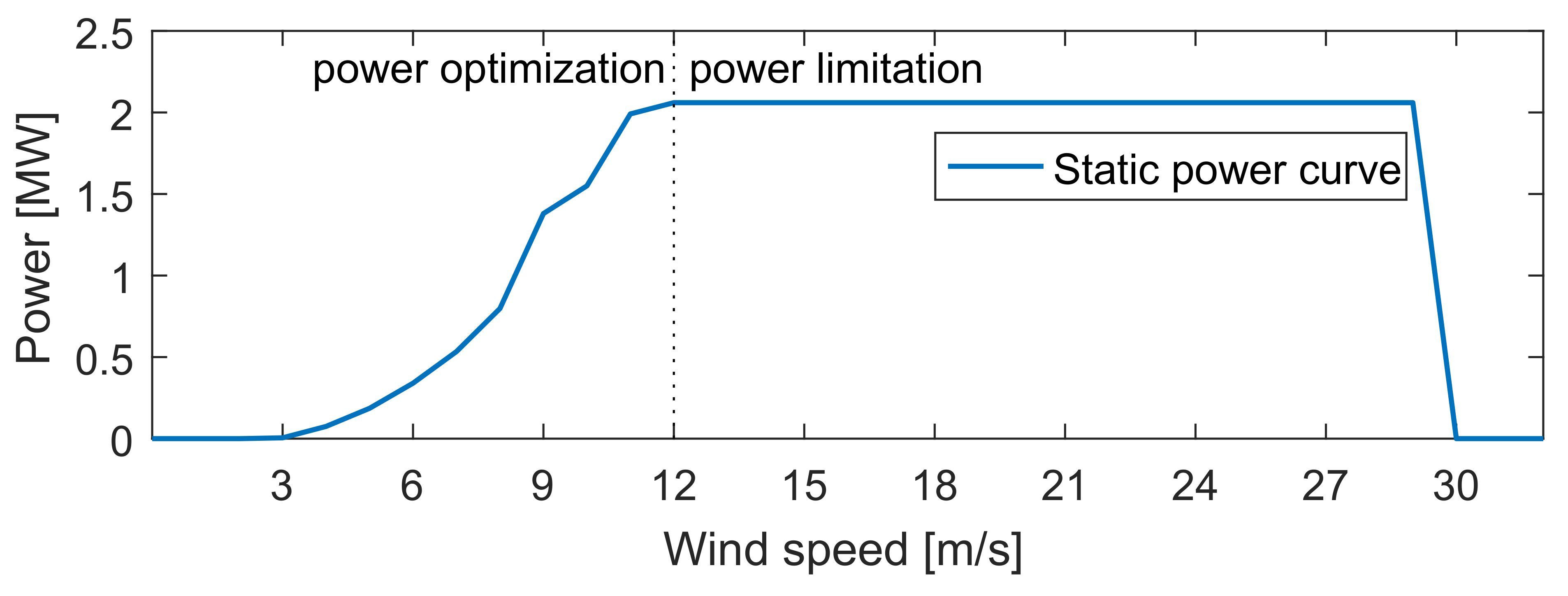
4.1. Wind Generation System Modeling and Validation
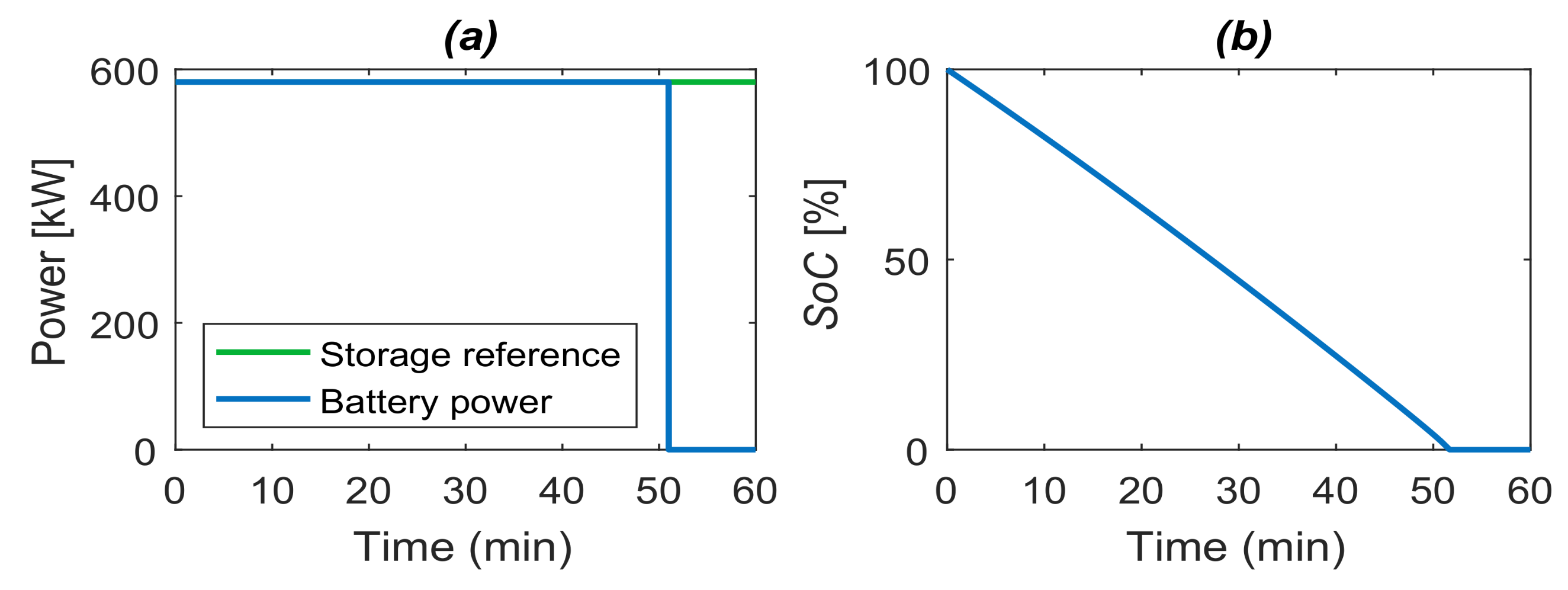
4.2. Li-ION Battery Modeling and Validation
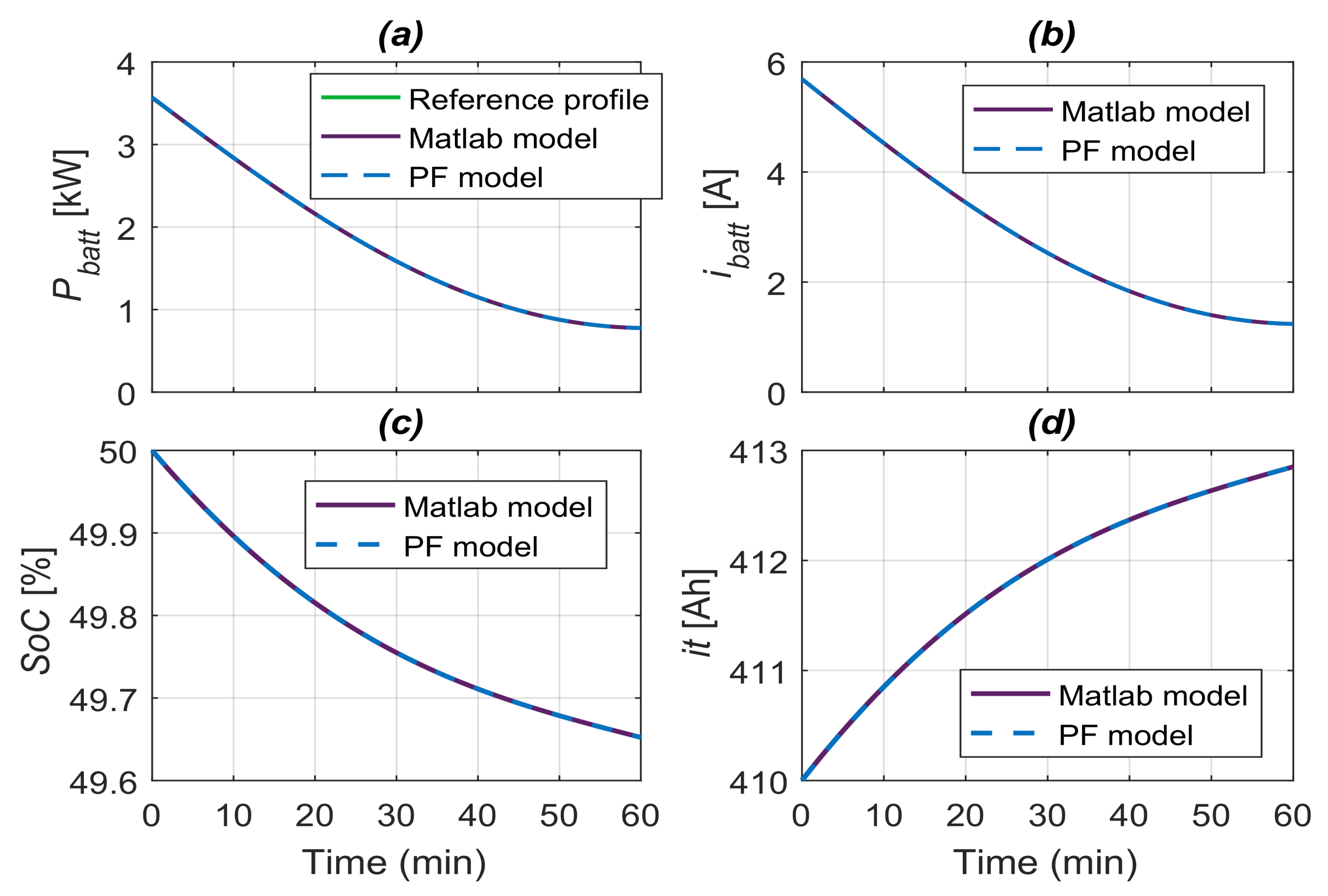
PowerFactory Model Validation
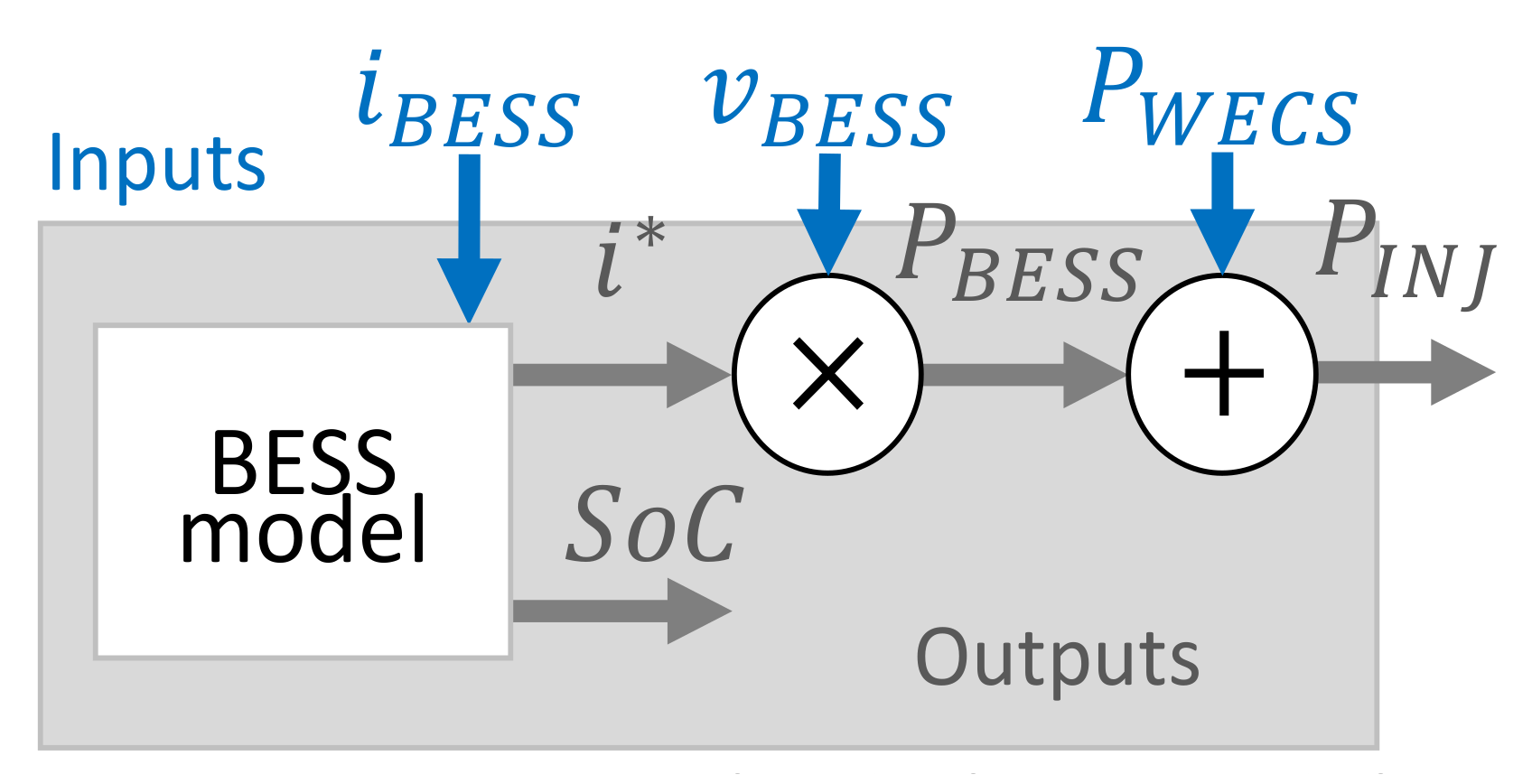
4.3. Storage System model for the MPC Strategy
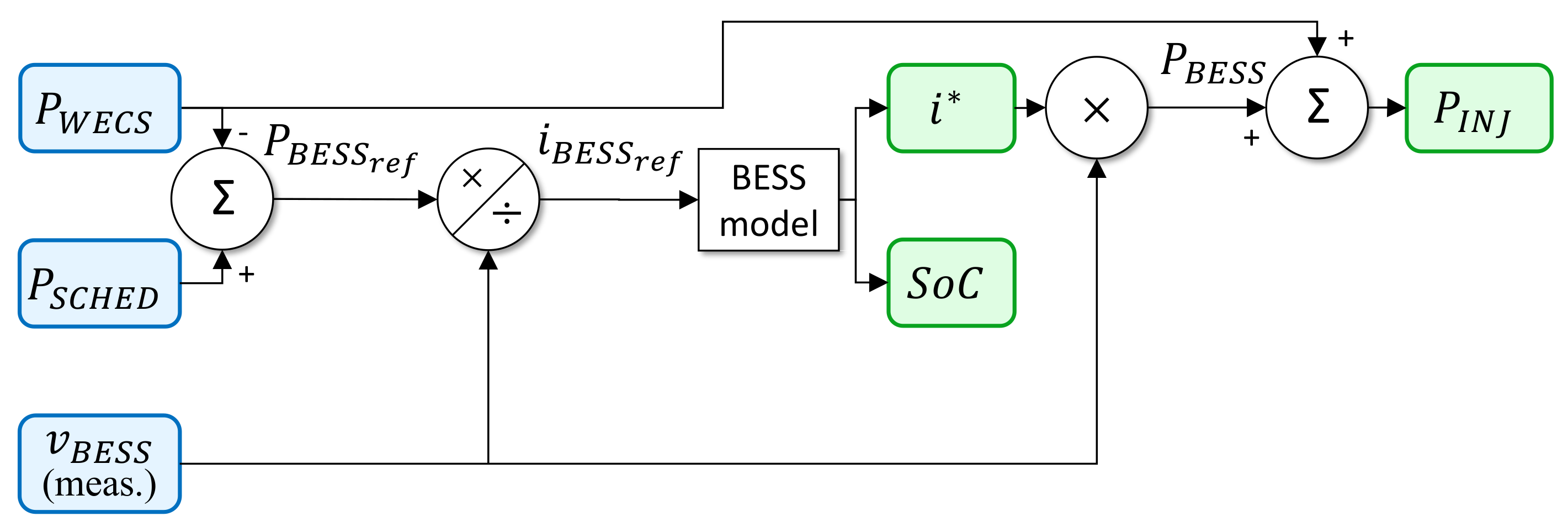
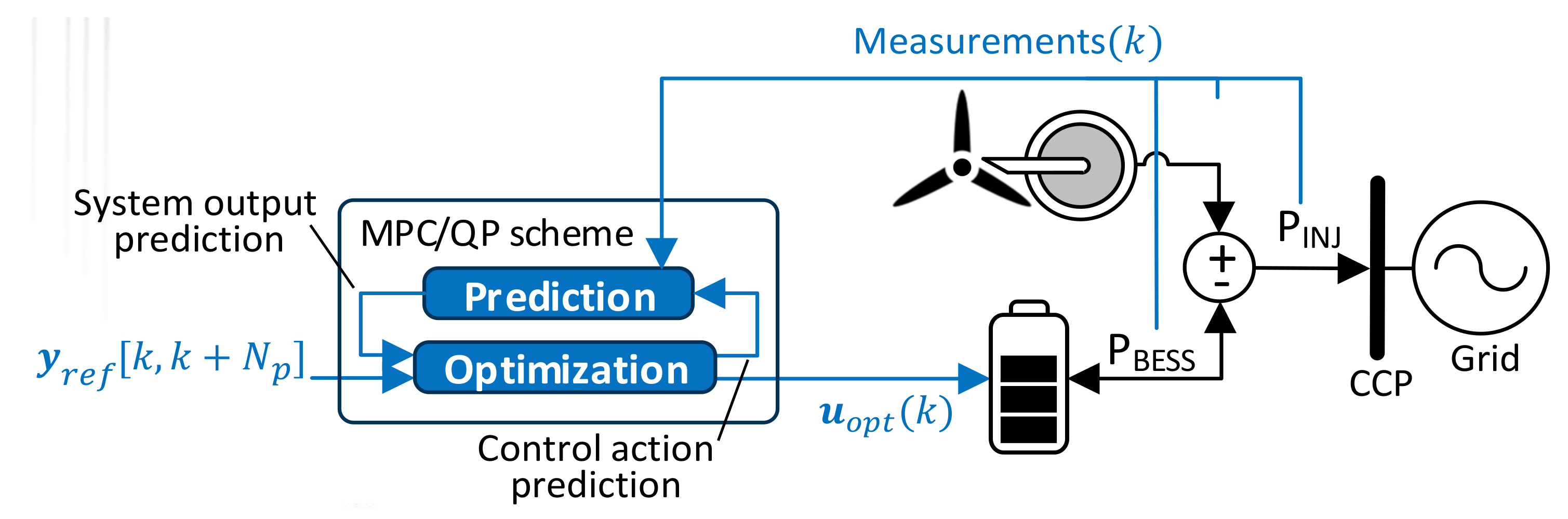
5. MPC Control Strategy
5.1. Energy Management with Respect to a Day-Ahead Power Injection Planning
5.1.1. Operational Objectives
- Forecasts and power injection band: the plant operation is based on 24 h of wind speed forecasts for the period 0:00–23:59 h for day D+1 (i.e., the next day, when the actual production is taking place). A scheduling algorithm represents the forecasted injection in the form of a half-hourly stepped profile.Such a profile is taken here as the day-ahead power injection schedule (). The injection band represented in Figure 17 is built from and established taking into consideration the fact that the energy storage system must be controlled so that the 30-min duration scheduled injection steps can be met. During the first year of operating the HPP, the BESS should allow the respect a tolerance region of of the installed power , above and below the scheduled injection. The band will be narrowed down to the second year and to from the third year.In this paper, the distance between and the bounds of the band is called injection tolerance and is set at of the installed capacity of the wind farm, , as required in the first year of the project.
- Favoring the BESS availability: A reference is defined at a . Seeking to keep the stored power at a half of BESS capacity means finding the right trade-off between charging or discharging the BESS, avoiding if possible the boundaries.
- Plant revenues and penalty system: Plant revenues are determined via a penalty system. Power injections with excursions of 60 consecutive seconds outside the limits are penalized with non-payment of the power supplied to the grid for the next 10 min. The plant revenue can then be calculated considering the energy selling price () as:where
5.1.2. Operational and Technical Constraints
- Maximal power injection: is constrained by a limit equal to the band upper boundary. With this, when searching for optimal solutions, the algorithm will not consider possible solutions that drive the power injection above the mentioned boundary. In line with this, , the upper limit for the power transfer, is computed according to the evolution of the commitment profile, as follows:with , the term gives . Conversely, the minimum injection occurs when the WTs are not generating power and the BESS is not delivering power. To avoid penalties, rather than setting constraints on both the upper and lower injection band limits, the constraint is placed on the band ceiling . This way, instead of allowing injections greater than the upper limit, extra available power can be used to charge the storage system. This constraint was defined through the state variable , which is a controlled output.
- Rate of change of power injected: according to the contractual specifications of the HPP operation, the speed at which varies (in MW/s) must be limited so that: (1), the time it takes to go from 0 to is in the range (5–30 min), and (2), the time it takes to go from to 0 is in the range (1–10 min). However, one single range of (1–5 min) is considered for both, positive and negative power injection variations. Moreover, as the constrained variable is the controller model input, , the limits are expressed in terms of current:where the use of the absolute value indicates that the equation is valid for both going from to 0, and vice versa. As noted, the lower limit is associated with the larger time in the range (5 min or 300 s), whereas the upper limit is related to the case where the passing takes place in 1 min (60 s). The reason for this is a shorter passing time implies a steeper slope, or a bigger rate of change limit. Making the limits for the rate of change of , in inequality form, gives:which are constraints for upward and downward steps of . In other words, these constraints limit the speed of change of to avoid abrupt changes in the power transferred towards the grid.
- State-of-charge: the BESS must be operated with depth-of-discharge maximal in accordance with the manufacturer’s recommendation. In addition, the linear model is valid if the is within and Hence, the is limited to the aforementioned range.
- BESS maximum charge/discharge currents: Considering the sign convention defined for BESS, the maximum continuous charge and discharge currents are, respectively, 3280 A and A.
5.2. Prediction and Optimization Strategy
5.3. Economic Optimization of the HPP Operation with Respect to a 24-H Commitment Profile
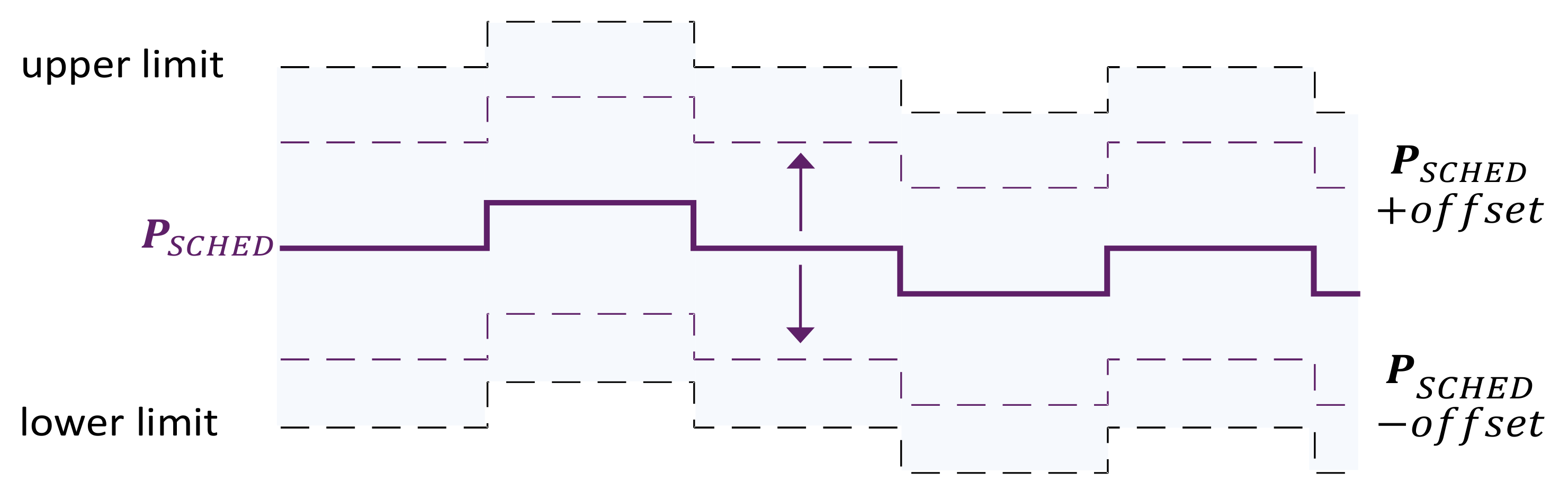
- Weights of the optimization objectives: Settings that can be modified to influence the power injection are the relative weights of the optimization objectives and the commitment , through the addition of a vertical offset, as represented in Figure 19. Such an offset that can be positive or negative.
- Other strategies may focus on maximizing of the energy stored in ESS or on keeping the control actions to a minimum, while the commitment failures are minimized.
5.4. Energy Management System KPIs
- Commitment Failure (CF %): The optimization problem consists of deciding on how the storage system is used (i.e., which part of the production is used to charge the BESS or how much power is to be discharged) as the wind turbines output instantly varies, to inject power into the island grid respecting a committed generation schedule. Then, the commitment profile is generated based on day-ahead forecast data. In addition, the disrespecting of the accepted injection region above and below the commitment may lead to commitment failures (triggered by injection band overtakes lasting 60 s) that are associated with economic penalties. Then, the commitment failures are calculated as the percentage of the time during which the penalty condition was active, or:
- Curtailment Power (): In some cases, losses can be presented due to a power overproduction by the wind turbines while the BESS is fully charged. This KPI allows these losses to be monitored and the effectiveness of the EMS proposed to be tested, which handles the way in which battery’s cycles respect the day-ahead commitment at the same time as minimizing these losses. To obtain this KPI, whenever , the lost power due to curtailment is calculated as:By considering the dissipated power, Equation (5) could be rewritten as:where the curtailed power is considered lost power. Then, the percentage of the power produced that was curtailed is obtained from:
- Not Supplied Power:Whenever a commitment failure has been triggered, the power not billed is calculated as:This means that the total remunerated injection is:The energy injected ( in MWh) is computed from the injected power by considering the time. Finally, the non-remunerated production (due to commitment failures) as a percentage is obtained by:
- Counting Battery Cycles: the lifetime of a battery is influenced by several factors, including the number of charge-discharge cycles. For this reason, correctly estimating battery deterioration is needed to establish an adequate operating region to maximize their lifetime, as well as to obtain the highest returns on investment. Thus, in order to keep track of the storage system’s use, partial charging and discharging cycles are considered as follows:where and are percentages (%) obtained from adding all the positive and negative changes in the , respectively. Those changes () are given by:Then, the storage system cycles (at DoD) are computed as:meaning that, when each and is equal to , are incremented by one cycle. The method used to count the cycles here is based on the approach introduced in Reference [50].
5.5. Rule-Based Strategy Operation
- If and , the targeted injection is the commitment (), and the power excess is stored.
- If ) but , the ESS is not charged or discharged.
6. Results
- Electricity tariff is decreased for a certain time (before and/or after the energy supply error).
- No purchase of electricity for a certain time (before and/or after the energy supply error).
- Obligation to disconnect the HPP after a certain number of errors noted.
- Re-invoicing by the distribution network manager and/or transport of the costs of mobilizing other means of production to compensate for the lack of energy supply compared to the forecast.
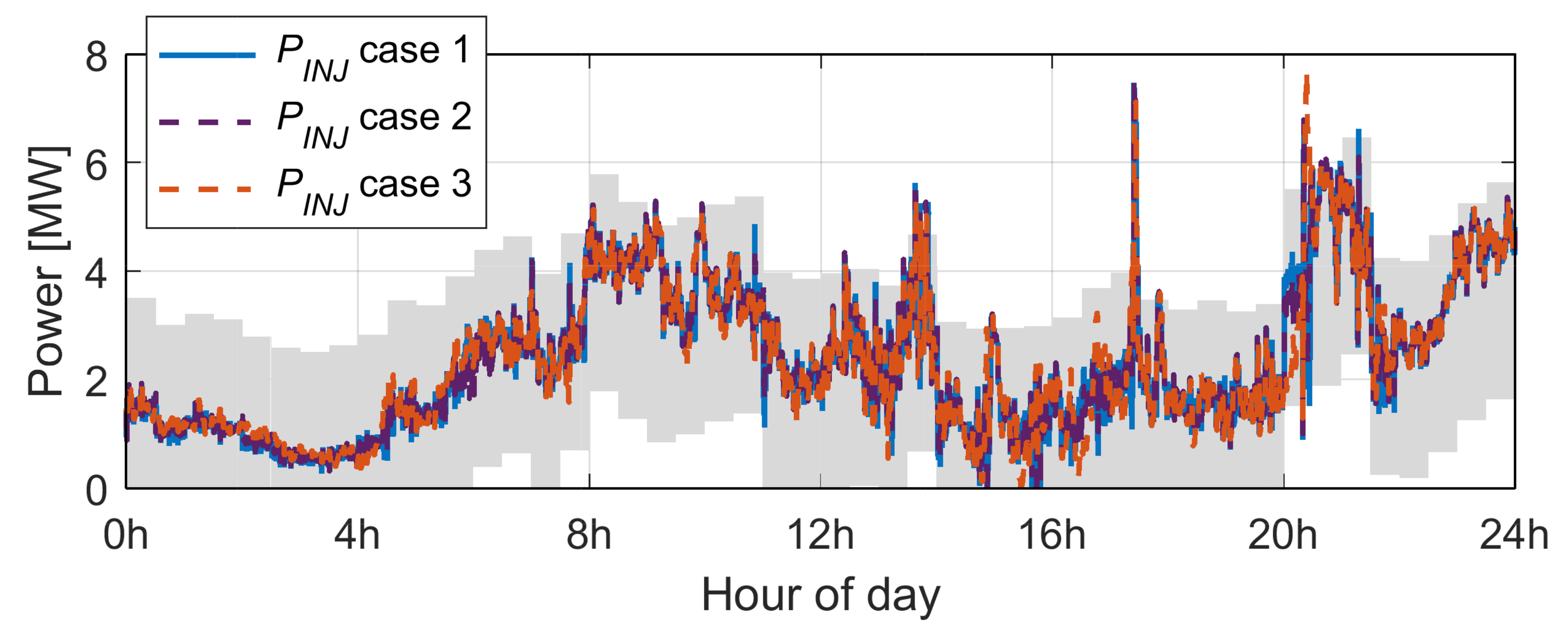
- weak wind zones (displayed in Figure 22 in violet), in which the average wind speeds and power productions are 4.8 m/s and 0.8 MW;
- medium wind zones (in blue), with average speeds of 7.2 m/s and average productions of MW; and
- strong wind zones (in gray), with average speeds of 9.2 m/s and average productions of MW.
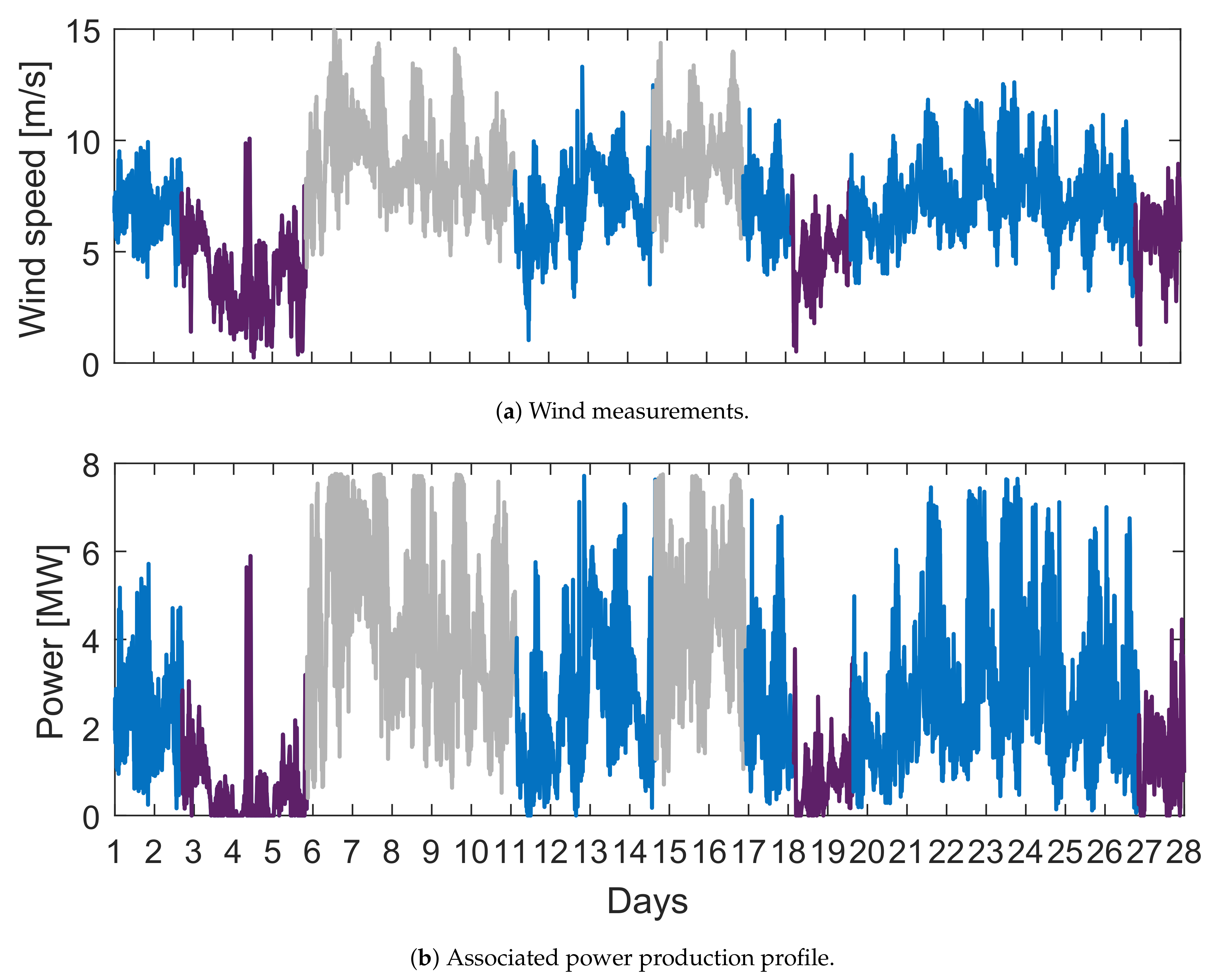
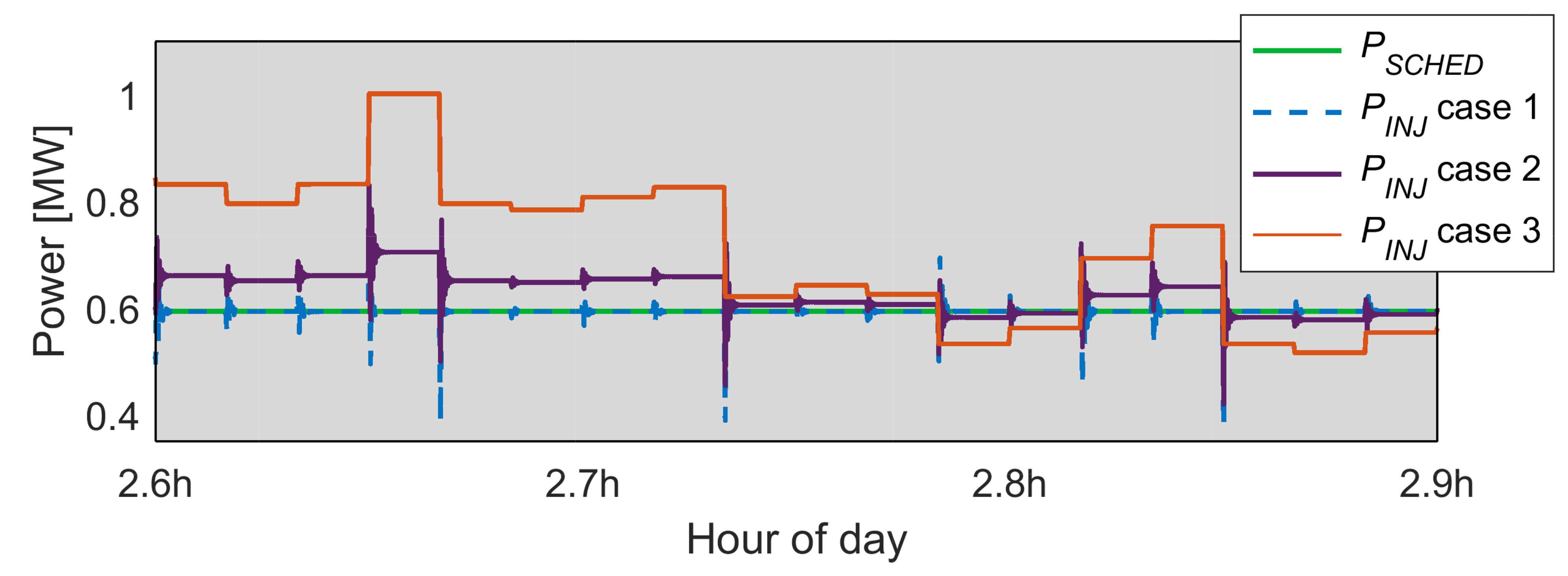
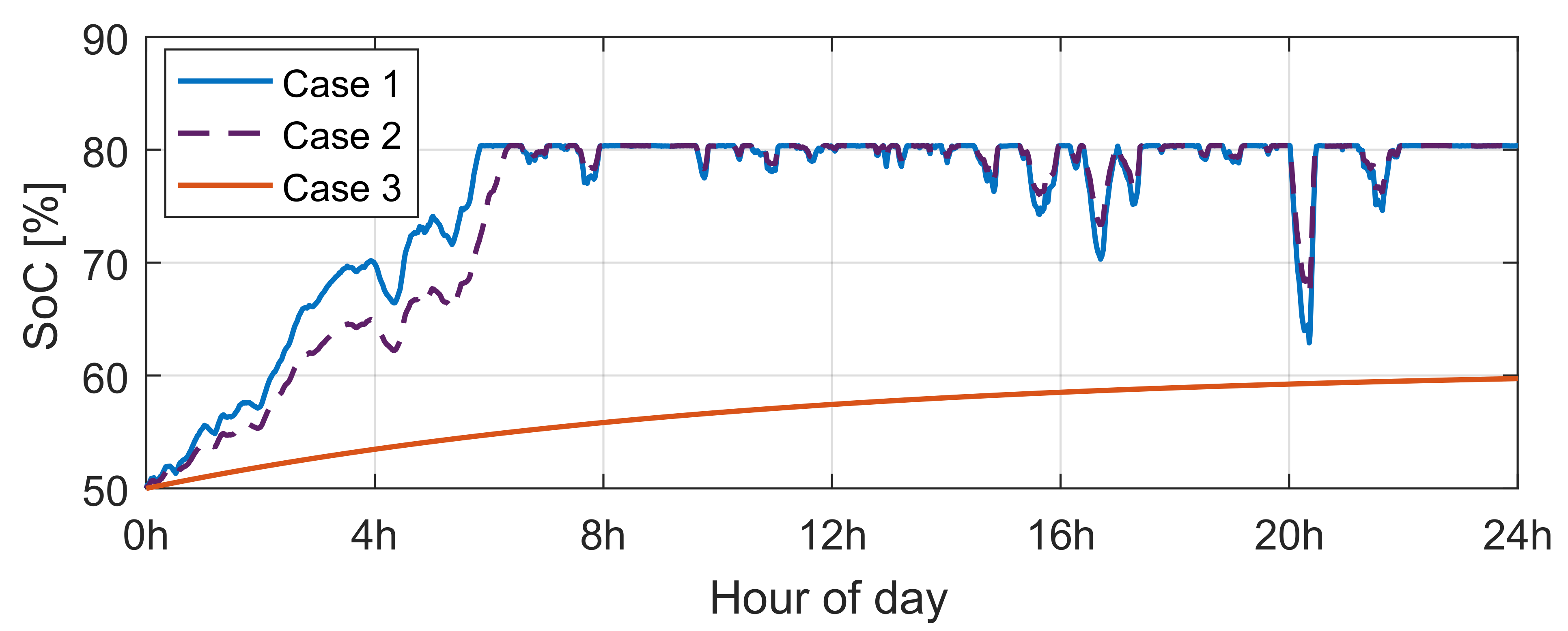
6.1. Scenario 1: Production Is Greater Than Expected
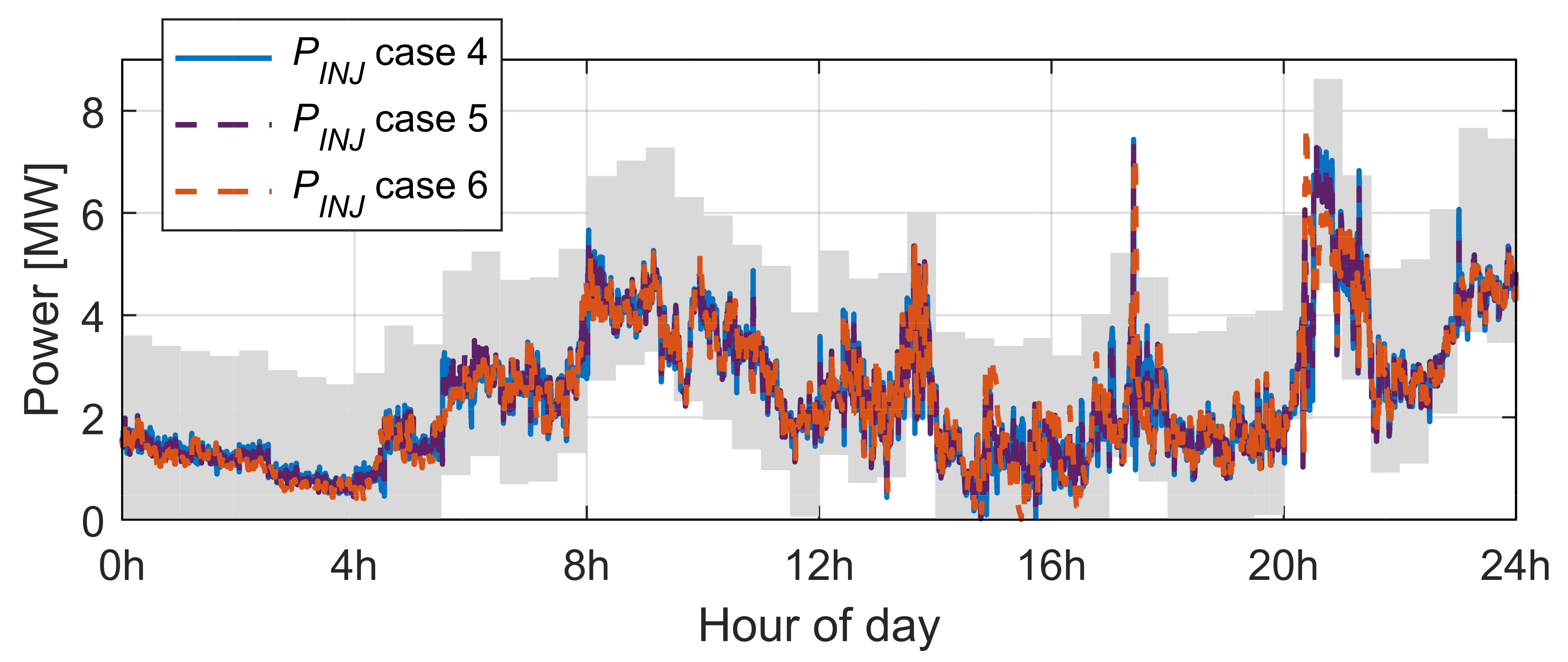
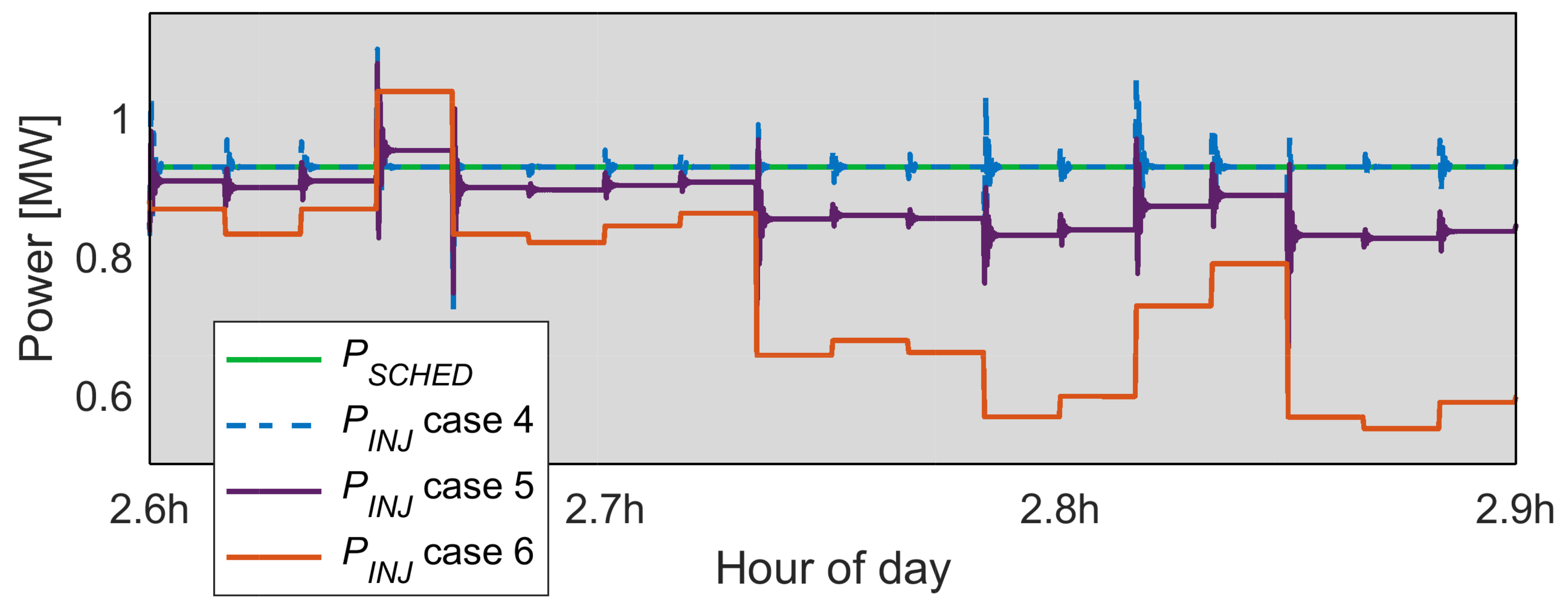
6.2. Scenario 2: Production Lower Than Commitment
- case 4, where the greatest weight was assigned to the -related objective () to prioritize minimizing the power injection’s tracking error,
- case 5, the same importance is given to the weight of both objectives, and
- case 6, the greatest weight was attributed to the minimizing the tracking error.
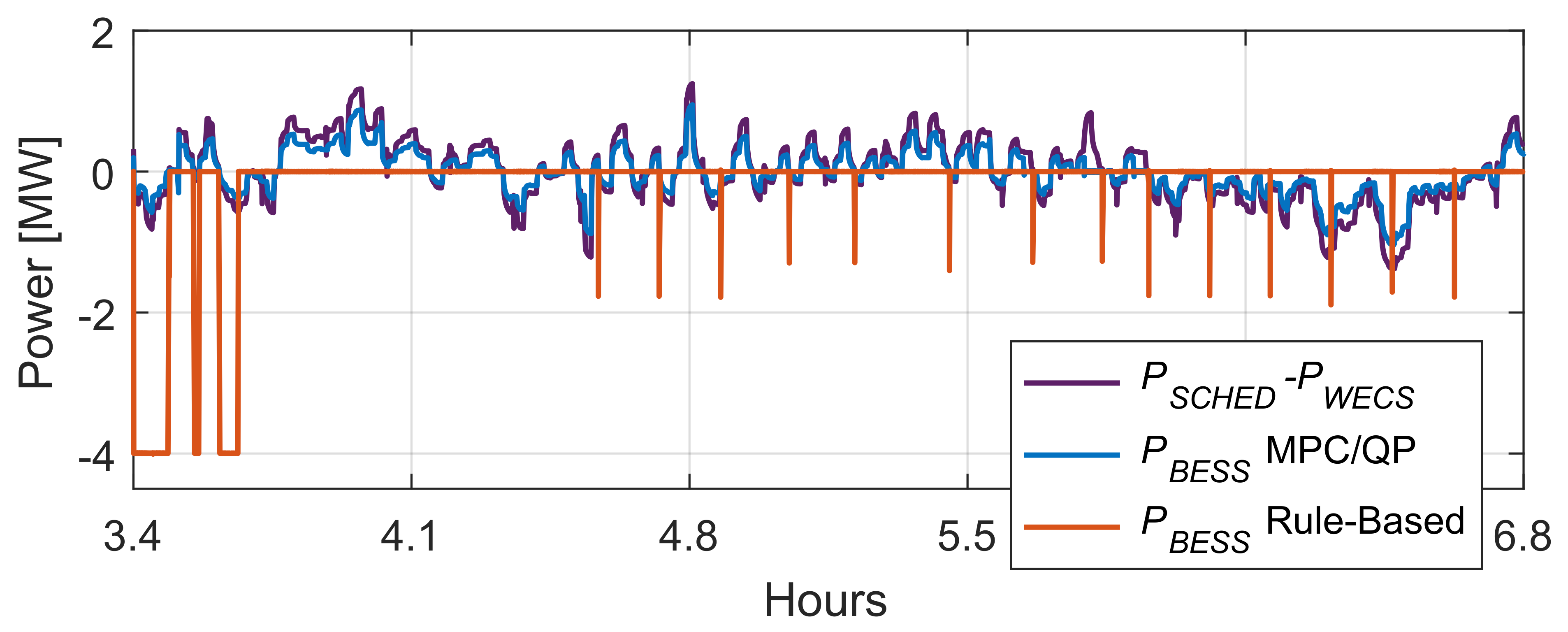
6.3. Comparison with a Rule-Based Strategy
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| EMS | Energy Management System |
| HPP | Hybrid Power Plant |
| MPC | Model Predictive Control |
| WT | Wind turbines |
| BESS | Battery Energy Storage System |
| RES | Renewable Energy Sources |
| EDF | Electricité de France |
| SoC | State-of-charge |
| DFIG | Doubly Fed Induction Generators |
| WECS | Wind Energy Conversion System |
| MILP | Mixed-Integer Linear Programming |
| KPIs | Key Performance Indicators |
References
- Chen, F.; Duic, N.; Alves, L.; Carvalho, M. Renewislands—Renewable energy solutions for islands. Renew. Sustain. Energy Rev. 2007, 11, 1888–1902. [Google Scholar] [CrossRef]
- El-Bidairi, K.S.; Nguyen, H.D.; Jayasinghe, S.; Mahmoud, T.S.; Penesis, I. A hybrid energy management and battery size optimization for standalone microgrids: A case study for Flinders Island, Australia. Energy Convers. Manag. 2018, 175, 192–212. [Google Scholar] [CrossRef]
- Jin, H.; Liu, P.; Li, Z. Dynamic modeling and design of a hybrid compressed air energy storage and wind turbine system for wind power fluctuation reduction. Comput. Chem. Eng. 2019, 122, 59–65. [Google Scholar] [CrossRef]
- Moeini-Aghtaie, M.; Dehghanian, P.; Fotuhi-Firuzabad, M.; Abbaspour, A. Multiagent Genetic Algorithm: An Online Probabilistic View on Economic Dispatch of Energy Hubs Constrained by Wind Availability. IEEE Trans. Sustain. Energy 2014, 5, 699–708. [Google Scholar] [CrossRef]
- Rodrígues, E.; Osório, G.; Godina, R.; Bizuayehu, A.; Lujano-Rojas, J.; Catalão, J. Grid code reinforcements for deeper renewable generation in insular energy systems. Renew. Sustain. Energy Rev. 2016, 53, 163–177. [Google Scholar] [CrossRef]
- Aidoo, I.; Sharma, P.; Hoff, B. Optimal controllers designs for automatic reactive power control in an isolated wind-diesel hybrid power system. Int. J. Electr. Power Energy Syst. 2016, 81, 387–404. [Google Scholar] [CrossRef]
- Sosnina, E.; Lipuzhin, I. A Study of Operation Modes of the Autonomous Power Supply System with Wind-Diesel Power Plant. In Proceedings of the 2018 IEEE PES Transmission Distribution Conference and Exhibition—Latin America (T&D-LA), Lima, Peru, 18–21 September 2018; pp. 1–5. [Google Scholar]
- Aliyu, H.; Agee, J. Electric energy from the hybrid wind-solar thermal power plants. In Proceedings of the 2016 IEEE PES PowerAfrica, Livingstone, Zambia, 28 June–3 July 2016; pp. 264–268. [Google Scholar]
- Liu, J.; Yao, Q.; Hu, Y. Model predictive control for load frequency of hybrid power system with wind power and thermal power. Energy 2019, 172, 555–565. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, M.; Chang, J.; Wang, X.; Tian, Y. Study on the combined operation of a hydro-thermal-wind hybrid power system based on hydro-wind power compensating principles. Energy Convers. Manag. 2019, 194, 94–111. [Google Scholar] [CrossRef]
- Pathak, G.; Singh, B.; Panigrahi, B. Wind–Hydro Microgrid and Its Control for Rural Energy System. IEEE Trans. Ind. Appl. 2019, 55, 3037–3045. [Google Scholar] [CrossRef]
- Liu, Y.; Qin, W.; Han, X.; Wang, P. Modelling of large-scale wind/solar hybrid system and influence analysis on power system transient voltage stability. In Proceedings of the 2017 12th IEEE Conference on Industrial Electronics and Applications (ICIEA), Siem Reap, Cambodia, 18–20 June 2017; pp. 477–482. [Google Scholar]
- Ding, Z.; Hou, H.; Yu, G.; Hu, E.; Duan, L.; Zhao, J. Performance analysis of a wind-solar hybrid power generation system. Energy Convers. Manag. 2019, 181, 223–234. [Google Scholar] [CrossRef]
- Abdeltawab, H.H.; Mohamed, Y.A.R.I. Market-Oriented Energy Management of a Hybrid Wind-Battery Energy Storage System Via Model Predictive Control With Constraint Optimizer. IEEE Trans. Ind. Electron. 2015, 62, 6658–6670. [Google Scholar] [CrossRef]
- Hu, J.; Shan, Y.; Xu, Y.; Guerrero, J. A coordinated control of hybrid AC/DC microgrids with PV-wind-battery under variable generation and load conditions. Int. J. Electr. Power Energy Syst. 2019, 104, 583–592. [Google Scholar] [CrossRef]
- El-Bidairi, K.S.; Nguyen, H.D.; Mahmoud, T.S.; Jayasinghe, S.; Guerrero, J.M. Optimal sizing of Battery Energy Storage Systems for dynamic frequency control in an islanded microgrid: A case study of Flinders Island, Australia. Energy 2020, 195, 117059. [Google Scholar] [CrossRef]
- Kennedy, N.; Miao, C.; Wu, Q.; Wang, Y.; Ji, J.; Roskilly, T. Optimal Hybrid Power System Using Renewables and Hydrogen for an Isolated Island in the UK. Energy Procedia 2017, 105, 1388–1393. [Google Scholar] [CrossRef]
- Katsigiannis, Y.; Karapidakis, E. Operation of wind-battery hybrid power stations in autonomous Greek islands. In Proceedings of the 2017 52nd International Universities Power Engineering Conference (UPEC), Heraklion, Greece, 28–31 August 2017; pp. 1–5. [Google Scholar]
- Obara, S.; Sato, K.; Utsugi, Y. Study on the operation optimization of an isolated island microgrid with renewable energy layout planning. Energy 2018, 161, 1211–1225. [Google Scholar] [CrossRef]
- Ntomaris, A.; Bakirtzis, A. Stochastic Scheduling of Hybrid Power Stations in Insular Power Systems With High Wind Penetration. IEEE Trans. Power Syst. 2016, 31, 3424–3436. [Google Scholar] [CrossRef]
- Notton, G.; Mistrushi, D.; Stoyanov, L.; Berberi, P. Operation of a photovoltaic-wind plant with a hydro pumping-storage for electricity peak-shaving in an island context. Sol. Energy 2017, 157, 20–24. [Google Scholar] [CrossRef]
- Wang, C.; Liu, Y.; Li, X.; Guo, L.; Qiao, L.; Lu, H. Energy management system for stand-alone diesel-wind-biomass microgrid with energy storage system. Energy 2016, 97, 90–104. [Google Scholar] [CrossRef]
- Luna, A.; Díaz, N.; Graells, M.; Vásquez, J.; Guerrero, J. Mixed-Integer-Linear-Programming-Based Energy Management System for Hybrid PV-Wind-Battery Microgrids: Modeling, Design, and Experimental Verification. IEEE Trans. Power Electron. 2017, 32, 2769–2783. [Google Scholar] [CrossRef]
- Menniti, D.; Pinnarelli, A.; Sorrentino, N.; Vizza, P.; Burgio, A.; Brusco, G.; Motta, M. A Real-Life Application of an Efficient Energy Management Method for a Local Energy System in Presence of Energy Storage Systems. In Proceedings of the 2018 IEEE International Conference on Environment and Electrical Engineering and 2018 IEEE Industrial and Commercial Power Systems Europe (EEEIC / I CPS Europe), Palermo, Italy, 12–15 June 2018; pp. 1–6. [Google Scholar]
- Bukar, A.; Tan, C. A review on stand-alone photovoltaic-wind energy system with fuel cell: System optimization and energy management strategy. J. Clean. Prod. 2019, 221, 73–88. [Google Scholar] [CrossRef]
- Petersen, L.; Iov, F.; Tarnowski, G.C. A Model-Based Design Approach for Stability Assessment, Control Tuning and Verification in Off-Grid Hybrid Power Plants. Energies 2019, 13, 49. [Google Scholar] [CrossRef]
- Zhang, Y.; Meng, F.; Wang, R.; Kazemtabrizi, B.; Shi, J. Uncertainty-resistant stochastic MPC approach for optimal operation of CHP microgrid. Energy 2019, 179, 1265–1278. [Google Scholar] [CrossRef]
- Tan, K.T.; Sivaneasan, B.; Peng, X.Y.; So, P.L. Control and Operation of a DC Grid-Based Wind Power Generation System in a Microgrid. IEEE Trans. Energy Convers. 2016, 31, 496–505. [Google Scholar] [CrossRef]
- Zhang, Y.; Meng, F.; Wang, R.; Zhu, W.; Zeng, X.J. A stochastic MPC based approach to integrated energy management in microgrids. Sustain. Cities Soc. 2018, 41, 349–362. [Google Scholar] [CrossRef]
- Xing, X.; Xie, L.; Meng, H. Cooperative energy management optimization based on distributed MPC in grid-connected microgrids community. Int. J. Electr. Power Energy Syst. 2019, 107, 186–199. [Google Scholar] [CrossRef]
- Tedesco, F.; Mariam, L.; Basu, M.; Casavola, A.; Conlon, M.F. Economic Model Predictive Control-Based Strategies for Cost-Effective Supervision of Community Microgrids Considering Battery Lifetime. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 1067–1077. [Google Scholar] [CrossRef]
- Zhang, X.; Bao, J.; Wang, R.; Zheng, C.; Skyllas-Kazacos, M. Dissipativity based distributed economic model predictive control for residential microgrids with renewable energy generation and battery energy storage. Renew. Energy 2017, 100, 18–34. [Google Scholar] [CrossRef]
- Chen, Y.; Deng, C.; Li, D.; Chen, M. Quantifying cumulative effects of stochastic forecast errors of renewable energy generation on energy storage SOC and application of Hybrid-MPC approach to microgrid. Int. J. Electr. Power Energy Syst. 2020, 117, 105710. [Google Scholar] [CrossRef]
- Tabar, V.S.; Abbasi, V. Energy management in microgrid with considering high penetration of renewable resources and surplus power generation problem. Energy 2019, 189, 116264. [Google Scholar] [CrossRef]
- Notton, G. Importance of islands in renewable energy production and storage: The situation of the French islands. Renew. Sustain. Energy Rev. 2015, 47, 260–269. [Google Scholar] [CrossRef]
- Belfort, A. Les Chiffres Clés de l’Énergie en Guadeloupe, 2016 ed.; Technical report; Observatoire régional de l’énergie et du climat de la Guadeloupe; Comité de l’OREC (ADEME, Région Guadeloupe, DEAL, EDF, Météo-France, SYMEG et Synergîle): Baie-Mahault, France, 2017. [Google Scholar]
- Marin, D. Intégration des éoliennes dans les réseaux électriques insulaires. Ph.D. Thesis, Ecole Centrale de Lille, Lille, France, 2009. [Google Scholar]
- Aguilera-González, A.; Vechiu, I.; Rodríguez, R.H.L.; Bacha, S. MPC Energy Management System For A Grid-Connected Renewable Energy/Battery Hybrid Power Plant. In Proceedings of the 7th International Conference on Renewable Energy Research and Applications (ICRERA 2018), Paris, France, 14–17 October 2018; pp. 738–743. [Google Scholar]
- Rueda, J.; Korai, A.; Cepeda, J.; Erlich, I.; Gonzalez-Longatt, F. Implementation of Simplified Models of DFIG-Based Wind Turbines for RMS-Type Simulation in DIgSILENT PowerFactory. In PowerFactory Applications for Power System Analysis; Springer International Publishing: Cham, Switzerland, 2014. [Google Scholar]
- Yazhou, L.; Mullane, A.; Lightbody, G.; Yacamini, R. Modeling of the wind turbine with a doubly fed induction generator for grid integration studies. IEEE Trans. Energy Convers. 2006, 21, 257–264. [Google Scholar]
- Tremblay, O.; Dessaint, L. Experimental validation of a battery dynamic model for EV applications. World Electr. Veh. J. 2009, 3, 289–298. [Google Scholar] [CrossRef]
- Saw, L.; Somasundaram, K.; Ye, Y.; Tay, A. Electro-thermal analysis of Lithium Iron Phosphate battery for electric vehicles. J. Power Sources 2014, 249, 231–238. [Google Scholar] [CrossRef]
- Rigo-Mariani, R. Méthodes de Conception Intégrée “Dimensionnement-Gestion” par Optimisation d’Un Micro-réseau avec Stockage. Ph.D. Thesis, Université de Toulouse, Toulouse, France, 2015. [Google Scholar]
- Hérnandez-Torres, D.; Turpin, C.; Roboam, X.; Sareni, B. Modélisation en flux d’énergie d’une batterie Li-Ion en vue d’une optimisation technico-économique d’un micro-réseau intelligent. In Proceedings of the Symposium de Génie Electrique (SGE’16), Grenoble, France, 7–9 March 2016; pp. 1–8. [Google Scholar]
- Camacho, E.; Bordons-Alba, C. Model Predictive Control; Springer Verlag: London, UK, 2007. [Google Scholar]
- Efheij, H.; Albagul, A.; Ammar Albraiki, N. Comparison of Model Predictive Control and PID Controller in Real Time Process Control System. In Proceedings of the 2019 19th International Conference on Sciences and Techniques of Automatic Control and Computer Engineering (STA), Sousse, Tunisia, 24–26 March 2019; pp. 64–69. [Google Scholar]
- Alamir, M. A Pragmatic Story of Model Predictive Control: Self-Contained Algorithms and Case-Studies; CreateSpace Independent Publishing Platform: Grenoble, France, 2013. [Google Scholar]
- Coleman, T.; Li, Y. A Reflective Newton Method for Minimizing a Quadratic Function Subject to Bounds on Some of the Variables. SIAM J. Optim. 1996, 6, 1040–1058. [Google Scholar] [CrossRef]
- Pramangioulis, D.; Atsonios, K.; Nikolopoulos, N.; Rakopoulos, D.; Grammelis, P.; Kakaras, E. A Methodology for Determination and Definition of Key Performance Indicators for Smart Grids Development in Island Energy Systems. Energies 2019, 12, 242. [Google Scholar] [CrossRef]
- Gundogdu, B.; Gladwin, D.T. A Fast Battery Cycle Counting Method for Grid-Tied Battery Energy Storage System Subjected to Microcycles. In Proceedings of the 2018 International Electrical Engineering Congress (iEECON), Krabi, Thailand, 7–9 March 2018; pp. 1–4. [Google Scholar]














| Symbol | Description | Unit | Value |
|---|---|---|---|
| Fully charged voltage | V | 3.95 | |
| Nominal voltage | V | 3.6 | |
| Exponential voltage | V | 3.9 | |
| Nominal capacity | Ah | 39 | |
| Maximum cell capacity | Ah | 41 | |
| Exponential capacity | Ah | 1 | |
| I | Nominal discharge current | A | 13.67 |
| Cell charge voltage limit | V | 4 | |
| Cell cut-off voltage | V | 2.7 |
| Parameter | Description | Unit | Value |
|---|---|---|---|
| Filtered current upper bound | A | ||
| Control amplitude lower bound | A | −6400 | |
| Control amplitude upper bound | A | 3280 | |
| State-of-charge upper limitation | % | 20 | |
| State-of-charge lower limitation | % | 80 | |
| Control actions rate of change lower bound | A/s | ||
| Control actions rate of change upper bound | A/s |
| Parameter | Description | Unit | Value |
|---|---|---|---|
| Weight of objective related to | - | 0, 50, 100 | |
| Weight of objective related to | - | 0, 50, 100 | |
| Weighting of the inputs control effort | - | 1 | |
| offset | Vertical displacement of | MW | 0 |
| SoC set-point level | % | 80 | |
| Optimization window length | - | 10 |
| Case | CF (%) | (MWh) | ||||
|---|---|---|---|---|---|---|
| Case 1 | 0 | 0 | 0.34 | 56.2 | 1.90 | 16.84 |
| Case 2 | 0 | 0 | 0.34 | 56.2 | 1.46 | 18.55 |
| Case 3 | 8.33 | 12.16 | 0 | 49.9 | 0.08 | 28.60 |
| Case | CF (%) | (MWh) | ||||
|---|---|---|---|---|---|---|
| Case 4 | 6.25 | 8.49 | 0 | 52.7 | 2.21 | 11.70 |
| Case 5 | 6.25 | 8.71 | 0 | 52.6 | 1.72 | 12.91 |
| Case 6 | 7.64 | 11.93 | 0 | 50.4 | 0.07 | 21.47 |
| Indicator | MPC | RB | MPC | RB | MPC | RB |
| 1.7 | 8.5 | 1.8 | 8.5 | 1.7 | 8.5 | |
| ) | 0.3 | 13.6 | 0.4 | 13.6 | 0.4 | 13.6 |
| 0 | 0 | 0 | ||||
| (MWh) | 1811.2 | 1504.5 | 1807.3 | 1504.5 | 1807.5 | 1504.5 |
| 45.6 | 15.8 | 91.2 | 15.8 | 111.7 | 15.8 | |
| 0.18 | 0.24 | 0.09 | 0.24 | 0.06 | 0.24 | |
| 20.3 | 27.7 | 27.2 | 27.7 | 28.7 | 27.7 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
López-Rodríguez, R.; Aguilera-González, A.; Vechiu, I.; Bacha, S. Day-Ahead MPC Energy Management System for an Island Wind/Storage Hybrid Power Plant. Energies 2021, 14, 1066. https://doi.org/10.3390/en14041066
López-Rodríguez R, Aguilera-González A, Vechiu I, Bacha S. Day-Ahead MPC Energy Management System for an Island Wind/Storage Hybrid Power Plant. Energies. 2021; 14(4):1066. https://doi.org/10.3390/en14041066
Chicago/Turabian StyleLópez-Rodríguez, Rubén, Adriana Aguilera-González, Ionel Vechiu, and Seddik Bacha. 2021. "Day-Ahead MPC Energy Management System for an Island Wind/Storage Hybrid Power Plant" Energies 14, no. 4: 1066. https://doi.org/10.3390/en14041066
APA StyleLópez-Rodríguez, R., Aguilera-González, A., Vechiu, I., & Bacha, S. (2021). Day-Ahead MPC Energy Management System for an Island Wind/Storage Hybrid Power Plant. Energies, 14(4), 1066. https://doi.org/10.3390/en14041066