Prediction of Extreme Wind Speed for Offshore Wind Farms Considering Parametrization of Surface Roughness
Abstract
1. Introduction
2. Theory and Method
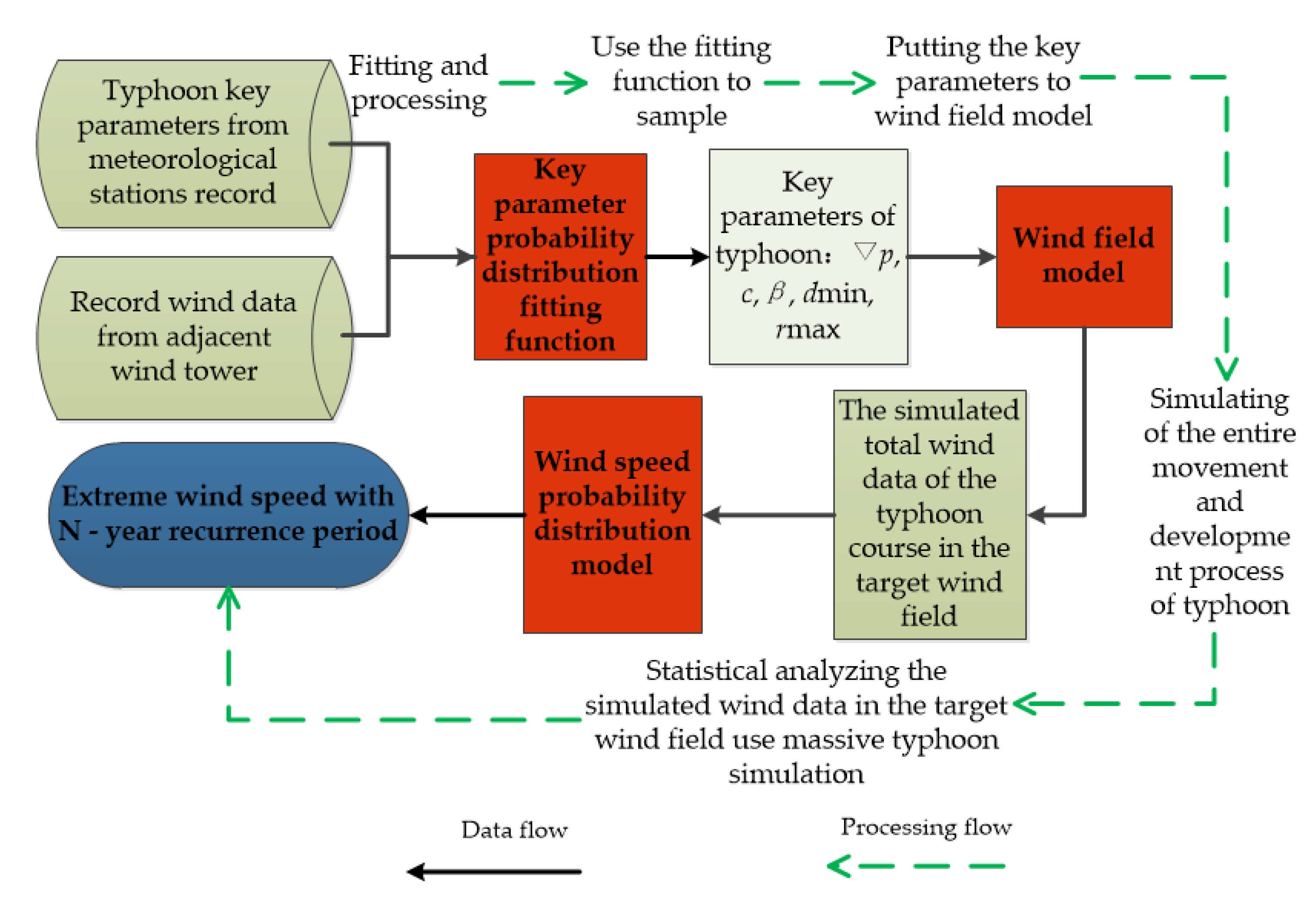
2.1. MCS and Process
- Collect typhoon key parameters record from meteorological stations and adjacent wind tower’s wind speed historical records.
- Fit and statistical process the data to get the key parameter probability distribution fitting function.
- Use the fitting function and Metropolis–Hastings algorithm (‘mhsample‘ function of Matlab software is applied in this paper [36]) to sample key typhoon parameters.
- Put the key typhoon parameters to YM wind model to simulate the entire movement and development process of typhoon and get the total wind data of the typhoon course.
- Repeat step 3–4 for 106 (or more) times to get massive wind data.
- Statistical analyze the massive wind data and get wind speed probability distribution model.
- Use probability distribution model (generalized extreme value theory in this paper) to get the EWS with a certain return period.
2.2. YM Typhoon Wind Field Model
2.3. Generalized Extreme Value Theory
2.4. Offshore Roughness Calculation Considering the Wind-Wave Coupling Effect
3. Result and Discussion
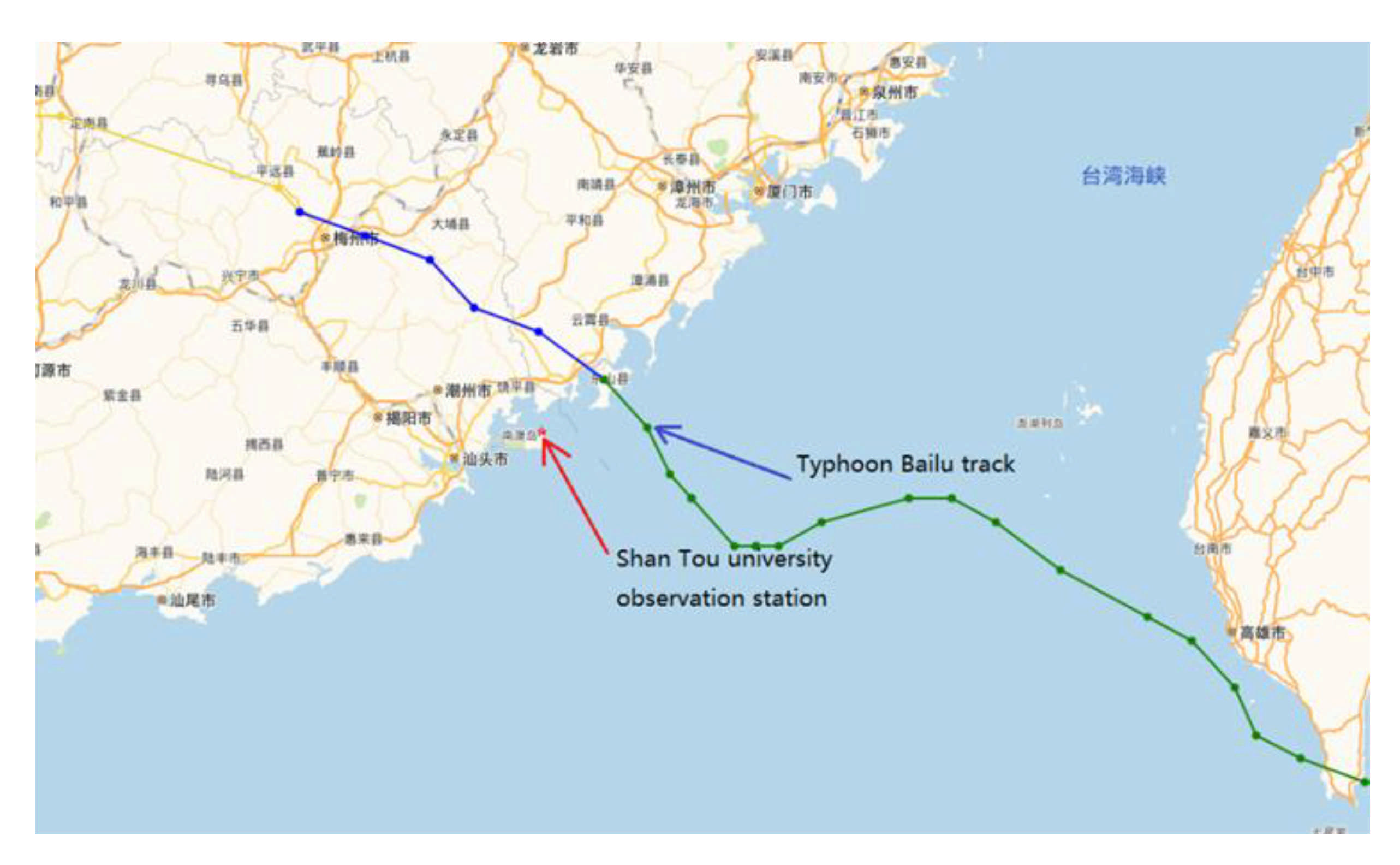
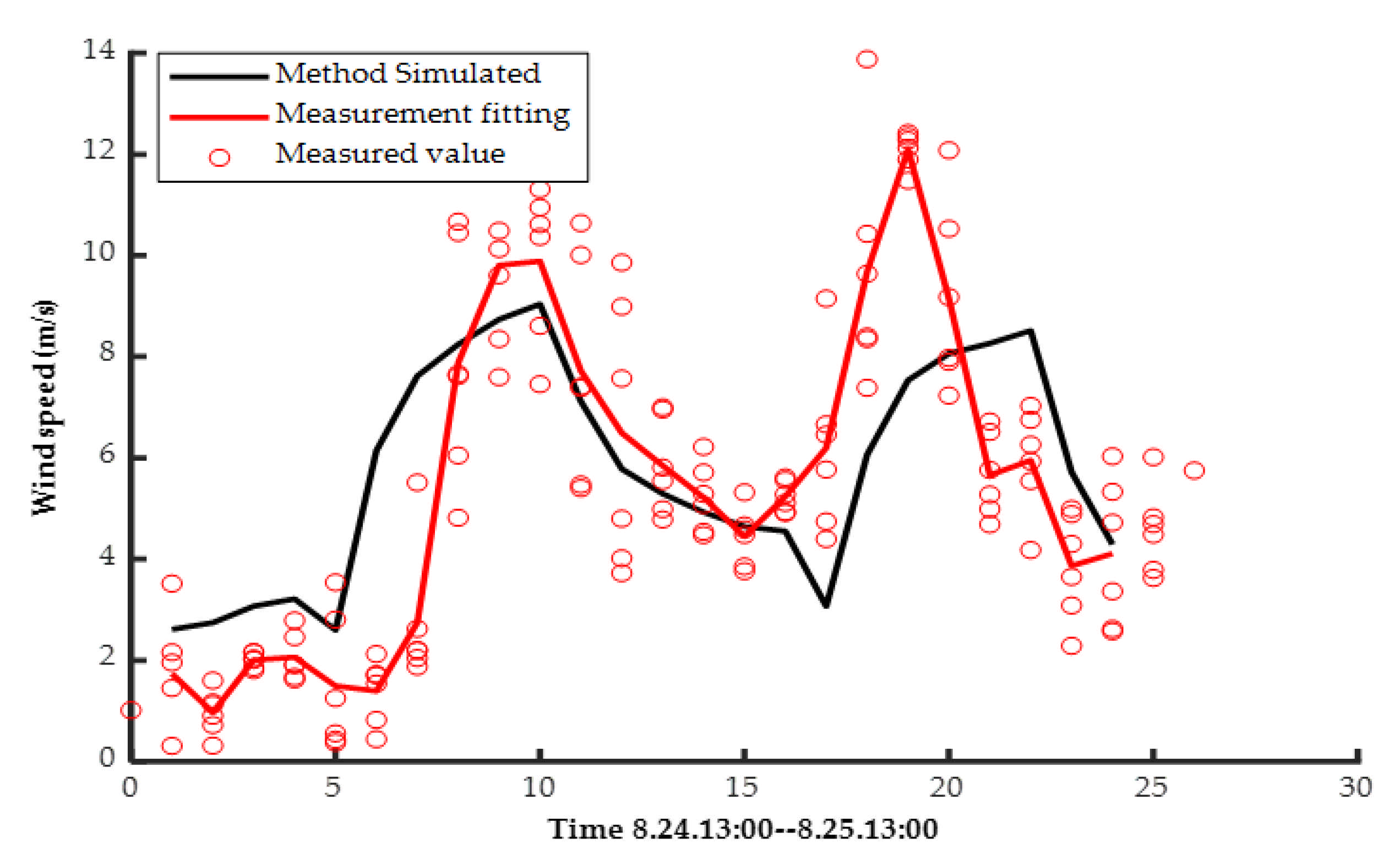
3.1. Parameters Setting and Verification of Parametric Wind Field Model
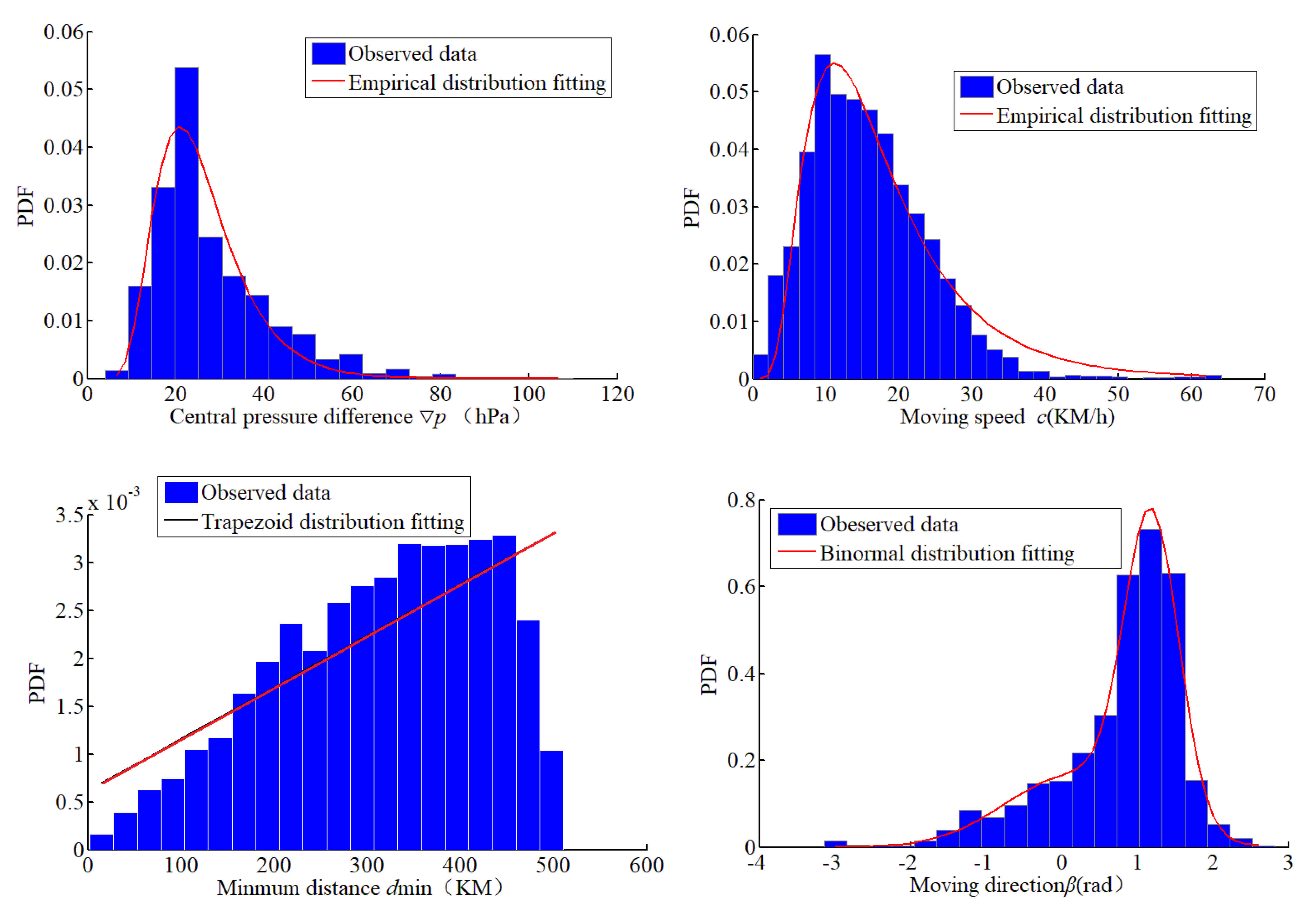
3.2. Statistics and Fitting of Critical Parameters of Typhoons
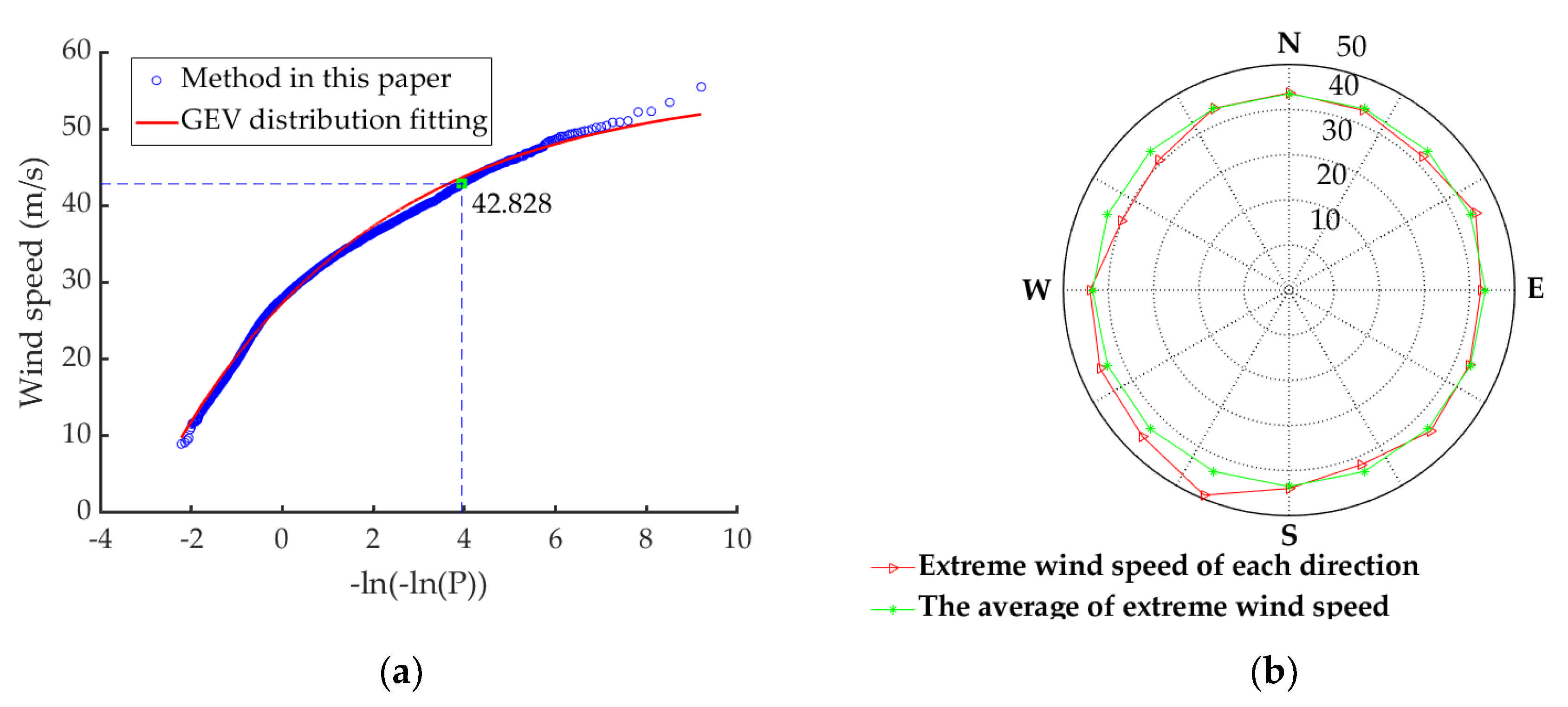
3.3. Prediction of EWS under the Influence of Typhoon without the Parametrization of Surface Roughness
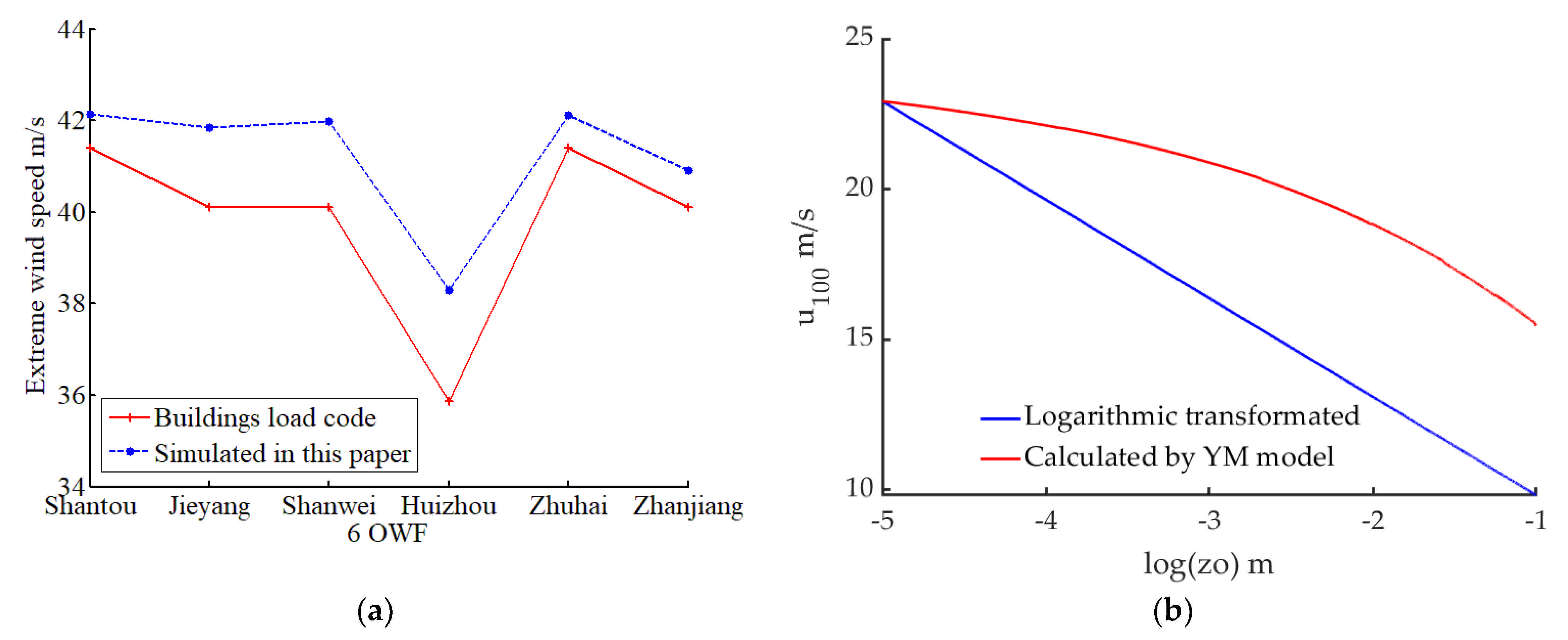
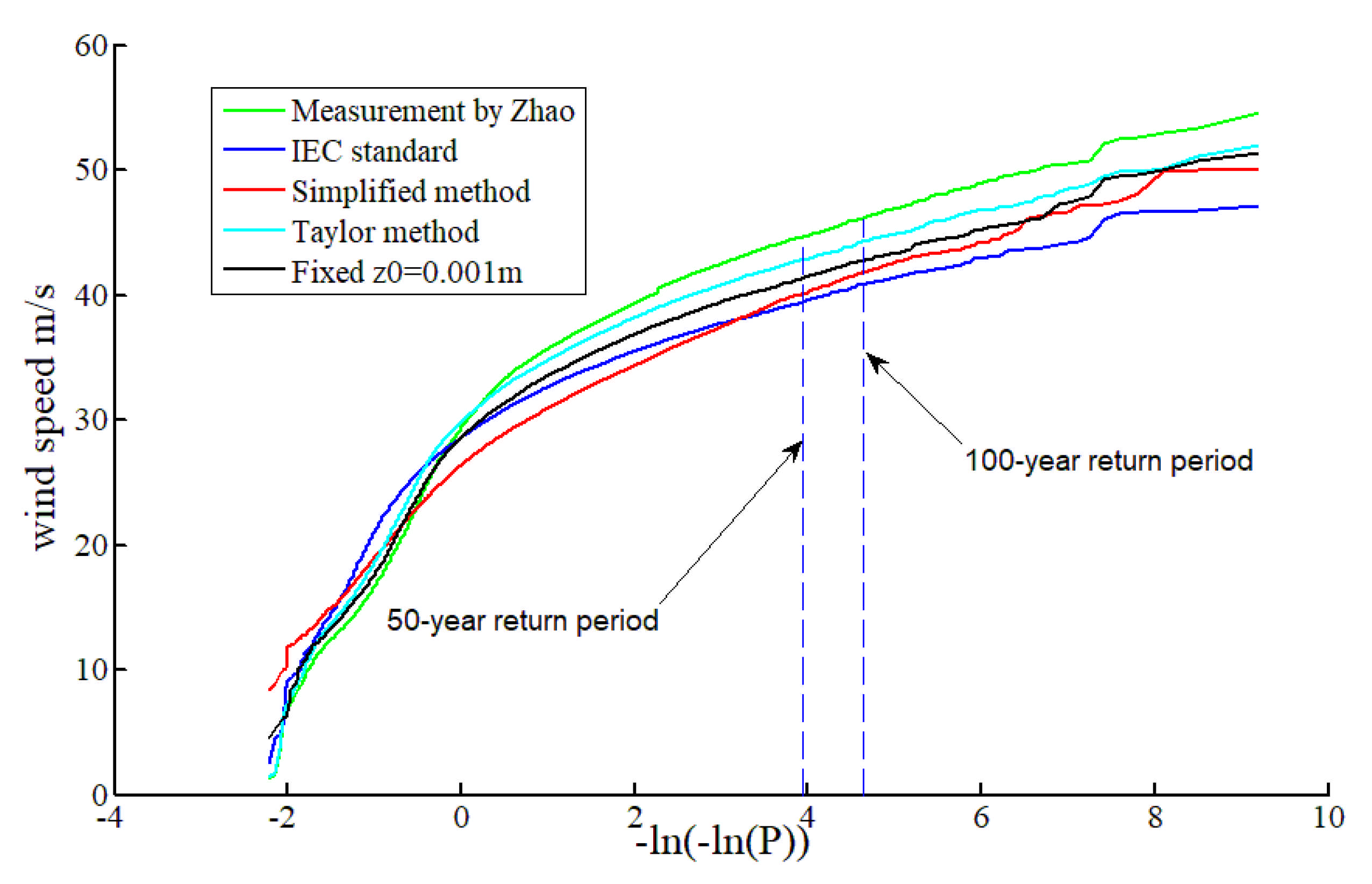
3.4. Prediction of EWS by Improving YM Model and Considering the Parametrization of Surface Roughness
3.5. Summary and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Song, L.L.; Mao, H.Q.; Qian, G.M. Analysis on the Wind Power by Tropical Cyclone. Taiyangneng Xuebao/Acta Energiae Solaris Sinica 2006, 27, 961–965. [Google Scholar]
- Ishihara, T.; Yamaguchi, A.; Takahara, K. An analysis of damaged wind turbines by typhoon Maemi. In Proceedings of the Sixth Asia-Pacific Conference on Wind Engineering (APCWE-VI), Seoul, Korea, 12–14 September 2005. [Google Scholar]
- Worsnop, R.P.; Lundquist, J.K.; Bryan, G.H. Gusts and shear within hurricane eyewalls can exceed offshore wind turbine design standards. Geophys. Res. Lett. 2016, 44, 6413–6420. [Google Scholar] [CrossRef]
- Guglielmo, D.; Filippo, P.; Flavio, P. Wind speed prediction for wind farm applications by Extreme Value Theory and Copulas. J. Wind. Eng. Ind. Aerodyn. 2015, 145, 229–236. [Google Scholar]
- IEC. IEC 61400-1: Edition Wind Turbines-Part 1: Design Requirements; IEC: Geneva, Switzerland, 2018; pp. 27–30. [Google Scholar]
- General Administration of Quality Supervision, Inspection and Quarantine and Standardization Administration of the People’s Republic of China. Wind Turbine Generator System under Typhoon Condition; GB/T31519; General Administration of Quality Supervision, Inspection and Quarantine and Standardization Administration of the People’s Republic of China: Beijing, China, 2016; p. 20.
- Ishihara, T.; Yamaguchi, A. Prediction of the extreme wind speed in the mixed climate region by using Monte Carlo simulation and measure-correlate-predict method. Wind Energ. 2015, 18, 171–186. [Google Scholar] [CrossRef]
- Zhao, L.; Ge, Y.J.; Song, L.L. Monte Carlo Simulation Analysis of Typhoon Extreme Value Wind Characteristics in Guangzhou. J. Tongji Univ. Nat. Sci. 2007, 35, 1034–1038. [Google Scholar]
- Xiao, Y.F.; Duan, Z.D.; Xiao, Y.Q. Typhoon wind hazard analysis for southeast China coastal regions. Struct. Saf. 2011, 33, 286–295. [Google Scholar] [CrossRef]
- Wang, J.C.; Quan, Y.; Gu, M. Assessment of the directional extreme wind speeds of typhoons via the Copula function and Monte Carlo simulation. Wind Struct. 2020, 30, 141–153. [Google Scholar]
- Fang, W.H.; Lin, W. A review on typhoon wind field modeling for disaster risk assessment. Prog. Phys. Geogr. 2013, 32, 852–867. [Google Scholar]
- Lin, N.; Emanuel, K.; Vanmarcke, E. 7 Physically-based hurricane risk analysis. In Extreme Natural Hazards, Disaster Risks and Societal Implications; Ismail-Zadeh, A., Urrutia Fucugauchi, J., Kijko, A., Takeuchi, K., Zaliapin, I., Eds.; Special Publications of the International Union of Geodesy and Geophysics; Cambridge University Press: Cambridge, UK, 2014; pp. 88–92. [Google Scholar]
- Dayal, K.; Cater, J.E.; Kingan, M.J. Evaluation of the WRF model for simulating surface winds and the diurnal cycle of wind speed for the small island state of Fiji. J. Phys. Conf. Ser. 2020, 1618, 1–12. [Google Scholar] [CrossRef]
- Ruiz-Salcines, P.; Salles, P.; Robles-Díaz, L.; Díaz-Hernández, G.; Torres-Freyermuth, A.; Appendini, C.M. On the Use of Parametric Wind Models for Wind Wave Modeling under Tropical Cyclones. Water 2019, 11, 2044. [Google Scholar] [CrossRef]
- Xu, Y.L. Windstorms and Cable-Supported Bridges. In Wind Effects on Cable-Supported Bridges; Xu, Y.L., Ed.; John Wiley & Sons Singapore Pte. Ltd.: Singapore, 2013; pp. 569–573. [Google Scholar]
- Vickery, P.J.; Twisdale, L.A. Wind-Field and Filling Models for Hurricane Wind-Speed Predictions. J. Struct. Eng. 1995, 121, 1700–1709. [Google Scholar] [CrossRef]
- Thompson, E.F.; Cardone, V.J. Practical modeling of hurricane surface wind fields. J. Waterw. Port Coast. Ocean Eng. 1996, 122, 195–205. [Google Scholar] [CrossRef]
- Batts, M.E.; Simiu, E.; Russell, L.R. Hurricane wind speeds in the United States. J. Struct. Div. 1980, 106, 2001–2016. [Google Scholar] [CrossRef]
- Yan, M.; Matsui, M.; Hibi, K. A numerical study of the wind field in a typhoon boundary layer. J. Wind. Eng. Ind. Aerodyn. 1997, 67, 437–448. [Google Scholar]
- Larsén, X.G.; Du, J.; Bolaños, R. Estimation of offshore extreme wind from wind-wave coupled modeling. Wind Energy 2019, 22, 1043–1057. [Google Scholar] [CrossRef]
- Charnock, H. A note on empirical wind-wave formulae. Q. J. R. Meteorol. Soc. 2010, 84, 443–447. [Google Scholar] [CrossRef]
- Edson, J.B.; Fairall, C.W. Similarity Relationships in the Marine Atmospheric Surface Layer for Terms in the TKE and Scalar Variance Budgets*. J. Atmos. Sci. 1998, 55, 2311–2328. [Google Scholar] [CrossRef]
- Taylor, P.K.; Yelland, M.J. The Dependence of Sea Surface Roughness on the Height and Steepness of the Waves. J. Phys. Oceanogr. 2000, 31, 572–590. [Google Scholar] [CrossRef]
- Zijlema, M.; Vledder, G.P.V.; Holthuijsen, L. Bottom friction and wind drag for wave models. Coast. Eng. 2012, 65, 19–26. [Google Scholar] [CrossRef]
- Edson, J.B.; Jampana, V.; Weller, R. On the Exchange of Momentum over the Open Ocean. J. Phys. Oceanogr. 2013, 43, 1589–1610. [Google Scholar] [CrossRef]
- Fan, Y.; Lin, S.J.; Held, I.M. Global ocean surface wave simulation using a coupled atmosphere–wave model. J. Clim. 2012, 25, 6233–6252. [Google Scholar] [CrossRef]
- Liu, B.; Liu, H.; Xie, L. A Coupled Atmosphere-Wave-Ocean Modeling System: Simulation of the Intensity of an Idealized Tropical Cyclone. Mon. Weather Rev. 2011, 139, 132–152. [Google Scholar] [CrossRef]
- Janssen, P.; Lionello, P.; Zambresky, L. On the interaction of wind and waves. Philos. Trans. R. Soc. Lond. Ser. Math. Phys. Sci. 1989, 329, 289–301. [Google Scholar]
- Jensen, R.E.; Cardone, V.J.; Cox, A.T. Performance of Third Generation Wave Models in Extreme Hurricanes. In Proceedings of the 9th International Workshop of Wave Hindcasting and Forecasting, Victoria, BC, Canada, 24–29 September 2006. [Google Scholar]
- Chalikov, D.V.; Makin, V.K. Models of the wave boundary layer. Bound.-Layer Meteorol. 1991, 56, 83–99. [Google Scholar] [CrossRef]
- Makin, V.K.; Kudryavtsev, V.N.; Mastenbroek, C. Drag of the sea surface. Bound.-Layer Meteorol. 1995, 73, 159–182. [Google Scholar] [CrossRef]
- Drost, E.J.F.; Lowe, R.J.; Ivey, G.N. The effects of tropical cyclone characteristics on Australia’s North West region. Cont. Shelf Res. 2017, 139, 35–53. [Google Scholar] [CrossRef]
- Guo, Y.; Hou, Y.; Liu, Z. Risk Prediction of Coastal Hazards Induced by Typhoon: A case study in the Coastal Region of Shenzhen, China. Remote Sens. 2020, 12, 1731. [Google Scholar] [CrossRef]
- Yan, Z.D.; Liang, B.C.; Wu, G.X. Ultra-long return level estimation of extreme wind speed based on the deductive method. Ocean Eng. 2020, 197, 106900–106912. [Google Scholar] [CrossRef]
- Cappé, O.; Godsill, S.J.; Moulines, E. An Overview of Existing Methods and Recent Advances in Sequential Monte Carlo; IEEE: Piscataway, NJ, USA, 2007; Volume 95, pp. 899–924. [Google Scholar]
- MathWorks. Available online: https://www.mathworks.com/help/stats/mhsample.html (accessed on 1 January 2021).
- Lettau, H.H. Physical and meteorological basis for mathematical models of urban diffusion processes. In Proceedings of Symposium on Multiple-Source Urban Diffusion Models; Arthur, C.S., Ed.; US Environmental Protection Agency: Durham, NC, USA, 1970; pp. 2.1–2.26. [Google Scholar]
- Helliwell, N.C. Wind over London. In Proceedings of the Wind Effects on Buildings and Structures; Saikon Co.: Tokyo, Japan, 1971; pp. 23–32. [Google Scholar]
- Kondo, J.; Yamazawa, H. Aerodynamic roughness over an inhomogeneous ground surface. Bound.-Layer Meteorol. 1986, 35, 331–348. [Google Scholar] [CrossRef]
- Simiu, E. Equivalent static wind load for tall building design. In Proceedings of the 4th International Conference, Munich, Germany, 26–30 July 2004. [Google Scholar]
- Wu, J. Wind stress and surface roughness at air-sea interface. J. Geophys. Res. 1969, 74, 444–455. [Google Scholar] [CrossRef]
- IEC. IEC 61400–3 Edition 1.0: Design Requirements for Offshore Wind Turbines Eoliennes; IEC: Geneva, Switzerland, 2019; pp. 30–40. [Google Scholar]
- Typhoon Network of the China Central Meteorological Station. Available online: http://typhoon.nmc.cn/web.html (accessed on 1 March 2020).
- Holland, G.J. An analytic model of the wind and pressure profiles in hurricanes. Mon. Weather Rev. 1980, 108, 1212–1218. [Google Scholar] [CrossRef]
- Jiang, Z.H.; HUA, F.; Qu, P. A New Scheme for Adjusting the Tropical Cyclone Parameter. Adv. Marine Sci. 2008, 26, 5–11. [Google Scholar]
- Ying, M.; Zhang, W.; Yu, H. An Overview of the China Meteorological Administration Tropical Cyclone Database. J. Atmos. Ocean. Technol. 2014, 31, 287–301. [Google Scholar] [CrossRef]
- SA/SNZ (Standard Australian/Standard New Zealand). Structural Design Actions—Wind Actions AS/NZS 1170.2-2002; Standards Australia and Standards New Zealand: Sydney, Australia; Wellington, New Zealand, 2002; pp. 6–20.
- Harper, B.A.; Kepert, J.D.; Ginger, J.D. Guidelines for Converting between Various Wind Averaging Periods in Tropical Cyclone Conditions; No. 1555; WMO: Geneva, Switzerland, 2010; pp. 4–16. [Google Scholar]
- MOHURD (Ministry of Housing and Urban-Rural Development of the People’s Republic of China). Load Code for the Design of Building Structures GB 50009-2012; MOHURD: Beijing, China, 2012; pp. 30–50.
- Zhao, Z.K.; Liu, C.X.; Li, Q.; Dai, G.-F.; Song, Q.-T.; Lv, W.-H. Typhoon air-sea drag coefficient in coastal regions. J. Geophys. Res. Oceans 2015, 120, 716–727. [Google Scholar] [CrossRef]

| Key Wind Parameter | Followed Probability Distribution | Probability Distribution Density Function |
|---|---|---|
| Poisson distribution | ||
| ∇p | Empirical distribution | |
| c | Empirical distribution | |
| dmin | Trapezoidal distribution | |
| β | Binormal distribution |
| Wind Farm and Located City | Lati (N) | Log (E) | λ | Β (b1,b2,b3,b4,b5) | ∇p | C | dmin |
|---|---|---|---|---|---|---|---|
| Wailuo, Zhanjiang | 20.57 | 110.65 | 4.72 | (0.41, 2.13, 0.87, 2.82, 0.34) | (1.64, 3.67, −0.23) | (0.98, 2.86, 0.40) | (0.21, 155) |
| Guishan, Zhuhai | 22.01 | 113.72 | 5.07 | (0.31, 1.54, 0.73, 2.73, 0.35) | (1.58, 3.72, −0.25) | (0.81, 2.78, 0.52) | (0.43, 98.3) |
| Huizhou, Gangkou | 22.30 | 114.97 | 5.11 | (0.46, 1.89, 0.91, 2.77, 0.31) | (1.54, 3.70, −0.25) | (0.79, 2.77, 0.53) | (0.50, 81.4) |
| Houhu, Shanwei | 22.75 | 116.12 | 4.98 | (0.47, 1.78,0.96, 2.76, 0.28) | (1.63, 3.66, −0.23) | (0.80, 2.77, 0.52) | (0.58, 61.9) |
| Shenquan, Jieyang | 22.64 | 116.27 | 5.15 | (0.49, 1.69, 0.98, 2.75, 0.30) | (1.62, 3.65, −0.23) | (0.80, 2.78, 0.52) | (0.56, 67.0) |
| Yangdong, Shantou | 23.36 | 117.01 | 5.04 | (0.51,1.82, 0.90, 2.75, 0.31) | (1.59, 3.66, −0.23) | (0.796,2.79,0.52) | (0.54, 61.8) |
| Wind Farm Site and Located City | Mean Value of EWS in All Directions (m/s) | Maximum EWS (m/s) | Wind Direction of Maximum EWS | Offshore Wind Farm and Located County | Wind Pressure Specified in Load Code (kN/m2) | Wind Speed Converted from Wind Pressure (m/s) | Relative Deviation (%) |
|---|---|---|---|---|---|---|---|
| Wanluo, Zhanjiang | 40.9 | 48.6 | 7 | Xuwen County | 0.75 | 40.1 | 2.0 |
| Guishan, Zhuhai | 42.2 | 51.5 | 12 | Wanshan District | 0.8 | 41.4 | 1.7 |
| Gangkou, Huizhou | 38.3 | 49.9 | 11 | Huidong County | 0.6 | 35.9 | 6.8 |
| Houhu, Shanwei | 42.0 | 48.9 | 11 | Lufeng City | 0.75 | 40.1 | 4.7 |
| Shenquan, Jieyang | 41.9 | 49.3 | 8 | Huilai County | 0.75 | 40.1 | 4.3 |
| Yangdong, Shantou | 42.8 | 49.7 | 10 | Nan’ao Island | 0.8 | 41.4 | 3.4 |
| Wind Farm Site | The Results with Wind-Wave Coupling | Relative Deviation (%) | |
|---|---|---|---|
| Wanluo, Zhanjiang | 40.9 | 43.8 | 7.0 |
| Guishan, Zhuhai | 42.1 | 44.6 | 5.8 |
| Gangkou, Huizhou | 38.3 | 43.2 | 12.7 |
| Houhu, Shanwei | 42.0 | 44.2 | 5.7 |
| Shenquan, Jieyang | 41.9 | 44.9 | 6.9 |
| Yangdong, Shantou | 42.8 | 44.5 | 3.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, X.; Chen, Y.; Yi, W.; Wang, Z. Prediction of Extreme Wind Speed for Offshore Wind Farms Considering Parametrization of Surface Roughness. Energies 2021, 14, 1033. https://doi.org/10.3390/en14041033
Ma X, Chen Y, Yi W, Wang Z. Prediction of Extreme Wind Speed for Offshore Wind Farms Considering Parametrization of Surface Roughness. Energies. 2021; 14(4):1033. https://doi.org/10.3390/en14041033
Chicago/Turabian StyleMa, Xinwen, Yan Chen, Wenwu Yi, and Zedong Wang. 2021. "Prediction of Extreme Wind Speed for Offshore Wind Farms Considering Parametrization of Surface Roughness" Energies 14, no. 4: 1033. https://doi.org/10.3390/en14041033
APA StyleMa, X., Chen, Y., Yi, W., & Wang, Z. (2021). Prediction of Extreme Wind Speed for Offshore Wind Farms Considering Parametrization of Surface Roughness. Energies, 14(4), 1033. https://doi.org/10.3390/en14041033





