Abstract
The paper proposes a novel hybrid feature selection (FS) method for day-ahead electricity price forecasting. The work presents a novel hybrid FS algorithm for obtaining optimal feature set to gain optimal forecast accuracy. The performance of the proposed forecaster is compared with forecasters based on classification tree and regression tree. A hybrid FS method based on the elitist genetic algorithm (GA) and a tree-based method is applied for FS. Making use of selected features, aperformance test of the forecaster was carried out to establish the usefulness of the proposed approach. By way of analyzing and forecasts for day-ahead electricity prices in the Australian electricity markets, the proposed approach is evaluated and it has been established that, with the selected feature, the proposed forecaster consistently outperforms the forecaster with a larger feature set. The proposed method is simulated in MATLAB and WEKA software.
1. Introduction
Efficient and consistent electricity price forecasting is vital for market participants in the preparation of appropriate risk management plans in an electricity market. The higher the complexity in the market, the greater the peril of producing an error in forecast. An appropriate forecasting method allows suppliers and buyers to detail the bidding strategies for moderate losses and to increase profit. The research for developing price forecasting tools in non-intervention markets is at an intermediary stage and a variety of forecasting models covering many free trade markets have emerged in recent years [1,2,3,4,5,6]. Since a price chain is extremely volatile with non-constant mean and variance, because of the mobile nature and inflexible condition of establishing real-time stability of demand and supply of electricity, short-term price prediction is a difficult task. Market clearing prices (MCP) are volatile in a deregulated power market because of being an auction market price forecasting is an important tool for such markets. The companies that do business in electricity markets make broad use of price forecasting methods either to propose or to evade against volatility while auctioning in a pool system. Market contenders are requested to communicate the bids in terms of quantities and prices. A corporation can regulate its own production/price schedule on its own cast and hourly pool prices. A good quality MCP forecast and its confidence interval evaluation can help utilities and autonomous power producers to present efficient bids. Electricity price forecasting has been focussed of several researchers in the field of electricity and various authors and researchers have published on this topic.
Time series, artificial neural networks (ANNs), regression, semi-parametric and non-parametric methods [7,8,9,10,11,12,13,14] are well known approaches used for electricity price forecasting. W K. Hubicka et al. [15] suggested a novel idea in vitality forecasting and have shown that averaging next day electricity price forecasts of a prescient model across 28- to 728-day alignment windows yields preferred outcomes over choosing only one ’ideal’ window length. A. Y. Alanis et al. [16] presented, a recurrent neural network for forecasting electricity price based on the extended Kalman filter with both cases one step ahead and n-step ahead and also include the stability proof using the Lyapunov methodology.
L. Wang et al. [17] represented a model for day ahead hourly price forecasting using stacked denoising autoencoders (SDA) and deep neural networks. The data used are from the market of Arkansas, Texas, Louisiana, Nebraska, and Indiana hub of US. Authors in [17] used forecasting of two types: day ahead hourly forecasting and the online forecasting. The results show that the SDA model is competent in forecasting the electricity prices accurately. H. Mosbah et al. [18] used a multilayer neural network in composite topologies for accurate forecasting using data of 2005 as a training set while predicting prices of January 2006 in the Australian market. MAPE and MSE are calculated to compare the best performance indices using diverse composite topologies.
P. Sarikprueck et al. [19] proposed a hybrid method for both spike and non-spike power market prices using clustering methods of three types including CART, stratification and K-means methods and validated the performance of the proposed model with the Electric Reliability Commission of Texas wholesale market price. The outcomes given in the suggested technique show a vital up-gradation over other usual methodologies. J. P. González et al. [20] introduced a recently developed forecasting technique which strives to generalize the ARMAX time series method to the L2Hilbert space. The proposed model consists of linear regression where useful parameters work on functional variables. The variables used are either historical values, or exogenous variables, or past observed innovations. German and Spanish electricity markets are considered for forecasting in the work.
Anamika et al. [21] presented, a combination of various methodology like feed forward neural networks (FFNN), wavelet transform (WT), fuzzy adaptive particle swarm optimization (FA-PSO) for price forecasting on Spanish electricity markets for the year 2002. K. Wang et al. [22] suggested a novel approach for electricity price forecasting which consists of three models, first they combined the relief-F algorithm and random forest (RF) and proposed a hybrid FS method based on GCA to remove the feature redundancy. Secondly, a combination of KPCA was utilized in feature extraction procedure to understand the dimensionality reduction. Finally, a support vector machine (SVM) classifier based on differential evolution (DE) was used to predict electricity price.
P. Li et al. [23] addressed the dynamic similar sub-series technique for the consideration of cumulative effect which is due to collection of effecting factors during several consecutive time intervals and which makes relatively large forecasting errors. R. Tahmasebifar et al. [24] considered the probabilistic interval variables which can affect future electricity price forecasting. The method consists of two steps, in the initial step, a new hybrid method is introduced to predict point forecasts which is a combination of ELM, WT, FS based on mutual information (MI), and bootstrap approaches and in second step, PSO algorithm is used for improving the forecast accuracy and evaluating the variance of the model.
O. Abedinia et al. [25] suggested an FS approach based on criteria of informationtheory with important contribution of modeling interaction in combination with redundancy and relevancy. The hybrid filter-wrapper approach is another fundamental outcome of this work. C. González et al. [26] proposed a method to efficiently find the important variables that dominate the forecasting of electricity price forecasting. CART, RF and bagging approaches were used for the accurate forecasting of electricity price in Iberian market. Historical data of 22 dominating factor such as load, price, hydro wind energy production, thermal generation hours etc., are used to efficiently forecast electricity price.
In this work electricity price forecasting is done using sequential minimization optimization (SMO) regression. The SMO regression algorithm followed by regression analysis is a powerful tool of decomposition for training SVM without the requirement of a quadratic programming (QP) solver. It is probable that SMO is the only SVM optimizer that exclusively exploits the quadratic form of the objective function and simultaneously uses the analytic solution of the size two cases. Since most of the objective functions have minimization criteria characteristics with set of constraints, for optimization purposes, such objective functions are represented in the form of Lagrange’s multipliers. These Lagrange multipliers contain a dual form of the primal set of the predefined objective functions minus linear constraints. The only problem with SMO is its convergence accuracy for non-sparse data sets, but a few modifications have been suggested by the researchers to cope with such limitations. The novel contributions made in this work are:
- A novel hybrid method based on elitist GA and tree based method for input FS in price prediction,
- SMO regression base SVM is used for prediction of price and result obtained is compared with classification tree (J48) [27] and regression tree [28] (bagging and M5P) with and without feature selection,
- Fixing the error margins during price prediction by applying the confidence interval, and
- Season-wise optimize FS to have a better forecasting accuracy.
The paper is organized as follows. The proposed methodology for price forecasting is summarized in Section 2. Section 3 of the paper explains the SMO regression. The methodology adopted for input FS using a novel hybrid method based on elitist GA and tree-based method is explained briefly in Section 4. Section 5 shows the outcomes and performance of the proposed methodology. Findings and concluding remarks are provided in Section 6.
2. Proposed Methodology
Forecasting of day-ahead prices with FS and without feature selection (WoFS) has been considered in this work. The present work emphasizes on an elitist GA and tree-based FS method for price forecasting. Forecast of electricity price on half hourly basis and for each day and all season, week-wise is considered. A comparison of forecasting accuracy has been made by using full feature set and that of reduce feature set, which validates the usefulness of the forecasting with a reduced feature set. The proposed methodology for comparison of different methods is shown in Figure 1. Figure 1 shows that electricity price forecasting is performed using SMO regression employing a full feature set and in parallel the same SMO regression is used with selected feature set. These two forecasting modes were compared to ascertain the superiority of FS. The result obtained from SMO Regression, WoFS and with FS methods is also compared with classification tree and regression tree.
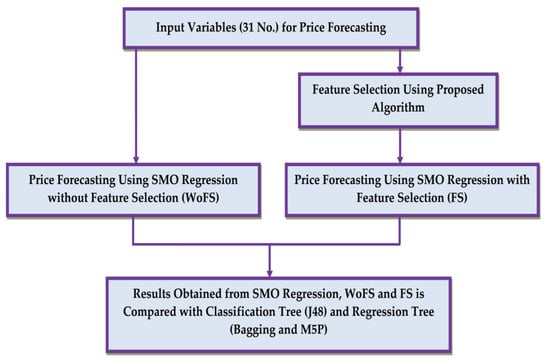
Figure 1.
Proposed methodology.
3. Sequential Minimal Optimization (SMO) Regression Algorithm
SMO regression was proposed by J. Platt (1998) as the SVM classifier design for the training of SVM (Vladimir Vapnik, 1979) by using the LIBSVM tool. SMO is used to optimize solutions of large QP without using extra matrix storage and QP optimization steps. It is probable that SMO is the only SVM optimizer that exclusively exploits the quadratic form of the objective function and it breaks large QP into sets of the smallest possible QP by using Osuna’s theorem. SMO consist two components one is analytic method and another is heuristic process. During the computation, at every step SMO uses only two Lagrange’s multiplier and solves it by using analytic method. Then by heuristic process it selects the best result to update the system to get new optimal value. This selection method needs very short and simple C coding. Therefore, it fastens the speed and omits the requirement of numerical QP optimization which requires an entire QP library routine or complex matrix algorithms.
3.1. Methodology
The SMO algorithm basically works with two steps and until convergence, the algorithm keeps repeating these steps in each iteration:
Step 1: Breaking of large QP problems into series of smallest possible QP problem. Find the most promising pair (µ1 and µ2).
Step 2: It solves small QP problems in a very fast manner compared to the QP optimization process because it consumes more time due to inner loops. It is important point to consider that it requires memory in proportion to the smallest possible samples taken under step 1. This enables it to handle a lot of training sets i.e., very large QP problems. Optimize µ1 and µ2 keeping other µ’s fixed.
A general quadratic problem has a quadratic objective function with linear constraints. A basic form is expressed by Equation (1).
where, is a vector of decision variable, contain the constant coefficients that would multiply the squared term and the a1 times a2 terms. Therefore, C needs to be multiplied two times by the column vector A. the linear term of model is defined by the coefficients are d1 and d2 in the vector. 0 defines the lower bound C is higher bound or upper bound in the constraint.
3.2. Calculation of SMO Regression
See Appendix A.
4. Input Feature Selection Using Proposed Algorithm
GA is based on the Darwinian theory of natural evolution. It is basically a heuristic search technique. In this approach no assumptions are made for relationship among features, while searching the space for feature selection. The genetic algorithm, when selecting any feature as per their importance to define the given data, decides by giving a sequence of Boolean values, allowing exploration of the feature space. It retains the features that benefit the classification task. By doing this it simultaneously avoids any local optima due to their intrinsic randomness. By using operators inspired by natural evolution such as selection, mutation and crossover, GA finds the solutions to optimize the problems. For any given dataset, FS is used to select dominating features among the pool of various feature so that handled data would be less and efficient. It is performed using an elitist technique of GA and tree based method.
In this method we select the dominant features of the input data set, which affects the process of forecasting on a priority basis. The 20% elite data from the large dataset to be presented in next generation has been selected, so that the next population is with features having classification accuracy not less than the previous generation. For the purpose of FS string of ‘0’ and ‘1’ are used in the manner of chromosome segments. In this chromosome ‘0’ shows that the specific feature corresponding to that index is not chosen and ‘1’ shows that the specific features is chosen. Here, the length of the chromosome is same as the number of features in given dataset. Computation is undertaken using data mining workbench WEKA. The fitness function is derived through tree and will be the stratified with 10-fold cross validation (10-FCV) classification accuracy. Consequently, we apply genetic operators, iteration by iteration until we met the stopping criteria. The set of selected features is the obtained chromosomes with optimal fitness function.
The mathematical definition of the fitness function for the proposed approach for feature selection is given below:
Fitness function = Classification accuracy
In this work, single site crossover with 0:5 probabilities is performed in every step through roulette wheel selection. The mutation is performed with probability of 0:005. Further, we include the elite chromosomes by keeping 20% elite chromosomes for the next generation. In this way it can be seen that the resulting population has the best chromosomes which have optimal or, best classification accuracy of the given data set. The flowchart of elitist GA and the tree-based method for FS is shown in Figure 2.
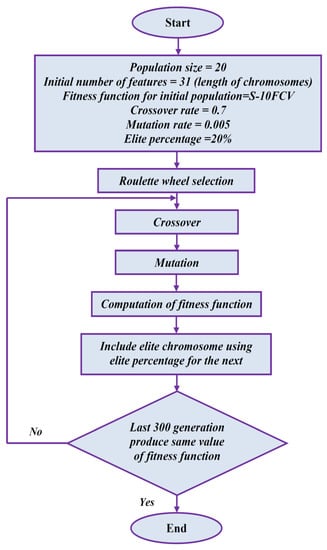
Figure 2.
Flow chart of feature selection using proposed algorithm.
5. Result and Discussion
The half hourly historical load and price data of New South Wales, Australia (taken from Australian Energy Market Operator (AEMO)), and weather data of Sydney City (www.weatherzone.com/au, accessed on 18 August 2019) has been taken from January 2014 to June 2016 for the forecasting. The elitist GA algorithm is performed in MATLAB software, whereas the formation of optimal regression tree was performed in WEKA software. The WEKA software was interfaced with MATLAB for performing all regression tree calculations. The final forecast was made using MATLAB Software. Electricity price, load, wind speed, temperature, and humidity are considered as input variable in the present study. Table 1 shows the list of input variables that may affect day ahead price forecasting. Table 1 shows the input feature set and the time delay relative to forecast hour. The input feature set is taken on the basis of various literatures.

Table 1.
List of input variables which affect electricity price forecasting.
Each data set consists of 31 input features. 2016 data sets are used in the one training set to predict the electricity price. The results obtained from the proposed work are explained in two sections. The importance of FS is discussed in first section and forecast accuracy in second section. The input variables for FS of electricity price forecasting are taken from Table 1 as input feature set. FS is performed in a weekly manner. 2016 data sets are used in the one training set to forecast the electricity price and was considered on the concept of similar weeks. Every data set consists of five similar weeks of the months of the previous year and the preceding week of the same year, e.g., if the input FS for price forecasting is to be done for the week of 22–28 August 2015, the training set would consist of the data corresponding to 15–21 August 2015, 22–28 August 2014, 15–21 August 2014, 8–14 August 2014, 29 August–04 September 2014, 05–11 September 2014. For obtaining the FS the classification accuracy of data for the classifier is calculated using 10-FCV. It means at least once complete data is tested by this method. In this way FS is the only method that can be used for conducting feature analysis. By the present studies a detailed feature analysis can be undertaken.
From Table 2 it is clear that the input variable price of present-day (Pr1) was selected in all the runs i.e., 36 times. At the same time, the price of the previous day (Pr4) was selected 22 times and the hour type (Hto) 24 times, which shows their relative importance accordingly. The load of immediate hour (Lo1) and previous day load (Lo4) was an important feature and selected 20 and 23 times respectively. The temperatures of the present day (Te1) selected more times than on the previous day. Wind speed of the previous day (Wi6) was selected more number of times than the same day. The humidity of the previous day (Hu6) was selected more times than on the same day. Effects of features can also be analyzed according to seasons. Table 2 also indicates the top 10 features selected most times.

Table 2.
Number of feature selected year wise highlighted on the top 10 features selected most times.
Table 3 indicates the season-wise importance of different features. From the Table 3 it is observed that Lo6 and Lo1 etc. are features which are assumed to have more importance during the winter season. Hu6 and Pr5 etc. are features which are assumed to have more importance during the spring season. Lo4 and Te5 etc. are features which are assumed to have more importance during the summer season. Pr1 is seem to be feature regardless of the season. These analysis indicated the relative importance of feature in terms of seasonal variations.

Table 3.
Number of times a feature selected season wise.
In this work, numerous error measures like root-mean square error (RMSE), mean absolute error (MAE), mean absolute percentage error (MAPE) and error variance (EV) are used for numerical accuracy assessment of the price forecasting as follows:
where Ap and Fp are actual and forecasted value of electricity price at time p and K is the length of forecast horizon and .
The electricity price forecasting is undertaken using SMO regression with the FS method for the New South Wales (NSW) electricity market. The average errors of each method for all seasons are calculated week-wise. Table 4 shows comparison between the SMO regression approach and seven other approaches (SMO regression, M5P, M5P+ FS, Bagging, Bagging+ FS, J48, J48+ FS), in terms of different error measures in terms of MAPE, RMSE, MAE and EV. It also summarizes the overall mean performance for each method, in the last column. Results show that the SMO regression+ FS methods perform well over all other methods used for the comparison. The error of four prior weeks are evaluated and arranged at the regular interval of half an hour from 00:00, 00:30, 01:00,...., up to 23:30 to evaluate the confidence interval for a day. Then, hourly standard deviation (δ) and 2δ are calculated for 95% confidence interval. The upper limit and lower limit calculation is as given below:
Upper Limit = Forecasted value + 2δ
Lower Limit = Forecasted value − 2δ

Table 4.
Comparison of forecast accuracy using different error measures.
The results of proposed model for winter, spring summer of NSW electricity market is depicted in Figure 3, Figure 4 and Figure 5 respectively. From the Table 4 it is clear that the proposed method (SMO regression+ FS) outperforms other methods in all seasons and for all error measures. Table 5 shows percentage improvement achieved by SMO+ FS over the considered approaches. It is observed that the SMO Reg+ FS gives 52.16% improvement over the J48 method. It can be seen that the SMO Reg+ FS has improved forecasting accuracy over all the methods considered for comparison.
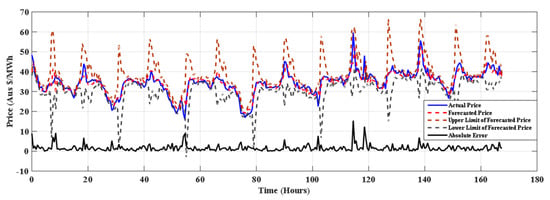
Figure 3.
Forecasting for 22–28 August 2015 in winter with SMO regression+ FS.
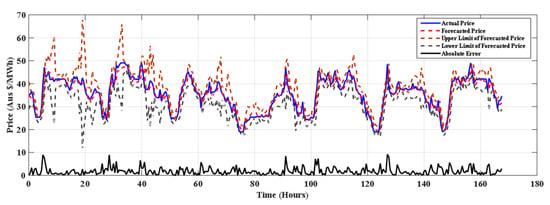
Figure 4.
Forecasting for 22–28 October 2015 in spring with SMO regression+ FS.
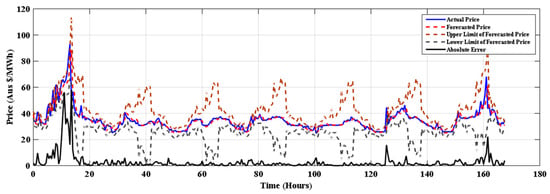
Figure 5.
Forecasting for 22–28 January 2016 in summer with SMO regression+ FS.

Table 5.
Improvement of error measures using SMO regression+ FS over other approaches.
Table 6 summarizes the daily MAPE corresponding to SMO regression and SMO regression+ FS. The daily errors for the winter, spring and summer seasons, using the SMO regression and SMO regression+ FS are depicted in Figure 6, Figure 7 and Figure 8. These results indicate that the performance of the SMO regression+ FS is generally better than the performance of the SMO regression.

Table 6.
Comparative daily MAPE corresponding to SMO regression and SMO regression+ FS.
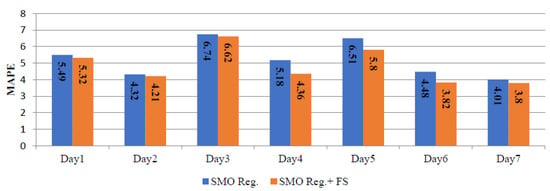
Figure 6.
Daily MAPE corresponding to SMO reg. and SMO reg.+ FS for winter season.
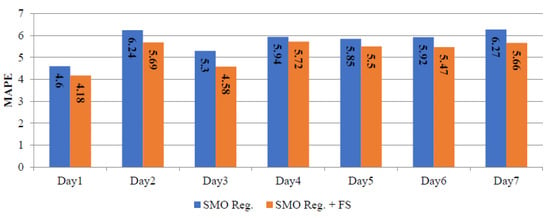
Figure 7.
Daily MAPE corresponding to SMO reg. and SMO reg.+ FS for spring season.

Figure 8.
Daily MAPE corresponding to SMO reg. and SMO reg.+ FS for summer season.
6. Conclusions
In this paper, a novel hybrid method for day ahead electricity price forecasting is presented. The elitist GA and tree-based method is used for input features selection. The forecasting is done for whole year with FS and WoFS. MAPE, RMES, MAE and EV have been calculated day-wise, week-wise and season-wise. The result obtained from SMO regression is compared with the results of classification tree (J48) and regression tree (bagging and M5P). It can be observed from the experimental results that SMO regression with FS method provides better forecast results of electricity prices than WoFS and SMO regression outperforms classification tree (J48) and regression tree (bagging and M5P)-based forecasters. It was observed that SMO regression+ FS could give improved accuracy (MAPE) in the range of 23.77 and 36.27 (for M5P and bagging) to 52.16 (for J48).
Author Contributions
Conceptualization, methodology and software, A.K.S. and A.S.P.; writing—original draft and formal analysis, A.K.S., A.S.P. R.M.E.; supervision and visualization, A.S.P. and R.M.E.; data curation, validation and investigation, A.K.S. and R.M.E.; writing—review and editing: U.S., S.M. and L.M.-P.; All authors have read and agreed to the published version of the manuscript.
Funding
The APC was funded by Ostfold University College, Halden, Norway.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The half hourly historical load and price data of New South Wales, Australia (taken from Australian Energy Market Operator (AEMO)) and weather data of Sydney City (www.weatherzone.com/au, accessed on 18 August 2019) has been taken for the forecasting.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| FS | Feature Selection |
| GA | Genetic Algorithm |
| MCP | Market Clearing Prices |
| ANN | Artificial Neural Network |
| SDA | Stacked Denoising Autoencoders |
| FFNN | Feed Forward Neural Networks |
| WT | Wavelet Transform: |
| FA-PSO | Fuzzy Adaptive Particle Swarm Optimization: |
| RF | Random Forest |
| SVM | Support Vector Machine |
| DE | Differential Evolution |
| MI | Mutual Information |
| SMO | Sequential Minimization Optimization |
| QP | Quadratic Programming |
| WoFS | Without Feature Selection |
| KKT | Karush–Kuhan–Tucker |
| 10-FCV | 10-Fold Cross Validation |
| AEMO | Australian Energy Market Operator |
| RMSE | Root-Mean Square Error |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| EV | Error Variance |
Appendix A
Calculation of SMO regression:
For a typical SMO algorithm, the dual form of the SVM minimized function and related calculations are given below from Equations (A1) to (A6).
where, ; K = kernel function subject to constraints:
Transforming the above sets of equations by,
Then the model objective function can be represented as,
To express analytically, the minimum of model objective function as a function of two parameters i.e., u and v, we have:
where are two constants, and
Representing the model objective function in terms of a single Lagrange’s multiplier by substituting for the constraint to be true after a step in parametric space keeping summative values of ‘’ be fixed:
Taking partial derivative w.r.t. and equating to zero, , we obtain:
where
The steps involved will minimize the global objective function, if any of the parameter violates the KKT (Karush–Kuhan–Tucker) conditions of regression i.e.,
If none of the parameters violates the KKT condition, the global minima have been reached.
References
- Tso, G.K.; Yau, K.K. Predicting electricity energy consumption: A comparison of regression analysis, decision tree and neural networks. Energy 2007, 32, 1761–1768. [Google Scholar] [CrossRef]
- Alghandoor, A.; Phelan, P.; Villalobos, R.; Phelan, B. US manufacturing aggregate energy intensity decomposition: The application of multivariate regression analysis. Int. J. Energy Res. 2008, 32, 91–106. [Google Scholar] [CrossRef]
- Zaza, F.; Paoletti, C.; LoPresti, R.; Simonetti, E.; Pasquali, M. Multiple regression analysis of hydrogen sulphide poisoning in molten carbonate fuel cells used for waste-to-energy conversions. Int. J. Hydrogen Energy 2011, 36, 8119–8125. [Google Scholar] [CrossRef]
- Kumar, U.; Jain, V. Time series models (Grey-Markov, Grey Model with rolling mechanism and singular spectrum analysis) to forecast energy consumption in India. Energy 2010, 35, 1709–1716. [Google Scholar] [CrossRef]
- Rumbayan, M.; Abudureyimu, A.; Nagasaka, K. Mapping of solar energy potential in Indonesia using artificial neural network and geographical information system. Renew. Sustain. Energy Rev. 2012, 16, 1437–1449. [Google Scholar] [CrossRef]
- Matallanas, E.; Castillo-Cagigal, M.; Gutiérrez, A.; Monasterio-Huelin, F.; Caamano-Martin, E.; Bote, D.M.; Jimenez-Leube, J. Neural network controller for active demand-side management with PV energy in the residential sector. Appl. Energy 2012, 91, 90–97. [Google Scholar] [CrossRef] [Green Version]
- Cheong, C.W. Parametric and non-parametric approaches in evaluating martingale hypothesis of energy spot markets. Math. Comput. Model. 2011, 54, 1499–1509. [Google Scholar] [CrossRef]
- Wesseh, P.K., Jr.; Zoumara, B. Causal independence between energy consumption and economic growth in Liberia: Evidence from a non-parametric bootstrapped causality test. Energy Policy 2012, 50, 518–527. [Google Scholar] [CrossRef]
- Hubicka, K.; Marcjasz, G.; Weron, R. A Note on Averaging Day-Ahead Electricity Price Forecasts across Calibration Windows. IEEE Trans. Sustain. Energy 2019, 10, 321–323. [Google Scholar] [CrossRef]
- Alanis, A.Y. Electricity prices forecasting using artificial neural networks. IEEE Lat. Am. Trans. 2018, 16, 105–111. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Z.; Chen, J. Short-term electricity price forecasting with stacked denoising autoencoders. IEEE Trans. Power Syst. 2017, 32, 2673–2681. [Google Scholar] [CrossRef]
- Mosbah, H.; El-Hawary, M. Hourly electricity price forecasting for the next month using multilayer neural network. Can. J. Electr. Comput. Eng. 2016, 39, 283–291. [Google Scholar] [CrossRef]
- Sarikprueck, P.; Lee, W.; Kulvanitchaiyanunt, A.; Chen, V.C.P.; Rosenberger, J. Novel Hybrid Market Price Forecasting Method With Data Clustering Techniques for EV Charging Station Application. IEEE Trans. Ind. Appl. 2015, 51, 1987–1996. [Google Scholar] [CrossRef]
- González, J.P.; San Roque, A.M.; Perez, E.A. Forecasting functional time series with a new Hilbertian ARMAX model: Applica-tion to electricity price forecasting. IEEE Trans. Power Syst. 2017, 33, 545–556. [Google Scholar] [CrossRef]
- Anamika; Peesapati, R.; Kumar, N. Electricity Price Forecasting and Classification Through Wavelet–Dynamic Weighted PSO–FFNN Approach. IEEE Syst. J. 2018, 12, 3075–3084. [Google Scholar] [CrossRef]
- Wang, K.; Xu, C.; Zhang, Y.; Guo, S.; Zomaya, A.Y. Robust Big Data Analytics for Electricity Price Forecasting in the Smart Grid. IEEE Trans. Big Data 2019, 5, 34–45. [Google Scholar] [CrossRef]
- Li, P.; Zhang, J.; Li, C.; Zhou, B.; Zhang, Y.; Zhu, M.; Ning, A. Dynamic Similar Sub-Series Selection Method for Time Series Forecasting. IEEE Access 2018, 6, 32532–32542. [Google Scholar] [CrossRef]
- Tahmasebifar, R.; Sheikh-El-Eslami, M.K.; Kheirollahi, R. Point and interval forecasting of real-time and day-ahead electricity prices by a novel hybrid approach. IET Gener. Transm. Distrib. 2017, 11, 2173–2183. [Google Scholar] [CrossRef]
- Abedinia, O.; Amjady, N.; Zareipour, H. A New Feature Selection Technique for Load and Price Forecast of Electrical Power Systems. IEEE Trans. Power Syst. 2017, 32, 62–74. [Google Scholar] [CrossRef]
- González, C.; Mira-McWilliams, J.; Juárez, I. Important variable assessment and electricity price forecasting based on regression tree models: Classification and regression trees, Bagging and Random Forests. IET Gener. Transm. Distrib. 2015, 9, 1120–1128. [Google Scholar] [CrossRef]
- Elattar, E.E.; Elsayed, S.K.; Farrag, T.A. Hybrid Local General Regression Neural Network and Harmony Search Algorithm for Electricity Price Forecasting. IEEE Access 2020, 9, 2044–2054. [Google Scholar] [CrossRef]
- Zhang, C.; Li, R.; Shi, H.; Li, F. Deep learning for day-ahead electricity price forecasting. IET Smart Grid 2020, 3, 462–469. [Google Scholar] [CrossRef]
- Zheng, K.; Wen, B.; Wang, Y.; Chen, Q. Impact of electricity price forecasting errors on bidding: A price-taker’s perspective. IET Gener. Transm. Distrib. 2020, 14, 6259–6266. [Google Scholar] [CrossRef]
- Zhang, D.; Li, Q.; Mugera, A.W.; Ling, L. A hybrid model considering cointegration for interval-valued pork price forecasting in China. J. Forecast. 2020, 39, 1324–1341. [Google Scholar] [CrossRef]
- Furqan, A.M.; Younis, S. Multi-Horizon Electricity Load and Price Forecasting using an Interpretable Multi-Head Self-Attention and EEMD-Based Framework. IEEE Access 2021, 9, 85918–85932. [Google Scholar]
- Huang, C.-J.; Shen, Y.; Chen, Y.-H.; Chen, H.-C. A novel hybrid deep neural network model for short-term electricity price forecasting. Int. J. Energy Res. 2021, 45, 2511–2532. [Google Scholar] [CrossRef]
- Srivastava, A.K.; Singh, D.; Pandey, A.S.; Maini, T. A Novel Feature Selection and Short-Term Price Forecasting Based on a Decision Tree (J48) Model. Energies 2019, 12, 3665. [Google Scholar] [CrossRef] [Green Version]
- Srivastava, A.K.; Singh, D.; Pandey, A.S. Short Term Load Forecasting Using Regression Trees: Ramdom Forest, Bagging & M5P. Int. J. Adv. Trends Comput. Sci. Eng. 2020, 9, 1898. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).