Deciding a Multicriteria Decision-Making (MCDM) Method to Prioritize Maintenance Work Orders of Hydroelectric Power Plants
Abstract
:1. Introduction
2. Support for Maintenance Decision-Making
2.1. Main MCDM Methods
2.2. Selecting an MCDM Method
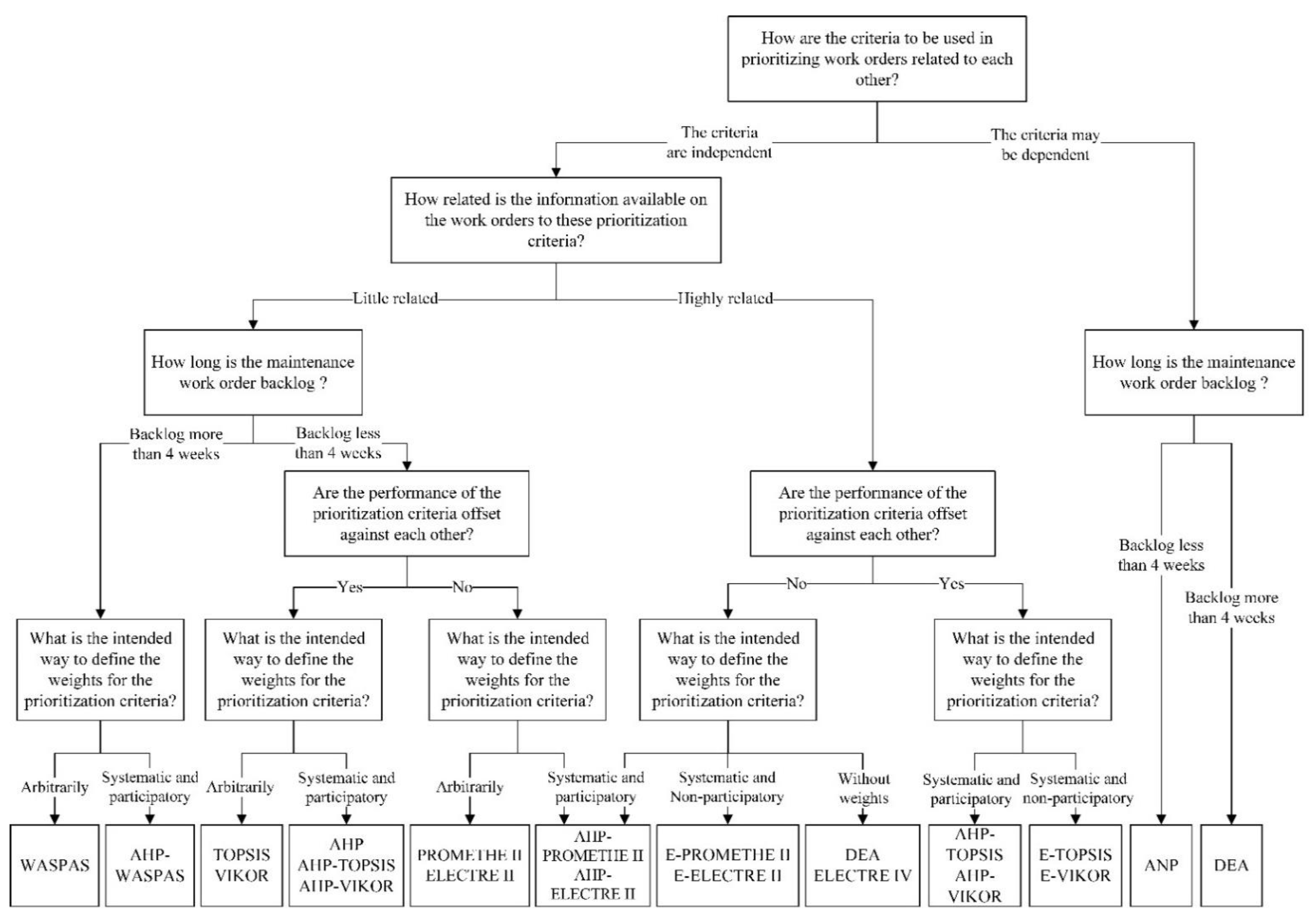
3. The Proposed Decision Tree Diagram for Deciding an MCDM Method to Prioritize Maintenance Work Orders
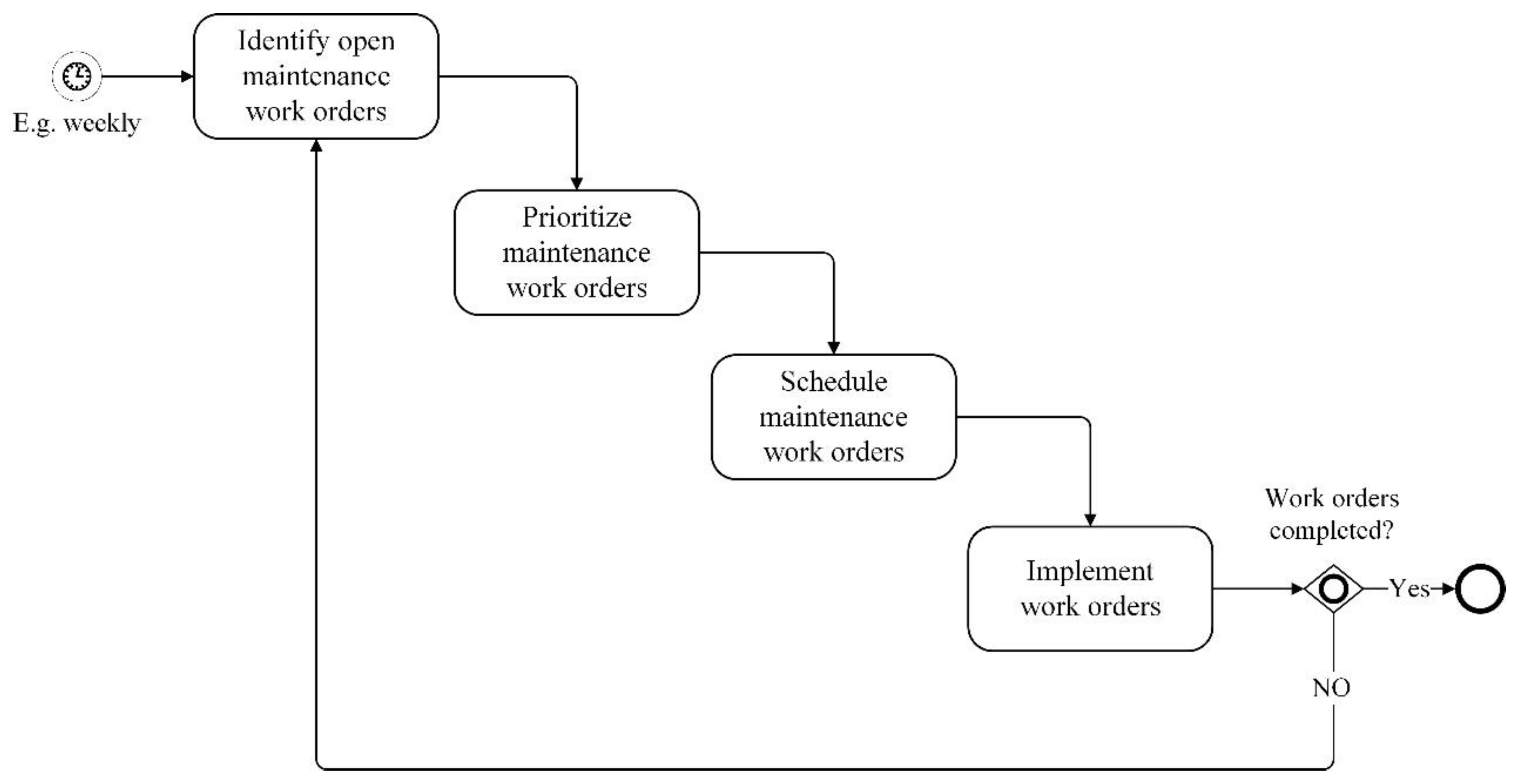
3.1. Using the Diagram
3.2. Other Points to Consider
4. Case Study
4.1. Selecting a Suitable MCMD Method
4.2. Prioritizing Maintenance Work Orders
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| MWO | Description | Location | System | MWOC | CAPA | MWOT | WT |
|---|---|---|---|---|---|---|---|
| 0018037 | Replace the spillway lifting gantry cable | Auxiliary equipment | Lifting Equipment | VH | MN | PV | 257 |
| 0018102 | External triennial inspection of the air-oil hydraulic accumulator | Generating unit 01 | Speed governor system | VL | MJ | PD | 232 |
| 0018163 | Lubrication of upstream lifting gantry elements | Auxiliary equipment | Lifting Equipment | VL | MN | PV | 223 |
| 0018186 | Replacement of corroded parts of the water intake grill | Generating unit 01 | Water intake | VH | EH | CO | 216 |
| 0018223 | External triennial inspection of the compressed air receiver | Auxiliary equipment | Compressed air | VL | MJ | PD | 213 |
| 0018425 | Analysis of the lubricating oil of the combined generator bearing | Generating unit 01 | Bearings | EL | EH | PD | 207 |
| 0018656 | Calibration of compressed air receiver pressure gauge | Auxiliary equipment | Compressed air | VL | MJ | PV | 198 |
| 0018834 | Electrical inspection of self-cleaning filter system | Generating unit 01 | Water circulation system | EL | MN | PD | 187 |
| 0018843 | Lubricating oil filtration of the combined generator bearing reservoir | Generating unit 01 | Bearings | VL | EH | PV | 187 |
| 0019862 | Fix air leakage from the compressor breather on compressor number 1 of 64 bar | Auxiliary equipment | Compressed air | VL | MJ | CO | 169 |
| 0019963 | Perform vibration analysis on exhaust fan of battery bank room | Auxiliary equipment | Exhaust and ventilation systems | EL | EL | PD | 166 |
| 0020396 | Level sensor adjustment of turbine cover | Generating unit 01 | Turbine | EL | EH | CO | 159 |
| 0021158 | Replacement of transmission belts of exhaust fan 01 | Auxiliary equipment | Exhaust and ventilation systems | VL | EL | PV | 156 |
| 0021245 | Chromatographic analysis of the insulating oil | Generating unit 01 | Step up transformer 7TR1 | VL | EH | PD | 153 |
| 0021269 | Internal triennial inspection of the compressed air receiver 25 bar | Auxiliary equipment | Compressed air | MO | MJ | PD | 150 |
| 0021526 | Analysis of the lubricating oil of the speed governor system | Generating unit 01 | Speed governor system | EL | MJ | PD | 146 |
| 0021589 | Electrical inspection of turbine guide motor pumps | Generating unit 01 | Bearings | EL | EH | PD | 135 |
| 0021783 | Electrical inspection of water intake grills cleaner | Generating unit 01 | Water intake | EL | EH | PD | 126 |
| 0021925 | Analysis of the lubricating oil of the guide turbine bearing | Generating unit 01 | Bearings | EL | EH | PD | 123 |
| 0021940 | Change the compressor lubricating oil of compressor number 1 of 8 bar | Auxiliary equipment | Compressed air | MO | MJ | PV | 120 |
| 0021963 | Cleaning of the electrical panels of the lifting equipment | Auxiliary equipment | Lifting Equipment | EL | MN | PV | 120 |
| 0022011 | Electrical inspection of the Step-up transformer 7TR1 | Generating unit 01 | Step up transformer 7TR1 | EL | EH | PD | 113 |
| 0022141 | Fix the leakage in the water intake grills cleaner hydraulic unit | Generating unit 01 | Water intake | MO | EH | CO | 112 |
| 0022229 | Electrical inspection of motorized valve 8 | Generating unit 01 | Water circulation system | EL | MN | PV | 111 |
| 0022239 | Perform vibration analysis on speed governor motor pump 2 | Generating unit 01 | Speed governor system | EL | MJ | PD | 111 |
| 0022241 | Electrical inspection of speed governor motor pump 2 | Generating unit 01 | Speed governor system | EL | MJ | PD | 111 |
| 0022251 | Cleaning of the excitation system elements | Generating unit 01 | Excitation system | EL | MJ | PV | 111 |
| 0022335 | Replacement of the combined bearing temperature sensor 4 | Generating unit 01 | Bearings | VL | EH | CO | 109 |
| 0022489 | Fix the leakage in the speed governor hydraulic unit | Generating unit 01 | Speed governor system | MO | MJ | CO | 106 |
| 0022681 | Exhaust fan 02 rotor balancing | Auxiliary equipment | Exhaust and ventilation systems | VL | EL | PV | 104 |
| 0022784 | Lubrication of water intake grills cleaner elements | Generating unit 01 | Water intake | VL | EH | PV | 102 |
| 0022855 | Calibration of air-oil hydraulic accumulator pressure gauge | Generating unit 01 | Speed governor system | VL | MJ | PV | 98 |
| 0023094 | Lubricate the bearings of the hydrant pump | Auxiliary equipment | Firefighting system | VL | EH | PV | 92 |
| 0023231 | Fix water leakage in the heat exchanger of guide turbine bearing | Generating unit 01 | Bearings | VL | EH | CO | 87 |
| 0023261 | Perform vibration analysis on combined generator bearing motor pump | Generating unit 01 | Bearings | EL | EH | PD | 85 |
| 0023346 | Annual preventive maintenance on compressor number 1 of 64 bar | Auxiliary equipment | Compressed air | MO | MJ | PV | 79 |
| 0023357 | Annual preventive maintenance on compressor number 2 of 64 bar | Auxiliary equipment | Compressed air | MO | MJ | PV | 79 |
| 0023582 | Perform motor circuit analysis on combined bearing motor pumps | Generating unit 01 | Bearings | VL | EH | PD | 75 |
| 0024023 | Thermographic analysis on the panels and relays of turbine | Generating unit 01 | Control and automation | EL | MN | PD | 65 |
| 0024051 | Thermographic analysis on the panels and relays of generator | Generating unit 01 | Control and automation | EL | MN | PD | 65 |
| 0024160 | Perform motor circuit analysis on speed governor motor pump 1 | Generating unit 01 | Speed governor system | VL | MJ | PV | 64 |
| 0024241 | Fix the oil leakage in the combine generator bearing | Generating unit 01 | Bearings | MO | MJ | CO | 62 |
| 0024283 | Replace temperature sensor 3 of excitation system | Generating unit 01 | Excitation system | VL | MJ | CO | 60 |
| 0024349 | Electrical inspection of overhead crane | Auxiliary equipment | Lifting Equipment | EL | MJ | PD | 56 |
| 0024386 | Change bearings on motor pump 2 of combine generator bearings | Generating unit 01 | Bearings | MO | EH | CO | 56 |
| 0024440 | Electrical inspection of compressor number 1 of 25 bar | Auxiliary equipment | Compressed air | EL | MJ | PD | 50 |
| 0024581 | Annual preventive maintenance on compressor number 1 of 8 bar | Auxiliary equipment | Compressed air | MO | MJ | PV | 43 |
| 0024648 | Preventive maintenance in the gasket box of turbine cover | Generating unit 01 | Turbine | VL | EH | PV | 43 |
| 0024649 | Electrical inspection of turbine cover motor pump 1 | Generating unit 01 | Turbine | EL | EH | PD | 43 |
| 0024681 | Modify position of speed governor motor pump 2 | Generating unit 01 | Speed governor system | VL | MJ | MD | 39 |
| 0024753 | Thermographic analysis of the Step-up transformer 7TR1 | Generating unit 01 | Step up transformer 7TR1 | EL | EH | PD | 38 |
| 0024762 | Cleaning and adjustment of inductive water intake gate 02 | Generating unit 01 | Water intake | EL | EH | PV | 37 |
| 0024810 | Cleaning the electrical panels of water intake gates | Generating unit 01 | Water intake | EL | MN | PV | 37 |
| 0024920 | Lubrication of overhead crane elements | Auxiliary equipment | Lifting Equipment | VL | MJ | PV | 36 |
| 0025128 | Inspection of the hydraulic actuation system of the water intake gate 01 | Generating unit 01 | Water intake | EL | EH | PD | 34 |
| 0025136 | Change the lubricating oil of the hydraulic unit | Generating unit 01 | Water intake | MO | EH | PV | 34 |
| 0025138 | Inspection of the hydraulic actuation system of the water intake gate 02 | Generating unit 01 | Water intake | EL | EH | PD | 34 |
| 0025209 | Inspection of the hydraulic actuation system of the water intake gate 03 | Generating unit 01 | Water intake | EL | EH | PD | 34 |
| 0025248 | Perform motor circuit analysis on guide bearing motor pumps | Generating unit 01 | Bearings | VL | EH | PD | 33 |
| 0025259 | Electrical inspection of excitation system | Generating unit 01 | Excitation system | EL | MN | PD | 33 |
| 0025562 | Electrical inspection of downstream lifting gantry | Auxiliary equipment | Lifting Equipment | EL | MN | PD | 28 |
| 0025651 | Cleaning the electrical panels of turbine | Generating unit 01 | Control and automation | EL | MN | PV | 24 |
| 0025669 | Electrical insulation tests of the rotor and stator | Generating unit 01 | Generator | MO | MJ | PV | 24 |
| 0025749 | Adjust position of the downstream surveillance camera | Auxiliary equipment | Vigilance camera system | EL | EL | CO | 22 |
| 0025779 | Hydraulic unit oil filtration | Generating unit 01 | Speed governor system | VL | MJ | PV | 20 |
| 0025841 | Cleaning the electrical panels of speed governor | Generating unit 01 | Control and automation | EL | MN | PV | 14 |
| 0025950 | Install online filtration system for lubricating oil | Generating unit 01 | Speed governor system | VH | EH | IP | 9 |
| 0025980 | Retighten circuit breaker connections on the speed governor panel | Generating unit 01 | Speed governor system | EL | MN | PV | 9 |
| 0026005 | Electrical inspection of compressor number 1 of 64 bar | Auxiliary equipment | Compressed air | EL | MJ | PD | 7 |
| 0026091 | Installation of an accelerometer for collecting vibration on the motor pumps | Generating unit 01 | Bearings | MO | EH | IP | 7 |
| 0026149 | Change bearings on motor pump 1 of speed governor system | Generating unit 01 | Speed governor system | MO | MJ | PV | 4 |
References
- Wisniewski, Z.; Blaszczyk, A. Changes in Maintenance Management Practices—Standards and Human Factor. Adv. Intell. Syst. Comput. 2018, 606, 348–354. [Google Scholar] [CrossRef]
- GFMAN. The Maintenance Framework, 1st ed.; The Global Forum on Maintenance & Asset Management (GFMAM): Kelowna, Canada, 2016. [Google Scholar]
- Ihemegbulem, I.; Baglee, D. ISO55000 Standard as a Driver for Effective Maintenance Budgeting. In Proceedings of the 2nd International Conference on Maintenance Engineering, Manchester, UK, 5–6 September 2017; p. 16. [Google Scholar]
- Ahuja, I.S.; Khamba, J. Total productive maintenance: Literature review and directions. Int. J. Qual. Reliab. Manag. 2008, 25, 709–756. [Google Scholar] [CrossRef] [Green Version]
- Da Silva, R.F.; De Souza, G.F.M. Asset management system (ISO 55001) and Total Productive Maintenance (TPM): A discussion of interfaces for maintenance management. Revista Gestão da Produção Operações e Sistemas 2020, 15, 288–313. [Google Scholar] [CrossRef]
- Haroun, A.E.; Duffuaa, S.O. Maintenance Organization; Springer: Singapore, 2009; pp. 3–15. [Google Scholar]
- ISO. ISO 55000—Asset Management—Overview, Principles and Terminology; ISO: Geneva, Switzerland, 2014. [Google Scholar]
- Wijnia, Y.; de Croon, J. The Asset Management Process Reference Model for Infrastructures. In 9th WCEAM Research Papers. Lecture Notes in Mechanical Engineering; Springer: Basel, Switzerland, 2015; pp. 447–457. [Google Scholar]
- Okoh, P.; Schjølberg, P.; Wilson, A. AMMP: A new maintenance management model based on ISO 55000. Infrastruct. Asset Manag. 2016, 3, 21–28. [Google Scholar] [CrossRef]
- ISO. ISO 55001—Asset Management—Management Systems—Requirements; ISO: Geneva, Switzerland, 2014. [Google Scholar]
- Goodwin, P.; Wright, G. Decision Analysis for Management Judgements, 5th ed.; John Wiley and Sons Ltd.: Hoboken, NJ, USA, 2014. [Google Scholar]
- Koornneef, H.; Verhagen, W.; Curran, R. A decision support framework and prototype for aircraft dispatch assessment. Decis. Support Syst. 2020, 135, 113338. [Google Scholar] [CrossRef]
- Özcan, E.; Ünlüsoy, S.; Eren, T. A combined goal programming—AHP approach supported with TOPSIS for maintenance strategy selection in hydroelectric power plants. Renew. Sustain. Energy Rev. 2017, 78, 1410–1423. [Google Scholar] [CrossRef]
- Melani, A.H.; Murad, C.A.; Netto, A.C.; Souza, G.F.; Nabeta, S.I. Maintenance Strategy Optimization of a Coal-Fired Power Plant Cooling Tower through Generalized Stochastic Petri Nets. Energies 2019, 12, 1951. [Google Scholar] [CrossRef] [Green Version]
- Saaty, T.L. The Analytic Hierarchy Process: Planning Setting Priorities, Resource Allocation; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Bevilacqua, M.; Braglia, M. The analytic hierarchy process applied to maintenance strategy selection. Reliab. Eng. Syst. Saf. 2000, 70, 71–83. [Google Scholar] [CrossRef]
- Belinelli, M.; Federal University of Technology; Zattar, I.C.; Da Silva, M.M.; Seleme, R.; De Souza, G.F.; Rodrigues, M.; De Oliveira, C.C.; Savoldi, A. Prioritization of the Industrial Maintenance Activities According its Ergonomics Risks using Multi-criteria Analysis AHP. Int. J. Eng. Trends Technol. 2018, 59, 214–222. [Google Scholar] [CrossRef]
- Ayag, Z.; Samanlioglu, F. Fuzzy AHP-GRA approach to evaluating energy sources: A case of Turkey. Int. J. Energy Sect. Manag. 2020, 14, 40–58. [Google Scholar] [CrossRef]
- Hwang, C.-L.; Yoon, K. Multiple Attribute Decision Making, 1st ed.; Springer: Berlin/Heidelberg, Germany, 1981. [Google Scholar]
- Bai, C.; Dhavale, D.; Sarkis, J. Integrating Fuzzy C-Means and TOPSIS for performance evaluation: An application and comparative analysis. Expert Syst. Appl. 2014, 41, 4186–4196. [Google Scholar] [CrossRef]
- Bertolini, M.; Esposito, G.; Romagnoli, G. A TOPSIS-based approach for the best match between manufacturing technologies and product specifications. Expert Syst. Appl. 2020, 159, 113610. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Network Process: Decision Making with Dependence and Feedback; RWS Publications: Pittsburgh, PA, USA, 2001. [Google Scholar]
- Zaim, S.; Turkyilmaz, A.; Acar, M.F.; Alturki, U.M.; Demirel, O.F. Maintenance strategy selection using AHP and ANP algorithms: A case study. J. Qual. Maint. Eng. 2012, 18, 16–29. [Google Scholar] [CrossRef]
- Saaty, T.L.; Vargas, L.G. Decision Making with the Analytic Network Process; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2006; Volume 282. [Google Scholar]
- Liu, P.C.Y.; Lo, H.-W.; Liou, J.J.H. A Combination of DEMATEL and BWM-Based ANP Methods for Exploring the Green Building Rating System in Taiwan. Sustainability 2020, 12, 3216. [Google Scholar] [CrossRef] [Green Version]
- Opricovic, S.; Tzeng, G.-H. A comparative analysis of the DEA-CCR model and the VIKOR method. Yugosl. J. Oper. Res. 2008, 18, 187–203. [Google Scholar] [CrossRef]
- Alinezhad, A.; Esfandiari, N. Sensitivity Analysis in the QUALIFLEX and VIKOR Methods. J. Optim. Ind. Eng. 2012, 10, 29–34. [Google Scholar]
- Brans, J.P. L’ingénièrie de la décision; Elaboration d’instruments d’aide à la décision. La méthode PROMETHEE. In L’aide à la Décision Nature, Instruments Perspect. d’Avenir; Nadeau, R., Landry, M., Eds.; Presses de l’Université Laval: Québec, QC, Canada, 1982; pp. 183–213. [Google Scholar]
- Brans, J.-P.; Mareschal, B. Promethee Methods. In Multiple Criteria Decision Analysis: State of the Art Surveys; International Series in Operations Research & Management Science; Springer: New York, NY, USA, 2005; Volume 78. [Google Scholar] [CrossRef]
- Chen, Y.-H.; Wang, T.-C.; Wu, C.-Y. Strategic decisions using the fuzzy PROMETHEE for IS outsourcing. Expert Syst. Appl. 2011, 38, 13216–13222. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Dyson, R.G.; Allen, R.; Camanho, A.S.; Podinovski, V.V.; Sarrico, C.S.; Shale, E.A. Pitfalls and Protocols in DEA. Eur. J. Oper. Res. 2001, 132, 245–259. [Google Scholar] [CrossRef]
- Roy, B.; Vanderpooten, D. The European school of MCDA: Emergence, basic features and current works. J. Multi-Criteria Decis. Anal. 1996, 5, 22–38. [Google Scholar] [CrossRef]
- Del Vasto-Terrientes, L.; Valls, A.; Slowinski, R.; Zielniewicz, P. ELECTRE-III-H: An outranking-based decision aiding method for hierarchically structured criteria. Expert Syst. Appl. 2015, 42, 4910–4926. [Google Scholar] [CrossRef]
- Żak, J.; Kruszyński, M. Application of AHP and ELECTRE III/IV Methods to Multiple Level, Multiple Criteria Evaluation of Urban Transportation Projects. Transp. Res. Procedia 2015, 10, 820–830. [Google Scholar] [CrossRef] [Green Version]
- Zavadskas, E.K.; Antucheviciene, J.; Saparauskas, J.; Turskis, Z. MCDM methods WASPAS and MULTIMOORA: Verification of robustness of methods when assessing alternative solutions. Econ. Comput. Econ. Cybern. Stud. Res. 2013, 47, 5–20. [Google Scholar]
- Chakraborty, S.; Zavadskas, E.K. Applications of WASPAS Method in Manufacturing Decision Making. Informatica 2014, 25, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Siksnelyte, I.; Zavadskas, E.K.; Streimikiene, D.; Sharma, D. An Overview of Multi-Criteria Decision-Making Methods in Dealing with Sustainable Energy Development Issues. Energies 2018, 11, 2754. [Google Scholar] [CrossRef] [Green Version]
- Huang, I.B.; Keisler, J.; Linkov, I. Multi-criteria decision analysis in environmental sciences: Ten years of applications and trends. Sci. Total Environ. 2011, 409, 3578–3594. [Google Scholar] [CrossRef] [PubMed]
- Velasquez, M.; Hester, P.T. An analysis of multi-criteria decision making methods. Int. J. Oper. Res. 2013, 10, 56–66. [Google Scholar]
- Kabir, G.; Sadiq, R.; Tesfamariam, S. A review of multi-criteria decision-making methods for infrastructure management. Struct. Infrastruct. Eng. 2014, 10, 1176–1210. [Google Scholar] [CrossRef]
- Behzadian, M.; Otaghsara, S.K.; Yazdani, M.; Ignatius, J. A state-of the-art survey of TOPSIS applications. Expert Syst. Appl. 2012, 39, 13051–13069. [Google Scholar] [CrossRef]
- Baumann, M.; Weil, M.; Peters, J.; Chibeles-Martins, N.; Moniz, A. A review of multi-criteria decision making approaches for evaluating energy storage systems for grid applications. Renew. Sustain. Energy Rev. 2019, 107, 516–534. [Google Scholar] [CrossRef]
- Gul, M.; Celik, E.; Aydin, N.; Gumus, A.T.; Guneri, A.F. A state of the art literature review of VIKOR and its fuzzy extensions on applications. Appl. Soft Comput. 2016, 46, 60–89. [Google Scholar] [CrossRef]
- Pohekar, S.; Ramachandran, M. Application of multi-criteria decision making to sustainable energy planning—A review. Renew. Sustain. Energy Rev. 2004, 8, 365–381. [Google Scholar] [CrossRef]
- Sabaei, D.; Erkoyuncu, J.; Roy, R. A Review of Multi-criteria Decision Making Methods for Enhanced Maintenance Delivery. Procedia CIRP 2015, 37, 30–35. [Google Scholar] [CrossRef] [Green Version]
- Cinelli, M.; Coles, S.R.; Kirwan, K. Analysis of the potentials of multi criteria decision analysis methods to conduct sustainability assessment. Ecol. Indic. 2014, 46, 138–148. [Google Scholar] [CrossRef] [Green Version]
- Durbach, I.N.; Stewart, T.J. Modeling uncertainty in multi-criteria decision analysis. Eur. J. Oper. Res. 2012, 223, 1–14. [Google Scholar] [CrossRef]
- Bouyssou, D. Using DEA as a Tool for MCDM: Some Remarks. J. Oper. Res. Soc. 1999, 50, 974. [Google Scholar] [CrossRef]
- Opricovic, S.; Tzeng, G.-H. Comparing DEA and MCDM Method; Springer: Singapore, 2003; pp. 227–232. [Google Scholar]
- Sarkis, J. A comparative analysis of DEA as a discrete alternative multiple criteria decision tool. Eur. J. Oper. Res. 2000, 123, 543–557. [Google Scholar] [CrossRef]
- Kheybari, S.; Rezaie, F.M.; Farazmand, H. Analytic network process: An overview of applications. Appl. Math. Comput. 2020, 367, 124780. [Google Scholar] [CrossRef]
- Si, S.-L.; You, X.-Y.; Liu, H.-C.; Zhang, P. DEMATEL Technique: A Systematic Review of the State-of-the-Art Literature on Methodologies and Applications. Math. Probl. Eng. 2018, 2018, 1–33. [Google Scholar] [CrossRef] [Green Version]
- Haddad, M.; Sanders, D. Selection of discrete multiple criteria decision making methods in the presence of risk and uncertainty. Oper. Res. Perspect. 2018, 5, 357–370. [Google Scholar] [CrossRef]
- Guitouni, A.; Martel, J.-M. Tentative guidelines to help choosing an appropriate MCDA method. Eur. J. Oper. Res. 1998, 109, 501–521. [Google Scholar] [CrossRef]
- Leite, I.M.S.; de Freitas, F.F.T. Análise Comparativa dos Métodos de Apoio Multicritério a Decisão: AHP, ELECTRE e PROMETHEE. XXXII Encontro Nac. Eng. Produção, Bento Gonçalves, RS: 2012. Available online: http://www.abepro.org.br/biblioteca/enegep2012_TN_STP_162_944_20906.pdf (accessed on 26 August 2020).
- Haddad, M.; Sanders, D.; Tewkesbury, G. Selecting a discrete multiple criteria decision making method for Boeing to rank four global market regions. Transp. Res. Part A Policy Pract. 2020, 134, 1–15. [Google Scholar] [CrossRef]
- Banihabib, M.E.; Hashemi-Madani, F.-S.; Forghani, A. Comparison of Compensatory and non-Compensatory Multi Criteria Decision Making Models in Water Resources Strategic Management. Water Resour. Manag. 2017, 31, 3745–3759. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z. A new logarithmic normalization method in games theory. Informatica 2008, 19, 303–314. [Google Scholar] [CrossRef]
- Vafaei, N.; Ribeiro, R.A.; Camarinha-Matos, L. Data normalisation techniques in decision making: Case study with TOPSIS method. Int. J. Inf. Decis. Sci. 2018, 10, 19. [Google Scholar] [CrossRef]
- Jahan, A.; Edwards, K.L. A state-of-the-art survey on the influence of normalization techniques in ranking: Improving the materials selection process in engineering design. Mater. Des. 2015, 65, 335–342. [Google Scholar] [CrossRef]
- Çelen, A. Comparative Analysis of Normalization Procedures in TOPSIS Method: With an Application to Turkish Deposit Banking Market. Informatica 2014, 25, 185–208. [Google Scholar] [CrossRef] [Green Version]
- Chan, F.T.; Prakash, A. Maintenance policy selection in manufacturing firms using the fuzzy MCDM approach. Int. J. Prod. Res. 2012, 50, 7044–7056. [Google Scholar] [CrossRef]
- Kahraman, C.; Onar, S.C.; Oztaysi, B. Fuzzy Multicriteria Decision-Making: A Literature Review. Int. J. Comput. Intell. Syst. 2015, 8, 637–666. [Google Scholar] [CrossRef] [Green Version]
- Bevilacqua, M.; Ciarapica, F.E.; Mazzuto, G. A Fuzzy Cognitive Maps Tool for Developing a RBI&M Model. Qual. Reliab. Eng. Int. 2016, 32, 373–390. [Google Scholar] [CrossRef]
- Saaty, T.L.; Vargas, L.G. Models, Methods, Concepts & Applications of the Analytic Hierarchy Process; Springer: New York, NY, USA, 2012; p. 345. [Google Scholar]
- Saaty, T.L. Decision making—The Analytic Hierarchy and Network Processes (AHP/ANP). J. Syst. Sci. Syst. Eng. 2004, 13, 1–35. [Google Scholar] [CrossRef]
- Da Silva, R.F.; Melani, A.H.A.; Michalski, M.A.; de, C.; de Souza, G.F.M.; Nabeta, S.I. Defining maintenance significant items based on ISO 55000 and AHP: A hydropower plant case study. In Proceedings of the 29th European Safety and Reliability Conference, Hannover, Germany, 22–26 September 2019; pp. 3437–3444. [Google Scholar]
- Şengül, Ü.; Eren, M.; Shiraz, S.E.; Gezder, V.; Şengül, A.B. Fuzzy TOPSIS method for ranking renewable energy supply systems in Turkey. Renew. Energy 2015, 75, 617–625. [Google Scholar] [CrossRef]
- Wei, C.-C.; Cheng, Y.-L.; Lee, K.-L. How to select suitable manufacturing information system outsourcing projects by using TOPSIS method. Int. J. Prod. Res. 2019, 57, 4333–4350. [Google Scholar] [CrossRef]
- Conejero, J.; Preciado, J.; Prieto, A.; Bas, M.; Bolós, V. Applying data driven decision making to rank vocational and educational training programs with TOPSIS. Decis. Support Syst. 2021, 142, 113470. [Google Scholar] [CrossRef]
| # | Method | Occurrence |
|---|---|---|
| 1 | Analytic Hierarchy Process (AHP) | 1286 |
| 2 | Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) | 816 |
| 3 | Analytic Network Process (ANP) | 406 |
| 4 | VIseKriterijumska Optimizacija I Kompromisno Resenje (VIKOR) | 380 |
| 5 | Preference Ranking Organization Method for Enrichment Evaluations (PROMETHEE) | 196 |
| 6 | Data Envelopment Analysis (DEA) | 141 |
| 7 | The Elimination et Choix Traduisant la Realité (ELECTRE) | 69 |
| 8 | Weighted Aggregated Sum Product Assessment (WASPAS) | 54 |
| Method | Features | Strengths | Weaknesses | References |
|---|---|---|---|---|
| AHP | This method was developed by Thomas Saaty in the 1970s and is currently one of the most popular MCDM methods. The AHP evaluates the criteria as well as the alternatives with respect to each criterion through pairwise comparison. As result, it obtains a vector of criteria weights and the priority vectors of the alternatives for each of the criteria. These vectors are synthesized to compose the global priority of the alternatives. | i. It calculates the inconsistency index which is important to ensure the consistent judgments of the decision makers; ii. Quick application compared to other methods; iii. It converts a complex problem into a simple, flexible and intuitive hierarchy; iv. It is a powerful technique when the criteria are independent. | i. Loss of information due to the high level of aggregation; ii. Difficulty in interpreting qualitative scale (e.g., “strongly”) due to human nature; iii. Its accuracy can vary widely in subjective problems; iv. The implementation is relatively inconvenient due to its complexity; v. It is cognitively demanding; vi. It is susceptible to the reversal of the classification; vii. The qualitative pairwise comparisons may imply uncertainty. | [15,16,17,18] |
| TOPSIS | This method is based on the calculation of the Euclidean distance to evaluate the distance between the ideal positive and negative solutions. Thus, the final classification of the alternatives occurs both in the shortest distance to the ideal positive solution and in the longest distance from the negative one. | i. It only depends on the weights and intrinsic characteristics of each alternative; ii. Quick application when compared to other MCDM methods; iii. Consistent and reliable; iv. Easy to implement and understandable principle; v. It works satisfactorily in different areas of application. | i. Loss of information due to the high level of aggregation; ii. It does not provide how to determine the weights for the different criteria. It is assumed that it already has this information; iii. The use of Euclidean distance does not consider the correlation of attributes. | [13,19,20,21] |
| ANP | This method was developed by Thomas Saaty as an expansion of AHP based on the Markov Chain concept. ANP mathematical modeling is characterized by a decision system that overcomes the problem of the interdependence of elements at all hierarchical levels and within the same level. | i. ANP has all the positive characteristics of AHP, including simplicity, flexibility, simultaneous use of quantitative and qualitative criteria, and the ability to review consistency in judgments; ii. It allows for dependence and includes independence and it has the ability to prioritize groups or clusters of elements. | i. It is sensitive to several criteria. As the number of criteria increases, the dimensions of the super matrices increase, which leads to the extension and/or impossibility of the resolution process; ii. The qualitative nature of comparisons made in pairs may imply uncertainty; iii. It also has the same weaknesses of the AHP. | [22,23,24,25] |
| VIKOR | From Serbian, VIKOR means “Multi-Criteria Optimization and Compromise Solution. It was developed by Serafim Opricovic and it aims to solve decision problems with conflicting criteria, through a viable compromise solution obtained by the data input (weights and criteria). | i. It is tolerant of deviations in values during the evaluation period; ii. Its algorithm can be performed without the interactive participation of decision makers. | i. Possible errors in calculation; ii. Linear normalization is necessary to solve multidimensional problems of criteria; iii. It does not provide how to determine the weights for the different criteria. | [26,27] |
| PROMETHEE | It was first introduced by J.P. Brans in the 1980s. It is a method of the outranking family with non-compensatory characteristics and consists of a preference function associated with each criterion, with the weights describing their relative importance. The initial definition of the method has distinguished between standards for a partial classification of alternatives (PROMETHEE I) or complete (PROMETHEE II). Then, later studies have created other extensions (III, IV, V, and VI). | i. It is easy to use and of low complexity; ii. It is particularly useful when there are difficulties in reconciling alternatives; iii. The advantages of this method are clarity and stability; iv. You can use qualitative and quantitative data. | i. Concerns with this method are centered on the dependence of quite arbitrary definitions of what constitutes outranking and the lack of axiomatic bases; ii. Very long computation process compared to other MCDM methods; iii. The method does not provide how to determine the weights for the different criteria; iv. It is difficult for the user to get a clear view of the problem when using many criteria. | [28,29,30] |
| DEA | Unlike most existing MCDMs, it does not use a common set of weights that can express the preferences of a decision maker. DEA mathematical modeling is based on the application of the linear programming technique to evaluate the relative efficiency of each alternative on a judgment scale ranging from 0 to 1. It identifies relationships between variables that other methods are not able to perform. | i. It does not use modeled preference information (e.g., weights or utility function); ii. It is capable of handling multiple inputs and outputs and it can discover relationships that may be hidden with other methods; iii. It can even be used for a pre-analysis, identifying the main efficient alternatives, and then applying a conventional MCDM method. | i. It does not deal with inaccurate data and assumes that all input and output data is exactly known. ii. It does not use a set of weights that express the preferences of the decision maker. iii. The user may not understand the logic and assumptions of the method for accepting them; iv. An efficient alternative in DEA could be the best or the worst compromise solution in an aggregation method. | [26,31,32] |
| ELECTRE | From French, ELECTRE means “Elimination and Choice Expressing Reality. It is a consistent MCDM belonging to the outranking family. Outranking are non-compensatory methods that were developed for situations in which there are a large number of alternatives with strong heterogeneity between criteria. Among its extensions, ELECTRE IV stands out as it does not use a common set of weights. | i. It is applicable even when information is missing; ii. It can use qualitative and quantitative data; iii. Weights are used as coefficients of importance so that compensation is not implied; iv. Its main advantage is that it takes into account uncertainty and imprecision. | i. Concerns with this method are centered on the dependence of quite arbitrary definitions of what constitutes outranking and the lack of axiomatic bases; ii. Very long computation process compared to other MCDM methods; iii. The method only draws attention to preference and ignores the level of difference between alternatives; iv. It consumes time without using specific software; v. It is considered quite difficult; | [33,34,35] |
| WASPAS | It is an elementary and compensatory multicriteria method introduced by E.K. Zavadskas. It is the only method that was developed by combining two MCDMs: WSM (Weighted Sum Model) and WPM (Weighted Product Model). Due to simple mathematical modeling and consistent result, it has been applied in the solution of many problems in several areas. | i. It consists of two mathematically-based techniques combined, WSM and WPM; ii. It is quite comprehensive in nature and it can be successfully applied to any decision-making situation; iii. It involves a simple and solid mathematical model. | i. Possible errors in calculation; ii. There is no consistency analysis process for the input data, so input data must be reliable for the result to be consistent. | [36,37] |
| # | Question | Possible Answer Options |
|---|---|---|
| 1 | How are the criteria to be used in prioritizing work orders related to each other? | The criteria are independent |
| The criteria can be dependent | ||
| 2 | How related is the information available on the work orders to these prioritization criteria? | Little related |
| Highly related | ||
| 3 | How long is the maintenance work order backlog? | Backlog more than 4 weeks |
| Backlog less than 4 weeks | ||
| 4 | Are the performance of the prioritization criteria offset against each other? | Yes |
| No | ||
| 5 | What is the intended way to define the weights for the prioritization criteria? | Arbitrary |
| Systematic and participatory (with AHP) | ||
| Systematic and non-participatory (with Entropy) | ||
| Without weights |
| # | Question | Answer |
|---|---|---|
| 1 | How are the criteria to be used in prioritizing work orders related to each other? | The criteria are independent |
| 2 | How related is the information available on the work orders to these prioritization criteria? | Highly related |
| 3 | How long is the maintenance work order backlog? | - |
| 4 | Are the performance of the prioritization criteria offset against each other? | Yes |
| 5 | What is the intended way to define the weights for the prioritization criteria? | Systematic and participatory (with AHP) |
| Weight | Criteria | Description | Performance |
|---|---|---|---|
| 0.101 | Maintenance work order cost (MWOC) | The total cost associated with the maintenance order (spare parts, labor, and logistics) | Extremally high to extremely low |
| 0.607 | Criticality of the associated physical asset (CAPA) | Score representing the degree of criticality of the associated physical asset in the service order | Extremally high to extremely low |
| 0.243 | Maintenance work order type (MWOT) | Classification of the maintenance service order according to its type of priority | A score of work order type |
| 0.048 | Waiting time (WT) | Days since the maintenance work order was opened in the CMMS for maintenance planning | Number of waiting days |
| Score | Definition | Description |
|---|---|---|
| 1 | Equal importance | Two criteria contribute equally to the prioritization of the MWO |
| 3 | Moderate importance | One criterion contributes slightly better to the prioritization of the MWO over another |
| 5 | Strong importance | One criterion contributes strongly better to the prioritization of the MWO over another |
| 7 | Very strong importance | One criterion contributes very strongly better to the prioritization of the MWO over another |
| 9 | Extreme importance | One criterion contributes extremely better to the prioritization of the MWO over another |
| MWOC | CAPA | MWOT | WT | |
|---|---|---|---|---|
| MWOC | 1 | 1/7 | 1/3 | 3 |
| CAPA | 7 | 1 | 3 | 9 |
| MWOT | 3 | 1/3 | 1 | 5 |
| WT | 1/3 | 1/9 | 1/5 | 1 |
| Scale | MWOC | CAPA | MWOT |
|---|---|---|---|
| 1 | Extremally low (EL) | Extremally low (EL) | Improvement (IP) |
| 3 | Very low (VL) | Minor (MN) | Modification (MD) |
| 5 | Moderate (MO) | Moderate (MO) | Corrective (CO) |
| 7 | Very high (VH) | Major (MJ) | Predictive (PD) |
| 9 | Extremally high (EH) | Extremally high (EH) | Preventive (PV) |
| Objective | Max. or Min. | Max. or Min. | Max. or Min. | |
|---|---|---|---|---|
| Criterion 1 | Criterion 2 | … | Criterion n | |
| Alternative 1 | x11 | x12 | … | x1n |
| Alternative 2 | x21 | x22 | … | x2n |
| Alternative 3 | x31 | x32 | … | x3n |
| … | … | … | … | … |
| Alternative m | xm1 | xm2 | … | xmn |
| wj (weight) | w1 | w2 | … | wn |
| MWO | Description | Location | CCi | Rank |
|---|---|---|---|---|
| 0018425 | Analysis of the lubricating oil of the combined generator bearing | Generating unit 01 | 0.914875 | 1 |
| 0018843 | Lubricating oil filtration of the combined generator bearing reservoir | Generating unit 01 | 0.912172 | 2 |
| 0021589 | Electrical inspection of turbine guide motor pumps | Generating unit 01 | 0.897340 | 3 |
| 0021783 | Electrical inspection of water intake grills cleaner | Generating unit 01 | 0.894533 | 4 |
| 0021925 | Analysis of the lubricating oil of the guide turbine bearing | Generating unit 01 | 0.893576 | 5 |
| 0022011 | Electrical inspection of the Step-up transformer 7TR1 | Generating unit 01 | 0.890321 | 6 |
| 0022784 | Lubrication of water intake grills cleaner elements | Generating unit 01 | 0.887751 | 7 |
| 0024762 | Cleaning and adjustment of inductive water intake gate 02 | Generating unit 01 | 0.886996 | 8 |
| 0023094 | Lubricate the bearings of the hydrant pump | Auxiliary equipment | 0.884327 | 9 |
| 0023261 | Perform vibration analysis on combined generator bearing motor pump | Generating unit 01 | 0.880757 | 10 |
| … | … | … | … | … |
| 0025562 | Electrical inspection of downstream lifting gantry | Auxiliary equipment | 0.382283 | 66 |
| 0018037 | Replace the spillway lifting gantry cable | Auxiliary equipment | 0.377074 | 67 |
| 0021158 | Replacement of transmission belts of exhaust fan 01 | Auxiliary equipment | 0.303835 | 68 |
| 0022681 | Exhaust fan 02 rotor balancing | Auxiliary equipment | 0.300278 | 69 |
| 0019963 | Perform vibration analysis on exhaust fan of battery bank room | Auxiliary equipment | 0.293832 | 70 |
| 0025749 | Adjust position of the downstream surveillance camera | Auxiliary equipment | 0.250726 | 71 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
da Silva, R.F.; Bellinello, M.M.; de Souza, G.F.M.; Antomarioni, S.; Bevilacqua, M.; Ciarapica, F.E. Deciding a Multicriteria Decision-Making (MCDM) Method to Prioritize Maintenance Work Orders of Hydroelectric Power Plants. Energies 2021, 14, 8281. https://doi.org/10.3390/en14248281
da Silva RF, Bellinello MM, de Souza GFM, Antomarioni S, Bevilacqua M, Ciarapica FE. Deciding a Multicriteria Decision-Making (MCDM) Method to Prioritize Maintenance Work Orders of Hydroelectric Power Plants. Energies. 2021; 14(24):8281. https://doi.org/10.3390/en14248281
Chicago/Turabian Styleda Silva, Renan Favarão, Marjorie Maria Bellinello, Gilberto Francisco Martha de Souza, Sara Antomarioni, Maurizio Bevilacqua, and Filippo Emanuele Ciarapica. 2021. "Deciding a Multicriteria Decision-Making (MCDM) Method to Prioritize Maintenance Work Orders of Hydroelectric Power Plants" Energies 14, no. 24: 8281. https://doi.org/10.3390/en14248281
APA Styleda Silva, R. F., Bellinello, M. M., de Souza, G. F. M., Antomarioni, S., Bevilacqua, M., & Ciarapica, F. E. (2021). Deciding a Multicriteria Decision-Making (MCDM) Method to Prioritize Maintenance Work Orders of Hydroelectric Power Plants. Energies, 14(24), 8281. https://doi.org/10.3390/en14248281









