Sensitivity Analysis and Power Systems: Can We Bridge the Gap? A Review and a Guide to Getting Started
Abstract
:1. Introduction
1.1. Sensitivity Analysis: A Quick Glance
1.1.1. Some Useful Definitions
1.1.2. Role of Sensitivity Analysis and Its Connection with Uncertainty Analysis
- Which model inputs produce the largest variation in the model output, where, and/or when?
- Which are the non-influential model inputs that can be confidently excluded from the analysis?
- Which parts of the input space produce model output values below or above a certain threshold?
- What is the impact on the model output in response to varying model inputs with respect to a baseline value?
- Does the model behavior agree with the modeler’s underlying assumptions?
- In which region of the input space does a specific condition remain optimal?
- How much would model-based inference change with alternative modeling assumptions?
1.1.3. Why So Many Sensitivity Analysis Techniques?
1.1.4. Classification of Sensitivity Analysis Methods
- Traditionally, it has been common practice across the scientific community, not only in the power system area, to adopt local SA approaches (e.g., [16,17,18,19,20]). In local SA, input variability is studied around just a specific baseline point , with the model inputs being varied over a small neighborhood (“locally”, indeed) around , which is usually the user’s operational/nominal point or what is believed to be the “appropriate” or “best known” configuration. Consequently, local sensitivity measures (such as , i.e., the model output partial derivative with respect to each of the model inputs), are dependent on the specific input space location at which they are computed. On the other hand, global SA approaches aim at exploring (at least conceptually) the whole input space, i.e., by encompassing the full range of model inputs’ variability and not only the neighborhood of [21]. It is worth noting that the applicability of local SA is valid only for “small” changes, and it is limited to just a small neighborhood around , unless the model is proven to be linear in all its inputs (whereby remains constant for any ). Importantly, if the model is nonlinear to a certain degree or large uncertainty affects the model inputs, as is often the case in power systems, local SA provides only an incomplete view of model sensitivity behavior and might offer misleading information when used for speculating upon model sensitivity behavior at a “global” level. On the other hand, global SA, though being generally more expensive than local SA, allows for the full accounting of model inputs’ uncertainty by pursuing a complete exploration of the input space;
- Besides the distinction between global and local, SA methods can be divided between OAT and AAT according to the sampling strategy viewpoint. In OAT approaches, the model inputs are varied one by one, in turn, while keeping all the others fixed at their baseline values. In AAT approaches, instead, the model inputs are simultaneously varied, e.g., as Monte Carlo simulations. The OAT sampling strategy is by far the most popular approach applied in SA, probably due to its inherent simplicity and intuitiveness [6,8]. In fact, changing one input at a time while holding all other inputs constant logically implies that whatever observed effect on the model output can be uniquely attributed to the specific perturbed input. However, as further discussed in Section 2, OAT approaches—though well matched to the analyst’s intuitive way of thinking—suffer from a major drawback: due to their nature, they cannot detect the presence of model inputs’ interactions, which thus remain unexplored. In other words, OAT strategies can reveal only the individual contribution of a given model input, whereas higher-order effects are allowed to emerge only via AAT designs, i.e., by moving (perhaps counter-intuitively at first glance) more than one input at a time.
1.1.5. Remark on Local and Global Sensitivity Analysis
1.1.6. Desirable Features of Sensitivity Analysis
- Ability to cope with scale/shape effects, i.e., incorporation of the whole variation range of the inputs and their distribution;
- Inclusion of multidimensional averaging, i.e., exploration of the input space at a global scale by simultaneously varying all inputs so as to let potential interactions emerge;
- Independence from any prior assumption on the model form, i.e., possibility to apply—and, more importantly, trust—the sensitivity measure regardless of the validity of specific model properties (an SA method possessing this property is “model-free”);
- Ability to deal with groups of model inputs, i.e., capacity to treat sets of inputs as if they were single inputs to facilitate the agility of result interpretation.
1.2. Sensitivity Analysis for Power Systems
1.3. Motivation and Objectives of the Paper
- There is a widely common conviction—see, e.g., the recent position paper [63] by a multidisciplinary authorship team with expertise in SA—that the benefits of SA, despite its wide potential, are not yet fully realized and its role in supporting modelers and experimenters is often not fully exploited across the different research fields. As demonstrated in this paper, this applies also to the power system community, due not only to terminology problems (e.g., what is really meant by “sensitivity analysis”), but supposedly also to the plethora of techniques available for performing SA, among which the (potentially beginner) SA user might easily get lost, remaining doubtful about the most suitable method for the application at hand;
- Although other SA reviews are available in different research fields (e.g., in the context of chemical [64], environmental [15], Earth-system [65], and hydrological [66] modeling), to the best of the authors’ knowledge, a thorough and up-to-date literature review on the usage of SA methods within the power system modeling community is missing;
- Unlike local SA, global SA techniques are undoubtedly less spread throughout the power system modeling community, being sometimes improperly applied or not even known (maybe because of partial communication among SA practitioners and SA final users, the relatively young age of global SA, the lack of statistical training, or the absence of discipline-specific application examples [6,27,63]).
- To provide (in Section 2) an introductory overview of the main SA methods available to the power system community, with particular focus on methodological bases, properties (weaknesses and strengths), and applicability boundaries, ultimately guiding the user in the best-fitting SA technique quest for the problem of concern;
- To present (in Section 3) a gap-filling systematic and critical literature review of the SA practice state-of-the-art in the power system field, with a suggested high-level categorization of power system applications according to the SA framework;
- To furnish (in Section 4) a ready-to-use and operational-oriented general workflow with illustration of the recommended steps for running global SA and a discussion of the user’s relevant choices.
1.4. Intended Audience for the Paper
1.5. Structure of the Paper
2. Operative Review of Sensitivity Analysis Methods
2.1. The Toy Example
2.2. Local Sensitivity Analysis Methods
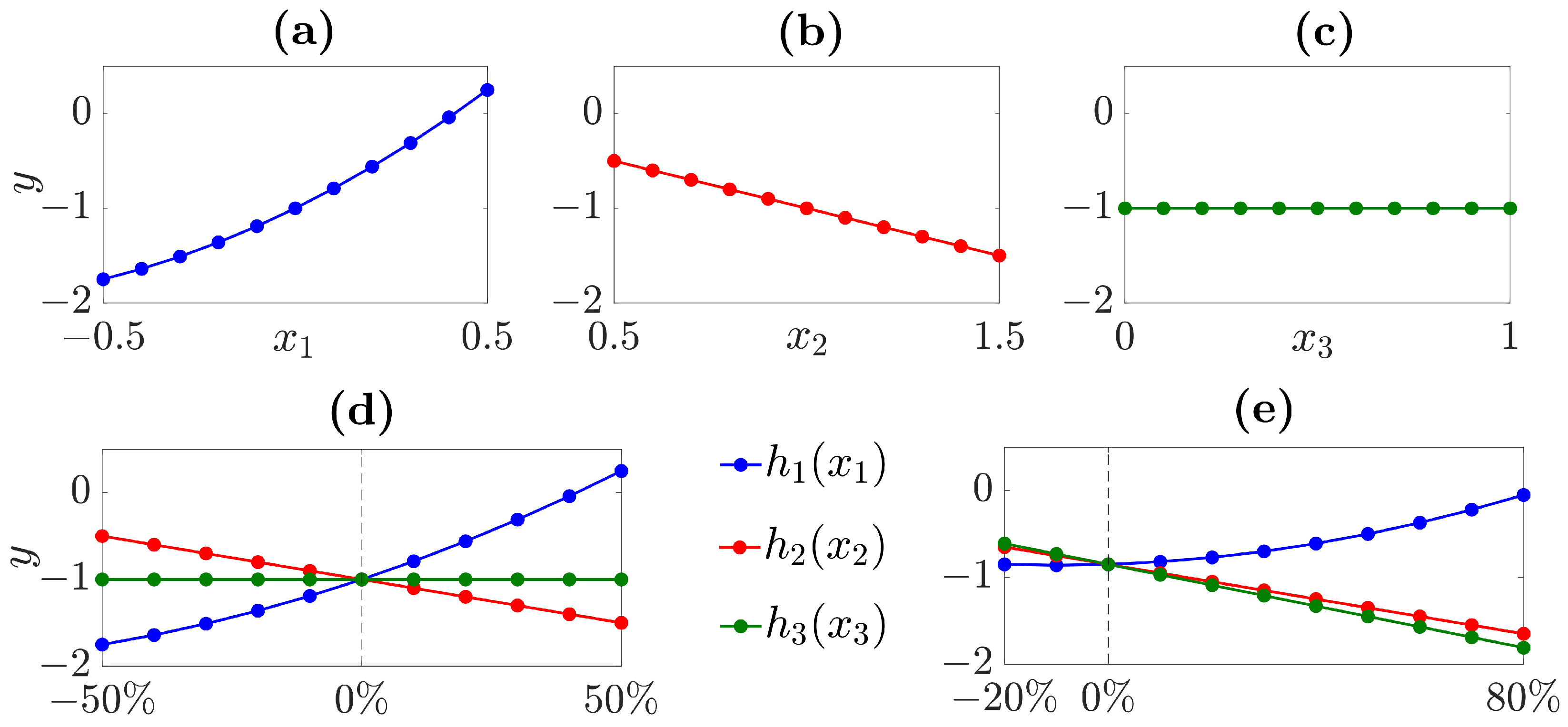
2.2.1. Tornado Diagram
2.2.2. One-Way Sensitivity Analysis
2.2.3. Scenario Analysis
- The “baseline” scenario, with all the model inputs kept at their base case values to study a reference situation;
- The “worst-case” scenario, with all the model inputs set to values that reflect some unfavorable behavior of the model;
- The “best-case” scenario, with all the model inputs set to values that produce a desirable configuration capturing some “well-behaved” pattern of the model.
2.2.4. Differential Sensitivity Analysis
2.3. Global Sensitivity Analysis Methods
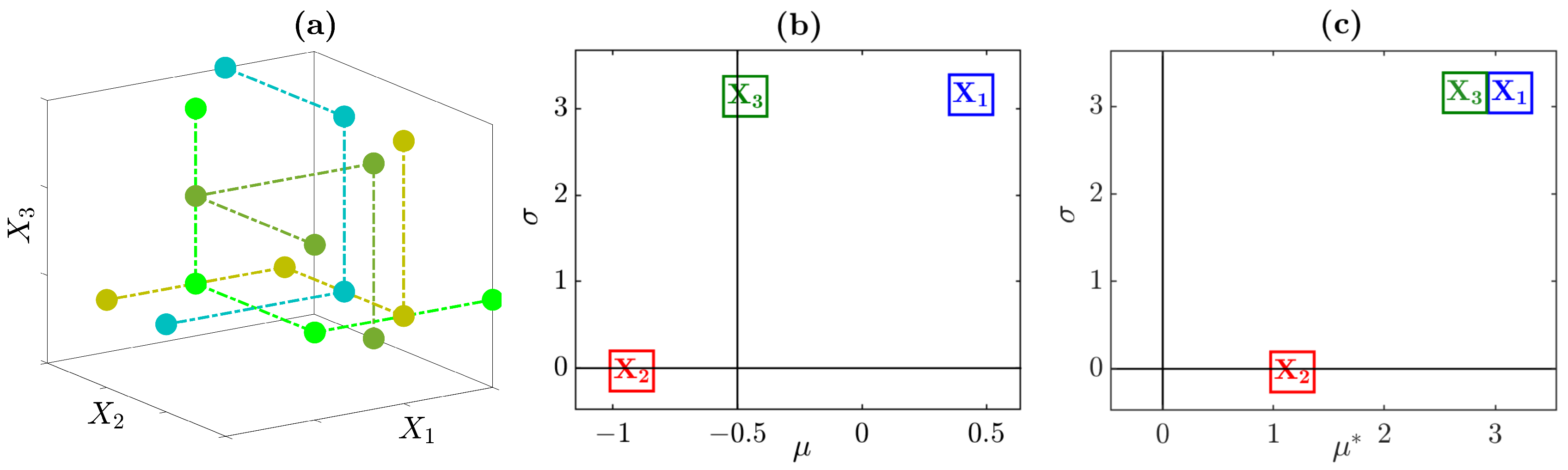
2.3.1. Morris Method
2.3.2. Correlation and Regression Analysis
2.3.3. Variance-Based Sensitivity Analysis
- if the model inputs are independent;
- if the model inputs are independent;
- if the model is additive (i.e., without interactions);
- measures how much is involved in interactions with other inputs;
- indicates the overall amount of interactions among inputs.
3. Status Quo of Sensitivity Analysis in the Power System Community
- A growing interest in the scientific community towards SA is observed in the recent years.
- The majority of published SAs tends to adopt local and OAT approaches, often relying on unjustified assumptions regarding the linearity degree of the model hence undermining the analysis credibility.
- A conceptual misunderstanding exists that leads to conflating the meaning of “sensitivity analysis” and “uncertainty analysis”, ultimately causing a degradation of the analysis quality.
- Spread practice is to perform a global UA (e.g., by Monte Carlo simulation) alongside with a local SA.
- Disciplines often based on large computer models (such as earth, environmental or energy sciences) surprisingly showcase rather low rates of global SA approaches.
3.1. Strategy for the Bibliometric Study
3.2. Review Criteria of the Bibliometric Study
3.2.1. Presence of Uncertainty and/or Sensitivity Analysis
3.2.2. Local/Global Sensitivity Analysis
- in local SA the model output uncertainty is studied in terms of variation of the model inputs around a specific baseline (e.g., Tornado diagram, one-way SA and differential SA) or by focusing just on a restricted set of model inputs’ combinations (e.g., scenario analysis);
- in global SA the model output uncertainty is studied by exploring the whole space of variability of the model inputs via OAT designs (e.g., in the Morris method) or AAT designs (e.g., in regression/correlation analysis, variance-based SA), without focusing only in a small neighborhood around a given nominal/operational point.
3.2.3. Method of Sensitivity Analysis
3.2.4. Paper Focus
- In model-focused papers the main concern of the publication is a specific algorithm/model, with SA serving purely as a support tool for evaluating the model sensitivity behavior under uncertainty. In this case the paper outcomes are application-oriented, i.e., mainly related to the model rather than to the SA method.
- In method-focused papers a specific SA method is introduced, developed or tested under various perspectives (e.g., numerical convergence, computational cost, scalability, etc.), whereas a model/algorithm is used only for the purpose of testing the SA method, whose performance is the main focus of the paper.
3.2.5. Model Type
3.2.6. Software for Sensitivity Analysis
3.3. Results of the Bibliometric Study
- the paper content actually did not perform any UA or SA (according to Definitions 1 and 2);
- the paper was the conference version of a journal article already reviewed (thus avoiding the presence of duplicates);
- the topic of the paper was not related to the power system field.
3.3.1. Presence of Uncertainty and/or Sensitivity Analysis
3.3.2. Local/Global Sensitivity Analysis
3.3.3. Method of Sensitivity Analysis
3.3.4. Paper Focus
- Ref. [41], where a fuzzy set theory based sensitivity index is developed in the context of reliability analysis of phasor measurement units;
- Ref. [180], where a “wind curtailment sensitivity index” and the respective sensitivity matrix are developed in the context of transmission network congestion;
- Ref. [52], where a strategy for optimal placement (in terms of number and location) of low voltage measurement devices is developed based on a “sensitivity order”;
- Ref. [19], where an analytical methodology is presented for calculating a set of well-known reliability indices (e.g., loss of load probability, expected power not supplied, loss of load frequency) with respect to variations in equipment failure and repair rates;
- Ref. [43], where a composite sensitivity factor based method is proposed in the context of distributed generation planning aggregating power loss and voltage sensitivity factors;
- Ref. [46], where a second-order differential SA method is proposed for assessing the optimal solution sensitivity in the context of power systems with embedded power electronics;
- Ref. [49], where a generator swing sensitivity index is proposed for evaluating the synchronous generator transient stability performance;
- Ref. [183], where three global sensitivity indices are proposed by combining principal component analysis and variance-based SA methods, considering correlated model inputs and multiple outputs for the study of microgrid operation;
- Ref. [186], where techniques for modeling the stochastic correlation between model inputs are implemented and evaluated from their performance viewpoint in the context of power system small-disturbance stability;
- Ref. [100], where a strategy based on the Morris method is applied for priority ranking of the model inputs whose correlation is modeled with the multivariate Gaussian copula method in the context of voltage and angular stability;
- Ref. [189], where a sequential experimental design based approach is used for building a surrogate model in the context of an all-electric warship AC/DC conversion system;
3.3.5. Model Type
3.3.6. Software for Sensitivity Analysis
3.3.7. Trend of Sensitivity Analysis over Time
3.4. Outcomes of the Bibliometric Study
3.4.1. Increased Interest in Sensitivity Analysis
3.4.2. Prevalence of Local Sensitivity Analysis Methods
3.4.3. Tendency to Perform Global Uncertainty Analysis Together with Local Sensitivity Analysis
3.4.4. Incorrect Beliefs Regarding Sensitivity Analysis
- Although the need for SA as a diagnostic tool is properly acknowledged, it is sometimes believed that local methods are the only viable approaches for running SA (clearly ignoring the existence of global SA techniques).
- Even if global SA is known, local SA is at times preferred to it and used under the specific motivation that the model at hand is “simple” and only a restricted amount of inputs are considered. In this regard, Section 2 has proved that even a not prohibitively complex model can conceal traps for the analyst and extreme care has to be taken when producing inferences by resorting to local and OAT SA methods. If the assumptions behind local and OAT SA methods are not valid, an uncertainty source locally not relevant might in fact reveal to be a key driver at a global scale or might gain importance because of its involvement in interactive effects with other inputs.
- Common arguments sometimes used in disfavor of global (especially variance-based) SA are, e.g., the computational burden (when high-dimensional systems are to be studied) or the inability to capture specific model properties (e.g., the direction of change produced in the model output by the inputs’ variability): these beliefs ultimately motivate the preference for local and OAT SA methods. As already discussed in Section 2.3.3 the computational cost to estimate Sobol indices can be effectively decreased by adopting alternative possibilities such as metamodel-based techniques (e.g., via PCE [140]) or sequential approaches (e.g., first performing an initial SA via cheap screening methods and then adopting a quantitative method). On the other hand certain model features of interest such as the sign of the effect, the input/output relationship, etc. can be easily retrieved at no additional cost by integrating graphical methods in the global SA workflow (e.g., scatter plots [109], CSM [160] and CSV [161] plots, CUSUNORO plots [162], cobweb plots [163]).
- When variance-based SA is used, the inputs’ ranking based on first order Sobol indices () is sometimes expected to be consistent with that obtained according to the total order Sobol indices (): such expected agreement between rankings might signalize a conceptual misunderstanding supposedly related to unclear knowledge of the SA settings. As discussed in Section 2.3.3, and convey two different concepts of input “importance” and might assume different values for the same input, hence the two associated rankings need not to be necessarily identical. In particular, produces a ranking of the inputs according to their individual contribution to the output uncertainty, whereas considers the overall effect of a specific input both alone and in synergy with other inputs. Therefore, as exemplified in Table 2, an input with small or null (i.e., almost negligible under the input prioritization setting) might have a significantly higher value of hence acquiring not negligible importance (under the input fixing setting) given its involvement in interactive effects.
3.4.5. High Level Categorization of Power System Applications
4. Global Sensitivity Analysis at Work: Ready-to-Use Workflow with a Technical Example
4.1. The System under Study
4.2. The Suggested Workflow
4.2.1. Define the Analysis Purpose
- Which of the system variability sources contributes to the system state uncertainty the most?
- Do any of the system variability sources have a negligible impact on the system state uncertainty?
- Does the model sensitivity behavior change over time?
- Do certain modeling choices affect the system state uncertainty?
4.2.2. Identify the Model
4.2.3. Identify the Model Output
4.2.4. Identify the Model Inputs
4.2.5. Characterize Model Input Uncertainty
4.2.6. Choose the Method for Sensitivity Analysis
- Purpose of the analysis—and potentially its final audience as well—in terms of the question the analyst is willing to answer (e.g., focus on a small neighborhood around an operational point or on the whole variability range, interest in input prioritization and/or model simplification, aim to understand the model structure, etc.);
- Model computational cost (in terms of number of model evaluations the analyst can afford), dependent on the model execution time and number of model inputs (e.g., for high-dimensional and time-consuming models, a low-cost SA such as the Morris method is more suitable than variance-based techniques, which might be too expensive);
- Prior model knowledge: if the model is very simple (e.g., linear and additive), local/OAT methods might be applied, whereas if the model properties are a priori unknown (e.g., in the case of “black box” models) or the model linearity assumption does not hold, global model-free methods (such as variance-based SA) are the recommended choice;
- Presence of constraints on the inputs (e.g., correlations between them, multivariate distribution properties, etc.).
- It can easily deal with all the goals stated in Questions 1–4;
- Neither the computational time (8 ms for model run by using an Intel® CoreTM i5-7200U CPU laptop with 8 GB RAM), nor the number of model inputs (five) are, in this case, a limiting factor;
- It does not rely on prior modeling assumptions (being model-free).
4.2.7. Generate the Input Sample
4.2.8. Evaluate the Model
4.2.9. Estimate Output Uncertainty
4.2.10. Extract the Sensitivity Measures and Interpret the Results
4.2.11. Iterate Sensitivity Analysis (if Needed)
4.2.12. Complement Sensitivity Analysis with Graphical Tools
5. Operative Hints and Remarks for Sensitivity Analysis
5.1. No One-Fits-All Method
5.2. Appropriately Frame the Sensitivity Analysis Question
5.3. Mind the Assumptions of the Sensitivity Analysis Method
5.4. Investigate the Impact of Discrete Model Inputs
5.5. Integrate Sensitivity Analysis Routines into the Modeling Workflow
5.6. Perform Uncertainty Analysis and Global Sensitivity Analysis in Tandem and Iteratively, Wherever Meaningful
5.7. Prefer Global Sensitivity Analysis Methods to Local and OAT Approaches in the Presence of the Inputs’ Uncertainty
5.8. Stimulate Participation in the Sensitivity Analysis Activity
5.9. Assess Sensitivity Analysis Robustness
5.10. Complement Sensitivity Analysis with Visualization Tools
6. Conclusions
- The status quo of SA within the power system community was reviewed via a systematic bibliometric study. Results showed that local SA is often the preferred choice (perhaps due to its inherent simplicity and long tradition or because of the “destructive honesty” of global SA [21]), but it is sometimes improperly adopted. An encouraging increasing trend of research works applying global SA has emerged, however, in the last decade. Nonetheless, a few wrong beliefs and systematic downsides still remain regarding SA: admitting their existence might be the foremost step towards an attempt to improve the situation;
- An introductory overview to getting started with the most widely adopted SA techniques was presented and detailed references were reported for promoting the user’s further engagement with the SA topic: being aware of the tremendous possibilities offered by the rich set of available SA techniques and understanding their underlying assumptions represent a crucial step for reaching a responsible use of SA. Knowing the merits, downsides, and applicability boundaries of each technique is in fact of paramount importance during the quest of the most suitable SA method to employ for the problem at hand. Moreover, awareness of the “behind-the-scenes” of each SA method might avoid the dangerous bad practice to adopt SA methods for research questions other than those for which the specific technique has been originally developed;
- A step-by-step and ready-to-use tutorial was presented to illustrate the global SA general workflow, with a description of recommended steps, critical aspects, and user-oriented hints. An up-to-date list of openly available software tools in the most common programming languages for running SA was also furnished to ultimately promote the integration of SA and its election as a routine “ingredient” of the power system modeling activity.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AAT | All-At-a-Time |
| covariance | |
| CSM | Contribution to the Sample Mean |
| CSV | Contribution to the Sample Variance |
| , | sensitivity measures of the Tornado diagram |
| DC | Direct Current |
| DoE | Design of Experiments |
| expected value | |
| EE | Elementary Effect |
| sensitivity measure of the one-way sensitivity analysis | |
| K | number of model inputs |
| LHS | Latin Hypercube Sampling |
| , , | sensitivity measures of the Morris method |
| OAT | One-At-a-Time |
| PCE | Polynomial Chaos Expansion |
| Probability Density Function | |
| PEAR | Pearson linear product moment correlation coefficient |
| coefficient of model determination | |
| , | sensitivity measures of the differential sensitivity analysis |
| first-order Sobol index | |
| second-order Sobol index | |
| standard deviation | |
| SA | Sensitivity Analysis |
| SPEAR | Spearman correlation coefficient |
| SRA | Scalability and Replicability Analysis |
| SRC | Standardized Regression Coefficient |
| U | Uniform probability density function |
| UA | Uncertainty Analysis |
| total-order Sobol index | |
| Var | variance |
References
- Taleb, N.N. The Black Swan: The Impact of the Highly Improbable, 1st ed.; Random House: New York, NY, USA, 2008. [Google Scholar]
- Nearing, G.S.; Gupta, H.V. Ensembles vs. information theory: Supporting science under uncertainty. Front. Earth Sci. 2018, 12, 653–660. [Google Scholar] [CrossRef]
- French, S. Modeling, making inferences and making decisions: The roles of sensitivity analysis. Top 2003, 11, 229–251. [Google Scholar] [CrossRef]
- European Commission. Impact Assessment Guidelines, SEC(2009) 92. Available online: https://ec.europa.eu/smart-regulation/impact/commission_guidelines/docs/iag_2009_en.pdf (accessed on 25 October 2021).
- United States Environmental Protection Agency. Guidance on the Development, Evaluation, and Application of Environmental Models. Available online: https://www.epa.gov/measurements-modeling/guidance-document-development-evaluation-and-application-environmental-models (accessed on 25 October 2021).
- Saltelli, A.; Aleksankina, K.; Becker, W.; Fennell, P.; Ferretti, F.; Holst, N.; Li, S.; Wu, Q. Why so many published sensitivity analyses are false: A systematic review of sensitivity analysis practices. Environ. Model. Softw. 2019, 114, 29–39. [Google Scholar] [CrossRef]
- Ferretti, F.; Saltelli, A.; Tarantola, S. Trends in sensitivity analysis practice in the last decade. Sci. Total Environ. 2016, 568, 666–670. [Google Scholar] [CrossRef]
- Saltelli, A.; Annoni, P. How to avoid a perfunctory sensitivity analysis. Environ. Model. Softw. 2010, 25, 1508–1517. [Google Scholar] [CrossRef]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis. The Primer; John Wiley & Sons, Ltd.: Chichester, UK, 2008. [Google Scholar]
- Ghanem, R.; Higdon, D.; Owhadi, H. Handbook of Uncertainty Quantification; Springer: New York, NY, USA, 2017. [Google Scholar]
- Saltelli, A.; Chan, K.; Scott, M. Sensitivity Analysis; John Wiley & Sons, Ltd.: Chichester, UK, 2000. [Google Scholar]
- Saltelli, A.; Tarantola, S.; Campolongo, F.; Ratto, M. Sensitivity Analysis in Practice: A Guide to Assessing Scientific Models; John Wiley & Sons, Ltd.: Chichester, UK, 2004. [Google Scholar]
- Cacuci, D. Sensitivity and Uncertainty Analysis, Volume I: Theory; Chapman & Hall/CRC: New York, NY, USA, 2003. [Google Scholar]
- Fisher, R.A. Statistical Methods for Research Workers, 5th ed.; Oliver and Boyd: Edinburgh, UK, 1935. [Google Scholar]
- Pianosi, F.; Beven, K.; Freer, J.; Hall, J.W.; Rougier, J.; Stephenson, D.B.; Wagener, T. Sensitivity analysis of environmental models: A systematic review with practical workflow. Environ. Model. Softw. 2016, 79, 214–232. [Google Scholar] [CrossRef]
- Turányi, T. Applications of sensitivity analysis to combustion chemistry. Reliab. Eng. Syst. Saf. 1997, 57, 41–48. [Google Scholar] [CrossRef]
- Pastres, R.; Franco, D.; Pecenik, G.; Solidoro, C.; Dejak, C. Local sensitivity analysis of a distributed parameters water quality model. Reliab. Eng. Syst. Saf. 1997, 57, 21–30. [Google Scholar] [CrossRef]
- Salehfar, H.; Trihadi, S. Application of perturbation analysis to sensitivity computations of generating units and system reliability. IEEE Trans. Power Syst. 1998, 13, 152–158. [Google Scholar] [CrossRef]
- Melo, A.; Pereira, M. Sensitivity analysis of reliability indices with respect to equipment failure and repair rates. IEEE Trans. Power Syst. 1995, 10, 1014–1021. [Google Scholar] [CrossRef]
- Lima, E. A sensitivity analysis of eigenstructures [in power system dynamic stability]. IEEE Trans. Power Syst. 1997, 12, 1393–1399. [Google Scholar] [CrossRef]
- Leamer, E.E. Sensitivity Analyses Would Help. Am. Econ. Rev. 1985, 75, 308–313. [Google Scholar]
- Snyman, J.A.; Wilke, D.N. Practical Mathematical Optimization, 2nd ed.; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Zio, E.; Podofillini, L. Accounting for components interactions in the differential importance measure. Reliab. Eng. Syst. Saf. 2006, 91, 1163–1174. [Google Scholar] [CrossRef]
- Wendell, R.E. The Tolerance Approach to Sensitivity Analysis in Linear Programming. Manag. Sci. 1985, 31, 564–578. [Google Scholar] [CrossRef]
- Rall, L.B. Automatic Differentiation: Techniques and Applications; Springer: Berlin/Heidelberg, Germany, 1981. [Google Scholar]
- Bischof, C.H.; Bücker, H.M.; Hovland, P.D.; Naumann, U.; Utke, J. (Eds.) Advances in Automatic Differentiation; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Azzini, I.; Listorti, G.; Mara, T.; Rosati, R. Uncertainty and Sensitivity Analysis for Policy Decision Making: An Introductory Guide; Publication Office of the European Union: Luxembourg, 2020. [Google Scholar]
- Saltelli, A.; Ratto, M.; Tarantola, S.; Campolongo, F. Sensitivity analysis practices: Strategies for model-based inference. Reliab. Eng. Syst. Saf. 2006, 91, 1109–1125. [Google Scholar] [CrossRef]
- Saltelli, A.; D’Hombres, B. Sensitivity analysis didn’t help. A practitioner’s critique of the Stern review. Glob. Environ. Chang. 2010, 20, 298–302. [Google Scholar] [CrossRef]
- Birnbaum, Z.W. On the Importance of Different Components in a Multicomponent System. In Proceedings of the Second International Symposium on Multivariate Analysis, Dayton, OH, USA, 17–22 June 1968; pp. 581–592. [Google Scholar]
- Pereira, M.V.F.; Pinto, L.M.V.G. Application of Sensitivity Analysis of Load Supplying Capability to Interactive Transmission Expansion Planning. IEEE Trans. Power Appar. Syst. 1985, 104, 381–389. [Google Scholar] [CrossRef]
- Giannitrapani, A.; Paoletti, S.; Vicino, A.; Zarrilli, D. Optimal Allocation of Energy Storage Systems for Voltage Control in LV Distribution Networks. IEEE Trans. Smart Grid 2017, 8, 2859–2870. [Google Scholar] [CrossRef]
- Brenna, M.; De Berardinis, E.; Delli Carpini, L.; Foiadelli, F.; Paulon, P.; Petroni, P.; Sapienza, G.; Scrosati, G.; Zaninelli, D. Automatic Distributed Voltage Control Algorithm in Smart Grids Applications. IEEE Trans. Smart Grid 2013, 4, 877–885. [Google Scholar] [CrossRef]
- Aghatehrani, R.; Kavasseri, R. Sensitivity-Analysis-Based Sliding Mode Control for Voltage Regulation in Microgrids. IEEE Trans. Sustain. Energy 2013, 4, 50–57. [Google Scholar] [CrossRef]
- Valverde, G.; Van Cutsem, T. Model Predictive Control of Voltages in Active Distribution Networks. IEEE Trans. Smart Grid 2013, 4, 2152–2161. [Google Scholar] [CrossRef] [Green Version]
- Weckx, S.; D’Hulst, R.; Driesen, J. Voltage Sensitivity Analysis of a Laboratory Distribution Grid With Incomplete Data. IEEE Trans. Smart Grid 2015, 6, 1271–1280. [Google Scholar] [CrossRef] [Green Version]
- Jhala, K.; Natarajan, B.; Pahwa, A. The Dominant Influencer of Voltage Fluctuation (DIVF) for Power Distribution System. IEEE Trans. Power Syst. 2019, 34, 4847–4856. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, T.; Gooi, H.B.; Masiello, R.D.; Katzenstein, W. Penetration Rate and Effectiveness Studies of Aggregated BESS for Frequency Regulation. IEEE Trans. Smart Grid 2016, 7, 167–177. [Google Scholar] [CrossRef]
- Preece, R.; Milanović, J.V. Assessing the Applicability of Uncertainty Importance Measures for Power System Studies. IEEE Trans. Power Syst. 2016, 31, 2076–2084. [Google Scholar] [CrossRef]
- Li, S.; Ma, Y.; Hua, Y.; Chen, P. Reliability Equivalence and Sensitivity Analysis to UHVDC Systems Based on the Matrix Description of the F&D Method. IEEE Trans. Power Deliv. 2016, 31, 456–464. [Google Scholar]
- Wang, Y.; Li, W.; Zhang, P.; Wang, B.; Lu, J. Reliability Analysis of Phasor Measurement Unit Considering Data Uncertainty. IEEE Trans. Power Syst. 2012, 27, 1503–1510. [Google Scholar] [CrossRef]
- Rodrigues, A.B.; Prada, R.B.; da Silva, M.D.G. Voltage Stability Probabilistic Assessment in Composite Systems: Modeling Unsolvability and Controllability Loss. IEEE Trans. Power Syst. 2010, 25, 1575–1588. [Google Scholar] [CrossRef]
- Zhang, C.; Xu, Y.; Dong, Z.; Ma, J. A composite sensitivity factor based method for networked distributed generation planning. In Proceedings of the 2006 Power Systems Computation Conference (PSCC), Genoa, Italy, 20–24 June 2016; pp. 1–7. [Google Scholar]
- Ehsan, A.; Yang, Q. Coordinated Investment Planning of Distributed Multi-Type Stochastic Generation and Battery Storage in Active Distribution Networks. IEEE Trans. Sustain. Energy 2019, 10, 1813–1822. [Google Scholar] [CrossRef]
- Wang, L.; Singh, C. Multicriteria Design of Hybrid Power Generation Systems Based on a Modified Particle Swarm Optimization Algorithm. IEEE Trans. Energy Convers. 2009, 24, 163–172. [Google Scholar] [CrossRef]
- Heidari, M.; Filizadeh, S.; Gole, A.M. Support Tools for Simulation-Based Optimal Design of Power Networks With Embedded Power Electronics. IEEE Trans. Power Deliv. 2008, 23, 1561–1570. [Google Scholar] [CrossRef]
- Gonzalez, A.; Echavarren, F.M.; Rouco, L.; Gomez, T. A Sensitivities Computation Method for Reconfiguration of Radial Networks. IEEE Trans. Power Syst. 2012, 27, 1294–1301. [Google Scholar] [CrossRef]
- Hiskens, I.; Alseddiqui, J. Sensitivity, Approximation, and Uncertainty in Power System Dynamic Simulation. IEEE Trans. Power Syst. 2006, 21, 1808–1820. [Google Scholar] [CrossRef] [Green Version]
- Aghamohammadi, M.R.; Beik Khormizi, A.; Rezaee, M. Effect of Generator Parameters Inaccuracy on Transient Stability Performance. In Proceedings of the 2010 Asia-Pacific Power and Energy Engineering Conference, Chengdu, China, 28–31 March 2010; pp. 1–5. [Google Scholar]
- Dui, X.; Zhu, G.; Yao, L. Two-Stage Optimization of Battery Energy Storage Capacity to Decrease Wind Power Curtailment in Grid-Connected Wind Farms. IEEE Trans. Power Syst. 2018, 33, 3296–3305. [Google Scholar] [CrossRef]
- Hashemi, S.; Østergaard, J.; Yang, G. A Scenario-Based Approach for Energy Storage Capacity Determination in LV Grids With High PV Penetration. IEEE Trans. Smart Grid 2014, 5, 1514–1522. [Google Scholar] [CrossRef]
- Cataliotti, A.; Cosentino, V.; Di Cara, D.; Tinè, G. LV Measurement Device Placement for Load Flow Analysis in MV Smart Grids. IEEE Trans. Instrum. Meas. 2016, 65, 999–1006. [Google Scholar] [CrossRef]
- Bandler, J.W.; El-Kady, M.A. A New Method for Computerized Solution of Power Flow Equations. IEEE Trans. Power Appar. Syst. 1982, 101, 1–10. [Google Scholar] [CrossRef]
- Gurram, R.; Subramanyam, B. Sensitivity analysis of radial distribution network—Adjoint network method. Int. J. Electr. Power Energy Syst. 1999, 21, 323–326. [Google Scholar] [CrossRef]
- Khatod, D.; Pant, V.; Sharma, J. A novel approach for sensitivity calculations in the radial distribution system. IEEE Trans. Power Deliv. 2006, 21, 2048–2057. [Google Scholar] [CrossRef]
- Christakou, K.; LeBoudec, J.Y.; Paolone, M.; Tomozei, D.C. Efficient Computation of Sensitivity Coefficients of Node Voltages and Line Currents in Unbalanced Radial Electrical Distribution Networks. IEEE Trans. Smart Grid 2013, 4, 741–750. [Google Scholar] [CrossRef] [Green Version]
- Tamp, F.; Ciufo, P. A Sensitivity Analysis Toolkit for the Simplification of MV Distribution Network Voltage Management. IEEE Trans. Smart Grid 2014, 5, 559–568. [Google Scholar] [CrossRef] [Green Version]
- Rocco, C.M.; Zio, E. Global Sensitivity Analysis in a Multi-State Physics Model of Component Degradation Based on a Hybrid State-Space Enrichment and Polynomial Chaos Expansion Approach. IEEE Trans. Reliab. 2013, 62, 781–788. [Google Scholar] [CrossRef] [Green Version]
- Chen, P.C.; Malbasa, V.; Dong, Y.; Kezunovic, M. Sensitivity Analysis of Voltage Sag Based Fault Location with Distributed Generation. IEEE Trans. Smart Grid 2015, 6, 2098–2106. [Google Scholar] [CrossRef]
- Hasan, K.N.; Preece, R.; Milanović, J.V. Priority Ranking of Critical Uncertainties Affecting Small-Disturbance Stability Using Sensitivity Analysis Techniques. IEEE Trans. Power Syst. 2017, 32, 2629–2639. [Google Scholar] [CrossRef] [Green Version]
- Ni, F.; Nijhuis, M.; Nguyen, P.H.; Cobben, J.F.G. Variance-Based Global Sensitivity Analysis for Power Systems. IEEE Trans. Power Syst. 2018, 33, 1670–1682. [Google Scholar] [CrossRef]
- Papaioannou, I.; Tarantola, S.; Rocha Pinto Lucas, A.; Kotsakis, E.; Marinopoulos, A.; Ginocchi, M.; Masera, M.; Olariaga-Guardiola, M. Smart Grid Interoperability Testing Methodology; Publication Office of the European Union: Luxembourg, 2018. [Google Scholar]
- Razavi, S.; Jakeman, A.; Saltelli, A.; Prieur, C.; Iooss, B.; Borgonovo, E.; Plischke, E.; Lo Piano, S.; Iwanaga, T.; Becker, W.; et al. The Future of Sensitivity Analysis: An essential discipline for systems modeling and policy support. Environ. Model. Softw. 2021, 137, 104954. [Google Scholar] [CrossRef]
- Saltelli, A.; Ratto, M.; Tarantola, S.; Campolongo, F. Sensitivity Analysis for Chemical Models. Chem. Rev. 2005, 105, 2811–2828. [Google Scholar] [CrossRef]
- Wagener, T.; Pianosi, F. What has Global Sensitivity Analysis ever done for us? A systematic review to support scientific advancement and to inform policy-making in earth system modeling. Earth-Sci. Rev. 2019, 194, 1–18. [Google Scholar] [CrossRef]
- Shin, M.J.; Guillaume, J.; Croke, B.; Jakeman, A. Addressing ten questions about conceptual rainfall–runoff models with global sensitivity analyses in R. J. Hydrol. 2013, 503, 135–152. [Google Scholar] [CrossRef]
- Marrel, A.; Iooss, B.; Da Veiga, S.; Ribatet, M. Global Sensitivity Analysis of Stochastic Computer Models with joint metamodels. Stat. Comput. 2012, 22, 833–847. [Google Scholar] [CrossRef] [Green Version]
- Moutoussamy, V.; Nanty, S.; Pauwels, B. Emulators for stochastic simulation codes. ESAIM: Proc. Surv. 2015, 48, 116–155. [Google Scholar] [CrossRef]
- Eschenbach, T.G. Spider plots versus Tornado Diagrams for Sensitivity Analysis. INFORMS J. Appl. Anal. 1992, 22, 40–46. [Google Scholar] [CrossRef]
- Rocco, C. Variability analysis of electronic systems: Classical and interval methods. In Proceedings of the Annual Reliability and Maintainability Symposium, Philadelphia, PA, USA, 13–16 January 1997; pp. 188–193. [Google Scholar]
- Bueno, E.A.B.; Utubey, W.; Hostt, R.R. Evaluating the effect of the white tariff on a distribution expansion project in Brazil. In Proceedings of the 2013 IEEE PES Conference on Innovative Smart Grid Technologies (ISGT Latin America), Sao Paulo, Brazil, 15–17 April 2013; pp. 1–8. [Google Scholar]
- Abdel-Karim, N.; Calderon, D.; Lauby, M.; Coleman, T.; Moura, J. Impact of wind and solar variability on the resource adequacy for North American bulk power system. In Proceedings of the 2016 International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), Beijing, China, 16–20 October 2016; pp. 1–8. [Google Scholar]
- Lemons, J.; Shrader-Frechette, K.; Cranor, C. The Precautionary Principle: Scientific Uncertainty and Type I and Type II Errors. Found. Sci. 1997, 2, 207–236. [Google Scholar] [CrossRef]
- Borgonovo, E.; Smith, C.L. A Study of Interactions in the Risk Assessment of Complex Engineering Systems: An Application to Space PSA. Oper. Res. 2011, 59, 1461–1476. [Google Scholar] [CrossRef]
- Gomes, V.M.; Assis, A.O.; Matias, C.A.; Saraiva, J.P.; Gomes, F.A.; Wainer, G.A.; Lima, B.S.; Magalhães, A.S.; Calixto, W.P.; Flores, P.H.R.; et al. Analytical method for calculating the sensitivity index of system parameters. In Proceedings of the 2017 CHILEAN Conference on Electrical, Electronics Engineering, Information and Communication Technologies (CHILECON), Pucon, Chile, 18–20 October 2017; pp. 1–6. [Google Scholar]
- Kërçi, T.; Milano, F. Sensitivity Analysis of the Interaction between Power System Dynamics and Unit Commitment. In Proceedings of the 2019 IEEE Milan PowerTech, Milan, Italy, 23–27 June 2019; pp. 1–6. [Google Scholar]
- Tasdighi, M.; Ghasemi, H.; Rahimi-Kian, A. Residential Microgrid Scheduling Based on Smart Meters Data and Temperature Dependent Thermal Load Modeling. IEEE Trans. Smart Grid 2014, 5, 349–357. [Google Scholar] [CrossRef]
- Amoiralis, E.I.; Tsili, M.A.; Georgilakis, P.S.; Kladas, A.G. Energy efficient transformer selection Implementing life cycle costs and environmental externalities. In Proceedings of the 2007 9th International Conference on Electrical Power Quality and Utilisation, Barcelona, Spain, 9–11 October 2007; pp. 1–6. [Google Scholar]
- Santos, S.F.; Fitiwi, D.Z.; Bizuayehu, A.W.; Shafie-khah, M.; Asensio, M.; Contreras, J.; Cabrita, C.M.P.; Catalão, J.P.S. Impacts of Operational Variability and Uncertainty on Distributed Generation Investment Planning: A Comprehensive Sensitivity Analysis. IEEE Trans. Sustain. Energy 2017, 8, 855–869. [Google Scholar] [CrossRef]
- Eschenbach, T.G.; McKeague, L.S. Exposition on Using Graphs for Sensitivity Analysis. Eng. Econ. 1989, 34, 315–333. [Google Scholar] [CrossRef]
- Stern, N. The Economics of Climate Change: The Stern Review; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Tietje, O. Identification of a small reliable and efficient set of consistent scenarios. Eur. J. Oper. Res. 2005, 162, 418–432. [Google Scholar] [CrossRef]
- Qiu, T.; Xu, B.; Wang, Y.; Dvorkin, Y.; Kirschen, D.S. Stochastic Multistage Coplanning of Transmission Expansion and Energy Storage. IEEE Trans. Power Syst. 2017, 32, 643–651. [Google Scholar] [CrossRef]
- Rodriguez-Calvo, A.; Cossent, R.; Frías, P. Scalability and replicability analysis of large-scale smart grid implementations: Approaches and proposals in Europe. Renew. Sustain. Energy Rev. 2018, 93, 1–15. [Google Scholar] [CrossRef]
- O’Brien, F. Scenario planning––Lessons for practice from teaching and learning. Eur. J. Oper. Res. 2004, 152, 709–722. [Google Scholar] [CrossRef]
- Peace, G.S. Taguchi Methods: A Hands-on Approach; Addison-Wesley: Reading, MA, USA, 1993. [Google Scholar]
- Xu, Y.; Yin, M.; Dong, Z.Y.; Zhang, R.; Hill, D.J.; Zhang, Y. Robust Dispatch of High Wind Power-Penetrated Power Systems Against Transient Instability. IEEE Trans. Power Syst. 2018, 33, 174–186. [Google Scholar] [CrossRef]
- Xie, X.; Zhang, Y.; Meng, K.; Dong, Z.Y.; Liu, J.; Tang, S. Impact of Utility-Scale Energy Storage Systems on Power System Transient Stability Considering Operating Uncertainties. In Proceedings of the 2019 IEEE Innovative Smart Grid Technologies—Asia (ISGT Asia), Chengdu, China, 21–24 May 2019; pp. 508–513. [Google Scholar]
- Borgonovo, E. Sensitivity analysis with finite changes: An application to modified EOQ models. Eur. J. Oper. Res. 2010, 200, 127–138. [Google Scholar] [CrossRef]
- Tortorelli, D.A.; Michaleris, P. Design sensitivity analysis: Overview and review. Inverse Probl. Eng. 1994, 1, 71–105. [Google Scholar] [CrossRef]
- Kettunen, J.; Salo, A.; Bunn, D.W. Optimization of Electricity Retailer’s Contract Portfolio Subject to Risk Preferences. IEEE Trans. Power Syst. 2010, 25, 117–128. [Google Scholar] [CrossRef]
- Zhao, C.; Wang, Q.; Wang, J.; Guan, Y. Expected Value and Chance Constrained Stochastic Unit Commitment Ensuring Wind Power Utilization. IEEE Trans. Power Syst. 2014, 29, 2696–2705. [Google Scholar] [CrossRef]
- Djukanovic, M.; Khammash, M.; Vittal, V. Sensitivity based structured singular value approach to stability robustness of power systems. IEEE Trans. Power Syst. 2000, 15, 825–830. [Google Scholar] [CrossRef]
- Song, G.; Kolmanovsky, I.; Gibson, A. Sensitivity Equations Based Experiment Design and Adaptive Compensation of Transient Fuel Dynamics in Port-Fuel Injection Engines. In Proceedings of the 2007 IEEE International Conference on Control Applications, Singapore, 1–3 October 2007; pp. 1388–1393. [Google Scholar]
- Griewank, A.; Walther, A. Evaluating Derivatives: Principles and Techniques of Algorithmic Differentiation, 2nd ed.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2008. [Google Scholar]
- Gustafsson, S.; Biro, T.; Cinar, G.; Gustafsson, M.; Karlsson, A.; Nilsson, B.; Nordebo, S.; Sjöberg, M. Electromagnetic Dispersion Modeling and Measurements for HVDC Power Cables. IEEE Trans. Power Deliv. 2014, 29, 2439–2447. [Google Scholar] [CrossRef] [Green Version]
- Souza Lima, E.; De Jesus Fernandes, L. Assessing eigenvalue sensitivities [power system control simulation]. IEEE Trans. Power Syst. 2000, 15, 299–306. [Google Scholar] [CrossRef]
- Borgonovo, E.; Plischke, E. Sensitivity analysis: A review of recent advances. Eur. J. Oper. Res. 2016, 248, 869–887. [Google Scholar] [CrossRef]
- Hasan, K.N.; Preece, R.; Milanović, J.V. Efficient identification of critical parameters affecting the small-disturbance stability of power systems with variable uncertainty. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar]
- Qi, B.; Hasan, K.N.; Milanović, J.V. Identification of Critical Parameters Affecting Voltage and Angular Stability Considering Load-Renewable Generation Correlations. IEEE Trans. Power Syst. 2019, 34, 2859–2869. [Google Scholar] [CrossRef] [Green Version]
- Rohadi, N.; Živanovic, R. Sensitivity analysis of a fault impedance measurement algorithm applied in protection of parallel transmission lines. In Proceedings of the 9th IET International Conference on Advances in Power System Control, Operation and Management (APSCOM 2012), Hong Kong, 18–21 November 2012; pp. 1–6. [Google Scholar]
- Liu, S.; Jin, D.; Ma, Z.; Wei, X.; Zhang, L. Survey of Morris and E-FAST algorithms based on power-generation operation and assistant decision model. In Proceedings of the 2015 8th International Conference on Ubi-Media Computing (UMEDIA), Colombo, Sri Lanka, 24–26 August 2015; pp. 344–349. [Google Scholar]
- Morris, M.D. Factorial sampling plans for preliminary computational experiments. Technometrics 1991, 33, 161–174. [Google Scholar] [CrossRef]
- Campolongo, F.; Cariboni, J.; Saltelli, A. An effective screening design for sensitivity analysis of large models. Environ. Model. Softw. 2007, 22, 1509–1518. [Google Scholar] [CrossRef]
- Campolongo, F.; Saltelli, A. Sensitivity analysis of an environmental model: An application of different analysis methods. Reliab. Eng. Syst. Saf. 1997, 57, 49–69. [Google Scholar] [CrossRef]
- Campolongo, F.; Tarantola, S.; Saltelli, A. Tackling quantitatively large dimensionality problems. Comput. Phys. Commun. 1999, 117, 75–85. [Google Scholar] [CrossRef]
- Iman, R.L.; Conover, W.J. The Use of the Rank Transform in Regression. Technometrics 1979, 21, 499–509. [Google Scholar] [CrossRef]
- Saltelli, A.; Marivoet, J. Non-parametric statistics in sensitivity analysis for model output: A comparison of selected techniques. Reliab. Eng. Syst. Saf. 1990, 28, 229–253. [Google Scholar] [CrossRef]
- Kleijnen, J.; Helton, J. Statistical analyses of scatterplots to identify important factors in large-scale simulations, 1: Review and comparison of techniques. Reliab. Eng. Syst. Saf. 1999, 65, 147–185. [Google Scholar] [CrossRef] [Green Version]
- Niederreiter, H. Random Number Generation and Quasi-Monte Carlo Methods; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1992. [Google Scholar]
- Sobol, I.; Kucherenko, S. On Global sensitivity analysis of quasi-Monte Carlo algorithms. Monte Carlo Methods Appl. 2005, 11, 83–92. [Google Scholar] [CrossRef]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code. Technometrics 1979, 21, 239–245. [Google Scholar]
- Helton, J.C. Uncertainty and sensitivity analysis techniques for use in performance assessment for radioactive waste disposal. Reliab. Eng. Syst. Saf. 1993, 42, 327–367. [Google Scholar] [CrossRef]
- Iman, R.; Campbell, J.; Helton, J. An approach to sensitivity analysis of computer models: Part I—Introduction, Input Variable Selection and Preliminary Variable Assessment. J. Qual. Technol. 1981, 13, 174–183. [Google Scholar] [CrossRef]
- Spearman, C. The Proof and Measurement of Association between Two Things. Am. J. Psychol. 1904, 15, 72–101. [Google Scholar] [CrossRef]
- Razavi, S.; Gupta, H. What do we mean by sensitivity analysis? The need for comprehensive characterization of “global” sensitivity in Earth and Environmental systems models: A Critical Look at Sensitivity Analysis. Water Resour. Res. 2015, 51, 3070–3092. [Google Scholar] [CrossRef]
- Larbi, M.; Stievano, I.S.; Canavero, F.G.; Besnier, P. Variability Impact of Many Design Parameters: The Case of a Realistic Electronic Link. IEEE Trans. Electromagn. Compat. 2018, 60, 34–41. [Google Scholar] [CrossRef]
- Sobol’, I.M. Sensitivity analysis for nonlinear mathematical models. Math. Model. Comput. Exp. 1993, 1, 407–414. [Google Scholar]
- Ishigami, T.; Homma, T. An importance quantification technique in uncertainty analysis for computer models. In Proceedings of the First International Symposium on Uncertainty Modeling and Analysis, College Park, MD, USA, 3–5 December 1990; pp. 398–403. [Google Scholar]
- Iman, R.L.; Hora, S.C. A Robust Measure of Uncertainty Importance for Use in Fault Tree System Analysis. Risk Anal. 1990, 10, 401–406. [Google Scholar] [CrossRef]
- Pearson, K. On the General Theory of Skew Correlation and Non-Linear Regression; Dulau and Co.: London, UK, 1905. [Google Scholar]
- Saltelli, A.; Annoni, P.; Azzini, I.; Campolongo, F.; Ratto, M.; Tarantola, S. Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index. Comput. Phys. Commun. 2010, 181, 259–270. [Google Scholar] [CrossRef]
- Cukier, R.I.; Fortuin, C.M.; Shuler, K.E.; Petschek, A.G.; Schaibly, J.H. Study of the sensitivity of coupled reaction systems to uncertainties in rate coefficients. I Theory. J. Chem. Phys. 1973, 59, 3873–3878. [Google Scholar] [CrossRef]
- Saltelli, A.; Tarantola, S. On the Relative Importance of Input Factors in Mathematical Models: Safety Assessment for Nuclear Waste Disposal. J. Am. Stat. Assoc. 2002, 97, 702–709. [Google Scholar] [CrossRef]
- Homma, T.; Saltelli, A. Importance measures in global sensitivity analysis of nonlinear models. Reliab. Eng. Syst. Saf. 1996, 52, 1–17. [Google Scholar] [CrossRef]
- Oreskes, N.; Shrader-Frechette, K.; Belitz, K. Verification, Validation, and Confirmation of Numerical Models in the Earth Science. Science 1994, 263, 641–646. [Google Scholar] [CrossRef] [Green Version]
- Sobol, I.; Tarantola, S.; Gatelli, D.; Kucherenko, S.; Mauntz, W. Estimating the approximation error when fixing unessential factors in global sensitivity analysis. Reliab. Eng. Syst. Saf. 2007, 92, 957–960. [Google Scholar] [CrossRef]
- Sobol, I.M. A Primer for the Monte Carlo Method, 1st ed.; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Saltelli, A. Making best use of model evaluations to compute sensitivity indices. Comput. Phys. Commun. 2002, 145, 280–297. [Google Scholar] [CrossRef]
- Jansen, M.J. Analysis of variance designs for model output. Comput. Phys. Commun. 1999, 117, 35–43. [Google Scholar] [CrossRef]
- Janon, A.; Klein, T.; Lagnoux-Renaudie, A.; Nodet, M.; Prieur, C. Asymptotic normality and efficiency of two Sobol index estimators. ESAIM: Probab. Stat. 2014, 18, 342–364. [Google Scholar] [CrossRef] [Green Version]
- Archer, G.E.B.; Saltelli, A.; Sobol’, I.M. Sensitivity measures, anova-like Techniques and the use of bootstrap. J. Stat. Comput. Simul. 1997, 58, 99–120. [Google Scholar] [CrossRef]
- Efron, B.; Stein, C. The Jackknife Estimate of Variance. Ann. Stat. 1981, 9, 586–596. [Google Scholar] [CrossRef]
- Joe, S.; Kuo, F. Remark on Algorithm 659: Implementing Sobol’s quasirandom sequence generator. ACM Trans. Math. Softw. 2003, 29, 49–57. [Google Scholar] [CrossRef]
- Saltelli, A.; Tarantola, S.; Chan, K.P.S. A Quantitative Model-Independent Method for Global Sensitivity Analysis of Model Output. Technometrics 1999, 41, 39–56. [Google Scholar] [CrossRef]
- Tarantola, S.; Gatelli, D.; Mara, T. Random balance designs for the estimation of first order global sensitivity indices. Reliab. Eng. Syst. Saf. 2006, 91, 717–727. [Google Scholar] [CrossRef] [Green Version]
- Mara, T. Extension of the RBD-FAST method to the computation of global sensitivity indices. Reliab. Eng. Syst. Saf. 2009, 94, 1274–1281. [Google Scholar] [CrossRef] [Green Version]
- Plischke, E. An effective algorithm for computing global sensitivity indices (EASI). Reliab. Eng. Syst. Saf. 2010, 95, 354–360. [Google Scholar] [CrossRef]
- Storlie, C.B.; Helton, J.C. Multiple predictor smoothing methods for sensitivity analysis: Description of techniques. Reliab. Eng. Syst. Saf. 2008, 93, 28–54. [Google Scholar] [CrossRef]
- Sudret, B. Global sensitivity analysis using polynomial chaos expansions. Reliab. Eng. Syst. Saf. 2008, 93, 964–979. [Google Scholar] [CrossRef]
- Blatman, G.; Sudret, B. Adaptive sparse polynomial chaos expansion based on least angle regression. J. Comput. Phys. 2011, 230, 2345–2367. [Google Scholar] [CrossRef]
- Oakley, J.E.; O’Hagan, A. Probabilistic sensitivity analysis of complex models: A Bayesian approach. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2004, 66, 751–769. [Google Scholar] [CrossRef] [Green Version]
- Sudret, B. Meta-models for structural reliability and uncertainty quantification. In Proceedings of the Asian-Pacific Symposium on Structural Reliability and its Applications (APSSRA’2012), Singapore, 23–25 May 2012; pp. 1–24. [Google Scholar]
- Krzykacz-Hausmann, B. Epistemic sensitivity analysis based on the concept of entropy. In Proceedings of the 3rd International Conference on Sensitivity Analysis of Model Output, Madrid, Spain, 18–20 June 2001; pp. 31–35. [Google Scholar]
- Borgonovo, E. A new uncertainty importance measure. Reliab. Eng. Syst. Saf. 2007, 92, 771–784. [Google Scholar] [CrossRef]
- Plischke, E.; Borgonovo, E.; Smith, C.L. Global sensitivity measures from given data. Eur. J. Oper. Res. 2013, 226, 536–550. [Google Scholar] [CrossRef]
- Kucherenko, S.; Tarantola, S.; Annoni, P. Estimation of global sensitivity indices for models with dependent variables. Comput. Phys. Commun. 2012, 183, 937–946. [Google Scholar] [CrossRef]
- Li, G.; Rabitz, H.; Yelvington, P.E.; Oluwole, O.O.; Bacon, F.; Kolb, C.E.; Schoendorf, J. Global Sensitivity Analysis for Systems with Independent and/or Correlated Inputs. J. Phys. Chem. A 2010, 114, 6022–6032. [Google Scholar] [CrossRef]
- Jacques, J.; Lavergne, C.; Devictor, N. Sensitivity analysis in presence of model uncertainty and correlated inputs. Reliab. Eng. Syst. Saf. 2006, 91, 1126–1134. [Google Scholar] [CrossRef]
- Xu, C.; Gertner, G.Z. Uncertainty and sensitivity analysis for models with correlated parameters. Reliab. Eng. Syst. Saf. 2008, 93, 1563–1573. [Google Scholar] [CrossRef]
- Mara, T.; Tarantola, S. Variance-based Sensitivity Indices for Models with Dependent Inputs. Reliab. Eng. Syst. Saf. 2011, 107, 115–121. [Google Scholar] [CrossRef] [Green Version]
- Mara, T.A.; Becker, W.E. Polynomial chaos expansion for sensitivity analysis of model output with dependent inputs. Reliab. Eng. Syst. Saf. 2021, 214, 107795:1–107795:12. [Google Scholar] [CrossRef]
- Owen, A.; Prieur, C. On Shapley Value for Measuring Importance of Dependent Inputs. SIAM/ASA J. Uncertain. Quantif. 2016, 5, 986–1002. [Google Scholar] [CrossRef] [Green Version]
- Sobol, I.; Kucherenko, S. A new derivative based importance criterion for groups of variables and its link with the global sensitivity indices. Comput. Phys. Commun. 2010, 181, 1212–1217. [Google Scholar] [CrossRef]
- Pianosi, F.; Wagener, T. A simple and efficient method for global sensitivity analysis based on cumulative distribution functions. Environ. Model. Softw. 2015, 67, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Spear, R.C.; Grieb, T.M.; Shang, N. Parameter uncertainty and interaction in complex environmental models. Water Resour. Res. 1994, 30, 3159–3169. [Google Scholar] [CrossRef]
- Liu, H.; Chen, W.; Sudjianto, A.; Chen, D. Relative Entropy Based Method for Probabilistic Sensitivity Analysis in Engineering Design. J. Mech. Des. 2005, 128, 326–336. [Google Scholar] [CrossRef]
- Razavi, S.; Gupta, H. A new framework for comprehensive, robust, and efficient global sensitivity analysis: 1. Theory. Water Resour. Res. 2015, 52, 423–439. [Google Scholar] [CrossRef] [Green Version]
- Razavi, S.; Gupta, H.V. A new framework for comprehensive, robust, and efficient global sensitivity analysis: 2. Application. Water Resour. Res. 2016, 52, 440–455. [Google Scholar] [CrossRef]
- Bolado-Lavin, R.; Castaings, W.; Tarantola, S. Contribution to the sample mean plot for graphical and numerical sensitivity analysis. Reliab. Eng. Syst. Saf. 2009, 94, 1041–1049. [Google Scholar] [CrossRef]
- Tarantola, S.; Kopustinskas, V.; Bolado-Lavin, R.; Kaliatka, A.; Ušpuras, E.; Vaišnoras, M. Sensitivity analysis using contribution to sample variance plot: Application to a water hammer model. Reliab. Eng. Syst. Saf. 2012, 99, 62–73. [Google Scholar] [CrossRef]
- Plischke, E. The Cusunoro Curve: A Visual Tool for Global Sensitivity Analysis. In Proceedings of the 29th European Safety and Reliability Conference (ESREL), Hannover, Germany, 22–26 September 2019; pp. 2748–2753. [Google Scholar]
- Kurowicka, D.; Cooke, R.M. Uncertainty Analysis with High Dimensional Dependence Modeling; John Wiley & Sons, Ltd.: Chichester, UK, 2006. [Google Scholar]
- Butler, M.P.; Reed, P.M.; Fisher-Vanden, K.; Keller, K.; Wagener, T. Identifying parametric controls and dependencies in integrated assessment models using global sensitivity analysis. Environ. Model. Softw. 2014, 59, 10–29. [Google Scholar] [CrossRef]
- Van Werkhoven, K.; Wagener, T.; Reed, P.; Tang, Y. Sensitivity-guided reduction of parametric dimensionality for multi-objective calibration of watershed models. Adv. Water Resour. 2009, 32, 1154–1169. [Google Scholar] [CrossRef]
- Norton, J. An introduction to sensitivity assessment of simulation models. Environ. Model. Softw. 2015, 69, 166–174. [Google Scholar] [CrossRef]
- Iooss, B.; Lemaître, P. A Review on Global Sensitivity Analysis Methods. In Uncertainty Management in Simulation-Optimization of Complex Systems: Algorithms and Applications; Dellino, G., Meloni, C., Eds.; Springer: Boston, MA, USA, 2015; pp. 101–122. [Google Scholar]
- Gupta, H.; Razavi, S. Chapter 20—Challenges and Future Outlook of Sensitivity Analysis. In Sensitivity Analysis in Earth Observation Modeling; Petropoulos, G.P., Srivastava, P.K., Eds.; Elsevier: Amsterdam, The Netherlands, 2017; pp. 397–415. [Google Scholar]
- Aien, M.; Hajebrahimi, A.; Fotuhi-Firuzabad, M. A comprehensive review on uncertainty modeling techniques in power system studies. Renew. Sustain. Energy Rev. 2016, 57, 1077–1089. [Google Scholar] [CrossRef]
- Kasturi, R.; Dorraju, P. Sensitivity Analysis of Power Systems. IEEE Trans. Power Appar. Syst. 1969, 88, 1521–1529. [Google Scholar] [CrossRef]
- Pauli, F.; Sulligoi, G.; Lughi, V.; Pavan, A.M. Grid parity in the Italian domestic PV market a sensitivity analysis. In Proceedings of the 2015 International Conference on Renewable Energy Research and Applications (ICRERA), Palermo, Italy, 22–25 November 2015; pp. 1477–1480. [Google Scholar]
- Macii, D.; Barchi, G.; Petri, D. Uncertainty sensitivity analysis of WLS-based grid state estimators. In Proceedings of the 2014 IEEE International Workshop on Applied Measurements for Power Systems Proceedings (AMPS), Aachen, Germany, 24–26 September 2014; pp. 1–6. [Google Scholar]
- Hsiao, T.; Shieh, C.; Lu, C. Reliability evaluation of a Taipower system protection scheme. In Proceedings of the IEEE PES Power Systems Conference and Exposition, New York, NY, USA, 10–13 October 2004; pp. 157–162. [Google Scholar]
- Choi, H.; Seiler, P.J.; Dhople, S.V. Propagating Uncertainty in Power Flow With the Alternating Direction Method of Multipliers. IEEE Trans. Power Syst. 2018, 33, 4124–4133. [Google Scholar] [CrossRef]
- Xu, X.; Yan, Z.; Shahidehpour, M.; Chen, S.; Wang, H.; Li, Z.; Zhou, Q. Maximum Loadability of Islanded Microgrids with Renewable Energy Generation. IEEE Trans. Smart Grid 2019, 10, 4696–4705. [Google Scholar] [CrossRef]
- Qi, B.; Milanovic, J.V. Identification of critical parameters affecting voltage stability in networks with renewable generations using sensitivity analysis methods. In Proceedings of the 2017 IEEE Manchester PowerTech, Manchester, UK, 18–22 June 2017; pp. 1–6. [Google Scholar]
- Alzate-González, N.; Mora-Flórez, J.; Pérez-Londoño, S. Methodology and software for sensitivity analysis of fault locators. In Proceedings of the 2014 IEEE PES Transmission Distribution Conference and Exposition—Latin America (PES T&D-LA), Medellin, Colombia, 10–13 September 2014; pp. 1–6. [Google Scholar]
- Taflanidis, A.; Loukogeorgaki, E.; Angelides, D. Analysis and design of offshore energy conversion devices under modeling uncertainties. In Proceedings of the OCEANS’11 MTS/IEEE KONA, Waikoloa, HI, USA, 19–22 September 2011; pp. 1–10. [Google Scholar]
- Lu, Z.; Xu, X.; Yan, Z.; Wang, H. Density-based Global Sensitivity Analysis of Islanded Microgrid Loadability Considering Distributed Energy Resource Integration. J. Mod. Power Syst. Clean Energy 2020, 8, 94–101. [Google Scholar] [CrossRef]
- Gu, Y.; Xie, L. Fast Sensitivity Analysis Approach to Assessing Congestion Induced Wind Curtailment. IEEE Trans. Power Syst. 2014, 29, 101–110. [Google Scholar] [CrossRef]
- Munikoti, S.; Jhala, K.; Lai, K.; Natarajan, B. Analytical Voltage Sensitivity Analysis for Unbalanced Power Distribution System. In Proceedings of the 2020 IEEE Power Energy Society General Meeting (PESGM), Montreal, QC, Canada, 2–6 August 2020; pp. 1–5. [Google Scholar]
- Saraiva, J.P.; Lima, B.S.; Gomes, V.M.; Flores, P.H.R.; Gomes, F.A.; Assis, A.O.; Reis, M.R.C.; Araújo, W.R.H.; Abrenhosa, C.; Calixto, W.P. Calculation of sensitivity index using one-at-a-time measures based on graphical analysis. In Proceedings of the 2017 18th International Scientific Conference on Electric Power Engineering (EPE), Kouty nad Desnou, Czech Republic, 17–19 May 2017; pp. 1–6. [Google Scholar]
- Wang, H.; Yan, Z.; Shahidehpour, M.; Xu, X.; Zhou, Q. Quantitative Evaluations of Uncertainties in Multivariate Operations of Microgrids. IEEE Trans. Smart Grid 2020, 11, 2892–2903. [Google Scholar] [CrossRef]
- Wang, L.; Mazumdar, M. Using a System Model to Decompose the Effects of Influential Factors on Locational Marginal Prices. IEEE Trans. Power Syst. 2007, 22, 1456–1465. [Google Scholar] [CrossRef]
- Hoeffding, W. A Class of Statistics with Asymptotically Normal Distribution. Ann. Math. Stat. 1948, 19, 293–325. [Google Scholar] [CrossRef]
- Hasan, K.N.; Preece, R. Influence of Stochastic Dependence on Small-Disturbance Stability and Ranking Uncertainties. IEEE Trans. Power Syst. 2018, 33, 3227–3235. [Google Scholar] [CrossRef]
- Wang, H.; Yan, Z.; Shahidehpour, M.; Zhou, Q.; Xu, X. Optimal Energy Storage Allocation for Mitigating the Unbalance in Active Distribution Network via Uncertainty Quantification. IEEE Trans. Sustain. Energy 2021, 12, 303–313. [Google Scholar] [CrossRef]
- Rosenblatt, M. Remarks on a Multivariate Transformation. Ann. Math. Stat. 1952, 23, 470–472. [Google Scholar] [CrossRef]
- Langston, J.; Martin, A.; Simpson, J.; Steurer, M.; Senroy, N.; Suryanarayanan, S.; Woodruff, S.L. Sequential Experimental Design Based Modeling of a Notional All-Electric Ship AC/DC Conversion System for Sensitivity and Uncertainty Analysis. In Proceedings of the 2007 IEEE Electric Ship Technologies Symposium, Arlington, VA, USA, 21–23 May 2007; pp. 261–266. [Google Scholar]
- Chen, P.C.; Malbasa, V.; Kezunovic, M. Sensitivity analysis of voltage sag based fault location algorithm. In Proceedings of the 2014 Power Systems Computation Conference, Wroclaw, Poland, 18–22 August 2014; pp. 1–7. [Google Scholar]
- Simonov, M.; Bertone, F.; Goga, K. Global Sensitivity Analysis Workflow Support to the EV Fleet Recharge Optimization Use Case. In Proceedings of the 2018 IEEE International Telecommunications Energy Conference (INTELEC), Torino, Italy, 7–11 October 2018; pp. 1–6. [Google Scholar]
- Ibrahim, M.N.; Zivanovic, R. Impact of CT saturation on phasor measurement algorithms: Uncertainty and sensitivity study. In Proceedings of the 2010 IEEE 11th International Conference on Probabilistic Methods Applied to Power Systems, Singapore, 14–17 June 2010; pp. 728–733. [Google Scholar]
- Marelli, S.; Sudret, B. UQLab: A Framework for Uncertainty Quantification in Matlab. In Proceedings of the 2nd International Conference on Vulnerability and Risk Analysis and Management (ICVRAM 2014), Liverpool, UK, 13–16 July 2014; pp. 2554–2563. [Google Scholar]
- Iooss, B.; Da Veiga, S.; Janon, A.; Pujol, G. Sensitivity: Global Sensitivity Analysis of Model Outputs, R Package Version 1.26.0. Available online: https://CRAN.R-project.org/package=sensitivity (accessed on 25 October 2021).
- Tarantola, S.; Becker, W. SIMLAB Software for Uncertainty and Sensitivity Analysis. In Handbook of Uncertainty Quantification; Ghanem, R., Higdon, D., Owhadi, H., Eds.; Springer: New York, NY, USA, 2017; pp. 1979–1999. [Google Scholar]
- Herman, J.; Usher, W. SALib: An open-source Python library for Sensitivity Analysis. J. Open Source Softw. 2017, 2, 97. [Google Scholar] [CrossRef]
- Kucherenko, S.; Zaccheus, O. SobolGSA. Available online: http://www.imperial.ac.uk/process-systems-engineering/research/free-software/sobolgsa-software/ (accessed on 25 October 2021).
- Puy, A.; Piano, S.L.; Saltelli, A.; Levin, S.A. sensobol: Computation of Variance-Based Sensitivity Indices. Version 1.0.3. Available online: https://cran.r-project.org/web/packages/sensobol (accessed on 25 October 2021).
- Pianosi, F.; Sarrazin, F.; Wagener, T. A Matlab toolbox for Global Sensitivity Analysis. Environ. Model. Softw. 2015, 70, 80–85. [Google Scholar] [CrossRef] [Green Version]
- Tong, C. PSUADE Reference Manual (Version 1.7). Available online: http://everest.msrc.sunysb.edu/tzhang/capt_tune/GCM_paras_tuner/sa/sampling/PSUADE_v1.7.5a/Doc/Manual/PsuadeRefManual.pdf (accessed on 25 October 2021).
- Baudin, M.; Lebrun, R.; Iooss, B.; Popelin, A.L. OpenTURNS: An Industrial Software for Uncertainty Quantification in Simulation. In Handbook of Uncertainty Quantification; Ghanem, R., Higdon, D., Owhadi, H., Eds.; Springer: New York, NY, USA, 2017; pp. 2001–2038. [Google Scholar]
- Razavi, S.; Sheikholeslami, R.; Gupta, H.V.; Haghnegahdar, A. VARS-TOOL: A toolbox for comprehensive, efficient, and robust sensitivity and uncertainty analysis. Environ. Model. Softw. 2019, 112, 95–107. [Google Scholar] [CrossRef]
- Eldred, M.; Dalbey, K.; Bohnhoff, W.; Adams, B.; Swiler, L.; Hough, P.; Gay, D.; Eddy, J.; Haskell, K. DAKOTA: A Multilevel Parallel Object-Oriented Framework for Design Optimization, Parameter Estimation, Uncertainty Quantification, and Sensitivity Analysis. Version 5.0, User’s Manual. Available online: https://www.osti.gov/servlets/purl/991842/ (accessed on 25 October 2021).
- Wu, W.; Hu, Z.; Song, Y.; Sansavini, G.; Chen, H.; Chen, X. Transmission Network Expansion Planning Based on Chronological Evaluation Considering Wind Power Uncertainties. IEEE Trans. Power Syst. 2018, 33, 4787–4796. [Google Scholar] [CrossRef]
- Alhasawi, F.B.; Milanovic, J.V. Ranking the Importance of Synchronous Generators for Renewable Energy Integration. IEEE Trans. Power Syst. 2012, 27, 416–423. [Google Scholar] [CrossRef]
- Leite da Silva, A.M.; Jardim, J.L.; de Lima, L.R.; Machado, Z.S. A Method for Ranking Critical Nodes in Power Networks Including Load Uncertainties. IEEE Trans. Power Syst. 2016, 31, 1341–1349. [Google Scholar] [CrossRef]
- Farret, F.A.; Simões, M.G. Micropower System Modeling with Homer. In Integration of Alternative Sources of Energy; Farret, F., Simões, M., Eds.; John Wiley & Sons: New York, NY, USA, 2006; pp. 379–418. [Google Scholar]
- Qin, C.; Zeng, Y.; Liu, Z.; Zhou, B.; Jin, X.; Chen, J. BTNRAS, A tool for Transmission Network Risk Assessment. In Proceedings of the IEEE PES Innovative Smart Grid Technologies, Tianjin, China, 21–24 May 2012; pp. 1–7. [Google Scholar]
- Alemazkoor, N.; Meidani, H. Fast Probabilistic Voltage Control for Distribution Networks With Distributed Generation Using Polynomial Surrogates. IEEE Access 2020, 8, 73536–73546. [Google Scholar] [CrossRef]
- Sandoval, E.H.; Anstett-Collin, F.; Basset, M. Sensitivity study of dynamic systems using polynomial chaos. Reliab. Eng. Syst. Saf. 2015, 104, 15–26. [Google Scholar] [CrossRef] [Green Version]
- Langston, J.; Taylor, J.; Hover, F.; Simpson, J.; Steurer, M.; Baldwin, T. Uncertainty Analysis for a Large-Scale Transient Simulation of a Notional All-Electric Ship Pulse Load Charging Scenario. In Proceedings of the 10th International Conference on Probablistic Methods Applied to Power Systems, Rincon, PR, USA, 25–29 May 2008; pp. 1–8. [Google Scholar]
- Rausch, M.; Sanders, W.H. Stacked Metamodels for Sensitivity Analysis and Uncertainty Quantification of AMI Models. In Proceedings of the 2020 IEEE International Conference on Communications, Control, and Computing Technologies for Smart Grids (SmartGridComm), Tempe, AZ, USA, 11–13 November 2020; pp. 1–7. [Google Scholar]
- Xu, Y.; Mili, L.; Zhao, J. Probabilistic Power Flow Calculation and Variance Analysis Based on Hierarchical Adaptive Polynomial Chaos-ANOVA Method. IEEE Trans. Power Syst. 2019, 34, 3316–3325. [Google Scholar] [CrossRef]
- Tang, J.; Ni, F.; Ponci, F.; Monti, A. Dimension-Adaptive Sparse Grid Interpolation for Uncertainty Quantification in Modern Power Systems: Probabilistic Power Flow. IEEE Trans. Power Syst. 2016, 31, 907–919. [Google Scholar] [CrossRef]
- D’Antona, G.; Monti, A.; Ponci, F.; Rocca, L. Maximum Entropy Multivariate Analysis of Uncertain Dynamical Systems Based on the Wiener–Askey Polynomial Chaos. IEEE Trans. Instrum. Meas. 2007, 56, 689–695. [Google Scholar] [CrossRef]
- Heidari, M.; Filizadeh, S.; Gole, A.M. Electromagnetic Transients Simulation-Based Surrogate Models for Tolerance Analysis of FACTS Apparatus. IEEE Trans. Power Deliv. 2013, 28, 797–806. [Google Scholar] [CrossRef]
- Wang, H.; Yan, Z.; Xu, X.; He, K. Evaluating Influence of Variable Renewable Energy Generation on Islanded Microgrid Power Flow. IEEE Access 2018, 6, 71339–71349. [Google Scholar] [CrossRef]
- Metropolis, N.; Ulam, S. The Monte Carlo Method. J. Am. Stat. Assoc. 1949, 44, 335–341. [Google Scholar] [CrossRef]
- Metropolis, N. The Beginning of the Monte Carlo method. In Los Alamos Science Special Issue; Los Alamos National Laboratory: Los Alamos, NM, USA, 1987; pp. 125–130. [Google Scholar]
- Smith, W. Worst case circuit analysis-an overview (electronic parts/circuits tolerance analysis). In Proceedings of the 1996 Annual Reliability and Maintainability Symposium, Las Vegas, NV, USA, 22–25 January 1996; pp. 326–334. [Google Scholar]
- Zio, E. The Monte Carlo Simulation Method for System Reliability and Risk Analysis; Springer: London, UK, 2013. [Google Scholar]
- D’Antona, G.; Davoudi, M. Effects of parameter and measurement uncertainties on the power system WLS state estimation. In Proceedings of the 2012 IEEE International Instrumentation and Measurement Technology Conference, Graz, Austria, 13–16 May 2012; pp. 1015–1020. [Google Scholar]
- Wang, P.; Zhang, Z.; Huang, Q.; Li, J.; Yi, J.; Lee, W.J. A novel approach to improve model generalization ability in dynamic equivalent of active distribution network. In Proceedings of the 2017 IEEE/IAS 53rd Industrial and Commercial Power Systems Technical Conference (I CPS), Niagara Falls, ON, Canada, 6–11 May 2017; pp. 1–8. [Google Scholar]
- Chua, L.O.; Lin, P.Y. Computer-Aided Analysis of Electronic Circuits: Algorithms and Computational Techniques; Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 1975. [Google Scholar]
- Atkinson, K.E. An Introduction to Numerical Analysis; John Wiley & Sons, Inc.: New York, NY, USA, 1988. [Google Scholar]
- Gamboa, F.; Janon, A.; Klein, T.; Lagnoux, A. Sensitivity indices for multivariate outputs. Comptes Rendus Math. 2013, 351, 307–310. [Google Scholar] [CrossRef] [Green Version]
- Lamboni, M.; Monod, H.; Makowski, D. Multivariate sensitivity analysis to measure global contribution of input factors in dynamic models. Reliab. Eng. Syst. Saf. 2011, 96, 450–459. [Google Scholar] [CrossRef]
- O’Hagan, A.; Buck, C.E.; Daneshkhah, A.; Eiser, J.R.; Garthwaite, P.H.; Jenkinson, D.J.; Oakley, J.E.; Rakow, T. Uncertain Judgements: Eliciting Experts’ Probabilities; John Wiley & Sons, Ltd.: Chichester, UK, 2006. [Google Scholar]
- Paleari, L.; Confalonieri, R. Sensitivity analysis of a sensitivity analysis: We are likely overlooking the impact of distributional assumptions. Ecol. Model. 2016, 340, 57–63. [Google Scholar] [CrossRef]
- Tarantola, S.; Giglioli, N.; Jesinghaus, J.; Saltelli, A. Can global sensitivity analysis steer the implementation of models for environmental assessments and decision-making? Stoch. Environ. Res. Risk Assess. 2002, 16, 63–76. [Google Scholar] [CrossRef]
- Kelleher, C.; Wagener, T. Ten guidelines for effective data visualization in scientific publications. Environ. Model. Softw. 2011, 26, 822–827. [Google Scholar] [CrossRef]
- Opathella, C.; Venkatesh, B. Managing Uncertainty of Wind Energy with Wind Generators Cooperative. IEEE Trans. Power Syst. 2013, 28, 2918–2928. [Google Scholar] [CrossRef]
- Khorashadi Zadeh, F.; Nossent, J.; Sarrazin, F.; Pianosi, F.; van Griensven, A.; Wagener, T.; Bauwens, W. Comparison of variance-based and moment-independent global sensitivity analysis approaches by application to the SWAT model. Environ. Model. Softw. 2017, 91, 210–222. [Google Scholar] [CrossRef] [Green Version]
- Sarrazin, F.; Pianosi, F.; Wagener, T. Global Sensitivity Analysis of environmental models: Convergence and validation. Environ. Model. Softw. 2016, 79, 135–152. [Google Scholar] [CrossRef] [Green Version]
- Kundur, P. Power System Stability and Control; McGraw-Hill, Inc.: New York, NY, USA, 1994. [Google Scholar]
- ASSET Project—A Holistic and Scalable Solution for Research, Innovation and Education in Energy Transition. Available online: https://energytransition.academy/ (accessed on 25 October 2021).
- EDDIE Project—Education for Digitalisation of Energy. Available online: https://www.eddie-erasmus.eu/ (accessed on 25 October 2021).












| SA Type | SA Method | Sampling Strategy | Sensitivity Measure | Computational Cost |
|---|---|---|---|---|
| Local SA | Tornado Diagram | OAT | , | ∼2K |
| One-Way SA | OAT | ≥2K | ||
| Scenario Analysis | AAT | — | Number of Scenarios | |
| Differential SA | OAT | ∼K | ||
| Global SA | Morris Method | OAT | , , | ∼10K |
| Correlation Analysis | AAT | >10K | ||
| Regression Analysis | AAT | >10K | ||
| Variance-Based SA | AAT | >10K (with Metamodel) or >100K (via Direct Estimation) |
| First-Order | Total-Order | Second-Order | Third-Order |
|---|---|---|---|
| UA | SA | Focus | Model Type | ||||
|---|---|---|---|---|---|---|---|
| Present Absent | 56% 44% | Local Global Absent | 66% 15% 19% | Method Model | 21% 79% | Linear Nonlinear Unclear | 4% 76% 20% |
| Software Tool | Programming Language | Reference | Software Tool | Programming Language | Reference |
|---|---|---|---|---|---|
| UQLab | MATLAB | [193] | sensitivity | R | [194] |
| SimLab | R | [195] | SALib | Python | [196] |
| SobolGSA | C#, MATLAB, Python | [197] | sensobol | R | [198] |
| SAFE | MATLAB, R, Python | [199] | PSUADE | C | [200] |
| OpenTURNS | Python, C++ | [201] | VARS-Tool | MATLAB, C | [202] |
| Dakota | C++ | [203] |
| Input Name | Description | |
|---|---|---|
| I | Current | |
| Resistance | ||
| Resistance | ||
| L | Inductance | |
| C | Capacitance |
| Input Name | First-Order | Total-Order |
|---|---|---|
| I | ||
| L | ||
| C |
| Input Name | ms | ms | ||
|---|---|---|---|---|
| First-Order | Total-Order | First-Order | Total-Order | |
| I | ||||
| L | ||||
| C | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ginocchi, M.; Ponci, F.; Monti, A. Sensitivity Analysis and Power Systems: Can We Bridge the Gap? A Review and a Guide to Getting Started. Energies 2021, 14, 8274. https://doi.org/10.3390/en14248274
Ginocchi M, Ponci F, Monti A. Sensitivity Analysis and Power Systems: Can We Bridge the Gap? A Review and a Guide to Getting Started. Energies. 2021; 14(24):8274. https://doi.org/10.3390/en14248274
Chicago/Turabian StyleGinocchi, Mirko, Ferdinanda Ponci, and Antonello Monti. 2021. "Sensitivity Analysis and Power Systems: Can We Bridge the Gap? A Review and a Guide to Getting Started" Energies 14, no. 24: 8274. https://doi.org/10.3390/en14248274
APA StyleGinocchi, M., Ponci, F., & Monti, A. (2021). Sensitivity Analysis and Power Systems: Can We Bridge the Gap? A Review and a Guide to Getting Started. Energies, 14(24), 8274. https://doi.org/10.3390/en14248274








