The Effect of Hydraulic Fracture Geometry on Well Productivity in Shale Oil Plays with High Pore Pressure
Abstract
:1. Introduction
2. Materials and Methods
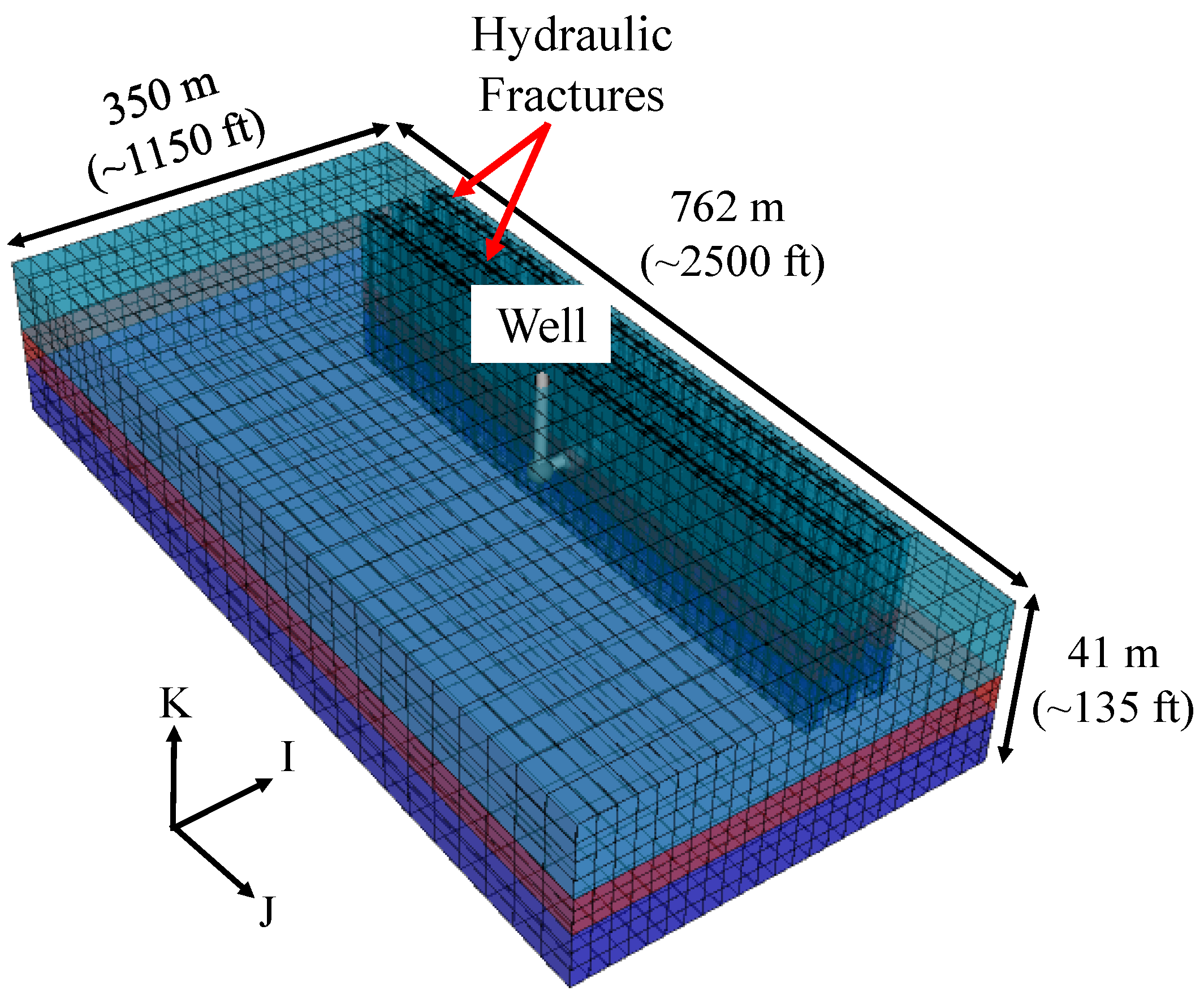
2.1. Numerical Simulation Model Description
2.2. Reservoir and Fluid Properties
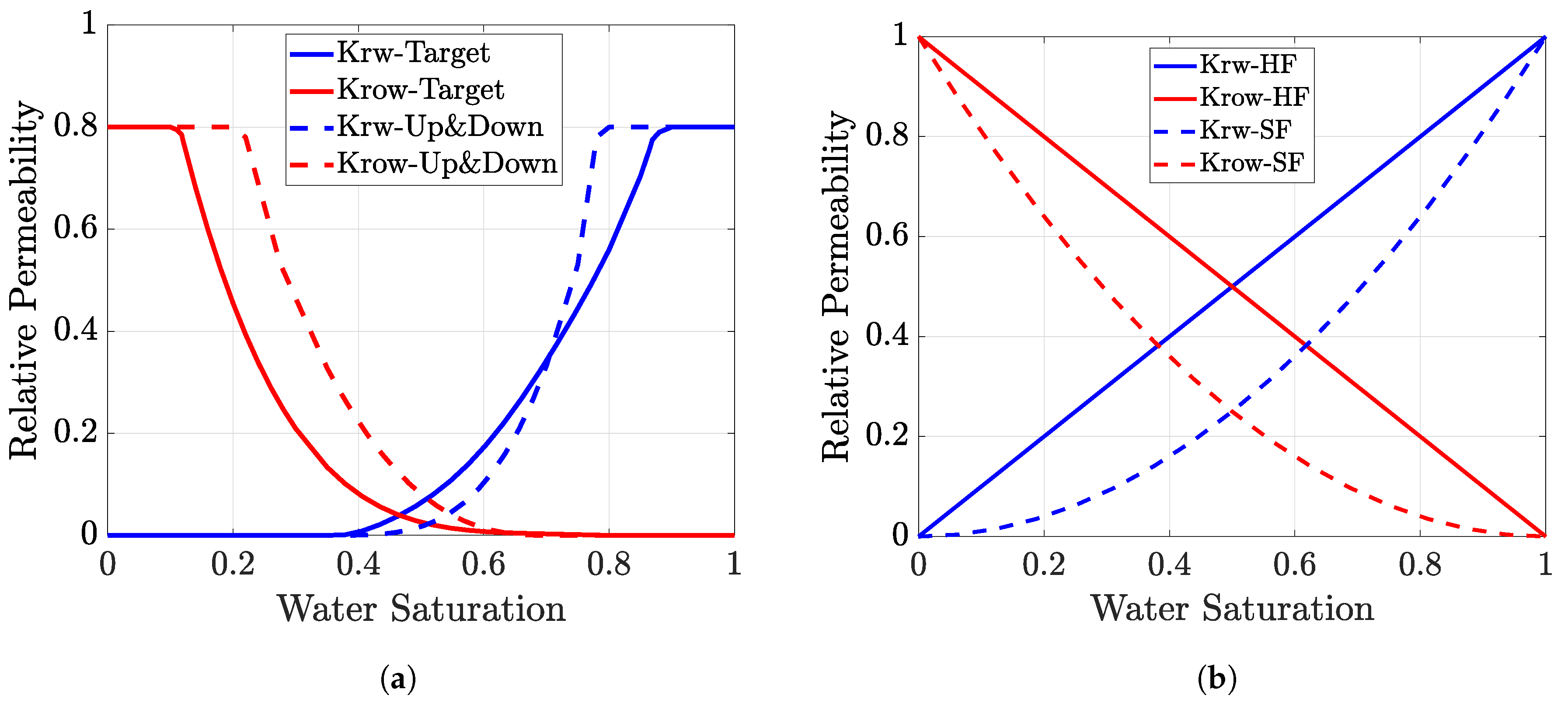
2.3. Relative Permeability Curves
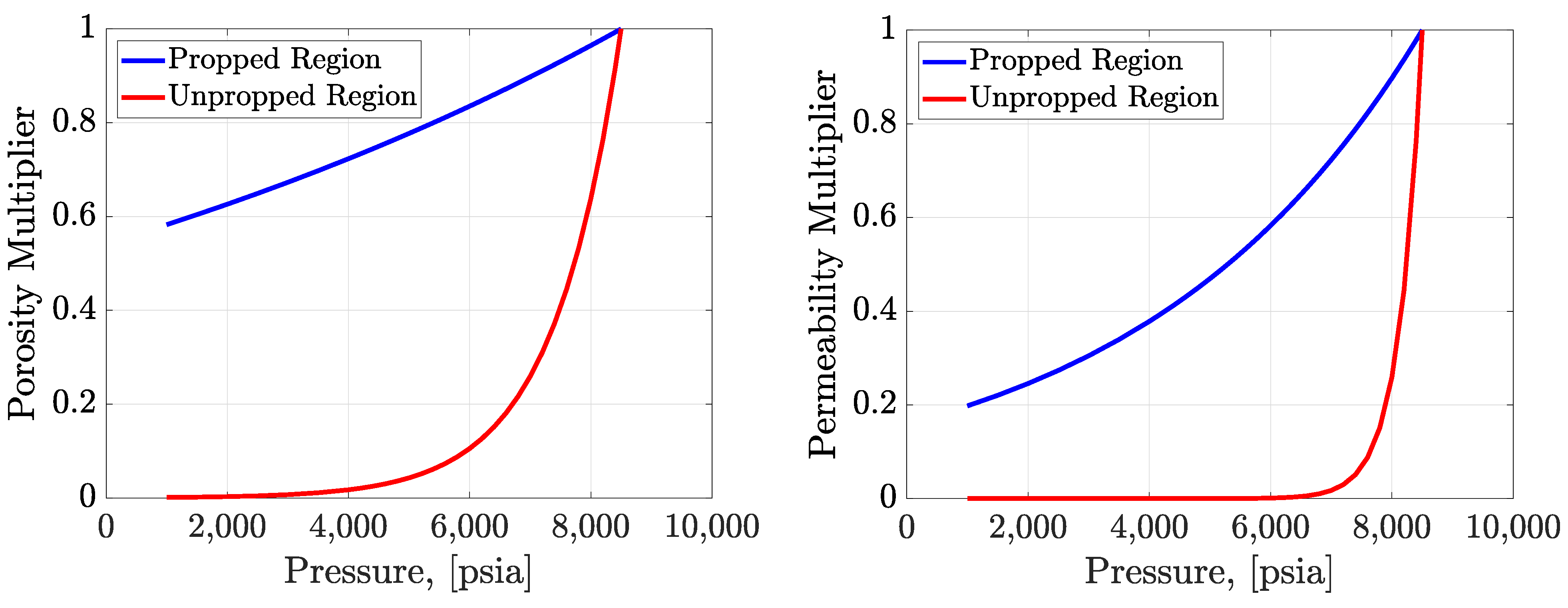
2.4. Pressure-Dependent Permeability
- –
- i: Initial porosity, fraction.
- –
- ki: Initial permeability, m2 (mD).
- –
- Pnet: Net pressure, MPa (psi). It is the difference between the initial pressure and the current pressure [55].
- –
- Cfrac: Coefficient of stress sensitivity, MPa−1 (psi−1).
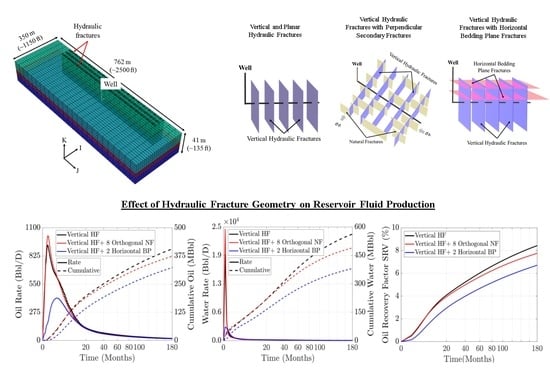
3. Hydraulic Fracture Geometry Scenarios
3.1. Reference Fracture Scenario: Vertical and Planar Hydraulic Fractures
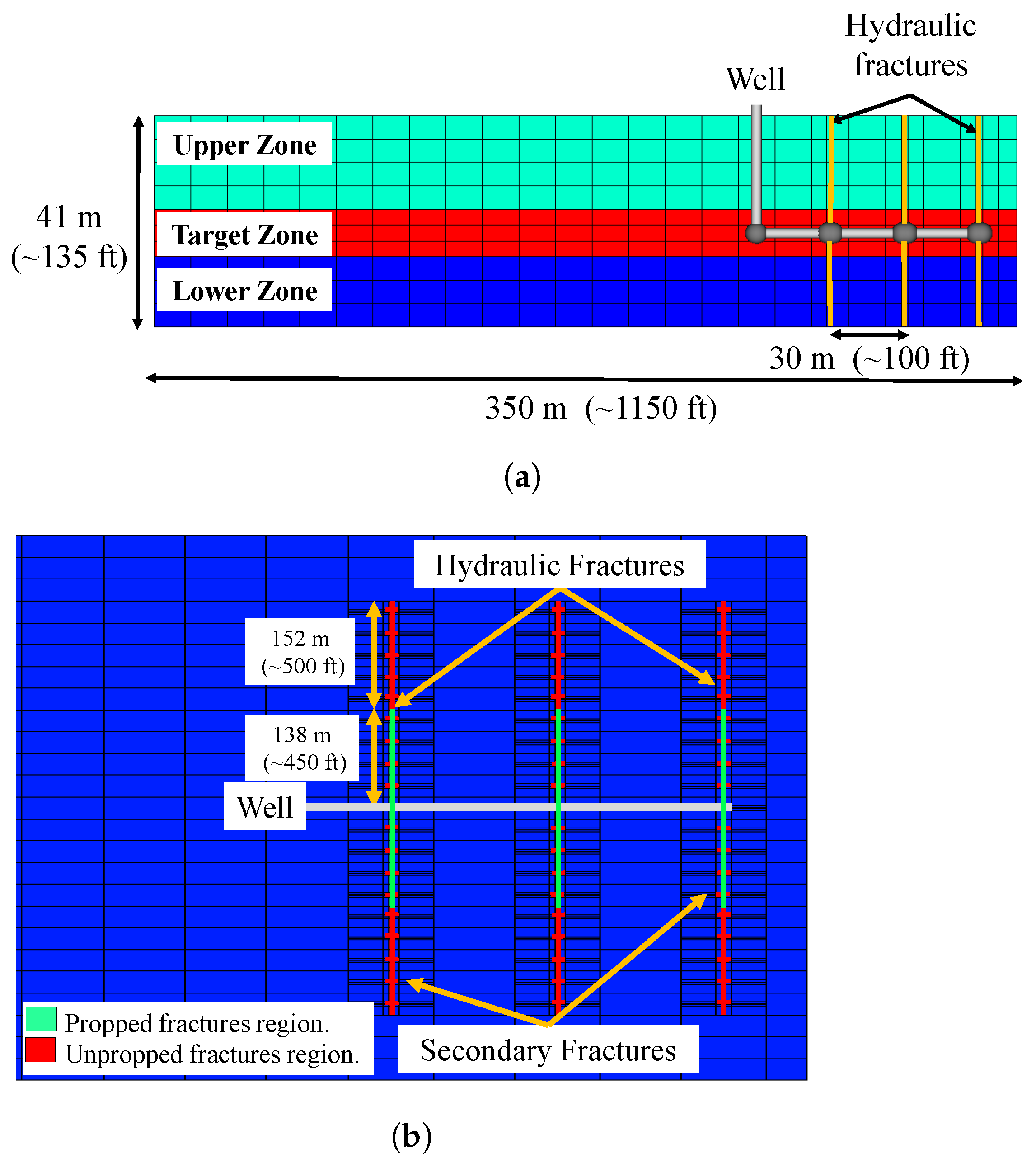
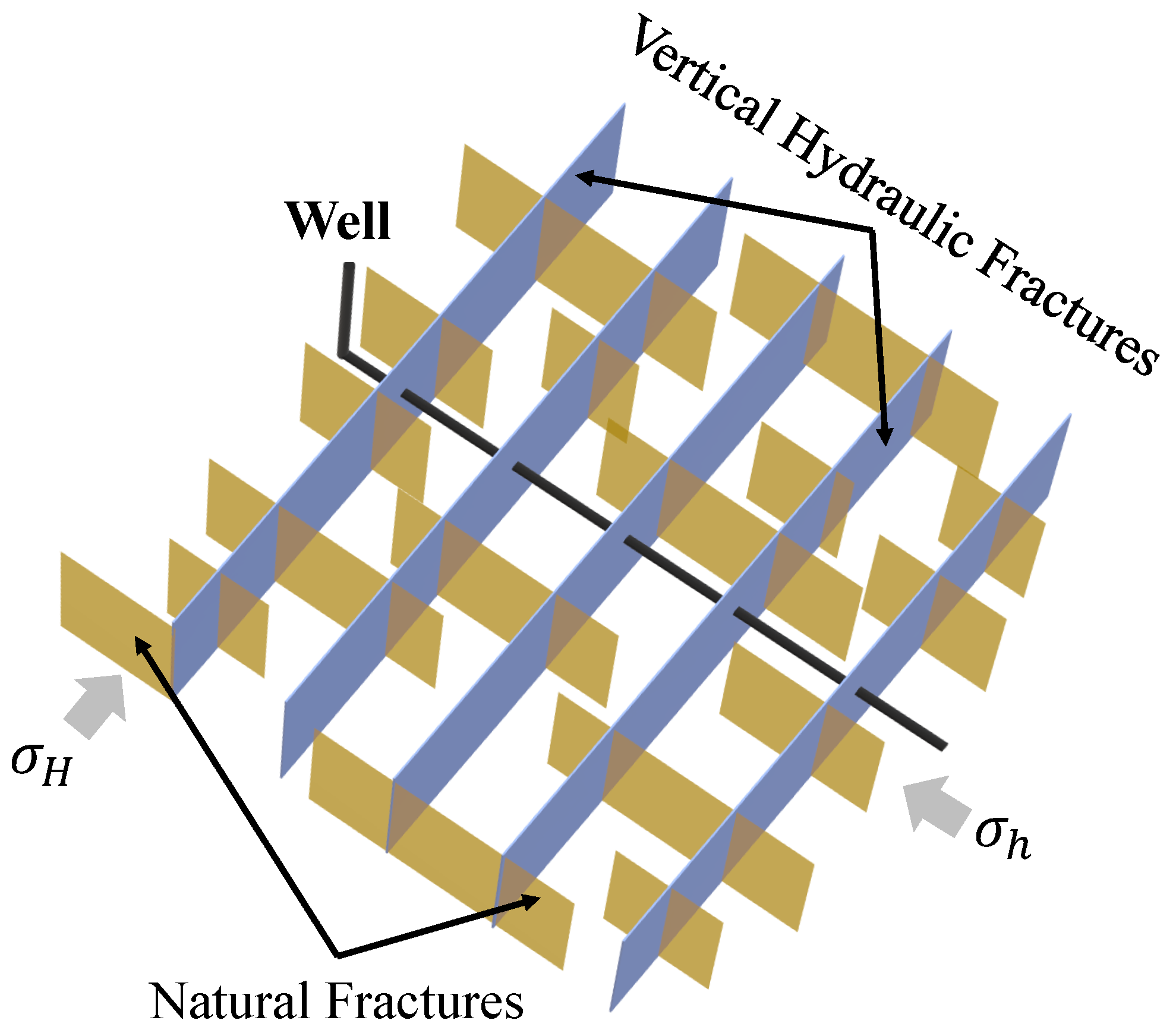
3.2. Second Fracture Scenario: Vertical Hydraulic Fractures with Perpendicular Secondary Fractures
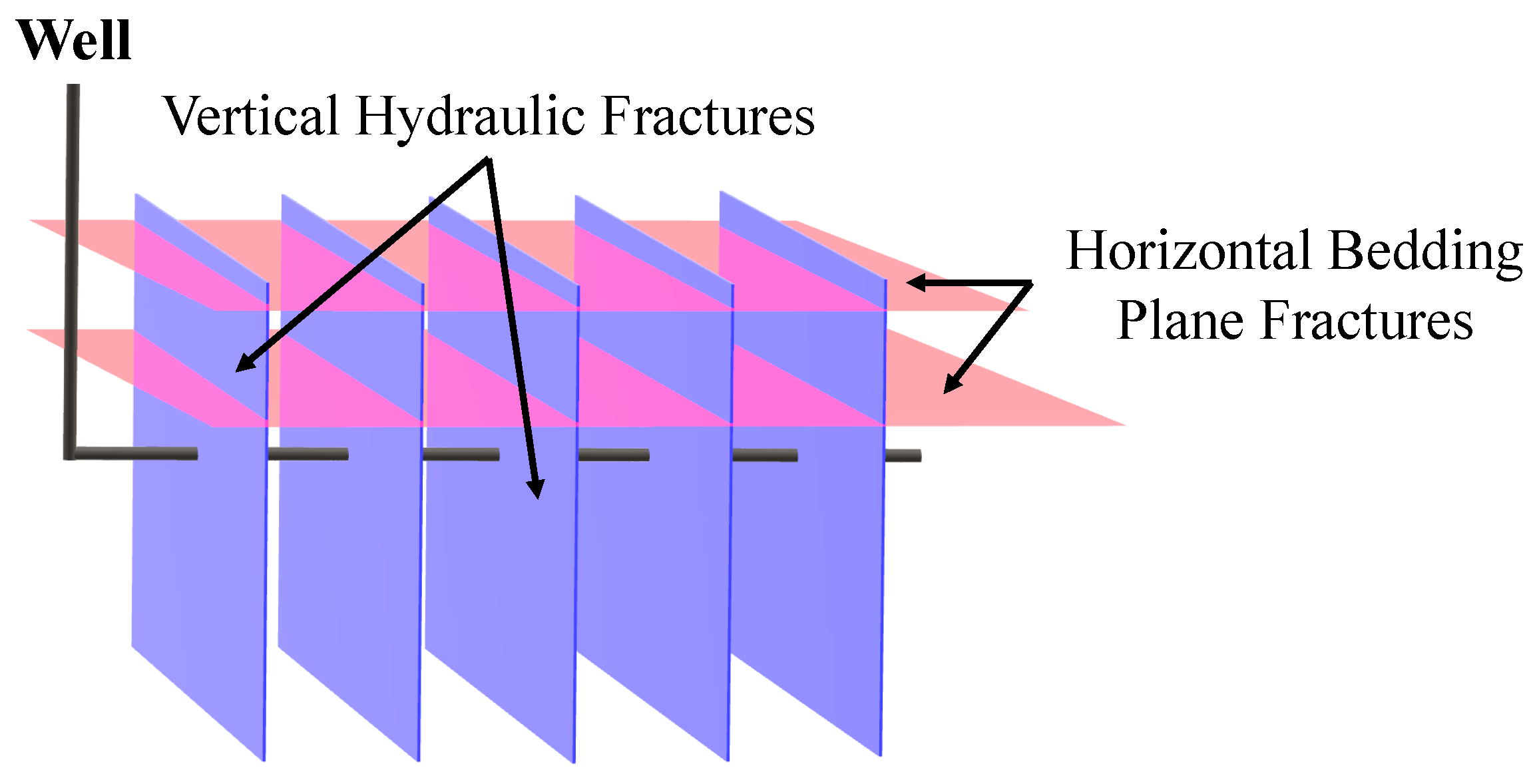
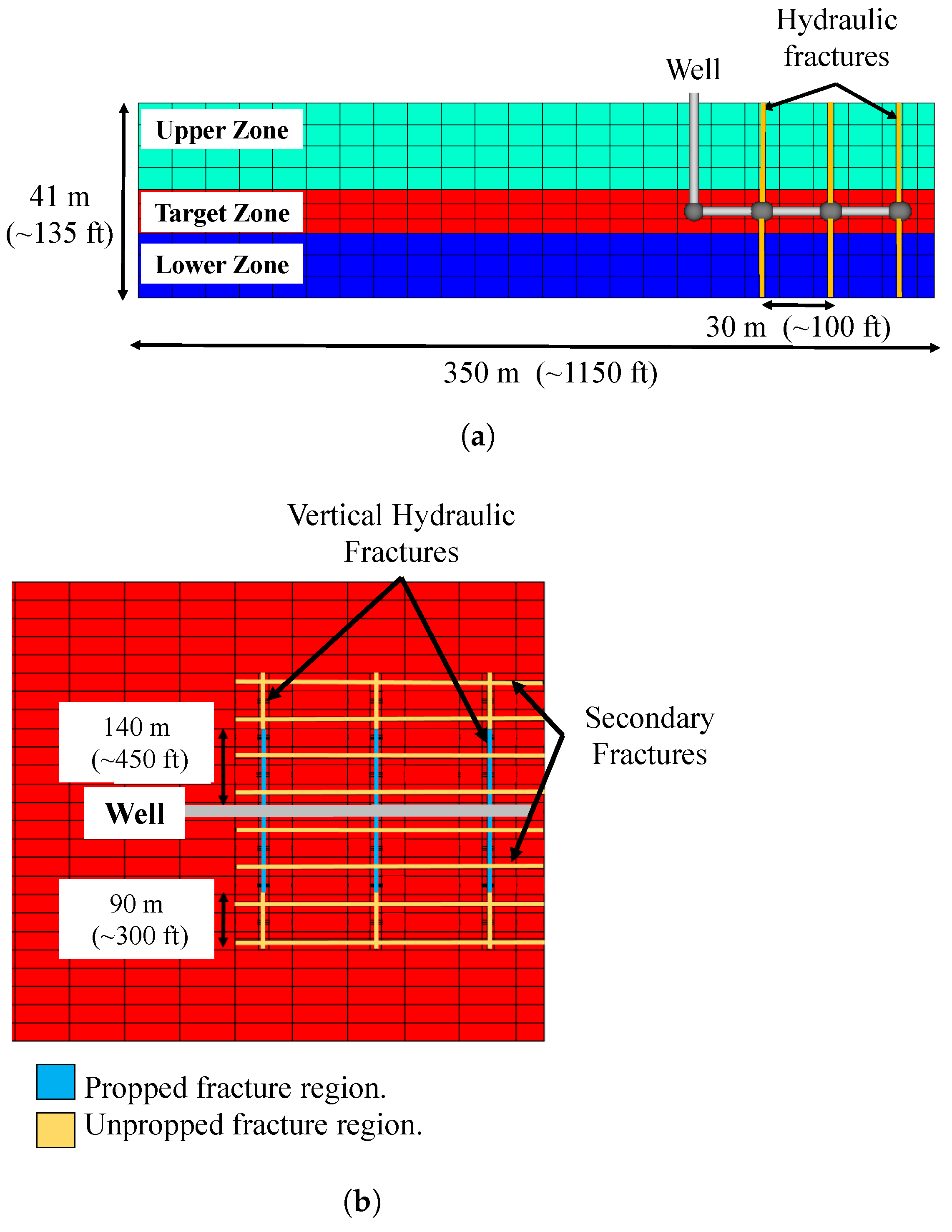
3.3. Third Fracture Scenario: Vertical Hydraulic Fractures with Horizontal Bedding Plane Fractures
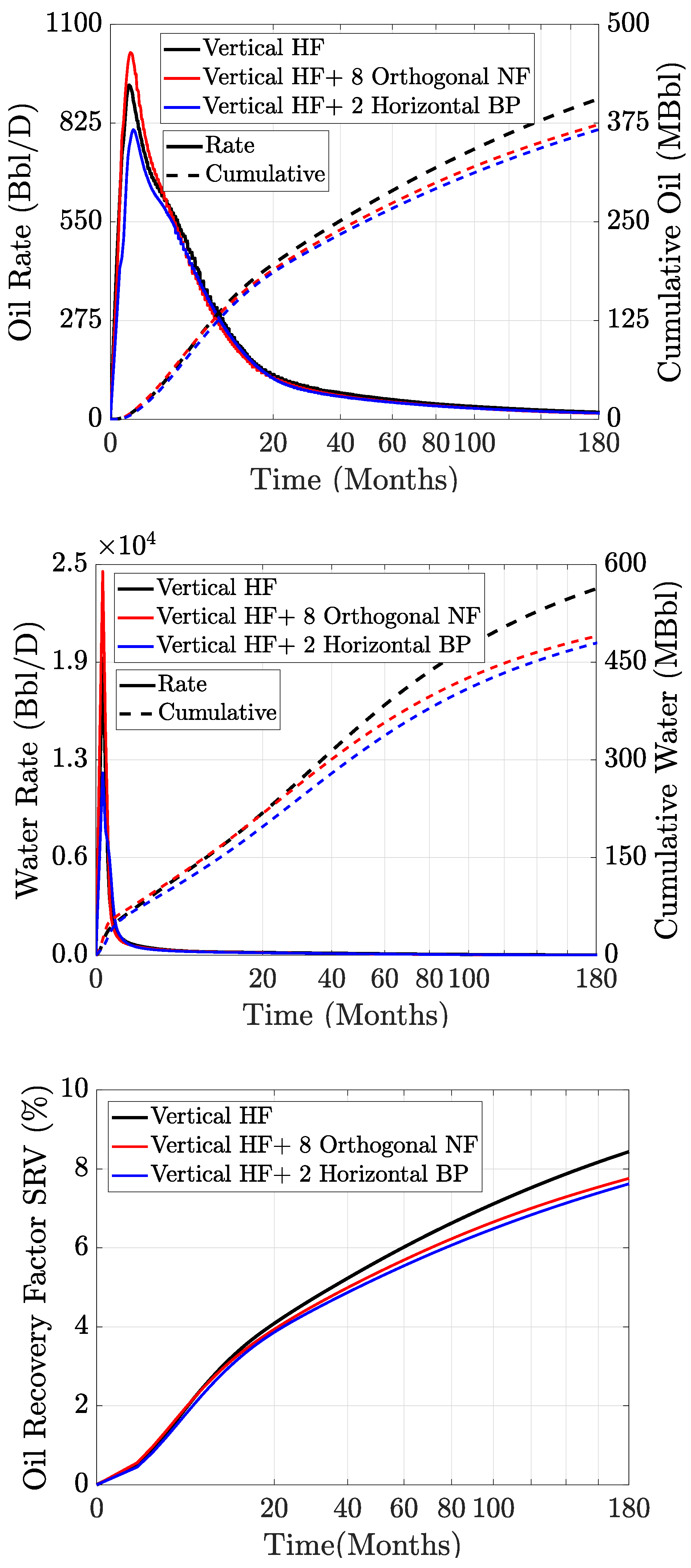
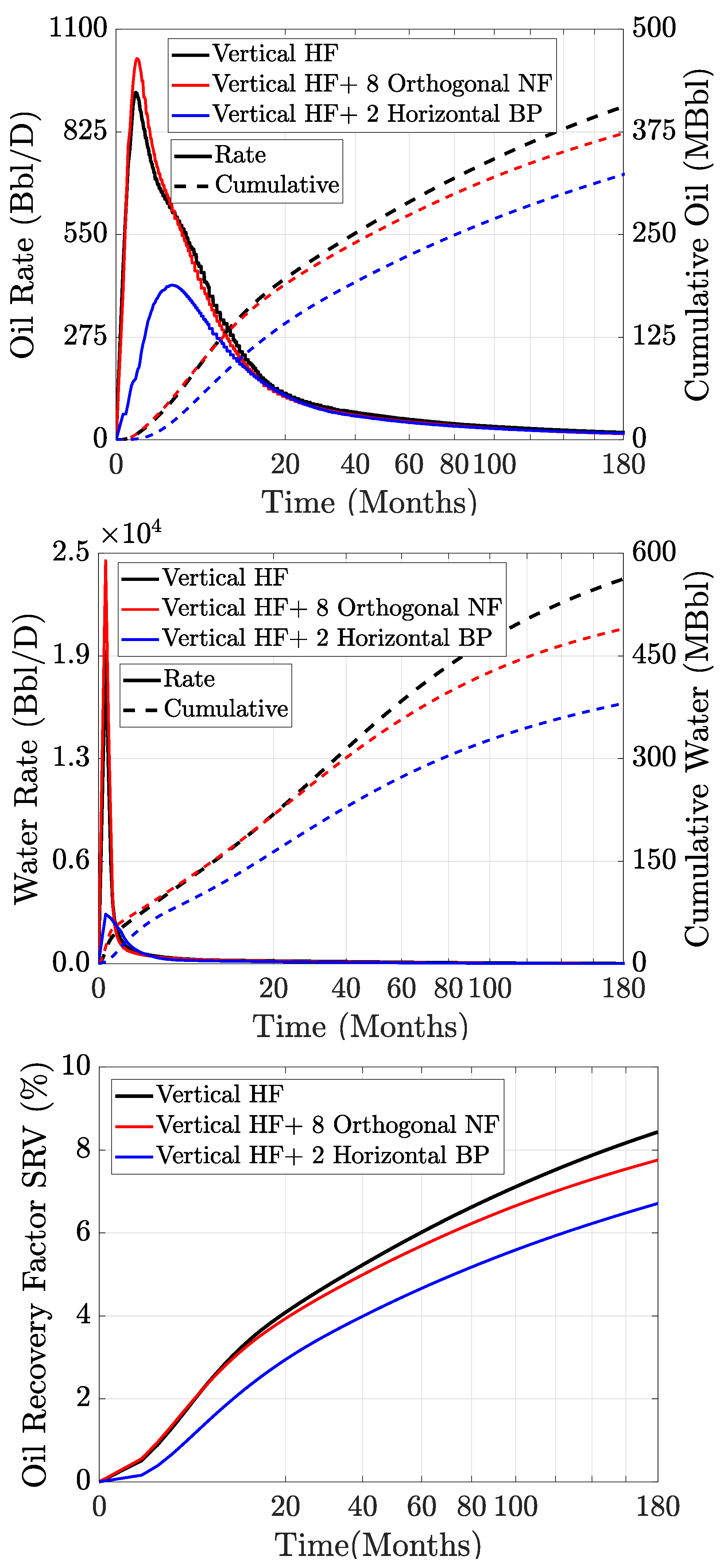
4. Results and Discussion
5. Conclusions
- The interactions among vertical hydraulic fractures and the orthogonal pre-existing natural fractures may initiate and hydraulically open secondary natural fractures. Our results show that these secondary fractures improve reservoir permeability and contribute to the initial hydrocarbon production when they reach conductivity similar to that of primary vertical hydraulic fractures. The presence of stimulated vertical orthogonal natural fractures enhances the initial oil production by about 10%.
- We allow the stimulation of secondary orthogonal natural fractures to reduce the vertical hydraulic fracture length and aperture. The shortened primary fracture length combined with the rapid closure of secondary natural fractures, reduce the stimulated reservoir volume and harms long-term production. Thus, our results show that these two factors can reduce the cumulative oil production at 15 years by about 8% compared with the scenario with vertical hydraulic fractures only.
- We assume that stimulation of the horizontal bedding planes reduces the primary vertical hydraulic fracture length and aperture. This may produce premature proppant screen-out and inefficient proppant placement into primary hydraulic fractures. Our results show that the lowered vertical hydraulic fracture conductivity combined with rapid horizontal fracture closure can reduce cumulative hydrocarbon production after 15 years by about 20% and the initial hydrocarbon production by about 50% compared with the vertical hydraulic fractures only (“ he reference fracture scenario”).
- In hydraulic fracturing, it is crucial to constrain the present-day in situ stress state (magnitudes and orientation) and pore pressure conditions to understand the initiation and propagation mechanisms that control the final stimulated reservoir volume geometry. Only then realistic hydrocarbon production forecasts can be obtained. The assumption of vertical, symmetrical, and planar fractures may lead to unreliable hydrocarbon production forecasts. This last finding agrees with the studies performed by previous researchers [6,35,36,69]. The simplification of hydraulic fracture geometry can overestimate hydrocarbon production, primarily if the modeled formation is characterized by high pore pressure and a small difference between the principal stresses. These conditions enhance the fracturing fluid leakage into natural fractures and/or bedding planes.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| BP | Bedding Planes |
| DK | Dual Permeability |
| HF | Hydraulic Fractures |
| LS-LR-DK | Locally Spaced-Logarithmically Refined-Dual Permeability |
| NF | Natural Fractures |
| RF | Recovery Factor |
| SF | Secondary Fractures |
| SRV | Stimulated Reservoir Volume |
| TOC | Total Organic Carbon |
Nomenclature
| Shmin | Minimum principal horizontal stress |
| SHmax | Maximum horizontal stress |
| Sv | Overburden stress |
| S3 | Least principal stress |
References
- Schenk, C. World Oil and Gas Resource Assessments; Central Energy Resources Science Center, USGS: Menlo Park, CA, USA, 2021. Available online: https://www.usgs.gov/centers/cersc/science/world-oil-and-gas-resource-assessments?qt-science_center_objects=0#qt-science_center_objects (accessed on 30 August 2021).
- Su, Y.; Ren, L.; Meng, F.; Xu, C.; Wang, W. Theoretical Analysis of the Mechanism of Fracture Network Propagation with Stimulated Reservoir Volume (SRV) Fracturing in Tight Oil Reservoirs. PLoS ONE 2015, 10, e0125319. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barree, R.D.; Conway, M.W.; Gilbert, J.V.; Woodroof, R.A. Evidence of Strong Fracture Height Containment Based on Complex Shear Failure and Formation Anisotropy. In Proceedings of the SPE Annual Technical Conference and Exhibition, Florence, Italy, 20–22 September 2010; Society of Petroleum Engineers: Florence, Italy, 2010; p. 20. [Google Scholar] [CrossRef]
- Ren, L.; Zhao, J.; Hu, Y. Hydraulic Fracture Extending into Network in Shale: Reviewing Influence Factors and Their Mechanism. Sci. World J. 2014, 2014, 847107. [Google Scholar] [CrossRef]
- Warpinski, N.R.; Mayerhofer, M.J.; Vincent, M.C.; Cipolla, C.L.; Lolon, E.P. Stimulating Unconventional Reservoirs: Maximizing Network Growth While Optimizing Fracture Conductivity. J. Can. Pet. Technol. 2009, 48, 39–51. [Google Scholar] [CrossRef]
- Yang, R.; Huang, Z.; Yu, W.; Li, G.; Ren, W.; Zuo, L.; Tan, X.; Sepehrnoori, K.; Tian, S.; Sheng, M. A Comprehensive Model for Real Gas Transport in Shale Formations with Complex Non-planar Fracture Networks. Sci. Rep. 2016, 6, 36673. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Liao, X.; Yu, W.; Sepehrnoori, K.; Zhao, X.; Li, X.; Sun, H. A Diagnostic Approach to Identify Complex Fracture Geometries in Unconventional Reservoirs Using a Semi-analytical Model. In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology Conference, Austin, TX, USA, 24–26 July 2017; p. 27. [Google Scholar] [CrossRef]
- Yu, W.; Xu, Y.; Weijermars, R.; Wu, K.; Sepehrnoori, K. A Numerical Model for Simulating Pressure Response of Well Interference and Well Performance in Tight Oil Reservoirs with Complex-Fracture Geometries Using the Fast Embedded-Discrete-Fracture-Model Method. SPE Reserv. Eval. Eng. 2017, 21. [Google Scholar] [CrossRef]
- Blanton, T.L. Propagation of Hydraulically and Dynamically Induced Fractures in Naturally Fractured Reservoirs. In Proceedings of the SPE Unconventional Gas Technology Symposium, Louisville, Kentucky, 18–21 May 1986; Society of Petroleum Engineers: Louisville, Kentucky, 1986; p. 15. [Google Scholar] [CrossRef]
- Chuprakov, D.A.; Prioul, R. Hydraulic Fracture Height Containment by Weak Horizontal Interfaces. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 3–5 February 2015; Society of Petroleum Engineers: The Woodlands, TX, USA, 2015; p. 17. [Google Scholar] [CrossRef]
- Li, H.; Zou, Y.; Valko, P.P.; Ehlig-Economides, C. Hydraulic Fracture Height Predictions in Laminated Shale Formations Using Finite Element Discrete Element Method. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 9–11 February 2016; Society of Petroleum Engineers: The Woodlands, TX, USA, 2016; p. 17. [Google Scholar] [CrossRef]
- Tang, J.; Wu, K.; Zeng, B.; Huang, H.; Hu, X.; Guo, X.; Zuo, L. Investigate effects of weak bedding interfaces on fracture geometry in unconventional reservoirs. J. Pet. Sci. Eng. 2018, 165, 992–1009. [Google Scholar] [CrossRef]
- Guo, Y.; Yang, C.; Wang, L.; Xu, F. Study on the Influence of Bedding Density on Hydraulic Fracturing in Shale. Arab. J. Sci. Eng. 2018, 43, 6493–6508. [Google Scholar] [CrossRef]
- Prabhakaran, R.; De Pater, H.; Shaoul, J. Pore pressure effects on fracture net pressure and hydraulic fracture containment: Insights from an empirical and simulation approach. J. Pet. Sci. Eng. 2017, 157, 724–736. [Google Scholar] [CrossRef]
- Blanton, h.L. An Experimental Study of Interaction Between Hydraulically Induced and Pre-Existing Fractures. In Proceedings of the SPE Unconventional Gas Recovery Symposium, Pittsburgh, Pennsylvania, 16–18 May 1982; Society of Petroleum Engineers: Pittsburgh, PA, USA, 1982; p. 13. [Google Scholar] [CrossRef]
- Beugelsdijk, L.J.L.; de Pater, C.J.; Sato, K. Experimental Hydraulic Fracture Propagation in a Multi-Fractured Medium. In Proceedings of the SPE Asia Pacific Conference on Integrated Modelling for Asset Management, Yokohama, Japan, 25–26 April 2000; Society of Petroleum Engineers: Yokohama, Japan, 2000; p. 8. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, M.; Jin, Y.; Guangqing, Z. Analysis of fracture propagation behavior and fracture geometry using a tri-axial fracturing system in naturally fractured reservoirs. Int. J. Rock Mech. Min. Sci. 2008, 45, 1143–1152. [Google Scholar] [CrossRef]
- Zhou, J.; Jin, Y.; Chen, M. Experimental investigation of hydraulic fracturing in random naturally fractured blocks. Int. J. Rock Mech. Min. Sci. 2010, 47, 1193–1199. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, M.; Zhang, G. Analysis of the Influence of a Natural Fracture Network on Hydraulic Fracture Propagation in Carbonate Formations. Rock Mech. Rock Eng. 2014, 47, 575–587. [Google Scholar] [CrossRef]
- Warpinski, N.R. Hydraulic Fracturing in Tight, Fissured Media. J. Pet. Technol. 1991, 43, 146–209. [Google Scholar] [CrossRef]
- de Pater, C.J.; Beugelsdijk, L.J.L. Experiments and numerical simulation of hydraulic fracturing in naturally fractured rock. In Proceedings of the Alaska Rocks 2005, The 40th U.S. Symposium on Rock Mechanics (USRMS), Anchorage, Alaska, 25–29 June 2005; American Rock Mechanics Association: Anchorage, Alaska, 2005; p. 12. [Google Scholar]
- Yushi, Z.; Shicheng, Z.; Zhou, T.; Xiang, Z.; Guo, T. Experimental Investigation into Hydraulic Fracture Network Propagation in Gas Shales Using CT Scanning Technology. Rock Mech. Rock Eng. 2015, 49. [Google Scholar] [CrossRef]
- Hou, B.; Zhang, R.; Zeng, Y.; Fu, W.; Muhadasi, Y.; Chen, M. Analysis of hydraulic fracture initiation and propagation in deep shale formation with high horizontal stress difference. J. Pet. Sci. Eng. 2018, 170, 231–243. [Google Scholar] [CrossRef]
- Izadi, G.; Moos, D.; Cruz, L.; Gaither, M.; Chiaramonte, L.; Johnson, S. Fully Coupled 3-D Hydraulic Fracture Growth in the Presence of Weak Horizontal Interfaces. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, The Woodlands, TX, USA, 24–26 January 2017; Society of Petroleum Engineers: The Woodlands, TX, USA, 2017; p. 15. [Google Scholar] [CrossRef]
- Huang, B.; Liu, J. Fully three-dimensional propagation model of horizontal borehole hydraulic fractures in strata under the effect of bedding planes. Energy Explor. Exploit. 2018, 36, 1189–1209. [Google Scholar] [CrossRef]
- Tang, J.; Zuo, L.; Xiao, L.; Wu, K.; Qian, B.; Yin, C.; Ehlig-Economides, C.; You, X. A 3-D Hydraulic Fracture Propagation Model Applied for Multiple-Layered Formation. In Proceedings of the International Petroleum Technology Conference, Beijing, China, 26–28 March 2019; p. 20. [Google Scholar] [CrossRef]
- Alalli, A.; Zoback, M. Microseismic evidence for horizontal hydraulic fractures in the Marcellus Shale, southeastern West Virginia. Lead. Edge 2018, 37, 356–361. [Google Scholar] [CrossRef]
- Celleri, H.M.; Castez, M.F.; Serebrinsky, S.; Sánchez, M.; Álvarez, J.P.; Winograd, E.A.; Vitolo, M. Hydraulic Fracture Propagation in Strike-Slip Regime With Weak Interfaces. In Proceedings of the 53rd U.S. Rock Mechanics/Geomechanics Symposium, New York, NY, USA, 23–26 June 2019; American Rock Mechanics Association: New York, NY, USA, 2019; p. 9. [Google Scholar]
- Nicholson, A.K.; Hawkes, R.V.; Bachman, R.C. Close Encounters in the 3rd Dimension: Using Diagnostic Fracture Injection Tests DFITs from the Alberta Duvernay Shale Formation to Quantify Simultaneous Horizontal- & Vertical-Plane Hydraulic Fracture Growth. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, The Woodlands, TX, USA, 5–7 February 2019; Society of Petroleum Engineers: The Woodlands, TX, USA, 2019; p. 21. [Google Scholar] [CrossRef]
- Kowan, J.; Schanken, L.; Jacobi, R. Conclusive Proof of Weak Bedding Planes in the Marcellus Shale and Proposed Mitigation Strategies. In Proceedings of the SPWLA 61st Annual Logging Symposium, Virtual, 24 June–29 July 2020. [Google Scholar] [CrossRef]
- Waters, G. Hydraulic Fracture Geometries in Laminated Rocks when Initiated from Horizontal Wells Drilled in Tectonically Stressed Environments. In Proceedings of the Second EAGE/SPE/AAPG Shale Gas Workshop, Dubai, United Arab Emirates, 21–24 September 2014; European Association of Geoscientists and Engineers: Dubai, United Arab Emirates, 2014; pp. 1–3. [Google Scholar] [CrossRef] [Green Version]
- Olorode, O.M.; Freeman, C.M.; Moridis, G.J.; Blasingame, T. High-Resolution Numerical Modeling of Complex and Irregular Fracture Patterns in Shale Gas and Tight Gas Reservoirs. In Proceedings of the SPE Latin America and Caribbean Petroleum Engineering Conference, Mexico City, Mexico, 16–18 April 2012; Society of Petroleum Engineers: Mexico City, Mexico, 2012; p. 25. [Google Scholar] [CrossRef] [Green Version]
- Yu, W.; Luo, Z.; Javadpour, F.; Varavei, A.; Sepehrnoori, K. Sensitivity analysis of hydraulic fracture geometry in shale gas reservoirs. J. Pet. Sci. Eng. 2014, 113, 1–7. [Google Scholar] [CrossRef]
- Yu, W.; Wu, K.; Sepehrnoori, K.; Xu, W. A Comprehensive Model for Simulation of Gas Transport in Shale Formation with Complex Hydraulic-Fracture Geometry. SPE Reserv. Eval. Eng. 2017, 20, 547–561. [Google Scholar] [CrossRef]
- Olorode, O.; Freeman, C.M.; Moridis, G.; Blasingame, T.A. High-Resolution Numerical Modeling of Complex and Irregular Fracture Patterns in Shale-Gas Reservoirs and Tight Gas Reservoirs. Spe Reserv. Eval. Eng. 2013, 16, 443–455. [Google Scholar] [CrossRef]
- Lin, M.; Chen, S.; Ding, W.; Chen, Z.; Xu, J. Effect of Fracture Geometry on Well Production in Hydraulic-Fractured Tight Oil Reservoirs. J. Can. Pet. Technol. 2015, 54, 183–194. [Google Scholar] [CrossRef]
- Xu, Y.; Cavalcante Filho, J.S.A.; Yu, W.; Sepehrnoori, K. Discrete-Fracture Modeling of Complex Hydraulic-Fracture Geometries in Reservoir Simulators. SPE Reserv. Eval. Eng. 2017, 20, 403–422. [Google Scholar] [CrossRef]
- Bartko, K.M.; Arnaout, I.H.; Asiri, K.S.; McClelland, K.M.; Mulhim, N.I.; Tineo, R.; Gurmen, M.N.; Al-Jalal, Z.; Pantsurkin, D.; Emelyanov, D.Y. From the Backyard Dune to Fracturing a Highly Tectonically Complex Formation in Saudi Arabia. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, The Woodlands, TX, USA, 24–26 January 2017; Society of Petroleum Engineers: The Woodlands, TX, USA, 2017; p. 18. [Google Scholar] [CrossRef]
- Ameen, M. Borehole Imaging of Natural Fractures and Stress Indicators in the Jurassic Carbonate Shale Plays, Eastern Saudi Arabia. In Proceedings of the Sixth EAGE Shale Workshop, Bordeaux, France, 28 April 2019. [Google Scholar] [CrossRef]
- Rubin, B. Accurate Simulation of Non Darcy Flow in Stimulated Fractured Shale Reservoirs. In Proceedings of the SPE Western Regional Meeting, Anaheim, CA, USA, 27–29 May; Society of Petroleum Engineers: Anaheim, CA, USA, 2010; p. 16. [Google Scholar] [CrossRef]
- Zhu, W.; He, X.; Khirevich, S.; Patzek, T.W. Fracture sealing and its impact on the percolation of subsurface fracture networks. Earth Space Sci. Open Arch. 2021, 30. [Google Scholar] [CrossRef]
- Chaudhary, A.S.; Ehlig-Economides, C.A.; Wattenbarger, R.A. Shale Oil Production Performance from a Stimulated Reservoir Volume. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 30 October–2 November 2011; Society of Petroleum Engineers: Denver, CO, USA, 2011; p. 21. [Google Scholar] [CrossRef] [Green Version]
- Aybar, U.; Yu, W.; Eshkalak, M.O.; Sepehrnoori, K.; Patzek, T. Evaluation of production losses from unconventional shale reservoirs. J. Nat. Gas Sci. Eng. 2015, 23, 509–516. [Google Scholar] [CrossRef]
- Al-Momin, A.; Kurdi, M.; Baki, S.; Mechkak, K.; Al-Saihati, A. Proving the Concept of Unconventional Gas Reservoirs in Saudi Arabia through Multistage Fractured Horizontal Wells. In Proceedings of the SPE Asia Pacific Unconventional Resources Conference and Exhibition, Brisbane, Australia, 9–11 November 2015; Society of Petroleum Engineers: Brisbane, Australia, 2015; p. 18. [Google Scholar] [CrossRef]
- Hakami, A.; Al-Mubarak, A.; Al-Ramadan, K.; Kurison, C.; Leyva, I. Characterization of carbonate mudrocks of the Jurassic Tuwaiq Mountain Formation, Jafurah basin, Saudi Arabia: Implications for unconventional reservoir potential evaluation. J. Nat. Gas Sci. Eng. 2016, 33, 1149–1168. [Google Scholar] [CrossRef]
- Zoback, M.D.; Kohli, A.H. Unconventional Reservoir Geomechanics: Shale Gas, Tight Oil, and Induced Seismicity; Cambridge University Press: Cambridge, MA, USA, 2019. [Google Scholar] [CrossRef]
- Abaza, B.; Baki, S.; Sadykov, A.; Mechkak, K.; Rueda, J. Determining the Magnitude of Interference among Adjacent Wells in a Saudi Arabian Unconventoinal Formation. In Proceedings of the International Petroleum Technology Conference, Dhahran, Saudi Arabia, 13–15 January 2020; International Petroleum Technology Conference: Dhahran, Saudi Arabia, 2020; p. 13. [Google Scholar] [CrossRef]
- Saputra, W.; Kirati, W.; Hughes, D.; Patzek, T. Forecast of Economic Gas production in the Marcellus. AAPG Bull. 2021. [Accepted]. [Google Scholar]
- Saputra, W.; Kirati, W.; Patzek, T.W. Generalized extreme value statistics, physical scaling and forecasts of gas production in the Haynesville shale. J. Nat. Gas Sci. Eng. 2021, 94, 104041. [Google Scholar] [CrossRef]
- Patzek, T.; Male, F.; Marder, M. A simple model of gas production from hydrofractured horizontal wells in shales. AAPG Bull. 2014, 98, 2507–2529. [Google Scholar] [CrossRef]
- Patzek, T.W.; Saputra, W.; Kirati, W. A Simple Physics-Based Model Predicts Oil Production from Thousands of Horizontal Wells in Shales. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 9–11 October 2017; Society of Petroleum Engineers: San Antonio, TX, USA, 2017; p. 26. [Google Scholar] [CrossRef] [Green Version]
- Saputra, W.; Kirati, W.; Patzek, T. Generalized Extreme Value Statistics, Physical Scaling and Forecasts of Oil Production in the Bakken Shale. Energies 2019, 12, 3641. [Google Scholar] [CrossRef] [Green Version]
- Al-Mulhim, N.I.; Korosa, M.; Ahmed, A.; Hakami, A.; Sadykov, A.; Baki, S.; Asiri, K.S.; Al Ruwaished, A. Saudi Arabia’s Emerging Unconventional Carbonate Shale Resources: Moving to Horizontals with an Integrated Engineering and Geosciences Approach. In Proceedings of the SPE Asia Pacific Unconventional Resources Conference and Exhibition, Brisbane, Australia, 9–11 November 2015; Society of Petroleum Engineers: Brisbane, Australia, 2015; p. 15. [Google Scholar] [CrossRef]
- Yu, W.; Hu, X.; Liu, M.; Wang, W. Investigation of the Effect of Natural Fractures on Multiple Shale-Gas Well Performance Using Non-Intrusive EDFM Technology. Energies 2019, 12, 932. [Google Scholar] [CrossRef] [Green Version]
- Liao, K.; Zhang, S.; Ma, X.; Yushi, Z. Numerical Investigation of Fracture Compressibility and Uncertainty on Water-Loss and Production Performance in Tight Oil Reservoirs. Energies 2019, 12, 1189. [Google Scholar] [CrossRef] [Green Version]
- Shar, M.; Abro, W.; Mahesar, A.; Lee, K. Simulation Study to Evaluate the Impact of Fracture Parameters on Shale Gas Productivity. Mehran Univ. Res. J. Eng. Technol. 2020, 39, 432–442. [Google Scholar] [CrossRef]
- Ivanova, A.; Mitiurev, N.; Cheremisin, A.; Orekhov, A.; Kamyshinsky, R.; Vasiliev, A. Characterization of Organic Layer in Oil Carbonate Reservoir Rocks and its Effect on Microscale Wetting Properties. Sci. Rep. 2019, 9, 10667. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ojha, S.P.; Misra, S.; Sinha, A.; Dang, S.; Tinni, A.; Sondergeld, C.; Rai, C. Relative Permeability and Residual Saturation Estimates for Organic-Rich Shale Samples from Bakken, Wolfcamp, Eagle Ford and Woodford Formations. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 9–11 October 2017; Society of Petroleum Engineers: San Antonio, TX, USA, 2017; p. 17. [Google Scholar] [CrossRef]
- Zoback, M.; Barton, C.; Brudy, M.; Castillo, D.; Finkbeiner, T.; Grollimund, B.; Moos, D.; Peska, P.; Ward, C.; Wiprut, D. Determination of stress orientation and magnitude in deep wells. Int. J. Rock Mech. Min. Sci. 2003, 40, 1049–1076. [Google Scholar] [CrossRef]
- Xiao, W.; Li, T.; Li, M.; Zhao, J.; Zheng, L.; Li, L. Evaluation of the stress sensitivity in tight reservoirs. Pet. Explor. Dev. 2016, 43, 115–123. [Google Scholar] [CrossRef]
- Dou, H.; Zhang, H.; Yao, S.; Sun, D.Z.T.; Ma, S.; Wang, X. Measurement and evaluation of the stress sensitivity in tight reservoirs. Pet. Explor. Dev. 2016, 43, 1116–1123. [Google Scholar] [CrossRef]
- Wang, H.; Ji, B.; Lv, C.; Zhang, L.; Li, X.; Cui, C.; Yu, H.; Nie, J. The stress sensitivity of permeability in tight oil reservoirs. Energy Explor. Exploit. 2019, 37, 1364–1376. [Google Scholar] [CrossRef]
- Aguilera, R. Effect of Fracture Compressibility on Gas-in-Place Calculations of Stress-Sensitive Naturally Fractured Reservoirs. In Proceedings of the SPE Unconventional Resources Conference/Gas Technology Symposium, Calgary, AB, Canada, 15–17 May 2006. [Google Scholar] [CrossRef]
- Zheng, S.; Manchanda, R.; Sharma, M.M. Modeling Fracture Closure with Proppant Settling and Embedment during Shut-In and Production. SPE Drill. Complet. 2020, 35, 668–683. [Google Scholar] [CrossRef]
- Shiozawa, S.; McClure, M. Simulation of proppant transport with gravitational settling and fracture closure in a three-dimensional hydraulic fracturing simulator. J. Pet. Sci. Eng. 2016, 138, 298–314. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Elsworth, D. Role of proppant distribution on the evolution of hydraulic fracture conductivity. J. Pet. Sci. Eng. 2018, 166, 249–262. [Google Scholar] [CrossRef]
- Zhang, W.; Thompson, K.E.; Reed, A.H.; Beenken, L. Relationship between packing structure and porosity in fixed beds of equilateral cylindrical particles. Chem. Eng. Sci. 2006, 61, 8060–8074. [Google Scholar] [CrossRef]
- Chunlou, L.; LaFollette, R.; Sookprasong, A.; Wang, S. Characterization of Hydraulic-Fracture Geometry in Shale-Gas Reservoirs. J. Pet. Technol. 2014, 66, 125–128. [Google Scholar] [CrossRef]
- Nandlal, K.; Weijermars, R. Drained rock volume around hydraulic fractures in porous media: Planar fractures versus fractal networks. Pet. Sci. 2019, 16, 1064–1085. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.J. Applied Petroleum Geomechanics; Gulf Professional Publishing: Cambridge, MA, USA, 2019; pp. 441–481. [Google Scholar] [CrossRef]
- Zhou, J.; Xue, C. Experimental Investigation of Fracture Interaction between Natural Fractures and Hydraulic Fracture in Naturally Fractured Reservoirs. In Proceedings of the SPE Europec featured at EAGE Conference and Exhibition, Vienna, Austria, 23–26 May 2011. [Google Scholar] [CrossRef]
- Jalili, S.; Ahangari, K. Effects of different stress regimes on hydraulic fracture geometry: A particle flow code approach. Innov. Infrastruct. Solut. 2017, 2. [Google Scholar] [CrossRef] [Green Version]
- Hubbert, M.K.; Willis, D.G. Mechanics Of Hydraulic Fracturing. Trans. AIME 1957, 210, 153–168. [Google Scholar] [CrossRef]
- Guo, T.; Zhang, S.; Zou, Y.; Xiao, B. Numerical simulation of hydraulic fracture propagation in shale gas reservoir. J. Nat. Gas Sci. Eng. 2015, 26, 847–856. [Google Scholar] [CrossRef]
- Lee, H.P.; Olson, J.E.; Holder, J.; Gale, J.F.W.; Myers, R.D. The interaction of propagating opening mode fractures with preexisting discontinuities in shale. J. Geophys. Res. Solid Earth 2015, 120, 169–181. [Google Scholar] [CrossRef]
- Tan, P.; Jin, Y.; Zhou, Y.; Hou, B.; Zhang, R.; Chang, Z.; Fan, M. Laboratory investigation of shale rock to identify fracture propagation in vertical direction to bedding. J. Geophys. Eng. 2018, 15. [Google Scholar] [CrossRef] [Green Version]
- Boggs, S., Jr. Carbonaceous Sedimentary Rocks, 2nd ed.; Cambridge University Press: Cambridge, MA, USA, 2009; pp. 527–555. [Google Scholar] [CrossRef]
- Weng, X.; Kresse, O.; Cohen, C.E.; Wu, R.; Gu, H. Modeling of Hydraulic Fracture Network Propagation in a Naturally Fractured Formation. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 24–26 January 2011; Society of Petroleum Engineers: The Woodlands, TX, USA, 2011; p. 18. [Google Scholar] [CrossRef]
- Cooke, M.L.; Underwood, C.A. Fracture termination and step-over at bedding interfaces due to frictional slip and interface opening. J. Struct. Geol. 2001, 23, 223–238. [Google Scholar] [CrossRef]
- Huang, B.; Liu, J. Experimental Investigation of the Effect of Bedding Planes on Hydraulic Fracturing Under True Triaxial Stress. Rock Mech. Rock Eng. 2017, 50, 2627–2643. [Google Scholar] [CrossRef]
- Rueda, J.; Valbuena, J.; Al-Momen, A.; Al-Mulhim, N. Applying Rate Transient Analysis (RTA) to Assist Fracturing Technique Selection in Unconventional Wells in Saudi Arabia. In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology Conference, Denver, CO, USA, 22–24 July 2019; Unconventional Resources Technology Conference: Denver, CO, USA, 2019; p. 10. [Google Scholar] [CrossRef]
- Rueda, J.; Valbuena, J.; Baki, S.; Mechkak, K.; Mohannad, M.; Momin, A.; Mulhim, N. Measuring Fracture Network Pressures during Fracturing and Production in Unconventionals in Saudi Arabia. In Proceedings of the SPE Middle East Oil and Gas Show and Conference, Manama, Bahrain, 18–21 March 2019; Society of Petroleum Engineers: Manama, Bahrain, 2019; p. 12. [Google Scholar] [CrossRef]
- Haider, S.; Saputra, W.; Patzek, T. The Key Factors That Determine the Economically Viable, Horizontal Hydrofractured Gas Wells in Mudrocks. Energies 2020, 13, 2348. [Google Scholar] [CrossRef]


| Layer | Thickness | Initial Water Saturation | Porosity | Permeability | |
|---|---|---|---|---|---|
| [m] | [ft] | [fraction] | [fraction] | [mD] | |
| Upper zone | 18 | 60 | 0.58 | 0.05 | 3.1 × 10 |
| Target zone | 9 | 30 | 0.20 | 0.07 | 14.0 × 10 |
| Lower zone | 14 | 45 | 0.60 | 0.04 | 2.0 × 10 |
| Parameter | SI Unit | Field Unit |
|---|---|---|
| Reservoir temperature | 138 ∘C | 280 ∘F |
| Initial reservoir pressure (a) | 58.6 MPa | 8500 psi |
| Vertical-horizontal permeability ratio (kv/kh) | 0.1 | 0.1 |
| Initial water saturation in the natural fracture network | 0.2 | 0.2 |
| Reservoir compressibility (b) | 1.0 × 10 Pa−1 | 6.9 × 10 psi−1 |
| Reservoir thickness | 41 m | 135 ft |
| Reservoir depth (c) | 3000 m | 10,000 ft |
| Natural fracture permeability (d) | 1.97 × 10 m2 | 200 mD |
| Natural fracture aperture (d) | 0.03 mm | 0.0001 ft |
| Natural fracture porosity | 0.0000067 | 0.0000067 |
| Number of stages (e) | 22 | 22 |
| Number of clusters per stage (e) | 3 | 3 |
| Hydraulic fracture spacing (f) | 30.5 m | 100 ft |
| Hydraulic fracture permeability | 1.97 × 10 m2 | 2000 mD |
| Hydraulic fracture propped half-length (f) | 137 m | 450 ft |
| Hydraulic fracture unpropped half-length | 152 m | 500 ft |
| Hydraulic fracture aperture (f) | 9 mm | 0.031 ft |
| Oil bubble point pressure | 23.44 MPa | 3400 psi |
| Oil API density | 45.6 | 45.6 |
| Oil density at stock tank conditions | 798.2 kg/m3 | 49.8 lbm/ft3 |
| Gas specific gravity | 0.8651 | 0.8651 |
| Water compressibility | 1.30 × 10 Pa−1 | 9.0 × 10 psi−1 |
| Water density at stock tank conditions | 996.9 kg/m3 | 62.2 lbm/ft3 |
| Parameter | Reference Fracture Scenario | Fracture Scenario #2 | Fracture Scenario #3 |
|---|---|---|---|
| Water rate peak [Bbl/d] | 18,992 | 24,546 | 11,666 |
| Oil rate peak [Bbl/d] | 931 | 1022 | 807 |
| Ultimate water production [MBbl] | 564 | 491 | 480 |
| Ultimate oil production [MBbl] | 407 | 374 | 368 |
| Recovery factor [%] | 8.5 | 7.7 | 7.6 |
| Comparison with reference scenario | |||
| Water rate peak [%] | - | 29 | −40 |
| Oil rate peak [%] | - | 10 | −13 |
| Ultimate water production [%] | - | −13 | −15 |
| Ultimate oil production [%] | - | −8 | −10 |
| Parameter | Reference Fracture Scenario | Fracture Scenario #2 | Fracture Scenario #3 |
|---|---|---|---|
| Water rate peak [Bbl/d] | 18,992 | 24,546 | 3027 |
| Oil rate peak [Bbl/d] | 931 | 1022 | 414 |
| Ultimate water production [MBbl] | 564 | 491 | 381 |
| Ultimate oil production [MBbl] | 407 | 374 | 324 |
| Recovery factor [%] | 8.5 | 7.7 | 6.7 |
| Comparison with reference scenario | |||
| Water rate peak [%] | - | 29 | −84 |
| Oil rate peak [%] | - | 10 | −55 |
| Ultimate water production [%] | - | −13 | −32 |
| Ultimate oil production [%] | - | −8 | −20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arias Ortiz, D.A.; Klimkowski, L.; Finkbeiner, T.; Patzek, T.W. The Effect of Hydraulic Fracture Geometry on Well Productivity in Shale Oil Plays with High Pore Pressure. Energies 2021, 14, 7727. https://doi.org/10.3390/en14227727
Arias Ortiz DA, Klimkowski L, Finkbeiner T, Patzek TW. The Effect of Hydraulic Fracture Geometry on Well Productivity in Shale Oil Plays with High Pore Pressure. Energies. 2021; 14(22):7727. https://doi.org/10.3390/en14227727
Chicago/Turabian StyleArias Ortiz, Daniela A., Lukasz Klimkowski, Thomas Finkbeiner, and Tadeusz W. Patzek. 2021. "The Effect of Hydraulic Fracture Geometry on Well Productivity in Shale Oil Plays with High Pore Pressure" Energies 14, no. 22: 7727. https://doi.org/10.3390/en14227727
APA StyleArias Ortiz, D. A., Klimkowski, L., Finkbeiner, T., & Patzek, T. W. (2021). The Effect of Hydraulic Fracture Geometry on Well Productivity in Shale Oil Plays with High Pore Pressure. Energies, 14(22), 7727. https://doi.org/10.3390/en14227727