Abstract
The test study area is the Miocene reservoir of Nam Con Son Basin, offshore Vietnam. In the study we used unsupervised learning to automatically cluster hydraulic flow units (HU) based on flow zone indicators (FZI) in a core plug dataset. Then we applied supervised learning to predict HU by combining core and well log data. We tested several machine learning algorithms. In the first phase, we derived hydraulic flow unit clustering of porosity and permeability of core data using unsupervised machine learning methods such as Ward’s, K mean, Self-Organize Map (SOM) and Fuzzy C mean (FCM). Then we applied supervised machine learning methods including Artificial Neural Networks (ANN), Support Vector Machines (SVM), Boosted Tree (BT) and Random Forest (RF). We combined both core and log data to predict HU logs for the full well section of the wells without core data. We used four wells with six logs (GR, DT, NPHI, LLD, LSS and RHOB) and 578 cores from the Miocene reservoir to train, validate and test the data. Our goal was to show that the correct combination of cores and well logs data would provide reservoir engineers with a tool for HU classification and estimation of permeability in a continuous geological profile. Our research showed that machine learning effectively boosts the prediction of permeability, reduces uncertainty in reservoir modeling, and improves project economics.
1. Introduction
One of the most challenging problems in reservoir analysis is predicting reservoir permeability when data is limited. A traditional approach to predicting permeability uses simple linear regression between core porosity and permeability (LogK = aPHI + b), Linear Multiple Regression (LMR) and Alternating Conditional Expectation (ACE) [1,2].
The novel approach which we have developed uses the Hydraulic Flow Unit (HU). The method classifies rock types using core data, then extrapolates the known hydraulic properties into the unknown based on pore scale fluid dynamics and geological parameters. This method was originally suggested by Amaefule et al. (1993) [3] and others [2,4,5]. Detailed studies confirmed that reservoir characterization can be improved by using HU to classify the reservoir rocks. Svirsky et al. (2004) [5] applied the method to describe reservoirs in a Siberian oil field. Guo et al. (2007) [6] used the rock quality index (RQI) and flow zone indicator (FZI) to classify clastic reservoirs of the Oriented basin, South America. Shenawi et al. (2009) [7] developed a variation of the HU technique and applied it to carbonate oil reservoirs in eight Saudi Arabian oilfields. Hossain et al. (2013) [8] used AI to estimate HU from predicted porosity and permeability. Sokhal et al. (2016) [9] used flow zone indicator (FZI) to predict rock type and permeability in Berkine basin in the Algerian Sahara.
So while core and log data provide relatively good data, it is still difficult to parameterize factors such as tortuosity, specific surface, or the radius of pores in a rock formation. Our study demonstrates that many of these problems can be solved using FZI and HU. These parameters can be combined to describe fluid flow in reservoir rock pores [10]. Thus, reservoir characterization using core and electric log data can be expressed as homogeneous hydraulic flow units (HU). FZI can be calculated from core data. FZI can then be transferred to HU groups using machine learning for FZI clustering [10].
Other studies tried to accomplish various supervised machine learning models for prediction reservoir characterization such as permeability, porosity, shear wave, and water saturation. Additionally, Linear Multiple Regression [1,11], Random Forest (RF) [12,13,14,15], Support Vector Machines [16,17], Boosted Tree and Artificial Neural Networks (ANN) were developed to improve predicting of FZI or permeability. Tang et al. (2004) [14] used statistical methods for classifying electric log facies from awest African clastic reservoir. Avseth et al. (2002) [18] used different multivariate statistical methods and a neural network for seismic lithofacies classification from well logs. Dubois et al. (2007) [19] tried to classify rock facies using various techniques in the Panoma gas field in Southwest Kansas. Wood (2019) [20] introduced new AI methods in classifying the Triassic reservoirs in the Hassi R’Mel gas field (Algeria). Researchers have more recently been interpolating or extrapolating missing well log data using machine learning methods and this work is ongoing [19,20,21,22,23,24,25].
In this paper, in order to answer the question reservoir engineers always ask: “How many hydraulic flow units do we need?” we took a two phase approach. In phase one, we not only applied traditional statistic methods for HU clustering of core data, including Histogram, Probability plot, Ward’s hierarchical algorithm and the Global Hydraulic Element (GHE) method [4,5,12], but also applied some unsupervised machine learning (ML) methods such as K mean, Self-Organize Map (SOM) and Fuzzy C mean (FCM). By comparing some of the unsupervised machine learning to deduce the optimal number of HU groups, we were then able to identify which unsupervised ML method is best for HU clustering in the reservoir.
In the second phase, we proposed a novel regression of supervised machine learning (ML) such as Artificial Neural Networks (ANN), Support Vector Machines (SVM), Boosted Tree (BT) and Random Forest (RF). These techniques were used to build the predict model of FZI in the zone of interest both for core and log data and application of that model to the uncored section and in the well without core data.
Since core and log data are an expensive and hard-won resource for reservoir characterization, it is crucial to maximize their use. By combining supervised and unsupervised machine learning methods and applying this technology to the available core and log data, we were able to significantly improve HU classification and prediction of the reservoir. Thus, this novel technique is a significant advance in the state of the art.
2. Geological Setting
The Nam Con Son Basin (NCSB) is from the Cenozoic age and is part of the southeastern continental shelf of Vietnam. It has an area of about 110,000 km2 (Figure 1). In general, the tectono-stratigraphic evolution of the basin during the Cenozoic can be subdivided into four major mega sequences: syn-rift 1, intra-rift, syn-rift 2, and post-rift. In the NCSB, rifting began in the late Eocene to early Oligocene. This began the North-South opening of the East Vietnam Sea. Seismic data suggests that the sediments are from the Eocene to Early Oligocene age. There is a major breakup unconformity at the top in the Early Oligocene. This early rifting was followed by thermal sag associated with the post-rift phase. During the Early Miocene, SW propagation of the East Vietnam Sea floor, spreading of the East Vietnam Sea to the NE of the basin and other regional tectonic forces impacted the NCSB. This eventually led to a second rifting phase followed by a regional uplift event in the late Middle Miocene as evidenced by the Mid-Miocene Unconformity. The post rift section during the late Miocene is marked by thermal sag and the deposition of the Mekong Delta sediments into the NCSB. This resulted in thermal maturation of the deeper section [26,27].
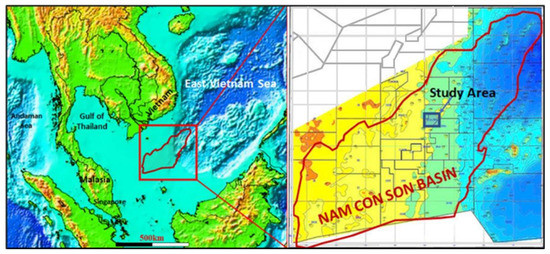
Figure 1.
Location map of the Nam Con Son Basin and study area.
The subsurface structure of the study area is complicated. Hydrocarbons of this basin have been discovered in Pre-Cenozoic basement and Miocene sandstone and carbonate. This study focuses only on the Miocene clastic reservoirs of the Dua Formation. Miocene clastics were deposited in paralic to shallow marine environments with sediment input from the north and west of the NCSB. The reservoirs are highly compartmentalized by NE-SW faulting [28].
3. Methodology and Dataset
3.1. Hydraulic Flow Unit (HU) Method Overview
A hydraulic flow unit is defined as that part of the reservoir volume comprising lithologies having reservoir characteristics, along with non-reservoir rocks and the fluids they contain. The flow unit has consistent physical characteristics that control fluid flow which are different from the characteristics of other reservoir volumes [29]. Each flow unit contains core data and electric log data that can be correlated and mapped between wells. The most important feature of HU is its ability to enable communication with other flow units. The pore geometry of a rock controls its hydraulic quality. Other authors have proposed a technique to discriminate hydraulic flow units (HU) within the reservoir by using core data porosity and permeability (Figure 2). We were able to use the hydraulic flow units in the reservoirs in the study area to create an improved reservoir model and to delineate potential new pay zones, and were able to increase potential reserves by 70% [5].
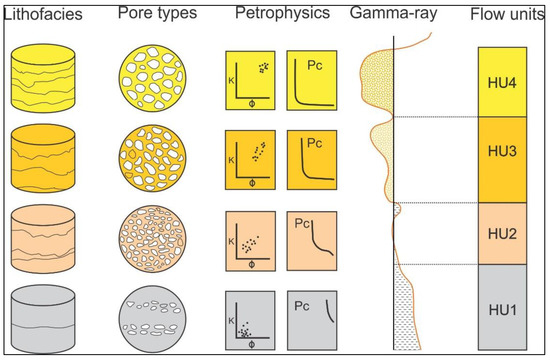
Figure 2.
The hydraulic flow units are defined based on lithofacies, reservoir properties and GR log response (modified after Ebanks et al., 1992) [30].
More recently, the concept of the HU has become an important tool for using flow zones to describe a reservoir. The Kozeny-Carman Equation (1) is the best formula to calculate permeability from the following parameters: rain size distribution, tortuosity, porosity, specific surface area, pore space geometry, fluid saturation and others [31,32].
where K is the permeability, Fs is the shape factor, Φe is the effective porosity, Sgr is the specific surface and τ is the tortuosity of pores.
Amaefule et al. (1993) [3] introduced two auxiliary factors: Φz, the normalized porosity—Equation (2); and RQI, the reservoir quality index—Equation (3). This results in a new formula—Equation (4), which defines the Flow Zone Indicator (FZI) in terms of porosity-permeability relationships, which accurately approximates the reservoir quality for a given sedimentary facies.
The basis of HU classification is to identify data classes that fall into that plot as a log-log graph of RQI versus Φz. Permeability is calculated from the HU of a sample by substituting for mean FZI porosity using Equation (5).
Based on Equations (1)–(4), we assume that units of constant FZI have invariable reservoir parameters that differ from the surrounding neighborhood. Proper division of the data set into units of constant FZI forms the basis for the HU construction, resulting in the best partial relationships of permeability versus porosity for each HU [33].
3.2. Applying Machine Learning for Hydraulic Flow Unit Classification and Prediction
Figure 3 details the workflow for applying machine learning to hydraulic flow unit classification and prediction.
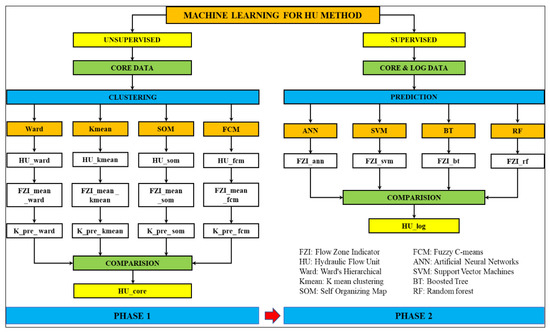
Figure 3.
The workflow for applying machine learning for Hydraulic flow unit classification and prediction in this study. On the left side, Phase 1 shows the process of applying unsupervised learning methods for HU clustering. We test four methods: Ward’s Hierarchical, K-mean, Ward’s Hierarchical, Fuzzy C-means (FCM), and Self-Organizing Map (SOM). On the right, Phase 2’s supervised learning algorithms include Support Vector Machines (SVM), Artificial Neural Networks (ANN), Random Forest (RF), and Boosted Tree (BT).
3.2.1. Unsupervised Learning Methods
This section introduces the unsupervised learning methods. For a more comprehensive overview, see Saxena et al. (2017) [34].
Ward’s Hierarchical Algorithm
Hierarchical clustering is a popular clustering technique. In Ward’s agglomerative hierarchical technique each data point forms a discrete cluster. Iteratively, similar discrete clusters merge into super clusters. The data point similarity is measured by summing the square of the distances between them. The hierarchical clustering output is a dendrogram that shows the cluster hierarchy [35].
This approach works well if the data is spherical, multivariate and normally distributed [1]. Additionally, the cluttering of this method is good only if there is an equal number of data points in each population. Ward’s Hierarchical clustering uses the following steps:
- Step 1:
- Calculate the proximity of individual points and consider all the data points as individual clusters,
- Step 2:
- Similar clusters are merged together and form as a single cluster,
- Step 3:
- Recalculate the proximity of new clusters,
- Step 4:
- Repeat steps 2 and 3 until termination conditions are reached.
K-Means Clustering
K-means clustering is a common unsupervised learning algorithm, which tries to group a data sets into K clusters so that items in the same cluster are close together and items in different clusters are more dispersed [35]. Hence, the K-means clustering process shrinks the distance between points in the same cluster and expands the distance between points when the clusters are different. The advantage of this clustering technique is speed. However, the problem with K-means is the number of clusters has to be known in advance, which is often a non-trivial task. Moreover, this method performs well with spherical clusters and when each cluster has equal numbers for observations. The algorithm works ineffectively with clusters of unusual size. The K-means method uses the following steps:
- Step 1:
- Choose the number of clusters K,
- Step 2:
- Select k random points from the data as center values,
- Step 3:
- Assign all the points to the closest cluster centers,
- Step 4:
- Recompute the new center values,
- Step 5:
- Repeat steps 3 and 4 until termination conditions are reached.
Self-Organizing Map (SOM)
The SOM algorithm [36] implemented in this study is an adaptive learning process. Neurons learn to represent discrete input data. The neuron that best approximates an input vector becomes the winning neuron. Other neurons learn to represent similar inputs. Neurons are then placed at the nodes in a lattice. This converts multi-dimensional data into a 1D and 2D discrete map [37]. The SOM clustering method uses the following steps:
- Step 1:
- Initialize random weight vector,
- Step 2:
- Choose random input vector from the training data,
- Step 3:
- Check all neurons to define the wining one that is the Best Matching Unit (BMU),
- Step 4:
- Update the neuron winner by calculating the neighborhood of the BMU, noting that the amount of neighbors decreases over time,
- Step 5:
- Repeat steps 2–4 until termination conditions are reached.
Fuzzy C-Means Clustering
Fuzzy clustering is a powerful unsupervised learning method for the analyzing data and constructing models. This is considered to be more natural than arbitrary hard clustering such as K-means. This method is derived from fuzzy logic, so it is suitable for solving ambiguous problems. The data points can belong to multiple clusters with different membership degrees [38]. Fuzzy C-means uses fuzzy partitioning. This means that a data point can belong to any or all groups. The degree of membership is graded between 0 and 1. This method also needs prior information on number clusters.
The fuzzy c-means clustering uses the following steps:
- Step 1:
- Set number of clusters k,
- Step 2:
- Randomly initialize k center values,
- Step 3:
- Calculate membership degree of each data point,
- Step 4:
- Calculate new center values,
- Step 5:
- Repeat steps 3 and 4 until termination conditions are reached.
3.2.2. Supervised Learning Methods
Support Vector Machines (SVM)
The SVM approach was originated by Vapnik in the 1960s [39,40] and was disregarded until recently. Now they have are considered to be a promising data driven estimator [41]. The SVM algorithm uses supervised learning. It is widely used to solve both linear and nonlinear problems. SVM creates a line or hyperplane that separates and divides the data into discrete classes. The algorithm finds the best line, or hyperplane to divide the data into two classes, maximizing the margin between the data points and the hyperplane. When the predicted value has the same sign as the actual value, then the cost is zero. Otherwise, we need to recalculate the loss value.
Boosted Trees (BT)
Decision trees are used for classification and regression problems. They are composed of vertices, which are written verifiable conditions, and leaves, in which answers are recorded (M classes for classification tasks) [42]. Boosting improves the performance of machine learning algorithms. Its essence lies in training each subsequent model using data from errors of previous models and further reducing errors [43]. This method can theoretically be used for any weak algorithm in order to reduce the learning error [44]. Gradient boosting of decision trees allows construction of an additive function as a sum of decision trees, iteratively and by analogy with the gradient descent method.
Artificial Neural Network (ANN)
ANN are statistical learning algorithms used in cognitive science and machine learning. They mimic neural networks which biologically form the central nervous systems. They work best in situations which approximate a function [45]. ANN works like a structure of the human brain: a neural system consisting of multiple layers, the first layer is the input data layer, followed by hidden neural layers that process data, relationships, and the influence of data on each other. Each layer contains neurons, which receive information from neurons in the previous data layer. The last layer is where the data is output. The learning process is repeated until the output of the ANN reaches the desired known value. An example of this technique is a back-propagation neural network. The learning process includes steps to calculate the output Y and comparing Y with the desired Z value; if the desired value is not reached (Δ = Z-Y large), then the weight must be adjusted, and the output recalculated until Δ equals 0 or becomes too small. The essential feature of the model is to manipulate these weights so that the error between the desired values and the predicted values is minimal.
Random Forests (RF)
RF was first described by Pavlov (1977, 1978) [46,47]. In this work, a set of labelled vertex rooted forests was considered with the assumption that probability distribution is uniform. Later, Pavlov (2000) [48] proposed the random forest with non-uniform distribution. Breiman (2001) proposed a new classification and regression method, also called a random forest [49]. This method is based on the construction of many decision trees, each of which comprises an original training sample. In the random forest method, when trees are formed at the vertex splitting stage, only a restricted number of randomly selected signs from the training sample can be used so that a complete leaf contains data from only one class. The classification is by voting of classifiers determined by individual trees. The regression assessment (RE) is calculated as the average RE of all trees [50].
Gradient Boosted Trees are very similar to Random Forests. They are both assembling methods: they combine decision trees to reduce the overfitting in each individual tree. However, the Gradient Boosted Trees differs from Random Forests in the way they build individual trees, and how the outputs are combined. While Random forests build the independent decision trees and combine them in parallel using bagging, Gradient boosted trees use a boosting method to combine weak learners so that each new tree corrects the errors of the previous one.
3.3. Dataset
The dataset of cores and well logs tested in this study was taken from the Miocene reservoir in the NCSB. Laboratory core measurements of effective porosity (Φe) and absolute permeability (K) were taken from various depths in the four wells. The study dataset included 587 core samples. Figure 4 shows all primary statistical analyses of the core data including basic statistics, histograms, distribution of K, Φe, FZI and cross plot of K versus Φe, and density.
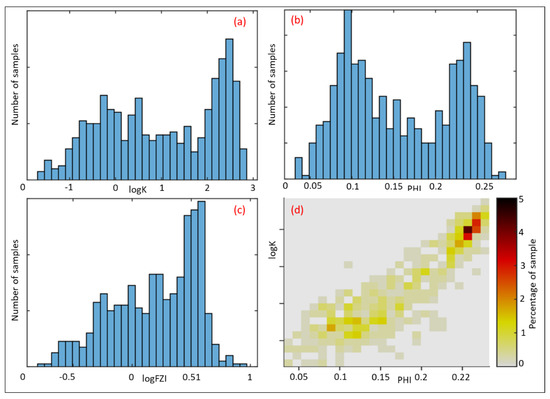
Figure 4.
The 587 cores data from 4 wells: (a) Histogram of permeability, (b) Porosity, (c) FZI and (d) Cross plot of permeability versus porosity and density of data.
Laboratory results (K, Φe) were combined with data from six logs including natural gamma ray intensity (GR), resistivity from LLD (short normal) and LLS (long normal), neutron porosity (NPHI), density (RHOB) and transit time interval (DT). Before applying machine learning techniques for FZI prediction, cores and logs data were depth matched for all study wells.
4. Results and Discussion
4.1. Unsupervised Machine Learning for HU Core Clustering
In the first phase of this study, based on 587 cores data from four wells in the study area, we analyzed data from FZI cores using Equation (4) and then applied statistical methods for FZI clustering. These techniques have been presented clearly by many researchers previously. They include Histogram, Probability plot and Ward’s hierarchical [1,3,5] and the Global Hydraulic Elements (GHE) method [4,51].
Figure 5 shows the results of HU classification from each of the traditional methods described above: (a) A histogram of FZI does not clearly reveal the distribution of groups; (b) A normal probability plot illustrates how the local slope changes according to selected groups with a constant FZI cluster; the straight lines connecting the selected sections of the probability plot can determine some groups of HU; (c) based on the Ward’s algorithm, the dendrogram clearly shows the FZI data clustering; (d) the GHE method proposed is a rapid and more straightforward approach to plot Φe and K on the pre-determined global hydraulic elements template. It can also divide core data into six groups [1,12].
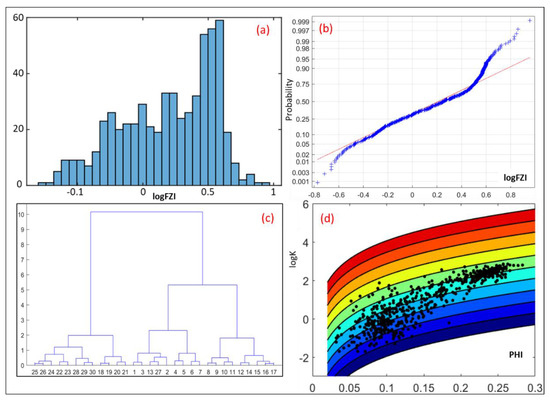
Figure 5.
Hydraulic flow unit classification base on core data: (a) Histogram of FZI, (b) Probability plot of FZI, (c) Dendrogram of FZI, (d) Dispersion plot of K_core versus PHI_core.
The objective of this optimization stage is to identify which training method clusters the best against the FZI core data, and to define the optimum group of HU core data to use for the Miocene reservoir section. In this study, we proposed three more methods: K-mean, SOM and Fuzzy C-means. FZI clustering was then transferred to HU groups. Figure 3 shows steps for applying unsupervised machine learning for each method above. In the first step we tried to divide the reservoir into groups from 2–10 HU, and then we could derive the FZI mean for each group. In the second step, we calculated permeability (K_pre) from each FZI mean using Equation (5). Table 1 shows correlation coefficient (R2) and root mean square error (RMSE) of K_core versus permeability calculated (K_pre) for each method in the clustering range from 2–10 HU.

Table 1.
The results of R2 and MRSE for unsupervised clustering range from 2–10 HU clusters.
The results of the unsupervised clustering machine learning methods are summarized in Table 1 and Figure 6. They clearly show when the number of HU increases from 2 to 10 the correlation coefficient of K_core versus K_pre for each method also increases from 0.896 to 0.995. Conversely the root mean square error decreases from 0.399 down to 0.086.
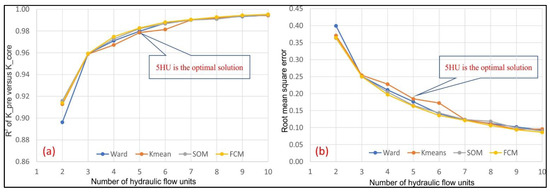
Figure 6.
Determination of the optimal number of HU groups by comparing machine learning clustering methods based on (a) the correlation coefficient (R2) of (K_pre versus K_core) and (b) the number of HU groups.
Figure 6 answers the question “How many hydraulic flow units do we need?”. In this case study, we can see clearly that 5 HU is the optimal solution for clustering of HU; the FCM method for highest R2 = 0.983, and RMSE for lowest RMSE = 0.163. These results suggest we use the FCM method for HU classification with core data section in Phase 1 on the workflow (Figure 3) Figure 7 compares the results of the 4 methods of unsupervised machine learning for 5 HU clustering. Figure 8a,b show results of applying FCM method for HU clustering with different HU groups, ranging from 3–10 HU. Table 2 shows the final simple statistics of porosity (PHI), permeability (K) and FZI from the results of FCM method for 5 HU groups.
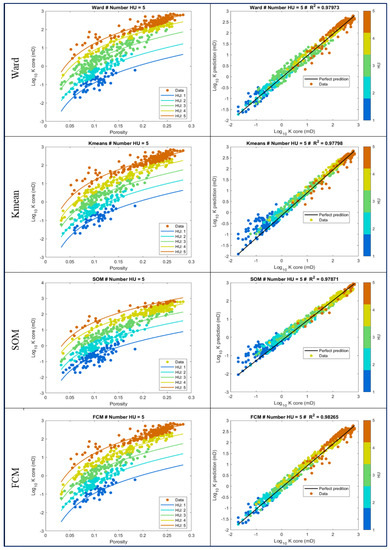
Figure 7.
The matrix cross plots between (K_core vs. PHI_core) and (K_core vs. K_pre) of four unsupervised machine learning methods show that the reservoir is divided into 5 HU groups.
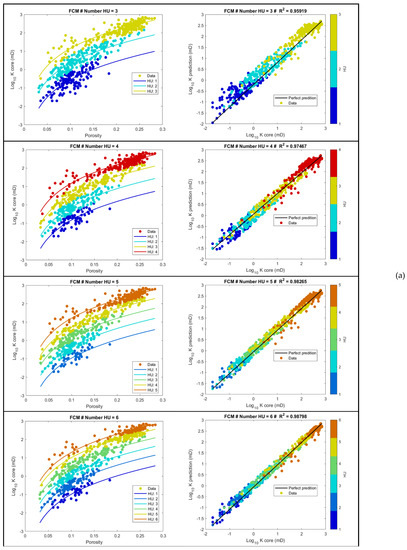
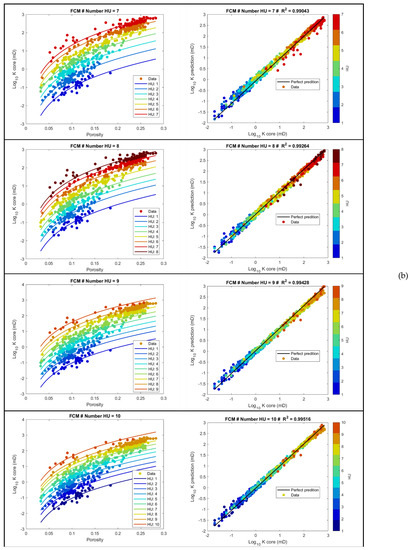
Figure 8.
The result of applying the FCM method to HU clustering: The cross plot of (K_core vs. PHI_core) and (K_core vs. K_pre) with different HU groups and ranging from 3–6 HU (a) and 7–10 HU (b).

Table 2.
The final simple statistics of PHI, K and FZI from the results of FCM method for 5 HU.
4.2. Supervised Machine Learning for HU Logs Prediction
4.2.1. Data Preparation
For training Machine Learning models, data preparation is critical to the success of training, validation and testing. To obtain the best results, the data needs to be clean and not corrupted. The logs must be properly calibrated, and environmentally corrected. Both log and core data must be accurately depth matched. The log data was recorded using differently calibrated tools with different scales. This error was fixed by normalizing the data.
Four wells with 587 core sample points were selected for HU clustering (Section 4.1). For this stage we selected one well which had a very high-density of cores, and six well logs for training, validation, and testing. Data preparation was done in three stages:
- -
- Data description,
- -
- Remove outliers,
- -
- Data standardization.
An outlier core in data is when an observed value is radically different from other observations. The outlier may be rare, distinct or does not fit in some way. Outliers are generally defined as samples that are exceptionally far from the mainstream of the core data set. In this study, to remove outliers and improve the signal to noise ratio in the data, we applied the Local Outlier Factor (LOF) method proposed by Breunig et al. (2000) [52]. The LOF method is best for finding outliers in a multidimensional dataset. After removing the outliers, the data was standardized by scaling to unit variance. We calculated the standard score of a sample by:
where: z is standard value; u is training sample mean; and s is training sample standard deviation.
After data preparation and removing outliers, the 302 remaining core data points were submitted to a supervised machine learning processing. Table 3 displays the basic statistics such as mean, standard deviation, minimum, maximum and three parts (25%, 50% and 75%) distribution of the six logs and FZI_core. Figure 9 shows the four log cures: DT, GR, RHOB, NPHI and FZI cores data with color responding to 5 HU and the cross plots between FZI core versus each log. Figure 10 shows the histograms of the six logs and FZI core data after removing outliers using the LOF method.

Table 3.
The statistic of the 6 logs (DT, GR, NPHI, RHOB, LLD, LLS,) and FZI core data after removing outliers.
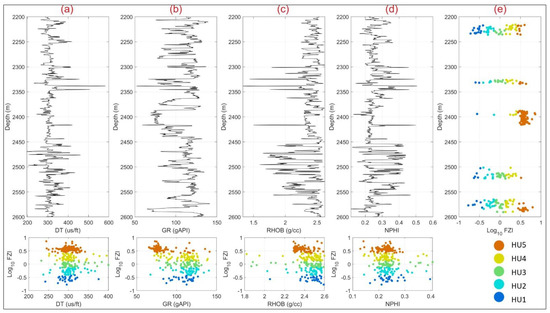
Figure 9.
The 4 log curves: DT, GR, RHOB, NPHI (a–d) and FZI cores color responding with 5 HU (e), and the cross plots between FZI core versus each log.
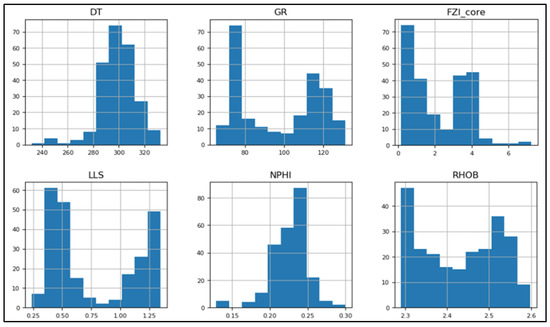
Figure 10.
The histogram of the logs (DT, GR, NPHI, RHOB, LLS,) and FZI core data after outlier removal.
4.2.2. Regression Machine Learning for FZI_log Prediction
The objective of this phase is to identify which training method is the best predictor for FZI core data combined with log data for predicting FZI_log based on the supervised machine learning methods. The four methods are ANN, SVM, BT and RF. These were selected for predicting FZI_log and then transferred to HU_log by using cutoff FZI max (Table 2). We then e estimated permeability log (K_log) by applying Equation (5) using each FZI mean for each HU groups from Table 2. To choose the best predictive supervised learning method, the four supervised learning methods were run simultaneously using the six logs combined with the core data to predict FZI logs; we ran several processing tests to find the best parameters for each method. The results indicate 70% data for training, 15% data for validation and 15% data for testing are optimal parameters. The results are summarized in Figure 11 and Table 4.
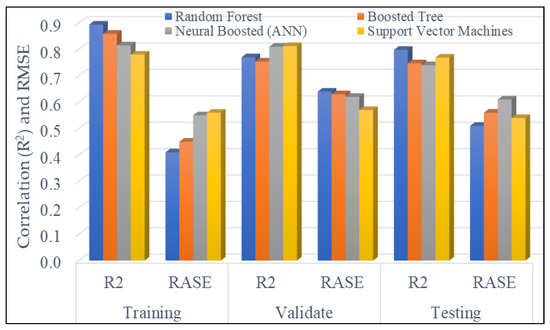
Figure 11.
The bar plots to display and compare 4 supervised machine learning methods to predict FZI log. The Random Forest method shows the best result with highest R2 = 0.894 and lowest RASE = 0.41 on the training section.

Table 4.
Summary results of R2 and RMSE after running four ML methods.
To compare four ML methods above, we examined the results of the three phases in the process. Figure 11 shows the bar plots and the summary results to compare the four supervised machine learning methods in order to predict FZI log. These include training, validation, and testing of each method. Table 4 shows evaluation standards. R2 and RMSE, used to grade the FZI log results.
- -
- For the R2: For training section, the Random Forest method shows the best result with R2 = 0.894 which is higher than BT (0.859), ANN (0.851) and SVM (0.78). For testing we also see that RF (0.798) is higher than BT (0.747), ANN (0.74) and SVM (0.769) showing better performance (Table 4).
- -
- For the RASE: For training, the Random Forest method shows RASE = 0.41 which is lower than BT (0.45), ANN (0.55) and SVM (0.56), and on testing we also see that RF (0.51) is lower than BT (0.56), ANN (0.61) and SVM (0.54) showing better performance (Table 4).
Figure 12 shows the cross plot of outcomes of four methods where we can observe and compare between target values (FZI_core) versus prediction (FZI_log) for training, validate and testing.
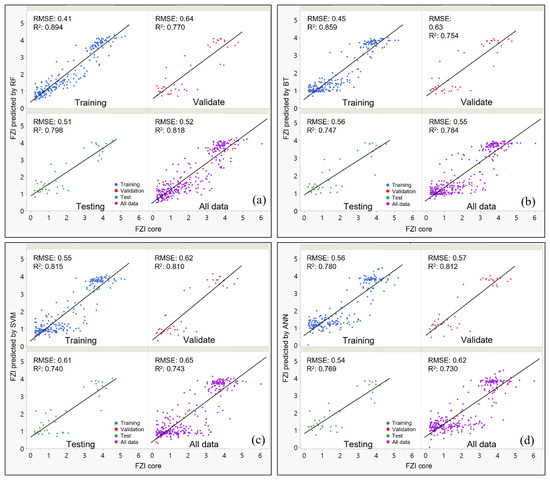
Figure 12.
The cross plots between FZI cores versus FZI prediction of 4 methods of supervised machine learning. For each method we can get the results: Training, validate and testing: (a) Random Forest (RF); (b) Boosted tree (BT); (c) Support vector machines (SVM) and (d) Neural Boosted (ANN).
After testing and comparing the models of each ML method above we decided to use the RF method to predict FZI logs for the full well log section. Figure 13 shows the results. The distribution of 5 HU groups depended on whether the section was clean sand reservoir type rock or shaly non reservoir rock. For reservoirs the distribution of the 5 HU groups for the well show a good correspondence with the GR logs. But HU1 and HU2 provide the best match in non-reservoir shale intervals.
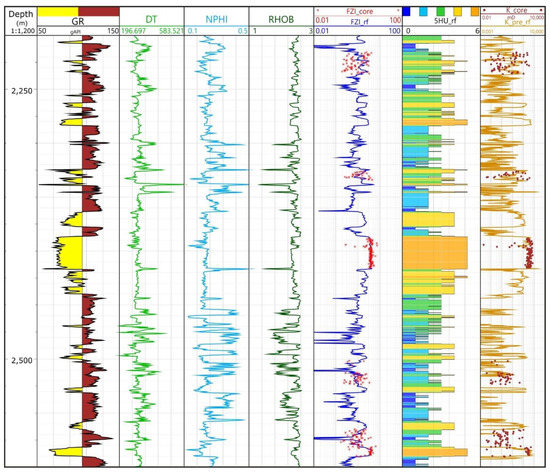
Figure 13.
The logs curves (GR, DT, NPHI, RHOB) and FZI prediction, HU classification and permeability estimated by applying the Random Forest method.
5. Conclusions
The study workflow combined supervised and unsupervised machine learning methods for hydraulic flow unit classification and prediction. Integrating both core and standard well log data for machine learning techniques improved the results over traditional methods. We used the results to estimate the permeability of the Miocene Reservoir of the Nam Con Son Basin. Key study conclusions are:
- Unsupervised machine learning is an effective way to quickly organize FZI data into clusters. We used the clustered data to rapidly determine the optimal number of HU groups for reservoir classification.
- We found the best clustering method for HU classification to be the Fuzzy Mean C technique. This showed the optimal division of the Miocene reservoir to be 5 HU.
- We examined four ML techniques. These were RF, ANN, SVM and BT. The RF results were clearly superior.
Finally, we used this workflow to predict HU logs from other wells. We used these predictions as input for a reservoir static model for media flow analysis in a further study.
Author Contributions
Introduction, H.Q.M.; geological setting, B.V.D.; methodology H.Q.M. and D.H.H.; data analysis T.K.H.; overview machine learning methods, K.D.T. and N.M.H.; applying unsupervised ML for HU cores classification H.Q.M., K.D.T., T.K.H. and N.V.K.; applying supervised ML for HU logs prediction K.D.T., D.H.H., T.K.H. and P.Q.N.; conclusions, H.Q.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research is funded by the Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number 105.99-2019.324 and National program on Mining and mineral processing under grand number CNKK.001/19.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This research is funded by the Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number 105.99-2019.324 and National program on Mining and mineral processing under grand number CNKK.001/19. The authors gratefully acknowledge the support given by Vietnam Petroleum Institute (VPI). Sincere thanks go to Pham Huy Giao and Pham Hong Trang of VPI for their support during manuscript preparation. Techlog® were used thanks to the university grant donation by Schlumberger to Hanoi University of Mining and Geology.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| ACE | Alternating Conditional Expectation |
| ANN | Artificial Neural Network |
| BT | Boosted Tree |
| DT | Sonic log |
| FCM | Fuzzy C mean |
| FZI | Flow zone indicator |
| GHE | Global Hydraulic Element |
| GR | Gamma-ray log |
| HU | Hydraulic flow unit |
| K | Permeability |
| LLD | Deep resistivity latero-log |
| LMR | Linear Multiple Regression |
| LSS | Shallow resistivity latero-log |
| NCSB | Nam Con Son Basin |
| NE | North-East |
| NPHI | Neutron porosity |
| PHI | Porosity |
| RF | Random Forest |
| RHOB | Density |
| RQI | Reservoir quality index |
| SOM | Self-Organize Map |
| SVM | Support Vector Machines |
| SW | South-West |
References
- Man, H.Q.; Jarzyna, J. Integration of Core, Well Logging and 2D Seismic Data to Improve a Reservoir Rock Model: A Case Study of Gas Accumulation in the NE Polish Carpathian Foredeep. Geol. Q. 2013, 57, 289–306. [Google Scholar] [CrossRef][Green Version]
- Abbaszadeh, M.; Fujii, H.; Fujimoto, F. Permeability Prediction by Hydraulic Flow Units—Theory and Applications. SPE Form. Eval. 1996, 11, 263–271. [Google Scholar] [CrossRef]
- Amaefule, J.O.; Altunbay, M.; Tiab, D.; Kersey, D.G.; Keelan, D.K. Enhanced Reservoir Description: Using Core and Log Data to Identify Hydraulic (Flow) Units and Predict Permeability in Uncored Intervals/Wells. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 3–6 October 1993; p. SPE-26436-MS. [Google Scholar]
- Corbett, P.; Ellabad, Y.; Mohammed, K.; Pososyaev, A. Global Hydraulic Elements—Elementary Petrophysics for Reduced Reservoir Modelling. In Proceedings of the 65th EAGE Conference & Exhibition, Stavanger, Norway, 2–5 June 2003; p. cp-6-00256. [Google Scholar]
- Svirsky, D.; Ryazanov, A.; Pankov, M.; Corbett, P.W.M.; Posysoev, A. Hydraulic Flow Units Resolve Reservoir Description Challenges in a Siberian Oil Field. In Proceedings of the SPE Asia Pacific Conference on Integrated Modelling for Asset Management, Kuala Lumpur, Malaysia, 29–30 March 2004; p. SPE-87056-MS. [Google Scholar]
- Guo, G.; Diaz, M.A.; Paz, F.J.; Smalley, J.; Waninger, E.A. Rock Typing as an Effective Tool for Permeability and Water-Saturation Modeling: A Case Study in a Clastic Reservoir in the Oriente Basin. SPE Reserv. Eval. Eng. 2007, 10, 730–739. [Google Scholar] [CrossRef]
- Shenawi, S.; Al-Mohammadi, H.; Faqehy, M. Development of Generalized Porosity-Permeability Transforms by Hydraulic Units for Carbonate Oil Reservoirs in Saudi Arabia. In Proceedings of the SPE/EAGE Reservoir Characterization & Simulation Conference, Abu Dhabi, UAE, 19–21 October 2009. [Google Scholar]
- Shujath Ali, S.; Hossain, M.E.; Hassan, M.R.; Abdulraheem, A. Hydraulic Unit Estimation From Predicted Permeability and Porosity Using Artificial Intelligence Techniques. In Proceedings of the North Africa Technical Conference and Exhibition, Cairo, Egypt, 15–17 April 2013. [Google Scholar]
- Abdallah, S.; Sid Ali, O.; Benmalek, S. Rock type and permeability prediction using flow-zone indicator with an application to Berkine Basin (Algerian Sahara). In SEG Technical Program Expanded Abstracts; Society of Exploration Geophysicists: Dallas, TX, USA, 2016; pp. 3068–3072. [Google Scholar]
- Quang, M.H.; Le An, N.; Jarzyna, J. Hydraulic flow unit classification from core data: Case study of the Z gas reservoir, Poland. JMES 2021, 62, 29–36. [Google Scholar] [CrossRef]
- Ha Quang, M.; Jarzyna, J. Integrating of Core and Logs and 2D Seismic Data to Improve 3D Hydraulic Flow Unit Modeling; European Association of Geoscientists & Engineers: Vienna, Austria, 2011; p. cp-238-00521. [Google Scholar]
- Matyasik, J.; Myśliwiec, M.; Leśniak, G.; Such, P. Relationship between Hydrocarbon Generation and Reservoir Development in the Carpathian Foreland (Poland). In Thrust Belts and Foreland Basins; Springer: Berlin/Heidelberg, Germany, 2007; pp. 413–427. ISBN 978-3-540-69425-0. [Google Scholar]
- Bressan, T.S.; Kehl de Souza, M.; Girelli, T.J.; Junior, F.C. Evaluation of Machine Learning Methods for Lithology Classification Using Geophysical Data. Comput. Geosci. 2020, 139, 104475. [Google Scholar] [CrossRef]
- Al-Mudhafar, W.J. Integrating Well Log Interpretations for Lithofacies Classification and Permeability Modeling through Advanced Machine Learning Algorithms. J. Pet. Explor. Prod. Technol. 2017, 7, 1023–1033. [Google Scholar] [CrossRef]
- Male, F.; Duncan, I.J. Lessons for Machine Learning from the Analysis of Porosity-Permeability Transforms for Carbonate Reservoirs. J. Pet. Sci. Eng. 2020, 187, 106825. [Google Scholar] [CrossRef]
- Al-Mudhafar, W.J. Integrating Component Analysis & Classification Techniques for Comparative Prediction of Continuous & Discrete Lithofacies Distributions. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 4–7 May 2015; Volume OnePetro; p. OTC-25806-MS. [Google Scholar]
- Al-Mudhafar, W.J. Integrating Kernel Support Vector Machines for Efficient Rock Facies Classification in the Main Pay of Zubair Formation in South Rumaila Oil Field, Iraq. Model. Earth Syst. Environ. 2017, 3, 12. [Google Scholar] [CrossRef]
- Ameur-Zaimeche, O.; Zeddouri, A.; Heddam, S.; Kechiched, R. Lithofacies Prediction in Non-Cored Wells from the Sif Fatima Oil Field (Berkine Basin, Southern Algeria): A Comparative Study of Multilayer Perceptron Neural Network and Cluster Analysis-Based Approaches. J. Afr. Earth Sci. 2020, 166, 103826. [Google Scholar] [CrossRef]
- Tang, H.; White, C.; Zeng, X.; Gani, M.; Bhattacharya, J. Comparison of Multivariate Statistical Algorithms for Wireline Log Facies Classification. In Proceedings of the AAPG Annual Meeting, Dallas, TX, USA, 30 June–1 July 2004. [Google Scholar]
- Baldwin, J.L.; Bateman, R.M.; Wheatley, C.L. Application Of A Neural Network To The Problem Of Mineral Identification From Well Logs. Log Anal. 1990, 31, SPWLA-1990-v31n5a1. [Google Scholar]
- Rogers, S.J.; Fang, J.H.; Karr, C.L.; Stanley, D.A. Determination of Lithology from Well Logs Using a Neural Network1. AAPG Bull. 1992, 76, 731–739. [Google Scholar] [CrossRef]
- Wong, P.M.; Jian, F.X.; Taggart, I.J. A Critical Comparison of Neural Networks and Discriminant Analysis in Lithofacies, Porosity and Permeability Predictions. J. Pet. Geol. 1995, 18, 191–206. [Google Scholar] [CrossRef]
- Avseth, P.; Mukerji, T. Seismic Lithofacies Classification From Well Logs Using Statistical Rock Physics. Petrophys.-SPWLA J. Form. Eval. Reserv. Descr. 2002, 43, SPWLA-2002-v43n2a1. [Google Scholar]
- Dubois, M.K.; Bohling, G.C.; Chakrabarti, S. Comparison of Four Approaches to a Rock Facies Classification Problem. Comput. Geosci. 2007, 33, 599–617. [Google Scholar] [CrossRef]
- Wood, D.A. Lithofacies and Stratigraphy Prediction Methodology Exploiting an Optimized Nearest-Neighbour Algorithm to Mine Well-Log Data. Mar. Pet. Geol. 2019, 110, 347–367. [Google Scholar] [CrossRef]
- Dung, B.V.; Tuan, H.A.; Van Kieu, N.; Man, H.Q.; Thanh Thuy, N.T.; Dieu Huyen, P.T. Depositional Environment and Reservoir Quality of Miocene Sediments in the Central Part of the Nam Con Son Basin, Southern Vietnam Shelf. Mar. Pet. Geol. 2018, 97, 672–689. [Google Scholar] [CrossRef]
- Tuan, N.Q.; Tri, T.V. Seismic Interpretation of the Nam Con Son Basin and Its Implication for the Tectonic Evolution. Indones. J. Geosci. 2016, 3, 127–137. [Google Scholar] [CrossRef]
- An, N.H. Assessement of Improved Oil Recovery Potential of Dai Hung Oil Field. Petrovietnam J. 2008, 8, 53–61. [Google Scholar] [CrossRef]
- Ebanks, W.J., Jr. Flow Unit Concept—Integrated Approach to Reservoir Description for Engineering Projects: Abstract. AAPG Bull. 1987, 71, 551–552. [Google Scholar]
- Ebanks, W.J., Jr.; Scheiling, M.H.; Atkinson, C.D. Flow Units for Reservoir Characterization; Morton-Thompson, D., Ed.; Development Geology Reference Manual; AAPG: Tulsa, OK, USA, 1992; ISBN 978-0-89181-660-7. [Google Scholar]
- Kozeny, J. Uber Kapillare Letung Des Wassers Im Boden, Sitzungsberichte. R. Acad. Sci. 1927, 136, 271–306. [Google Scholar]
- Carman, P.C. Fluid Flow through Granular Beds. Trans. Inst. Chem. Eng. 1937, 15, 150–167. [Google Scholar] [CrossRef]
- Jarzyna, J.; Man, H.Q. Hydraulic Units Differentiated in Reservoir Rock to Facilitate Permeability Determinations for Flow Modeling in Gas Deposit. Prz. Geol. 2009, 57, 996–1003. [Google Scholar]
- Saxena, A.; Prasad, M.; Gupta, A.; Bharill, N.; Patel, O.P.; Tiwari, A.; Er, M.J.; Ding, W.; Lin, C.-T. A Review of Clustering Techniques and Developments. Neurocomputing 2017, 267, 664–681. [Google Scholar] [CrossRef]
- Abbas, M.A.; Al Lawe, E.M. Clustering Analysis and Flow Zone Indicator for Electrofacies Characterization in the Upper Shale Member in Luhais Oil Field, Southern Iraq. In Proceedings of the Abu Dhabi International Petroleum Exhibition & Conference, Abu Dhabi, UAE, 12 November 2019. [Google Scholar]
- Kohonen, T. The Self-Organizing Map. Proc. IEEE 1990, 78, 1464–1480. [Google Scholar] [CrossRef]
- Dixit, N.; McColgan, P.; Kusler, K. Machine Learning-Based Probabilistic Lithofacies Prediction from Conventional Well Logs: A Case from the Umiat Oil Field of Alaska. Energies 2020, 13, 4862. [Google Scholar] [CrossRef]
- Suganya, R.; Shanthi, R. Fuzzy C-Means Algorithm—A Review. Int. J. Sci. Res. Publ. 2012, 2, 3. [Google Scholar]
- Vapnik, V. Pattern Recognition Using Generalized Portrait Method. Autom. Remote Control 1963, 24, 774–780. [Google Scholar]
- Vapnik, V. A Note on One Class of Perceptrons. Autom. Remote Control 1964, 24, 821–837. [Google Scholar]
- Rodriguez-Galiano, V.; Sanchez-Castillo, M.; Chica-Olmo, M.; Chica-Rivas, M. Machine Learning Predictive Models for Mineral Prospectivity: An Evaluation of Neural Networks, Random Forest, Regression Trees and Support Vector Machines. Ore Geol. Rev. 2015, 71, 804–818. [Google Scholar] [CrossRef]
- Kaftannikov, I.L.; Parasich, A.V. Decision Tree’s Features of Application in Classification Problems. Bull. S. Ural State Univ. Ser. Comput. Technol. Autom. Control Radioelectron. 2015, 15, 26–32. [Google Scholar] [CrossRef][Green Version]
- Salakhutdinova, K.I.; Lebedev, I.S.; Krivtsova, I.E. Gradient Boosting Trees Method in the Task of Software Identification. Sci. Tech. J. Inf. Technol. Mech. Opt. 2018, 18, 1016–1022. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. Experiments with a New Boosting Algorithm; Morgan Kaufmann Publishers Inc.: Bari, Italy, 1996; pp. 148–156. [Google Scholar]
- Jothilakshmi, S.; Gudivada, V.N. Chapter 10—Large Scale Data Enabled Evolution of Spoken Language Research and Applications. In Handbook of Statistics; Gudivada, V.N., Raghavan, V.V., Govindaraju, V., Rao, C.R., Eds.; Elsevier: Amsterdam, The Netherlands, 2016; Volume 35, pp. 301–340. ISBN 0169-7161. [Google Scholar]
- Pavlov, J.L. Limit Theorems for the Number of Trees of a given Size in a Random Forest. Math. USSR-Sb. 1977, 32, 335–345. [Google Scholar] [CrossRef]
- Pavlov, Y.L. The Asymptotic Distribution of Maximum Tree Size in a Random Forest. Theory Probab. Its Appl. 1978, 22, 509–520. [Google Scholar] [CrossRef]
- Pavlov, Y.L. Random Forests; VSP: Utrecht, The Netherlands, 2000; ISBN 90-6764-314-9. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Chistiakov, S.P. Random Forests: An Overview. Proc. Karelian Sci. Cent. Russ. Acad. Sci. 2013, 4, 117–136. [Google Scholar]
- Corbett, P.; Potter, D. Petrotyping: A Basemap and Atlas for Navigating through Permeability and Porosity Data for Reservoir Comparison and Permeability Prediction. In Proceedings of the International Symposium of the Society of Core Analysts (SCA2004-30), Abu Dhabi, UAE, 5–9 October 2004. [Google Scholar]
- Breunig, M.M.; Kriegel, H.P.; Ng, R.T.; Sander, J. LOF: Identifying DensityBased Local Outliers. SIGMOD Rec. 2000, 29, 93–104. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).