Effect of Adding Surfactants to a Solution of Fertilizer on the Granulation Process
Abstract
:1. Introduction
2. Materials and Methods
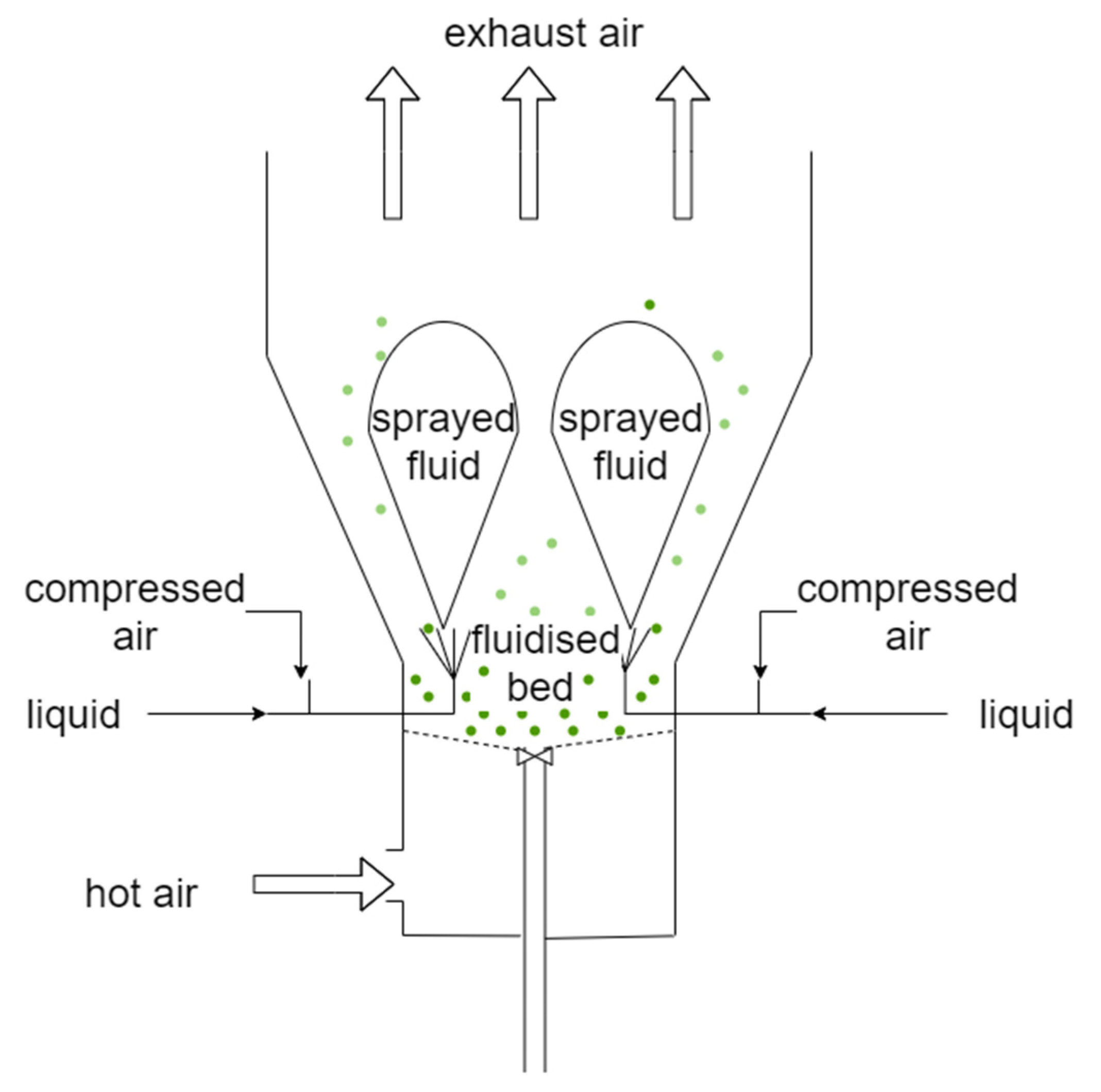
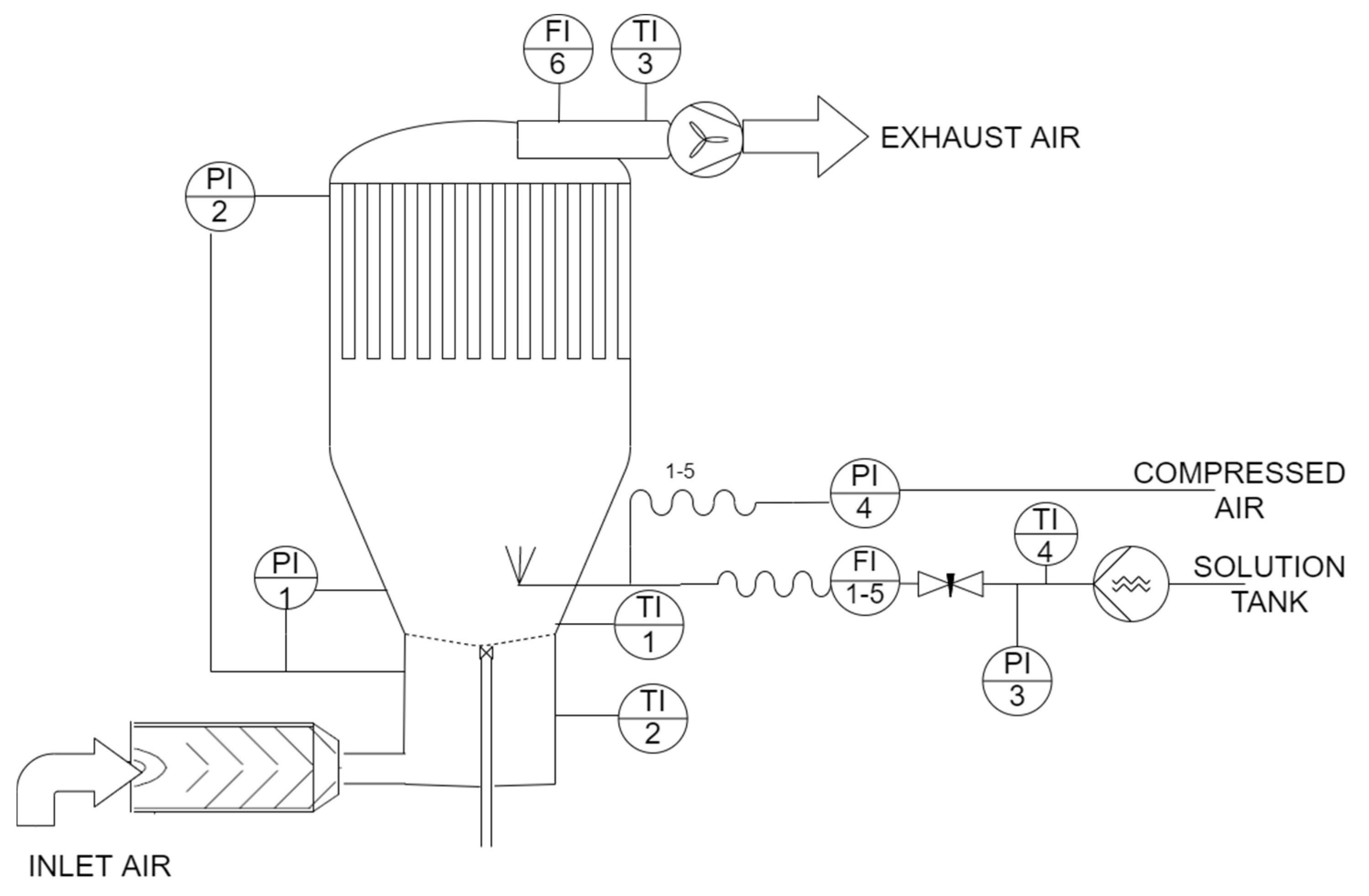
2.1. Experimental Setup and Procedure
- TI—temperature sensors (TI 1—temperature of the fluidized bed; TI 2—temperature of the inlet air; TI 3—temperature of the exhaust air),
- PI—pressure measurement or the measurement of pressure drop,
- FI—process air flow sensor (FI 6) or liquid flow sensor (FI 1–5).
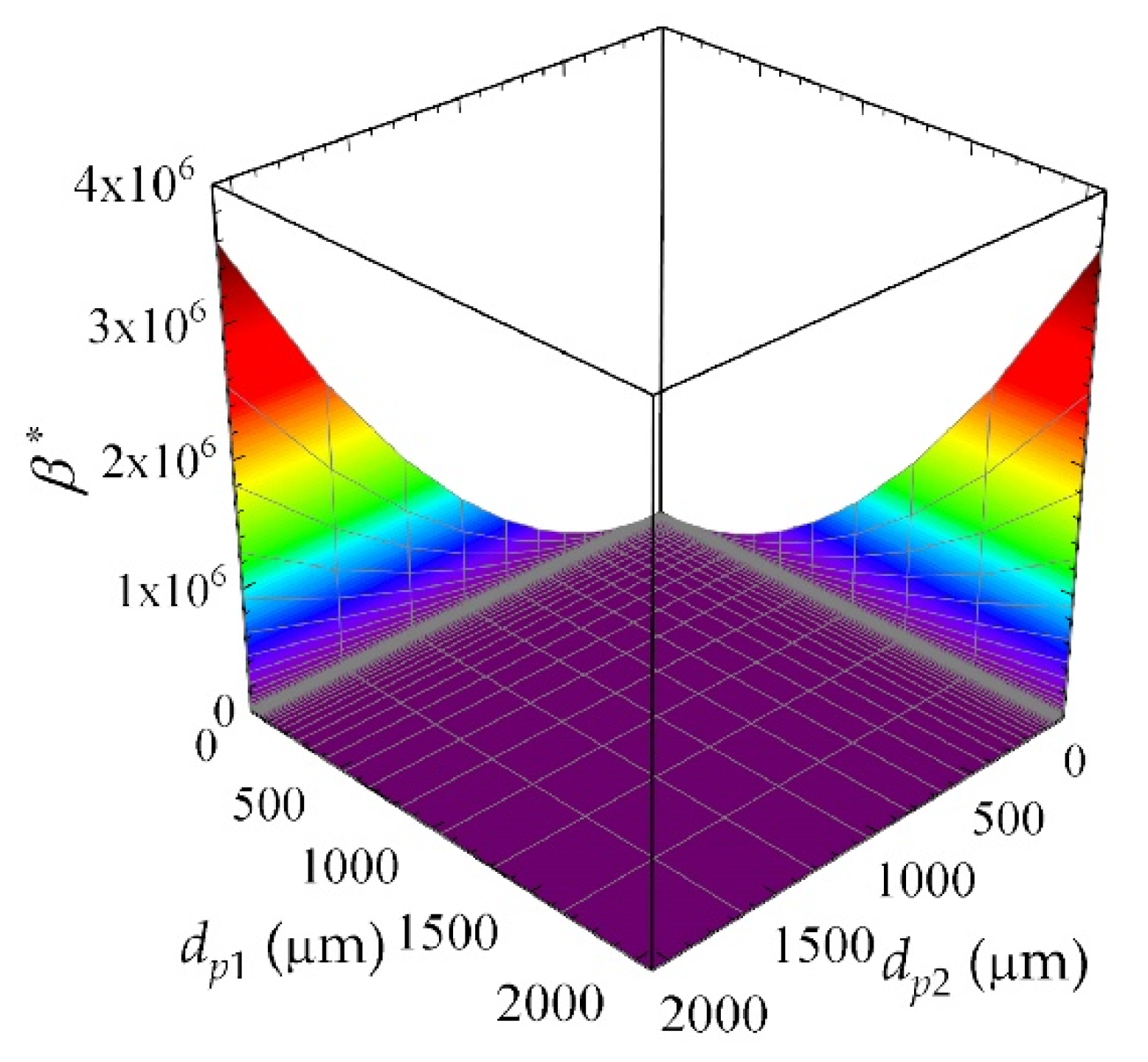
2.2. Population Balance Modeling
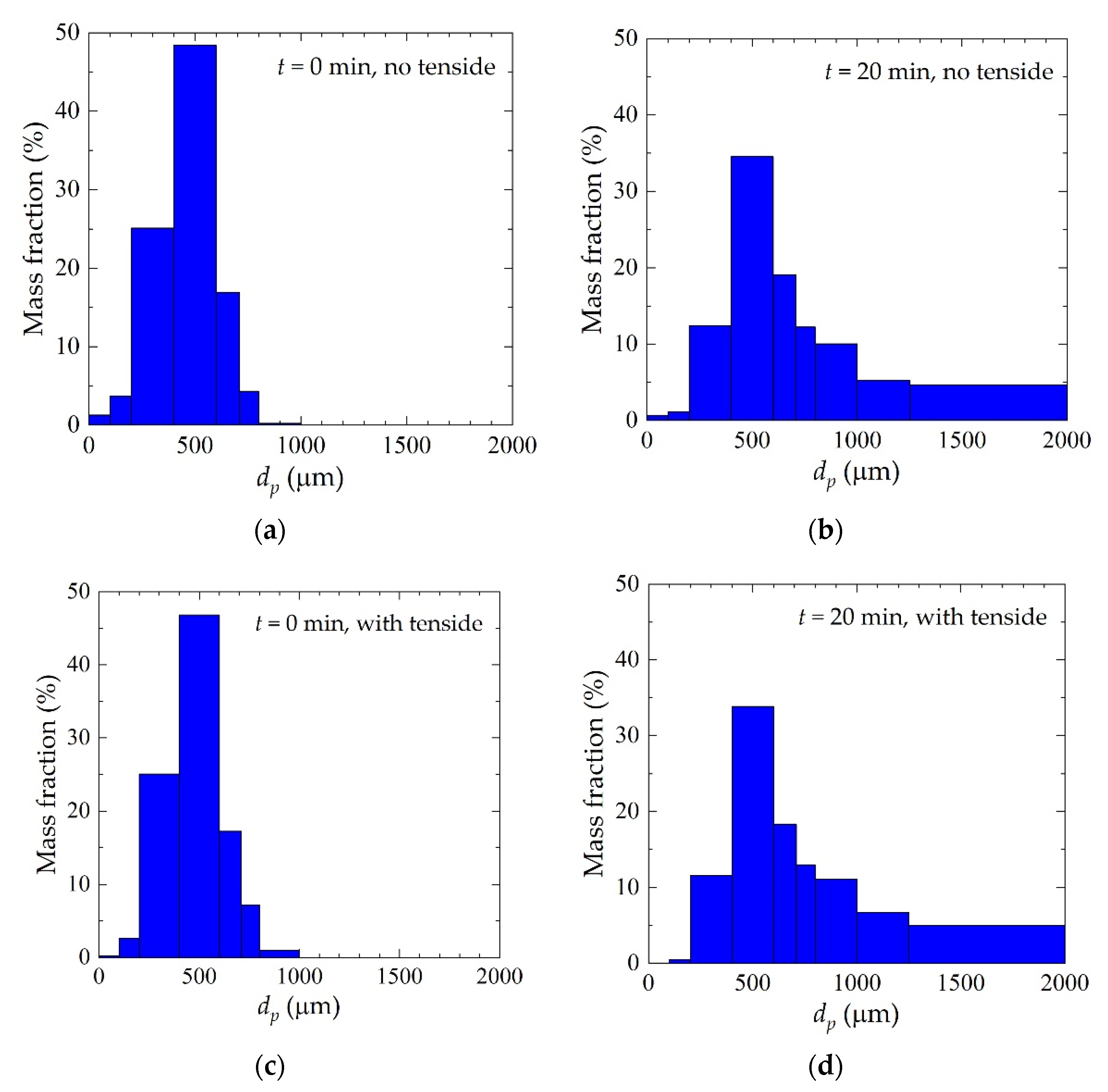
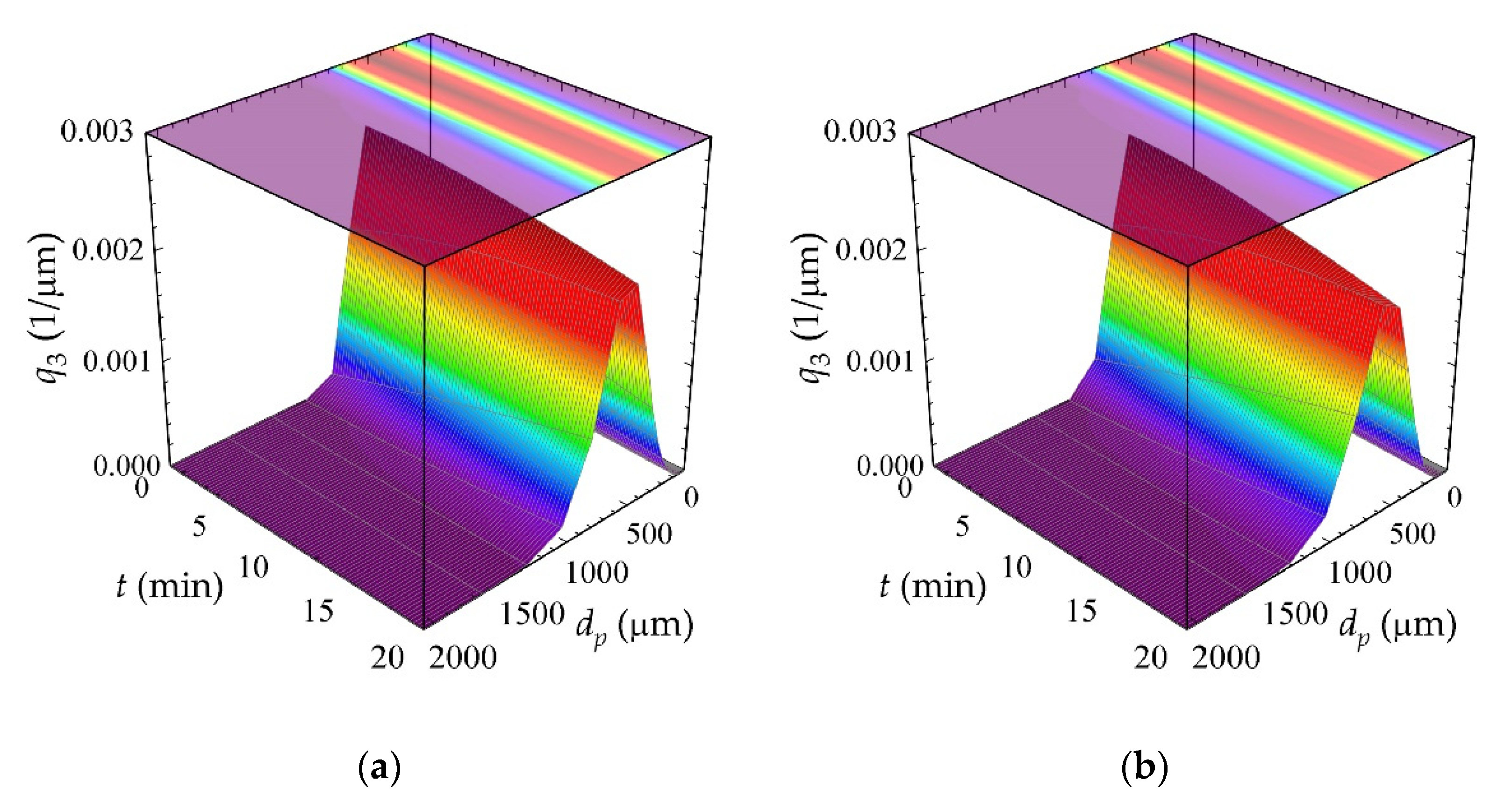
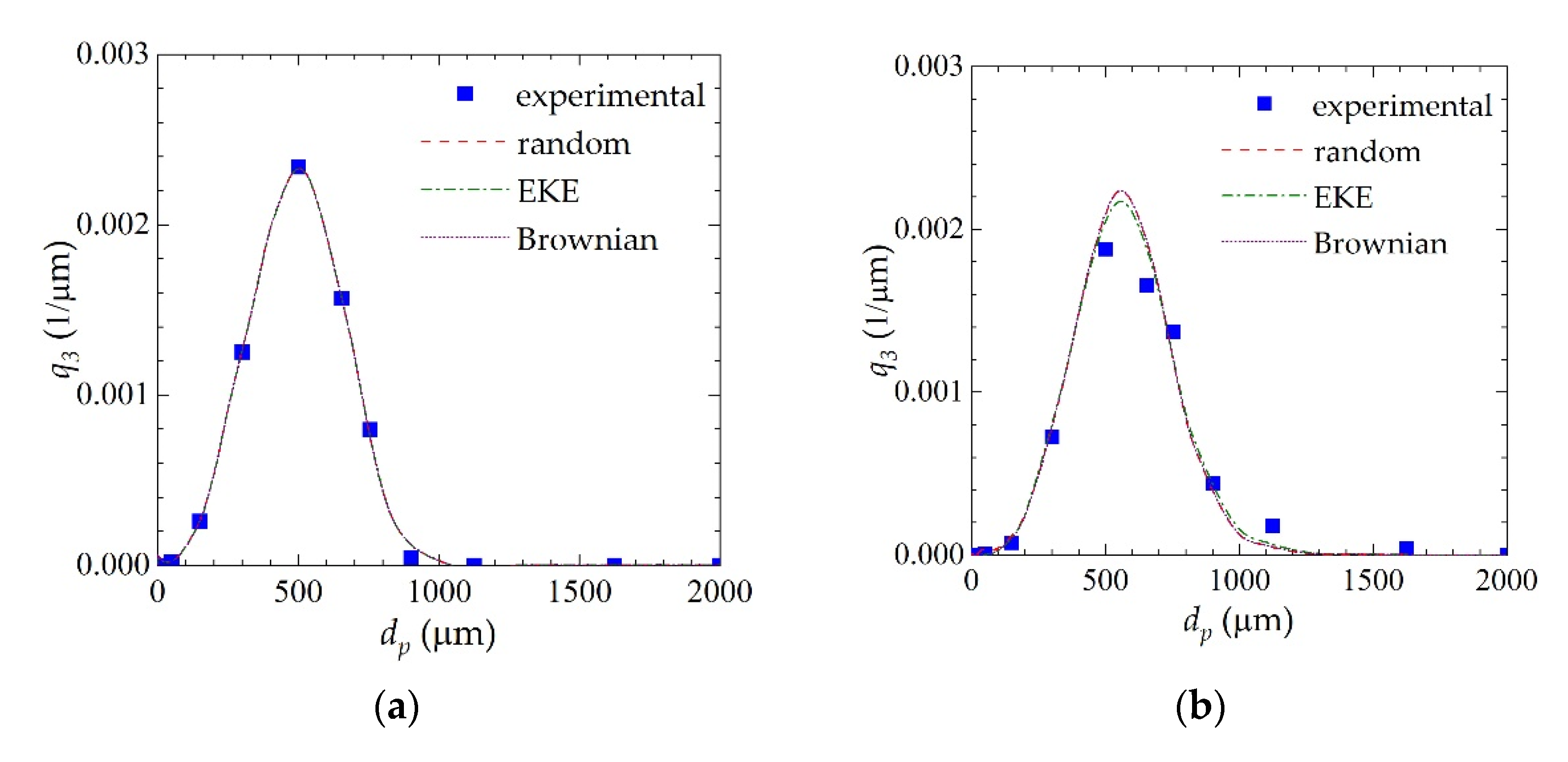
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Litster, J.D.; Ennis, B.J. The Science and Engineering of Granulation Process; Particle Technology Series; Springer Science & Business Media: New York, NY, USA, 2004; Volume 15. [Google Scholar]
- Kwiatek, J.; Siuda, R.; Gluba, T.; Olejnik, T.P.; Obraniak, A.; Marszałek-Gubiec, A.; Pietrasik, T. Granulation of limestone powder with selected binding liquids. Przem. Chem. 2018, 97, 1542–1548. [Google Scholar]
- Xu, J.; Yang, S.; Ren, Q.; Yang, G. Investigation of granulation calcined under the eutectic temperature in the fluidized bed. Constr. Build. Mater. 2021, 302, 124169. [Google Scholar] [CrossRef]
- Yohe, G.R. Binding materials used in making pellets and briquets. Ind. Miner. 1964, 19. Available online: https://www.ideals.illinois.edu/bitstream/handle/2142/43127/bindingmaterials19yohe.pdf?sequence=2 (accessed on 14 July 2021).
- Ficzere, M.; Meszaros, L.A.; Madarasz, L.; Novak, M.; Nagy, Z.K.; Galata, D.L. Indirect monitoring of ultralow dose API content in continuous wet granulation and tableting by machine vision. Int. J. Pharm. 2021, 607, 121008. [Google Scholar] [CrossRef]
- Chen, J.; Yang, H.; Xu, C.-M.; Cheng, J.-G.; Lu, Y.-W. Preparation of ZrO2 microspheres by spray granulation. Powder Technol. 2021, 385, 234–241. [Google Scholar] [CrossRef]
- Iveson, S.M.; Litster, J.D.; Hapgood, K.; Ennis, B.J. Nucleation, growth and breakage phenomena in agitated wet granulation processes: A review. Powder Technol. 2001, 117, 3–39. [Google Scholar] [CrossRef]
- Quatrini, E.; Li, X.; Mba, D.; Costantino, F. Fault diagnosis of a granulator operating under time-varying conditions using canonical variate analysis. Energies 2020, 13, 4427. [Google Scholar] [CrossRef]
- Fulop, G.; Domokos, A.; Galata, D.; Szabo, E.; Gyurkes, M.; Szabo, B.; Farkas, A.; Madarasz, L.; Demuth, B.; Lender, T.; et al. Integrated twin-screw wet granulation, continuous vibrational fluid drying and milling: A fully continuous powder to granule line. Int. J. Pharm. 2021, 594, 120126. [Google Scholar] [CrossRef]
- Maksakov, A.; Palis, S. Koopman-based data-driven control for continuous fluidized bed spray granulation with screen-mill-cycle. J. Process Control 2021, 103, 48–54. [Google Scholar] [CrossRef]
- Turchiuli, C.; Eloualia, Z.; El Mansouri, N.; Dumoulin, E. Fluidised bed agglomeration: Agglomerates shape and end-use properties. Powder Technol. 2005, 157, 168–175. [Google Scholar] [CrossRef]
- Soldati, R.; Zanelli, C.G.; Cavani, G.; Battaglioli, L.; Guarini, G.; Melandri, C.; Piancastelli, A.; Dondi, M. Powder rheology and compaction behavior of novel micro-granulates for ceramic tiles. Powder Technol. 2020, 374, 111–120. [Google Scholar] [CrossRef]
- Fries, L.; Dosta, M.; Antonyuk, S.; Palzer, S. Moisture distribution in fluidized beds with liquid injection. Chem. Eng. Technol. 2011, 34, 1076–1084. [Google Scholar] [CrossRef]
- Iveson, S.M.; Wauters, P.A.L.; Forres, S.; Litster, J.D.; Meesters, G.M.H.; Scarlett, B. Growth regime map for liquid-bound granules: Further development and experimental validation. Powder Technol. 2001, 117, 83–97. [Google Scholar] [CrossRef]
- Rao, N.N. Simulations for Modelling of Population Balance Equations of Particulate Processes Using Discrete Particle Model (dpm). Ph.D. Thesis, Otto-von-Guericke Universität, Magdeburg, Germany, 2009. [Google Scholar]
- Bück, A.; Dürr, R.; Schmidt, M.; Tsotsas, E. Model predictive control of continuous layering granulation in fluidised beds with internal product classification. J. Process Control 2016, 45, 65–75. [Google Scholar] [CrossRef]
- Neugebauer, C.; Diez, E.; Bück, A.; Palis, S.; Heinrich, S.; Kienle, A. On the dynamics and control of continuous fluidized bed layering granulation with screen-mill-cycle. Powder Technol. 2019, 354, 765–778. [Google Scholar] [CrossRef]
- Przywara, M.; Dürr, R.; Otto, E.; Kienle, A.; Antos, D. Process behavior and product quality in fertilizer manufacturing using continuous hopper transfer pan granulation—Experimental investigations. Processes 2021, 9, 1439. [Google Scholar] [CrossRef]
- Adetayo, A.A.; Litster, J.D.; Pratsinis, S.E.; Ennis, B.J. Population balance modelling of drum granulation of materials with wide size distribution. Powder Technol. 1995, 82, 37–49. [Google Scholar] [CrossRef]
- Heinrich, S.; Peglow, M.; Ihlow, M.; Henneberg, M.; Mörl, L. Analysis of start-up process in continuous fluidized bed spray granulation by population balance modelling. Chem. Eng. Sci. 2002, 57, 4369–4390. [Google Scholar] [CrossRef]
- Drechsler, J.; Peglow, M.; Heinrich, S.; Ihlow, M.; Mörl, L. Investigating the dynamic behavior of fluidized bed spray granulation processes applay numerical simulation tools. Chem. Eng. Sci. 2005, 60, 3817–3833. [Google Scholar] [CrossRef]
- Kumar, J.; Warnecke, G.; Peglow, M.; Heinrich, S. Comparison of numerical method for solving population balance equations incorporating aggregation and breakage. Powder Technol. 2009, 189, 218–229. [Google Scholar] [CrossRef]
- Golovin, I.; Strenzke, G.; Dürr, R.; Palis, S.; Bück, A.; Tsotsas, E.; Kienle, A. Parameter identification for continuous fluidized bed spray agglomeration. Processes 2018, 6, 246. [Google Scholar] [CrossRef] [Green Version]
- Ramkrishna, D. Population Balances; Academic Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Hounslow, M.J. A discretized population balance for continuous systems at steady state. AIChE J. 1990, 36, 106–116. [Google Scholar] [CrossRef]
- Dacanal, G.C.; Menegalli, F.C. Experimental study and optimization of the agglomeration of acerola powder in a conical fluid bed. Powder Technol. 2009, 188, 187–194. [Google Scholar] [CrossRef]
- Stevens, P.J. Formulation of sprays to improve the efficacy of foliar fertilisers. N. Z. J. For. Sci. 1994, 24, 27–34. [Google Scholar]
- Wang, X.Z.; Liu, D.Y.; Zhang, W.; Wang, C.J.; Cakmak, I.; Zou, C.Q. An effective strategy to improve grain zinc concention of winter wheat, Aphids prevention and farmers’ income. Field Crop. Res. 2015, 184, 74–79. [Google Scholar] [CrossRef]
- Prom-u-thai, C.; Rerkasem, B.; Yazici, A.; Cakmak, I. Zinc priming promotes seed germination and seedling vigor of rice. J. Plant Nutr. Soil Sci. 2012, 175, 482–488. [Google Scholar] [CrossRef]
- Sawan, Z.M.; Hafez, S.A.; Basyony, A.E. Effect of phosphorus fertilization and foliar application of chelated zinc and calcium on seed, protein and oil yields and oil properties of cotton. J. Agric. Sci. 2001, 136, 191–198. [Google Scholar] [CrossRef]
- Niewiadomska, A.; Sulewska, H.; Wolna-Maruwka, A.; Ratajczak, K.; Waraczewska, Z.; Budka, A. The influence of bio-stimulants and foliar fertilizers on yield, plant features, and the level of soil biochemical activity in white lupine (Lupinus albus L.) cultivation. Agronomy 2020, 10, 150. [Google Scholar] [CrossRef] [Green Version]
- ISO. PN-EN ISO7837-2000; ISO: Geneva, Switzerland, 2011. [Google Scholar]
- ISO. PN-EN ISO 845:2000; ISO: Geneva, Switzerland, 2000. [Google Scholar]
- Hounslow, M.J.; Ryall, R.L.; Marshall, V.R. A discretized population balance for nucleation, growth, and aggregation. AIChE J. 1988, 34, 1821–1832. [Google Scholar] [CrossRef]
- Vreman, A.W.; Van Lare, C.E.; Hounslow, M.J. A basic population balance model for fluid bed spray granulation. Chem. Eng. Sci. 2009, 64, 4389–4398. [Google Scholar] [CrossRef] [Green Version]
- Hulburt, H.M.; Katz, S. Some problems in particle technology: A statistical mechanical formulation. Chem. Eng. Sci. 1964, 19, 555–574. [Google Scholar] [CrossRef]
- Cronin, K.; Ortiz, F.J.; Ring, D.; Zhang, F. A new-time dependent rate constant of coalescence kernel for modelling of fluidized bed granulation. Powder Technol. 2021, 379, 321–334. [Google Scholar] [CrossRef]
- Liu, L.X.; Litster, J.D. Population balance modelling of granulation with a physically based coalescence kernel. Chem. Eng. Sci. 2002, 57, 2183–2791. [Google Scholar] [CrossRef]
- Kapur, P.C. Kinetics of granulation by non-random coalescence mechanism. Chem. Eng. Sci. 1972, 27, 1863–1869. [Google Scholar] [CrossRef]
- Hounslow, M.J. The population balance as a tool for understanding particle rate processes. KONA Powder Part. J. 1998, 16, 179–193. [Google Scholar] [CrossRef] [Green Version]
- Hounslow, M.J.; Peterson, J.M.K.; Instone, T. Tracer studies of high-shear granulation: II. Population balance modeling. AIChE J. 2001, 47, 1984–1999. [Google Scholar] [CrossRef]
- Rajniak, P.; Sepanek, F.; Dhanasekharan, K.; Fan, R.; Mancinelli, C.; Chern, R.T. A combined experimental and computational study of wet granulation in a Wuster fluid bed granulator. Powder Technol. 2009, 189, 190–201. [Google Scholar] [CrossRef]
- Štěpánek, F.; Rajniak, R.; Mancinelli, C.; Chern, R.T.; Ramachandran, R. Distribution and accessibility of binder in wet granules. Powder Technol. 2009, 189, 376–384. [Google Scholar] [CrossRef]



| Sample 1,2 | Granule Density [kg/m3] | Bulk Density [kg/m3] | Tapped Bulk Density [kg/m3] |
|---|---|---|---|
| A1 | 1779 | 1000 | 1140 |
| A2 | 1772 | 890 | 950 |
| B1 | 1510 | 730 | 800 |
| B2 | 1571 | 680 | 780 |
| Test | Random | EKE | Brownian |
|---|---|---|---|
| Without tenside | 2.656 × 10−13 | 1.890 × 10−12 | 6.103 × 10−14 |
| With tenside | 3.446 × 10−13 | 2.497 × 10−12 | 8.136 × 10−14 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Michałek, B.; Ochowiak, M.; Bizon, K.; Włodarczak, S.; Krupińska, A.; Matuszak, M.; Boroń, D.; Gierczyk, B.; Olszewski, R. Effect of Adding Surfactants to a Solution of Fertilizer on the Granulation Process. Energies 2021, 14, 7557. https://doi.org/10.3390/en14227557
Michałek B, Ochowiak M, Bizon K, Włodarczak S, Krupińska A, Matuszak M, Boroń D, Gierczyk B, Olszewski R. Effect of Adding Surfactants to a Solution of Fertilizer on the Granulation Process. Energies. 2021; 14(22):7557. https://doi.org/10.3390/en14227557
Chicago/Turabian StyleMichałek, Bernard, Marek Ochowiak, Katarzyna Bizon, Sylwia Włodarczak, Andżelika Krupińska, Magdalena Matuszak, Dominika Boroń, Błażej Gierczyk, and Radosław Olszewski. 2021. "Effect of Adding Surfactants to a Solution of Fertilizer on the Granulation Process" Energies 14, no. 22: 7557. https://doi.org/10.3390/en14227557
APA StyleMichałek, B., Ochowiak, M., Bizon, K., Włodarczak, S., Krupińska, A., Matuszak, M., Boroń, D., Gierczyk, B., & Olszewski, R. (2021). Effect of Adding Surfactants to a Solution of Fertilizer on the Granulation Process. Energies, 14(22), 7557. https://doi.org/10.3390/en14227557










