1. Introduction
Climate change and its consequences are as present and pressing as never before. Carbon emissions are agreed to be an important driver of this phenomenon, and carbon emissions from households constitute a large part of nationwide emissions, e.g., 40% of emissions in the UK are due to personal transport and heating [
1]. Households and their energy consumption, as a major source of carbon emissions, are thus a target of policy intervention. As countries fall behind on their carbon emission reduction targets, it is likely that more ambitious policies will have to be pursued in order to avoid the worst effects of climate change [
2]. One such policy is personal carbon trading (PCT), a type of cap-and-trade scheme where households are allocated allowances for carbon emissions from personal consumption. This paper focuses on PCT and assumes that no other upstream carbon tax or trade schemes are in place. It should be noted, however, that other approaches to limit carbon emissions exist. For example, carbon taxes or other carbon trading schemes, such as the EU’s Emmissions Trading System, assign “a visible carbon price to the purchase and use of fossil-fuel-based energy” ([
3], p. 1). These approaches target the carbon emission from small- and medium-sized firms, which then transfer the additional costs of the carbon price to the final consumers. Thus, these types of emission reduction approaches are sometimes called “upstream” carbon prices. The second type of emission reduction approach targets carbon emissions “downstream”, i.e., on the individual level. Here, PCT, which addresses personal consumption from individuals and households, is the most prominent policy. In order to avoid “double-pricing of certain emissions” ([
3], p. 2)—that is, a carbon price upstream as well as downstream—any effective PCT scheme must be carefully embedded into other measures of carbon abatement.
PCT is an umbrella term used for various downstream carbon budgeting schemes [
4]. (Parag and Fawcett [
5], p. 25) give a comprehensive overview of all existing schemes so far and show how they vary in “inclusiveness, the scope of emissions they cover, the rules and procedures for allocating, surrendering, and trading carbon units, and the level of individual engagement”. Nonetheless, a number of questions arise for the exact configuration of the PCT scheme:
Commitment: PCT schemes may be mandatory or voluntary. Mandatory schemes may be less politically desirable but more effective at reducing emissions. Voluntary PCT schemes may be more popular but less effective, as only those who can most easily reduce emissions and exhibit more “sustainable” behavior will likely join the PCT scheme.
Rate of reduction: Schemes must determine the rate at which carbon allowances are reduced per period. In determining this rate, factors such as the desired total emission reduction, economic hardship due to buying carbon allowance, and public compliance with the scheme must be considered.
Equity: The allocation of allowances in a PCT scheme may take into account factors that have an impact on individual CO2 emissions, such as health conditions, number of children, place of residence, etc. Alternatively, schemes can assign all participants an equal number of allowances or assign them based on auction processes, which may alter the political viability of a PCT scheme.
Scope: PCT schemes can address a variety of CO2 emissions from personal consumption, such as mobility or home energy, or they may address personal emissions as a whole.
Few pilot PCT projects exist, so it is not yet clear how to set up the most effective, most politically feasible, and most ethically acceptable PCT scheme. Voluntary real-world field experiments are limited to the Norfolk Island Carbon/Health Evaluation Study (NICHE), CarbonDAQ in the United Kingdom [
6], and CitiCAP in Lahti, Finland. The latter project is the latest pilot, which aimed to investigate how a PCT scheme can impact transportation in the city of Lahti [
7]. The scheme was voluntary and part of a large-scale city development project funded by the European Regional Development Fund. A fairly high number (2500) of citizens registered and initially took part via a smartphone application developed for the project. However, a considerably lower number (136) of participants maintained their commitment until the end of the project phase and 20% of participants admitted having cheated. Moreover, increases in CO
2 price did not have a significant effect on consumer behavior. The results from these first implementations of PCT indicate that more insights about the configuration of a PCT scheme are needed.
To help address this gap, we present the only currently available, maintained, and working agent-based model (ABM) for PCT. Our ABM studies optimum configurations for PCT schemes in a relatively inexpensive manner (as compared to real pilot projects), as it allows for testing counterfactuals and conducting experiments on an artificial population, e.g., the model can investigate the optimal reduction rate or initial allowance allocation. In addition, our model is written in NetLogo, a simple agent-based modeling software, and it can easily be adapted to new theoretical findings of PCT schemes or data from pilot projects. Thus, this ABM can help to drastically improve the conceptual foundations of PCT.
The remainder of this paper is organized as follows:
Section 2 summarizes the status of PCT modeling and the existing literature on PCT schemes.
Section 3 gives a brief introduction to agent-based models, followed by
Section 4, in which our ABM for simulating a PCT scheme is outlined.
Section 5 outlines how the ABM was initialized, and in
Section 6, the simulation results are presented. The paper ends with a discussion of the simulation results in
Section 7 and the conclusions in
Section 8.
2. Status of PCT Modeling
PCT was first introduced by David Fleming as Domestic Tradable Quotas, later called Tradable Energy Quotas [
8,
9]. At the same time, Mayer Hillman and Tina Fawcett introduced the term Personal Carbon Allowances [
10]. These two proposals, Tradable Energy Quotas and Personal Carbon Allowances, are the most discussed PCT proposals [
11]; nonetheless, other PCT proposals have been brought forward by researchers [
12,
13,
14,
15,
16,
17,
18]. As these contributions investigated optimal designs for PCT schemes, others have investigated the public acceptance of a PCT scheme [
19] and how to best integrate a PCT scheme into policy agendas [
20,
21,
22]. Most recently, Fuso Nerini et al. [
3] proposed combining a personal carbon allowance with artificial intelligence to extend the concept to goods and services and make the policy more efficient.
There are two distinct approaches to modeling PCT schemes: general equilibrium models and agent-based models. Li et al. [
23] examined consumer welfare with an equilibrium model, where consumers face two optimization problems: the optimal consumption of non-energy commodities given a monetary budget restraint and the optimal consumption of energy commodities given the carbon allowance budget restraint. Other researchers mostly followed this approach to model the PCT scheme. Most notably, Li et al. [
23] yielded three major findings. The authors concluded, first, that a PCT would be progressive, as poorer households have fewer emissions. Second, a buffer effect exists between the energy price and allowance price, which leads to the total energy price and the energy demand remaining stable. Third, with a decrease in emission rates, the welfare loss of over-emitters decreases; however, the welfare change is still far less than zero ([
23], p. 9). Fan et al. [
24], utilizing numerical simulations, concluded that allowance caps are inversely related to allowance prices and the allowance price level depends on high CO
2 rates. If greener energy sources reduce energy’s carbon footprint, allowance prices are also reduced. In another study, Fan et al. [
25] further investigated the buffer and price effect in a PCT scheme. A third paper by Fan et al. [
26] suggests that a PCT scheme is effective since consumers reduce their electricity consumption in response. However, consumers with varying income levels will respond differently to an allowance price change. Fan et al. [
27] supplemented this by constructing a model with a dynamic programming approach that includes banking, i.e., saving allowances, and they found results in line with the results delineated above.
In contrast to the equilibrium and optimization models presented above, a few studies have employed an approach rooted in complexity science and modeled a PCT scheme with agent-based models (ABMs). The first ABM was published by Kempener [
28] as a working paper in the Science and Technology Policy Research (SPRU) Electronic Working Paper Series. His model, implemented in AnyLogic, simulates a personal carbon trading scheme, where households have empirically derived and heterogeneous demographic characteristics and reduce demand for emissions based on economic and social motivations. In particular, this study analyzes the effectiveness and efficiency of the PCT scheme by investigating whether the absolute amount of emissions is reduced over time and whether the carbon price represents the marginal costs of abating emissions ([
28], p. 9). The results suggest that the allowance price increases if the initial allowance allocation decreases. However, though Kempener’s model considers households as heterogeneous entities, it does not consider households’ sizes and motivational factors explicitly, nor does it include different annual reduction rates. Moreover, this ABM is no longer working nor accessible. To address this gap, Seidl [
29] built an agent-based model to simulate a PCT scheme, which is employed in this paper in a slightly varied form. Its setup and the details of its configuration are described in
Section 4.
4. Model Structure
The improved agent-based model for PCT, implemented in NetLogo (Version 6.1.2-beta2) (for further details on NetLogo, see [
33]), extends and adapts a model developed for the Swedish Energimyndigheten [
29,
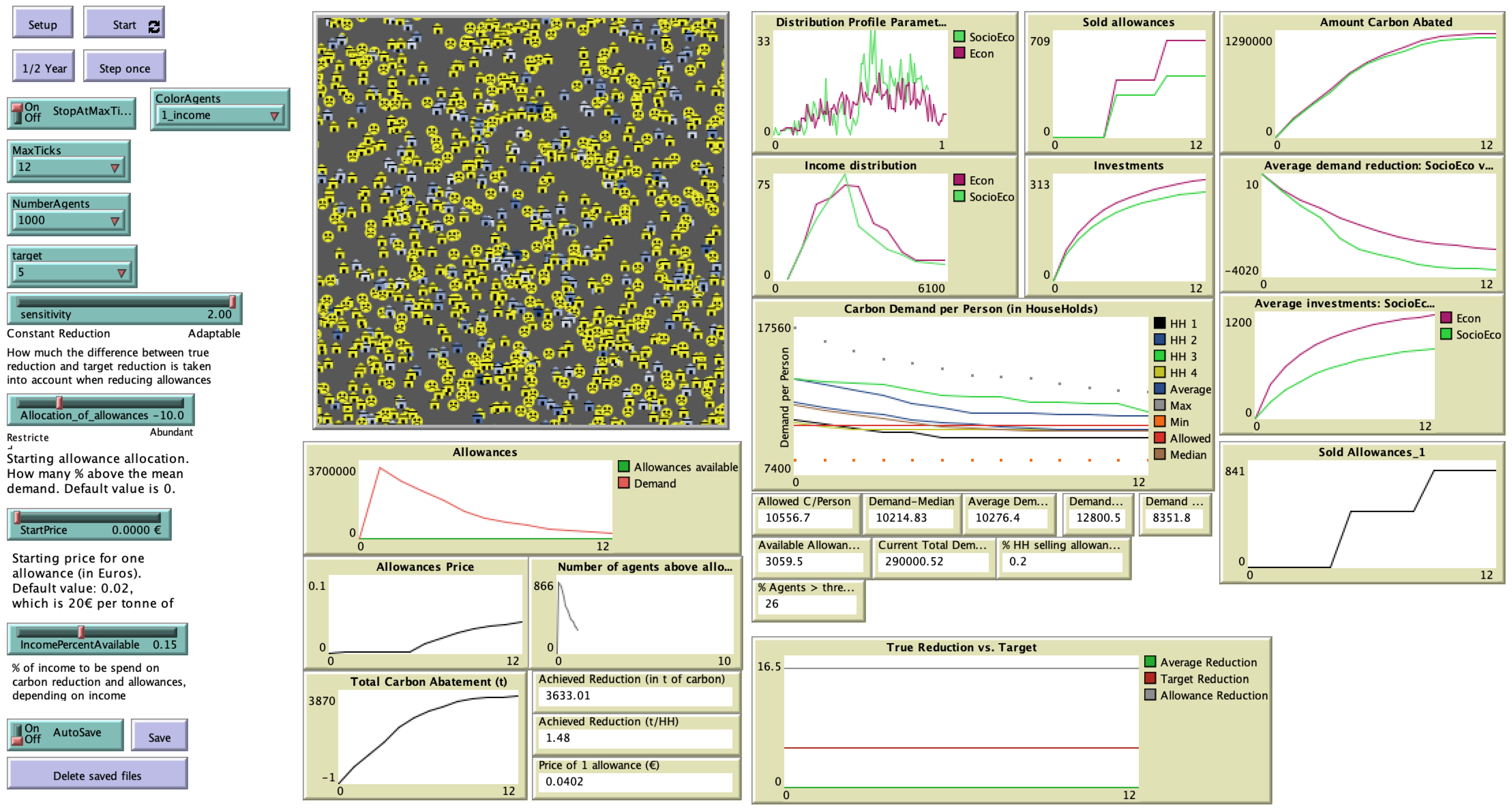
34]. The model simulates a PCT scheme with an initial distribution of allowances, a yearly reduction in allowances, and allowance trade among households. Users of the model can change the duration of the PCT scheme, the number of households, the amount of income available to spend on allowances, and the initial conditions of the scheme (for an example of the user interface, see
Figure 1). The model outputs, among other variables, the total amount of emissions reductions, allowance prices over time, and the number of households requiring allowances.
Households, which are the agents of this model, reduce emissions based on income, economic and socio-ecological motivation, and non-linear abatement costs. The environment for these agents is composed of other households, and agents are more likely to sell allowances if the majority of their neighbors do so. They are also more likely to sell allowances if they have sold in the past. Households are of five different size categories, ranging from one to five or more members. Children are not explicitly considered. Households are also categorized into ten income groups, from a minimum of EUR 500 to a maximum of EUR 6000 per month in steps of EUR 500. Households are also heterogeneous with respect to their socio-ecological and economic motivation values according to [
35,
36]. The socio-ecological motivation is represented in a parameter ranging from zero to one to denote how much an agent is motivated by socio-ecological concerns, resulting in investing more in carbon abatement measures. In parallel, the economic motivation is a parameter from zero to one, which denotes how much an agent is motivated by economic concerns, resulting in greater investment if doing so is profitable. Through this motivation, each household can abate one ton of CO
2 for every EUR 2000 invested. However, costs for more drastic reductions increase non-linearly—see [
37]—and extensions are possible [
23]. As a result of these combinations of motivations, agents can apply different strategies to reduce their amount of carbon emissions. First, this can be achieved by buying carbon-saving appliances or changing their lifestyle due to socio-economic motivation, e.g., refraining from flying and car use. Second, this can be achieved by investing in carbon abatement due to economic motivation, e.g., investing in alternative energy systems.
Household demographic data and behaviors are empirically based on studies conducted in the UK and Germany. The income distribution is derived from [
35], and the energy demand of households based on their income is taken from German statistics [
38]. Details on how much carbon households can abate from investment or lifestyle changes are derived from [
39]. The distribution of socio-economic and economic motivations is taken from [
40], as the authors investigated potential behaviors in response to a personal carbon allowance system (such as the use of public transport or cycling, the use of a small or fuel-efficient car, etc.). We do not differentiate the various behavioral responses but use their probabilities for behavior subgroups in our model.
Allowance trading is modeled as follows. First, allowances to produce carbon by fossil energy use are allocated to all agents (households). All agents receive the same number of allowances; that is, this simulation considers a PCT regime where all consumers are given the same carbon emission rights, even though their initial demand varies by income and number of household members. In each time step, representing a month, allowances can be traded to those agents whose demand is higher than the allowances received. If an agent’s neighbors are selling, it is more likely to sell, too. Allowance prices are then calculated from demand and supply by a simple market model [
41].
Instead of a constant allocation rate or constant annual reduction, we implemented an innovative method of adaptive allocation; the model specifies a “target” reduction per year with a sensitivity to reaching this target. To reduce emissions by the target rate, each year, or every twelve time steps, the model reduces the amount of allowances available by a percentage equal to the target plus the sensitivity multiplied by the difference between the average emissions reductions in the previous year and the target. For instance, if the target is 2% of CO
2 reduction and the average reduction in the previous year is only 1%, then, with a sensitivity of 1, the model will reduce the amount of allowances allocated in the following year by
Thus, if sensitivity is high, the model will more swiftly adapt the number of allowances to meet the emissions target, just as policymakers may adapt a PCT scheme’s parameter based on its previous performance. To our knowledge, our model is the first to emulate this mechanism.
Finally, there are various output facilities (see
Figure 1) for the user to track the ongoing simulation at runtime. First, the ‘View’ depicts the generated households, symbolized as houses with different colors. Currently, there are three different shadings implemented: blue colors according to income, green according to the degree of socio-ecological motivation, and orange according to the number of household members. The model also provides certain real-time figures of average household emissions reductions, maximum and minimum reductions, percentage of households selling, etc.
For a more detailed description of the model, we refer the reader to
Appendix A.
6. Simulation Results
Table 2 outlines the results of the simulation. Each dependent, or outcome, variable is regressed on each independent, or predictor, variable. Controls are not necessary, because NetLogo’s BehaviorSpace resembles a laboratory experiment, and so each independent variable is uncorrelated with the other. The third column gives the coefficient on the independent variable, i.e., the effect of increasing the independent variable by 1 unit (or increasing the model length to 60 months or the number of agents to 30,000) on the outcome variable. The fourth column gives the intercept, or the predicted value of the outcome variable if the independent variable equals 0, and the fifth column provides the R
2, or the proportion of the outcome variable’s variance explained by its relationship to the independent variable. Where applicable, standard errors are given, and asterisks note statistical significance.
A number of results are noteworthy. First, the initial price and the reduction target both impact the average price over the runtime. Although not reported in the results in
Table 2, the effect of the initial price on the average price holds when restricting the sample to prices in the final time step of each simulation, suggesting significant path dependence. These are potential policy entry points to leverage the success of a PCT scheme. For example, setting a lower initial price for allowances will decrease allowances’ average price over the course of the simulation without decreasing the emissions reduction (as the initial price is uncorrelated with emissions reduction; see
Table 2).
Second, as expected, the strength of emissions reductions decreases the number of allowances available: for every percentage point increase in the emissions reduction target, the number of available allowances decreases by 177. The length of the simulation also decreases the number of allowances: 60-month-long simulations had 275 fewer allowances available per time step, i.e., per month, than 12-month-long simulations.
Third, the initial allocation of allowances is a strong predictor of the (a) number of allowances available, (b) allowance price, (c) number of households exceeding their allowances, and (d) emissions reduction. In regard to the (a) number of allowances available, they were strongly predicted by the initial allocation. For every percentage point increase above the initial average demand in initial allowances, there were nearly 100 more allowances available on average in each month; in results not reported, this effect holds when restricting the sample to allowances in the final time step of each simulation. Indeed, the initial allowance allocation explains roughly 65% of the variation in available allowances, suggesting significant path dependence in the number of allowances available. In regard to the (b) allowances price, for every percentage point increase above the initial average demand in initial allowances, the average allowances price decreases by EUR 0.2, most likely because increased initial allocation increases the number of allowances available, which decreases prices. While seemingly marginal, this effect explains 28.1% of the average price’s variation.
The effect is also large for (c) allowance exceeders: for every percentage point increase above the initial average demand in initial allowances, roughly 7 percentage points of fewer households exceed their threshold. Initial allocations account for 55% of the variation in this outcome. In other words, if each household receives 10% less initial allowances in the beginning of the PCT scheme, on average, 38% of households will need to buy allowances each month, while, if each receives 10% more than the initial average demand, only 7% of households will buy allowances each month. In fact, while the magnitude of emission reduction increases the number of allowance exceeders—the more emissions are reduced, the lower allowances are, so the more households need to buy allowances—this variable explains only 12% of the variation in allowance exceeders, which is far less than that explained by the initial allowance allocation. Once again, this is because an increase in initial allowances increases the number of allowances available each month, which naturally decreases the number of exceeders. Similarly, because initial allowance allocation impacts the number of allowances, which, in turn, (d) impact emissions, a more generous initial allowance allocation significantly decreases the magnitude of emissions reductions. For every percentage point increase in the initial average demand for emissions in initial allowance allocations, emissions abatement decreases by 3 tons of carbon per household. Indeed, the initial allocation of allowances explains 11% of the variation in emissions reductions.
For comparison, emissions reductions targets only explain 5% of the variation in carbon abatement, although, as expected, the marginal effect is stronger: for every percentage point increase in the emissions reduction target, 10 more tons of carbon per household are abated. Of course, the strongest predictor of abatement is the length of each simulation, as longer simulations have more time to reduce carbon.
Interestingly, the ability of policymakers to adapt allowance allocations (sensitivity) to reach their reduction target is not strongly correlated with any outcome, except for price. However, even for price, the effect of sensitivity is quite insubstantial; sensitivity only explains 0.2% of the price’s variation. As, to our knowledge, our model is the first to examine sensitivity in personal carbon trading schemes, this surprising result may require further research.
To demonstrate the strength of ABMs’ ability to study the dynamics of PCT schemes and to examine the dynamics of price and emissions in relation to sensitivity and emissions reductions targets,
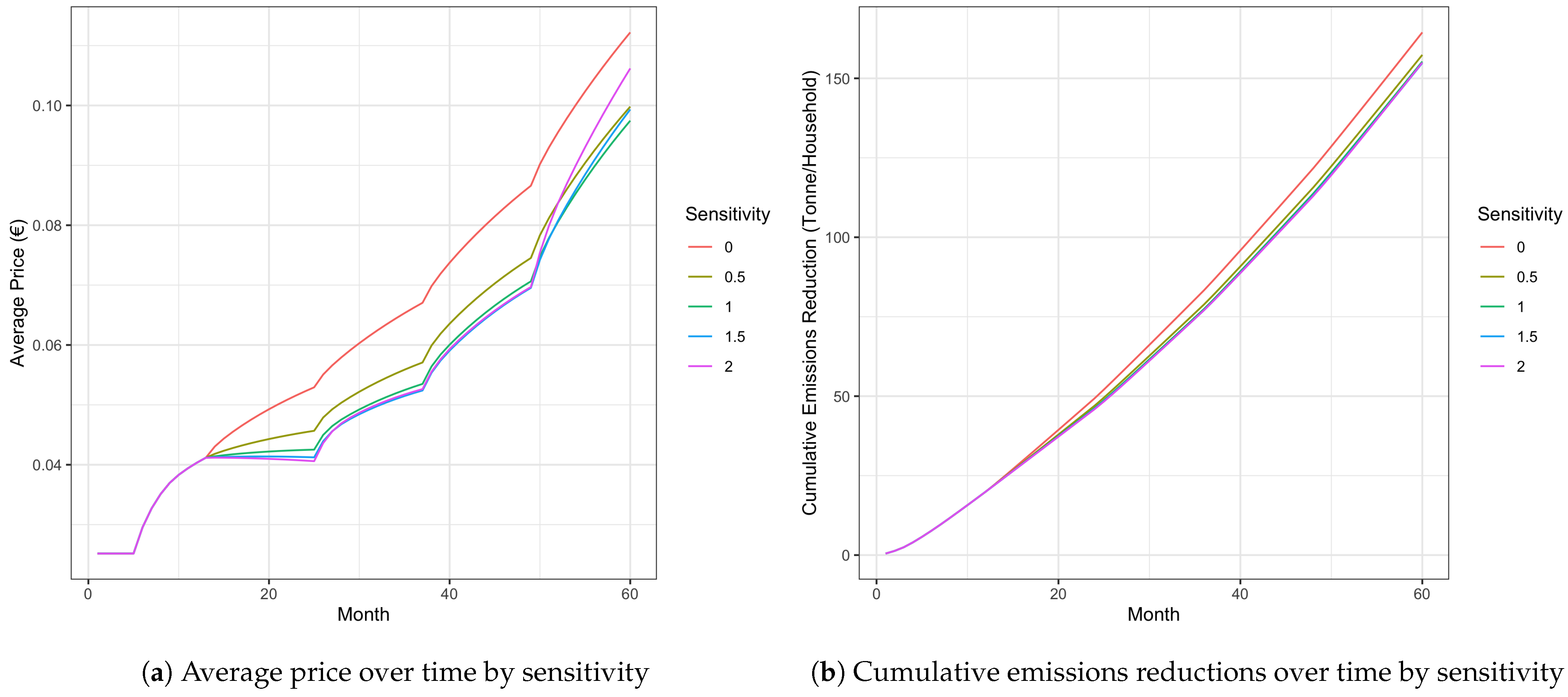
Figure 2a,
Figure 2b,
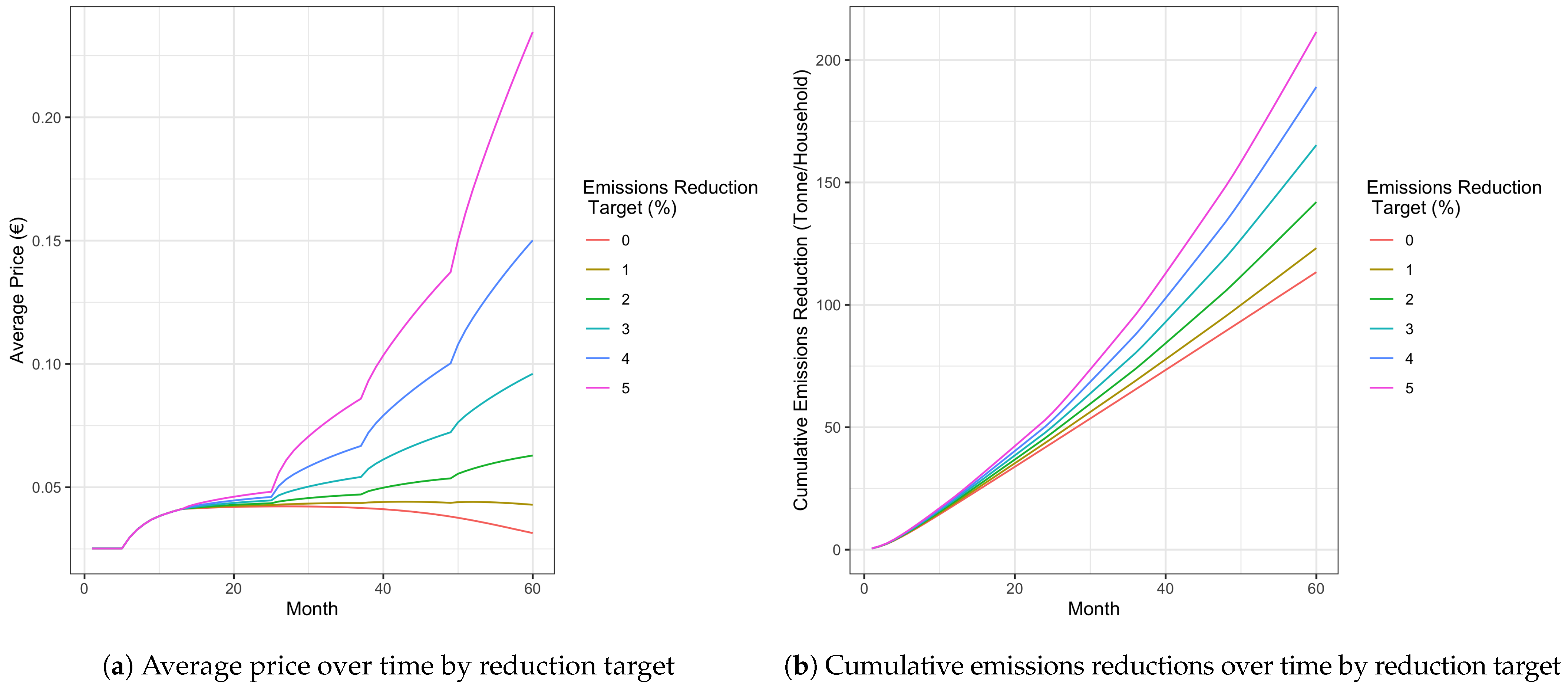
Figure 3a and
Figure 3b plot price or emissions reductions, averaged over every simulation with 60 ticks by their sensitivity or reduction target, for each month. As each independent variable is uncorrelated, averaging each run over variables other than sensitivity or reduction target averages out any spurious effects. Only simulations with 60 ticks were plotted because policymakers in the model only adjust the allocation of allowances every 12 months; thus, sensitivity has no impact on simulations with exactly 12 months.
Figure 2a shows how the average price for allowances increases over time, depending on the sensitivity chosen at the simulation start. Clearly, sensitivity decreases the price of allowances in each month. Moreover, prices increase at the beginning of every 12-month period, as this is when policymakers adjust the allocation of allowances in accordance with their emissions reductions targets.
Figure 2b demonstrates that the ability of policymakers to adapt allowance allocations does not impact cumulative emissions, as suggested by
Table 2.
Figure 3a, however, indicates that stronger reduction targets significantly and non-linearly impact the allowance price, and that this difference increases with the number of months. Similarly,
Figure 3b confirms that emissions reductions targets do increase carbon abatement, and that targets’ impact on abatement is mostly concentrated in the later months of each simulation, i.e., the difference in abatement between each reduction target increases with the number of months.
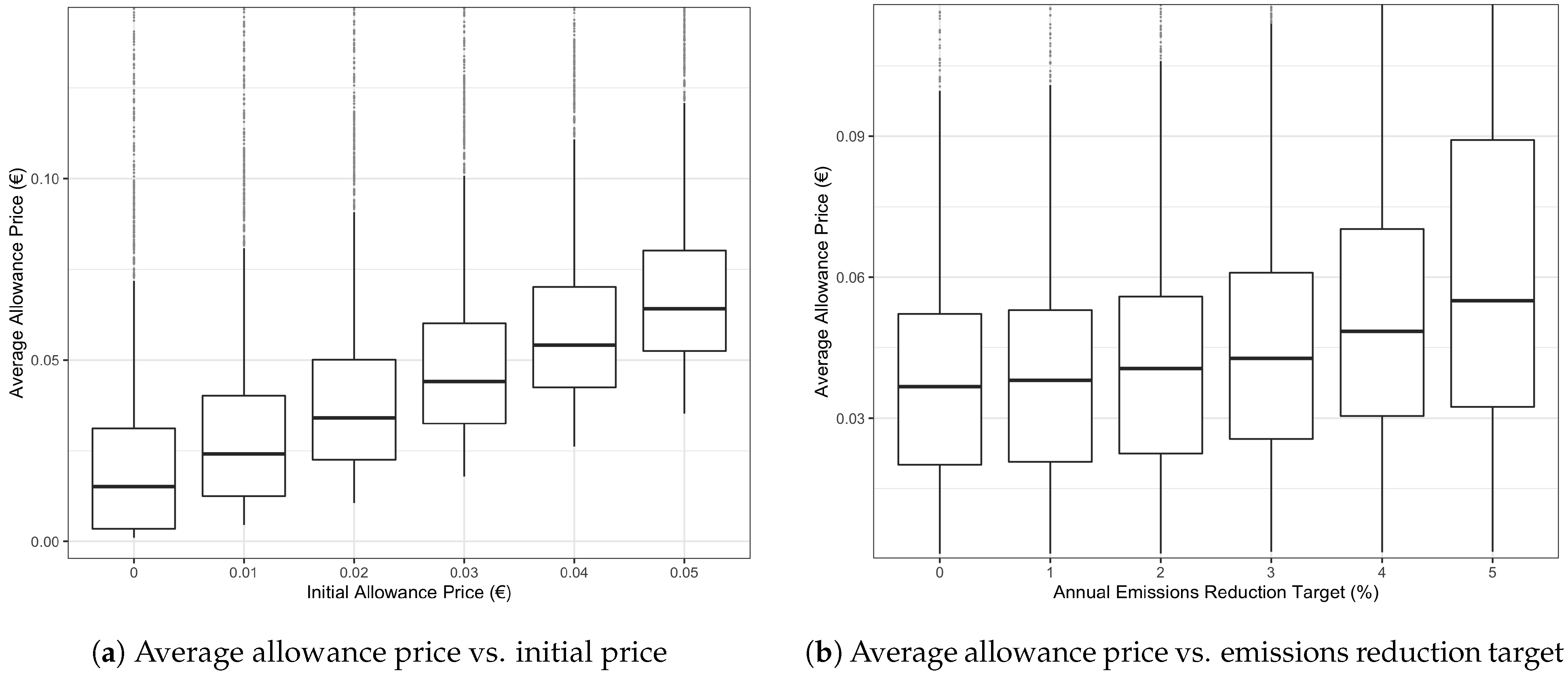
For visualization purposes, we also plotted the most significant results as box-plots, where the bar represents the median and the box the 25 and 75 percentiles, respectively. The whiskers comprise any values within the 1.5 times interquartile range of the percentiles. Due to the presence of outliers and in order to make the plots more readable, any values above the 95th percentile or below the 5th percentile of the y-axis value are excluded.
Figure 4a illustrates that the average price for allowances is influenced by the initial price. The higher the initial price for allowances, the higher the price over time. Moreover,
Figure 4b illustrates that the emissions target set at the start influences the average allowance price in each run.
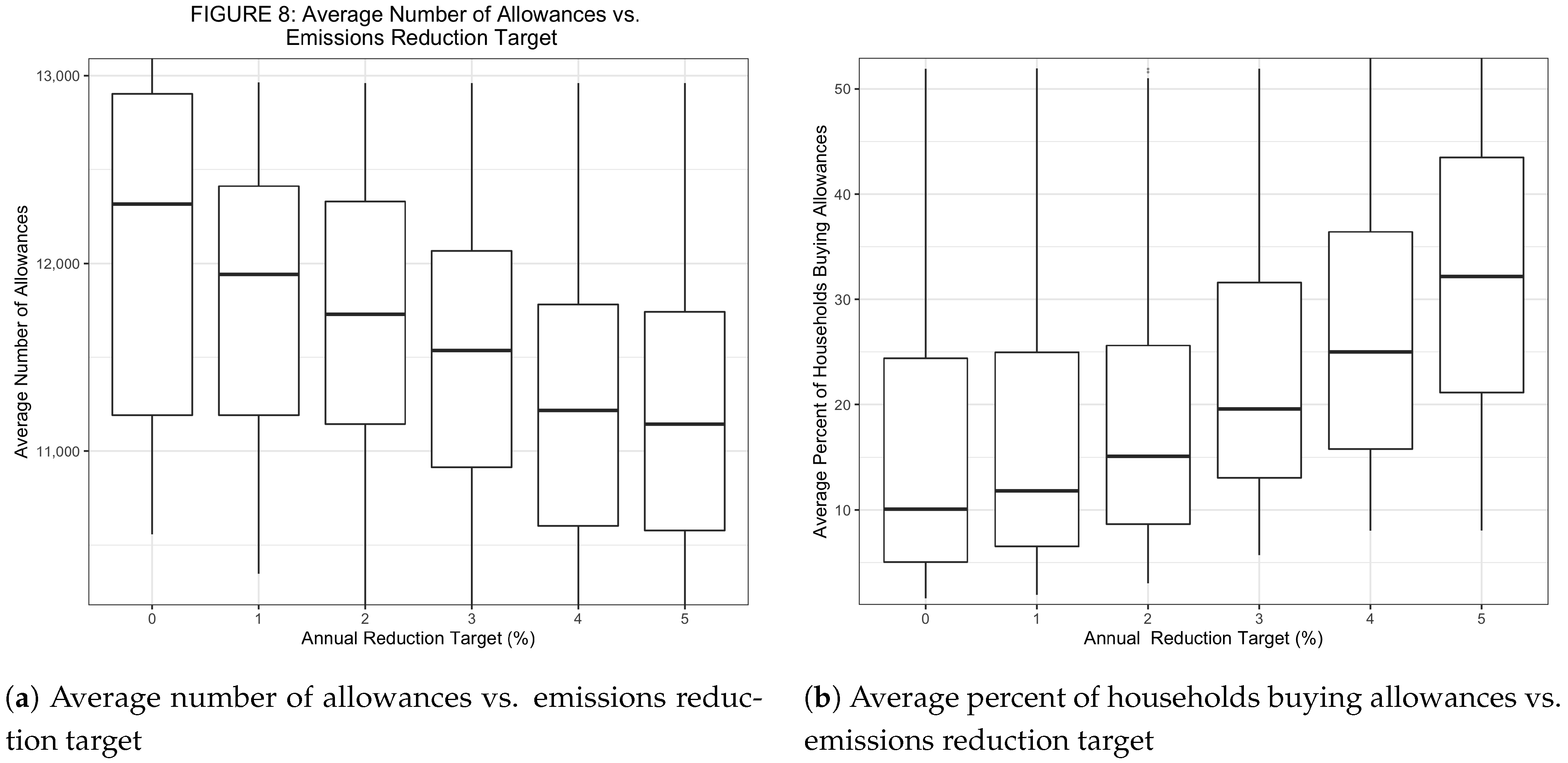
In
Figure 5a, one can see how an increasing reduction target decreases the average number of available allowances. Of course, with a higher reduction target, the annual allocation of allowances is lower and thus households are placed under more pressure to reduce their emissions. This can be seen in
Figure 5b, which shows that with more demanding reduction targets, more households have to buy allowances.
7. Discussion
In this simulation study, we outline a model of personal carbon trading in an artificial population of heterogeneous agents. We present an innovative agent-based model simulating a PCT scheme under a series of specific conditions. In our experiments, we varied different variables, such as the initial price, the income available to spend on allowances, the initial allowance availability, and the target reduction.
In general, our model of PCT schemes shows results that are generally intuitive, but some may need explanation or further research. For instance, while the initial price intuitively should be “swamped out” and be uncorrelated with the average price, our results indicate that average prices, even after 12 or 60 months, are strongly positively correlated with the initial price set by policymakers. Similarly, the initial allocation of allowances has an impact on the number of allowances available later in the model, which, in turn, implies that the initial allocation has a strong impact on price, the number of households buying allowances, and emission reductions.
An essential dependent variable of a PCT scheme is the actual reduction in carbon emissions. Intuition suggests that the initial reduction target is relevant, but in our simulations, increasing this target or the sensitivity did not notably decrease the cumulative emissions. Nonetheless, together with the initial allocation of allowances, these variables influence the simulation results to a certain degree, especially in later time steps. In other words, the effects need time to evolve. For more significant short-term effects, one would set the initial allocation to be more restrictive. However, this could result in social problems for two reasons. First, it is questionable whether such a PCT scheme would be even implemented or fail in the planning stage due to public hesitancy regarding such restrictive allocations. Second, a low initial allocation might place unjustifiable financial stress on households during the scheme. In addition, a PCT scheme that is set up in such a way might encourage cheating on a large scale, since cheating was already committed by approximately 20% of participants in the voluntary pilot project in Lahti, Finland.
As our model is an ABM, we were able to examine the dynamics of price and emissions reductions relative to the PCT schemes’ ability to adapt allocations and their targeted emissions reduction. Our results tentatively suggest that, if a PCT setup and design impacts the outcome of emissions consumption, then the majority of this impact occurs in the later months of the PCT. For instance, in
Figure 3b, the amount of emissions reduced is largely the same in simulations with 0% and 5% targets for the first 24 months. These simulations’ carbon abatements only begin to diverge after two years. These results suggest that longer PCT schemes are more sensitive to input parameters and are more effective at reducing carbon only if they are executed for their full timeframe.
Finally, to our knowledge, our project is the first to investigate the impact of policymakers’ ability to adapt the allocation of allowances to their emissions targets, but our results suggest that this ability to adapt (or to adjust “sensitivity”) has little impact on price, the number of allowances available, the number of allowance buyers, and emissions reductions. This is likely because policymakers both increase and decreases the number of allowances available, depending on the previously achieved emissions reduction. Because these increases and decreases in allowance allocation impact prices, emissions, etc., it seems that the effects of allowance increases and decreases roughly negate each other. It should be noted that most previous ABMs on PCT included a fixed rate of reduction—see, for example, [
28]—which could lead to more economic hardship and less social acceptance. Here, we see potential for further research in the direction proposed in this paper: an adjustable emissions reduction could function as a feedback mechanism for the population in the PCT scheme and have thus a beneficial effect on the PCT schemes’ effectiveness. Of course, further work is needed to confirm our results.
In spite of our novel contributions, there are limitations in our model of PCT. First, we lack coherent data from one country or community, and thus our results are not directly applicable to any specific context. Admittedly, this is true for any modeling approach on PCT to date, as no results in the literature can be used to emulate a specific scheme. However, there is value for future research and policy to investigate the impacts of a novel policy and explore the dynamics that could emerge if implemented [
43,
44]. Another point for improvement is the interaction between agents. With more data on specific social networks or social influence in general, the model can simulate social influence effects more realistically, as agents may ignore price signals. Often, in real-world projects, mutual influence is assumed to have an effect on consumption choices via social comparison and descriptive norms [
45,
46]. For instance, in Lahti’s pilot study, participants were informed via a smartphone app how they performed in terms of weekly CO
2. However, users did pay less attention to these notifications or the simulated prices in the app; rather, other constraints were relevant for daily mobility decisions, e.g., the weather or personal preferences. However, our model ignores these effects, and, to our knowledge, there are no data on mutual influence concerning the performance in a PCT scheme.
One specific strength of our ABM is its adaptability, as this model could be easily adapted to new, more detailed data sources that may be available in the future. This is vital for the development of PCT schemes: more detailed empirical data on PCT and more simulation results are necessary for real-world trials and experiments to be carried out. Supporting our claim that empirical analysis and modeling should go hand in hand to explore possible strategies for PCTs, (Fuso Nerini et al. [
3], p. 6) state: “Voluntary PCA [personal carbon allowances, the authors] initiatives and PCA-like schemes will be essential to trial various designs. Evidence from those trials should be incorporated into models that evaluate the impacts of various designs on different income groups. Participatory research methods and engagement with a wide range of stakeholders could help to advance the knowledge of this policy option”.
8. Conclusions
Some careful conclusions can be derived from our simulation study. Our results indicate that there exists high path dependence in the allowance price, i.e., initial price had a strong impact on later price, as well as in allowance allocation. The latter, in turn, implies that initial allowance allocation has strong impacts on allowance price, the number of households exceeding their allowances, and emissions reduction. Furthermore, our results suggest that policymakers may use these initial prices or allowance allocation to render a PCT scheme more effective or politically feasible. For instance, initial prices may be set lower to decrease prices for the entire duration of the PCT scheme without impacting emissions reductions. Similarly, policymakers may allocate allowances more generously relative to initial demand in order to decrease allowance prices and households’ need to buy them, though this would significantly decrease the amount of carbon emissions reduced.
The adaptive allocation rate also proved to be an interesting extension to earlier model versions with static rates or prescribed reduction steps, though our results suggested that sensitivity has little impact on key model outcomes. Even so, it could hint towards a potentially fruitful, empirically informed comparative study, as well as an evaluation of the relationship between sensitivity and emissions reductions. For implementing a successful PCT scheme, we need both the compliance of participants and noteworthy carbon abatement. A rate that steers CO2 abatement according to the actual citizens’ behavior appears to be a worthwhile idea for empirical trials.
From our results, we conclude that it is worthwhile to pursue modeling experiments with artificial societies as long as we do not have sufficient data from empirical trials. The lack of empirical data is a serious constraint. We would be able to build more powerful models with current empirical backing, particularly concerning actual participants’ behavior within a specific PCT scheme. Importantly, such data would always be locally specific (depending on the scope, such as a city (e.g., Lahti) or a larger scale). Thus, we propose small-scale projects that produce data in different political and spatial contexts. Then, we should implement these data into ABM in order to simulate prototypical populations.