Optimal Design of a Flyback Microinverter Operating under Discontinuous-Boundary Conduction Mode (DBCM)
Abstract
:1. Introduction
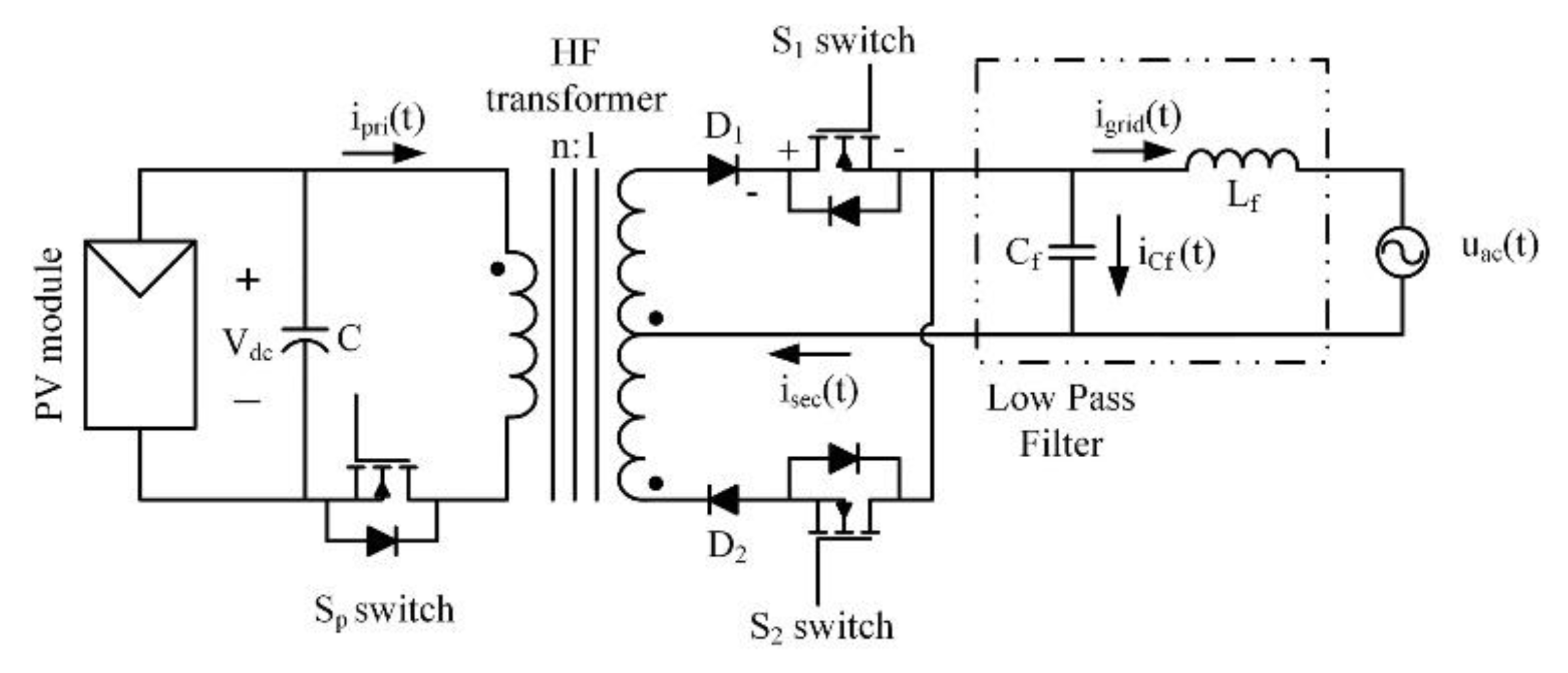
2. Power Losses in Hybrid DBCM
2.1. Semiconductor Losses
2.2. Transformer Losses
3. Design Optimization Process for DBCM
3.1. Objective Function
3.2. Design Constraints
- The core peak flux density (which for the case of the flyback microinverter operated in DBCM is for ωt = π/2 at maximum input power) must be lower than the ferrite material maximum flux density to avoid core saturation.
- The window utilization factor for the given core type, which is the ratio of the area of all the transformer windings to the transformer window, must be lower or equal to the maximum permitted value (for the windings to fit).
3.3. Optimization Sequence
4. Optimization Algorithm Verification
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Nomenclature
| PCL,SW,pri | Conduction losses of the primary switch (W). |
| Ipri,rms | RMS current value of the primary transformer side (A). |
| Rds,pri | ON-resistance of the primary switch (Ω). |
| ipri | Instant current value of the primary transformer side (A). |
| Ipri,rms,DCM | RMS current value of the primary transformer side during the DCM segment of DBCM (A). |
| Ipri,rms,BCM | RMS current value of the primary transformer side during the i-BCM segment of DBCM (A). |
| Vdc | Input voltage (V). |
| L1 | Transformer primary winding inductance (H). |
| dp | Peak duty cycle when in DCM. |
| fs | DCM switching frequency (Hz). |
| m | Ratio of the utility grid half cycle period to the DCM switching period. |
| ton,p | Peak ON-time of the primary side switch when in i-BCM (s). |
| ton,p,max | ton,p at nominal power (s). |
| k | Number of switching cycles during a utility grid half cycle for DBCM operation. |
| k1 | Νumber of switching cycles until ωt = α. |
| k2 | Number of switching cycles until ωt = π − α. |
| λ | Ratio of the input voltage to the peak grid voltage. |
| n | Transformer turns ratio. |
| α | Transition angle between DCM and BCM (rad). |
| PCL,SW,sec | Conduction losses of the secondary switches (W). |
| Isec,rms | RMS current value of each of the secondary transformer side windings (A). |
| Rdc,sec | ON-resistance of the secondary switches (Ω). |
| Isec,rms,DCM | RMS current value of each of the secondary transformer side windings during the DCM segment of DBCM (A). |
| Isec,rms,BCM | RMS current value of each of the secondary transformer side windings during the i-BCM segment of DBCM (A). |
| PCL,d | Conduction losses of the diodes (W). |
| Isec,avg | Average current value of each of the transformer secondary side windings current (A). |
| Vd | Diode forward voltage (V). |
| isec | Instant current value of the secondary transformer side (A). |
| PPV | Inverter input power (W). |
| PPV,nom | Maximum inverter input power (W). |
| uac | Instant voltage value of the utility grid (V). |
| Vacrms | RMS voltage value of the utility grid (V). |
| PSL | Semiconductor switching losses (W). |
| PSL,DCM | Semiconductor switching losses for the DCM segment of DBCM (W). |
| PSL,BCM | Semiconductor switching losses for the i-BCM segment of DBCM (W). |
| tf | Current fall time of the primary switch (s). |
| Pdc,z | DC copper losses of the winding z (W). |
| Pac,z | AC copper losses of the winding z (W). |
| Iz,avg | Average current value of the winding z (A). |
| Iz,rms | RMS current value of the winding z (A). |
| Fr,z | Resistance factor of the winding z. |
| PCore | Transformer core losses (W). |
| ΔBi | Flux swing during each switching cycle i (T). |
| αiGSE,βiGSE, kiGSE | Parameters of the Steinmetz equation loss formula. |
| Bi | Transformer core magnetic flux density at time ti (Τ). |
| η | Converter efficiency at a given power level. |
| Pi | Converter input power at a given power level (W). |
| Po | Converter output power at a given power level (W). |
| PLosses | Converter losses at a given power level (W). |
| PSi | Converter semiconductor losses at a given power level (W). |
| Pxfmr | Converter transformer losses at a givern power level (W). |
| PCL | Converter semiconductor conduction losses at a given power level (W) |
| PSW | Converter semiconductor switching losses at a given power level (W). |
| Vpri | Voltage of the primary switch when in OFF state (V). |
| Vpri,p | Maximum value of Vpri (V). |
| Vsec | Voltage of each secondary switch when in OFF state (V). |
| Vsec,p | Maximum value of Vsec (V). |
| toff,p | OFF-time of the primary switch at ωt = π/2 (s). |
| Vacp | Utility grid voltage value at ωt = π/2 (V). |
| Ipri,p | Peak current value of the primary transformer side at ωt = π/2 (A). |
| Isec,p | Peak current value of the secondary transformer side at ωt = π/2 (A). |
| ΔVCf | Voltage fluctuation of filter capacitor (V). |
| tq | Time segment during which the filter capacitor is charged at ωt = π/2 (s). |
| igrid | Instant value of the converter current supplied to the grid (A). |
| Igrid,p | Value of the converter current supplied to the grid at ωt = π/2 (A). |
| iCf | Instant current value of the filter capacitor (A). |
| fs,avg | Average converter switching frequency (Hz). |
| J | Current density of the transformer windings (A/mm2). |
| Bp | Maximum operational flux density (T). |
Appendix A
References
- Liu, B.; Duan, S.; Cai, T. Photovoltaic DC-building-module-based BIPV system—Concept and design considerations. IEEE Trans. Power Electron. 2011, 26, 1418–1429. [Google Scholar] [CrossRef]
- Leuenberger, D.; Biela, J. PV-module-integrated AC inverters (AC modules) with subpanel MPP tracking. IEEE Trans. Power Electron. 2017, 32, 6105–6118. [Google Scholar] [CrossRef]
- Voglitsis, D.; Papanikolaou, N.; Kyritsis, A. Incorporation of harmonic injection in an interleaved flyback inverter for the implementation of an active anti-islanding technique. IEEE Trans. Power Electron. 2017, 32, 8526–8543. [Google Scholar] [CrossRef]
- Kjaer, S.B.; Pedersen, J.K.; Blaabjerg, F. A review of single-phase grid-connected inverters for photovoltaic modules. IEEE Trans. Ind. Appl. 2005, 41, 1292–1306. [Google Scholar] [CrossRef]
- Quan, L.; Wolfs, P. A review of the single phase photovoltaic module integrated converter topologies with three dc link con-figurations. IEEE Trans. Power Electron. 2008, 23, 1320–1333. [Google Scholar] [CrossRef] [Green Version]
- Meneses, D.; Blaabjerg, F.; García, Ó.; Cobos, J.A. Review and comparison of step-up transformerless topologies for photovoltaic AC-module application. IEEE Trans. Power Electron. 2013, 28, 2649–2663. [Google Scholar] [CrossRef] [Green Version]
- Freddy, T.K.S.; Rahim, N.A.; Hew, W.-P.; Che, H.S. Comparison and analysis of single-phase transformerless grid-connected PV inverters. IEEE Trans. Power Electron. 2014, 29, 5358–5369. [Google Scholar] [CrossRef]
- Feng, X.; Wang, F.; Wu, C.; Luo, J.; Zhang, L. Modeling and comparisons of aggregated flyback microinverters in aspect of harmonic resonances with the grid. IEEE Trans. Ind. Electron. 2019, 66, 276–285. [Google Scholar] [CrossRef]
- Chen, M.; Zheng, R.; Fu, Y.; Qi, J.; Han, F.; Jiang, F.; Yao, W. An analog control strategy with multiplier-less power calcu-lation circuit for flyback microinverter. IEEE Trans. Power Electron. 2021, 36, 8617–8621. [Google Scholar] [CrossRef]
- Falconar, N.; Beyragh, D.S.; Pahlevani, M. An adaptive sensorless control technique for a flyback-type solar tile microin-verter. IEEE Trans. Power Electron. 2020, 35, 13554–13562. [Google Scholar] [CrossRef]
- Hasan, R.; Hassan, W.; Xiao, W. PV microinverter solution for high voltage gain and soft switching. IEEE Trans. Emerg. Sel. Top. Power Electron. 2021, in press. Available online: https://ieeexplore.ieee.org/document/9362130 (accessed on 28 October 2021). [CrossRef]
- Kyritsis, A.; Tatakis, E.C.; Papanikolaou, N. Optimum design of the current-source flyback inverter for decentralized grid-connected photovoltaic systems. IEEE Trans. Energy Convers. 2008, 23, 281–293. [Google Scholar] [CrossRef]
- Zhang, Z.; He, X.-F.; Liu, Y.-F. An optimal control method for photovoltaic grid-tied-interleaved flyback microinverters to achieve high efficiency in wide load range. IEEE Trans. Power Electron. 2013, 28, 5074–5087. [Google Scholar] [CrossRef]
- Nanakos, A.C.; Tatakis, E.C.; Papanikolaou, N.P. A weighted-efficiency-oriented design methodology of flyback inverter for ac photovoltaic modules. IEEE Trans. Power Electron. 2012, 27, 3221–3233. [Google Scholar] [CrossRef]
- Hu, H.; Harb, S.; Kutkut, N.H.; Shen, Z.J.; Batarseh, I. A single-stage microinverter without using eletrolytic capacitors. IEEE Trans. Power Electron. 2013, 28, 2677–2687. [Google Scholar] [CrossRef]
- Zengin, S.; Deveci, F.; Boztepe, M. Decoupling capacitor selection in DCM flyback PV microinverters considering harmonic distortion. IEEE Trans. Power Electron. 2012, 28, 816–825. [Google Scholar] [CrossRef]
- Gao, M.; Chen, M.; Zhang, C.; Qian, Z. Analysis and implementation of an improved flyback inverter for photovoltaic AC module applications. IEEE Trans. Power Electron. 2013, 29, 3428–3444. [Google Scholar] [CrossRef]
- Nanakos, A.C.; Christidis, G.C.; Tatakis, E.C. Weighted efficiency optimization of flyback micro-inverter under improved boundary conduction mode (i-BCM). IEEE Trans. Power Electron. 2015, 30, 5548–5564. [Google Scholar] [CrossRef]
- Li, Y.; Oruganti, R. A low cost flyback CCM inverter for AC module application. IEEE Trans. Power Electron. 2011, 27, 1295–1303. [Google Scholar] [CrossRef]
- Edwin, F.F.; Xiao, W.; Khadkikar, V. Dynamic modeling and control of interleaved flyback module-integrated converter for pv power applications. IEEE Trans. Ind. Electron. 2013, 61, 1377–1388. [Google Scholar] [CrossRef]
- Thang, T.V.; Thao, N.M.; Jang, J.H.; Park, J.H. Analysis and design of grid-connected photovoltaic systems with multiple-integrated converters and a pseudo-dc-link inverter. IEEE Trans. Ind. Electron. 2014, 61, 3377–3386. [Google Scholar] [CrossRef]
- Christidis, G.C.; Nanakos, A.C.; Tatakis, E.C. Hybrid discontinuous/boundary conduction mode of flyback microinverter for AC–PV modules. IEEE Trans. Power Electron. 2015, 31, 4195–4205. [Google Scholar] [CrossRef]
- Christidis, G.C.; Nanakos, A.C.; Tatakis, E.C. Analysis of a flyback current source inverter under hybrid DCM-BCM operation. In Proceedings of the 2015 17th European Conference on Power Electronics and Applications (EPE’15 ECCE-Europe), Geneva, Switzerland, 8–10 September 2015; pp. 1–10. [Google Scholar]
- Dimitrakakis, G.; Tatakis, E.; Rikos, E. A semiempirical model to determine HF copper losses in magnetic components with nonlayered coils. IEEE Trans. Power Electron. 2008, 23, 2719–2728. [Google Scholar] [CrossRef]
- Venkatachalam, K.; Sullivan, C.R.; Abdallah, T.; Tacca, H. Accurate prediction of ferrite core loss with nonsinusoidal waveforms using only Steinmetz parameters. In Proceedings of the 2002 IEEE Computers in Power Electronics Conference, Mayaguez, PR, USA, 3–4 June 2002; pp. 36–41. [Google Scholar]
- Steinmetz, C.P. On the law of hysteresis. In Proceedings of the 1984 IEEE International Conference on Robotics and Automation (ICRA), Atlanta, GA, USA, 13–15 March 1984; pp. 197–221. [Google Scholar]
- Wolfram, S. The Mathematica Book, 5th ed.; Wolfram Media: Champaign, IL, USA, 2004. [Google Scholar]
- European Committee for Electrotechnical Standardization (CENELEC). Overall Efficiency of Photovoltaic Inverters; European Standard EN 50530; CENELEC: Brussels, Belgium, 2010. [Google Scholar]
- Dixon, L.H. Magnetics design for switching power supplies. In Unitrode Seminars; Texas Instruments: Dallas, TX, USA, 2001. [Google Scholar]
- Gradshteyn, S.; Ryzhik, I.M.; Jeffrey, A. Table of Integrals, Series, and Products, 5th ed.; Academic Press: San Francisco, CA, USA, 1994. [Google Scholar]








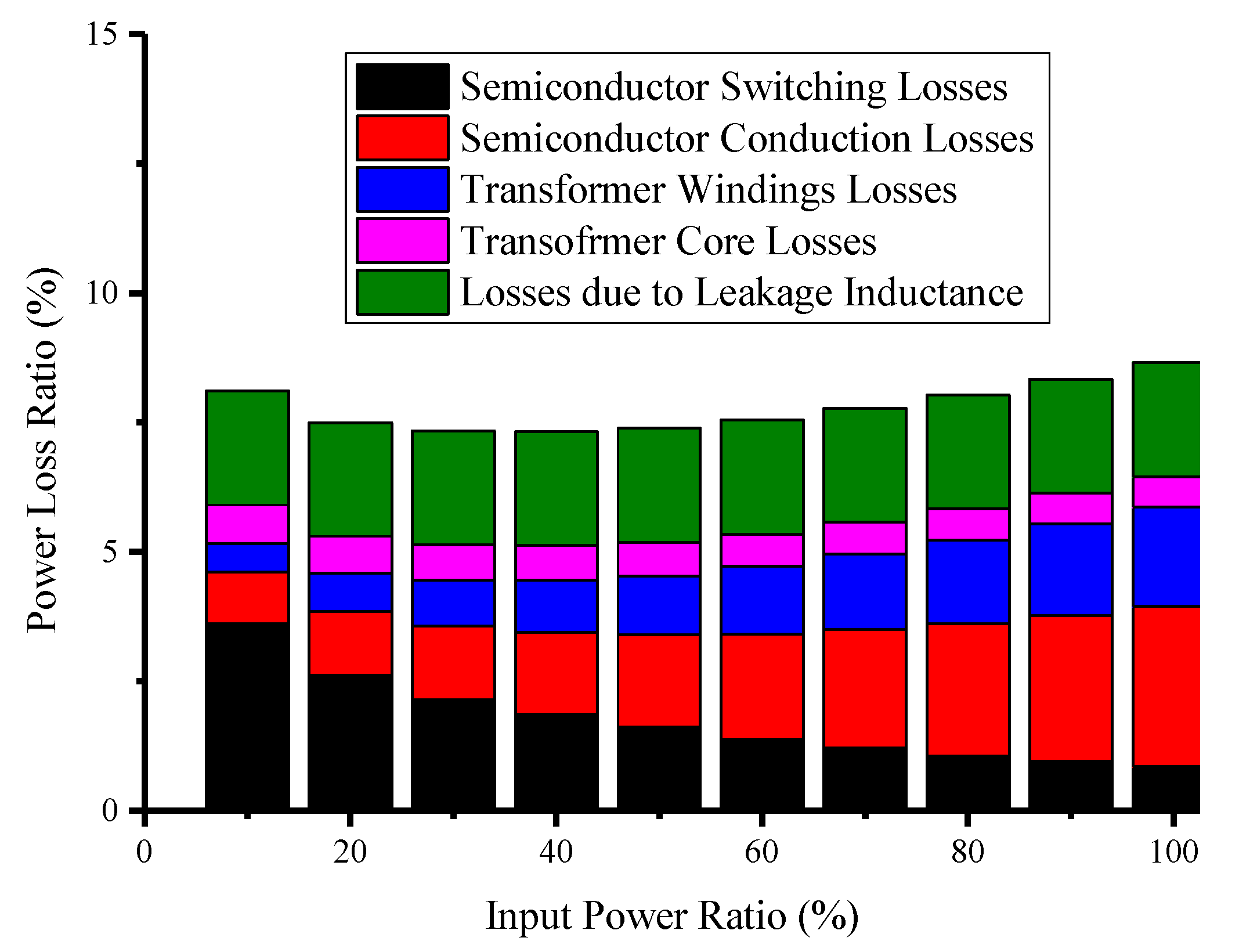
| Power Level | 5% | 10% | 20% | 30% | 50% | 75% | 100% |
|---|---|---|---|---|---|---|---|
| EU | 0.03 | 0.06 | 0.13 | 0.1 | 0.48 | 0 | 0.2 |
| CEC | 0 | 0.04 | 0.05 | 0.12 | 0.21 | 0.53 | 0.05 |
| Specifications | Design Constraints | Optimization Independent Variables | Design Values |
|---|---|---|---|
| STC: PPV,max = 180 W/Vdc = 36 V | Peak Flux Density: 280 mT | n = 0.129 | SP: IXFX180N15 |
| 0 °C: PPV,max = 205 W/Vdc = 40 V | Maximum. Transformer Fill Factor: 35% | f = 29 kHz | S1, S2: IXFX26N120 |
| 60 °C: PPV,max = 140 W/Vdc = 31 V | Maximum MOSFET breakdown voltage: 1200 V | tonp,max = 37.2 us | D1, D2: STTH1512G |
| Grid: 230 V/50 Hz | J = 4.1 A/mm2 | Turns = 19:147 | |
| Cf = 440 nF | Bp = 280 mT | L1 = 41.2 μH | |
| Core Type: ETD54 | Leakage inductance ratio: 2.2% | ||
| Material: 3F3 | Core gap = 3.41 mm |
| Maximum Power | Input Voltage | Measured Efficiency | Calculated Efficiency | Calculated Efficiency of [18] (i-BCM) |
|---|---|---|---|---|
| 205 W | 40 V | 92.15% | 92.27% | 91.59% |
| 180 W | 36 V | 92.24% | 92.43% | 91.38% |
| 140 W | 31 V | 92.35% | 92.35% | 91.51% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Christidis, G.; Nanakos, A.; Tatakis, E. Optimal Design of a Flyback Microinverter Operating under Discontinuous-Boundary Conduction Mode (DBCM). Energies 2021, 14, 7480. https://doi.org/10.3390/en14227480
Christidis G, Nanakos A, Tatakis E. Optimal Design of a Flyback Microinverter Operating under Discontinuous-Boundary Conduction Mode (DBCM). Energies. 2021; 14(22):7480. https://doi.org/10.3390/en14227480
Chicago/Turabian StyleChristidis, Georgios, Anastasios Nanakos, and Emmanuel Tatakis. 2021. "Optimal Design of a Flyback Microinverter Operating under Discontinuous-Boundary Conduction Mode (DBCM)" Energies 14, no. 22: 7480. https://doi.org/10.3390/en14227480
APA StyleChristidis, G., Nanakos, A., & Tatakis, E. (2021). Optimal Design of a Flyback Microinverter Operating under Discontinuous-Boundary Conduction Mode (DBCM). Energies, 14(22), 7480. https://doi.org/10.3390/en14227480







