Field-Based Prediction Models for Stop Penalty in Traffic Signal Timing Optimization
Abstract
:1. Introduction and Background
2. Methodology
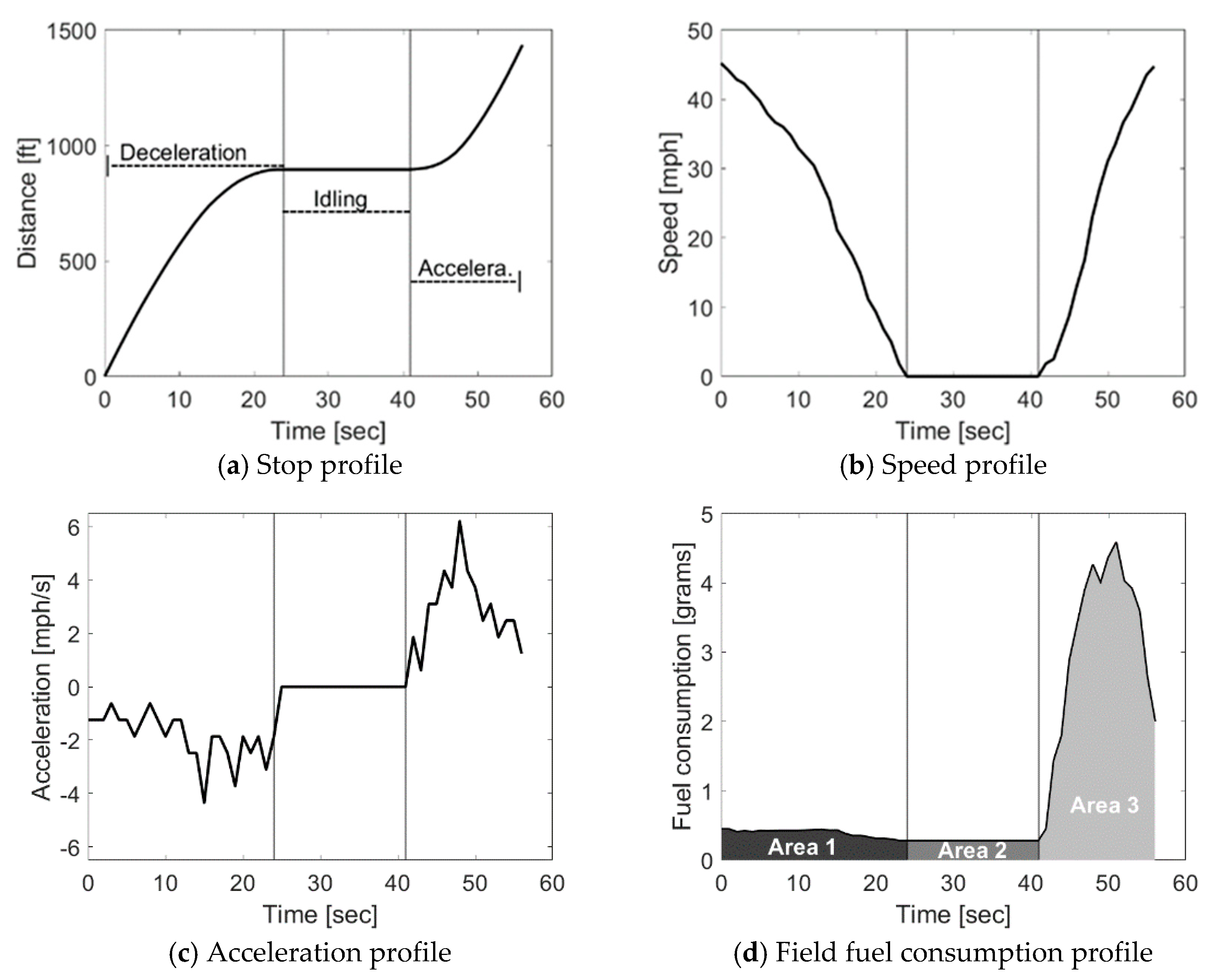
2.1. Overview of the Stop Penalty Derivation
2.2. Factors Impacting Stop Penalty
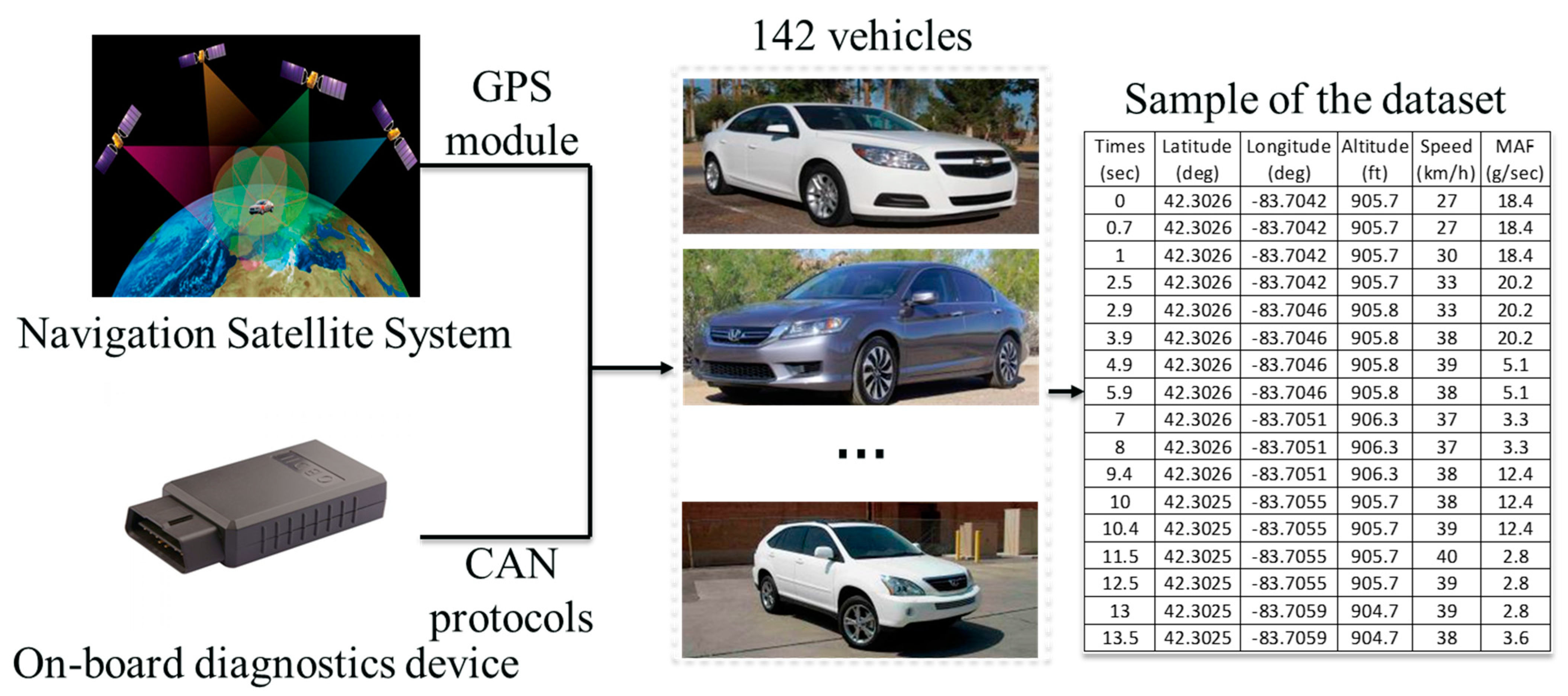
2.3. Collection of Field Data
2.4. Data Preparation
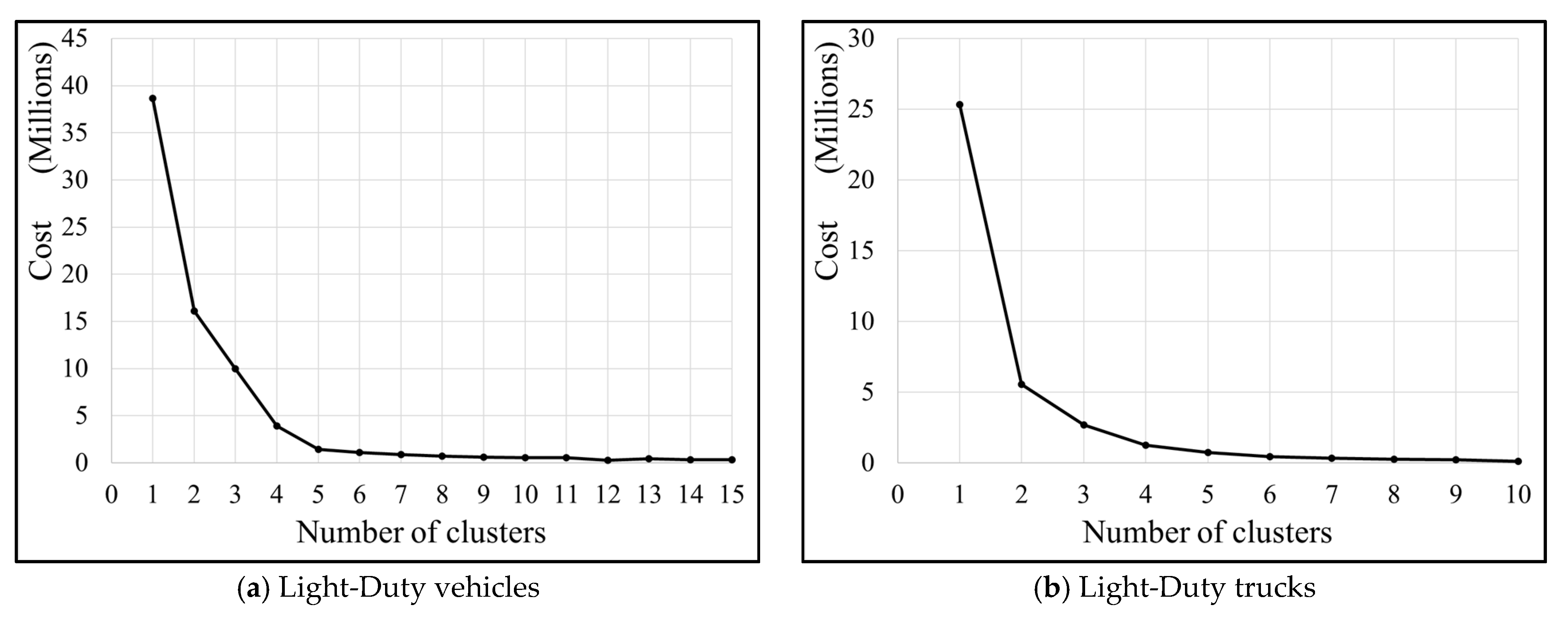
2.4.1. Vehicle Classification
2.4.2. Instantaneous Fuel Consumption Rates
2.4.3. Cruising Speeds and CSSPs
2.4.4. Road Gradient
2.5. Machine Learning (ML) Models
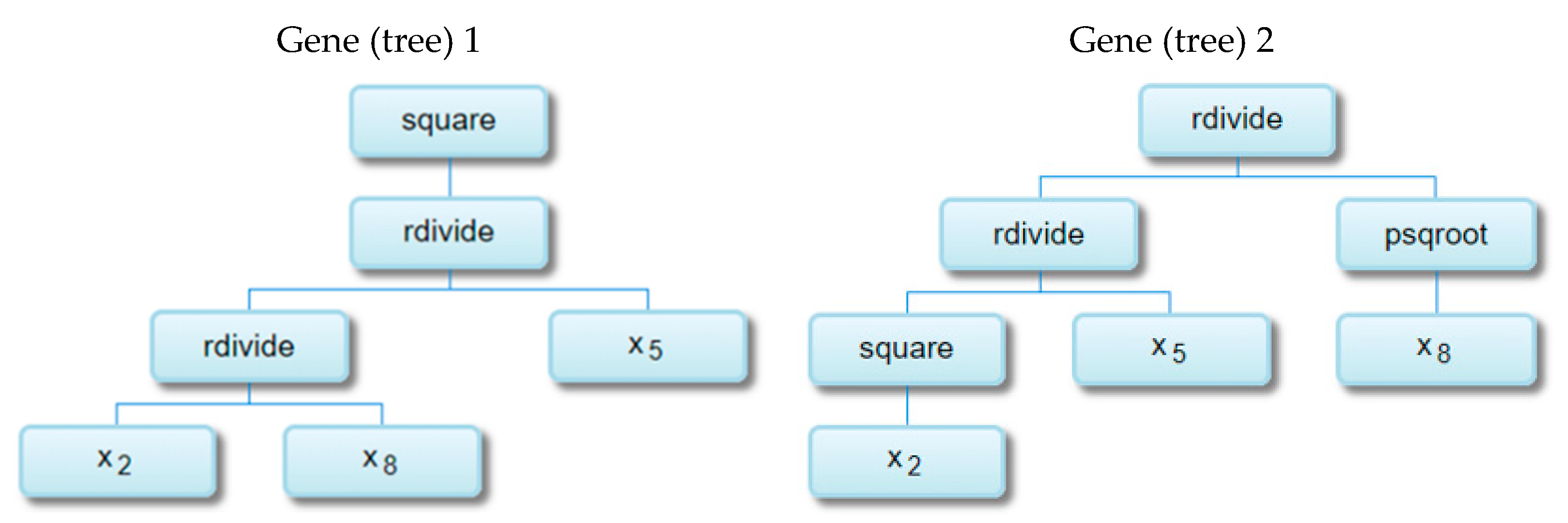
2.5.1. Multigene Genetic Programming
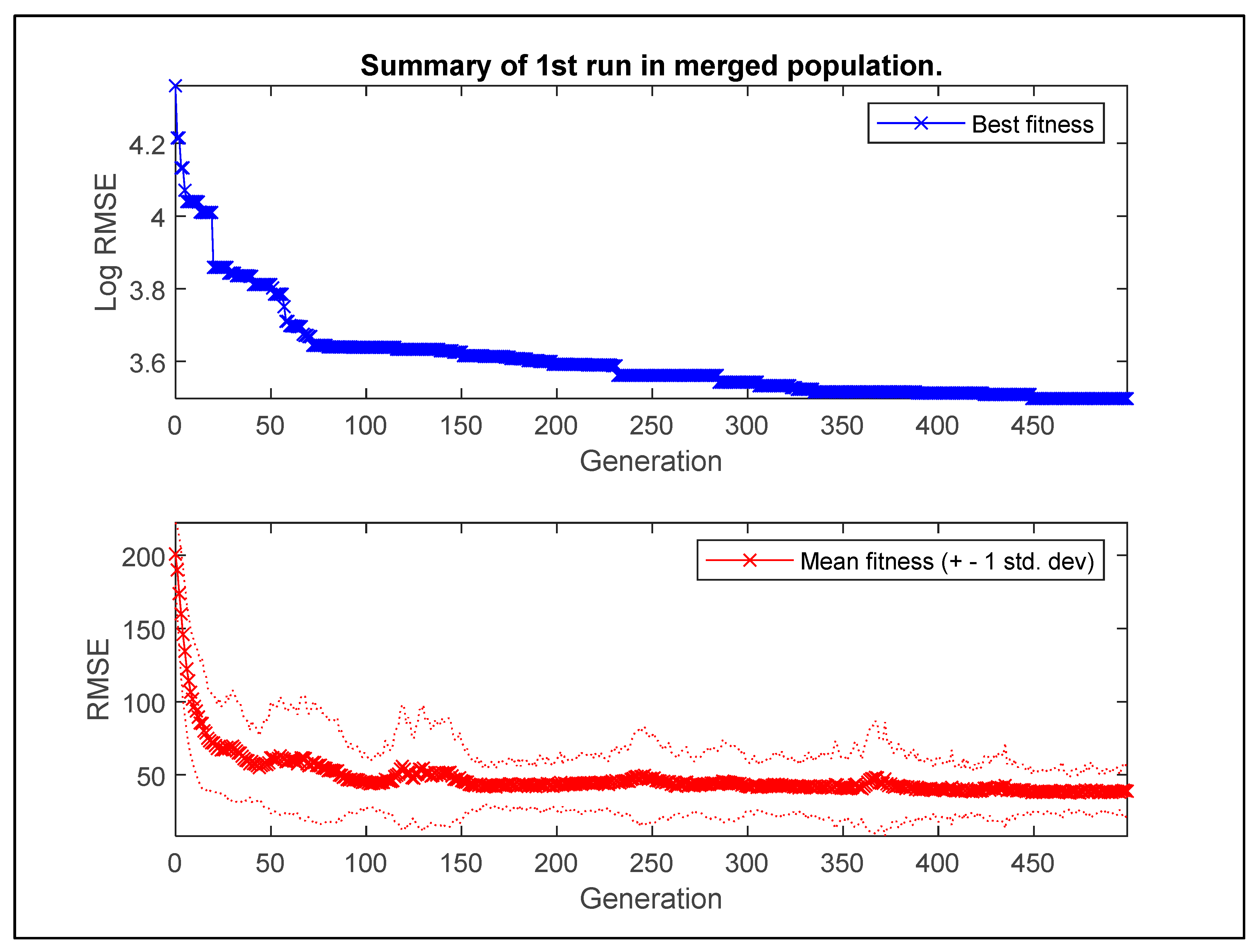
2.5.2. Development of MGGP Models
3. Results and Discussion
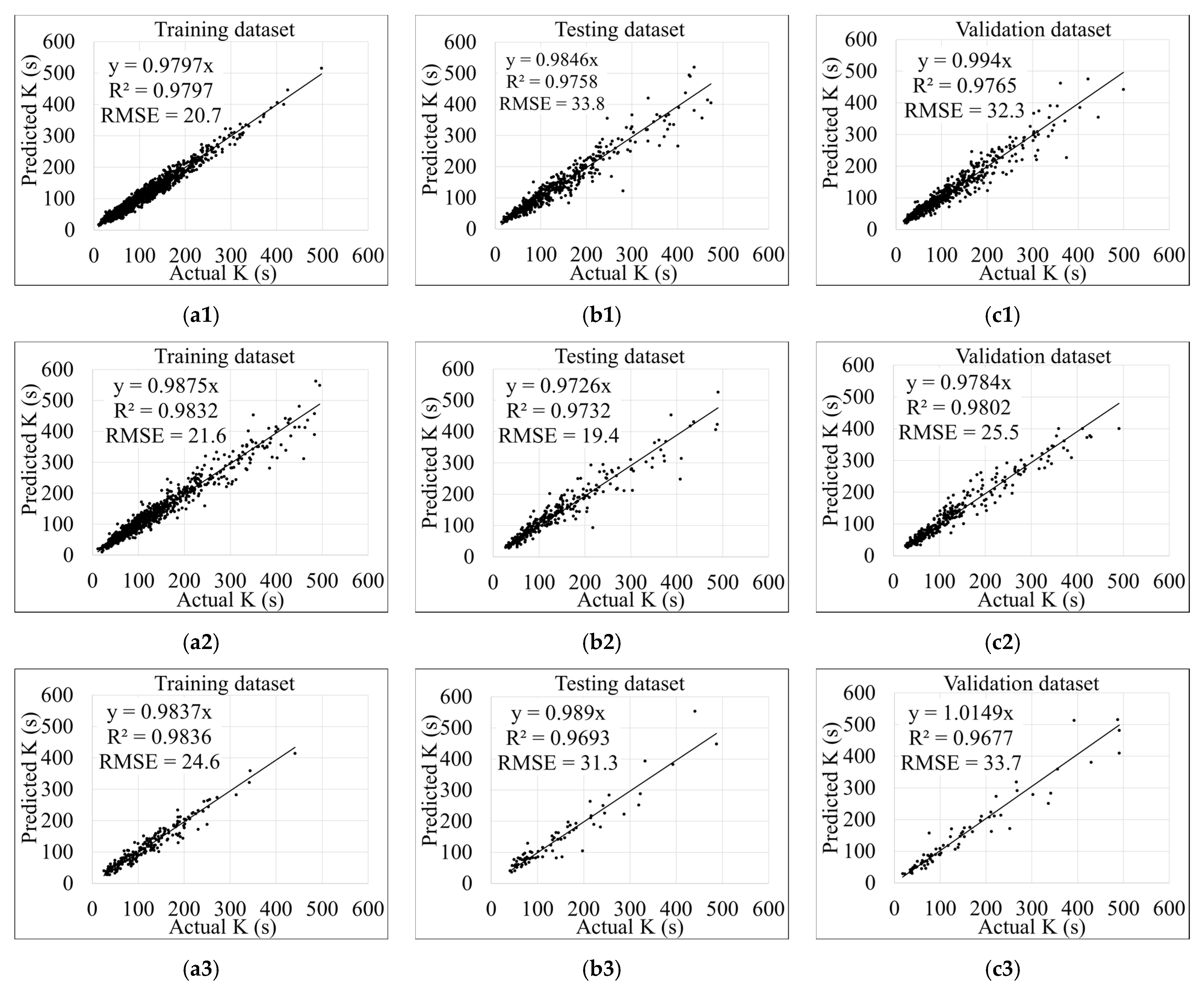
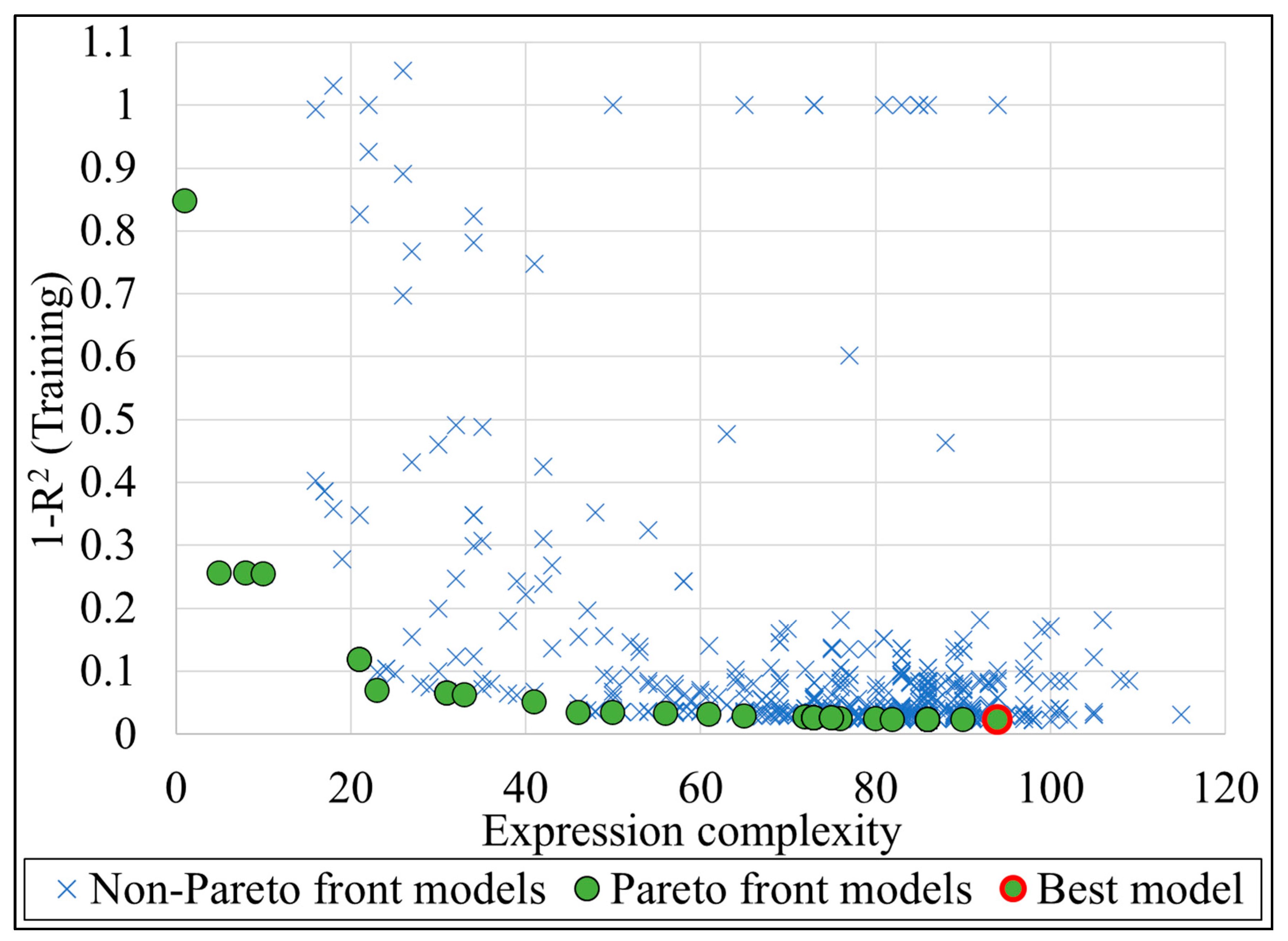
3.1. Models Training, Testing, and Validation
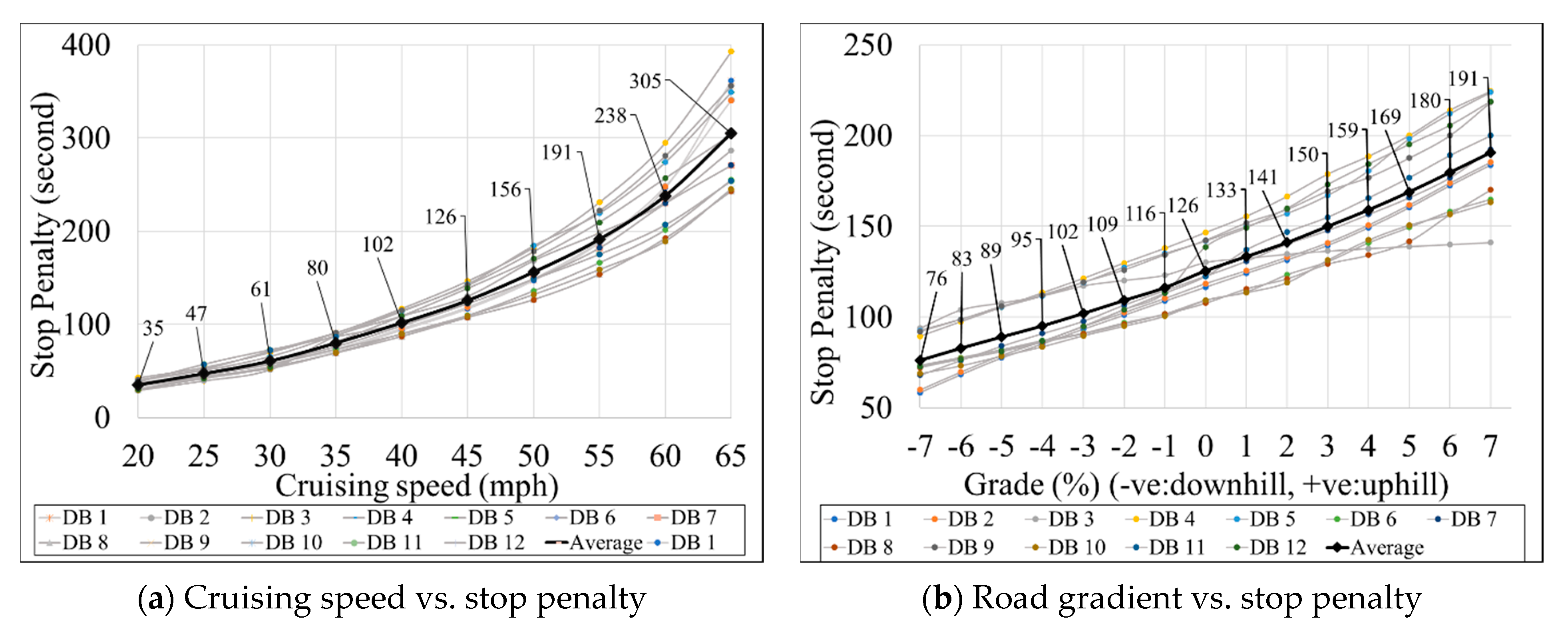
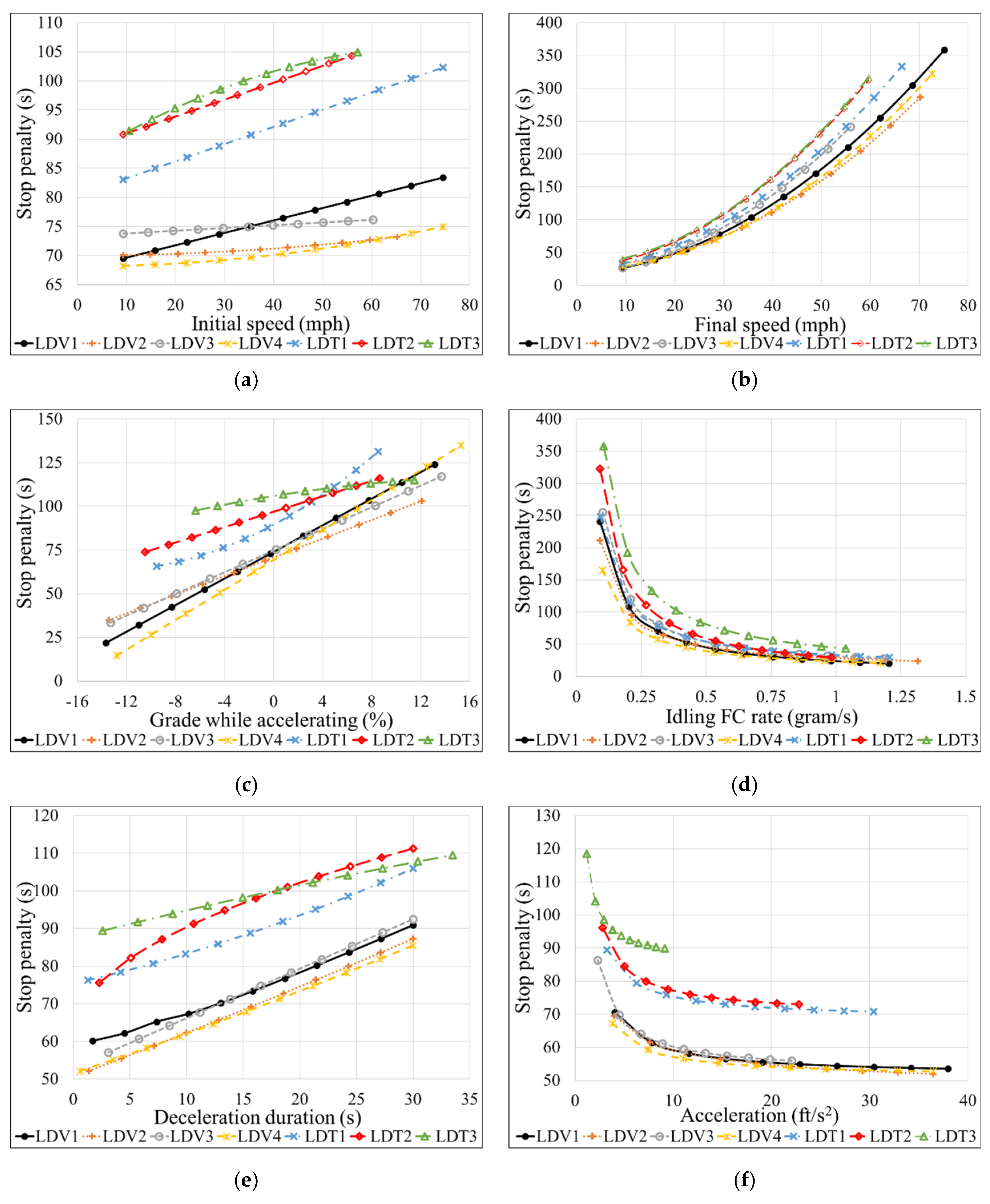
3.2. Parametric Analysis
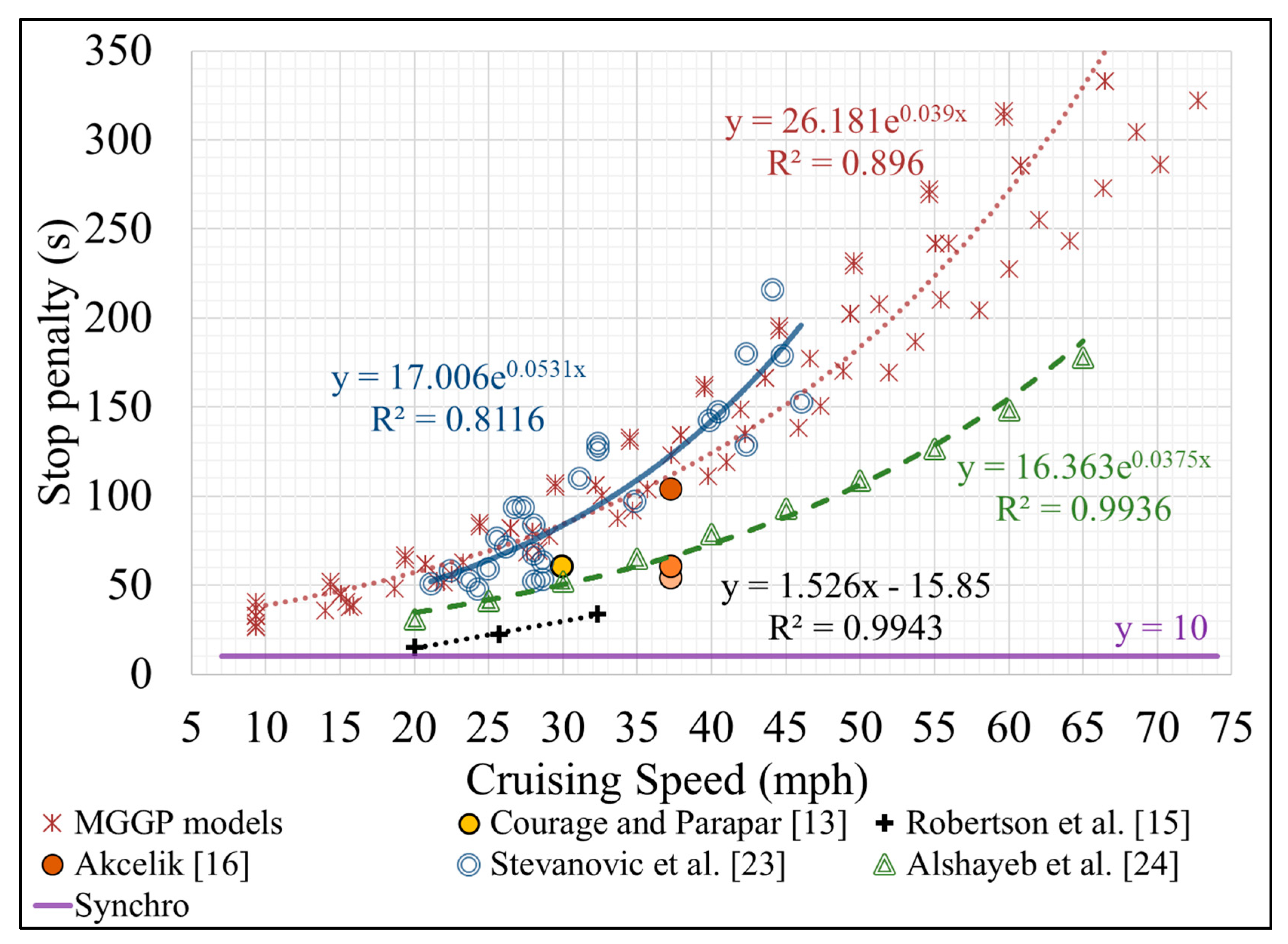
3.3. Comparison of Stop Penalties from Various Studies
- FC measurements were collected in the field, unlike Alshayeb et al. [24], whose stop penalties were simulation-based.
- Large number of LDVs and LDTs were included, whereas most previous studies used less than three vehicles.
- The tested fleet consisted of modern vehicles, whereas tested vehicles in the previous studies, except for Stevanovic et al. [23], are old for contemporary standards.
- Tested vehicles covered long distances, resulting in a significantly larger dataset than those used in the previous studies.
- The models cover multiple factors impacting the stop penalty (vehicle type, cruising speed, road gradient, FC idling rate, driving behavior, and decelerating duration), whereas most of the previous studies investigated only the impact of the cruising speed.
4. Conclusions and Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- McMichael, A.J.; Haines, J.A.; Slooff, R.; Sari Kovats, R.; World Health Organization. Climate Change and Human Health: An Assessment; World Health Organization: Geneva, Switzerland, 1996. [Google Scholar]
- Hannah, L. Climate Change Biology; Academic Press: Cambridge, MA, USA, 2021. [Google Scholar]
- Fast Facts on Transportation Greenhouse Gas Emissions [Internet]. EPA. Environmental Protection Agency; [updated on 8 July 2021; cited on 22 July 2021]. Available online: https://www.epa.gov/greenvehicles/fast-facts-transportation-greenhouse-gas-emissions (accessed on 3 November 2021).
- Pope, C.A., III; Burnett, R.T.; Thun, M.J.; Calle, E.E.; Krewski, D.; Ito, K.; Thurston, G.D. Lung cancer, cardiopulmonary mortality, and long-term exposure to fine particulate air pollution. JAMA 2002, 287, 1132–1141. [Google Scholar] [CrossRef] [Green Version]
- Rakha, H.; Ding, Y. Impact of stops on vehicle fuel consumption and emissions. J. Transp. Eng. 2003, 129, 23–32. [Google Scholar] [CrossRef]
- Alshayeb, S. Evaluation of Theoretical and Practical Signal Optimization Tools in Microsimulation Environment. Master’s Thesis, Florida Atlantic University, Boca Raton, FL, USA, 2019. [Google Scholar]
- Alshayeb, S.; Stevanovic, A.; Mitrovic, N.; Dimitrijevic, B. Impact of Accurate Detection of Freeway Traffic Conditions on the Dynamic Pricing: A Case Study of I-95 Express Lanes. Sensors 2021, 21, 5997. [Google Scholar] [CrossRef]
- Dobrota, N.; Stevanovic, A.; Mitrovic, N. Development of assessment tool and overview of adaptive traffic control deployments in the US. Transp. Res. Rec. 2020, 2674, 464–480. [Google Scholar] [CrossRef]
- Gavric, S.; Sarazhinsky, D.; Stevanovic, A.; Dobrota, N. Evaluation of Pedestrian Timing Treatments for Coordinated Signalized Intersections. In Proceedings of the Transportation Research Board 101st Annual Meeting, Washington, DC, USA, 9–13 January 2022. [Google Scholar]
- Stevanovic, A.; Dobrota, N.; Mitrovic, N. NCHRP 20-07/Task 414: Benefits of Adaptive Traffic Control Deployments-A Review of Evaluation Studies; Technical Report, Final Report; Transportation Research Board of the National Academies: Washington, DC, USA, 2019. [Google Scholar]
- Shayeb, S.A.; Dobrota, N.; Stevanovic, A.; Mitrovic, N. Assessment of Arterial Signal Timings Based on Various Operational Policies and Optimization Tools. Transp. Res. Rec. 2021. [Google Scholar] [CrossRef]
- Bauer, C.S. Some energy considerations in traffic signal timing. Traffic Eng. 1975, 45, 19–25. [Google Scholar]
- Courage, K.G.; Parapar, S.M. Delay and fuel consumption at traffic signals. Traffic Eng. 1975, 45, 23–27. [Google Scholar]
- Cohen, S.L.; Euler, G. Signal Cycle Length and Fuel Consumption and Emissions; Transportation Research Record: Thousand Oaks, CA, USA, 1978. [Google Scholar]
- Robertson, D.I.; Lucas, C.F.; Baker, R.T. Coordinating Traffic Signals to Reduce Fuel Consumption; Transport and Road Research Laboratory: London, UK, 1981. [Google Scholar]
- Akcelik, R. Fuel efficiency and other objectives in traffic system management. Traffic Eng. Control. 1981, 22, 54–65. [Google Scholar]
- “Brian” Park, B.; Yun, I.; Ahn, K. Stochastic optimization for sustainable traffic signal control. Int. J. Sustain. Transp. 2009, 3, 263–284. [Google Scholar] [CrossRef]
- Liao, T.Y. A fuel-based signal optimization model. Transp. Res. Part D Transp. Environ. 2013, 23, 1–8. [Google Scholar] [CrossRef]
- Stevanovic, A.; Stevanovic, J.; So, J.; Ostojic, M. Multi-criteria optimization of traffic signals: Mobility, safety, and environment. Transp. Res. Part C Emerg. Technol. 2015, 55, 46–68. [Google Scholar] [CrossRef] [Green Version]
- Road Research Laboratory. TRANSYT: A Traffic Network Study Tool. 1969. Available online: https://trid.trb.org/view/115048 (accessed on 3 November 2021).
- David, H.; John, A. Synchro Studio 7 User Guide; Trafficware, Ltd.: Houston, TX, USA, 2006; pp. 4–6. [Google Scholar]
- America, P.T. PTV Vistro User Manual; PTV AG: Karlsruhe, Germany, 2014. [Google Scholar]
- Stevanovic, A.; Shayeb, S.A.; Patra, S.S. Fuel Consumption Intersection Control Performance Index. Transp. Res. Rec. 2021. [Google Scholar] [CrossRef]
- Al Shayeb, S.; Stevanovic, A.; Effinger, J.R. Investigating Impacts of Various Operational Conditions on Fuel Consumption and Stop Penalty at Signalized Intersections. Int. J. Transp. Sci. Technol. 2021. [Google Scholar] [CrossRef]
- Ardalan, T.; Liu, D.; Kaisar, E. Truck Tonnage Estimation Using Weigh-In-Motion (WIM) Data in Florida. In Proceedings of the Transportation Research Board 99th Annual Meeting, Washington, DC, USA, 12–16 January 2020. [Google Scholar]
- Alshayeb, S.; Stevanovic, A.; Dobrota, N. Impact of Various Operating Conditions on Simulated Emissions-Based Stop Penalty at Signalized Intersections. Sustainability 2021, 13, 10037. [Google Scholar] [CrossRef]
- Department of Energy. Available online: https://www.energy.gov/ (accessed on 3 November 2021).
- Idaho National Laboratory. INL. 2021. Available online: https://inl.gov/ (accessed on 3 November 2021).
- Driver-Centric Fleet Management Solutions [Internet]. ISAAC Instruments. 2021 [updated 2021 Jul 9 cited 2021 Jul 22]. Available online: https://isaacinstruments.com/en/ (accessed on 3 November 2021).
- Huang, Z. Clustering large data sets with mixed numeric and categorical values. In Proceedings of the 1st Pacific-Asia Conference on Knowledge Discovery and Data Mining (PAKDD), Singapore, 23–24 February 1997; pp. 21–34. [Google Scholar]
- Yadav, J.; Sharma, M. A Review of K-mean Algorithm. Int. J. Eng. Trends Technol. 2013, 4, 2972–2976. [Google Scholar]
- Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A k-means clustering algorithm. J. R. Stat. Soc. Ser. C (Appl. Stat.) 1979, 28, 100–108. [Google Scholar] [CrossRef]
- An, F.; Barth, M.; Norbeck, J.; Ross, M. Development of comprehensive modal emissions model: Operating under hot-stabilized conditions. Transp. Res. Rec. 1997, 1587, 52–62. [Google Scholar] [CrossRef] [Green Version]
- Park, S.; Rakha, H.; Ahn, K.; Moran, K. Virginia tech comprehensive power-based fuel consumption model (VT-CPFM): Model validation and calibration considerations. Int. J. Transp. Sci. Technol. 2013, 2, 317–336. [Google Scholar] [CrossRef] [Green Version]
- Hillier, V.A.; Coombes, P. Hillier’s Fundamentals of Motor Vehicle Technology; Nelson Thornes: Cheltenham, UK, 2004. [Google Scholar]
- National Geospatial PROGRAM. The National Map. (n.d.). Retrieved 12 September 2021. Available online: https://www.usgs.gov/core-science-systems/national-geospatial-program/national-map (accessed on 3 November 2021).
- Iqbal, M.S.; Ardalan, T.; Hadi, M.; Kaisar, E.I. Developing Guidelines for Implementing Transit Signal Priority (TSP) and Freight Signal Priority (FSP) Using Simulation Modeling and Decision Tree Algorithm. In Proceedings of the Transportation Research Board 100th Annual Meeting, Washington, DC, USA, 5–29 January 2021. [Google Scholar]
- Martínez-Ballesteros, M.; Troncoso, A.; Martínez-Álvarez, F.; Riquelme, J.C. Mining quantitative association rules based on evolutionary computation and its application to atmospheric pollution. Integr. Comput. Aided Eng. 2010, 17, 227–242. [Google Scholar] [CrossRef] [Green Version]
- Roy, R.; Bhatt, P.; Ghoshal, S.P. Evolutionary computation based three-area automatic generation control. Expert Syst. Appl. 2010, 37, 5913–5924. [Google Scholar] [CrossRef]
- Zhang, Q.; Barri, K.; Jiao, P.; Salehi, H.; Alavi, A.H. Genetic programming in civil engineering: Advent, applications and future trends. Artif. Intell. Rev. 2021, 54, 1863–1885. [Google Scholar] [CrossRef]
- Koza, J.R.; Koza, J.R. Genetic Programming: On the Programming of Computers by Means of Natural Selection; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Gandomi, A.H.; Alavi, A.H. A new multi-gene genetic programming approach to nonlinear system modeling. Part I: Materials and structural engineering problems. Neural Comput. Appl. 2012, 21, 171–187. [Google Scholar] [CrossRef]
- Searson, D.P.; Leahy, D.E.; Willis, M.J. GPTIPS: An open source genetic programming toolbox for multigene symbolic regression. In Proceedings of the International Multiconference of Engineers and Computer Scientists, Hongkong, China, 17–19 March 2010; Volume 1, pp. 77–80. [Google Scholar]
- Claffey, P.J. Running Costs of Motor Vehicles as Affected by Road Design and Traffic; NCHRP Report; Transportation Research Board: Washington, DC, USA, 1971. [Google Scholar]


| Variable | Description |
|---|---|
| Total cost function of the k-prototype algorithm | |
| Number of clusters | |
| Cluster | |
| Cost of assigning numerical objects in cluster i | |
| Cost of assigning categorical objects in cluster i | |
| Within-cluster sum of squares | |
| Numerical object number j in cluster i | |
| Mean point of the centroid of cluster (i) | |
| Number of numerical objects in each cluster i | |
| Categorical prototype number j in cluster i | |
| Number of categorical objects in cluster i | |
| Set of all unique values in the categorical attribute j | |
| LDV | Light-duty vehicle |
| LDT | Light-duty truck |
| Input Parameter | LDV1 Model | LDV2 Model | LDV3 Model | LDV4 Model | LDT1 Model | LDT2 Model | LDT3 Model | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Min | Max | Min | Max | Min | Max | Min | Max | Min | Max | Min | Max | Min | Max | |
| (mph) | 9.32 | 74.56 | 9.32 | 65.24 | 9.32 | 60.27 | 9.32 | 74.56 | 9.32 | 74.56 | 9.32 | 55.92 | 10.56 | 57.17 |
| (mph) | 9.32 | 75.19 | 9.32 | 70.21 | 9.32 | 55.92 | 9.32 | 72.7 | 9.32 | 66.49 | 9.32 | 59.65 | 9.32 | 59.65 |
| (%) | −13.67 | 13.16 | −13.43 | 12.08 | −13.29 | 13.69 | −12.8 | 15.28 | −9.54 | 8.55 | −10.48 | 8.65 | −6.36 | 11.49 |
| (gram/sec) | 0.09 | 1.2 | 0.09 | 1.314 | 0.1 | 1.18 | 0.1 | 1.17 | 0.09 | 1.21 | 0.09 | 0.98 | 0.1 | 1.04 |
| (sec) | 1.7 | 30 | 1.4 | 30 | 3.1 | 30 | 0.6 | 30 | 1.3 | 30 | 2.3 | 30 | 2.6 | 33.5 |
| (ft/sec2) | 0.28 | 37.97 | 0.39 | 36.45 | 0.1 | 22.02 | 0.16 | 36.45 | 0.24 | 30.38 | 0.59 | 22.78 | 0.3 | 9.11 |
| Attribute * | Options/Value |
|---|---|
| Function set | +, −, x, /, log, sqrt, square |
| Population size | 800 |
| Number of generations | 500 |
| Maximum number of genes allowed in an individual | 6 |
| Maximum tree depth | 4 |
| Tournament size | 80 |
| Tournament type | Pareto (probability = 1) |
| Elite fraction | 0.7 |
| Number of inputs | 8 |
| Constants range | [−10, 10] |
| Complexity measure | Node count |
| Model | Equation # |
|---|---|
| LDV1 | |
| (20) | |
| LDV2 | |
| (21) | |
| LDV3 | |
| (22) | |
| LDV4 | |
| (23) | |
| LDT1 | |
| (24) | |
| LDT2 | |
| (25) | |
| LDT3 | |
| (26) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alshayeb, S.; Stevanovic, A.; Park, B.B. Field-Based Prediction Models for Stop Penalty in Traffic Signal Timing Optimization. Energies 2021, 14, 7431. https://doi.org/10.3390/en14217431
Alshayeb S, Stevanovic A, Park BB. Field-Based Prediction Models for Stop Penalty in Traffic Signal Timing Optimization. Energies. 2021; 14(21):7431. https://doi.org/10.3390/en14217431
Chicago/Turabian StyleAlshayeb, Suhaib, Aleksandar Stevanovic, and B. Brian Park. 2021. "Field-Based Prediction Models for Stop Penalty in Traffic Signal Timing Optimization" Energies 14, no. 21: 7431. https://doi.org/10.3390/en14217431
APA StyleAlshayeb, S., Stevanovic, A., & Park, B. B. (2021). Field-Based Prediction Models for Stop Penalty in Traffic Signal Timing Optimization. Energies, 14(21), 7431. https://doi.org/10.3390/en14217431