Three-Phase State Estimation of a Low-Voltage Distribution Network with Kalman Filter
Abstract
1. Introduction
2. Formulation of the State Estimation Problem
2.1. Single-Phase State Estimation
2.2. The Kalman Filter Implementation
2.3. Three-Phase Formulation
- The first br-rows of Yp contain the longitudinal admittances;
- The last N-rows of Yp contain the shunt admittances;
- Yp is a band matrix;
- Matrix A is constructed as for the single-phase case, with a 1 or −1 in correspondence to the sending and receiving nodes of the oriented branch.
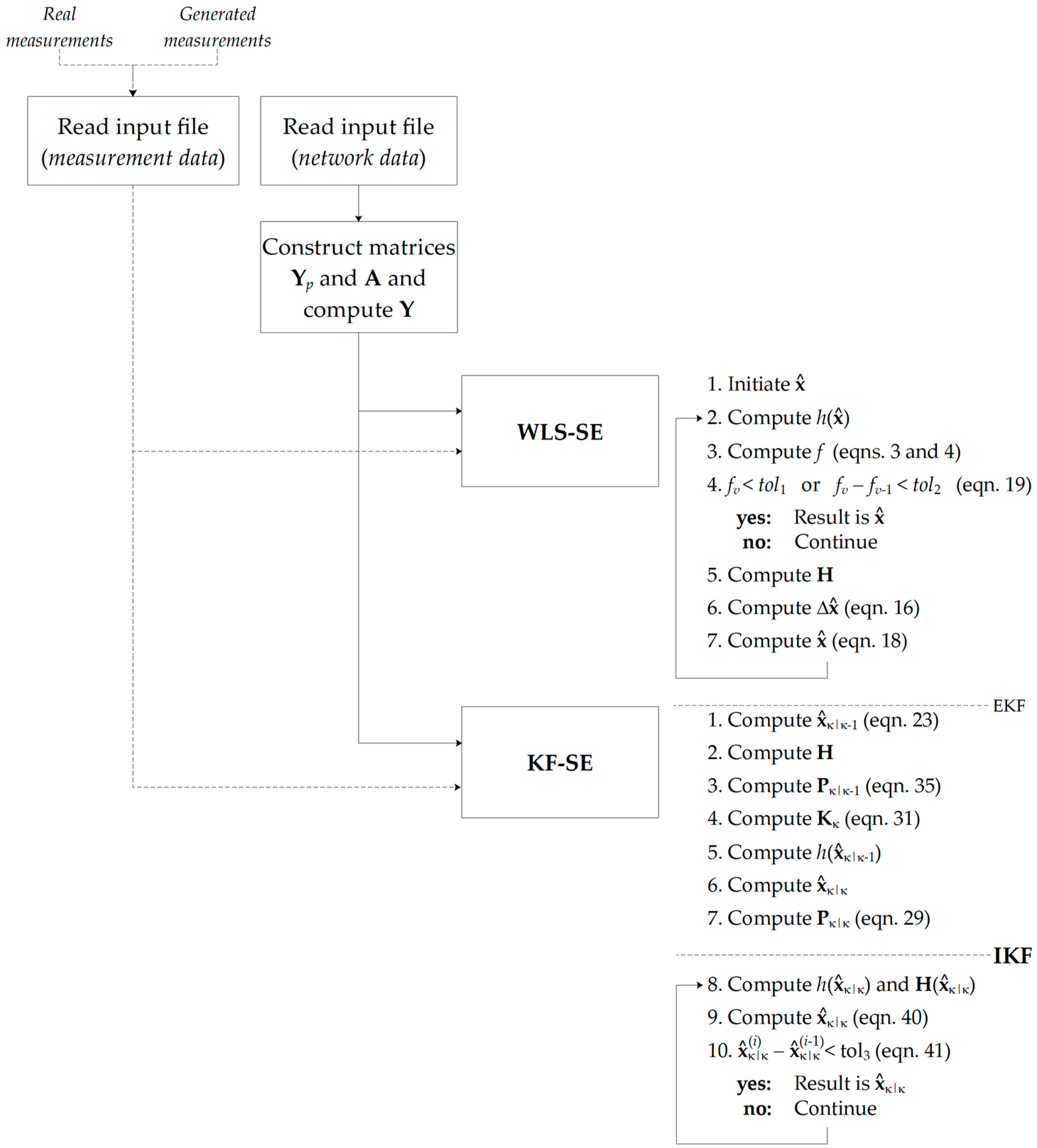
2.4. State Estimation Algorithm Implementation
- For lines, sending and arriving nodes, line impedances, and shunt admittances;
- For transformers, sending and arriving nodes, rated voltages and power, and pu data;
- For shunt elements (e.g., capacitor banks), connection nodes, and rated voltage and power;
- States of circuit breakers.
- For loads and generating units, measurements of active and reactive powers, voltage magnitudes and phases, and current magnitudes;
- For lines, measurements of active and reactive transmitted powers, and current magnitudes.
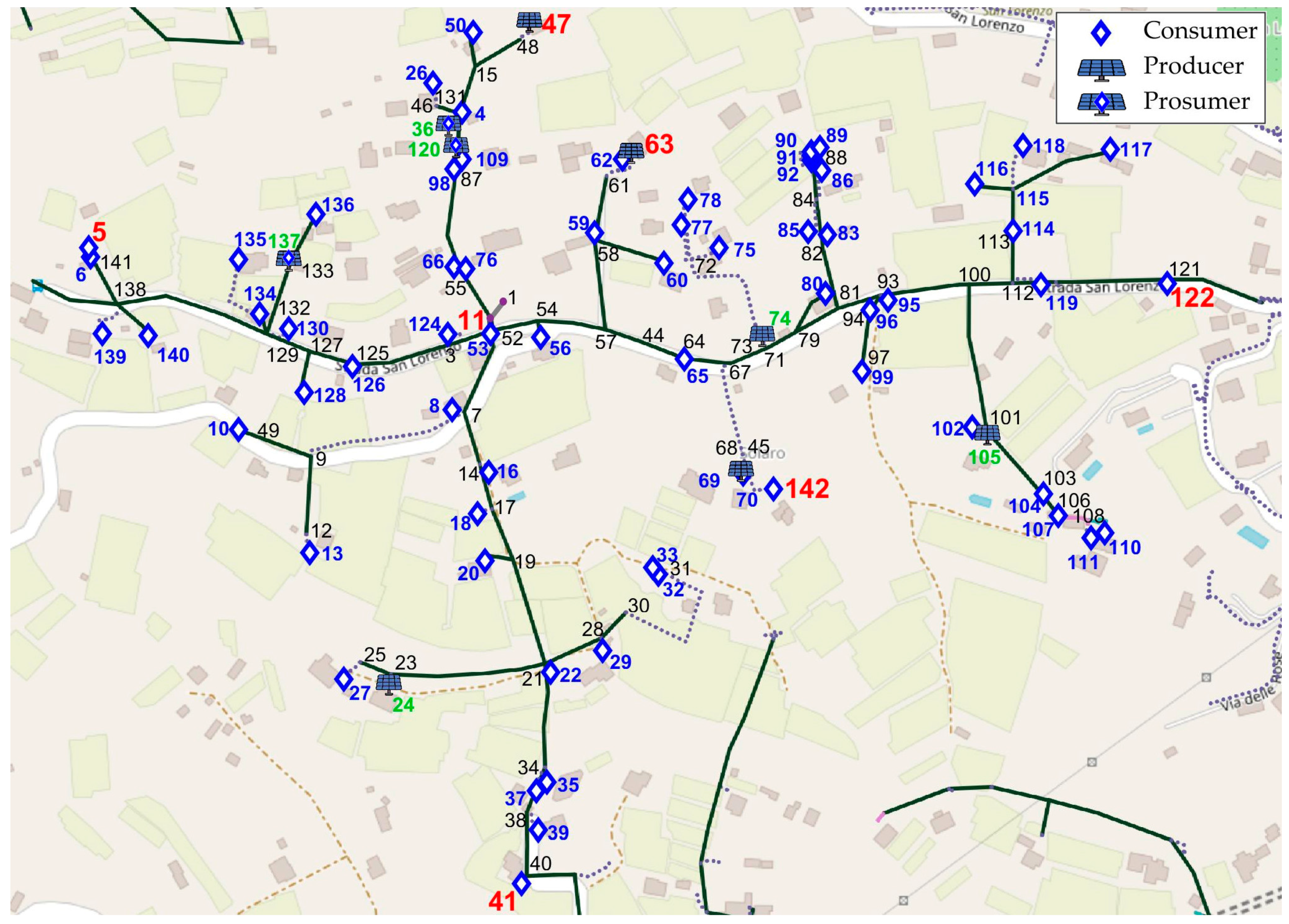
3. The Low-Voltage Network
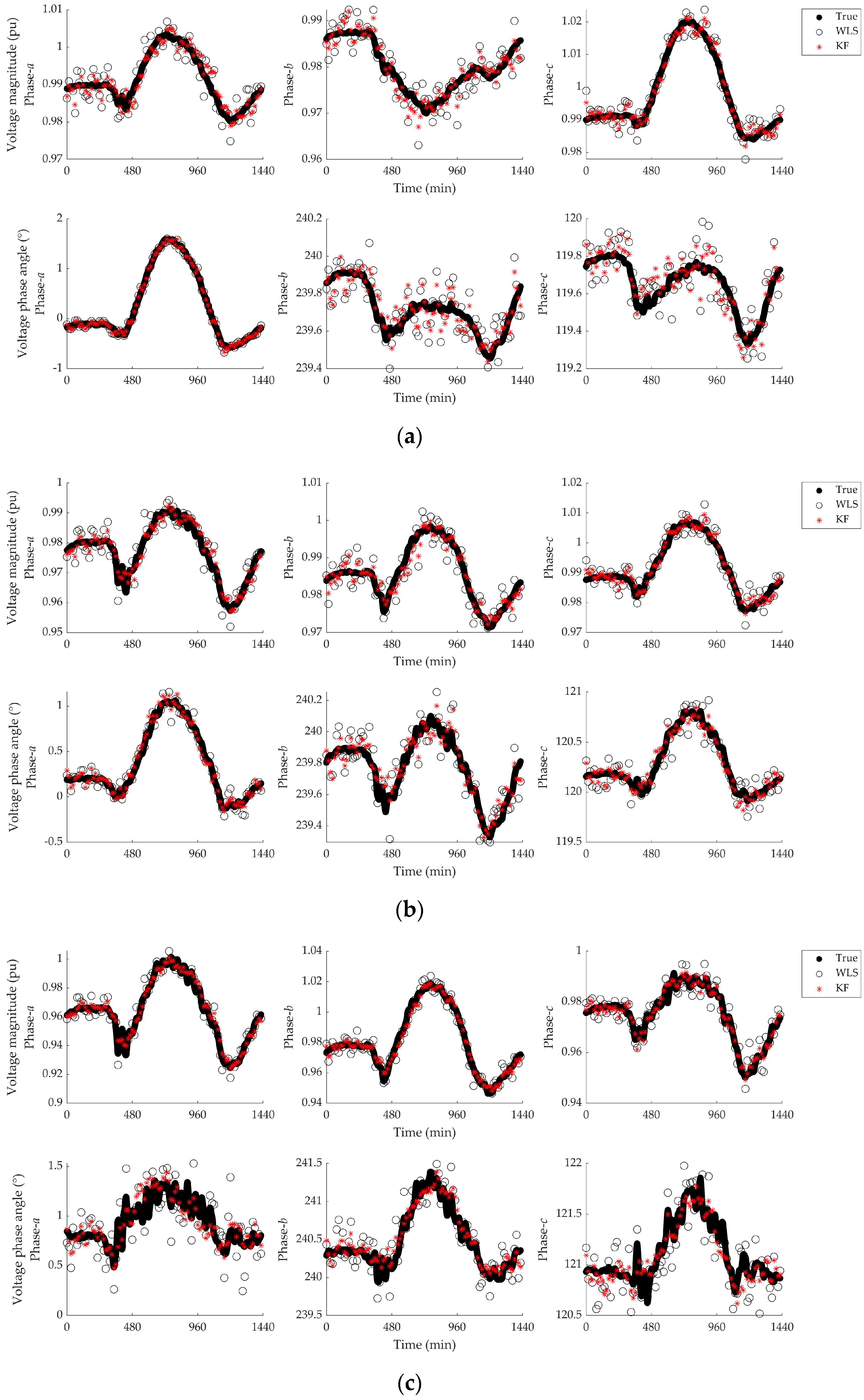
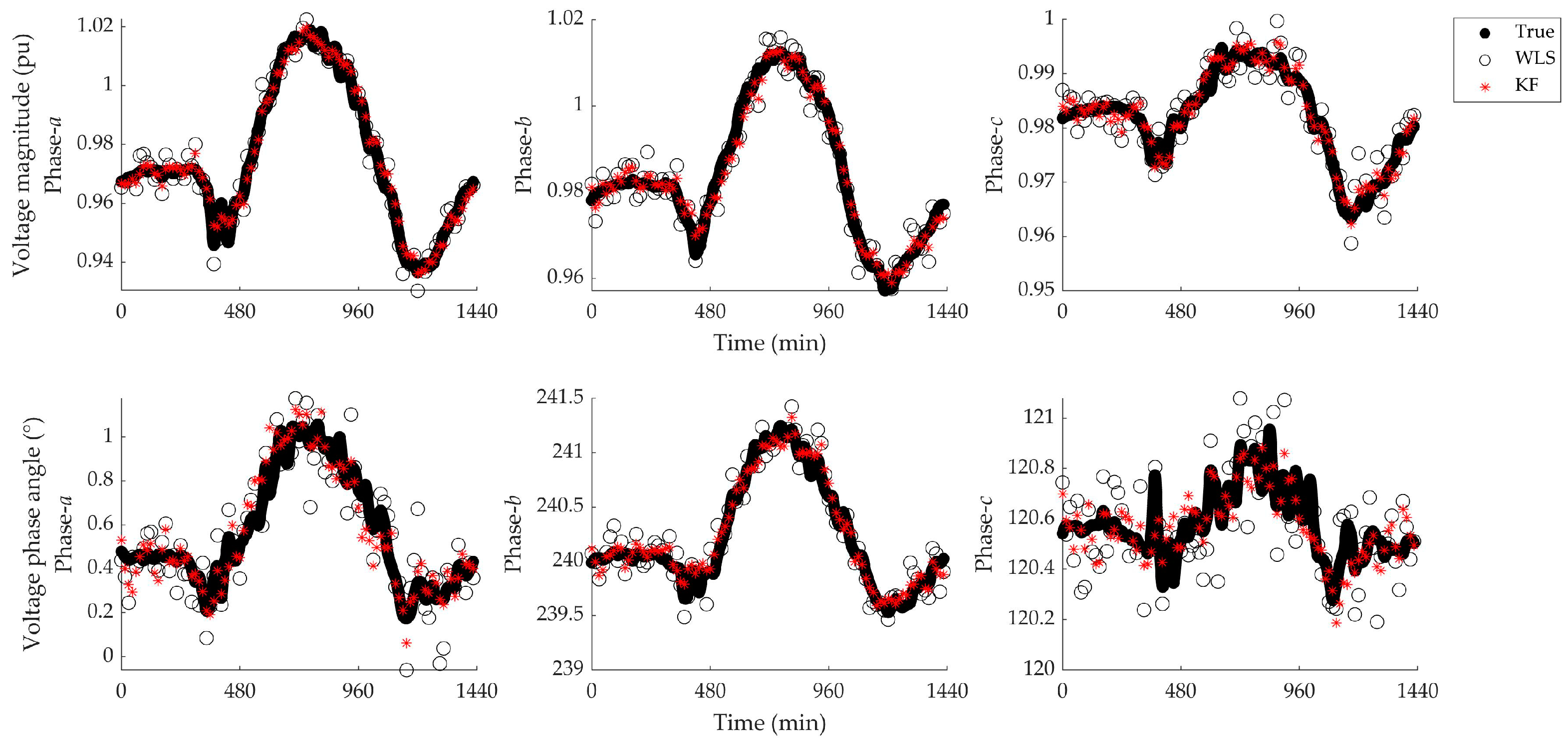
4. Test Results
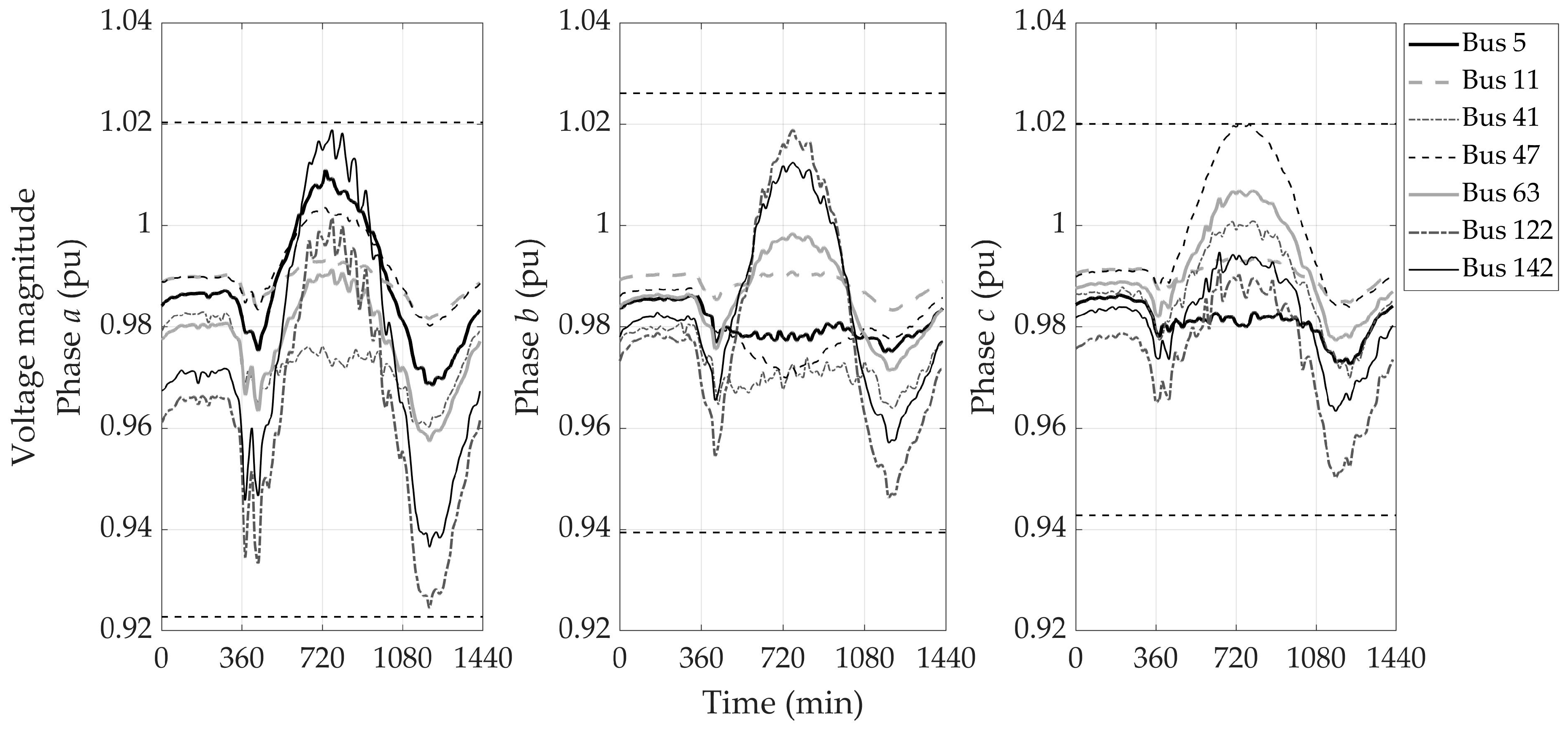
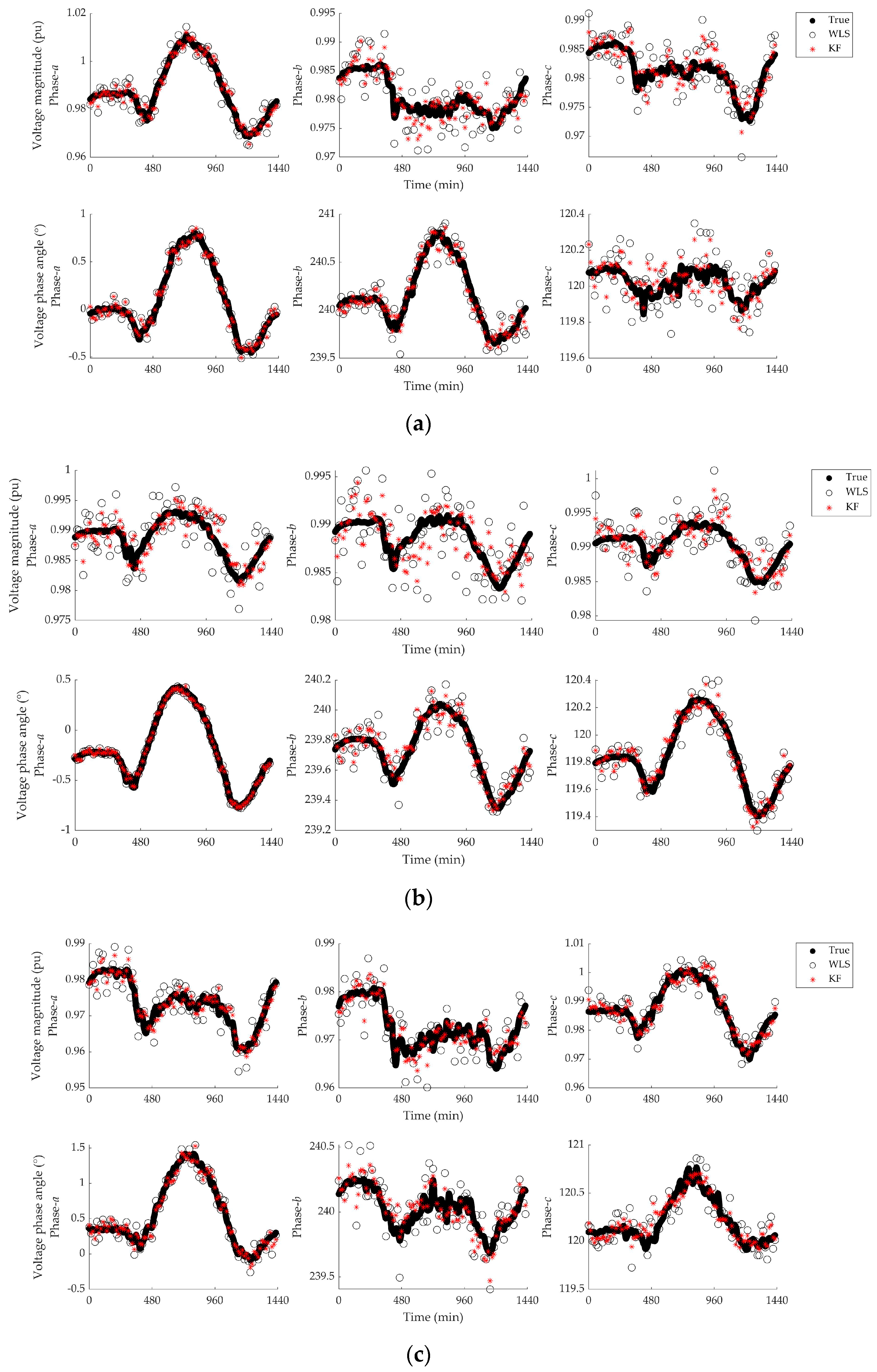
4.1. Base Case
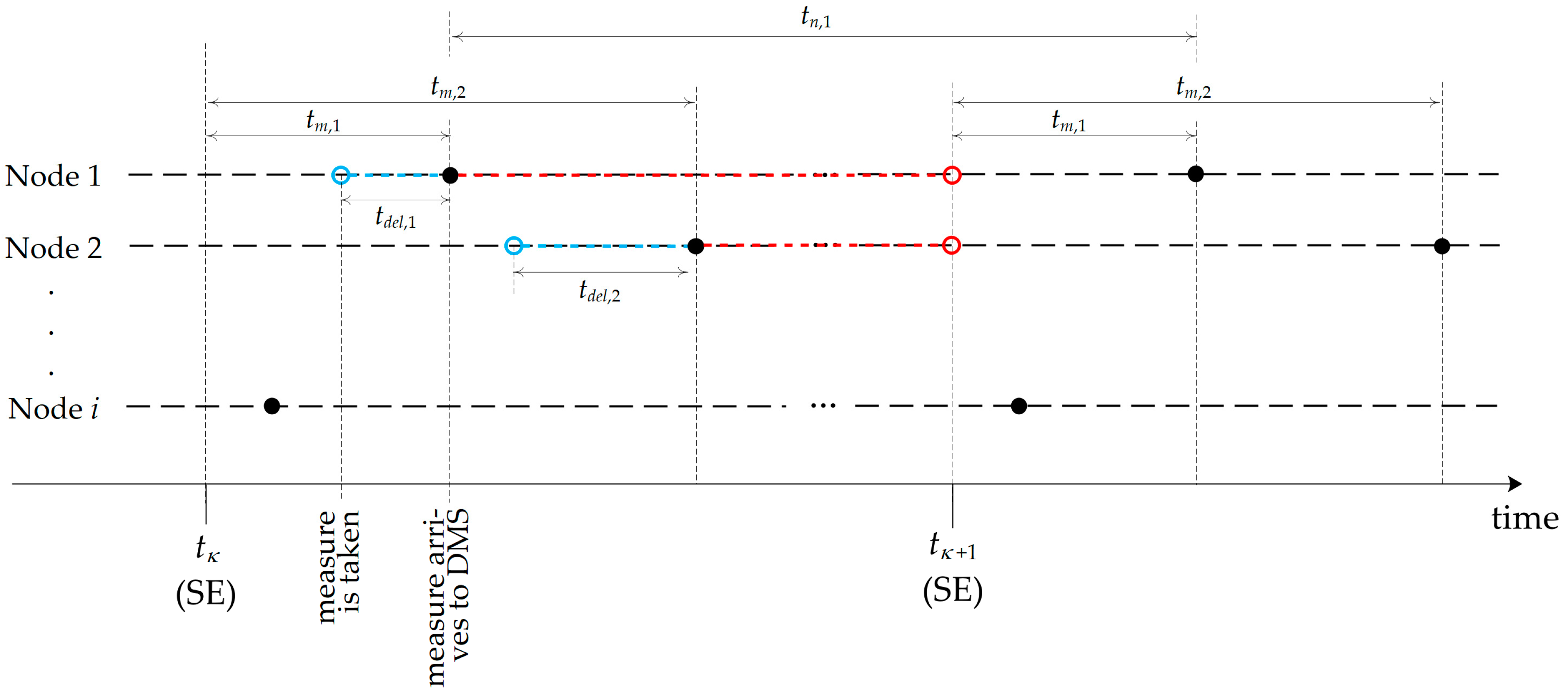
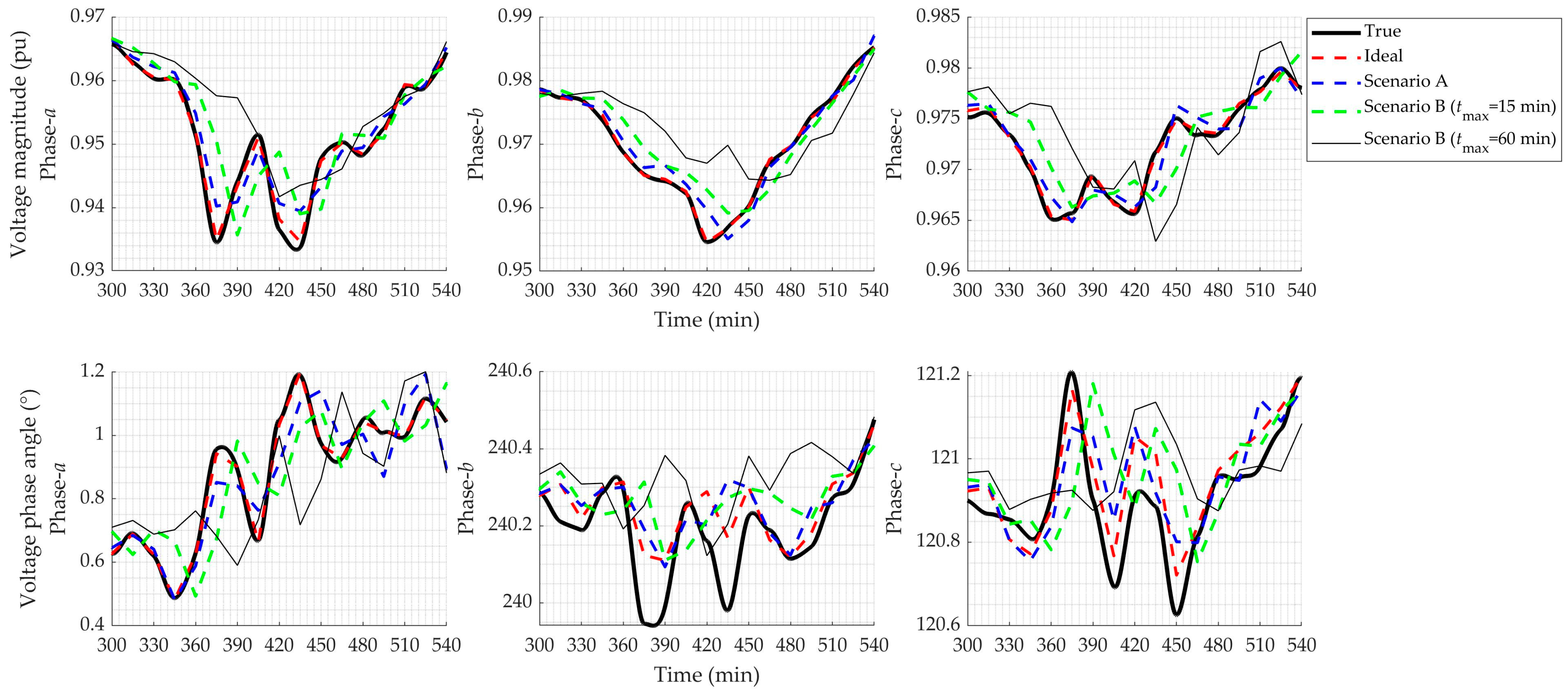
4.2. Influence of Measurement Nonsynchronicity and Time Delays
5. Conclusions and Future Development
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Nomenclature
| Acronyms | |
| DKF | Discrete Kalman filter |
| DMS | Distribution management system |
| DSO | Distribution system operator |
| EKF | Extended Kalman filter |
| IKF | Iterated Kalman filter |
| KF | Kalman filter |
| LV | Low voltage |
| MV | Medium voltage |
| PMU | Phasor measurement unit |
| PV | Photovoltaic |
| SE | State estimation |
| SM | Smart meter |
| WLS | Weighted least squares |
| List of variables 1 | |
| N | Number of nodes |
| A | Branch–bus incidence matrix |
| p1, p2, p3, p | Number of single-phase, two-phase, and three-phase buses, and total number of buses |
| br1, br2, br3, br | Number of single-phase, two-phase, and three-phase branches, and total number of branches |
| n | Number of state variables |
| m1, m2, m3, m | Number of single-phase, two-phase, and three-phase measurements, and total number of measurements |
| x, x | State variables |
| Estimated state | |
| h(x) | Relation between measurements and state variables |
| H | Measurement Jacobian matrix |
| e, e | Measurement noise (error) |
| σ | Measurement standard deviation |
| R | Measurement noise covariance matrix |
| y, Y, Y, Yp | Admittance, admittance matrix element, admittance matrix, and primitive admittance matrix |
| δ, V | Phase angle and magnitude of the voltage phasor |
| z, z | Measurements |
| w, W | Weights of the measurement errors |
| f | Objective function |
| v | Weighted least squares iteration index |
| i | Iterated Kalman filter iteration index |
| G | Gain matrix |
| ν, ν | Process noise |
| q, Q | Process noise covariance elements and matrix |
| φ, Ф | State-transition function and matrix |
| κ | Time instant index |
| S | Innovation covariance matrix |
| K | Kalman gain |
| Pκ|κ, Pκ|κ−1 | Estimation and prediction error covariance matrices at κ-instant |
| aad | Average absolute deviation |
| 1 Bold letters represent either vectors or matrices. | |
References
- Vaahedi, E. Practical Power System Operation; El-Hawary, M., Ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2014; ISBN 9781118915110. [Google Scholar]
- Primadianto, A.; Lu, C.N. A Review on Distribution System State Estimation. IEEE Trans. Power Syst. 2017, 32, 3875–3883. [Google Scholar] [CrossRef]
- Abur, A.; Expósito, A.G. Power System State Estimation: Theory and Implementation; CRC Press: Boca Raton, FL, USA, 2004; ISBN 0203913671. [Google Scholar]
- Zhao, J.; Gómez-Expósito, A.; Netto, M.; Mili, L.; Abur, A.; Terzija, V.; Kamwa, I.; Pal, B.; Singh, A.K.; Qi, J.; et al. Power System Dynamic State Estimation: Motivations, Definitions, Methodologies, and Future Work. IEEE Trans. Power Syst. 2019, 34, 3188–3198. [Google Scholar] [CrossRef]
- Zanni, L. Power-System State Estimation Based on PMUs: Static and Dynamic Approaches—From Theory to Real Implementation; École Polytechnique Fédérale de Lausanne: Lausanne, Switzerland, 2017. [Google Scholar]
- Blood, E.A.; Krogh, B.H.; Ilić, M.D. Electric power system static state estimation through Kalman filtering and load forecasting. In Proceedings of the IEEE Power and Energy Society 2008 General Meeting: Conversion and Delivery of Electrical Energy in the 21st Century, PES, Pittsburgh, PA, USA, 20–24 July 2008. [Google Scholar]
- Sarri, S.; Paolone, M.; Cherkaoui, R.; Borghetti, A.; Napolitano, F.; Nucci, C.A. State estimation of Active Distribution Networks: Comparison between WLS and iterated kalman-filter algorithm integrating PMUs. In Proceedings of the 3rd IEEE PES Innovative Smart Grid Technologies Conference Europe, Berlin, Germany, 14–17 October 2012. [Google Scholar]
- Sarri, S.; Zanni, L.; Popovic, M.; Le Boudec, J.Y.; Paolone, M. Performance Assessment of Linear State Estimators Using Synchrophasor Measurements. IEEE Trans. Instrum. Meas. 2016, 65, 535–548. [Google Scholar] [CrossRef]
- Brüggemann, A.; Görner, K.; Rehtanz, C. Evaluation of extended Kalman filter and particle filter approaches for quasi-dynamic distribution system state estimation. CIRED Open Access Proc. J. 2017, 1, 1755–1758. [Google Scholar] [CrossRef][Green Version]
- Valverde, G.; Terzija, V. Unscented Kalman filter for power system dynamic state estimation. IET Gener. Transm. Distrib. 2011, 5, 29–37. [Google Scholar] [CrossRef]
- Zhou, N.; Huang, Z.; Li, Y.; Welch, G. Local sequential ensemble Kalman filter for simultaneously tracking states and parameters. In Proceedings of the 2012 North American Power Symposium, NAPS 2012, Champaign, IL, USA, 9–11 September 2012. [Google Scholar]
- Dehghanpour, K.; Wang, Z.; Wang, J.; Yuan, Y.; Bu, F. A Survey on State Estimation Techniques and Challenges in Smart Distribution Systems. IEEE Trans. Smart Grid 2019, 10, 2312–2322. [Google Scholar] [CrossRef]
- Ahmad, F.; Rasool, A.; Ozsoy, E.; Sekar, R.; Sabanovic, A.; Elitaş, M. Distribution system state estimation-A step towards smart grid. Renew. Sustain. Energy Rev. 2018, 81, 2659–2671. [Google Scholar] [CrossRef]
- Durgaprasad, G.; Thakur, S.S. Robust dynamic state estimation of power systems based on M-Estimation and realistic modeling of system dynamics. IEEE Trans. Power Syst. 1998, 13, 1331–1336. [Google Scholar] [CrossRef]
- Mestav, K.R.; Luengo-Rozas, J.; Tong, L. Bayesian State Estimation for Unobservable Distribution Systems via Deep Learning. IEEE Trans. Power Syst. 2019, 34, 4910–4920. [Google Scholar] [CrossRef]
- Zamzam, A.S.; Sidiropoulos, N.D. Physics-Aware Neural Networks for Distribution System State Estimation. IEEE Trans. Power Syst. 2020, 35, 4347–4356. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, G.; Giannakis, G.B. Real-Time Power System State Estimation and Forecasting via Deep Unrolled Neural Networks. IEEE Trans. Signal Process. 2019, 67, 4069–4077. [Google Scholar] [CrossRef]
- Gahrooei, Y.R.; Khodabakhshian, A.; Hooshmand, R.-A. A New Pseudo Load Profile Determination Approach in Low Voltage Distribution Networks. IEEE Trans. Power Syst. 2018, 33, 463–472. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, Y.; Dinavahi, V. Robust Forecasting-Aided State Estimation for Power System Against Uncertainties. IEEE Trans. Power Syst. 2020, 35, 691–702. [Google Scholar] [CrossRef]
- Kong, X.; Zhang, X.; Zhang, X.; Wang, C.; Chiang, H.-D.; Li, P. Adaptive Dynamic State Estimation of Distribution Network Based on Interacting Multiple Model. IEEE Trans. Sustain. Energy 2021, 1. [Google Scholar] [CrossRef]
- Zhao, J.; Netto, M.; Mili, L. A Robust Iterated Extended Kalman Filter for Power System Dynamic State Estimation. IEEE Trans. Power Syst. 2017, 32, 3205–3216. [Google Scholar] [CrossRef]
- Mohammed, I.; Geetha, S.J.; Shinde, S.S.; Rajawat, K.; Chakrabarti, S. Modified Re-Iterated Kalman Filter for Handling Delayed and Lost Measurements in Power System State Estimation. IEEE Sens. J. 2020, 20, 3946–3955. [Google Scholar] [CrossRef]
- Paolone, M.; Le Boudec, J.-Y.; Sarri, S.; Zanni, L. Static and recursive PMU-based state estimation processes for transmission and distribution power grids. In Advances in Power System Modelling, Control and Stability Analysis; Milano, F., Ed.; The Institution of Engineering and Technology: London, UK, 2016; ISBN 978-1-78561-001-1. [Google Scholar]
- Alimardani, A.; Therrien, F.; Atanackovic, D.; Jatskevich, J.; Vaahedi, E. Distribution System State Estimation Based on Nonsynchronized Smart Meters. IEEE Trans. Smart Grid 2015, 6, 2919–2928. [Google Scholar] [CrossRef]
- Nainar, K.; Iov, F. Smart meter measurement-based state estimation for monitoring of low-voltage distribution grids. Energies 2020, 13, 5367. [Google Scholar] [CrossRef]
- Bessone, E.; Bianchi, S.; Massucco, S.; Nucci, C.A.; Pentolini, M.; Raco, F. The PODCAST project–optimizing distribution networks with renewable energy sources. In Proceedings of the 2018 AEIT International Annual Conference, Bari, Italy, 3–5 October 2018; pp. 1–6. [Google Scholar]
- Zhu, J.; Abur, A. Effect of Phasor Measurements on the Choice of Reference Bus for State Estimation. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–5. [Google Scholar]
- Wang, S.; Zhao, J.; Huang, Z.; Diao, R. Assessing Gaussian assumption of PMU measurement error using field data. IEEE Trans. Power Deliv. 2018, 33, 3233–3236. [Google Scholar] [CrossRef]
- Sorenson, H.W. Least-Squares Estimation. From Gauss To Kalman. IEEE Spectr. 1970, 7, 63–68. [Google Scholar] [CrossRef]
- Gelb, A.; Kasper, J.F.; Nash, R.A.; Price, C.F.; Sutherland, A.A. Applied Optimal Estimation; Gelb, A., Ed.; The MIT Press: Cambridge, MA, USA; London, UK, 1974; ISBN 0-262-20027-9. [Google Scholar]
- Arrillaga, J.; Arnold, C.P. Computer Analysis of Power Systems; John Wiley & Sons Ltd.: Christchurch, New Zealand, 1990; ISBN 0-471-92760-0. [Google Scholar]
- Debs, A.S.; Larson, R.E. A Dynamic Estimator for Tracking the State of a Power System. IEEE Trans. Power Appar. Syst. 1970, PAS-89, 1670–1678. [Google Scholar] [CrossRef]
- Zanni, L.; Sarri, S.; Pignati, M.; Cherkaoui, R.; Paolone, M. Probabilistic assessment of the process-noise covariance matrix of discrete Kalman filter state estimation of active distribution networks. In Proceedings of the 13th International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), Durham, UK, 7–10 July 2014. [Google Scholar]
- Kemal, M.; Sanchez, R.; Olsen, R.; Iov, F.; Schwefel, H.P. On the trade-off between timeliness and accuracy for low voltage distribution system grid monitoring utilizing smart meter data. Int. J. Electr. Power Energy Syst. 2020, 121, 106090. [Google Scholar] [CrossRef]

| Standard Deviations | |
|---|---|
| Voltage magnitude—σE | 0.653 V (0.2% of Emax) |
| Voltage phase angle—σδ | 1 mrad |
| Power—σS | 40 W (0.2% of 20 kW) |
| WLS-SE | KF-SE | ||||
|---|---|---|---|---|---|
| qi = 1 × 10−6 | qi = 1 × 10−5 | qi = 1 × 10−4 | qmag = 6.5 × 10−4 qang = 3.0 × 10−5 (Optimized) | ||
| aad (magnitude) | 2.68 × 10−3 | 7.50 × 10−3 | 5.66 × 10−3 | 2.74 × 10−3 | 1.92 × 10−3 (−28.4%) |
| aad (phase angle) | 0.095 | 0.108 | 0.077 | 0.077 | 0.070 (−25.9%) |
| WLS-SE | ||||
|---|---|---|---|---|
| Ideal | Asynchronous (Scenario A) | Asynchronous (Scenario B) | ||
| aad (magnitude) | 2.68 × 10−3 | 2.73 × 10−3 (+2.0%) | tmax = 15 min | tmax = 60 min |
| 3.08 × 10−3 (+14.8%) | 3.43 × 10−3 (+27.8%) | |||
| aad (phase angle) | 0.095 | 0.098 (+3.4%) | tmax = 15 min | tmax = 60 min |
| 0.107 (+13.1%) | 0.117 (+23.7%) | |||
| KF-SE | ||||
| Ideal | Asynchronous (Scenario A) | Asynchronous (Scenario B) | ||
| aad (magnitude) | 1.92 × 10−3 | 2.10 × 10−3 (+9.4%) | tmax = 15 min | tmax = 60 min |
| 2.39 × 10−3 (+24.4%) | 2.94 × 10−3 (+53.1%) | |||
| aad (phase angle) | 0.070 | 0.073 (+3.8%) | tmax = 15 min | tmax = 60 min |
| 0.078 (+11.1%) | 0.085 (+21.2%) | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Napolitano, F.; Rios Penaloza, J.D.; Tossani, F.; Borghetti, A.; Nucci, C.A. Three-Phase State Estimation of a Low-Voltage Distribution Network with Kalman Filter. Energies 2021, 14, 7421. https://doi.org/10.3390/en14217421
Napolitano F, Rios Penaloza JD, Tossani F, Borghetti A, Nucci CA. Three-Phase State Estimation of a Low-Voltage Distribution Network with Kalman Filter. Energies. 2021; 14(21):7421. https://doi.org/10.3390/en14217421
Chicago/Turabian StyleNapolitano, Fabio, Juan Diego Rios Penaloza, Fabio Tossani, Alberto Borghetti, and Carlo Alberto Nucci. 2021. "Three-Phase State Estimation of a Low-Voltage Distribution Network with Kalman Filter" Energies 14, no. 21: 7421. https://doi.org/10.3390/en14217421
APA StyleNapolitano, F., Rios Penaloza, J. D., Tossani, F., Borghetti, A., & Nucci, C. A. (2021). Three-Phase State Estimation of a Low-Voltage Distribution Network with Kalman Filter. Energies, 14(21), 7421. https://doi.org/10.3390/en14217421







