Reconfiguration Strategy for DC Distribution Network Fault Recovery Based on Hybrid Particle Swarm Optimization
Abstract
:1. Introduction
- (1)
- Considering the topological characteristics of DC distribution, the network structure is equivalently simplified to improve the search efficiency in the DNR process;
- (2)
- An adaptive coding strategy is designed to make the generated solutions satisfy the topological constraints. This strategy can improve the evolution efficiency of particles in the particle search process without judging infeasible solutions;
- (3)
- To avoid the algorithm from falling into premature, the idea of Lévy flight (LF) is introduced to improve the global search ability and convergence speed of the particles.
2. Modeling of DC Distribution Network Restoration Reconfiguration
2.1. Mathematical Model of Converters
2.2. The Calculation of Power Flow in Medium Voltage DC Distribution Network
2.3. Mathematical Model for Recovery Reconfiguration
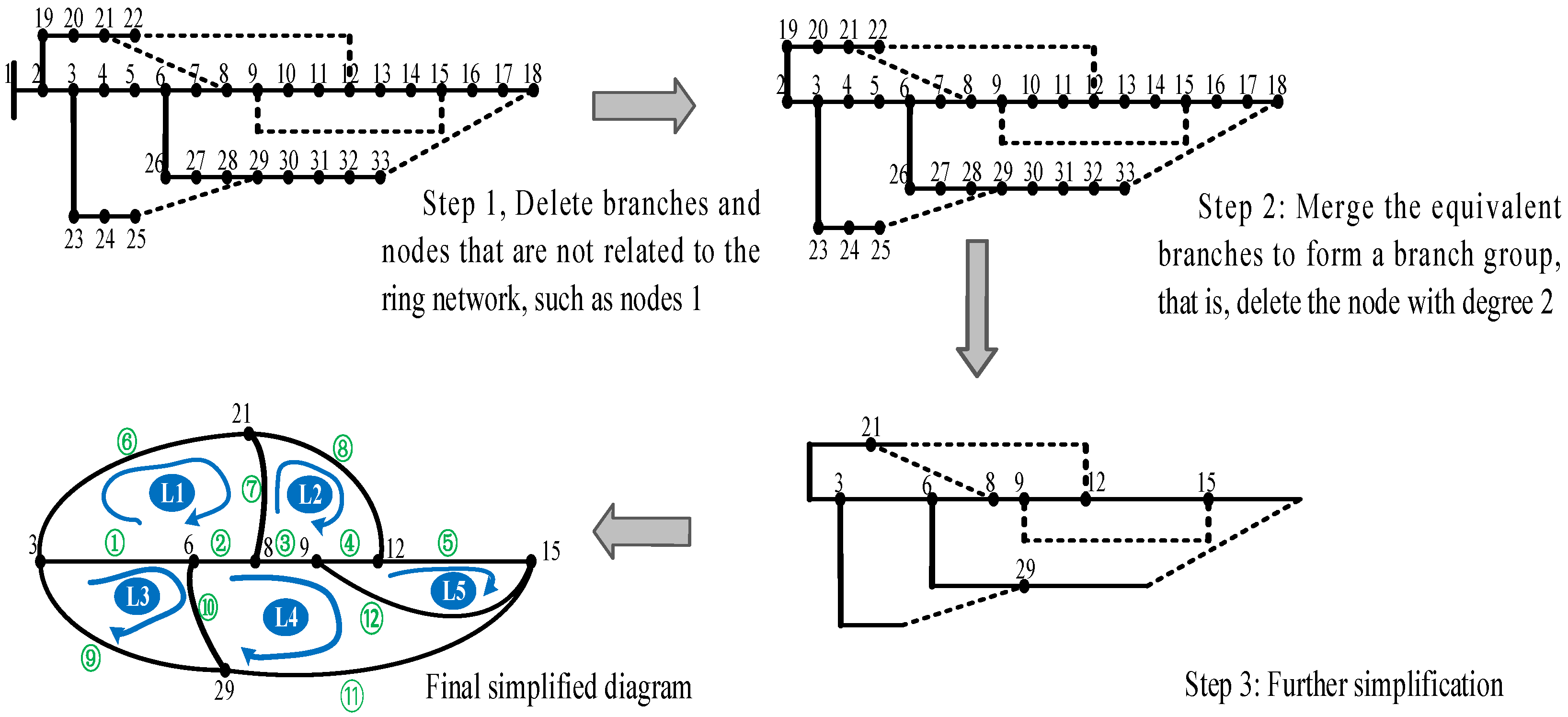
3. Simplification and Coding of Power Distribution Networks
3.1. Simplification of Power Distribution Networks
- (1)
- Some branches that already exist in radial branches need to be ignored. For example, the branch between node 1 and node 2, which is involved in splitting, will form an island that does not satisfy the radial constraint. Therefore, the first step should be to eliminate the branches that are not related to the ring network first;
- (2)
- Branches that have the same effect need to be disconnected. For example, disconnecting any two branches between node 3 and node 6 will have the same effect for disconnected loops, although the tide of the system will change accordingly. Therefore, in the second step, the concept of degree in graph theory is introduced to eliminate the nodes with 2°. The remaining equivalent branches are merged to form a set of branches with the two end nodes as branches.
3.2. Coding Method
4. HPSO Algorithm
4.1. Branched Group Selection Optimization Based on Adaptive BPSO
| Algorithm 1: Adaptive coding algorithm. | |
| Input: loop branch group and nodal branch incidence matrix | |
| Output: | |
| 1 | Initialization: ; is the sigmoid parameter of BPSO; |
| 2 | whiledo |
| 3 | while do |
| 4 | Pick a random value r uniformly from |
| 5 | Set ; |
| 6 | while do |
| 7 | Set ; |
| 8 | end |
| 9 | if then |
| 10 | ; |
| 11 | else |
| 12 | go to step 6; |
| 13 | end |
| 14 | Update ; |
| 15 | Set |
| 16 | end |
| 17 | Derive ; |
| 18 | end |
4.2. LF-Based Improved DPSO for Intra-Group Optimization
- (1)
- If the particle i being optimized is set to 0, it means that the branch group in this dimension has no previously selected branches. Therefore, the individual and global extremes have no guiding effect on this particle and the velocity of this particle does not change in this dimension and retains the last value, see the first case of (19). However, since this iteration needs to find the internal optimization of the branching group, the position of this dimension should be determined by randomly selecting a branching path, see the first case of (20);
- (2)
- If the value of the optimized particle is not set to 0, it is further divided into the following cases:
- ①
- If the individual extreme value and global extreme value velocity is 0, it cannot affect the particle velocity in this dimension. There is no guidance for non 0 particles, the velocity does not change, the position from the branch group randomly chooses a path, see the second case of (19) and (20);
- ②
- If the individual extreme and the global extreme are all non 0, both are guided at this time, and can be updated according to the particle iteration formula after joining the LF, see the third case of (19) and (20);
- ③
- If one of the individual and one of the global poles is 0 and one is not 0, the poles in the 0 state cannot be guided, and the poles in the non 0 state are guided to the velocity. The corresponding item is changed to a random value from the velocity space, LF is added to enhance the particle search ability, see the fourth and fifth cases of (19) and the 3rd case of (20).
5. Case Study
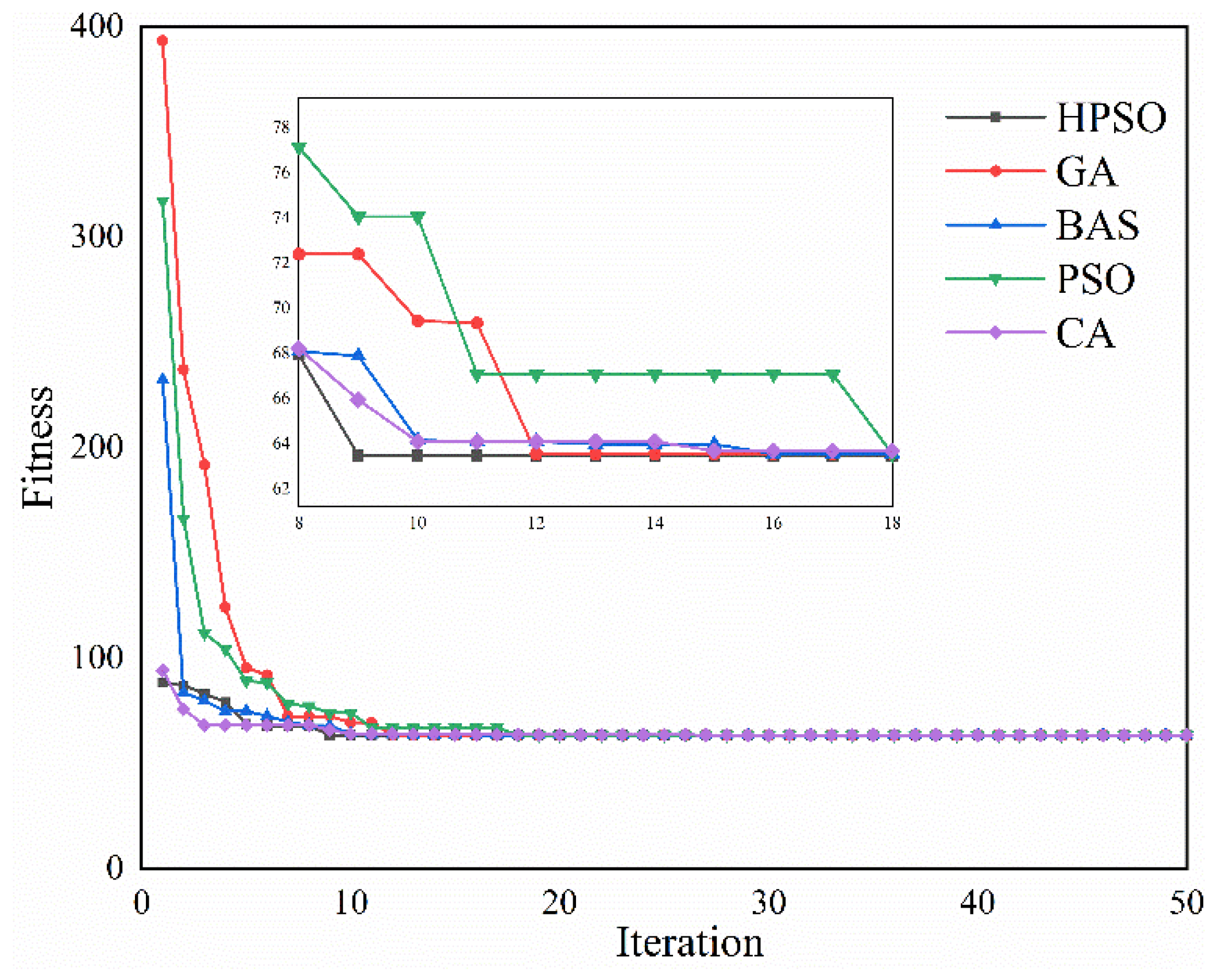
5.1. Comparison of Differen Metaheuristic t Algorithms
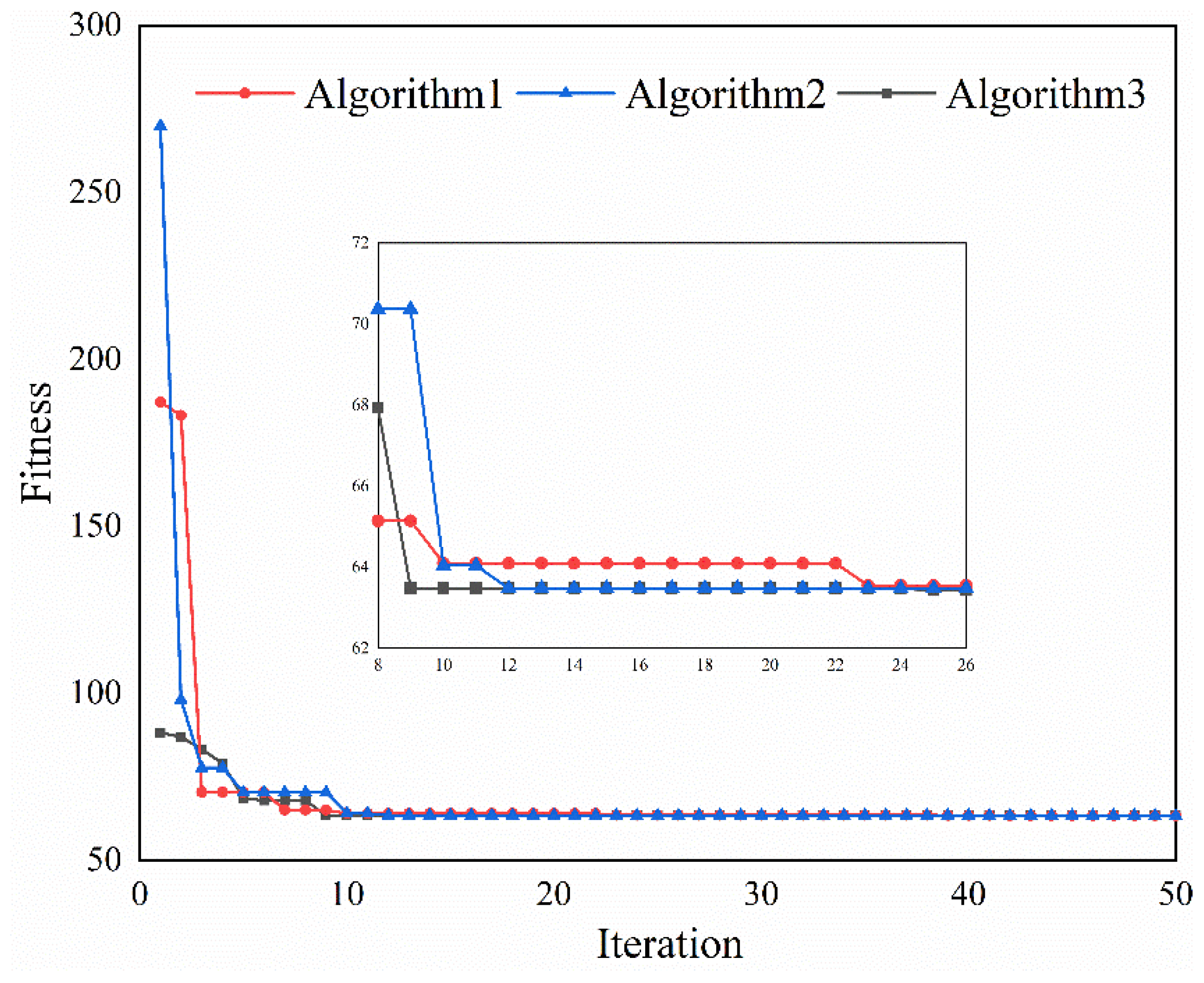
5.2. Comparison of Different Algorithms
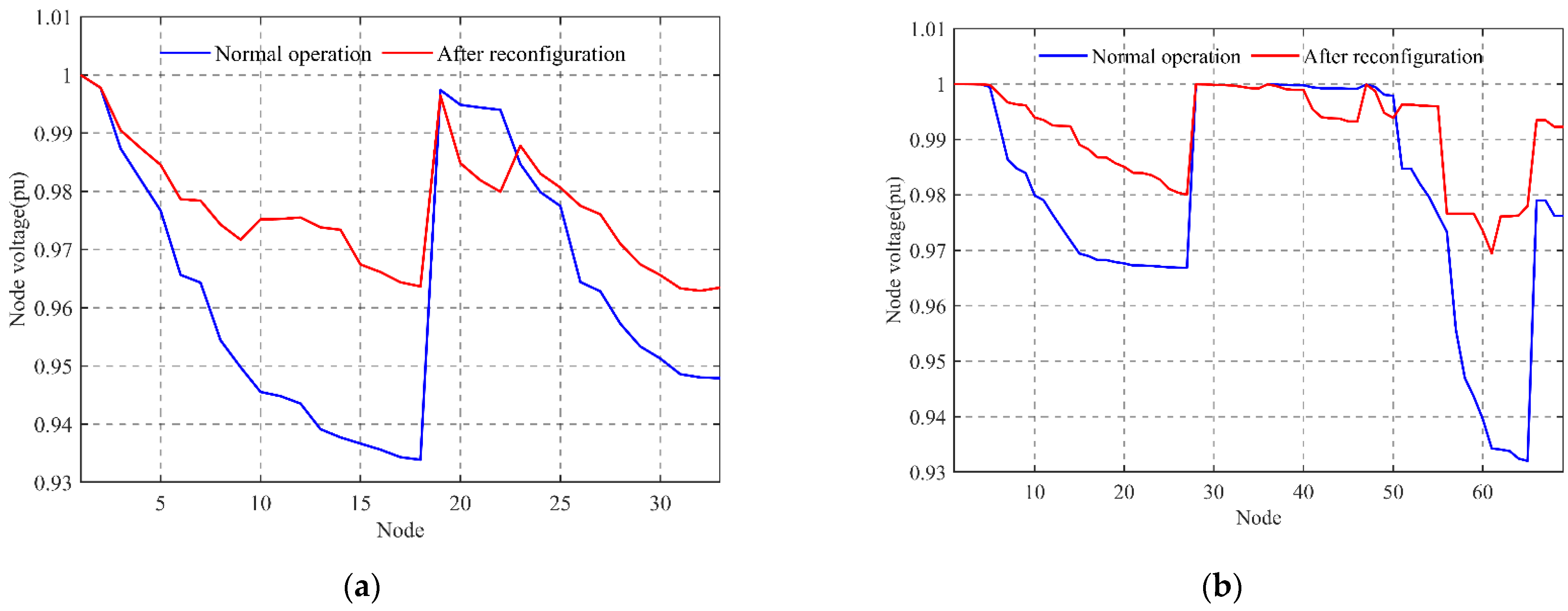
5.3. Validity Analysis of Conclusions
6. Conclusions
- (1)
- The improved BPSO based on the adaptive solution strategy can remove the judgment process of infeasible solutions and improve the efficiency of population evolution;
- (2)
- The improved DPSO based on LF idea can avoid the population from getting into local optimum, and find the global optimal solution faster;
- (3)
- The equivalent simplification of the distribution network reduces the problem dimension, and the special coding can further improve the computational efficiency.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AC | Alternating current |
| AI | Artificial intelligence |
| BPSO | Binary particle swarm algorithm |
| BAS | Beetle Antennae search |
| CA | Cuckoo algorithm |
| CSC | Current source converter |
| DPSO | Discrete particle swarm algorithm |
| DNR | Distribution network reconfiguration |
| DC | Direct current |
| GA | Genetic algorithm |
| HPSO | Hybrid particle swarm algorithm |
| LF | Lévy flight |
| MILP | Mixed-integer linear programming |
| PSO | Particle swarm algorithm |
| SFS | Stochastic fractal search |
| VSC | Voltage source converter |
| Nomenclature | |
| A. Mathematical model of converters | |
| Ps, Qs | Active power and reactive power on the AC bus |
| Pc, Qc | Active power and reactive power on the AC side |
| Pdc, Qdc | Active power and reactive power on the DC side |
| Us, δs | Voltage amplitude and phase angle of the AC bus |
| Uc, δc | Voltage amplitude and phase angle of the AC side |
| Internal losses of the converter | |
| a, b, c | The respective coefficients of the fitted quadratic functions for converter current and active losses |
| SN, | The rated capacity of the converter and the rated voltage of the DC side |
| SB, | Reference capacity and the reference voltage |
| I, G, U | Nodal current matrix, nodal conductance matrix, nodal voltage matrix |
| kj | Operation status |
| A, i | Node-branch correlation matrix and current vector |
| Ui,max, Ui,min | Upper and lower voltage |
| Ii,max | Upper current |
| B. HPSO algorithm | |
| Pid, Pgd | Global optimal solution and individual optimal solution |
| vid, xid | Particle speed and particle position |
| c1, c2 | Inertial System of Evolutionary Algorithm |
| α | Step control quantity |
| s | Step size |
| Gaussian normal distribution | |
| Standard normal distribution | |
| C. Other Symbols | |
| Lévy (·) | The random search path |
| Point-to-point multiplication | |
| rand (·) | Random rounding method |
| round (·) | Rounding to the nearest integer |
| r (·) | Random value |
| Sigmoid (·) | Sigmoid function |
References
- Li, J.; Li, D.; Zheng, Y.; Yao, Y.; Tang, Y. Unified Modeling of Regionally Integrated Energy System and Application to Optimization. Int. J. Electr. Power Energy Syst. 2022, 134, 107377. [Google Scholar] [CrossRef]
- Kumar, Y.; Das, B.; Sharma, J. Multiobjective, Multiconstraint Service Restoration of Electric Power Distribution System with Priority Customers. IEEE Trans. Power Deliv. 2008, 23, 261–270. [Google Scholar] [CrossRef]
- Chen, T.-H.; Huang, W.-T.; Gu, J.-C.; Pu, G.-C.; Hsu, Y.-F.; Guo, T.-Y. Feasibility Study of Upgrading Primary Feeders from Radial and Open-Loop to Normally Closed-Loop Arrangement. IEEE Trans. Power Syst. 2004, 19, 1308–1316. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; He, L.; Liu, F.; Li, C.; Cao, Y.; Shahidehpour, M. Flexible Voltage Control Strategy Considering Distributed Energy Storages for DC Distribution Network. IEEE Trans. Smart Grid 2019, 10, 163–172. [Google Scholar] [CrossRef]
- Ma, J.; Zhu, M.; Cai, X.; Li, Y.W. DC Substation for DC Grid—Part I: Comparative Evaluation of DC Substation Configurations. IEEE Trans. Power Electron. 2019, 34, 9719–9731. [Google Scholar] [CrossRef]
- Li, X.; Zhu, M.; Li, Y.; Cai, X. Cascaded MVDC Integration Interface for Multiple DERs with Enhanced Wide-Range Operation Capability: Concepts and Small-Signal Analysis. IEEE Trans. Power Electron. 2020, 35, 1182–1188. [Google Scholar] [CrossRef]
- Debnath, S.; Qin, J.; Bahrani, B.; Saeedifard, M.; Barbosa, P. Operation, Control, and Applications of the Modular Multilevel Converter: A Review. IEEE Trans. Power Electron. 2015, 30, 37–53. [Google Scholar] [CrossRef]
- Romero, R.; Franco, J.F.; Leão, F.B.; Rider, M.J.; de Souza, E.S. A New Mathematical Model for the Restoration Problem in Balanced Radial Distribution Systems. IEEE Trans. Power Syst. 2016, 31, 1259–1268. [Google Scholar] [CrossRef] [Green Version]
- Khushalani, S.; Solanki, J.M.; Schulz, N.N. Development of Three-Phase Unbalanced Power Flow Using PV and PQ Models for Distributed Generation and Study of the Impact of DG Models. IEEE Trans. Power Syst. 2007, 22, 1019–1025. [Google Scholar] [CrossRef]
- Baran, M.E.; Wu, F.F. Optimal Capacitor Placement on Radial Distribution Systems. IEEE Trans. Power Deliv. 1989, 4, 725–734. [Google Scholar] [CrossRef]
- Shirmohammadi, D.; Hong, H.W. Reconfiguration of Electric Distribution Networks for Resistive Line Losses Reduction. IEEE Trans. Power Deliv. 1989, 4, 1492–1498. [Google Scholar] [CrossRef]
- Helmi, A.M.; Carli, R.; Dotoli, M.; Ramadan, H.S. Efficient and Sustainable Reconfiguration of Distribution Networks via Metaheuristic Optimization. IEEE Trans. Autom. Sci. Eng. 2021, 1–17. [Google Scholar] [CrossRef]
- Muhammad, M.A.; Mokhlis, H.; Naidu, K.; Amin, A.; Franco, J.F.; Othman, M. Distribution Network Planning Enhancement via Network Reconfiguration and DG Integration Using Dataset Approach and Water Cycle Algorithm. J. Mod. Power Syst. Clean Energy 2020, 8, 86–93. [Google Scholar] [CrossRef]
- Tran, T.T.; Truong, K.H.; Vo, D.N. Stochastic Fractal Search Algorithm for Reconfiguration of Distribution Networks with Distributed Generations. Ain Shams Eng. J. 2020, 11, 389–407. [Google Scholar] [CrossRef]
- Song, C.; Luo, Q.; Shi, F. Genetic Algorithms for Optimization of Complex Nonlinear System. In Proceedings of the 2008 International Conference on Computer Science and Software Engineering, Wuhan, China, 12–14 December 2008; Volume 1, pp. 378–381. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95–International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Wang, J.; Chen, H. BSAS: Beetle Swarm Antennae Search Algorithm for Optimization Problems. arXiv 2018, arXiv:1807.10470. [Google Scholar]
- Rajabioun, R. Cuckoo Optimization Algorithm. Appl. Soft Comput. 2011, 11, 5508–5518. [Google Scholar] [CrossRef]
- Gao, S.; Gao, Y.; Zhang, Y.; Li, T. Adaptive Cuckoo Algorithm with Multiple Search Strategies. Appl. Soft Comput. 2021, 106, 107181. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Nguyen, T.T. An Improved Cuckoo Search Algorithm for the Problem of Electric Distribution Network Reconfiguration. Appl. Soft Comput. 2019, 84, 105720. [Google Scholar] [CrossRef]
- Souza, E.S.; Romero, R.; Franco, J.F. Restoration of Electrical Distribution Systems Using a Relaxed Mathematical Model. J. Control. Autom. Electr. Syst. 2018, 29, 259–269. [Google Scholar] [CrossRef] [Green Version]
- Scarabaggio, P.; Grammatico, S.; Carli, R.; Dotoli, M. Distributed Demand Side Management with Stochastic Wind Power Forecasting. IEEE Trans. Control. Syst. Technol. 2021, 1–16. [Google Scholar] [CrossRef]
- Raposo, A.A.M.; Rodrigues, A.B.; da Guia da Silva, M. Robust Meter Placement for State Estimation Considering Distribution Network Reconfiguration for Annual Energy Loss Reduction. Electr. Power Syst. Res. 2020, 182, 106233. [Google Scholar] [CrossRef]
- Li, Y.; Xiao, J.; Chen, C.; Tan, Y.; Cao, Y. Service Restoration Model with Mixed-Integer Second-Order Cone Programming for Distribution Network with Distributed Generations. IEEE Trans. Smart Grid 2019, 10, 4138–4150. [Google Scholar] [CrossRef]
- De Oliveira, L.W.; Seta, F.D.S.; de Oliveira, E.J. Optimal Reconfiguration of Distribution Systems with Representation of Uncertainties through Interval Analysis. Int. J. Electr. Power Energy Syst. 2016, 83, 382–391. [Google Scholar] [CrossRef]
- Fathabadi, H. Power Distribution Network Reconfiguration for Power Loss Minimization Using Novel Dynamic Fuzzy C-Means (DFCM) Clustering Based ANN Approach. Int. J. Electr. Power Energy Syst. 2016, 78, 96–107. [Google Scholar] [CrossRef]
- De Macedo Braz, H.D.; de Souza, B.A. Distribution Network Reconfiguration Using Genetic Algorithms with Sequential Encoding: Subtractive and Additive Approaches. IEEE Trans. Power Syst. 2011, 26, 582–593. [Google Scholar] [CrossRef]
- Whitley, D. A Genetic Algorithm Tutorial. Stat. Comput. 1994, 4, 65–85. [Google Scholar] [CrossRef]

| Algorithm | Parameter Value |
|---|---|
| PSO | |
| CA | |
| GA | |
| BAS | |
| HPSO |
| Cases | Item | PSO [16] | CA [18] | GA [28] | BAS [17] | HPSO |
|---|---|---|---|---|---|---|
| Modified IEEE 33-node | Average of all solutions/kW | 89.6352 | 90.6112 | 89.4715 | 89.3116 | 88.8219 |
| Average running time/s | 8.2731 | 11.1605 | 13.1567 | 8.9731 | 8.0690 | |
| Number of successes | 39 | 32 | 41 | 45 | 49 | |
| Modified IEEE 69-node | Average of all solutions/kW | 65.3672 | 68.0190 | 64.1037 | 65.4786 | 63.4467 |
| Average running time/s | 11.6358 | 14.7432 | 18.7623 | 12.4552 | 10.9651 | |
| Number of successes | 32 | 25 | 34 | 31 | 38 |
| Cases | Item | IBPSO | IDPSO | HPSO |
|---|---|---|---|---|
| Modified IEEE 33-node | Average of all solutions/kW | 91.5374 | 89.5214 | 88.8219 |
| Average running time/s | 6.7528 | 9.3566 | 8.0690 | |
| Number of successes | 41 | 47 | 49 | |
| Modified IEEE 69-node | Average of all solutions/kW | 65.0637 | 63.8612 | 63.4467 |
| Average running time/s | 9.3746 | 13.8473 | 10.9651 | |
| Number of successes | 27 | 39 | 38 |
| Cases | Item | Closed Switch | Network Loss/kW | Minimum Voltage/pu |
|---|---|---|---|---|
| Modified IEEE 33-node | Normal operation | 33, 34, 35, 36, 37 | 135.2760 | 0.9338 |
| After reconfiguration | 7, 9, 14, 32, 37 | 88.8114 | 0.9629 | |
| Improved IEEE 69 case | Normal operation | 69, 70, 71, 72, 73 | 143.4278 | 0.9320 |
| After reconfiguration | 14, 55, 61, 69, 70 | 63.4263 | 0.9695 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, M.; Li, J.; Li, J.; Yuan, X.; Xu, J. Reconfiguration Strategy for DC Distribution Network Fault Recovery Based on Hybrid Particle Swarm Optimization. Energies 2021, 14, 7145. https://doi.org/10.3390/en14217145
Yang M, Li J, Li J, Yuan X, Xu J. Reconfiguration Strategy for DC Distribution Network Fault Recovery Based on Hybrid Particle Swarm Optimization. Energies. 2021; 14(21):7145. https://doi.org/10.3390/en14217145
Chicago/Turabian StyleYang, Minsheng, Jianqi Li, Jianying Li, Xiaofang Yuan, and Jiazhu Xu. 2021. "Reconfiguration Strategy for DC Distribution Network Fault Recovery Based on Hybrid Particle Swarm Optimization" Energies 14, no. 21: 7145. https://doi.org/10.3390/en14217145
APA StyleYang, M., Li, J., Li, J., Yuan, X., & Xu, J. (2021). Reconfiguration Strategy for DC Distribution Network Fault Recovery Based on Hybrid Particle Swarm Optimization. Energies, 14(21), 7145. https://doi.org/10.3390/en14217145








