1. Introduction
Solar energy can be used as a renewable heat source for different processes, such as solar fuels production, electricity, and process heat. These are among the most important in solar energy due to the development of technology and the production of electricity used in various applications, such as buildings, mobility, and manufacturing [
1]. The concentrated solar irradiance allows achieving a high energy density to carry out these processes. The technologies that concentrate the irradiance imply lenses or mirrors that redirect the solar rays to an area smaller than the receiving area. The difference between these technologies is their concentrating process, for example, the parabolic dish, parabolic trough, linear fresnel reflector, central tower, and solar furnace [
2]. However, the transformation of concentrated solar radiation into thermal power is a considerable challenge that has been solved using a solar receiver [
1].
The solar irradiance distribution produced by solar concentrating systems is usually non-uniform, which causes a non-uniform temperature distribution in the receiver, causing damage to the material and affecting the heat transfer process, as well as the performance of the system [
3]. The solar irradiance distribution depends on the technology and optical configuration to produce concentrated solar radiation. Therefore, studying irradiance distributions will allow us to better understand the problem by determining a volume around the focal zone where the radiation density is uniform; this volume is known as an isosurface [
4], but does not provide a solution to achieve an almost homogeneous flux. The effective volume is built by connecting and interpolating 2D irradiance distribution images obtained in successive adjacent planes. The superimposition of the set of effective volumes obtained in different directions around the focal axis will build an isosurface. Irradiance flux depends on the position and the direction of the plane used for the calculation, so an effective volume will not present a uniform distribution flux, as the radiation along the tangential and horizontal planes will have different values [
4,
5].
Effective volumes refer to empty volumes created from equal intensities of irradiance distribution obtained from irradiance distributions received on parallel flat surfaces along one direction from the optical axis. It is the generation of three-dimensional images from two-dimensional planes scanned in one direction (some authors named this volume the protosurface [
4,
5,
6]). Therefore, it is possible to calculate the information between the bidimensional planes by interpolation, and all those points will correspond to the same irradiance level. By changing the direction in which planes are scanned, due to slight deviation from the optical axis of the concentrating system, another set of effective volumes is generated.
Experimental methods, such as indirect and direct, and measurement-supported simulation methods have been described in the literature to reveal the radiative flux distribution produced by a concentrating solar system obtaining acceptable results. The simulation-based techniques can provide more information about solar flux maps though it only serves to validate. These simulation-based methods use mathematical procedures to predict the result of the radiative process performed by the concentrating solar system. These mathematical procedures (Ray tracing simulation), based on different methods, such as Simple Ray Tracing, Convolution Ray Tracing, and Monte Carlo Ray Tracing [
4,
5], have been combined with solar simulators, showing acceptable results [
6]. While direct methods use a flux sensor that provides information about the irradiative flux, indirect methods use digital cameras to measure the solar radiation reflected on a diffuse surface [
7]. These methods have been used for evaluating R&D projects on concentrating solar systems to reveal the irradiance distribution in bidimensional planes. Previous studies reveal an irradiance distribution in volumetric receivers but not generating a uniform radiative flux volume through the application of the MCRT method, where the source of the concentrated solar radiation considered is a point focus concentrator [
3,
8,
9,
10,
11].
Du et al. [
12] reported a combined technique of X-ray-computed tomography to rebuild a realistic porous absorber with the MCRT to obtain the distribution of radiative flux that is closest to reality; this is not an irradiance distribution provided by the concentrating system itself. At the same time, Ali et al. made theoretical assumptions to simulate the operating conditions of the receiver [
1]. Eccher et al. [
13] compared the experimental concentrated solar radiation spot and one obtained by simulation without making any variation to the global optical error. The concentrating system, in this case, is a parabolic concentrator. The difference between the spots is attributed to the imperfections and deviations of the concentrator design due to the manufacturing process, again without determining the value of the global optical error and without considering the experimental conditions. Wang et al. [
14] assumed theoretical values of direct normal irradiance, reflectivity, and the number of rays for simulations. Ray tracing has been validated with reproducible results confirmed by the experiments in concentrators and is widely accepted [
5,
15,
16].
Riveros-Rosas et al. [
4] reported the generation of isosurfaces produced by different concentrating systems, such as a parabolic dish, a rectangular plate with parabolic curvature, and a concentrator of spherical facet with a parabolic profile, by applying a numerical model varying the optical error of the mirrors. At the same time, Perez-Enciso et al. [
5] reported the validation of effective volumes generated by a solar furnace and those experimentally obtained with an established optical error of the mirror, obtaining consistent results.
In summary, theoretical and experimental methods have been described in the literature to obtain the irradiance distribution produced by concentrating solar systems and the irradiance distribution obtained in volumetric receivers. However, the generation of effective volumes from theoretical-experimental methodologies for parabolic dish collectors to determine homogeneous irradiance distributions has not been reported in the literature.
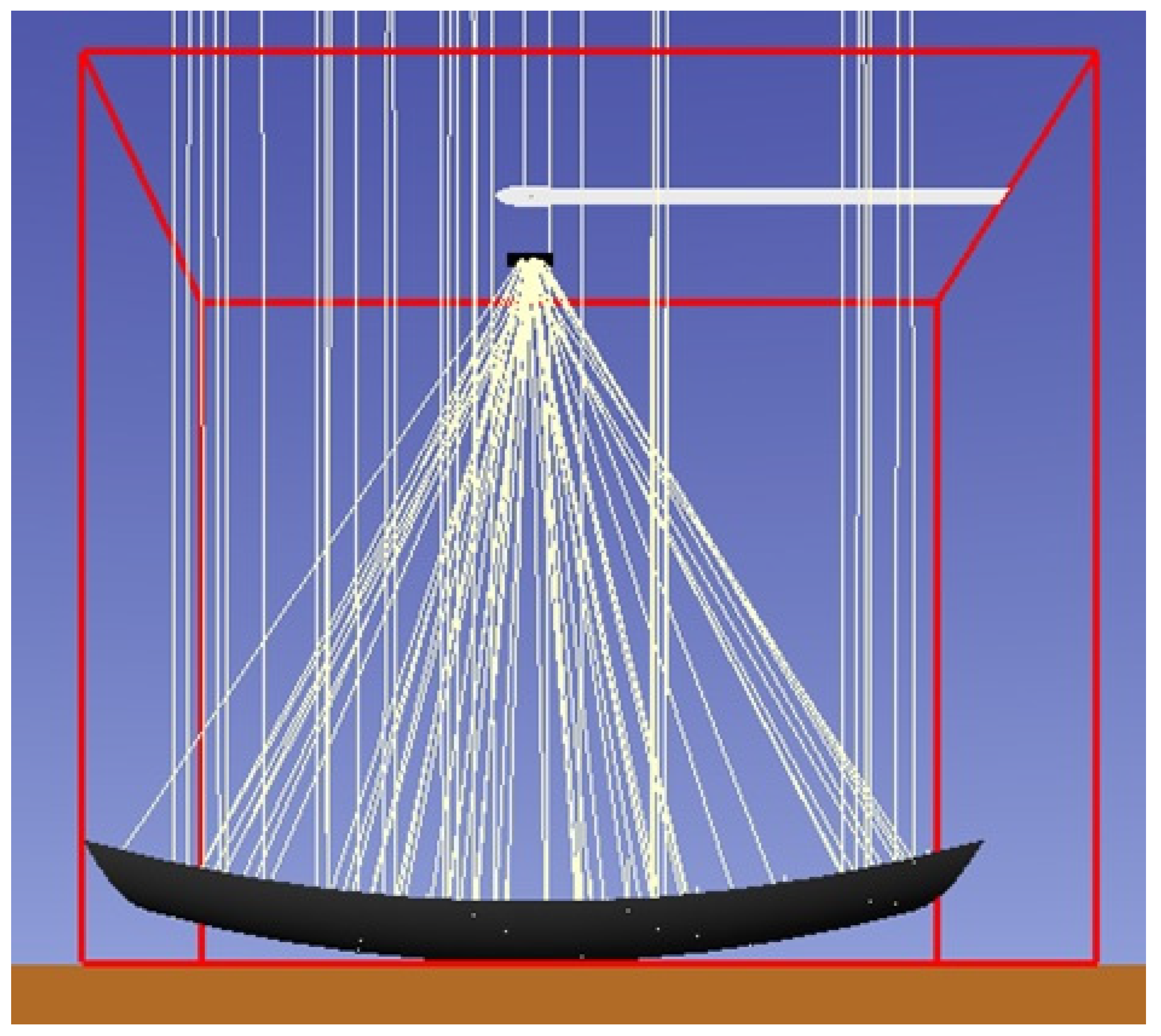
This study aims to reveal the irradiance flux distribution produced by the second surface parabolic dish concentrating system (
Figure 1), developed and built by researchers at the University of Arizona [
17], to produce electricity using high-efficiency photovoltaic cells. According to the literature, this type of concentrating technology presents extremely non-uniform radiation distribution [
15,
16,
18], thus its study is important. In this study, a validation of a numerical model to build effective volumes and compare with those built from experimental data is presented. The construction of effective volumes in the direction perpendicular to the focal axis of the concentrating system is the first step in generating an isosurface. An isosurface might help to reduce flux peaks and assist in designing a special receiver for this concentrating solar system.
From this study, cylinders with regular edges are expected as effective volumes because of the geometry of the concentrating mirror. Nevertheless, and according to the literature, the presence of errors in the surfaces could generate a type of optical anomaly and is likely to be aggravated by other factors, such as mechanical efforts produced by gravity and the support of the mirror, thermal efforts from the environmental temperature, the inclination of the optical system, and wind speed and direction [
19].
2. Methodology
This theoretical-experimental study aims to generate the effective volumes produced by a point-focus concentrating system, whose physical characteristics are described in
Table 1. Before generating effective volumes, it is necessary to estimate the global optical error of the concentrating system considering the operating conditions, which are different from (controlled) the laboratory conditions. This part is explained in
Section 2.4.
The section below describes the experimental set used to scan the images to determine the optical error and the effective volumes generation. After this, the ray-tracing simulation is described, and the effective volumes generation process is presented.
2.1. Experimental Set
The Camera-Target Method (CTM) is an indirect method since its result only describes the irradiance distribution profiles but not their values. It is also considered a low-cost method to obtain basic optical parameters [
20]. CTM uses a charge-coupled device (CCD) camera that records the radiative flux brightness distribution on a diffuse surface located perpendicularly to the optical axis of the parabola at different distances. In addition, the intensity of the concentrated radiation reflected by the parabolic dish was calibrated using a circular radiometer, which is considered a direct method. The advantages of the CTM are fast measurements and high spatial resolution and reliability [
7]. Therefore, this method has been used in several projects to evaluate optical systems since the 1970s [
5,
16,
18,
20,
21,
22,
23,
24,
25,
26,
27]. In addition, the diffuse surface has a diffuse reflection feature, meaning that regardless of the incident angle of radiation, this type of surface reflects in all directions.
A Pike Technologies 8 bits 210 CCD camera (
Figure 2a) was used (Fitchburg, WI, USA), to which a filter with linear response to light intensity was adapted. The camera’s dynamic range must be set at the highest flux intensity and kept constant during the experiment. This camera was selected due to its linear response to a wide range of intensities and high signal quality. This camera has a matrix of 1920 × 1080 pixels, capable of resolving 256 levels of gray.
For this experiment, a Refrigerated Lambertian Flat Plate (RLFP) (
Figure 2b) was used, from Instituto de Energías Renovables, Universidad Nacional Autónoma de Mexico, Temixco, Morelos, Mexico. RLFP is made of the junction of an aluminum plate and a nylamid plate. The aluminum plate is subjected to a sandblasting process to achieve a uniform surface and remove any paint residue, grease, and rust. The nylamid plate has inlets and outlets for the coolant flow (
Figure 2c). The RLFP was mounted on a linear actuator automatically moved by a control program along the optical axis to facilitate the experiment. To chill the RLFP, two heat exchangers connected in parallel with a total removal capacity of 800 W and a mass flow of 1 Lpm were required.
The RLFP has an opening where a circular radiometer was placed (
Figure 2b) (Vatell Corporation, Christiansburg, VA, USA). Its operation is based on receiving concentrated solar radiation on a thin circular surface of constantan attached to a circular copper block. The energy absorbed by the constantan surface flows radially towards a chilled copper block, acting as a heat reservoir at a constant temperature. As a result of this radial distribution from heat flow, the constantan’s surface temperature is higher than the temperature of the copper block. This temperature difference was measured with a thermocouple and could be related through a constant with the radiation intensity [
28].
The combination of indirect and direct methods provides enough information to reveal irradiance distribution profiles and their values. Since the concentrating solar system only operates with direct normal irradiance, it must be in the tracking mode, making the procedure difficult because both the concentrating system and RLFP are in motion (
Figure 3).
2.2. Ray Tracing Simulation
In this study, ray-tracing simulations were performed to characterize the concentrating system, simulating the response behavior of the real system of an event taking place over time [
29].
Our approach was based on the Monte Carlo method, which allows mathematical and physical problems to be solved by random variable simulation. The statistical simulation of the radiative transfer phenomenon is based on the emission, reflection, and absorption of the surfaces of the optical system [
30]. To carry out the Monte Carlo Ray Tracing simulations, the physical properties of the optical system and the environmental conditions were considered (
Figure 4).
Tonatiuh v.2.2.4, an optical modeling computer package, was used to carry out the ray-tracing simulation. This free-license software was developed by the National Renewable Energy Center of Spain, in Sarriguren, Navarra, Spain (CENER) and the University of Texas at Brownsville (UTB) with the support of the National Renewable Energy Laboratory (NREL) [
31]. The number of rays was established through a ray stability study carried out considering the parameters described in
Table 1, as well as a direct normal irradiance of 1000 W/m
2, a standard sun shape, and a circumsolar ratio value of 0.02, which were determined experimentally by image analysis of the actual sun (
Figure 5). A ray stability study is essential to eliminate the effect of the number of rays for the numerical resolution [
32]. Therefore, variation of the maximum power regarding the number of rays was analyzed. The mesh size for the experimental images was 500 × 500, and for simulated images was set at 250 × 250.
The simulation was carried out considering the receiver was located in the focal zone, and the number of rays varied from 0.01 to 40 million. Considered uncertainty is 4.0%.
Table 2 shows that from 5 million rays, uncertainty stays below the set value but has a little variation. Twenty million rays was the value selected for the simulations.
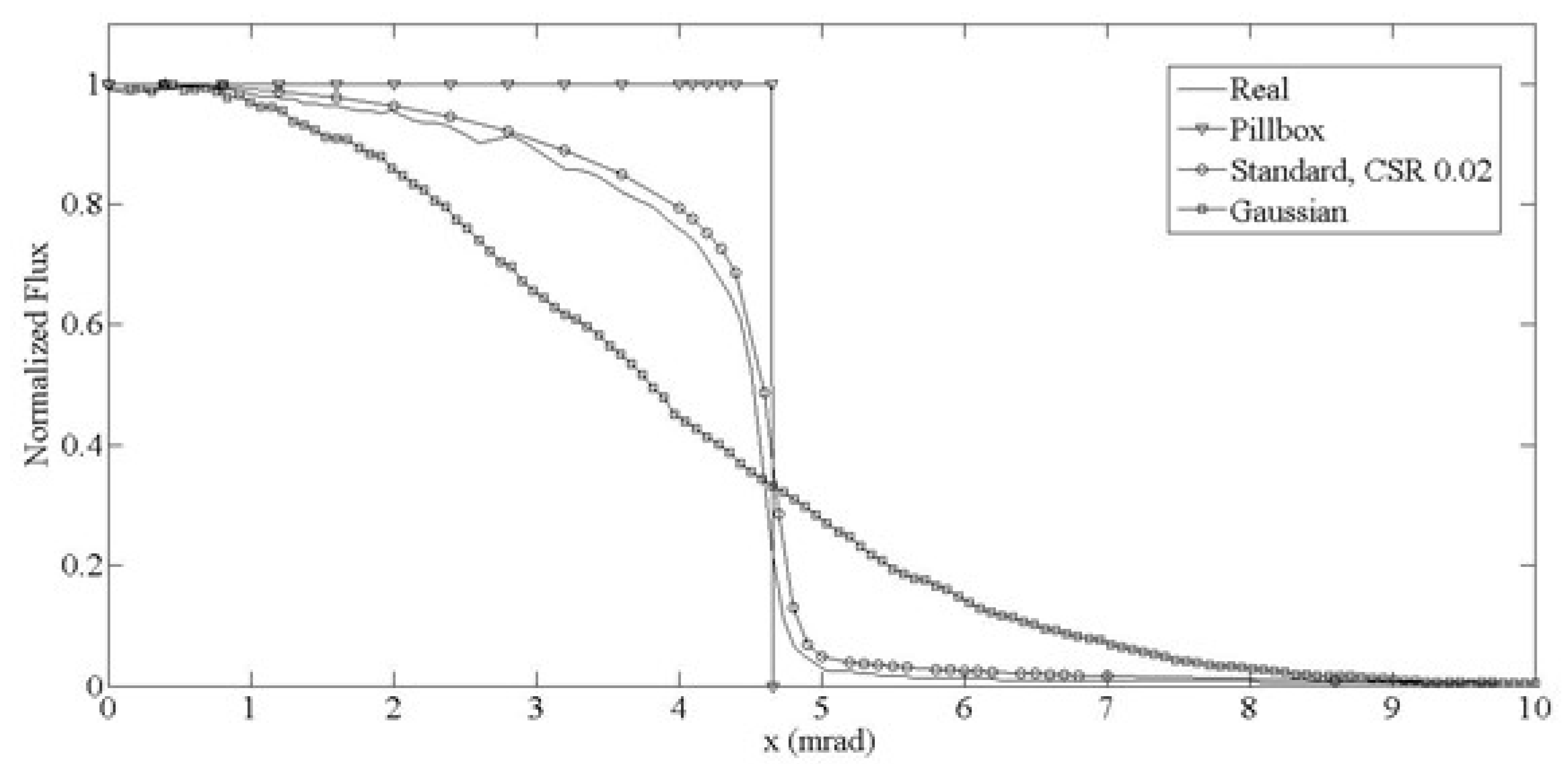
The circumsolar ratio, csr, represents the proportion of radiation incidents from the circumsolar region with respect to the total direct irradiance. It results from the scattering of direct sunlight through small angles due to atmospheric molecules and aerosols. Though it could be used as an approximated value [
33], if experimental conditions are desired to reproduce in the simulation process, this value must be experimentally determined. A photograph of the solar disc was scanned (
Figure 5), with the previously described CCD camera equipped with linear filters allowing an unsaturated image immediately after the application of the CTM to be obtained. After this, the solar irradiance distribution profiles in the center of the scanned image were analyzed and compared to different sun shapes produced by the software-varying csr value. The csr was determined by tying the theoretical value with the experimental one (
Figure 6) [
34].
2.3. Global Optical Error of the System
The optical error of the mirror is described by the difference between the diameter of the real sun and the diameter of the degraded sun produced by the concentrator mirror; it can be approximated with a normal distribution.
Microscopic or roughness errors are associated with the substrate material, whereas macroscopic or slope errors cause a deviation in the direction of the reflected cone due to the surface slope errors. The slope deviation duplicates the error angle and is related to the manufacturing process. In summary, the global optical error of a reflective surface is the junction of these microscopic and macroscopic errors and is calculated as shown in Equation (1) [
22].
where
is the global optical error,
stands for the roughness error, and
refers to the slope error. In addition to the optical errors of the concentrator mirror described previously, deviation caused by tracking
), displacement, control systems, data logger, and sun shape (
) must be considered as a part of the global optical error of the system. Therefore, Equation (1) must consider these parameters (Equation (2)) [
19]. If these parameters are omitted from the formula, the global optical error of the system could be underestimated. Some of these parameters were also affected by non-controlled conditions, such as solar irradiance, environmental temperature, and wind speed and direction.
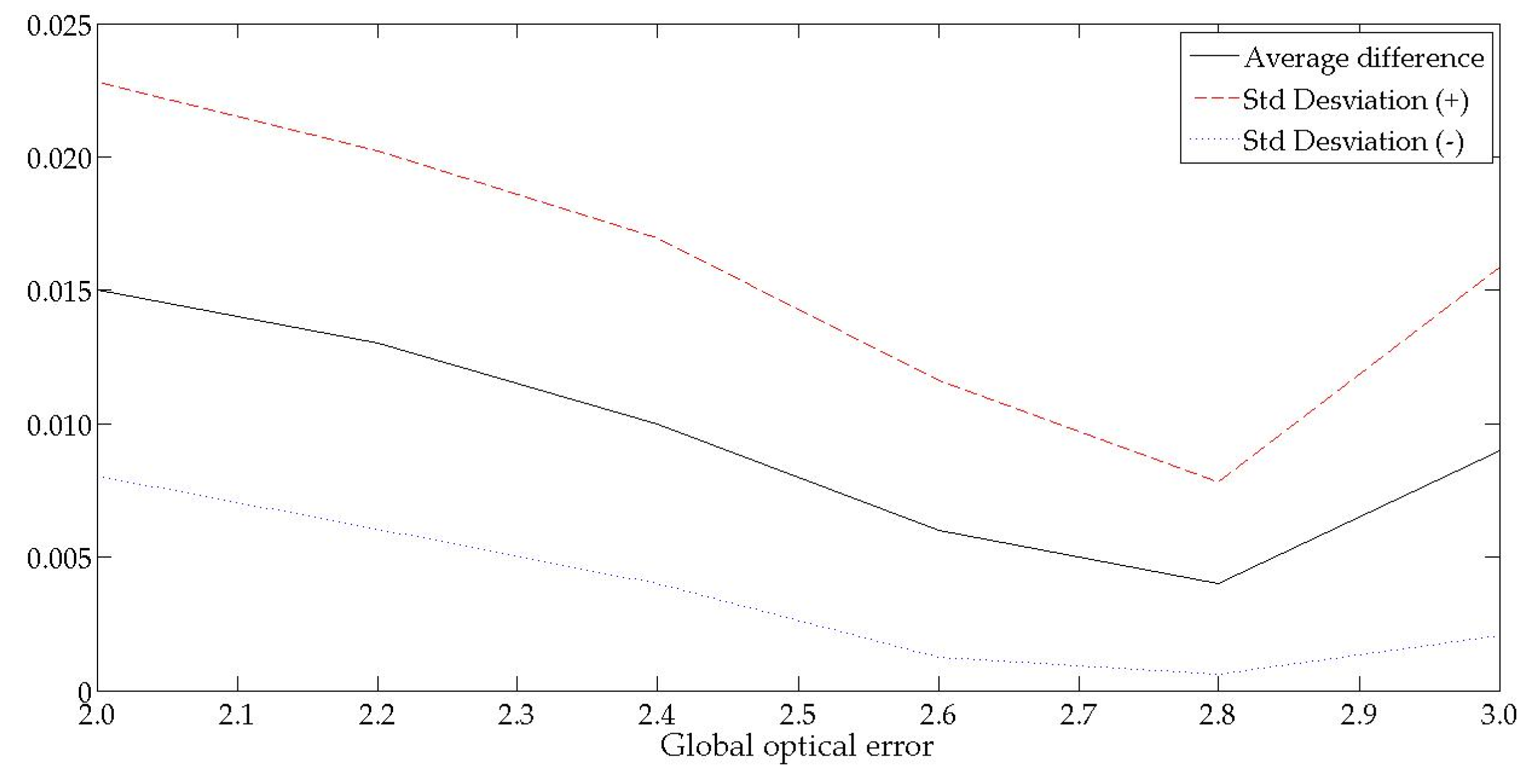
The global optical error of the system was calculated by comparing the irradiance distribution profiles from the experimental and theoretical scanned images in the focal zone of the concentrating system, evaluating them in vertical and horizontal axes of the concentrated solar radiation centroid. First, a quantitative approximation was carried out by varying the theoretical optical error around the real error, allowing an approximate error interval to be estimated. Theoretical irradiance distribution profiles were generated, varying the error in the determined interval. The global optical error of the system was estimated when the average difference between the experimental profile and the theoretical one presented the smallest standard deviation. The described method only calculates the global optical error of the system by comparing irradiance distribution profiles, but not by one of the terms described in Equation (2).
2.4. Generation of Effective Volumes
To generate the effective volumes, the irradiance distribution images produced by the concentrating system on the RLFP were scanned experimentally. Once the global optical error of the system was obtained, the theoretical irradiance distribution images were acquired.
The concentrating system must be in operating mode during the image scanning process. The images were scanned from 1.4 to 1.6 m from the vertex of the parabola mirror with 0.002 m between them (
Figure 7). A total of 31 bidimensional and parallel planes to the optical axis of the concentrator mirror were scanned. Therefore, information between bidimensional planes is generated by interpolation through commands made in MATLAB 2014a, and the build of three-dimensional images of different irradiance levels is obtained.
3. Results and Discussion
3.1. Global Optical Error of the System
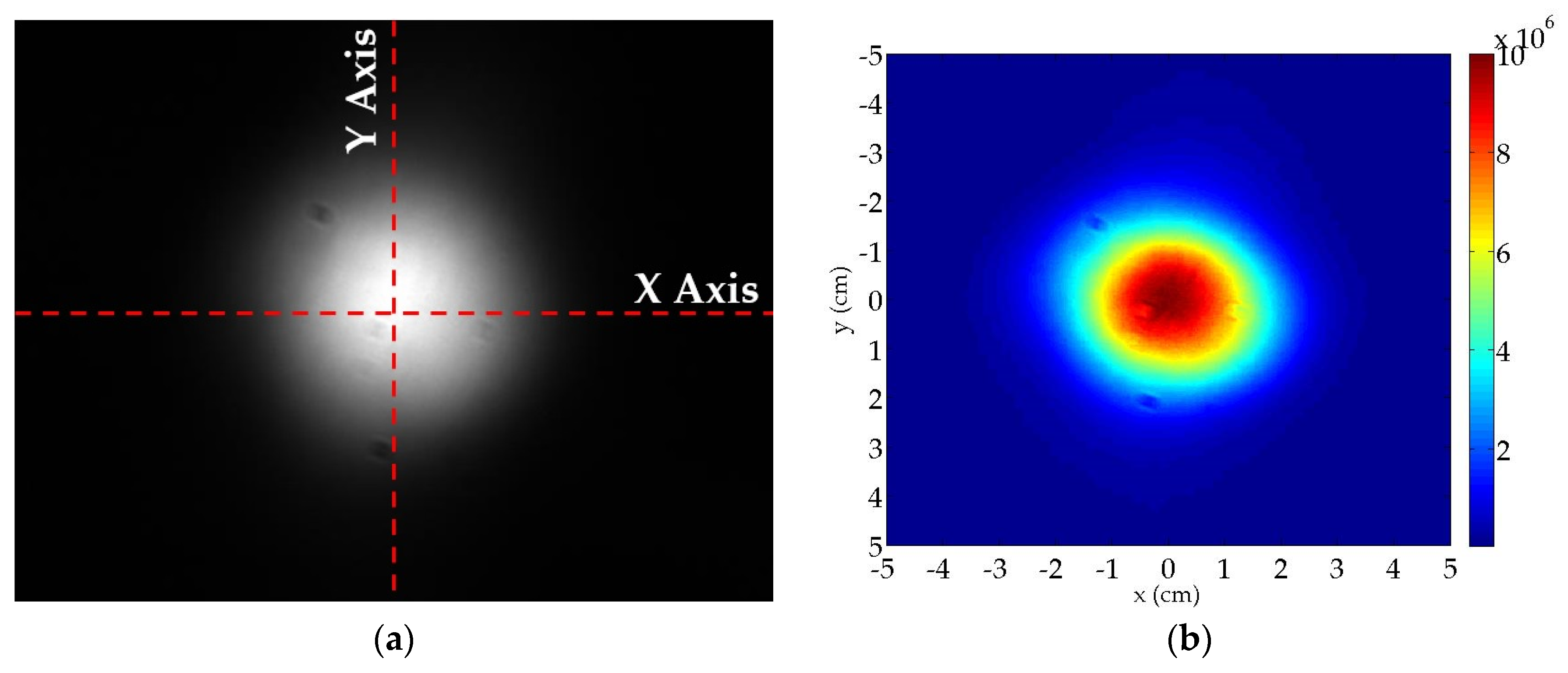
The scanned image at the focal zone in the concentrating system is shown in
Figure 8a. From this image, irradiance distribution profiles were obtained as shown with red lines. These profiles have a gaussian distribution through the applied methodology described in
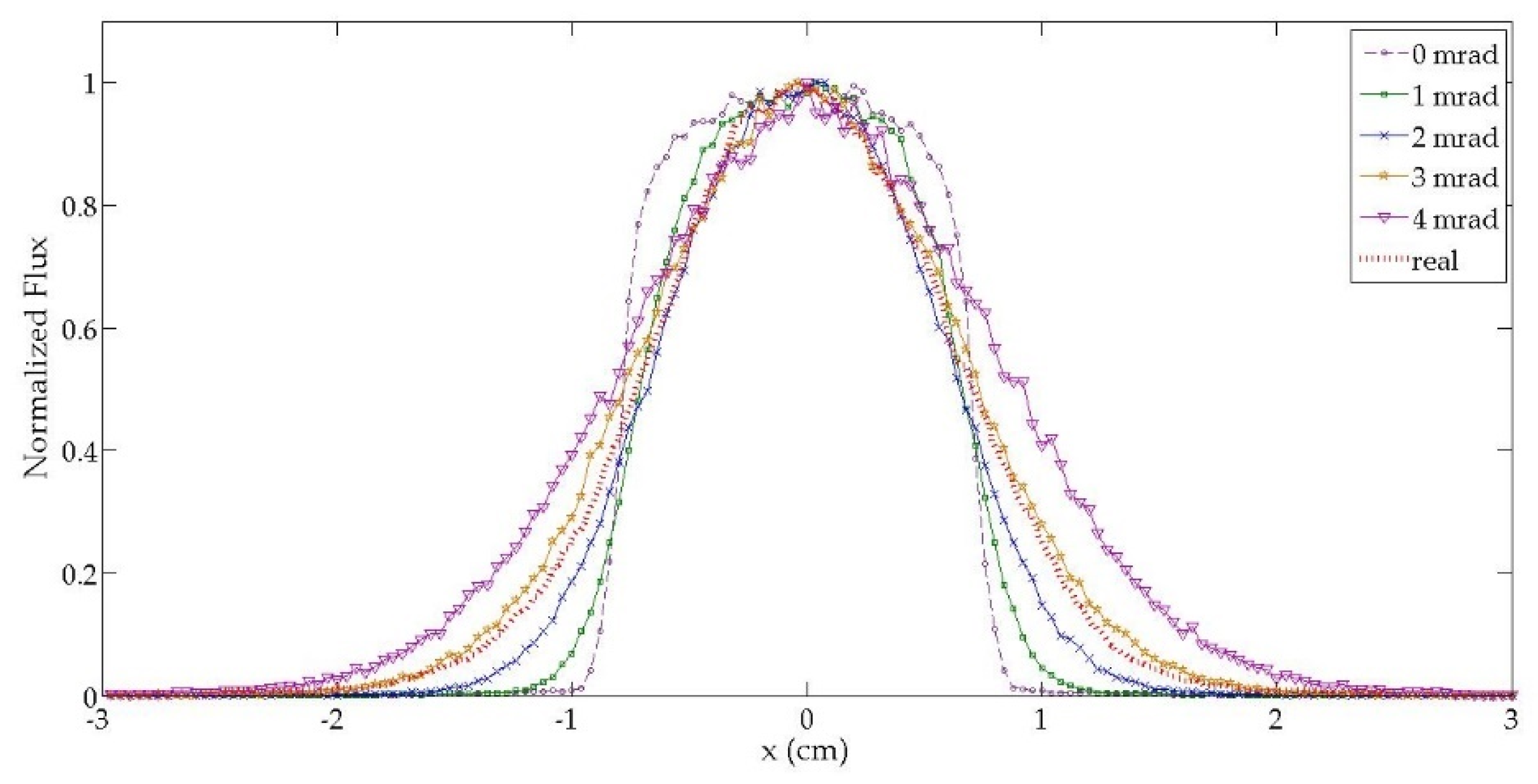
Section 2.3. The quantitative approximation is set between 2.0 and 3.0 mrad due to the real profile being between these values (
Figure 9). The qualitative approximation was determined by varying the error from 2.0 to 3.0 mrad (
Figure 10). The global optical error of the system was calculated at 2.8 mrad; thus this value presented the lowest standard deviation. The maximum value registered by the circular radiometer was 10 MW/m
2.
3.2. Effective Volumes
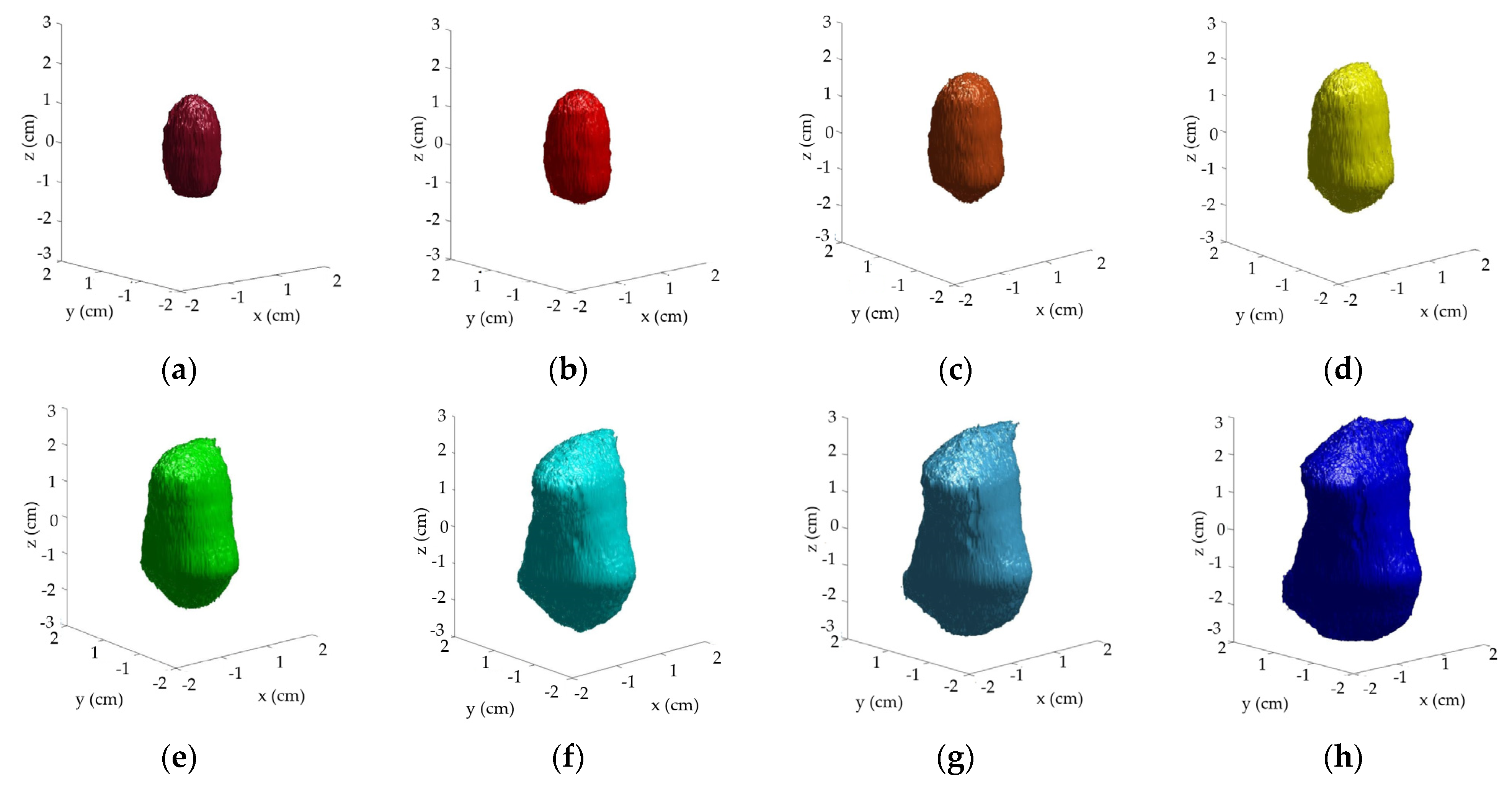
The real and theoretical effective volumes are presented in
Figure 11 and
Figure 12, respectively. Different uniform irradiance levels are shown, as seen in those figures. It is evident that the higher the flux value, the smaller the surface. For a flux value of 10 MW/m
2, theoretical effective volumes present a length in the
z-axis of ~2 cm and 1 cm in the
x and
y axes, while in experimental ones, lengths of less than 2 cm in the
z-axis and 1 cm in the
x and
y-axes were observed.
Comparing the shapes of theoretical and experimental effective volumes, some differences and trends can be seen.
Considering the shapes of effective volumes, theoretical and experimental types show differences between them. For theoretical effective volumes, higher irradiance levels present oval shapes, which are transformed into a cylinder for decreasing values. For experimental effective volumes, smaller flux presents a twist in the extreme side of the surfaces.
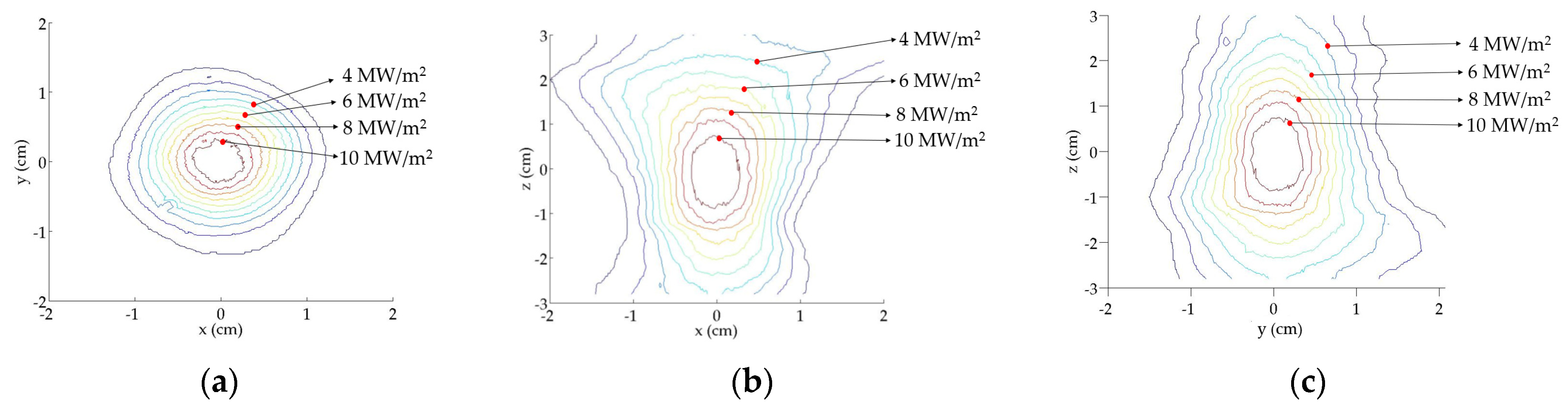
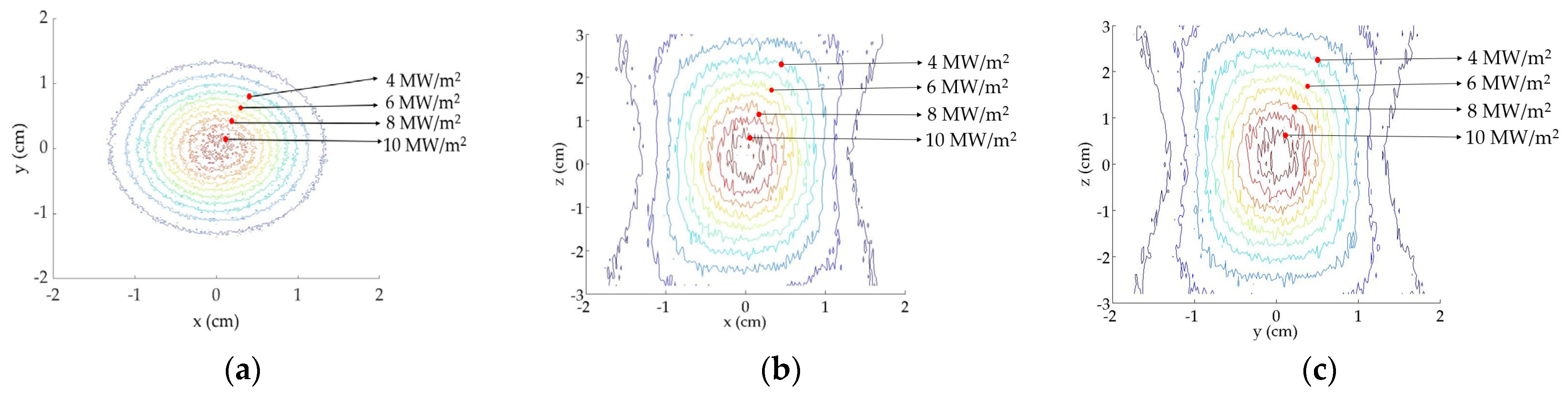
Experimental and theoretical isolines located at the focal zone in the
xy,
xz and
yz planes are shown in
Figure 13 and
Figure 14, respectively. Both experimental and theoretical
xy planes present a circular distribution and are very similar to each other because the images were scanned in this plane, whereas the other planes (
xz and
yz) differ from each other. In addition, in
Figure 13b,c, the twist can be appreciated at the smaller fluxes, while in
Figure 14b,c, this is not present.
Table 3 presents a quantitative comparison of the isolines shown in the previous figures. Areas from each flux were compared, taking as reference the real area to calculate the difference between them. The results show that theoretical irradiance area values are overestimated, presenting the smallest difference on the
xy plane at 10 MW/m
2 with 7.6% and the largest at 4 MW/m
2 on the
xz plane with 174%.
3.3. Discussion
The methodology established calculated the global optical error and obtained acceptable results. The optical imaging system evaluated the reproduced image of the sun, including the optical error that degrades the images. This error was calculated as 2.8 mrad. This points out the difference in the diameters of the real sun and the degraded sun produced by the system.
The theoretical effective volumes may not be considered as ideal ones due to the global optical error introduced. To build theoretical effective volumes that reproduce the experimental results, previous authors consider that some parameters used for simulation might be changed. Varying the focal length of the axes (x and y) could help reproduce the twist seen in the extreme sides of the experimental effective volumes. This twist could be due to mechanical efforts, thermal efforts, or wind speed and direction. However, determining the origin of this discovery is beyond the scope of this work.
The global optical error was determined on the xy plane. This explains the smallest difference comparing the theoretical and experimental isolines presented in this plane.
The low flux effective volumes are difficult to model because of the different sources of errors. These sources of errors are non-homogeneous and draw back from the gaussian distribution of the errors.
4. Conclusions
A novel theoretical-experimental methodology has been established to calculate the global optical error of the system and to generate different irradiance level surfaces produced by a parabolic dish concentrating system. These effective volumes obtained in the direction perpendicular to the focal axis are the first step in building uniform irradiance distribution surfaces. This helps reduce the peaks flux in the solar receivers, thus improving the performance of the overall system. To generate isosurfaces produced by this concentrating system, experimental and theoretical data must be collected in successive parallel planes, along several different directions, they must be superimposed to create an isosurface.
Several difficulties were presented during the development of the experimental methodology caused by the motion of the concentrating solar system, which must be due to the operating mode of scanning the images, as well as the cooling system, making the process difficult.
In contrast to previous studies, the experimental effective volumes were generated considering a global optical error of the system revealed at 2.8 mrad under operating conditions; this considers errors of the concentrating mirror, tracking system, control system, sun shape, and circumsolar ratio. In addition, theoretical effective volumes were generated from the established error, and a qualitative and quantitative comparison was made through isolines.
Differences between theoretical and real effective volumes were found, both in shape and dimensions. The highest flux revealed was 10 MW/m2, and the lowest was 4.5 MW/m2. Higher flux theoretical effective volumes presented an oval shape; by decreasing the flux value, they are transformed into an ellipsoid. Higher flux experimental effective volumes also presented oval shapes by decreasing the flux value, a twist in the extreme sides was observed. This twist could be due to mechanical efforts, thermal efforts, or wind direction and speed; however, determining the origin is not important for this work because the determination of the global optical error of the system is done in the focal zone—high-intensity region—whereas this error might not be revealed at low-intensity regions.