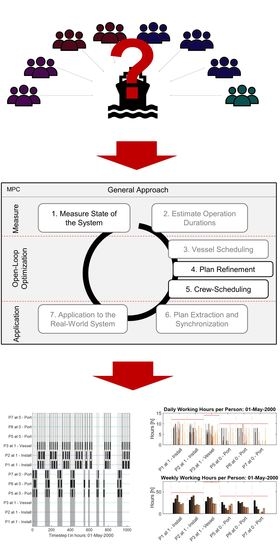
A Crew Scheduling Model to Incrementally Optimize Workforce Assignments for Offshore Wind Farm Constructions
Abstract
:1. Introduction
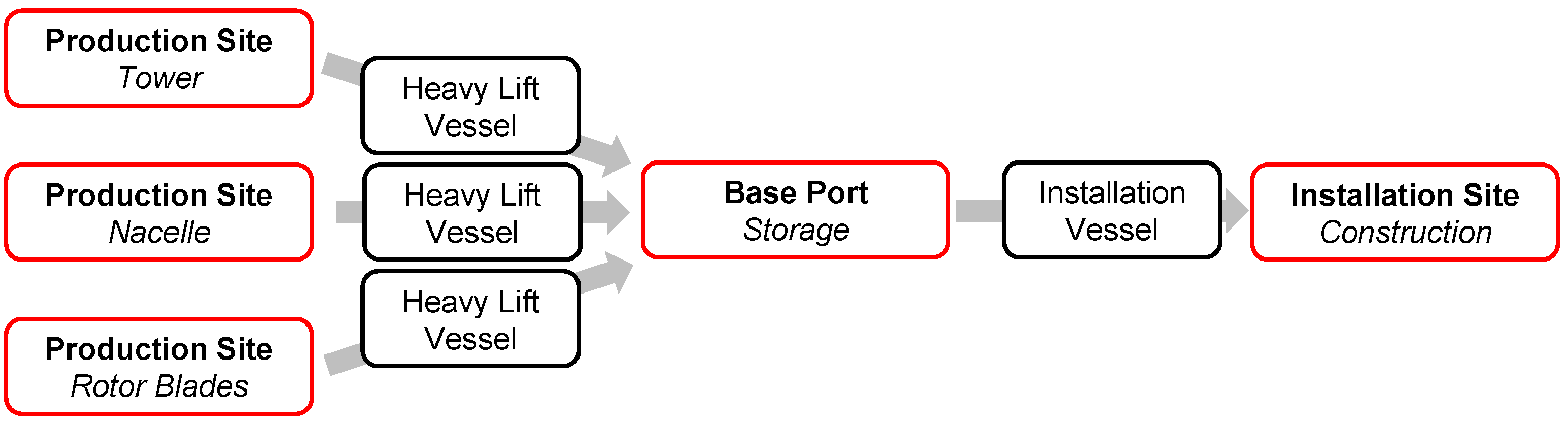
2. Process Description
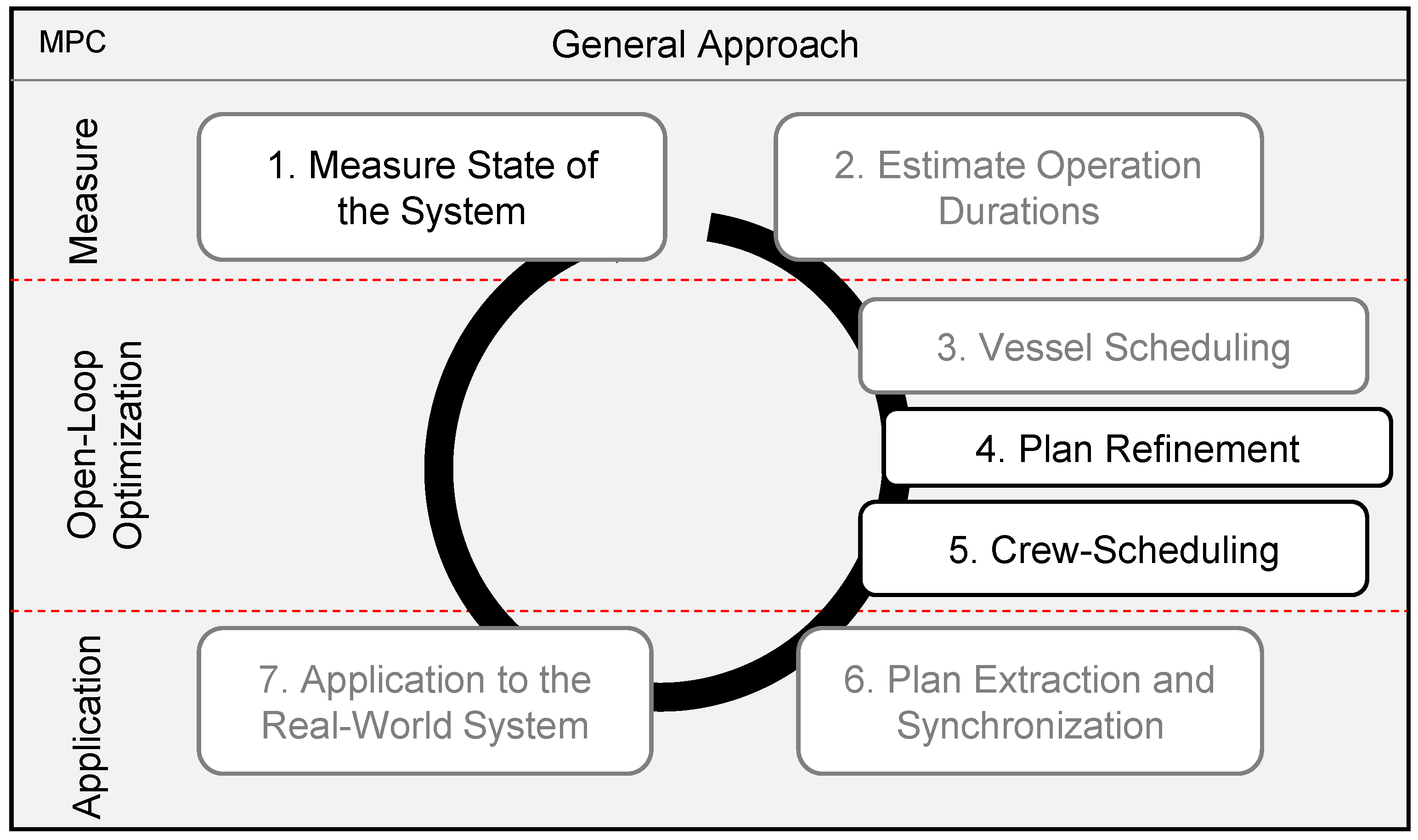
2.1. Planning and Scheduling of Offshore-Operations
2.2. Conclusion and Research Gap
3. Literature Review and Requirements Analysis
3.1. Description of the Investigated Crew Scheduling Problem
3.2. Requirement-Analysis
3.3. Literature Review on Models for Offshore Crew Scheduling
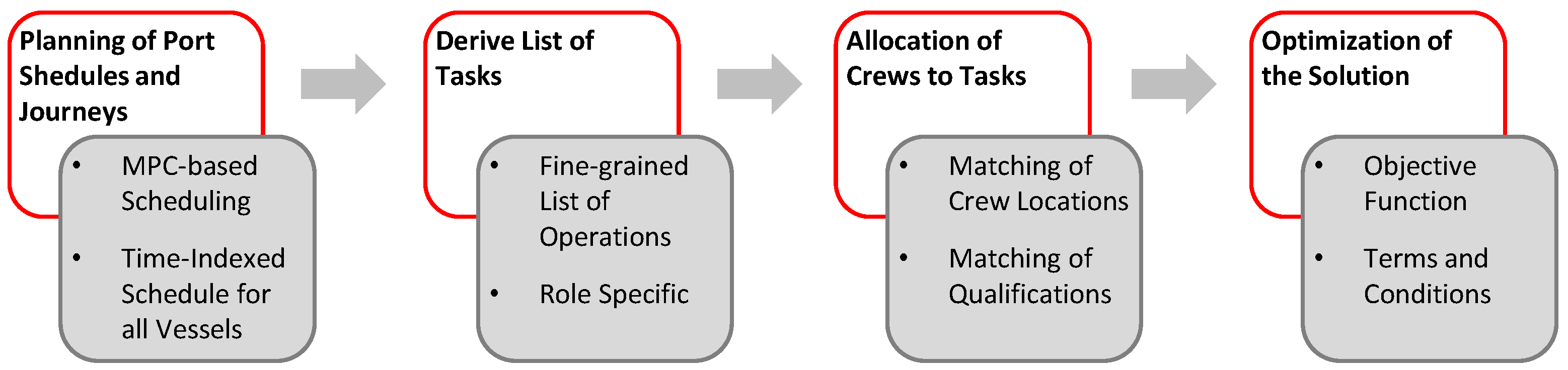
4. Workforce-Management Framework
4.1. Model Design Based on the Requirements and General Assumptions
4.2. System State for the Crew Scheduling (Model Parameters)
4.3. Decision Variables and Cost Function
4.4. Constraints
5. Experiments and Results
5.1. Scenario Description
5.2. Experimental Results
5.2.1. Base Scenario
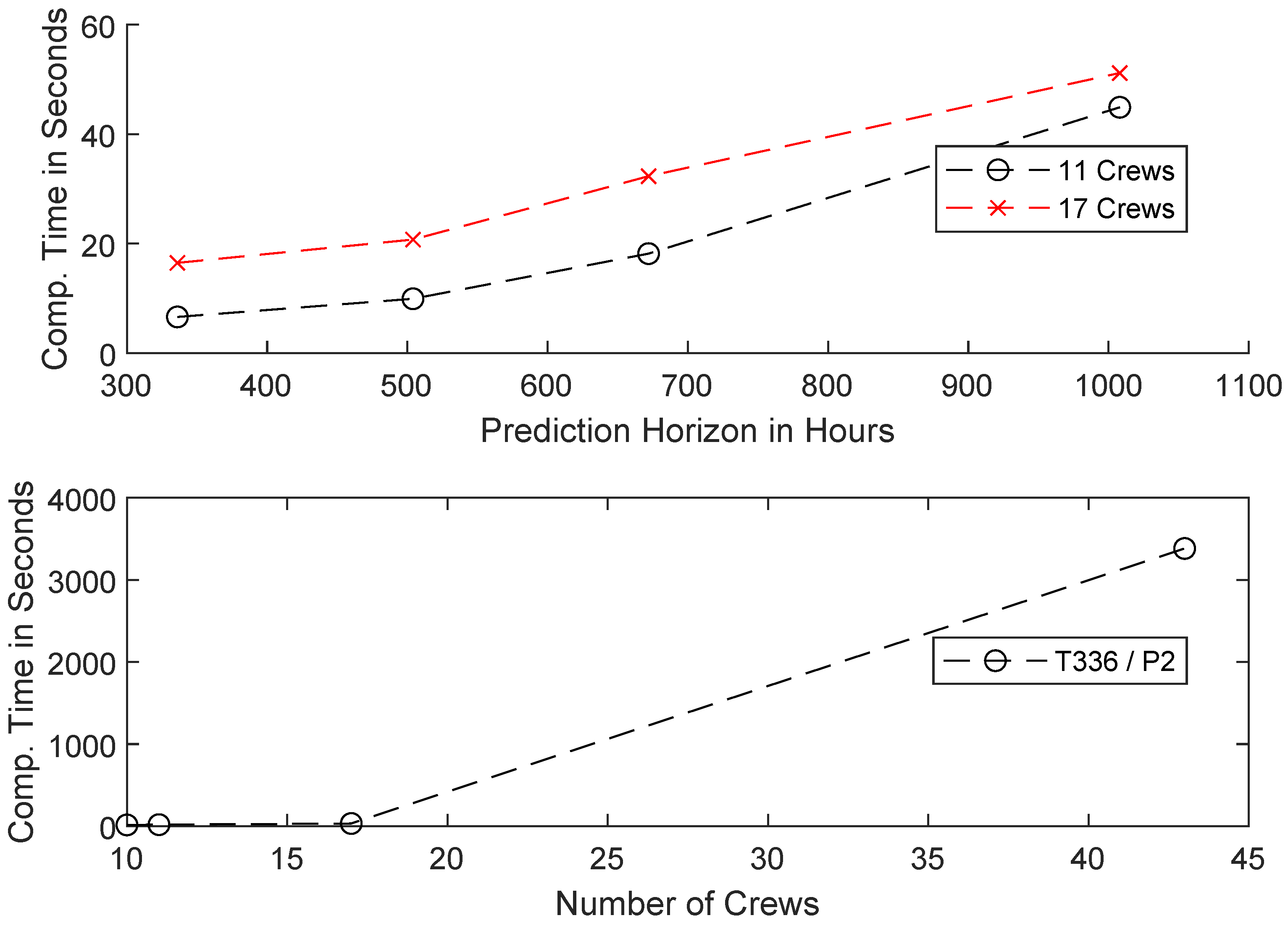
5.2.2. Extended Scenario and Computational Times
6. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- REN21. Renewables 2021 Global Status Report. 2021. Available online: https://www.ren21.net/reports/global-status-report/ (accessed on 14 September 2021).
- BVGassociates. Guide to an Offshore Wind Farm. 2019. Available online: https://bvgassociates.com/publications/ (accessed on 14 September 2021).
- Beinke, T.; Ait Alla, A.; Oelker, S.; Freitag, M. Demand for Special Vessels for the Decommissioning of Offshore Wind Turbines in the German North Sea—A Simulation Study. In Proceedings of the 30th International Ocean and Polar Engineering Conference (ISOPE), Virtual, 1–16 October 2020; Chung, J.S., Akselsen, O.M., Jin, H., Kawai, H., Lee, Y., Matskevitch, D., Eds.; ISOPE: Cupertino, CA, USA, 2020; pp. 480–484. [Google Scholar]
- Breton, S.; Moe, G. Status, Plans and Technologies for Offshore Wind Turbines in Europe and North America. Renew. Energy 2009, 34, 646–654. [Google Scholar] [CrossRef]
- Dewan, A.; Asgarpour, M.; Savenije, R. Commercial Proof of Innovative Offshore Wind Installation Concepts Using Ecn Install Tool; ECN: Petten, The Netherlands, 2015. [Google Scholar]
- Muhabie, Y.T.; Rigo, P.; Cepeda, M.; D’Agosto, M.A. A Discrete-event Simulation Approach to Evaluate the Effect of Stochastic Parameters on Offshore Wind Farms Assembly Strategies. Ocean Eng. 2018, 149, 279–290. [Google Scholar] [CrossRef]
- Ait Alla, A.; Oelker, S.; Lewandowski, M.; Freitag, M.; Thoben, K.D. A Study of New Installation Concepts of Offshore Wind Farms by Means of Simulation Model. In Proceedings of the Twenty-seventh International Ocean and Polar Engineering Conference (ISOPE), San Francisco, CA, USA, 25–30 June 2017; Chung, J.S., Triantafyllou, M.S., Langen, I., Eds.; ISOPE: Cupertino, CA, USA, 2017; pp. 607–612. [Google Scholar]
- Vis, I.F.; Ursavas, E. Assessment Approaches to Logistics for Offshore Wind Energy Installation. Sustain. Energy Technol. Assess. 2016, 14, 80–91. [Google Scholar] [CrossRef] [Green Version]
- Oelker, S.; Lewandowski, M.; Ait Alla, A.; Ohlendorf, J.H.; Haselsteiner, A.F. Logistikszenarien Für Die Errichtung Von Offshore-windparks—Herausforderungen Der Wirtschaftlichkeitsbetrachtung Neuer Logistikkonzepte. Ind. 4.0 Manag. 2017, 33, 24–28. [Google Scholar]
- Rippel, D.; Jathe, N.; Lütjen, M.; Freitag, M. Evaluation of Loading Bay Restrictions for the Installation of Offshore Wind Farms Using a Combination of Mixed-integer Linear Programming and Model Predictive Control. Appl. Sci. 2019, 9, 5030. [Google Scholar] [CrossRef] [Green Version]
- Rippel, D.; Jathe, N.; Becker, M.; Lütjen, M.; Szczerbicka, H.; Freitag, M. A Review on the Planning Problem for the Installation of Offshore Wind Farms. IFAC-PapersOnLine 2019, 52, 1337–1342. [Google Scholar] [CrossRef]
- Scholz-Reiter, B.; Karimi, H.R.; Lütjen, M.; Heger, J.; Schweizer, A. Towards a Heuristic for Scheduling Offshore Installation Processes. In Proceedings of the 24th International Congress on Condition Monitoringand and Diagnostics Engineering Management. Advances in Industrial Integrated Asset Management, Birmingham, UK, 30 May–1 June 2011; Maneesh, S., Rao, R., Liyanage, J.P., Eds.; COMADEM International: Birmingham, UK, 2011; pp. 999–1008. [Google Scholar]
- Ait Alla, A.; Quandt, M.; Lütjen, M. Simulation-based Aggregate Installation Planning of Offshore Wind Farms. Int. J. Energy 2013, 7, 23–30. [Google Scholar]
- Kerkhove, L.P.; Vanhoucke, M. Optimised Scheduling for Weather Sensitive Offshore Construction Projects. Omega 2017, 66, 58–78. [Google Scholar] [CrossRef]
- Ursavas, E. A Benders Decomposition Approach for Solving the Offshore Wind Farm Installation Planning at the North Sea. Eur. J. Oper. Res. 2017, 258, 703–714. [Google Scholar] [CrossRef]
- Barlow, E.; Tezcaner Öztürk, D.; Revie, M.; Akartunalı, K.; Day, A.H.; Boulougouris, E. A Mixed-method Optimisation and Simulation Framework for Supporting Logistical Decisions during Offshore Wind Farm Installations. Eur. J. Oper. Res. 2018, 264, 894–906. [Google Scholar] [CrossRef] [Green Version]
- Irawan, C.A.; Wall, G.; Jones, D. An Optimisation Model for Scheduling the Decommissioning of an Offshore Wind Farm. OR Spectr. 2019, 41, 513–548. [Google Scholar] [CrossRef]
- Lange, K.; Rinne, A.; Haasis, H.D. Planning Maritime Logistics Concepts for Offshore Wind Farms: A Newly Developed Decision Support System. Lect. Notes Comput. Sci. Comput. Logist. 2012, 7555, 142–158. [Google Scholar]
- Beinke, T.; Ait Alla, A.; Freitag, M. Resource Sharing in the Logistics of the Offshore Wind Farm Installation Process Based on a Simulation Study. Int. J. E-Navig. Marit. Econ. 2017, 7, 42–54. [Google Scholar] [CrossRef]
- Quandt, M.; Beinke, T.; Ait Alla, A.; Freitag, M. Simulation Based Investigation of the Impact of Information Sharing on the Offshore Wind Farm Installation Process. J. Renew. Energy 2017, 2017, 11. [Google Scholar] [CrossRef] [Green Version]
- Cheng, M.Y.; Wu, Y.F.; Wu, Y.W.; Ndure, S. Fuzzy Bayesian schedule risk network for offshore wind turbine installation. Ocean Eng. 2019, 188, 106238. [Google Scholar] [CrossRef]
- Peng, S.; Szczerbicka, H.; Becker, M. Modeling and Simulation of Offshore Wind Farm Installation with Multi-Leveled CGSPN. In Proceedings of the 30th International Ocean and Polar Engineering Conference (ISOPE), Virtual, 11–16 October 2020; Chung, J.S., Akselsen, O.M., Jin, H., Kawai, H., Lee, Y., Matskevitch, D., Eds.; ISOPE: Cupertino, CA, USA, 2020; pp. 472–479. [Google Scholar]
- Moher, D.; Liberati, A.; Tetzlaff, J.; Altman, D.G. Preferred reporting items for systematic reviews and meta-analyses: The PRISMA statement. PLoS Med. 2009, 6, e1000097. [Google Scholar] [CrossRef] [Green Version]
- van den Bergh, J.; Beliën, J.; de Bruecker, P.; Demeulemeester, E.; de Boeck, L. Personnel scheduling: A literature review. Eur. J. Oper. Res. 2013, 226, 367–385. [Google Scholar] [CrossRef]
- Gopalakrishnan, B.; Johnson, E.L. Airline Crew Scheduling: State-of-the-Art. Ann. Oper. Res. 2005, 140, 305–337. [Google Scholar] [CrossRef]
- John, O.; Gailus, S.; Rizvanolli, A.; Rauer, R. An Integrated Decision Support Tool for Hours of Work and Rest Compliance Optimization during Ship Operations. In Proceedings of the 13th International Conference on Computer and IT Applications in the Maritime Industries, COMPIT’14, Redworth, UK, 12–14 May 2014; Bertram, V., Ed.; Schriftenreihe Schiffbau, Technology University Verlag Schriftenreihe Schiffbau: Hamburg, Germany, 2014; pp. 245–257. [Google Scholar]
- Bundesamt für Justiz und Verbraucherschutz. Verordnung über die Arbeitszeit bei Offshore-Tätigkeiten; Bundesamt für Justiz and Verbraucherschutz: Berlin, Germany, 2013. [Google Scholar]
- Bundesamt für Justiz and Verbraucherschutz. Seearbeitsgesetz (SeeArbG); Bundesamt für Justiz and Verbraucherschutz: Berlin, Germany, 2021. [Google Scholar]
- Colli, N.; Mache, S.; Harth, V.; Mette, J. Physische und psychische Gesundheit von Offshore-Beschäftigten. Zentralblatt für Arbeitsmedizin Arbeitsschutz und Ergon 2017, 67, 176–178. [Google Scholar] [CrossRef]
- Hammer, G.; Röhrig, R. Qualification Requirement Analysis Offshore Wind Energy Industry. Tech. Rep. 2005. Available online: http://pcoe.nl/@api/deki/files/1919/=15final_report_qrs.pdf (accessed on 21 October 2021).
- Leggate, A.; Sucu, S.; Akartunalı, K.; van der Meer, R. Modelling crew scheduling in offshore supply vessels. J. Oper. Res. Soc. 2018, 69, 959–970. [Google Scholar] [CrossRef]
- Sucu, S. Solving Crew Scheduling Problem in Offshore Supply Vessels: Heuristics and Decomposition Methods. Ph.D. Thesis, University of Strathclyde, Glasgow, Scotland, 2017. [Google Scholar]
- Giachetti, R.E.; Damodaran, P.; Mestry, S.; Prada, C. Optimization-based decision support system for crew scheduling in the cruise industry. Comput. Ind. Eng. 2013, 64, 500–510. [Google Scholar] [CrossRef] [Green Version]
- Damodaran, P.; Mestry, S.; Zuniga, M.; Perez, J.; Brearley, R.; Arteta, B. A mathematical model for scheduling shipboard crew in cruise lines. In Proceedings of the IIE Annual Conference Expo 2010 Proceedings, Boston, MA, USA, 23–25 June 2010. [Google Scholar]
- Sereno, V.M.; Reinhardt, L.B.; Guericke, S. Exact Methods and Heuristics for the Liner Shipping Crew Scheduling Problem. In Computational Logistics; Cerulli, R., Raiconi, A., Voß, S., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2018; Volume 11184, pp. 363–378. [Google Scholar] [CrossRef]
- Leggate, A. A Vessel Crew Scheduling Problem: Formulations and Solution Methods. Ph.D. Thesis, University of Strathclyde, Glasgow, Scotland, 2016. [Google Scholar]
- Rizvanolli, A.; John, O. Ein gemischt-ganzzahliges lineares Optimierungs- modell zur Ermittlung des minimal notwendigen Bedarfes an Seefahrern zur Besetzung eines Schiffes. In Entscheidungsunterstützung in Theorie und Praxis; Spengler, T., Fichtner, W., Geiger, M.J., Rommelfanger, H., Metzger, O., Eds.; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2017; pp. 87–107. [Google Scholar] [CrossRef]
- Rizvanolli, A.; Heise, C.G. Efficient Ship Crew Scheduling Complying with Resting Hours Regulations. In Operations Research Proceedings 2016; Fink, A., Fügenschuh, A., Geiger, M.J., Eds.; Operations Research Proceedings; Springer International Publishing: Cham, Switzerland, 2018; pp. 535–541. [Google Scholar] [CrossRef]

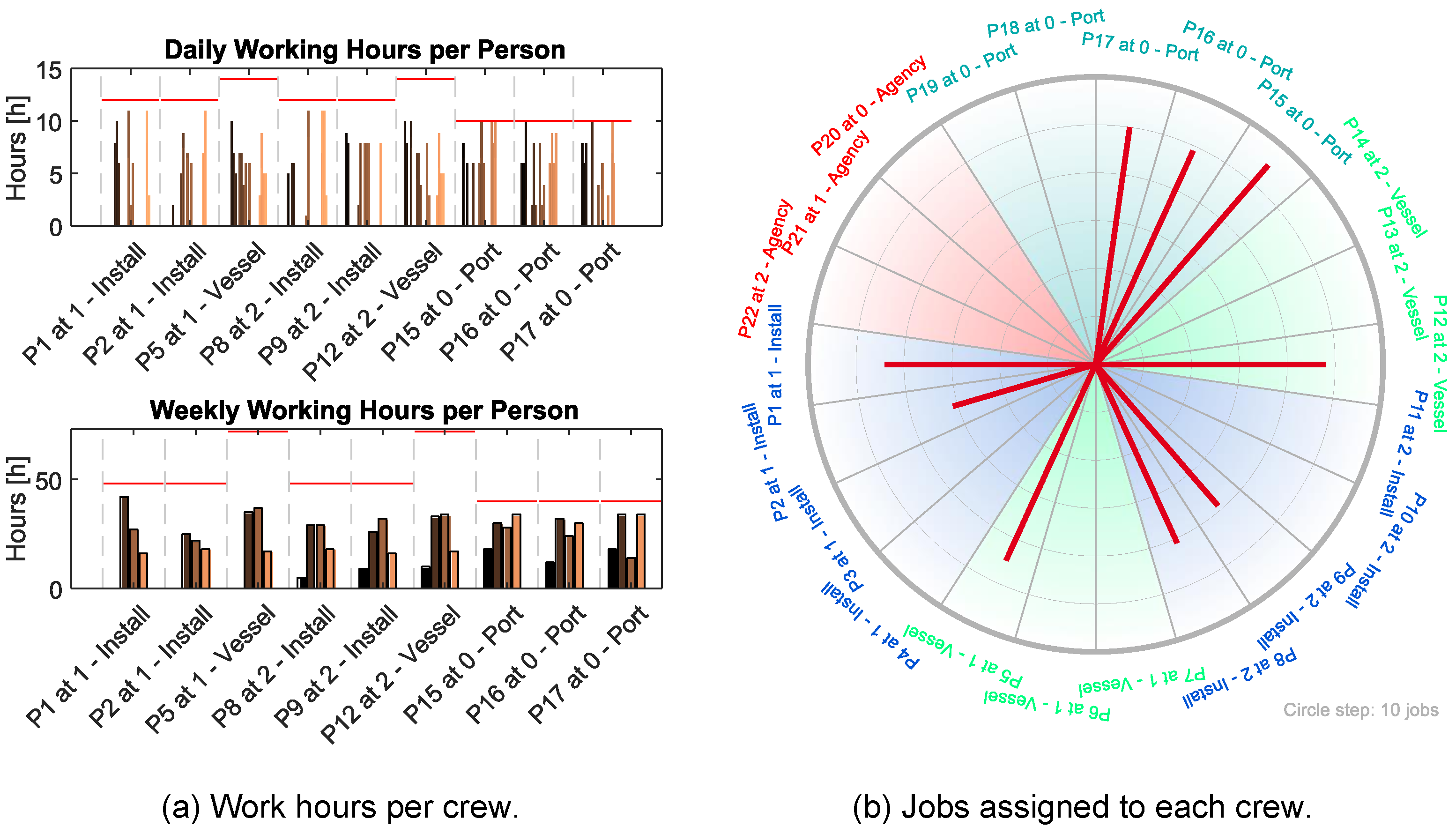
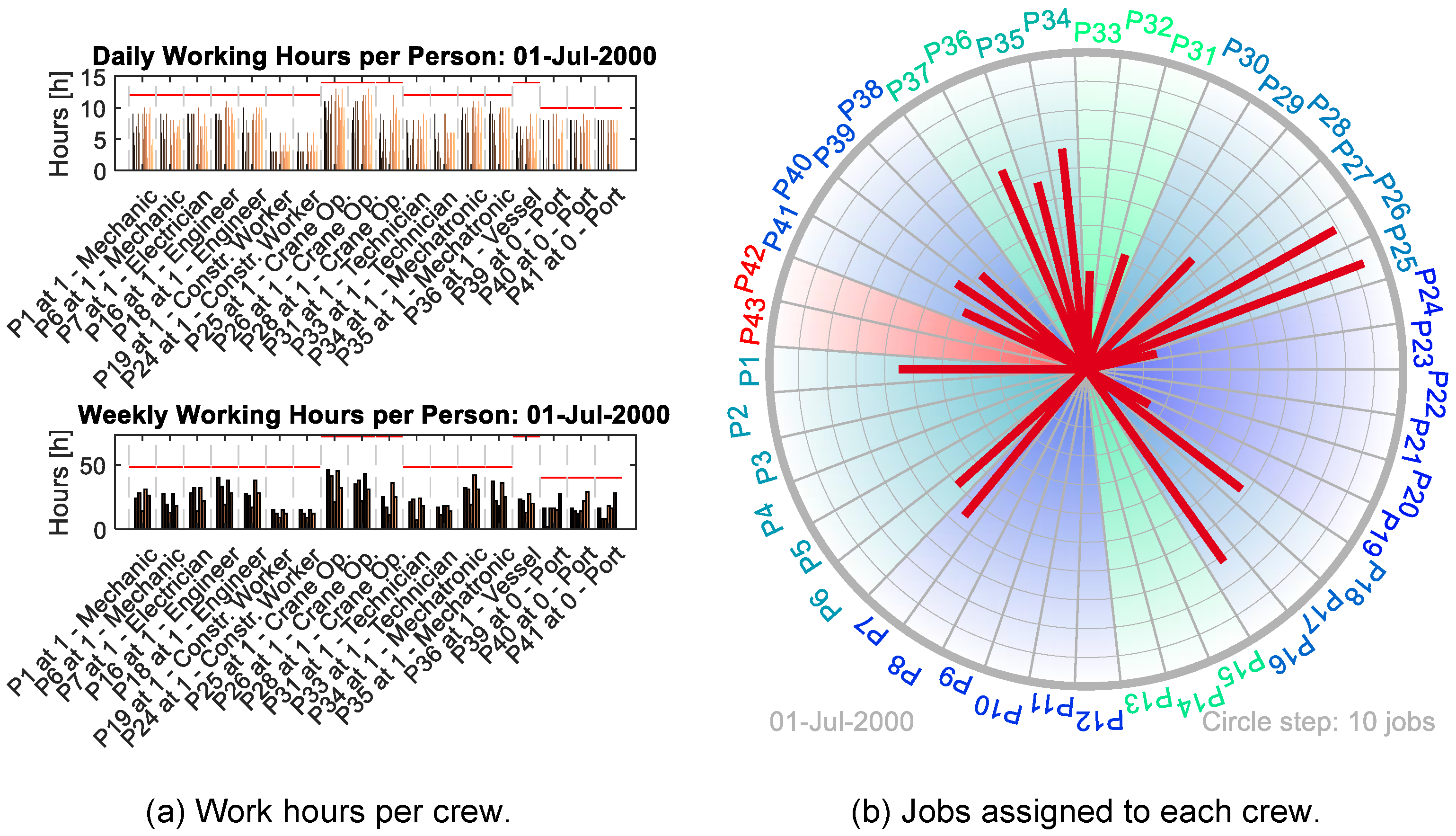
| Operation | Base-Duration | Max. Wind | Max. Wave | Responsible |
|---|---|---|---|---|
| [h] | [m/s] | [m] | Crew | |
| Load Tower | 3 | 12 1 | 5 1 | Port Crew |
| Load Nacelle | 2 | 12 1 | 5 1 | Port Crew |
| Load Hub | 1 | 12 1 | 5 1 | Port Crew |
| Load Blade | 2 | 12 1 | 5 1 | Port Crew |
| Traveling | 4 | 21 | 2.5 | Vessel Crew |
| (Re-)Positioning | 1 | 14 | 2.0 | Vessel Crew |
| Jack-up/-down | 2 | 14 | 1.8 | Vessel Crew |
| Install Tower | 3 | 12 | 2.5 2 | Project Crew |
| Install Nacelle | 3 | 12 | 2.5 2 | Project Crew |
| Install Hub | 2 | 12 | 2.5 2 | Project Crew |
| Install Blade | 2 | 10 | 2.5 2 | Project Crew |
| Publication | Objective | Domain | Horizon |
|---|---|---|---|
| Damodaran et al. (2010) [34] | Min. Cost | Cruise-Lanes | 1 Year |
| Giachetti et al. (2013) [33] | Min. Trip Cost | Cruise-Lanes | 240 Days |
| John et al. (2014) [26] | Min. Cost | Shipping Lines | One Trip |
| Sereno et al. (2018) [35] | Min. Trip Cost | Shipping Lines | 1 Year |
| Leggate (2016) [36] | Min. Cost | Offshore Supply | 3+ Months |
| Sucu (2017) [32] | Min. Cost | Offshore Supply | 3+ Months |
| Leggate et al. (2018) [31] | Min. Cost and | Offshore Supply | 3+ Months |
| Min. Num Changes | |||
| Rizvanolli and John (2017) [37] | Min. Crew | Container Transp. | One Trip |
| Rizvanolli and Heise (2018) [38] | Min. Crew | Container Transp. | One Trip |
| Parameter | Symbol | Unit | Domain |
|---|---|---|---|
| Sets and Indices | |||
| Prediction Horizon | Hours | ||
| Set of Persons/Crews | Persons | - | |
| Set of Jobs | Jobs | - | |
| Set of Locations | Locations | - | |
| Set of Skills | Skills | - | |
| Rule Sets | Rulesets | - | |
| Job Information | |||
| Job Start Instance | Hour | ||
| Job End Instance | Hour | ||
| Job Duration | Hours | ||
| Location of Job | Location | ||
| Assignment of Req. Skills to Jobs | Experience | ||
| Personnel Information | |||
| Assignment of Ruleset to Persons | Index | ||
| Assignment of Skills to Persons | Experience | ||
| Cost per Person | Currency | ||
| Ruleset Information | |||
| Maximum Daily Workload | Hours | ||
| Maximum Weekly Workload | Hours | ||
| Rest Period | Hours | ||
| Length of Breaks | Hours | ||
| Break Interval (One Break each) | Hours | ||
| Current State Information | |||
| Availability of Person | Unavailable | Binary | |
| Location of Personnel | Location | ||
| Presence of Person at Job Location | At Location | Binary | |
| Index of Next Week | Hours | ||
| Index of Next Day | Hours | ||
| Needs to Start Rest Today | Requires | Binary | |
| Needs to End Rest Today | Requires | Binary | |
| Hours Worked Today | Hours | ||
| Hours Worked This Week | Hours | ||
| Free Time at End of the Last Iteration | Hours | ||
| Parameter | Port Crew | Vessel Crew | Project Crew | Agency |
|---|---|---|---|---|
| Maximum Daily Workload | 14 | 12 | 10 | 24 |
| Maximum Weekly Workload | 72 | 48 | 40 | 168 |
| Rest Period | 6 | 11 | 11 | 0 |
| Length of Breaks | 1 | 1 | 1 | 0 |
| Break Interval | 10 | 10 | 8 | 0 |
| Number per Location | 5 | 3 | 4 | 1 |
| Inst. Tower | Inst. Nacelle | Inst. Blade | Inst. Hub | |
|---|---|---|---|---|
| Mechanic | 2 | 1 | 2 | 2 |
| Electrician | 1 | 2 | 1 | 2 |
| Welder | 1 | 0 | 0 | 0 |
| Engineer | 1 | 1 | 1 | 1 |
| Construction Worker | 2 | 0 | 0 | 0 |
| Crane Operator | 1 | 1 | 2 | 2 |
| Technician | 1 | 1 | 0 | 1 |
| Result | |||
|---|---|---|---|
| Key-Performance Indicator | All | One Vessel | Two Vessels |
| Average Number of Jobs Scheduled | 390.92 | ||
| Average Project Duration | 771 h | 1007 h | 535 h |
| Average Number of Planning Iterations | 2.75 | 3.17 | 2.33 |
| Total Number of Plan Interruptions | 10.0 | 4.00 | 6.00 |
| Average Optimization Time per Iteration | 25.25 s | 18.17 s | 32.32 s |
| Average Port Crews Required | 3.17 | 3.00 | 3.33 |
| Average Vessel Crews Required | 1.50 | 1.00 | 2.00 |
| Average Project Crews Required | 3.17 | 2.17 | 4.17 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rippel, D.; Foroushani, F.A.; Lütjen, M.; Freitag, M. A Crew Scheduling Model to Incrementally Optimize Workforce Assignments for Offshore Wind Farm Constructions. Energies 2021, 14, 6963. https://doi.org/10.3390/en14216963
Rippel D, Foroushani FA, Lütjen M, Freitag M. A Crew Scheduling Model to Incrementally Optimize Workforce Assignments for Offshore Wind Farm Constructions. Energies. 2021; 14(21):6963. https://doi.org/10.3390/en14216963
Chicago/Turabian StyleRippel, Daniel, Fatemeh Abasian Foroushani, Michael Lütjen, and Michael Freitag. 2021. "A Crew Scheduling Model to Incrementally Optimize Workforce Assignments for Offshore Wind Farm Constructions" Energies 14, no. 21: 6963. https://doi.org/10.3390/en14216963
APA StyleRippel, D., Foroushani, F. A., Lütjen, M., & Freitag, M. (2021). A Crew Scheduling Model to Incrementally Optimize Workforce Assignments for Offshore Wind Farm Constructions. Energies, 14(21), 6963. https://doi.org/10.3390/en14216963