Shaft Voltage Reduction Method Using Carrier Wave Phase Shift in IPMSM
Abstract
:1. Introduction
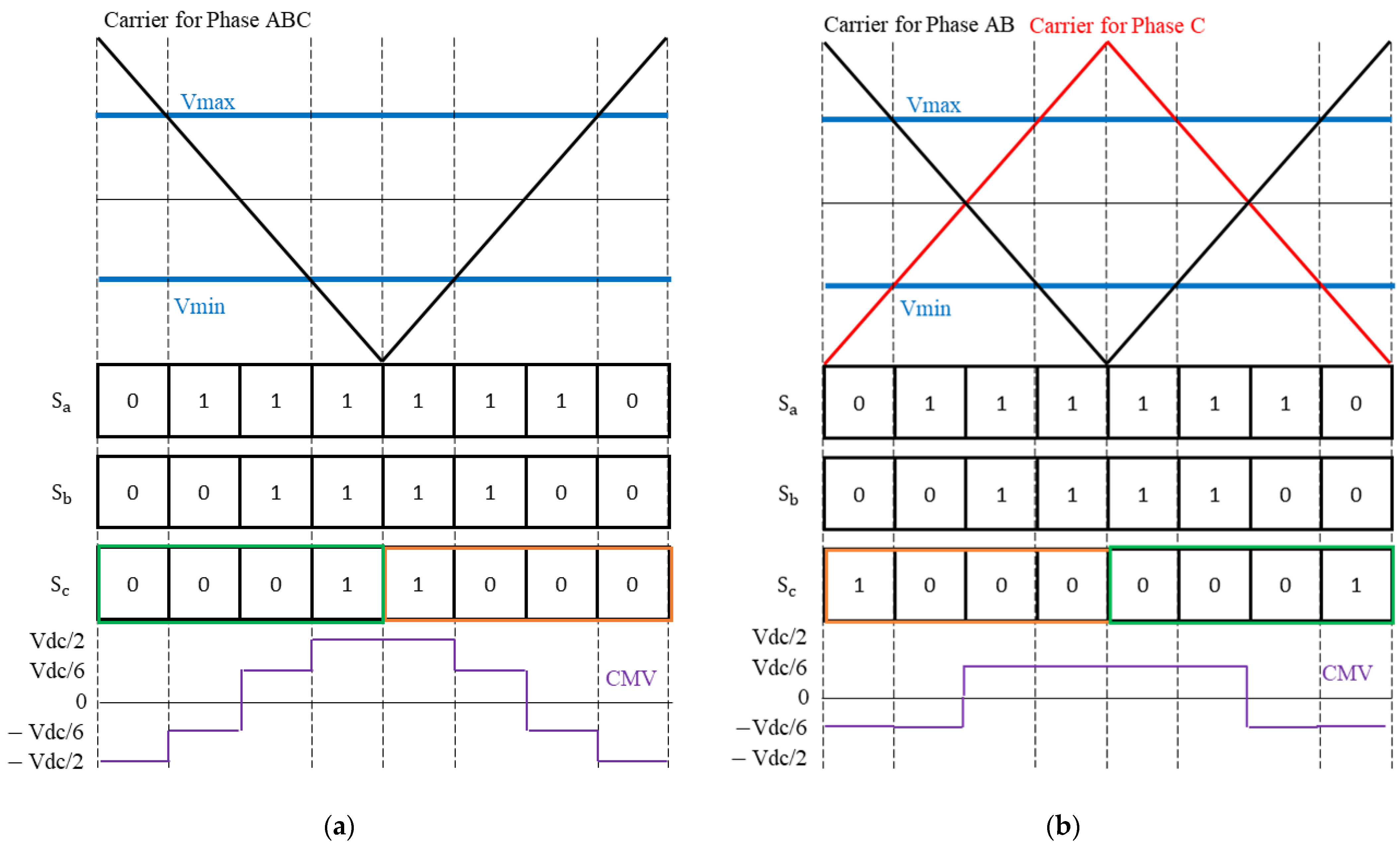
2. CMV and Switching States
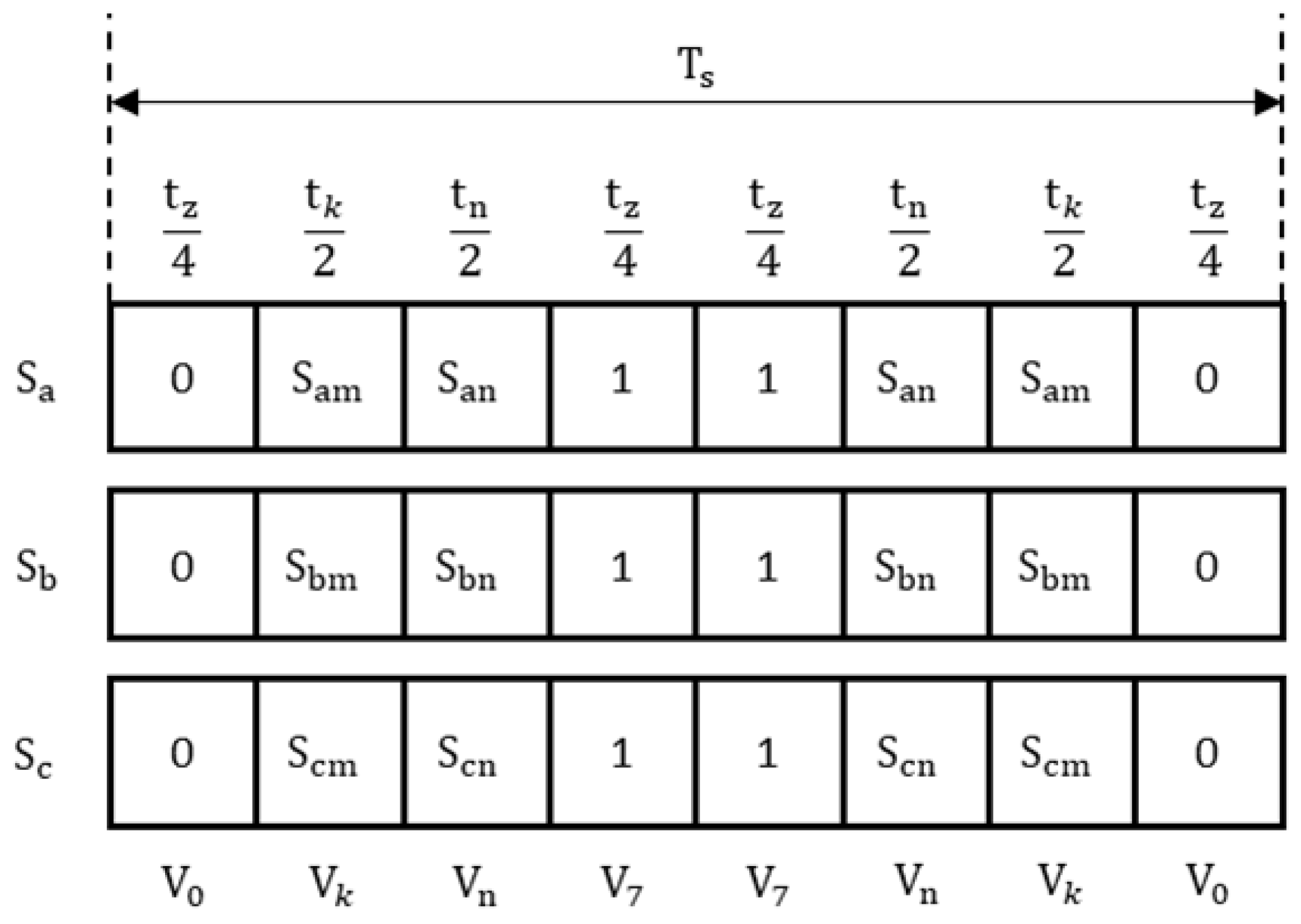
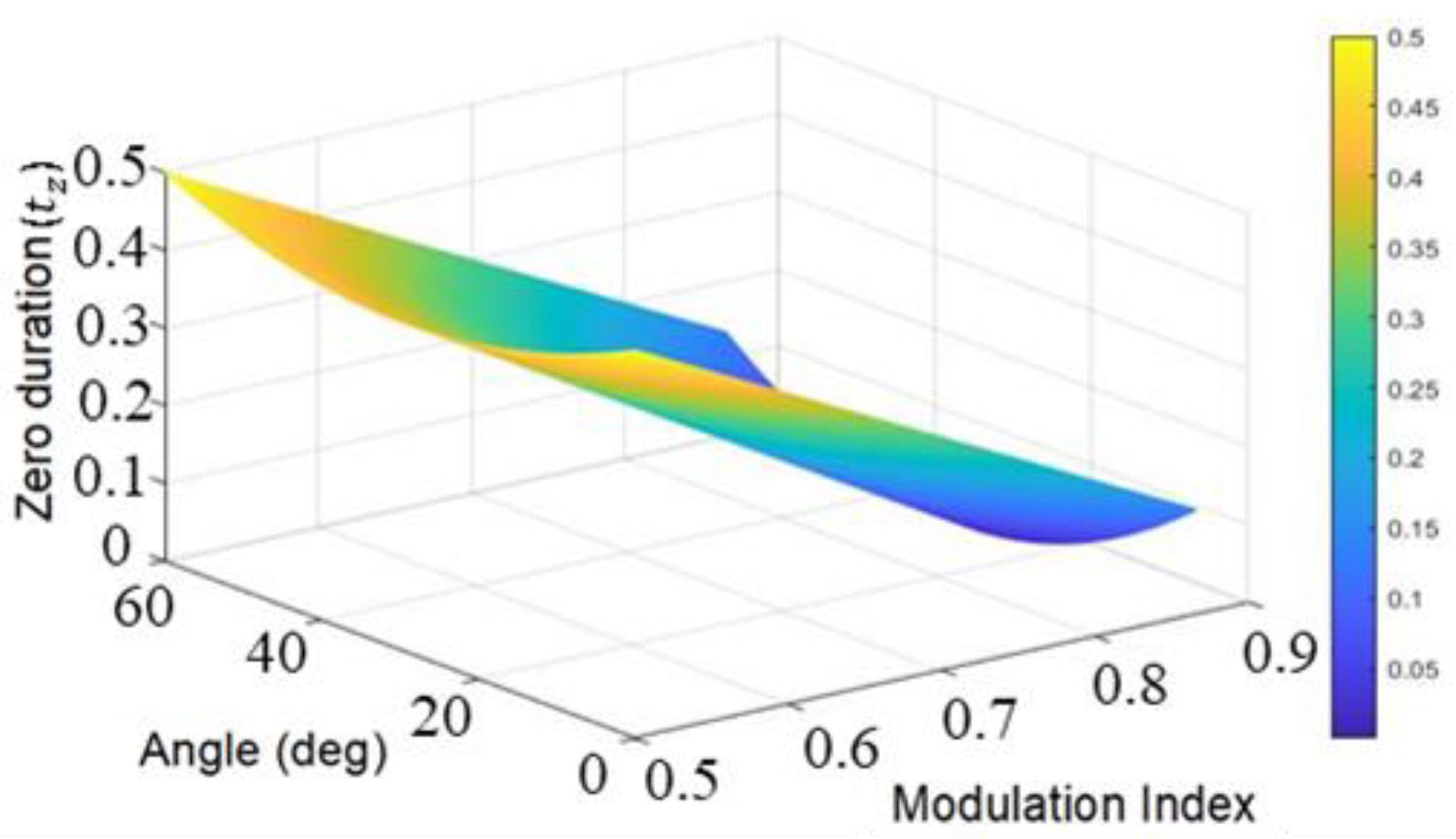
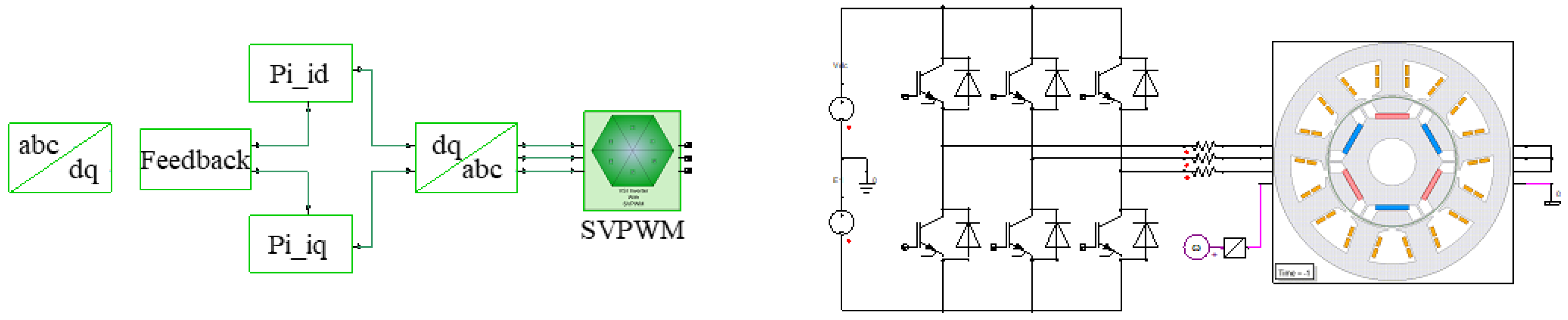
3. Carrier Wave Phase Shift in SVPWM
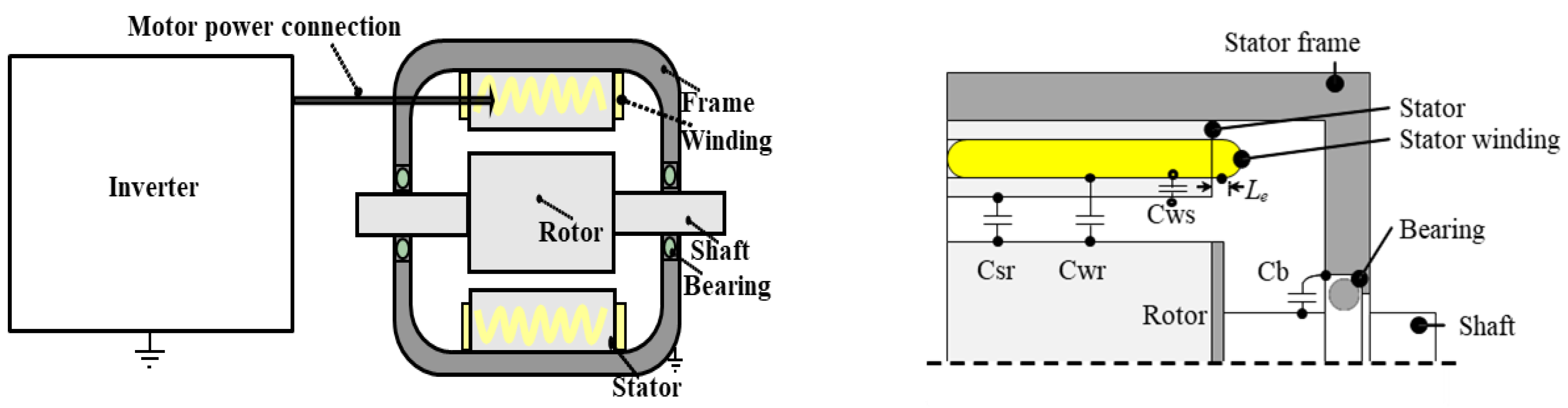
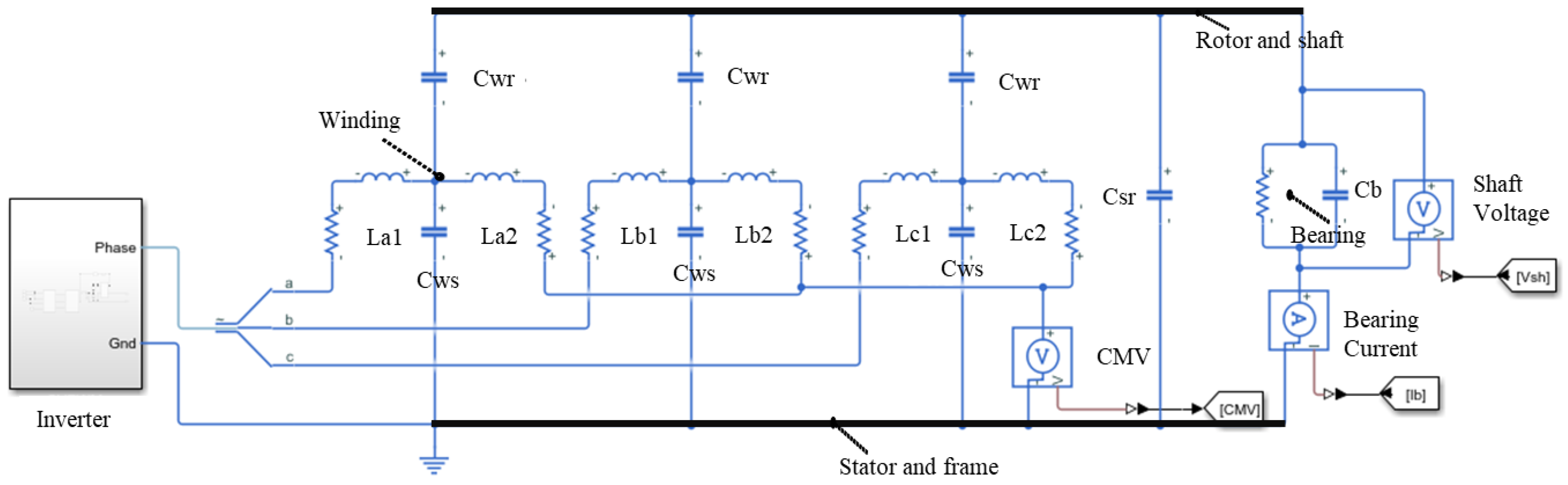
4. Equivalent Circuit Model
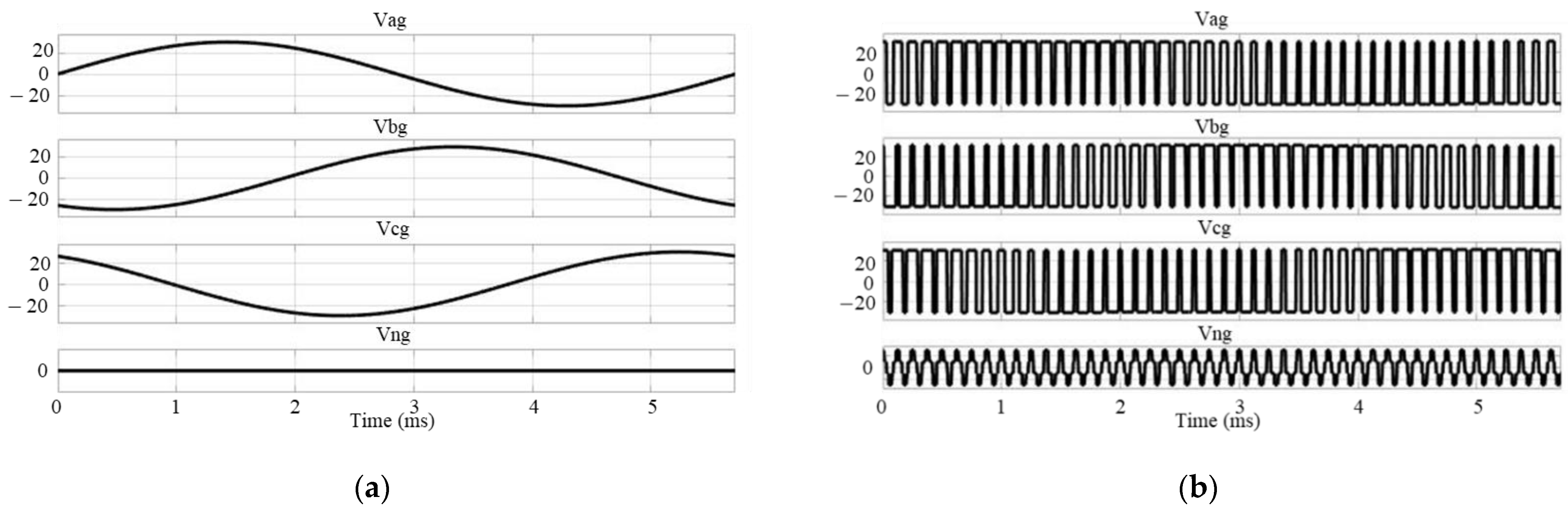
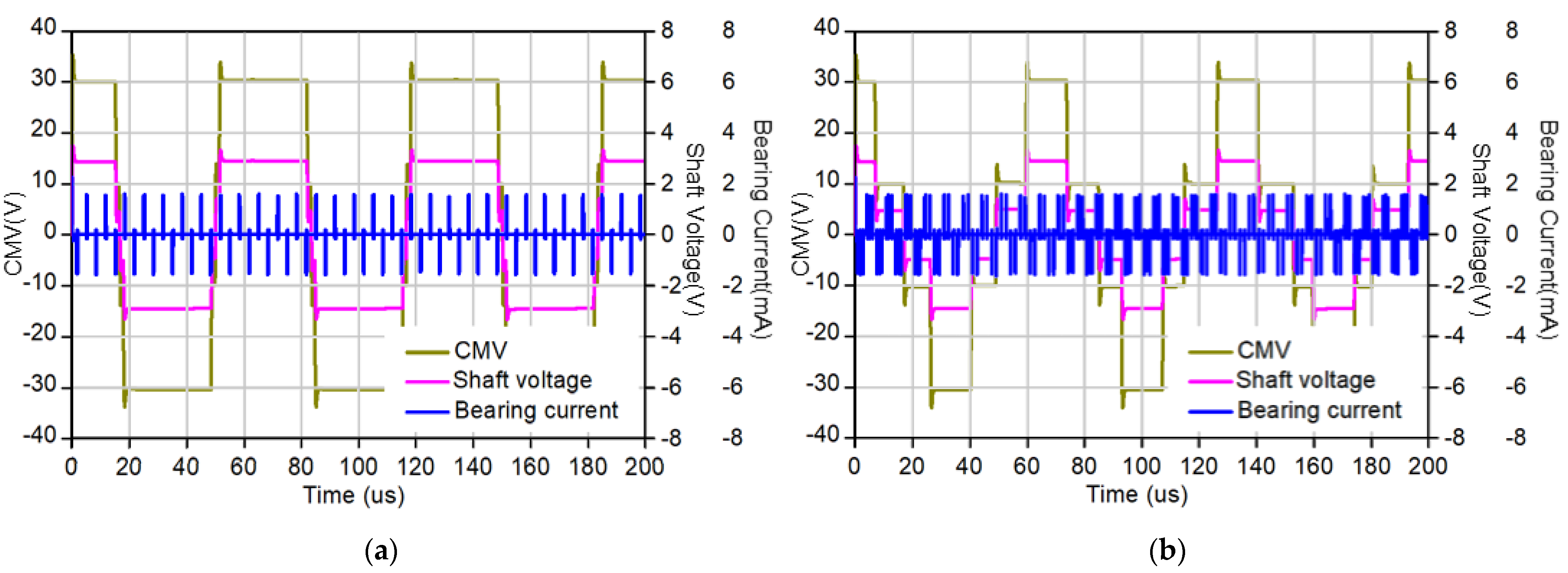
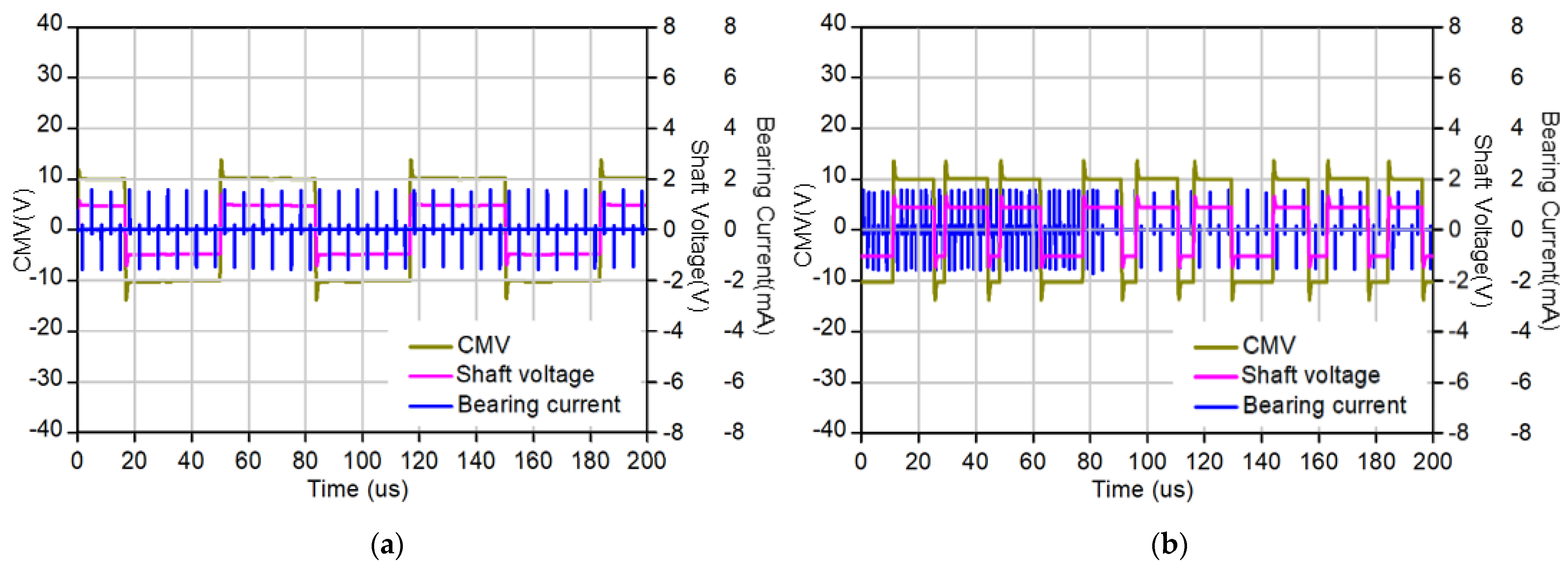
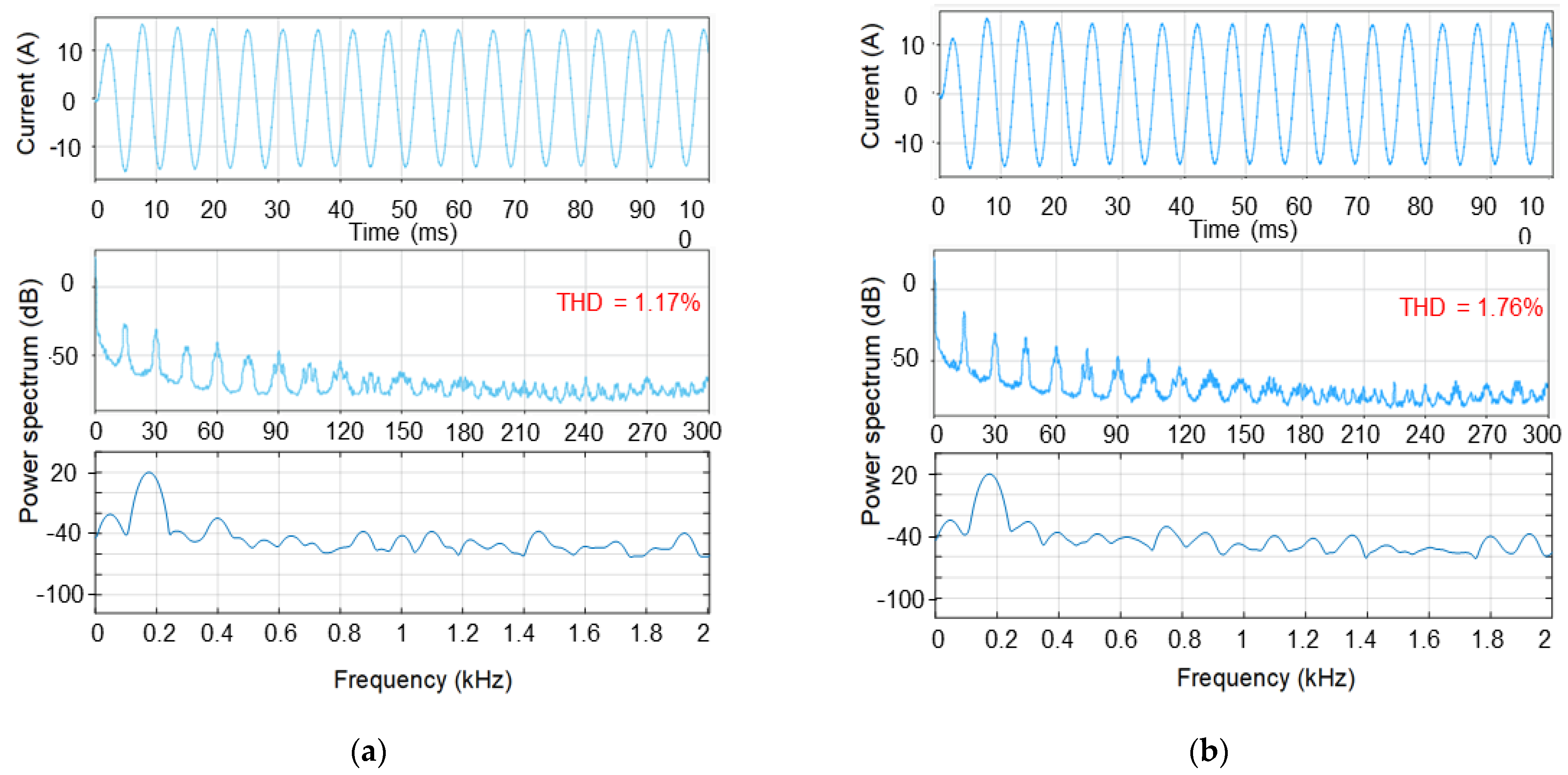
5. Simulation Results
- A.
- Shaft Voltage and Bearing Current
- B.
- Changes of input and output
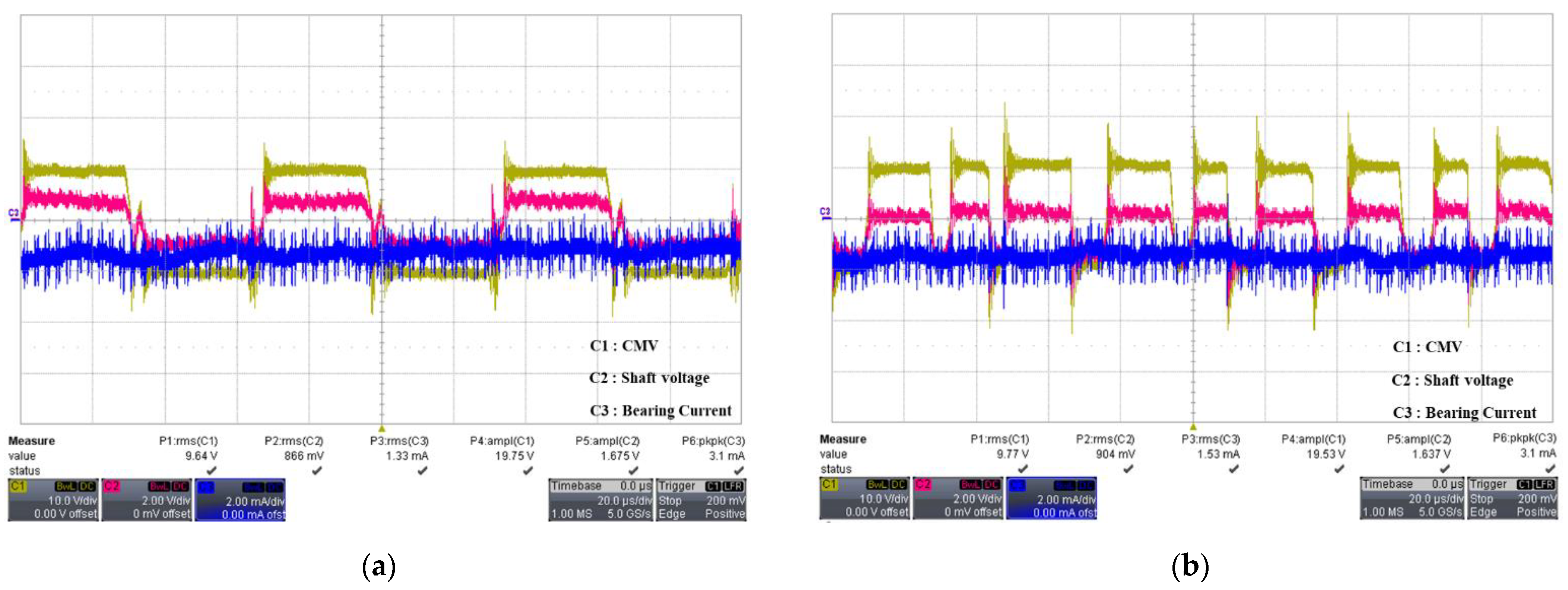
6. Experiment Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Park, J.-K.; Jeong, C.-L.; Lee, S.-T.; Hur, J. Early detection technique for stator winding inter-turn fault in bldc motor using input impedance. IEEE Trans. Ind. Appl. 2014, 51, 240–247. [Google Scholar] [CrossRef]
- Park, J.-K.; Hur, J. Detection of Inter-Turn and dynamic eccentricity faults using stator current frequency pattern in IPM-Type BLDC Motors. IEEE Trans. Ind. Electron. 2015, 63, 1771–1780. [Google Scholar] [CrossRef]
- Hong, J.; Park, S.; Hyun, D.; Kang, T.-J.; Bin Lee, S.; Kral, C.; Haumer, A. Detection and classification of rotor demagnetization and eccentricity faults for pm synchronous motors. IEEE Trans. Ind. Appl. 2012, 48, 923–932. [Google Scholar] [CrossRef]
- Ebrahimi, B.M.; Faiz, J. Demagnetization Fault diagnosis in surface mounted permanent magnet synchronous motors. IEEE Trans. Magn. 2013, 49, 1185–1192. [Google Scholar] [CrossRef]
- Esfahani, E.; Wang, S.; Sundararajan, V. Multisensor wireless system for eccentricity and bearing fault detection in induction motors. IEEE ASME Trans. Mechatron. 2014, 19, 818–826. [Google Scholar] [CrossRef]
- Ebrahimi, B.M.; Roshtkhari, M.J.; Faiz, J.; Khatami, S.V. Advanced eccentricity fault recognition in permanent magnet synchronous motors using stator current signature analysis. IEEE Trans. Ind. Electron. 2014, 61, 2041–2052. [Google Scholar] [CrossRef]
- Jin, X.; Zhao, M.; Chow, T.W.S.; Pecht, M. Motor bearing fault diagnosis using trace ratio linear discriminant analysis. IEEE Trans. Ind. Electron. 2014, 61, 2441–2451. [Google Scholar] [CrossRef]
- Blodt, M.; Granjon, P.; Raison, B.; Rostaing, G. Models for bearing damage detection in induction motors using stator current monitoring. IEEE Trans. Ind. Electron. 2008, 55, 1813–1822. [Google Scholar] [CrossRef] [Green Version]
- Prieto, M.D.; Cirrincione, G.; Espinosa, A.G.; Ortega, J.A.; Henao, H. Bearing fault detection by a novel condition-monitoring scheme based on statistical-time features and neural networks. IEEE Trans. Ind. Electron. 2013, 60, 3398–3407. [Google Scholar] [CrossRef]
- Immovilli, F.; Cocconcelli, M.; Bellini, A.; Rubini, R. Detection of generalized-roughness bearing fault by spectral-kurtosis energy of vibration or current signals. IEEE Trans. Ind. Electron. 2009, 56, 4710–4717. [Google Scholar] [CrossRef]
- Stack, J.; Harley, R.; Habetler, T. An Amplitude modulation detector for fault diagnosis in rolling element bearings. IEEE Trans. Ind. Electron. 2004, 51, 1097–1102. [Google Scholar] [CrossRef]
- Chen, S.; Lipo, T.A.; Fitzgerald, D. Modeling of motor bearing currents in PWM inverter drives. IEEE Trans. Ind. Appl. 1996, 32, 1365–1370. [Google Scholar] [CrossRef]
- Busse, D.; Erdman, J.; Kerkman, R.; Schlegel, D.; Skibinski, G. System electrical parameters and their effects on bearing currents. IEEE Trans. Ind. Appl. 1997, 33, 577–584. [Google Scholar] [CrossRef]
- Zare, F.; Adabi, J.; Nami, A.; Ghosh, A. Common mode voltage in a motor drive system with PFC. In Proceedings of the 14th International Power Electronics and Motion Control Conference EPE-PEMC 2010, Ohrid, Macedonia, 6–8 September 2010; pp. T4-57–T4-64. [Google Scholar] [CrossRef]
- Isomura, Y.; Yamamoto, K.; Morimoto, S.; Maetani, T.; Watanabe, A.; Nakano, K. Study of the further reduction of shaft voltage of brushless dc motor with insulated rotor driven by pwm inverter. IEEE Trans. Ind. Appl. 2014, 50, 3738–3743. [Google Scholar] [CrossRef]
- Bai, B.; Wang, Y.; Wang, X. Suppression for discharging bearing current in variable-frequency motors based on electromagnetic shielding slot wedge. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar] [CrossRef]
- Park, J.-K.; Thusitha, W.; Choi, S.-J.; Hur, J. Shaft-to-frame voltage suppressing approach by applying eletromagnetic shield in IPMSM. In Proceedings of the 2017 IEEE International Electric Machines and Drives Conference (IEMDC), Miami, FL, USA, 21–24 May 2017; pp. 1–7. [Google Scholar]
- Lee, S.-T.; Park, J.-K.; Jeong, C.-L.; Rhyu, S.-H.; Hur, J. Shaft-to-frame voltage mitigation method by changing winding-to-rotor parasitic capacitance of IPMSM. IEEE Trans. Ind. Appl. 2019, 55, 1430–1436. [Google Scholar] [CrossRef]
- Guo, Y.; Li, Z.; Li, H.; Zhang, X. Dual carrier based PWMstrategy for common-mode voltage reduction of three-phase voltage source inverters. IEICE Electron. Express 2018, 15, 20180994. [Google Scholar]
- Cacciato, M.; Consoli, A.; Scarcella, G.; Testa, A. Reduction of common-mode currents in PWMinverter motor drives. IEEE Trans. Ind. Appl. 1999, 35, 469–476. [Google Scholar] [CrossRef]
- Un, E.; Hava, A.M. A Near-State PWM method with reduced switching losses and reduced common-mode voltage for three-phase voltage source inverters. IEEE Trans. Ind. Appl. 2009, 45, 782–793. [Google Scholar] [CrossRef]
- Hava, A.M.; Ün, E. Performance analysis of reduced common-mode voltage PWM Methods and comparison with standard PWM methods for three-phase voltage-source inverters. IEEE Trans. Power Electron. 2009, 24, 241–252. [Google Scholar] [CrossRef]
- Janabi, A.; Wang, B. Hybrid SVPWM Scheme to Minimize the common-mode voltage frequency and amplitude in voltage source inverter drives. IEEE Trans. Power Electron. 2018, 34, 1595–1610. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhong, Y.; Gao, H.; Yuan, L.; Lu, T. Hybrid selective harmonic elimination PWM for common-mode voltage re-duction in three-level neutral-point- clamped inverters for variable speed induction drives. IEEE Trans. Power Electron. 2021, 27, 1152–1158. [Google Scholar] [CrossRef]
- Kwak, S.; Mun, S.-K. Model predictive control methods to reduce common-mode voltage for three-phase voltage source inverters. IEEE Trans. Power Electron. 2015, 30, 5019–5035. [Google Scholar] [CrossRef]
- Park, J.-K.; Wellawatta, T.R.; Choi, S.-J.; Hur, J. Mitigation Method of the Shaft Voltage According to Parasitic Capacitance of the PMSM. IEEE Trans. Ind. Appl. 2017, 53, 4441–4449. [Google Scholar] [CrossRef]
- Park, J.-K.; Wellawatta, T.R.; Ullah, Z.; Hur, J. New Equivalent Circuit of the IPM-Type BLDC Motor for Calculation of Shaft Voltage by Considering Electric and Magnetic Fields. IEEE Trans. Ind. Appl. 2016, 52, 3763–3771. [Google Scholar] [CrossRef]


| Space Vector | Switch State | Load Phase Voltage | CMV | ||
|---|---|---|---|---|---|
| [0 0 0] | 0 | 0 | 0 | ||
| [1 0 0] | |||||
| [1 1 0] | |||||
| [0 1 0] | |||||
| [0 1 1] | |||||
| [0 0 1] | |||||
| [1 0 1] | |||||
| [1 1 1] | 0 | 0 | 0 | ||
| Item | Appearance | Value | Units |
|---|---|---|---|
| p | No. of poles | 6 | |
| S | No. of slots | 9 | |
| DC Link voltage | 60 | V | |
| Switching Frequency | 15 | kHz | |
| Rated Speed | 3500 | RPM | |
| T | Rated Torque | 1.3 | N∙m |
| P | Rated Power | 400 | W |
| I | Rated Current | 10.32 | Arms |
| R | Stator resistance | 0.07 | ohm |
| Parasitic capacitance between winding and stator | 79.98 | pF | |
| Parasitic capacitance between winding and rotor | 8.73 | pF | |
| Parasitic capacitance between stator and rotor | 61.1 | pF | |
| parasitic capacitance between bearing and shaft | 186.8 | pF |
| Traditional | Proposed Method | ||||
|---|---|---|---|---|---|
| 500 rpm | 3500 rpm | 500 rpm | 3500 rpm | ||
| CMV | Peak-to-peak | 60 V | 60 V | 20 V | 20 V |
| RMS | 28.12 V | 17.95 V | 9.42 V | 9.42 V | |
| Shaft Voltage | Peak-to-peak | 5.28 V | 5.28 V | 1.72 V | 1.72 V |
| RMS | 2.48 V | 1.58 V | 0.87 V | 0.81 V | |
| Bearing Current | Peak-to-peak | 6.1 mA | 5.4 mA | 3.2 mA | 3.1 mA |
| RMS | 0.19 mA | 0.18 mA | 0.15 mA | 0.13 mA | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Im, J.-H.; Lee, Y.-K.; Park, J.-K.; Hur, J. Shaft Voltage Reduction Method Using Carrier Wave Phase Shift in IPMSM. Energies 2021, 14, 6924. https://doi.org/10.3390/en14216924
Im J-H, Lee Y-K, Park J-K, Hur J. Shaft Voltage Reduction Method Using Carrier Wave Phase Shift in IPMSM. Energies. 2021; 14(21):6924. https://doi.org/10.3390/en14216924
Chicago/Turabian StyleIm, Jun-Hyuk, Yeol-Kyeong Lee, Jun-Kyu Park, and Jin Hur. 2021. "Shaft Voltage Reduction Method Using Carrier Wave Phase Shift in IPMSM" Energies 14, no. 21: 6924. https://doi.org/10.3390/en14216924
APA StyleIm, J.-H., Lee, Y.-K., Park, J.-K., & Hur, J. (2021). Shaft Voltage Reduction Method Using Carrier Wave Phase Shift in IPMSM. Energies, 14(21), 6924. https://doi.org/10.3390/en14216924








