Abstract
The recently issued EN ISO 52016-1 technical standard provides a new simplified dynamic method for the building energy performance assessment. Since an extensive validation of the EN ISO 52016-1 hourly method is still missing, the present work investigates the effect of the main modelling assumptions—related to the heat balance on the outdoor and the indoor envelope surfaces—on the building thermal behaviour. The model validation was carried out by assessing the accuracy variation consequent to the application of the EN ISO 52016-1 modelling assumptions to a detailed dynamic calculation tool (EnergyPlus). To guarantee a general validity of the outcomes, two buildings, two levels of thermal insulation, and two Italian climatic zones were considered, for a total of eight case studies. To explore different applications of the standard method, the analysis was performed both under a free-floating condition—to evaluate the accuracy of the model in predicting the indoor operative temperatures—and to assess the annual energy needs for space heating and cooling. Results show that the assumptions related to the definition of the external convective and the shortwave (solar) radiation heat transfer lead to non-negligible inaccuracies in the EN ISO 52016-1 hourly model.
1. Introduction
In the last decade, different calculation methods were developed to address the issue of improving energy efficiency in buildings. According to the required level of accuracy or detail, as well as for the specific purpose, different calculation models can be found. Generally, they are categorised into quasi-steady state monthly or seasonal methods, and dynamic hourly methods, which can be either detailed or simplified [1]. All these methods should guarantee the compliance with requirements of robustness, repeatability, transparency, accuracy, and simplicity. The simplicity of the assessment, as well as the reproducibility of results, made the quasi-steady state methods to be widely applied over the years, especially for annual evaluations; however, individual month evaluations may lead to large errors [1]. On the other hand, detailed dynamic methods allow to obtain accurate results, often requiring not easily accessible detailed input data. In the middle, the simplified hourly methods are instead considered to be able to allow a sufficient level of accuracy, while guaranteeing the simplicity of the assessment.
Among the simplified hourly methods, the EN ISO 52016-1 technical standard hourly method [2] allows to take into account the effect of dynamic interactions, challenging the need for too detailed input data from the user [3]. To address this challenge, the hourly method is based on assumptions and simplifications selected as to guarantee a balance between the accuracy and the simplicity of the assessment. However, the modelling assumptions introduced by this simplified method may lead to inaccurate predictions in the energy consumption of buildings in both design phases and energy audits. Assessing the accuracy of the simplified method is thus of foremost importance, also considering the possible application of the EN ISO 52016-1 simplified method for legislative verifications, such as the checks on the compliance with the energy performance (EP) requirements, which is currently under discussion, for example, in Italy. Therefore, the effects related to the introduction of its modelling assumptions need to be investigated.
1.1. Validation Techniques of the Building Energy Models
Three approaches are commonly used for the building energy model validation: the analytical verification, the comparative testing, and the empirical validation [4]. The first technique consists in the comparison of the results of the tested model with the known analytical solution for an isolated heat transfer mechanism. However, its use is limited to the cases for which an analytical solution can be derived. In the empirical validation, the tested calculation method results are instead compared to monitored data from a real building. Finally, the comparative testing approach consists in the comparison of the results of the tested model to itself or to other codes. Although it relies on the accuracy of the model to which the tested one is compared, the inter-model comparison approach can be a very powerful approach to identify errors and to assess the accuracy of the tested model [5]. The comparative testing approach has been widely applied in the validation of building energy performance calculation models, and it proved its valuable capabilities in code debugging activities [6,7], in assessing the accuracy of building energy performance calculation models [8,9], and in the validation of several simulation programs. The main weakness of the comparative testing approach, if applied in inter-model comparisons, concerns the achievement of a sufficient input equivalence to ensure that each model is using comparable data [10]. Several research studies have introduced approaches for minimizing the errors due to differences in the input data [11,12]. However, input equivalence is not always a straightforward issue [13], and it may be difficult to reach a global equivalence in the input, which may lead to misleading results.
The presented validation techniques are generally coupled into comprehensive methodologies for the building energy model validation. Alongside the Solar Energy Research Institute (SERI) methodology [14], these testing techniques are also included in the European Union PASSYS Project methodology [15]. The PASSYS approach highlights two fundamental aspects related to the model validation. Firstly, it suggests that the model validation should be applied not only to the whole calculation model, but also to its single components. The main advantage of such validation method is the possibility to clearly detect inaccuracies in the algorithms or in the assumptions related to single portions of the tested calculation method [15]. Secondly, it includes a critical literature review in which the theory behind the different heat transfer processes is evaluated, and possible alternatives are investigated. The importance of this last aspect is also highlighted in the “Management of Information” System (MIS), a prototype tool developed by the IEA Annex 21 Subtask A [5] to assist the program development and validation. The developers and users are asked to document each choice made in terms of solving algorithm, or assumed simplification, or level of detail. Through the MIS, it is therefore possible to easily catch the causes of the discrepancies, for example while conducting several simulations or in validation activities.
1.2. Validation Studies of the EN ISO 52016-1 Hourly Model
Since its release in 2017, the assessment of the accuracy of the EN ISO 52016-1 simplified hourly method has been the central topic of a growing, but not yet sufficient, body of literature. Most of these studies apply the comparative testing validation approach to the whole model, and they allowed the authors to highlight the effect of some modelling options of the EN ISO 52016-1 hourly model on the accuracy of the method. Zakula et al. [12] tested the accuracy of the new simplified method by comparing it with the detailed dynamic method of TRNSYS (Transient System Simulation Tool) for ten Croatian reference buildings, characterised by different levels of thermal insulation, geometrical characteristics and building uses, and two climatic zones. Their results suggested that the simplified method tends to underestimate the heating needs and to overestimate the cooling needs compared to TRNSYS for the majority of buildings. Nevertheless, the Coefficient of Variation of Root Mean Square Error (cvRMSE), calculated on an hourly basis, satisfied the ASHRAE Guidelines-14 [16] for most of the considered case studies. Moreover, the Authors also showed that the use of fixed window solar properties (i.e., solar angle-independent), as introduced by the EN ISO 52016-1 hourly method, leads to significant discrepancies in the outcomes. This analysis was extended in [17], in which the authors provided a novel framework for the EN ISO 52016-1 accuracy assessment. The presented validation approach was applied to more than 147 thousand buildings; it revealed that the simplification in the modelling of the total solar energy transmittance has a significant impact in the accuracy of the simplified hourly method especially for intermediate climates. Improvements to the EN ISO 52016-1 hourly method were presented and evaluated as well. Similar results were also achieved by Kamaraj [18], who applied the Building Energy Simulation Test (BESTEST) approach [19] to evaluate the accuracy of the new standard in comparison with the TRNSYS model. Ballarini et al. [20] analysed the discrepancy between the results of the EN ISO 52016-1 hourly method and the detailed dynamic calculation model of EnergyPlus. Moreover, the authors proposed a validation methodology to identify the causes of deviations between the two models [11]. The proposed methodology consists in splitting the contributions of the air heat balance equation by dynamic driving force. This approach allowed the authors to detect the use of constant surface heat transfer coefficients as the main cause of deviation in the outcomes. The effect of single assumptions on the simulation results have been so far investigated by Mazzarella et al. [21]. The authors applied an analytical single process approach for the validation of the EN ISO 52016-1 conduction heat transfer model and of an improved version of this, introduced in the Italian National Annex of the standard.
1.3. Aims of the Research Work
Besides the investigations presented in literature, an extensive evaluation of the single modelling assumptions of the EN ISO 52016-1 hourly method is still missing and should be addressed with the aim to detect possible inaccuracies and to consider alternative calculation options. Within this framework, the present study is aimed at assessing the accuracy of the assumptions related to the envelope outdoor and indoor surface heat balance, specified in the EN ISO 52016-1 technical standard. A single-process validation approach fitting into the comparative testing technique is proposed, and it is aimed to:
- detect the modelling assumptions of the simplified hourly method on different levels, such as the modelling of the thermo-physical phenomena, the neglecting of some physical phenomena, the determination or the temporal discretisation of specific calculation parameters, or the definition of calculation boundary conditions,
- minimise the uncertainty in the validation of a calculation method due to inconsistencies in the input data,
- highlight the expected accuracy and limitations of the model for different applications [12], and thus answer to the question: “Is it good enough for [whatever purpose]?” [5].
To these purposes, the assumptions of the simplified method are analysed in comparison with the full detailed dynamic calculation model of EnergyPlus, and documented (topic 1). The documented simplifications are then tested one-at-a-time through a parametric analysis. To control and discard the so called “external errors” (input data) [4], the analysis is carried out by testing each calculation assumption on a detailed dynamic EnergyPlus model. Such approach allows to reach an overall input equivalence (topic 2), and to clearly investigate the “internal errors” (modelling options and assumptions). To assess whether the simplified EN ISO 52016-1 hourly method is suitable for different applications, and if its modelling simplifications are appropriate for specific purposes (topic 3), the effect the EN ISO 52016-1 modelling assumptions is evaluated in both predictions of the annual energy needs for heating and cooling, and of the hourly thermal loads and internal temperatures. Since the assumptions may influence the accuracy of a simulation depending on the building being analysed [4], different building categories, levels of thermal insulation of the building envelope and weather conditions are considered to guarantee a general validity of the outcomes.
A preliminary study was published by the same Authors [22], where the simplifications related to the outdoor surface heat balance were outlined and tested considering two case studies in three Italian climatic zones. The present work builds on the previous one by considering also the EN ISO 52016-1 assumptions of the indoor surface heat balance. A larger number of case studies (considering different geometries, levels of thermal insulation, and climatic zones) were considered to assess the accuracy of the simplified model. Moreover, the analysis was deepened evaluating both thermal loads and indoor operative temperatures.
2. Materials and Methods
2.1. Simplified Modelling of External Driving Forces
Four types of assumption can be applied to the building loads calculation models. In particular, the simplifications may be related to the mathematical models used either to describe a phenomenon or to define specific calculation parameters. The assumed assumptions may also concern the temporal discretisation of the calculation parameters, as well as the definition of calculation boundary conditions. Referring to these assumption types, the simplifications introduced by the EN ISO 52016-1 hourly method applied to the outside surface heat balance are analysed in the present paragraph, as well as documented and compared with the full detailed dynamic calculation model of EnergyPlus.
2.1.1. Convective Heat Transfer
The external convective heat transfer phenomenon is described by means of the classical formulation for the convective heat transfer by both the EN ISO 52016-1 simplified method and the detailed method of EnergyPlus. The areal heat flux transferred between the outdoor surface and the environment (qconv,ext, expressed in W·m−2) is calculated as
where hc,ext is the external convective heat transfer coefficient (in W·m−2·K−1), and Tair,ext and Tsurf are the temperatures (in K) of the outdoor air and of the surface, respectively.
In EN ISO 52016-1, the convective heat transfer coefficient (used in Equation (1)) is defined by applying the wind-speed correlation (forced convection) presented in EN ISO 6946 [23], as
where v is the wind speed (in m·s−1). On the other hand, EnergyPlus offers a wide selection of calculation models for the hc,ext determination; for the sake of the present study, the Thermal Analysis Research Program (TARP) algorithm [24] was assumed as reference. According to the TARP formulation, the external convection is split into its natural and forced components, and hc,ext is calculated as the sum of the respective heat transfer coefficients. The forced component is calculated by means of the Sparrow et al. formulation [25], which takes into account the surface geometrical characteristics, roughness and wind exposure, and the wind speed. The natural component is instead calculated by means of three different formulations for vertical, upward, and downward facing surfaces [24].
In the EN ISO 52016-1 hourly method, a time-independent (constant over the calculation period) convective heat transfer coefficient is assumed, while a timestep variable coefficient is adopted in EnergyPlus, if not explicitly required by the user.
Finally, outdoor air temperatures and wind speed relative to the site (used in Equations (1) and (2)) are considered in the simplified method, while local values calculated at the height above ground of the surface centroid are assumed in EnergyPlus.
2.1.2. Longwave Radiation Heat Transfer
The external longwave radiation heat transferred between the surface, the sky, and the ground (qlwr, expressed in W·m−2) is calculated by applying the Stefan-Boltzmann law in EnergyPlus, as
where ε is the surface thermal emissivity, σ is the Stefan-Boltzmann constant (5.67 × 10−8 W·m−2·K−4), while Tgnd, Tsky, Tair and Tsurf are respectively the ground, the sky, the outdoor air and the surface temperatures (in K), and Fgnd, Fsky and Fair are the view factors between the surface and the ground, the sky and the air, respectively. The linearised formulation is instead applied in the simplified hourly method of the EN ISO 52016-1 technical standard; the qlwr (in W·m−2) is calculated as
where hr,ext is the external radiative heat transfer coefficient (in W·m−2·K−1), Tsurf and Tair are the surface and the outdoor air temperatures (in K), respectively, and ΔTsky is the difference between the outdoor air temperature and the apparent sky temperature (in K).
The radiative heat transfer coefficient used in Equation (4) is assumed time-independent and is calculated by means of the EN ISO 6946 formulation [23], as
where Tm is the average temperature of the surface and of its surroundings (in K). Moreover, the determination of the view factor between the surface and the sky, which is used in Equations (3) and (4), takes into account the presence of external obstacles—such shadings or other buildings—in EnergyPlus, while this aspect is not considered in the simplified method.
Finally, the apparent sky temperature is determined by applying a direct model [26] in the simplified hourly method; a constant difference between the apparent sky and the air temperature is assumed [2]. In EnergyPlus, instead, the sky temperature is determined by applying an atmospheric emissivity model; in particular, the Clark-Allen correlation [27] is applied. As for the convective heat transfer, site values and local values of the outdoor air temperature are assumed by the simplified and by the detailed method, respectively.
2.1.3. Solar (Shortwave) Radiation
The solar gains on any exterior surface are a combination of the absorption of direct and diffuse solar radiation both in the EN ISO 52016-1 hourly method and in EnergyPlus. In case of shaded surfaces, both the methods consider the reduction of the direct radiation reaching the surface by means of the sunlit fraction, while the shadowing of the diffuse solar radiation component is considered only by EnergyPlus through a correction factor. This factor takes into account the angle between the surface and the sky, and the radiance distribution of the sky.
As far as the definition of the solar radiation entering the zone through the transparent envelope is concerned, the simplified and the detailed methods differ under two main aspects. Firstly, the total transmitted solar radiation is assumed to be completely shortwave radiation in EN ISO 52016-1, while EnergyPlus takes into account the effect from the absorption of solar radiation, and its emission as longwave radiation.
Secondarily, the solar properties of windows are considered solar-angle-dependent in EnergyPlus, and are determined by means of the Fresnel’s equation, while a weighted time average value of the total solar energy transmittance (g-value or SHGC) is assumed over the simulation period in EN ISO 52016-1. This is calculated by means of the exposure correction factor (Fw), as
where ggl,n is the total solar energy transmittance at normal incidence. The solar properties of windows are considered time-independent in EN ISO 52016-1, and the Fw factor is assumed constant over the calculation period. On the other hand, a solar angle-dependent Fw is considered in the Italian National Annex (NA) to EN ISO 52016-1; it is calculated as a weighted average of a Fw factor for diffuse radiation (assumed equal to 0.8 over the calculation period) and a Fw factor for beam solar radiation. The latter is calculated on a timestep basis accordingly to the empirical model introduced by Karlsson and Roos [28].
2.2. Simplified Modelling of Internal Driving Forces
As done for the external driving forces in Section 2.1, in the present section the simplifications introduced by the EN ISO 52016-1 hourly method applied to the inside surface heat balance are compared with the full detailed dynamic calculation model of EnergyPlus, and documented.
2.2.1. Convective Heat Transfer
Similar to the external convective heat transfer, the areal heat flux transferred between the surface and the indoor environment (qconv,int, expressed in W·m−2) is calculated both in the EN ISO 52016-1 simplified method and in the detailed method of EnergyPlus as
where hc,int is the internal convective heat transfer coefficient (in W·m−2·K−1), and Tair,int and Tsurf are the indoor air and the surface temperatures (in K), respectively.
In Equation (7), constant values of the convective heat transfer coefficient over the simulation period are applied in the EN ISO 52016-1 hourly method, and are derived from the EN ISO 13798 [29] technical standard, in accordance with the direction of the heat flux. The definition of hc,int on a timestep basis is instead performed by means of the TARP algorithm [24] in EnergyPlus, assumed as a reference for the sake of the present study.
2.2.2. Longwave Radiation Heat Transfer
In both EN ISO 52016-1 and EnergyPlus, the longwave radiation heat transfer includes the radiation exchange between the surfaces facing the thermal zone, and the radiation from internal sources.
The longwave radiation heat transferred between the zone surfaces is determined by means of the Stefan-Boltzmann law in EnergyPlus, while its linearised formulation is considered in EN ISO 52016-1. In particular, it is calculated as
where eli refers to the considered surface, and elk refers to the other surfaces facing the thermal zone, A is surface area (in m2), hr,int is the radiative heat transfer coefficient (in W·m−2·K−1), θsurf is the indoor surface temperature (in K). As for the external radiative heat transfer coefficient, also the internal coefficient is assumed time-independent, and it is calculated by means of the EN ISO 6946 formulation (Equation (5)). Although this approach represents a simplification in the modelling on the considered physical phenomenon, this assumption was not tested in the present work. In fact, the temperature difference between the surfaces facing the thermal zone can be considered negligible, thus this approach may influence the energy behaviour of a building in a negligible way.
As far as the radiation from internal sources is concerned, both the models define a radiative and convective split for the heat introduced into the thermal zone from the equipment. However, the models differ as regards the distribution of the radiative part over the surfaces. In particular, in EN ISO 52016-1, the radiative fraction of internal gains is uniformly distributed over the surfaces (qlwr,int, expressed in W·m−2), as
where Atot is the sum of the surface areas facing the thermal zone—including thermal mass surfaces—(in m2), fint,c is the convective fraction of internal gains, and Φint is the total internal heat gains (in W). In EnergyPlus, instead, the radiant fraction of internal gains is distributed proportionally to the surface area and the surface emissivity (Φlwr,int, expressed in W), as
where eli refers to the considered surface, and elk refers to the other surfaces facing the thermal zone, and A and ε are the surface area (in m2) and the emissivity, respectively. The other parameters are described in Equation (9).
Although both the models are not completely realistic, alternative methods are not easily applicable, since they would require knowledge of the placement and the surface temperature of all equipment [30].
2.2.3. Solar (Shortwave) Radiation
As far as the solar radiation transmitted into a thermal zone is concerned, the EN ISO 52016-1 method and EnergyPlus differ under three aspects. Firstly, the solar heat gains are considered to be all radiative heat gains in EnergyPlus; on the other hand, a fraction of solar heat entering the zone through the glazing is considered to be immediately transferred to the internal air [31] in EN ISO 52016-1. Secondly, the radiative fraction of solar heat gains is distributed uniformly over the zone surfaces in the simplified method (qswr,sol, expressed in W·m−2), as
where Atot is the sum of the surface areas facing the thermal zone—including thermal mass surfaces—(in m2), fsol,c is the convective fraction of solar gains, and Φsol is the total solar heat gains (beam plus diffuse solar radiation, in W). In EnergyPlus, instead, different approaches for the distribution of solar radiation are offered. For the sake of the present study, the “full exterior with reflections” distribution model of EnergyPlus was assumed as a reference. According to this approach, beam solar radiation entering the zone is assumed to fall on the floor, where it is absorbed according to the floor solar absorptance coefficient. The reflected solar radiation by the floor is added to the transmitted diffuse radiation (and eventual shortwave radiation from the lighting system), which is then distributed over the internal surfaces proportionally to the surface area and the surface solar absorptance (Φswr,sol, expressed in W), as
where eli refers to the considered surface, and elk refers to the other surfaces facing the thermal zone, A, α and ρ are, respectively, the surface area (in m2), the absorption and the reflection coefficients, and Φsol,diff is the diffuse solar radiation (transmitted solar radiation plus reflected beam solar radiation, in W). Finally, the solar reflectance is defined for transparent surfaces as
where τ is the direct solar transmission coefficient of the transparent surface. This represents the “lost” fraction of the solar radiation entering the zone that is reflected back to the external environment. In the EN ISO 52016-1 hourly method, instead, the solar radiation back reflection is not considered.
ρ = 1 − α − τ
2.3. Methodology
The effect of the above modelling options on the model accuracy is investigated in the present work by applying a code-to-code comparison methodology. A case-study approach was used to facilitate the achievement of the research goals. The procedure applied is summarised in Figure 1.
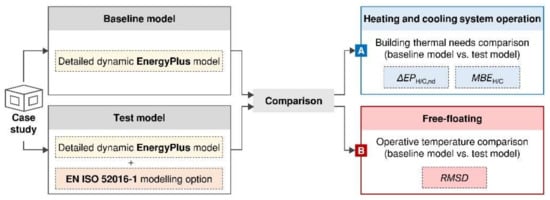
Figure 1.
Methodology framework applicable for the energy need (A) and the indoor temperature (B) evaluations.
Firstly, an energy model is created in EnergyPlus for the considered case study (baseline model). The considered assumptions are then implemented one-at-the-time in the detailed model (test model). In this way, an overall input equivalence between the baseline and the test model is achieved, and the only difference between them is related to the tested modelling option. The effect of the modelling assumptions on the accuracy of the model is evaluated for two different situations. Firstly, the variation in the annual sensible energy needs for heating and cooling is assessed for each test model, in comparison with the baseline model (Path A in Figure 1). Secondly, the errors in the prediction of the indoor operative temperatures are evaluated in a free-floating situation. These two different analyses allow to determine the expected accuracy of the model for different purposes, such as the energy performance evaluation or the energy requirements compliance check (Path A), or the energy audits or the thermal comfort evaluations (Path B).
Two statistical indexes were calculated to numerically assess the accuracy of the models. In particular, the hourly mean bias error (MBE) was used for the annual energy needs evaluation, and was calculated as specified in [16]:
where ΦH/C is the heating (H) or cooling (C) load (in W) at timestep t, for the test model and for the baseline, respectively, and n is the number of timesteps considered for the calculation (8760 for annual evaluations). The MBE is expressed as a percentage error, and measures how closely the predicted hourly heating or cooling loads corresponds to the baseline data. The variations in the energy needs are considered acceptable with MBE values in the range of ±10% (when using hourly data) [16]. The root-mean-square deviation (RMSD) was instead used to measure the variability in the prediction of the indoor operative temperatures (in K), and was calculated as
where θop is the indoor operative temperature at timestep t, for the test model and for the baseline, respectively, and n is the number of timesteps considered for the calculation (8760 for annual evaluations). In this case, acceptable deviations in the prediction of the indoor operative temperatures are considered for RMSD values lower than 0.5 K [32].
The procedure presented is applied separately for each tested modelling option. All simulations were performed through the Python applicative pyEp [33], which implements the Ptolemy EnergyPlus’s external interface.
3. Application
3.1. Case Studies
The cases considered in the present study are two buildings, an office module and a residential apartment unit, each one characterised by two levels of thermal insulation of the building envelope and sited into two different Italian climatic zones, for a total of four variants for two case studies.
A thermally uninsulated or scarcely insulated existing building (referred as ExtB from so on) was assumed as first; a well-insulated building envelope (referred as DM from so on), in compliance with the Italian minimum energy performance requirements for new buildings as specified by the Interministerial Decree of 26 June 2015 [34], was considered as well. The case studies were assumed to be placed in Milan (Northern Italy) and Palermo (Southern Italy).
The residential case study is an apartment unit of a multi-storey residential building (Figure 2a), representative of the Italian residential existing building stock, built in the period 1946-76 [35]. The main geometrical characteristics of the case study are presented in Table 1. It was assumed to be adjacent to identical residential units; thus, only the South-, West- and North-oriented façades are exposed to the outdoor environment. The internal partitions were assumed as adiabatic components, and were explicitly modelled for the sake of internal mass. The South-oriented façade is characterised by two windows of 2.8 m2 area each, shaded by an overhang of 1 m depth; the North-oriented façade is instead characterised by two windows of 1.5 m2 and 2.0 m2 areas, respectively. As concerns the existing building variant (ExtB), the external walls are made of uninsulated hollow brick masonry with air gap (Uwall,res,ExtB = 1.1 W·m−2·K−1), while the transparent components are characterised by a single glazing with wooden frame (Uwin,res,ExtB = 4.9 W·m−2·K−1, gres,ExtB = 0.85).
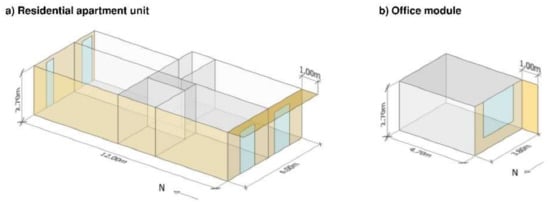
Figure 2.
3D visualization of the residential apartment unit (a) and of the office module (b) case studies.

Table 1.
Main geometrical data of the case studies.
The office module is a single office (Figure 2b, Table 1) of a multi-storey office building, representative of the Italian existing office building stock, built in the 90s [36]. As for the residential unit, the office module was assumed to be adjacent to identical conditioned offices. The only exposed building envelope component (West-oriented façade) is characterised by a window of 4.8 m2 area, shaded by a side fin of 1 m depth. As concerns the existing building variant (ExtB), the external wall is made of a prefabricated concrete wall (Uwall,off,ExtB = 0.8 W·m−2·K−1) with interposed low thickness thermal insulation material, while the window is a double-glazing unit with wooden frame (Uwin,off,ExtB = 2.8 W·m−2·K−1, goff,ExtB = 0.75).
For both the case studies, the thermo-physical features of the opaque envelope components where derived from the UNI/TR 11552 technical report [37] that provides typical Italian building components. As concerns the well-insulated building variants (DM), the opaque and transparent building envelope components were modified in order to achieve the thermal transmittance values of the reference building, as specified by the Italian legislation [34] for the considered climatic zones (Table 2).

Table 2.
Thermal transmittance values of the reference building in accordance with Interministerial Decree of 26 June 2015 [34].
A standard user behaviour, regarding the occupancy profile, internal heat sources, ventilation air flow rate, and HVAC operation, was assumed for both the case studies, and was derived from the draft of the Italian Annex of the EN 16798-1 technical standard [39]. The ideal load air system of EnergyPlus was considered to evaluate the energy needs for heating and cooling, considering a dead band internal temperature set point of 20 °C and 26 °C, respectively. The HVAC system was instead switched off all year long in the indoor operative temperature evaluation (free-floating condition).
The evaluations were carried out using the International Weather for Energy Calculations (IWEC) data file [40] for the cities of Milan and Palermo.
3.2. Modelling Options
From the documentation analysis presented in Section 2, fourteen different modelling options were selected to be tested. In this paragraph, a detailed description of the parameters used in the tested modelling assumptions is provided. For some of these, the implementation in EnergyPlus was not straightforward. The strategies used for the correct modelling of these assumptions are therefore outlined.
With regards to the external convection heat transfer (External CV) assumptions, the TARP algorithm [24] was adopted in the baseline model for the definition of the external convection heat transfer coefficient; four evaluation steps were considered instead in the test models, representing increasing levels of simplifications in its determination.
- HC-Vw-av. The effect of a lack of detailed input data regarding the wind speed was assessed. In particular, the convective heat transfer coefficient was considered time-dependent and was calculated by means of the TARP algorithm [24]. Differently from the baseline model, the forced component is calculated by implementing annual average wind speed values; specifically, wind speeds of 0.9 and 3.8 m·s−1 were used for Milan and Palermo, respectively.
- HC-V. The effect of the formulation specified in Equation (2) for the hc,ext determination was evaluated. The convective heat transfer coefficient was considered variable on a timestep basis, and the site hourly wind speed was used.
- HC-Cw-av. The annual average wind speed was implemented in Equation (2) to calculate an average heat transfer coefficient, assumed constant over the simulation period.
- HC-Cst. The effect of the hc,ext standard values was evaluated, assuming a constant convective heat transfer coefficient equal to 20 W·m−2·K−1 over the simulation period, calculated by means of the reference wind speed value of 4 m·s−1 (Equation (2)).
As far as the external longwave heat transfer (External LW) is concerned, the heat transferred between the surface and the external environment is assessed by means of Equation (3) in the baseline model. In particular, the Clark and Allen correlation [27] is used for the apparent sky temperature determination. Three evaluation steps were considered for the sake of the present study.
- SKY. The influence of the direct sky temperature model for the apparent sky temperature calculation was assessed; specifically, the sky temperature was assumed 11 °C below the outdoor air temperature.
- HR. In EnergyPlus, the external net longwave radiation heat flux is calculated by applying the Stefan-Boltzmann law. Thus, the definition of the radiative heat transfer coefficients as input values was not possible. To assess the influence of the linearisation of the longwave heat transfer (Equation (4)), a simple modelling strategy was applied. Firstly, the outdoor surface emittances were set equal to 0 to annul the external longwave heat transfer automatically calculated by EnergyPlus. Then, an additional heat balance term, calculated as specified in Equation (4), was added to the external surface of the envelope components. The standard radiative heat transfer coefficient (hr,ext) equal to 4.14 W·m−2·K−1 was used, and was calculated by assuming a surface emissivity equal to 0.9 and a reference mean temperature of 0 °C [23]. The EnergyPlus’s calculated view factor between the surface and the sky (Fsky) was assumed, as well as the Clark and Allen [27] calculated sky temperature.
- HR-EU. The parameters described for the HR test model were used in this step, while the apparent sky temperature was calculated as direct difference from outdoor air (11 °C).
Due to software limitations, the HR and HR-EU modelling assumptions were implemented only on the opaque building envelope components.
Concerning the solar radiation entering the zone through windows (External SW), two steps were considered.
- GV-EU. The effect of considering the solar radiation entering the thermal zone as all shortwave radiation was assessed. To this purpose, the direct solar transmission coefficient of windows was set equal to the g-value (at normal incidence), while 0 was assumed for the absorption factor. The glazing solar properties were considered time- and solar angle-independent, by assuming a constant exposure factor (FW in Equation (6)) equal to 0.9 over the simulation period [2].
- GV-ITA. The parameters described for the GV-EU test model were used in this step, while the glazing solar properties were considered solar angle- and time-dependent, by assuming a variable exposure factor (FW in Equation (6)) calculated by means of the Italian National Annex approach [28].
For both GV-EU and GV-ITA, the assumptions were implemented by means of the EnergyPlus Energy Management System (EMS) [41].
About the internal convection heat transfer (Internal CV), the variation in the accuracy of the model resulting from the use of the standard values of the heat transfer coefficient was assessed, compared to the baseline implementing the TARP algorithm [24] for the definition of the internal convective heat transfer coefficients. Specifically,
- HC-Cst. A constant value of the convective heat transfer coefficient was considered over the simulation period, whose determination depends on the direction of the heat flow. As specified by the EN ISO 6946 technical standard [23], the hc,int values were assumed equal to 5.0, 2.5 and 0.7 W·m−2·K−1, for horizontal, upward and downward heat fluxes, respectively.
As introduced, the linearisation of the internal longwave heat transfer (Internal LW) was not tested in the present work. Instead, the effect of the uniform distribution of the radiant fraction of internal gains was assessed, as follows.
- IG. Firstly, only the convective fraction of internal gains (occupancy, appliances, and lighting) was set as input data in the EnergyPlus model (test model). Then, their radiative fraction was directly applied to the internal surfaces as additional heat balance term, calculated for each timestep as in Equation (9).
Finally, three assumptions were tested as regards the solar radiation and solar heat gains (Internal SW) in the thermal zone, as follows.
- BR. The assumption of EN ISO 52016-1 to not consider a fraction of solar radiation that is reflected back outside the zone from windows was evaluated. To this purpose, the “lost” solar radiation (Equation (13)) was added as an additional heat balance term to each surface, proportionally to the respective surface areas and solar absorption factors (Equation (12)).
- UD. The effect of the uniform distribution of solar radiation on the internal surfaces, specified by the EN ISO 52016-1 hourly method, was evaluated. A simple modelling procedure was applied; the internal surface solar absorption was set equal to 0 to annul the absorbed solar radiation automatically calculated by EnergyPlus. Then, the global (beam plus diffuse) solar radiation entering the zone at each timestep was distributed uniformly on the internal surfaces (Equation (11)). Solar heat gains were considered all radiant heat gains.
- UD-CSG. The influence of the fraction of solar radiation directly transferred to the internal air as convective heat gain was evaluated. The modelling approach of UD was applied. Differently from the UD test model, the solar radiation distributed over the internal surfaces was decreased by a 10%, considered as a convective heat gain.
4. Results
The effects of the tested modelling options on the thermal behaviour of the case studies are presented in this section. In Section 4.1, the deviations of the annual energy needs for heating and cooling, evaluated through the comparison with the baseline model results (EnergyPlus full detailed method), are presented for each case study variant. The errors in the prediction of the indoor operative temperatures are instead presented in Section 4.2.
4.1. Energy Needs Evaluation
4.1.1. Simplified Modelling of the External Driving Forces
Figure 3 shows the deviations in the energy needs for heating and cooling for the tested modelling assumptions. The labels represent the variation of both heating and cooling energy needs (ΔEPH/C,nd), while the red and bold highlighted values represent the tested assumptions for which the mean bias error (MBE) exceeds the acceptable value (±10% [16]). Significant discrepancies between the baseline and the test models are highlighted when the EN ISO 52016-1 assumptions related to the definition of the external convective heat transfer coefficients are concerned. Generally, an increase of the annual energy needs for heating, and a decrease in the one for cooling occur for all the case study variants. Firstly, the effect related to the lack of specific input data regarding the local wind speed was assessed. The use of an average wind speed value for the determination of the hcs following the TARP algorithm (HC-Vw-av, variable heat transfer coefficient) leads to negligible variations in the cooling energy needs for all the considered building variants. In fact, the energy needs for cooling decreases with variations within −0.3 kWh·m−2, with respective Mean Bias Errors (MBEs) lower than −1%. Slightly increases occur instead in the energy needs for heating, especially for the residential apartment unit at the existing building (ExtB) insulation level in Milan (i.e., ΔEPH,nd equal to +1.3 kWh·m−2, and MBE equal to +2%). Negligible variations instead are reported for the cooling dominated climatic zone (Palermo), as well as for the well-insulated case studies (DM) in Milan.
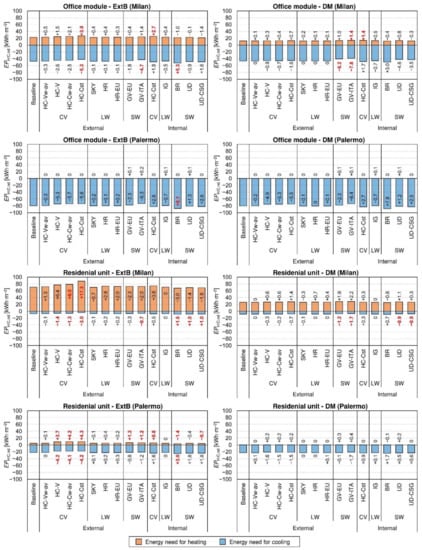
Figure 3.
Deviations of the energy needs for heating and cooling for the tested modelling assumptions and case study variants.
The use of a constant value of the heat transfer coefficient, calculated considering either an average (HC-Cw-av) or a reference wind speed (HC-Cst), leads to the highest variations of the energy need for heating among all the tested modelling assumptions. This is particularly true for the apartment unit at the ExtB insulation level in both climatic zones. In Palermo for the HC-Cst assumption, EPH,nd variations of +4.2 kWh·m−2 (compared to 5.2 kWh·m−2 of the baseline), and EPC,nd variations of −4.3 kWh·m−2 (compared to 22.2 kWh·m−2 of the baseline) are reported, with MBEs both exceeding the acceptable values (+83% and −19% for the heating and the cooling needs, respectively). Comparable situations occur in Milan for both the HC-Cw-av and HC-Cst tests (for heating, +11% and +24%, respectively; for cooling, −19% and −42%, respectively). Consistent discrepancies occur also for the ExtB office module in Milan when the HC-Cst assumption is implemented; in this case, the variations in the energy needs for heating and cooling are characterised by MBEs equal to +17% and −11%, respectively. Nevertheless, the implementation of the reference hc values specified by the EN ISO 13798 technical standard [29] leads to acceptable variations of the energy needs for all case studies characterised by the DM insulation level (e.g., for the DM apartment unit in Milan, +5% and −9% for the heating and the cooling energy needs, respectively), as well as for the existing office module in Palermo.
Finally, a decrease in the model accuracy occurs when variable external heat transfer coefficients, calculated by means of the EN ISO 6946 formulation (Equation (2)), are considered. In fact, this formulation applied on a timestep basis leads to increases in the heating needs comparable to the HC-Cw-av assumption for the all the considered cases (e.g., +9% for the ExtB residential building in Milan), as well as decreases in the cooling needs (e.g., −19% for the ExtB residential building in Milan). These similarities in the results can be explained by analysing the convective coefficient profiles shown in Figure 4, in which the different hc,ext hourly profiles (dashed lines in Figure 4) for the residential apartment unit (ExtB) in Milan are presented for a typical winter week (from 13 to 19 January). The hourly thermal loads are presented as well. The hc,ext values calculated by means of the formulation in Equation (2) on an hourly basis (HC-V) are consistently higher than the ones calculated by means of the TARP algorithm, using either a variable (baseline model) or an average constant wind speed (HC-Vw-av). Higher convection heat transfer rates occur for the HC-V assumption, leading to the reported discrepancies between the outcomes both on the annual energy needs and on the hourly thermal loads. The HC-Cw-av assumption leads to similar results to HC-V, since the constant hc,ext used in HC-Cw-av can be considered an average mean value of the hourly HC-V values. However, since HC-V is sensitive to the hourly fluctuation of the wind speed, slightly discrepancies can be highlighted between HC-Cw-av and HC-V. In particular, the HC-V test model tends to overestimate the hc values with respect to the baseline when high values of wind speed are reported, and thus to overestimate heating loads, while the HC-Cw-av constant value is similar to the baseline one.
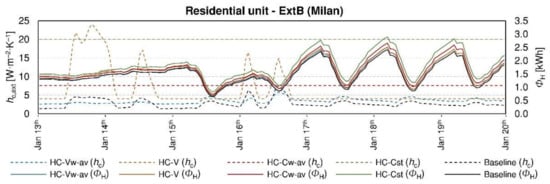
Figure 4.
Existing residential unit in Milan: hourly heating loads and hc,ext values in a winter period for the analysed modelling assumptions.
As far as the modelling assumptions related to the longwave heat transfer phenomenon are concerned, a general increase in the energy need for heating and a decrease in the one for cooling can be observed. The linearisation of the longwave heat transfer phenomenon (HR and HR-EU) results to influence the energy need of the case studies more than the simplified definition of the sky temperature (SKY). For example, the energy need for heating increases of +2.8 and +0.7 kWh·m−2 for the residential unit in Milan, for the existing building and the DM insulation levels, respectively, when the standard constant hr,ext and the EnergyPlus sky temperature are considered (HR). The introduction of the EN ISO 52016-1 assumption related to the sky temperature definition (HR-EU) shows comparable results with the HR modelling option. This is due to the fact that the actual average difference between the apparent sky and the outdoor air temperatures is similar to the reference value of 11 °C (i.e., equal to 11.5 °C for Milan, and 11.2 °C for Palermo) used in the simulations. Likewise, good agreements between the baseline and the test models can be found when the sky temperature is assumed to be 11°C below the external air temperature (SKY). In fact, the variation in the energy need for heating is around ±0.5 kWh·m−2 for all the case studies, with mean errors within ±2%. For all the considered case study variants, the modelling assumptions related to the external longwave radiation guarantee a variation in the accuracy of the calculation model never exceeding the MBE assumed limits (±10%).
When the solar radiation entering the thermal zone is considered as all shortwave radiation, and the glazing parameters are considered to be solar angle- and time-independent (GV-EU), the energy need for heating slightly increases compared to the baseline model, while the energy need for cooling decreases. The same trend occurs also for the GV-ITA test model.
4.1.2. Simplified Modelling of the Internal Driving Forces
The implementation of a time-independent internal convective heat transfer coefficient (HC-Cst), calculated for reference conditions [23], leads to a general increase of the energy needs for both heating and cooling. Differently from the external convective heat transfer, the simplification introduced by the EN ISO 52016-1 on the definition and time discretisation of the internal convective heat transfer coefficients guarantees an acceptable level of accuracy for almost all the considered cases. In fact, the average errors in the prediction of the energy needs for cooling vary between +3% and +7% for all the considered case studies. As for the energy needs for heating, good agreements between the baseline and the test models are reported for the office module in Palermo (i.e., ΔEPH,nd equal to 0 kWh·m−2 for both the ExtB and the DM insulation levels), and for the ExtB residential apartment in Milan (i.e., ΔEPH,nd equal to +3.6 kWh·m−2, corresponding to MBEs of +5%).
The simplification related to the uniform distribution of the radiant fraction of internal gains on the internal surfaces does not affect the accuracy of the model. The extent of the variation in the energy needs for both heating and cooling is negligible for the residential apartment; in fact, they range within a ±0.1 kWh·m−2 variation, with relative mean bias errors tending towards 0%. For the office module, in which the internal heat gains are consistently higher than in the residential building (overall 28 W·m−2 compared to 7.6 W·m−2), the variations in the energy needs are slightly higher (e.g., +0.5 and −0.7 kWh·m−2 for heating and cooling, respectively, for the well-insulated office module in Milan); the MBE values never exceed the acceptable values.
As introduced, the EN ISO 52016-1 hourly method does not consider back reflection of solar radiation to the external environment (BR). As expected, a decrease in the energy needs for space heating occurs due to the higher solar gains; an increase in the energy needs for cooling is reported, as well. This trend is particularly clear for the case studies characterised by the existing building insulation level; in fact, the high values of windows solar transmittance (typical for low-performance transparent building components) entail a high amount of back reflected solar radiation (baseline model), and thus higher solar gains in the test models. For example, the energy need for cooling of the ExtB office building in Palermo increases of +8.1 kWh·m−2 compared to the baseline model, while a decrease of −3.0 kWh·m−2 is reported for the ExtB residential apartment in Milan. Similar variations also occur for the case studies in Palermo, when the DM level of thermal insulation is considered (e.g., for the office module, −3% and +7% of the energy needs for heating and cooling, respectively). For four out of eight cases considered, the variations in the energy needs exceed the accepted ranges.
Generally, considering a uniform distribution of solar radiation on the zone surfaces (UD) leads to a slight increase of the annual energy needs for heating, and a decrease in the one for cooling, in the heating dominated climatic zone (Milan), while an opposite trend is reported in Palermo (cooling dominated). The EN ISO 52016-1 solar distribution approach causes a consistent underestimation of the surface solar heat gain for the floor, while a higher solar radiation amount is distributed over the surfaces facing the outdoor environment, compared to the baseline model. Finally, the same trend, but with opposite signs, is reported when a fraction of solar radiation is considered to be immediately transferred to the internal air (UD-CSG). In fact, this approach leads to a decrease in the energy need for heating, and an increase in the energy need for cooling, with respect to the UD test model. If compared to the baseline model, the UD and UD-CSG variants show an opposite deviation on the energy needs for heating and cooling that, if applied together, they might produce compensations in the results. The variations of the heating energy needs are almost negligible for all the considered case studies, while a general increase in the energy needs for cooling occurs. The effect of this assumption is particularly consistent in the office module, which is characterised by a noteworthy transparent surface with respect to the conditioned volume. The solar radiation immediately transferred to the air consists in an annual average additional heat gain equal to 2.5 W·m−2 for the office module, compared to 0.9 W·m−2 for the apartment unit.
4.2. Operative Temperatures Evaluation
The errors in the prediction of the indoor operative temperatures are presented in Figure 5 for a winter month (orange squared dots), and for a summer month (blue circle dots). In particular, a free-floating simulation was performed for each tested assumption and for each case study variant, and the effect of the simplifications was assessed for two months (from 15 January to 15 February—referred as Winter month, and from 15 July to 15 August—referred as Summer month). Each chart in Figure 5 reports the results for each of the eight cases considered. The dashed red line in each chart represents the assumed root-mean-squared deviation acceptable limit (0.5 K).
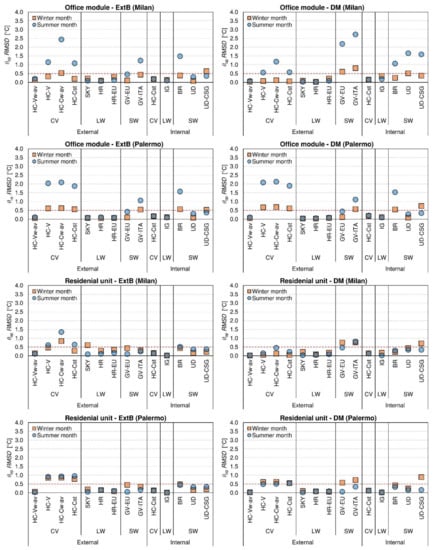
Figure 5.
Operative temperature RMSDs for a winter and a summer month for the tested modelling assumptions and case study variants.
The evaluations on the operative temperatures partially confirm the findings of the previous analysis on the annual energy needs for heating and cooling.
As far as the existing building insulation level is concerned, the accuracy of the model in predicting the indoor operative temperatures results to be not sensitive to the modelling assumptions related to the longwave radiation heat transfer (on both the internal and external surfaces), and to the inside heat convection. The simplified algorithms used in the determination of the external convective heat transfer coefficients (HC-V, HC-Cw-av, and HC-Cst) are the simplifications that lead to consistent discrepancies in the operative temperature estimation in all the ExtB cases. Discrepancies in the prediction of the indoor operative temperatures also occur when the back reflection of the solar radiation entering the thermal zone is neglected (BR test case), as well as when a weighted g-value is considered in the simulations (GV-EU and GV-ITA), especially in the office module case study due to its large windowed surface (compared to the conditioned volume).
The results related to the well-insulated buildings are consistently different between the office module and the residential unit. The residential apartment results to be less sensitive to the modelling assumptions related to the external heat convection than the office building, for which RMSDs between 0.55 and 1.2 °C are reported for Milan and around 2.0 °C for Palermo in summer, if either an hourly variable (HC-V) or constant heat transfer coefficient (HC-Cw-av and HC-Cst) is applied. Differently from the ExtB building, in the well-insulated building the GV assumptions (GV-EU and GV-ITA) result to influence more the winter-performance than the summer one; however, the acceptable variance of the indoor operative temperatures is not guaranteed for both summer and winter, for all the considered cases.
5. Discussion
The validation of the EN ISO 52016-1 hourly calculation method was carried out—limited to the heat transfer phenomena on the outdoor and the indoor envelope surfaces—by assessing the loss of accuracy of a detailed dynamic EnergyPlus energy model when the simplifications introduced by the EN ISO 52016-1 technical standard are implemented.
It can be drawn that, generally, the use of an average wind speed value (in absence of other detailed information) does not influence the accuracy of the model, both for the annual energy needs evaluation and for the hourly temperature predictions, for all the case studies. In the same way, the analysis allowed to understand that the EN ISO 52016-1 assumptions related to the external and internal longwave radiation heat transfer can guarantee a high level of accuracy in the outcomes while assuring the simplicity of the assessment. The same conclusion can be drawn for the simplified determination of the apparent sky temperature. On the other hand, the simplifications on the external heat transfer coefficients lead to significant inaccuracies in the calculation model, as well as the ones applied to the shortwave (solar) heat transfer.
In some situations, the effect of some of the tested assumptions is different for the annual EP and for the hourly operative temperature evaluation. It is thus of crucial importance to understand for which purposes and conditions the simplifications are applicable or not. The results presented in Section 4 allowed the Authors to answer to the question: “Is it good enough for [whatever purpose]?” [5], referred to the EN ISO 52016-1 hourly method applied to two building use categories, with different thermal insulation levels and located in two representative Italian climatic zones.
In Figure 6, the results of the analysis are summarised for the heating/winter (left-hand side) and the cooling/summer period (right-hand side) through a comparison table. For each considered case study variant, check marks (✓) and crosses (✗) are assigned to the tested assumptions, if the variation limits (i.e., MBE for the energy needs evaluation, and RMSD for the hourly temperature evaluation) are, respectively, verified or not. It is thus possible to draw some considerations on the expected level of accuracy for the different evaluation purposes (i.e., annual energy performance evaluation and hourly temperature estimation), as follows.
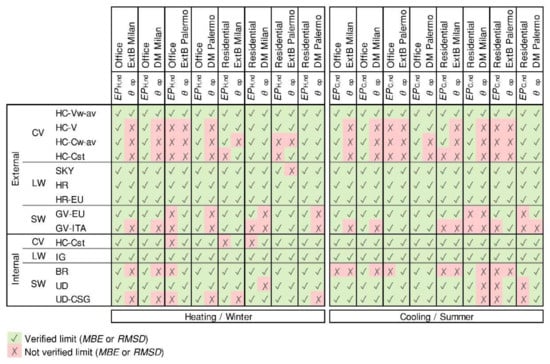
Figure 6.
Summary of the results for the annual energy performance and the hourly operative temperature evaluations.
- The simplified determination of the external convective heat transfer coefficient generally leads to inaccuracies for uninsulated buildings. In well-insulated buildings, instead, good agreements can be obtained for annual energy performance evaluations, while significant errors are committed in the prediction of the indoor operative temperatures, especially in the warm season. Thus, the EN ISO 52016-1 simplifications on the external convection heat transfer may be applied in the design phases, or for compliance checks, for new buildings. However, for energy audits of existing buildings, or for thermal comfort evaluations, it may be preferable to use more accurate calculation models.
- The use of a constant indoor convective heat transfer coefficient may lead to inaccuracies in the estimation of the energy need for heating for uninsulated buildings, while its application in the prediction of the indoor operative temperatures can be considered.
- Inaccuracies in the temperature prediction occur when the simplification on the solar radiation entering into the zone is considered (i.e., back reflection and convective solar gains). However, generally they guarantee an acceptable accuracy in terms of energy needs estimation.
6. Conclusions
In the present work, the effect of the specific simplifying modelling assumptions introduced by the EN ISO 52016-1 hourly method on the accuracy of a detailed dynamic simulation method was quantified. The modelling assumptions that may lead to non-negligible inaccuracy in the outcomes were identified. A single process validation approach, based on a detailed documentation analysis, was proposed, and applied to identify at which extent the modelling assumptions can affect the accuracy of the model. Specifically, fourteen modelling options related to the envelope outdoor and indoor surfaces heat balance were tested on different case studies. To guarantee a general validity of the outcomes, two buildings (with different geometrical characteristics and building uses), two levels of thermal insulation (uninsulated or scarcely insulated, and well insulated), and two climatic zones were considered.
The research also underlined important aspects as regards the EN ISO 52016-1 hourly model validation. Firstly, the effectiveness of different modelling options seems to be strictly related to the accuracy in the definition of the considered parameters. For example, the use of a simplified model for the convective heat transfer coefficient calculation resulted to negatively affect the accuracy of the energy need assessment, even if applied on a timestep basis. This may indicate that the discrepancies are caused by a simplification of the equation used for the parameter definition rather than by a variation in its temporal discretisation. Therefore, it would be preferable to select detailed approaches.
Moreover, the results of the research proved the advantages of performing the validation separately for the different assumptions. The proposed approach led in fact to clearly detect specific inaccuracies in the modelling assumptions that a whole-model approach would not have allowed to identify. Therefore, the use of single component validation approaches should be enhanced to guarantee a complete and extensive energy performance assessment validation.
Finally, it was shown how different assumptions may be suitable for different applications. Therefore, it is necessary to firstly define the purpose of the application of the calculation method to correctly address its validation, and to decide the level of modelling detail [5] for eventual implementations of the method.
Considering these aspects, the research outcomes are intended to address the model validation as to contribute to the enhancement of the standardisation activity. Further works will include in-depth analyses of the modelling options here tested and the exploration of alternative calculation methods for the definition of the parameters involved. These further researches will be addressed to increase the accuracy of the simplified dynamic methods, while guaranteeing the simplicity of the building energy performance assessment.
Author Contributions
Conceptualization, G.D.L., I.B. and V.C.; Formal analysis, G.D.L. and F.B.M.D.; Investigation, G.D.L. and F.B.M.D.; Methodology, G.D.L., I.B. and V.C.; Supervision, V.C.; Visualization, G.D.L. and F.B.M.D.; Writing—Original draft, G.D.L.; Writing—Review & Editing, I.B. and V.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- European Committee for Standardization (CEN). EN ISO 13790, Energy Performance of Buildings—Calculation of Energy Use for Space Heating and Cooling; CEN: Brussels, Belgium, 2007. [Google Scholar]
- European Committee for Standardization (CEN). EN ISO 52016-1, Energy Performance of Buildings—Energy Needs for Heating and Cooling, Internal Temperatures and Sensible and Latent Heat Loads—Part 1: Calculation Procedures; CEN: Brussels, Belgium, 2016. [Google Scholar]
- van Dijk, D. EN ISO 52016 1: The new International Standard to calculate building energy needs for heating and cooling, internal temperature and heating and cooling loads. In Proceedings of the Building Simulation 2019: 16th Conference of IBPSA, Rome, Italy, 2–4 September 2019; pp. 4061–4068. [Google Scholar]
- Judkoff, R.; Wortman, D.; O’Doherty, B.; Burch, J. A Methodology for Validating Building Energy Analysis Simulations; Technical Report NREL/TP-550-42059; National Renewable Energy Laboratory: Golden, CO, USA, 2008.
- Bloomfield, D.P. An overview of validation methods for energy and environmental software. In ASHRAE Transactions: Symposia; American Society of Heating, Refrigerating and Air-Conditioning Engineers: Seattle, WA, USA, 1999; Volume 105, pp. 685–693. [Google Scholar]
- Beausoleil-Morrison, I.; Griffith, B.; Vesanen, T.; Weber, A. A demonstration of the effectiveness of inter-program comparative testing for diagnosing and repairing solution and coding errors in building simulation programs. J. Build. Perform. Simul. 2009, 2, 63–73. [Google Scholar] [CrossRef]
- Buonomano, A. Code-to-Code Validation and Application of a Dynamic Simulation Tool for the Building Energy Performance Analysis. Energies 2016, 9, 301. [Google Scholar] [CrossRef] [Green Version]
- Beausoleil-Morrison, I. Inter-model comparison of embedded-tube radiant floor models in BPS tools. J. Build. Perform. Simul. 2016, 9, 190–209. [Google Scholar]
- Raslan, R.; Davies, M. Results variability in accredited building energy performance compliance demonstration software in the UK: An inter-model comparative study. J. Build. Perform. Simul. 2010, 3, 63–85. [Google Scholar] [CrossRef]
- Bloomfield, D. Appraisal techniques for methods of calculating the thermal performance of buildings. Build. Serv. Eng. Technol. 1985, 6, 13–20. [Google Scholar] [CrossRef]
- Ballarini, I.; Costantino, A.; Fabrizio, E.; Corrado, V. A Methodology to Investigate the Deviations between Simple and Detailed Dynamic Methods for the Building Energy Performance Assessment. Energies 2020, 13, 6217. [Google Scholar] [CrossRef]
- Zakula, T.; Bagaric, M.; Ferdelji, N.; Milovanovic, B.; Mudrinic, S.; Ritosa, K. Comparison of dynamic simulations and the ISO 52016 standard for the assessment of building energy performance. App. Energy 2019, 254, 113553. [Google Scholar] [CrossRef]
- Neymark, J.; Kummert, M.; Judkoff, R. Developing Equivalent Surface Heat Transfer Input Parameters for Updated Standard 140/BESTEST Thermal Fabric Test Cases. In Proceedings of the Building Simulation 2019: 16th Conference of IBPSA, Rome, Italy, 2–4 September 2019; pp. 4570–4577. [Google Scholar]
- Judkoff, R. Validation of Building Energy Analysis simulation programs at the solar energy research institute. Energy Build. 1998, 10, 221–239. [Google Scholar] [CrossRef]
- Jensen, S.O. Validation of building energy simulation programs: A methodology. Energy Build. 1995, 22, 133–144. [Google Scholar] [CrossRef]
- American Society for Heating Refrigerating Air-conditioning Engineers (ASHRAE). Guideline 14—Measurement of Energy, Demand, and Water Savings; ASHRAE: Atlanta, GA, USA, 2014. [Google Scholar]
- Zakula, T.; Badun, N.; Ferdelji, N.; Ugrina, I. Framework for the ISO 52016 standard accuracy prediction based on the in-depth sensitivity analysis. Appl. Energy 2021, 298, 117089. [Google Scholar] [CrossRef]
- Kamaraj, S.V. Dynamic Building Modelling Using an Extensive RC Network according to ISO 52016: Numerical Implementation and Testing. Ph.D. Thesis, Politecnico di Milano, Milan, Italy, 2008. [Google Scholar]
- Judkoff, R.; Wortman, D.; O’Doherty, B.; Burch, J. Building Energy Simulation Test (BESTEST) and Diagnostic Method; National Renewable Energy Laboratory: Golden, CO, USA, 1998.
- Ballarini, I.; Costantino, A.; Fabrizio, E.; Corrado, V. The dynamic model of EN ISO 52016-1 for the energy assessment of buildings compared to simplified and detailed simulation methods. In Proceedings of the Building Simulation 2019: 16th Conference of IBPSA, Rome, Italy, 2–4 September 2019; pp. 3847–3854. [Google Scholar]
- Mazzarella, L.; Scoccia, R.; Colombo, P.; Motta, M. Improvement of EN ISO 52016-1:2017 hourly heat transfer thought a wall assessment: The Italian National Annex. Energy Build. 2020, 210, 109758. [Google Scholar] [CrossRef]
- De Luca, G.; Bianco Mauthe Degerfeld, F.; Ballarini, I.; Corrado, V. The Effect of the External Driving Forces Modelling on the Calculated Building Energy Need Through the Use of Dynamic Simulation. In Proceedings of the Building Simulation 2021: 17th Conference of IBPSA, Bruges, Belgium, 1–3 September 2021. in press. [Google Scholar]
- European Committee for Standardization (CEN). EN ISO 6946, Building Components and Building Elements—Thermal Resistance and Thermal Transmittance—Calculation Methods; CEN: Brussels, Belgium, 2017. [Google Scholar]
- Walton, G.N.; National Bureau of Standards. Thermal Analysis Research Program Reference Manual. NBSSIR 83-2655; U.S. Department of Commerce: Washington, DC, USA, 1983. [Google Scholar]
- Sparrow, E.M.; Ramsey, J.W.; Mass, E.A. Effect of Finite Width on Heat Transfer and Fluid Flow about an Inclined Rectangular Plate. J. Heat Transf. 1979, 101, 204. [Google Scholar] [CrossRef]
- Evangelisti, L.; Guattari, C.; Asdrubali, F. On the sky temperature models and their influence on buildings energy performance: A critical review. Energy Build. 2019, 183, 607–625. [Google Scholar] [CrossRef]
- Clark, G.; Allen, C. The Estimation of Atmospheric Radiation for Clear and Cloudy Skies. In Proceedings of the 2nd National Passive Solar Conference, Philadelphia, PA, USA, 16–18 March 1978. [Google Scholar]
- Karlsson, J.; Roos, A. Modelling the angular behaviour of the total solar energy transmittance of windows. Sol. Energy 2000, 69, 312–329. [Google Scholar] [CrossRef]
- European Committee for Standardization (CEN). EN ISO 13789, Thermal Performance of Buildings—Transmission and Ventilation Heat Transfer Coefficients—Calculation Method; CEN: Brussels, Belgium, 2017. [Google Scholar]
- U.S. Department of Energy. EnergyPlus™ Version 9.4.0 Documentation: Engineering Reference; National Renewable Energy Laboratory: Golden, CO, USA, 2020.
- European Committee for Standardization (CEN). EN ISO 52017, Energy Performance of Buildings—Sensible and Latent Heat Loads and Internal Temperatures—Part 1: Generic Calculation Procedures; CEN: Brussels, Belgium, 2017. [Google Scholar]
- European Committee for Standardization (CEN). EN ISO 13791, Thermal Performance of Buildings—Calculation of Internal Temperatures of a Room in Summer without Mechanical Cooling—General Criteria and Validation Procedures; CEN: Brussels, Belgium, 2012. [Google Scholar]
- pyEp 0.9.4.4. Available online: https://pypi.org/project/pyEp/ (accessed on 10 July 2021).
- Italian Republic. Inter-Ministerial Decree of 26 June 2015, Applicazione delle Metodologie di Calcolo delle Prestazioni Energetiche e Definizione delle Prescrizioni e dei Requisiti Minimi Degli Edifici. Off. J. Ital. Repub. 2015, 162, 39. [Google Scholar]
- Loga, T.; Diefenbach, N.; Stein, B. Typology Approach for Building Stock Energy Assessment. Main Results of the TABULA Project; Institut Wohnen und Umwelt GmbH: Darmstadt, Germany, 2012. [Google Scholar]
- Italian Ministry of the Economic Development and Ministry of the Environment. Updating of the Italian Application of the Cost-Optimal Calculation Methodology for the Minimum Energy Performance Requirements (Directive 2010/31/EU Art. 5); Italian Ministry of the Economic Development and Ministry of the Environment: Rome, Italy, 2018.
- Italian Organisation for Standardisation (UNI). UNI/TR 11552, Opaque Envelope Components of Buildings—Thermo-Physical Parameters; UNI: Rome, Italy, 2014. [Google Scholar]
- Italian Organisation for Standardisation (UNI). UNI 10349-3, Heating and Cooling of Buildings—Climatic Data—Part 3: Accumulated Temperature Differences (Degree-Days) and Other Indices; UNI: Rome, Italy, 2016. [Google Scholar]
- European Committee for Standardization (CEN). EN 16798-1, Energy Performance of Buildings—Ventilation for Buildings—Part 1: Indoor Environmental Input Parameters for Design and Assessment of Energy Performance of Buildings Addressing Indoor Air Quality, Thermal Environment, Lighting and Acoustics—Module M1-6; CEN: Brussels, Belgium, 2019. [Google Scholar]
- EnergyPlus Weather Data Sources. Available online: https://energyplus.net/weather/sources (accessed on 10 July 2021).
- EnergyPlus. Available online: https://energyplus.net/ (accessed on 10 July 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).