Control of WPT Transmitter Coils for Power Distribution to Two Receiver Coils without Feedback
Abstract
:1. Introduction
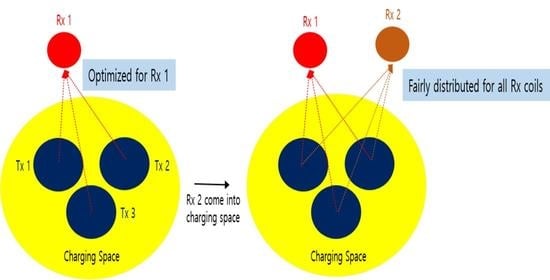
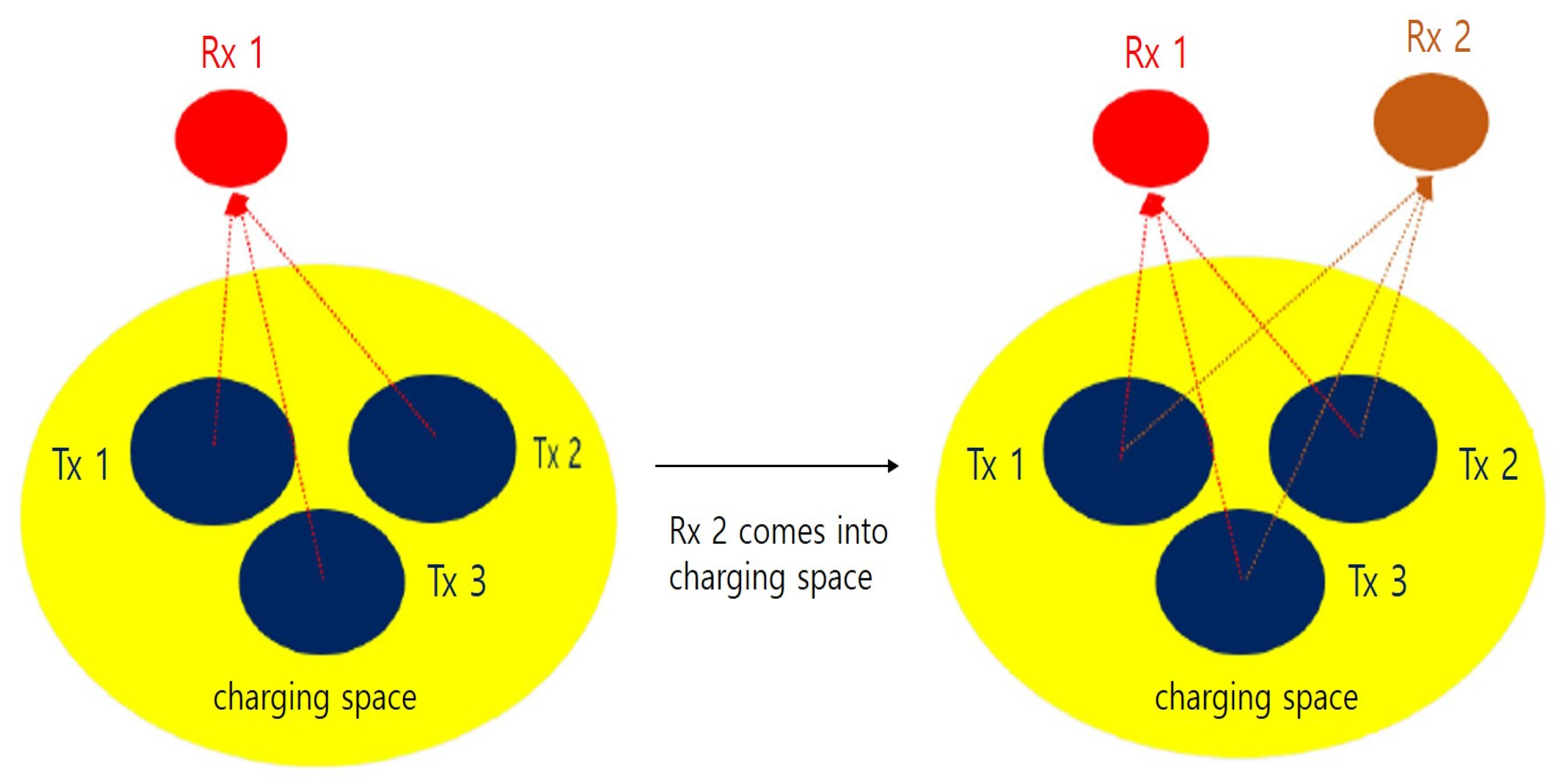
2. Description of System Architecture and Proposed Scenario
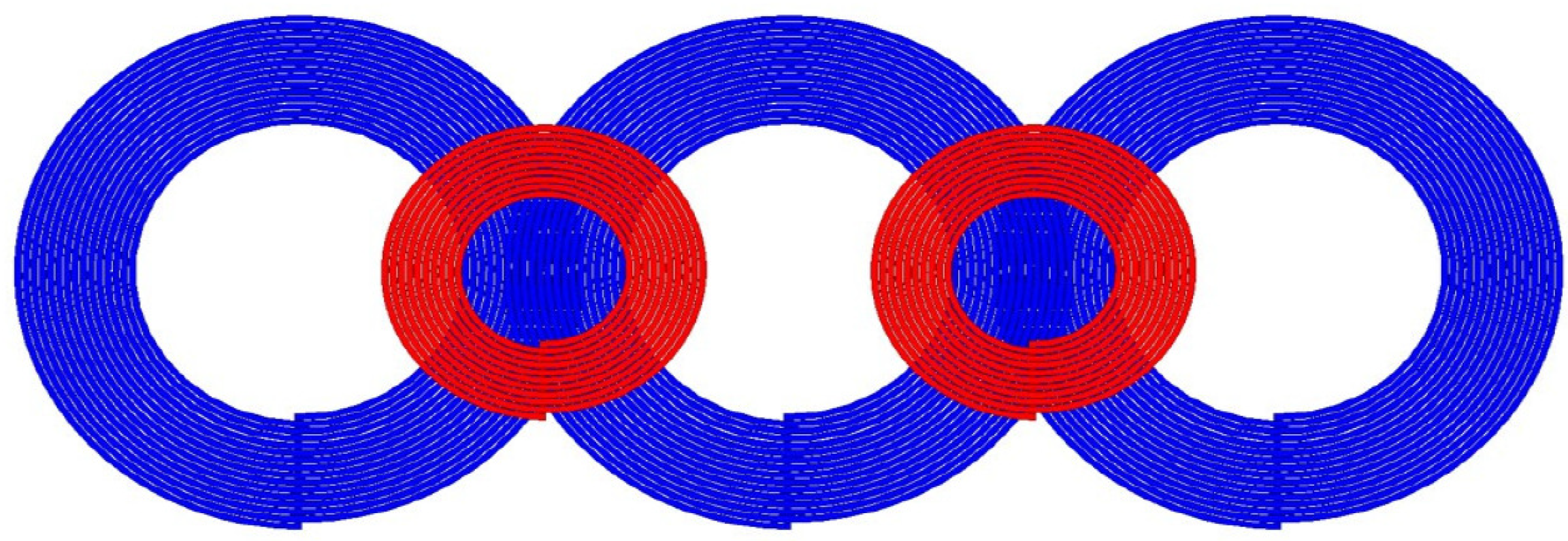
2.1. System Architecture
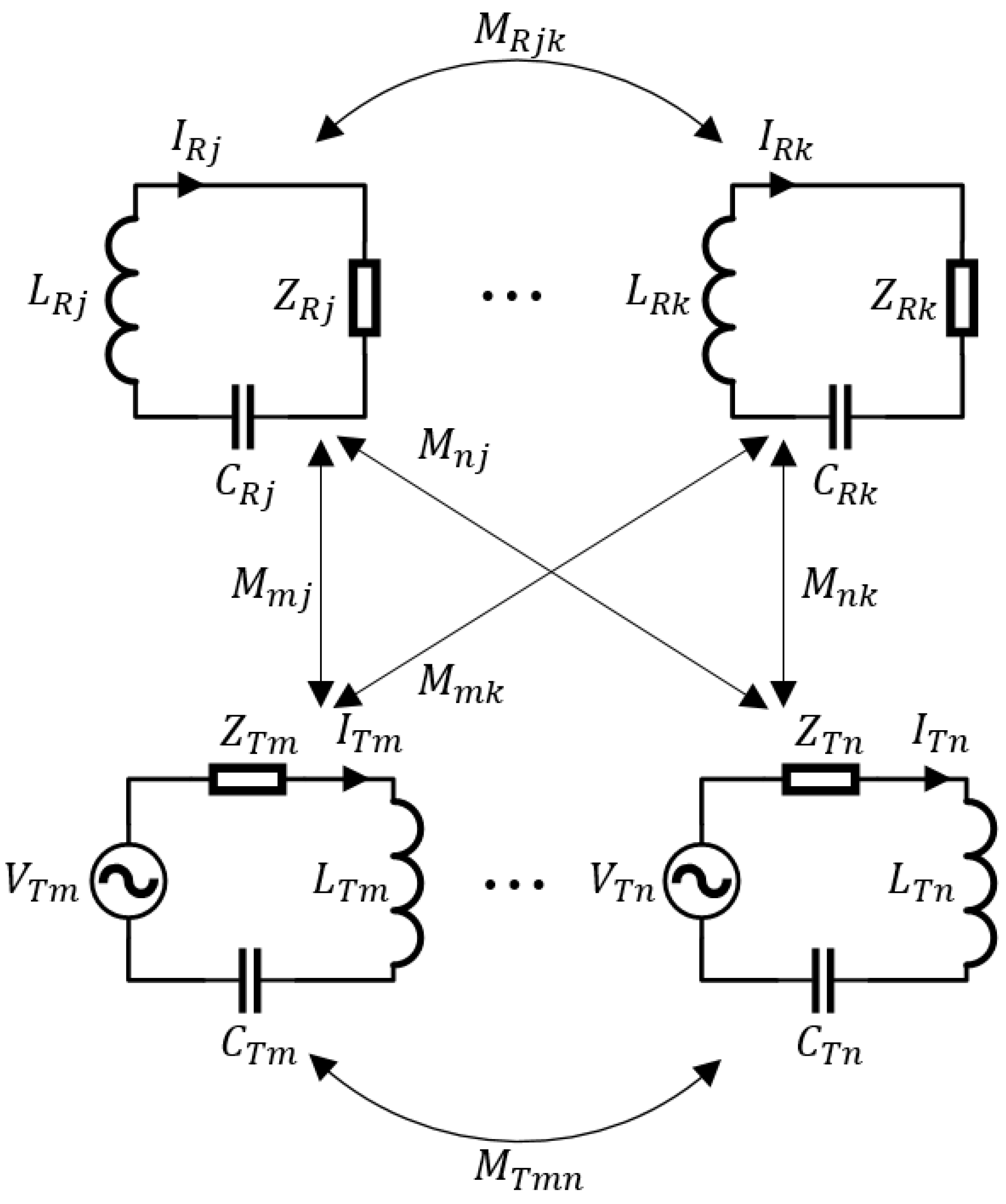
2.2. Circuit Equation
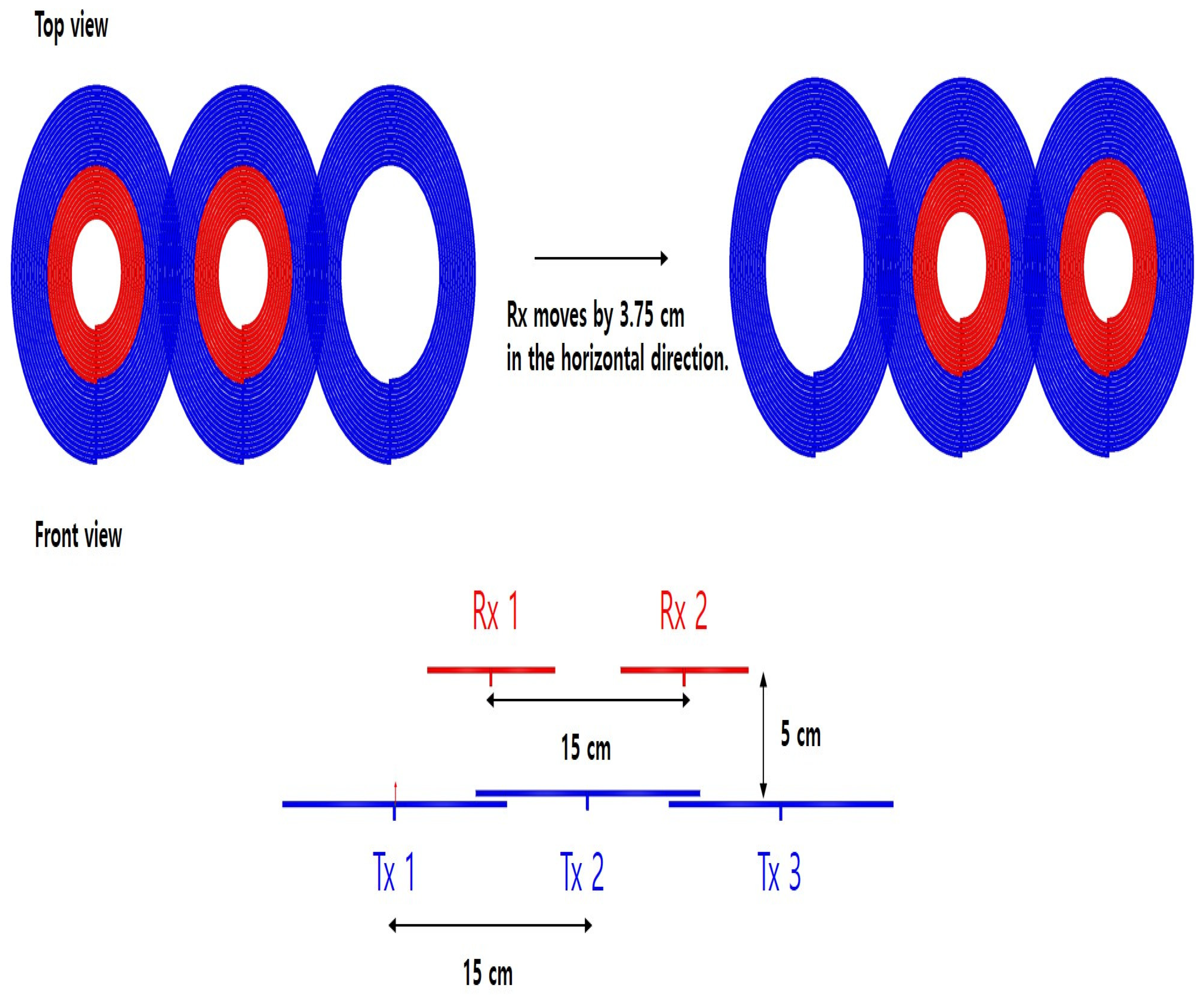
2.3. Problem Formulation and Simulation
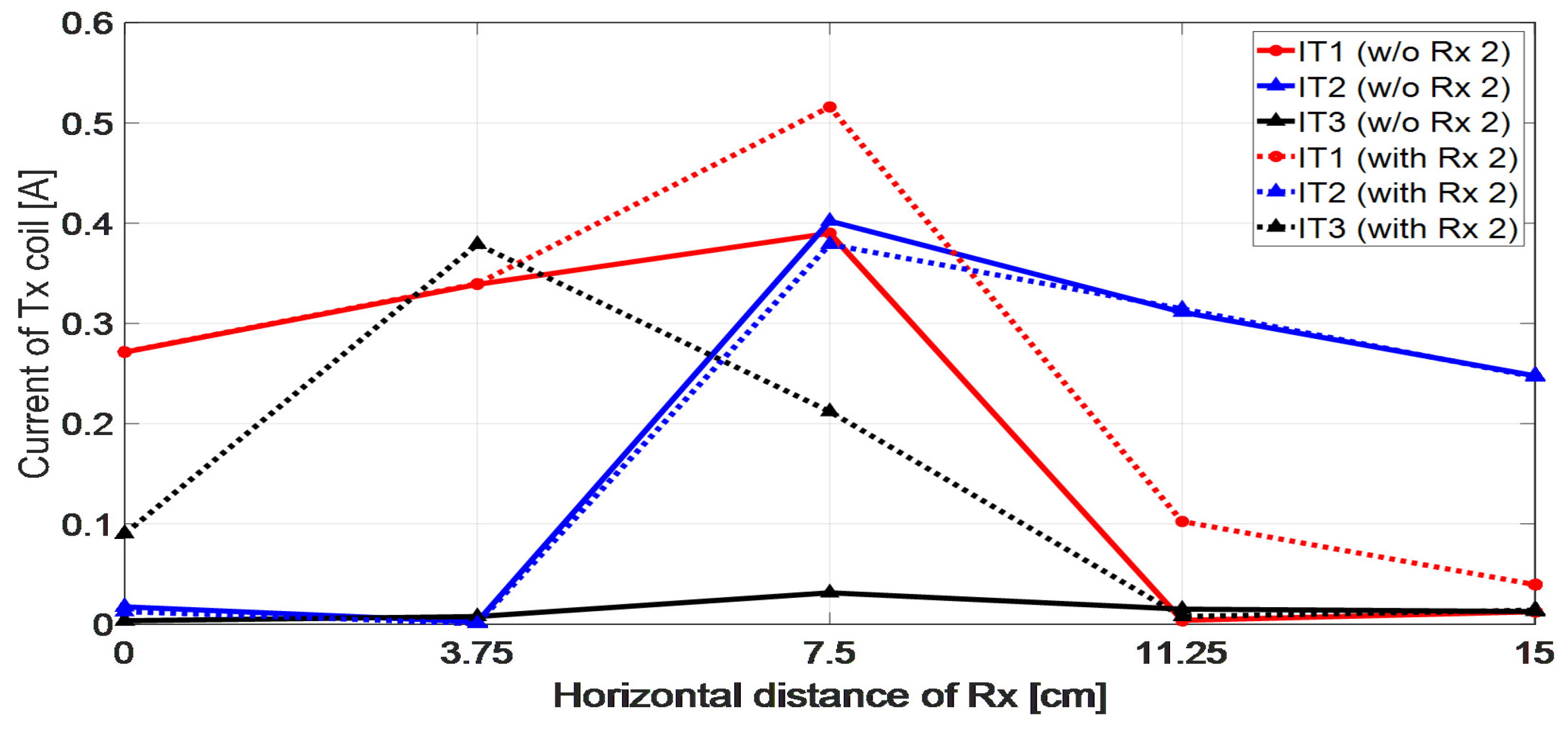
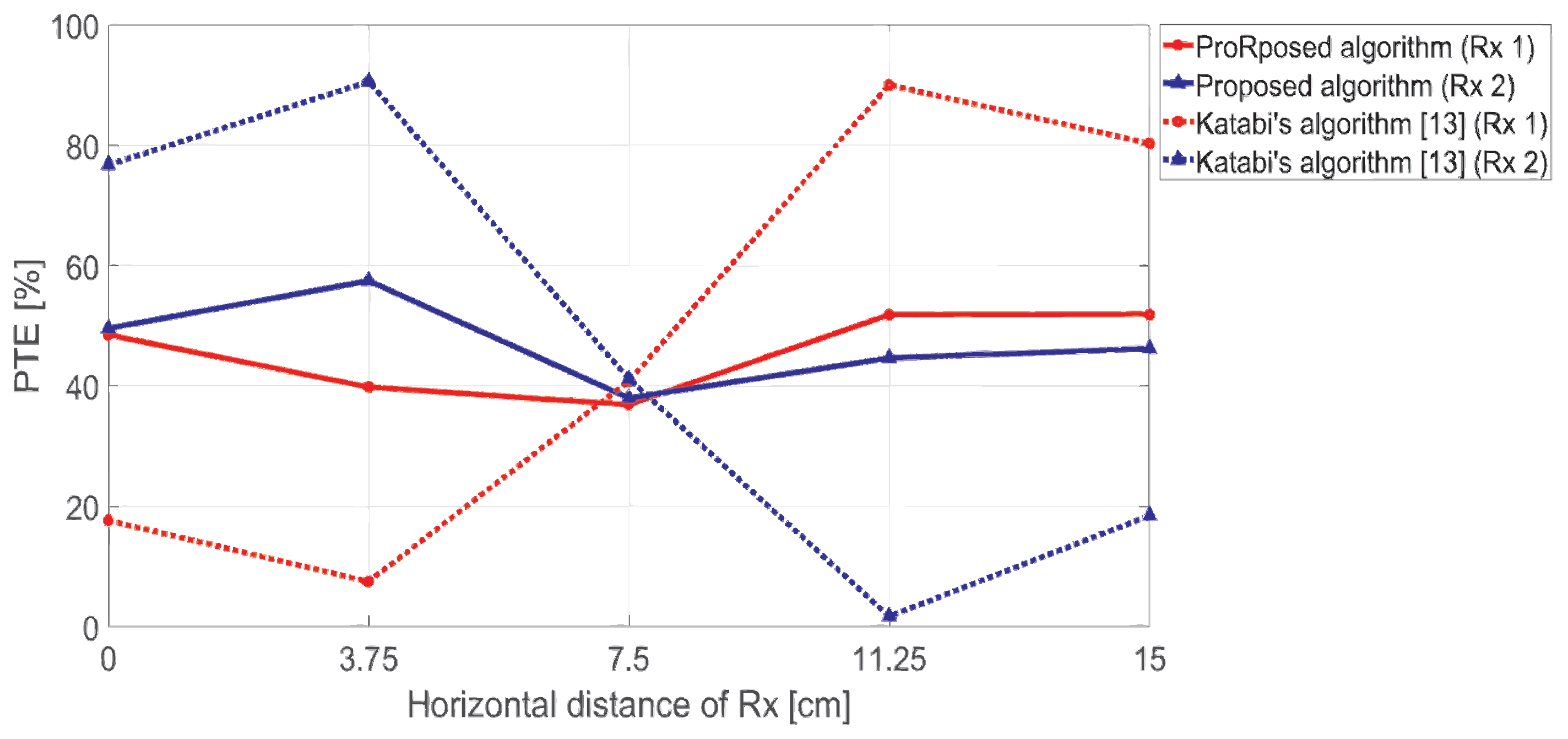
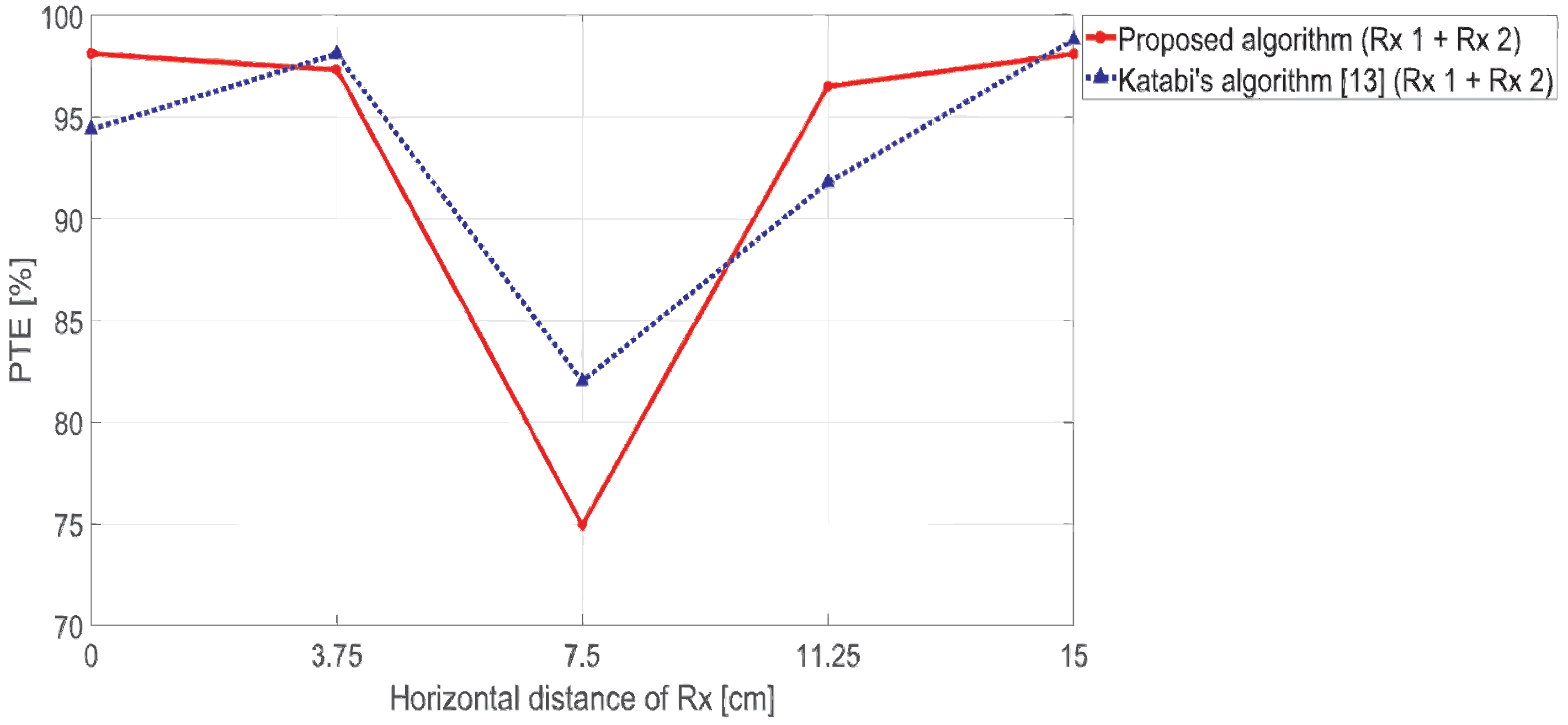
3. Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Indexes | |
| R | Rx coil indexes |
| T | Tx coil indexes |
| Parameters | |
| Current of i-th Tx coil | |
| Current of i-th Rx coil | |
| Voltage of i-th Tx coil | |
| Voltage of i-th Rx coil | |
| Impedance of i-th Tx coil | |
| Impedance of i-th Rx coil | |
| Mutual inductance between i-th Tx coil and j-th Rx coil | |
| Mutual inductance between i-th Tx coil and j-th Tx coil | |
| Mutual inductance between i-th Rx coil and j-th Rx coil | |
| resonant frequency | |
| eigenvector | |
| weight factor |
References
- Zhang, H.; Gao, S.P.; Ngo, T.; Wu, W.; Guo, Y.X. Wireless power transfer antenna alignment using intermodulation for two-tone powered implantable medical devices. IEEE Trans. Microw. Theory Tech. 2019, 67, 1708–1716. [Google Scholar] [CrossRef]
- Yan, Z.; Song, B.; Zhang, Y.; Zhang, K.; Mao, Z.; Hu, Y. A rotation-free wireless power transfer system with stable output power and efficiency for autonomous underwater vehicles. IEEE Trans. Power Electron. 2018, 34, 4005–4008. [Google Scholar] [CrossRef]
- Park, J.H.; Kim, J.H.; Shin, Y.J.; Park, B.J.; Kim, W.S.; Cheong, S.J.; Ahn, S.Y. Toroidal-Shaped Coils for a Wireless Power Transfer System for an Unmanned Aerial Vehicle. J. Electromagn. Eng. Sci. 2019, 19, 48–55. [Google Scholar] [CrossRef]
- Kim, Y.W.; Boo, S.H.; Kim, G.Y.; Kim, N.Y.; Son, L.B. Wireless Power Transfer Efficiency Formula Applicable in Near and Far Fields. J. Electromagn. Eng. Sci. 2019, 19, 239–244. [Google Scholar] [CrossRef]
- Lee, H.W.; Boo, S.H.; Kim, G.Y.; Lee, B.S. Optimization of Excitation Magnitudes and Phases for Maximum Efficiencies in a MISO Wireless Power Transfer System. J. Electromagn. Eng. Sci. 2020, 20, 16–22. [Google Scholar] [CrossRef] [Green Version]
- Kim, G.Y.; Son, L.B. Design of Wireless Power and Information Transfer Systems Considering Figure of Merit for Information. J. Electromagn. Eng. Sci. 2020, 20, 241–247. [Google Scholar] [CrossRef]
- Dan, H.; Chao, Y.; Xu, G.; Liu, Z.; Han, H.; Su, M.; Sun, Y. An Extremum Seeking Algorithm based on Square Wave for Three-Dimensional Wireless Power Transfer System to Achieve Maximum Power Transmission. IEEE Trans. Ind. Appl. 2021. Available online: https://ieeexplore.ieee.org/document/9496216 (accessed on 16 September 2021).
- Yan, Z.; Yang, B.; Liu, H.; Chen, C.; Waqas, M.; Mai, R.; He, Z. Efficiency improvement of wireless power transfer based on multitransmitter system. IEEE Trans. Power Electron. 2020, 35, 9011–9023. [Google Scholar] [CrossRef]
- Huh, S.; Ahn, D. Two-transmitter wireless power transfer with optimal activation and current selection of transmitters. IEEE Trans. Power Electron. 2017, 33, 4957–4967. [Google Scholar] [CrossRef]
- Jadidian, J.; Katabi, D. Magnetic MIMO: How to charge your phone in your pocket. In Proceedings of the 20th Annual International Conference on Mobile Computing and Networking, Maui, HI, USA, 7–11 September 2014; pp. 495–506. [Google Scholar]
- Cao, G.; Zhou, H.; Zhang, H.; Xu, J.; Yang, P.; Li, X.Y. Requirement-driven magnetic beamforming for mimo wireless power transfer optimization. In Proceedings of the 2018 15th Annual IEEE International Conference on Sensing, Communication, and Networking (SECON), Hong Kong, China, 11–13 June 2018; pp. 1–9. [Google Scholar]
- Gao, T.; Wang, X.; Jiang, L.; Hou, J.; Yang, Y. Research on power distribution in multiple-input multiple-output magnetic coupling resonance wireless power transfer system. Electr. Eng. 2021, 1–8. [Google Scholar]
- Qi, C.; Huang, S.; Chen, X.; Wang, P. Multi-Frequency Modulation to Achieve an Individual and Continuous Power Distribution for Simultaneous MR-WPT System with an Inverter. IEEE Trans. Power Electron. 2021, 36, 12440–12455. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, C.; Xiao, Y.; Liu, S. Separate power allocation and control method based on multiple power channels for wireless power transfer. IEEE Trans. Power Electron. 2020, 35, 9046–9056. [Google Scholar] [CrossRef]
- Lee, S.B.; Kim, M.; Jang, I.G. Determination of the Optimal Resonant Condition for Multireceiver Wireless Power Transfer Systems Considering the Transfer Efficiency and Different Rated Powers with Altered Coupling Effects. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 9, 2384–2393. [Google Scholar] [CrossRef]
- Le-Huu, H.; Seo, C. Dual-Band Free-Positioning Transmitting Coil for Multiple-Receiver Wireless Power Transfer. IEEE Access 2021, 9, 107298–107308. [Google Scholar] [CrossRef]
- Xie, X.; Xie, C.; Li, L. Wireless power transfer to multiple loads over a long distance with load-independent constant-current or constant-voltage output. IEEE Trans. Transp. Electrif. 2020, 6, 935–947. [Google Scholar] [CrossRef]
- Park, S.; Choi, W. Transmitter Current Control and Receiver Coil Selection in Magnetic MIMO Power Transfer Systems. IEEE Wirel. Commun. Lett. 2020, 9, 1782–1785. [Google Scholar] [CrossRef]
- Shi, L.; Kabelac, Z.; Katabi, D.; Perreault, D. Wireless power hotspot that charges all of your devices. In Proceedings of the 21st Annual International Conference on Mobile Computing and Networking, Paris, France, 7–11 September 2015; pp. 2–13. [Google Scholar]
- Shi, L. Orientation-Indepedent Wireless Charging of Multiple Mobile Devices at a Distance. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2016. [Google Scholar]
- Gharanjik, A.; Soltanalian, M.; Shankar, M.R.B.; Ottersten, B. Grab-n-Pull: A max-min fractional quadratic programming framework with applications in signal and information processing. Signal Process. 2019, 160, 1–12. [Google Scholar] [CrossRef]
- Kurs, A.; Karalis, A.; Moffatt, R.; Joannopoulos, J.D.; Fisher, P.; Soljačić, M. Wireless power transfer via strongly coupled magnetic resonances. Science 2007, 317, 83–86. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Karipidis, E.; Sidiropoulos, N.D.; Luo, Z.Q. Quality of Service and Max-Min Fair Transmit Beamforming to Multiple Cochannel Multicast Groups. IEEE Trans. Signal Process. 2008, 56, 1268–1279. [Google Scholar] [CrossRef] [Green Version]
| Term | Definition | Explanation |
|---|---|---|
| Current of Tx, Rx coil | ||
| Voltage of Tx, Rx coil | ||
| Impedance of Tx, Rx coil | ||
| Mutual inductance between Tx and Rx coil | ||
| Mutual inductance between Tx(Rx) and Tx(Rx) coil | ||
| Horizontally Moved 0 cm | 3.75 cm | 7.5 cm | 11.25 cm | 15 cm | |
|---|---|---|---|---|---|
| [nH] | 2920.34 | 2345.96 | 985.8 | 30.71 | −159.06 |
| [nH] | −184.61 | −15.45 | 1016.21 | 2550.12 | 3195.03 |
| [nH] | −35.98 | −52.2 | −78.85 | −121.65 | −161.19 |
| Horizontally Moved 0 cm | 3.75 cm | 7.5 cm | 11.25 cm | 15 cm | |
|---|---|---|---|---|---|
| Horizontally Moved 0 cm | 3.75 cm | 7.5 cm | 11.25 cm | 15 cm | |
|---|---|---|---|---|---|
| [nH] | 2920.07 | 2345.97 | 984.51 | 104.03 | −159.26 |
| [nH] | −183.41 | −14.77 | 1017.27 | 2374.55 | 3198.45 |
| [nH] | −36 | −52.24 | −78.84 | −114.82 | −160.78 |
| [nH] | −158.61 | −120.63 | −78.47 | −54.79 | −35.85 |
| [nH] | 3198.89 | 2565.54 | 1035.46 | 69.36 | −181.91 |
| [nH] | −161.72 | 22.52 | 969.29 | 2177.21 | 2919.35 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heo, J.; Park, S.; Kim, S.-W.; Cho, I.-K.; Hong, S.; Park, Y.B. Control of WPT Transmitter Coils for Power Distribution to Two Receiver Coils without Feedback. Energies 2021, 14, 6828. https://doi.org/10.3390/en14206828
Heo J, Park S, Kim S-W, Cho I-K, Hong S, Park YB. Control of WPT Transmitter Coils for Power Distribution to Two Receiver Coils without Feedback. Energies. 2021; 14(20):6828. https://doi.org/10.3390/en14206828
Chicago/Turabian StyleHeo, Jun, Sungyeal Park, Sang-Won Kim, In-Kui Cho, Songnam Hong, and Yong Bae Park. 2021. "Control of WPT Transmitter Coils for Power Distribution to Two Receiver Coils without Feedback" Energies 14, no. 20: 6828. https://doi.org/10.3390/en14206828
APA StyleHeo, J., Park, S., Kim, S.-W., Cho, I.-K., Hong, S., & Park, Y. B. (2021). Control of WPT Transmitter Coils for Power Distribution to Two Receiver Coils without Feedback. Energies, 14(20), 6828. https://doi.org/10.3390/en14206828