Abstract
Energy storage, both short- and long-term, will play a vital role in the energy system of the future. One storage technology that provides high power and capacity and that can be operated without carbon emissions is compressed air energy storage (CAES). However, it is widely assumed that CAES plants are not economically feasible. In this context, a mixed-integer linear programming (MILP) model of the Huntorf CAES plant was developed for revenue maximization when participating in the day-ahead market and the minute-reserve market in Germany. The plant model included various plant variations (increased power and storage capacity, recuperation) and a water electrolyzer to produce hydrogen to be used in the combustion chamber of the CAES plant. The MILP model was applied to four use cases that represent a market-orientated operation of the plant. The objective was the maximization of revenue with regard to price spreads and operating costs. To simulate forecast uncertainties of the market prices, a rolling horizon approach was implemented. The resulting revenues ranged between EUR 0.5 Mio and EUR 7 Mio per year and suggested that an economically sound operation of the storage plant is possible.
1. Introduction
To implement a renewable energy system in Germany, both short- and long-term emission-free energy storage will be vital, as well as hydrogen for long-term storage and in the traffic and industry sectors [1]. Short-term storage systems are defined by a discharging duration of less than 24 h. Respectively, a long-term energy storage system presents a discharging duration of 24 h or more. If 90% of the energy consumption in Germany is to be covered by renewable energies, roughly 7 GW of short-term storage and 16 GW of long-term storage will be needed [2]. With a short-term storage discharging duration of on average 4 h, this accounts for a storage capacity of 28 GWh. Regarding long-term energy storage, a storage capacity of 24 TWh to 32 TWh was estimated with a discharging duration of 1500 h to 2000 h.
Compressed air energy storage (CAES) systems are classified as short-term storage, although the classification depends heavily on the geological conditions of the salt cavern. This storage technology uses compressed air stored in an underground salt cavern. The world’s first plant was commissioned in 1978 in Huntorf, Germany. Until today, only one additional plant has been put into operation in McIntosh, USA [3]. These CAES plants use natural gas for reheating the compressed air before expansion. It is also possible to reheat the compressed air by combusting hydrogen. If hydrogen is produced with an electrolyzer powered by renewable energies, the CAES plant emits no carbon dioxide. Another approach is the adiabatic CAES plant: if the excess heat of the compression is stored and used to reheat the compressed air before expansion, the CAES plant does not consume any fuel.
The German energy market currently offers two possibilities for the Huntorf plant to generate revenue: the day-ahead market or intraday market and the tertiary-operating-reserve market. Since the startup time of the Huntorf plant in charging and discharging mode is around 8 min [4], the supply of primary or secondary operating reserve is not a use case for this plant. In this paper, the revenue maximization in the day-ahead market and the minute-reserve market was modeled and evaluated.
To this extent, a mixed-integer linear programming (MILP) model of the CAES plant was created. MILP modeling has been the subject of various research approaches regarding energy storage plants. Moreno et al. [5] showed that the proposed MILP model of a hybrid energy storage plant facilitates the participation in different markets and enables robust scheduling. In [6], a MILP model of a CAES plant was presented that co-optimizes the participation in the energy and ancillary service markets. A similar approach was shown in [7]. Wolf et al. [8] developed a MILP model of an adiabatic CAES plant co-located with a wind farm for multifunctional commitment optimization. A nonlinear optimization model of a CAES plant with a detailed thermoeconomic model was used in [9] to reduce wind curtailment and CO2 emissions. Ghalelou et al. [10] presented a MILP model that incorporates a CAES plant, thermal units, and a demand–response program with the objective of reducing operating costs.
1.1. CAES Plant in Huntorf
Compressed air energy storage consists, similar to an open gas turbine cycle, of a compressor, a combustion chamber, a gas turbine, and a synchronous machine. However, a CAES plant also includes a compressed air storage. This results in the time-independent air compression and generation of electrical energy. During charging mode, the CAES plant uses electrical energy to compress and store ambient air. In discharging mode, the compressed air is reheated by using natural gas and then expanded to ambient pressure. The electrical energy is fed into the grid. The synchronous machine can work as a motor or as a generator by decoupling it from either the turbine or the compressor [11]. The process flow diagram of a CAES plant is shown in Figure 1.
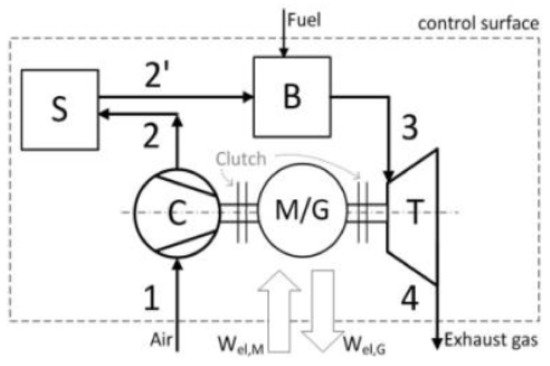
Figure 1.
Process flow diagram of a CAES plant with C—compressor, S—storage, B—combustion chamber, T—turbine, and M/G—motor/generator (synchronous machine) [11].
The Huntorf plant has a rated power of 321 MW in discharging mode. The discharging duration is roughly 8 h at rated power. In charging mode, the plant provides 68 MW for around 24 h, as the air mass flow of the compressor (108 kg/s) is much smaller than the air mass flow of the combustion chamber (455 kg/s). Since the compressed air is cooled down to ambient temperature before storage and reheated before entering the gas turbine, the Huntorf plant is considered as a diabatic CAES plant. Natural gas is used in both the high- and low-pressure combustion chamber to reheat the air before expansion. The compressed air is stored in solution-mined underground salt caverns [4]. The combined volume of the two air caverns is 310,000 m3. The salt cavern operates at a pressure range from 43 bar to 70 bar [12]. Kaiser et al. estimated a round-trip efficiency of 33% of the Huntorf plant based on exergetic considerations [13].
Originally, the Huntorf plant was commissioned to store excess power during off-peak load periods and supply electricity during high-load periods. However, due to decreasing operating hours, the plant has primarily been used for providing tertiary operating reserve (minute reserve) since its commission [14].
1.2. Research Review
Multiple studies analyzed the ability and feasibility of diabatic and adiabatic CAES plants to level fluctuating wind generation. Lund et al. [15] conducted a system economic analysis of a CAES plant and concluded that a CAES plant cannot store all excess renewable energy within the scenario on its own and is less attractive than other load leveling approaches. However, a study by Succar et al. [3] stated that the combination of wind power plants and a CAES plant showed investment costs that were similar to those of other baseload power plants with low carbon emissions. Bullough et al. [16] concluded that an adiabatic CAES plant facilitates better integration of fluctuating wind power and increases wind power utilization. The economic analysis of Denholm et al. [17] led to the conclusion that co-locating a CAES plant with a wind farm rather than with the load site improves the utilization capacity of transmission-constrained electrical grids. Nabil et al. [18] added peak shaving and demand-side management to the list of possible applications of CAES besides the integration of more renewable power generation plants, in particular wind farms. Drury et al. [19] stated that the participation in the energy and control reserve markets can make CAES plants profitable, depending on the market design, but adiabatic CAES would need further revenue possibilities. In [20], a profit-based unit commitment model was introduced with the aim of the profit maximization of a generation company whose portfolio includes CAES and concentrating solar power units. The results showed that the profit increases by more than 4% compared to a generation portfolio based solely on thermal power plants. Jakiel et al. [21] showed that the roll-out of wind power plants leads to the improvement of market conditions for adiabatic CAES plants, which are emission-free and thus not affected by fuel and emission price changes. The research project ADELE-ING [22] proposed that the investment costs of adiabatic CAES are as low as those of hydropower storage plants and partially adiabatic CAES plants present an additional 30% cost reduction. The business economic analysis of [15] showed that the feasibility of CAES plants strongly depends on the structure of the ancillary service markets. It is widely assumed that CAES plants cannot be operated profitably. Therefore, no more than two diabatic plants have been put into operation to date. Recent research focused on adiabatic compressed air energy storage technologies because this technology promises a higher efficiency and zero emissions. However, no adiabatic CAES has been put into operation as of now. Barbour et al. [23] stated that the difficulties include the availability of suitable off-the-shelf components, unrealistic assumptions in theoretical research, and the irreversibility of the cycle.
The simulation of a stand-alone CAES plant that is fueled with hydrogen produced on-site with an electrolysis has not been performed in recent research. Most studies analyze the micro- or macro-economic benefit of either a diabatic CAES fueled with natural gas or an adiabatic CAES plant. Hamedi et al. [24] conducted an eco-emission analysis on a microgrid including compressed air and power-to-gas energy storage technologies. However, the gas from the power-to-gas process is only used for covering the gas demand and not for the CAES process. The combination of a hydrogen-fueled CAES and an electrolysis offers two main advantages: The CAES operation is carbon-emission-free without the usage of an expensive heat exchanger, and the electrolysis offers an additional, flexible load in charging mode that can participate in the energy market independently of the compressor of the CAES plant. Furthermore, the addition of hydrogen storage increases the storage capacity of the combined storage plant. This paper shows that hydrogen-fueled CAES plants can play a vital part in the future emission-free energy system. To this end, the economic viability of such a plant was assessed. The aim was to analyze to what extent the Huntorf CAES plant can be operated economically and which plant enhancement yields the highest revenue increase.
2. Materials and Method
The CAES plant model used a mixed-integer linear programming approach. The performance of the plant was described using a linear objective function and linear constraints. The model included eight plant variations and four use cases. The objective function and the constraints differed depending on the plant variation and the use case. The model was implemented in MATLAB R2020b by MathWorks using the CPLEX toolbox Version 12.10 by IBM.
The model included eight plant variations to analyze the benefit of the current state of the plant and possible plant enhancements. The plant variations are shown in Table 1. The enhancements included the increase of the storage capacity of the compressed air storage by increasing the maximum pressure in the salt cavern (variation C+) and the use of excess exhaust heat for preheating the fuel (recuperation (variation R)). Plant variation CP+R is a retrofit of the Huntorf plant. It unites the two prior mentioned enhancement possibilities (C+ and R) and additionally includes the increase of the rated charging and discharging power. Another enhancement is the addition of a water electrolysis to produce hydrogen, which is burned in the high-pressure combustion chamber to reduce the CO2 emissions of the plant (variations H20 to H470). Within this scope, the storage capacity of the hydrogen storage equals the amount of hydrogen needed for a full discharging cycle of the compressed air storage. Three values for the rated power of the electrolysis were analyzed: 20 MW (a currently economically and technologically reasonable value), 120 MW (hydrogen storage is fully charged in the same amount of time as the compressed air storage), and 470 MW (hydrogen storage is fully charged in the same amount of time as the compressed air storage is fully discharged). Plant variation CP+RH is a combination of the retrofit of CP+R with hydrogen production and combustion in both combustion chambers. This plant variations represents a CO2-emission-free storage power plant.

Table 1.
Plant variations of the MILP model.
Figure 2 shows the process flowchart of the Huntorf CAES plant and the plant variations. The base plant model Huntorf and plant variations C+, R, and CP+R use only natural gas in the combustion chambers. In plant variations H20, H120, and H470, hydrogen is used in the high-pressure combustion chamber and natural gas is used in the low-pressure combustion chamber. For the retrofit CP+RH, hydrogen fuels both combustion chambers.
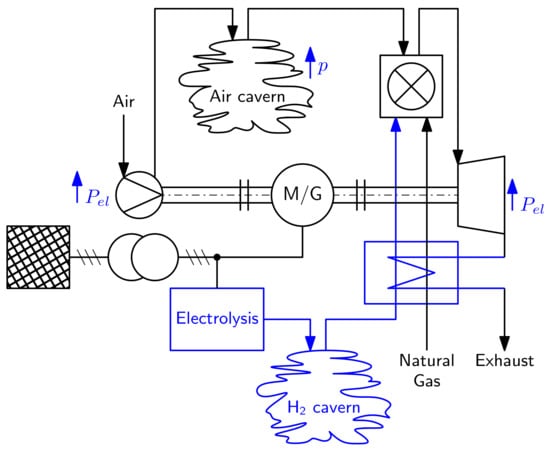
Figure 2.
Process flowchart of the Huntorf CAES plant (black) with additional components of the plant variations (blue).
Within the scope of this research, it was assumed that the combustion of hydrogen in the existing high- and low-pressure combustion chambers is possible with only little modification of the plant. The plant parameters are shown in Table A3 in the Appendix A.
The MILP model was applied to four use cases, shown in Table 2, which represent a market-orientated operation of the plant. The objective of these use cases was the maximization of revenue. Within use case DA, the plant stores energy when the energy prices are low and sells energy when the energy prices are high. For use case MR, the participation in the day-ahead market is paired with the minute-reserve market. Both the revenue at the day-ahead market and the minute-reserve market are highly dependent on the quality of the price forecast. For use cases DAF and MRF, a model is developed that simulates the uncertainty of a seven-day forecast paired with a rolling horizon optimization approach. It was assumed that the Huntorf plant is a price taker, and therefore, the participation of the plant in the market has no effect on the market prices.

Table 2.
Use cases of the MILP model.
2.1. Input Data
The day-ahead market is one of two energy stock markets and one of four possibilities to buy or sell electricity in Germany. The day-ahead auction on the European Energy Exchange stock market (EPEX) spot trades electricity until 12:00 p.m. for the next day in one-hour blocks. The day-ahead market price is the market clearing price. The day-ahead market prices for 2015 to 2019 were retrieved from [25].
The minute reserve (also called tertiary control reserve) is the third instance of control reserve in the German electricity market. The minute reserve is to be activated within 15 min and distinguishes between positive and negative reserve. The positive minute reserve is the generation capacity that can be activated in case of an underproduction of electricity in the German electricity market. The negative minute reserve is the load capacity or the ability to decrease electricity generation if the generation is greater than the load in the electricity grid [26].
Both the provision of minute-reserve power (positive and negative) and the call for electrical energy (positive and negative) are refunded. Therefore, the tenders distinguish between capacity price and energy price. The activation is based on a merit-order-list where the market participants are refunded based on their tender (pay-as-bid method). Only market participants who are allocated for tendering capacity can tender energy [26].
The MILP model requires the definition of the capacity price () and energy price (), both positive and negative, prior to the optimization. The binary vectors indicate whether the Huntorf tender is lower than the market clearing price (MCP) (here, and ) at instant t.
In October of 2018, the tendering process for minute reserve changed: the granting depended on a tender that was dependent on the capacity price, the energy price, and a weighting factor. The weighting factor was determined quarterly. In November 2020, the tendering process was changed again. Presently, the provision of power and the call for energy are tendered separately [26]. Because of this change, the year 2019 was omitted in the analysis of yearly revenue for use cases MR and MRF. The minute reserve-market prices for 2015 to 2018 were retrieved from [25].
The carbon price in Germany was set to EUR 25/t in 2021. By 2025, the price will rise to EUR 55/t. Starting in 2026, the emission allowances will be auctioned off (§10 BEHG (Brennstoffemissionshandelsgesetz of 12 December 2019, which has been changed by Article 1 of the law of 3 November 2020)). The specific carbon dioxide emissions of natural gas are / [27]. The price of natural gas is also expected to rise in the future. The International Energy Agency [28] predicts a rise of 30% by 2040 compared to 2020.
In the MILP model, the price for carbon dioxide emissions was added to the natural gas price, and price increases were taken into account.
For use cases DAF and MRF, the uncertainty of electricity price forecasts was considered. Electricity price forecasting is important for all market participants and is therefore researched extensively. The influencing factors are complex [29]. It was assumed that the day-ahead and minute-reserve market prices could be predicted for seven days ahead [30]. However, the forecast of the electricity price is highly dependent on the weather forecast, since transmission capacity and both the generation and the consumption of energy depend on the weather conditions. The forecast therefore grows more uncertain for a longer forecasting horizon. The objective of this research was not to develop a model to predict energy prices, but to simulate the uncertainty of a price forecast. To this end, Equations (4) and (5) were developed.
represents the day-ahead market price with forecast uncertainty, whereas is the real price. The uncertainty was modeled with a random number r, which was generated using a normal distribution with (expected value) and (deviation). The predicted prices were limited by a corridor , which was dependent on the maximum price per year (). T is the length of the forecast.
The usability of this approach was determined by calculation the mean average error (MAE), the mean average percentage error (MAPE), and the symmetric mean average percentage error (sMAPE). The MAE of this forecast was 7.734. Compared to the results of Ugurlu et al. [31], the forecast simulation can be ranked between a naive method and an artificial neural network (ANN) approach. Delarue et al. [32] stated that the MAPE of typical time series price forecasts is around 20%, while it can decrease to 10% or lower for adequately trained ANN approaches. The MAPE of this forecast simulation was 23.1%. The sMAPE equaled 26.35%, which is greater than the sMAPE of all forecasting methods described in [33]. This led to the conclusion that the forecasting simulation was worse than a forecasting approach the plant operator would use. Thus, the results for the use cases with forecasting uncertainties can be viewed as worst-case scenarios.
The uncertainty was implemented in the MILP model with the use of a rolling horizon optimization approach with an optimization horizon of one day and a forecast horizon of seven days [34,35]. For use case MRF, the forecast uncertainty for the capacity price for the minute reserve was simulated in the same way as the forecast uncertainty of the day-ahead market prices. However, the deviation from the original prices started at the beginning of the second day of the prediction. This was implemented to prevent a situation where the real market clearing price was higher than the tendered price, but the predicted MCP was lower, which would result in an allocation of power or energy within the model even though the tender would not have been accepted in reality.
2.2. Plant Model
The decision variables of the MILP model are shown in Table A2, and the input parameters are shown in Table A3. The indices used for variables and parameters are shown in Table A1. For DA and DAF, equaled 1 h, and for the use cases MR and MRF, was 15 min (0.25 h).
2.2.1. Constraints
Constraints (8)–(13) model the CAES plant. The energy balance of the compressed air storage was calculated with Constraint (8). Parameter is the round-trip efficiency.
The power in charging mode is not adjustable and defined as follows:
The power in discharging mode can be adjusted between a minimal value and the rated value.
Constraint (11) ensures that the plant does not operate in charging and discharging mode simultaneously.
Constraints (12) and (13) define the startup variables: variables and equal one if the plant starts operating in charging mode and discharging mode, respectively, at instant t.
Constraints (14)–(16) were included in the plant variations with electrolysis (H20, H120, H470, and CP+RH). Constraint (14) describes the energy balance of the hydrogen storage and defines the state of charge. Parameter is the electrolysis efficiency in , and and describe the hydrogen consumption during discharging mode.
The power of the electrolyzer was defined in the same way as the power of the CAES plant in discharging mode.
The startup variable of the electrolyzer was defined as follows.
Constraints (17)–(32) were added or adjusted for use cases MR and MRF. The called minute-reserve power was added to the energy balance:
Negative minute-reserve power is not adjustable, because the plant would be operating in charging mode.
When tendering positive minute-reserve power, the power can be adjusted because the plant will operate in discharging mode if the positive minute reserve is called upon.
If the plant is allocated for the provision of minute-reserve power () and the energy offer price is lower than the market clearing price (), minute-reserve energy is called upon.
The plant can either provide positive or negative minute reserve or participate in the day-ahead market in charging or discharging mode, which is ensured by Constraint (22).
However, the minute-reserve power can only be tendered if the MCP is higher than the tender of the plant.
The startup variables for the provision of minute-reserve energy were defined with Constraints (25) and (26), where equals , which was not included in the decision vector to reduce the model size.
The minute-reserve power is offered in four-hour blocks. The state of charge of the compressed air storage has to be sufficient to provide minute-reserve energy at the tendered power for four hours. is the set of time steps at the beginning of a four-hour block.
The tendered power is constant for a four-hour block.
In the day-ahead market, energy is traded in one-hour blocks. is the set of time steps at the beginning of a one-hour block.
The following Constraints (33)–(40) were added to the model for plant variations with electrolysis to model the minute-reserve tendering with the electrolyzer. Constraint (33) describes the energy balance of the hydrogen storage.
The power of the electrolyzer was assumed to be continuously adjustable between a minimal value and the rated value.
The power with which minute-reserve energy is provided equals the power that is tendered for minute-reserve power.
Minute-reserve power can only be tendered if the tendered price is lower than the MCP.
The startup variable for the electrolyzer when providing minute-reserve energy was defined with Constraint (37).
The SOC of the hydrogen storage at the beginning of each four-hour block has to be sufficient to provide minute-reserve energy with the tendered power for four hours.
The tendered minute-reserve power is constant within a four-hour block, and the power with which the plant operates in the day-ahead-market is constant within a one-hour block.
2.2.2. Objective Function
The objective function for use cases DA and DAF aims at maximizing the revenue when participating in the day-ahead market and was defined as follows:
Equation (42) describes the revenue when selling electrical energy in the day-ahead market in discharging mode. With Equation (43), the costs of buying electrical energy in the day-ahead market during charging mode are calculated. Equation (44) estimates the fuel costs for natural gas during discharging mode. Parameters and model the linear behavior of the natural gas consumption of the plant during discharging mode. Equations (45) and (46) estimate the costs for each startup of the plant.
For plant variations including electrolysis (H20, H120, H470, and CP+RH), the objective function was adjusted according to Equation (47). Electricity for the electrolyzer is bought in the day-ahead market (), and startup costs of the electrolyzer were added ().
with
For use cases MR and MRF, the revenue for tendered minute-reserve power (, Equation (50)) was added as a cost component with a positive sign to the objective function.
For plant variations with electrolysis, this revenue component is defined as:
The revenue for the provision of minute-reserve energy is not included in the objective function because the model included a fixed-energy-price tender. The plant provides energy if it provides power and if the energy price tender is less than or equal to the MCP. The first condition was optimized, and the second condition could not be controlled.
3. Results
The results of the MILP optimization are the time series of the power of the CAES plant, the power of the electrolyzer (if present), as well as the time series of the state of charge of both the compressed air storage and the hydrogen storage (if present). The simulation results were analyzed and compared with a set of the criteria, which included the revenue and plant parameters such as operating hours and carbon emissions. The yearly revenue included operating costs such as energy purchase in the day-ahead market for charging mode and electrolysis, natural gas and carbon emission costs, and startup costs. The startup costs represent the cost of the wear of the components. The revenue corresponds to the objective functions of use cases DA and DAF. For use cases MR and MRF, the proceeds for providing energy in the minute-reserve market were added to the results of the objective function to calculate the revenue since these proceeds were omitted during the optimization. The revenue did not include investment costs for plant enhancements.
3.1. Revenue
Figure 3 shows the revenue for the participation in the day-ahead market (use case DA) for years 2015 to 2019 and the average per year. The current Huntorf plant resulted in an average yearly revenue of EUR 1.2 Mio. The fossil retrofit (CP+R) showed the highest average revenue with almost EUR 7 Mio per year. This plant variation is a combination of plant variations C+ and R with the addition of a higher rated power in charging and discharging mode. The Plant variation with recuperation (R) showed a significant increase in revenue compared to the current plant, whereas the plant variation with increased storage capacity (C+) only showed a slight increase. In conclusion, the improvement of fuel consumption due to recuperation has a higher impact on the revenue than the increase in storage capacity and power, because the costs for natural gas and carbon dioxide emissions are an extensive factor of the revenue.
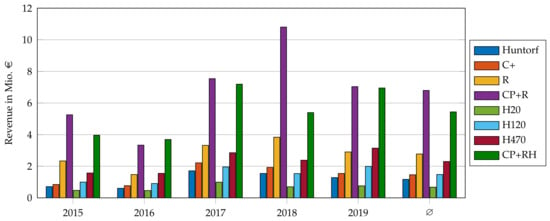
Figure 3.
Yearly revenue of use case DA.
The yearly revenue of plant variations including electrolysis depends on the rated power of the electrolyzer: higher rated powers result in higher revenues if investment costs are omitted. With high rated power, the electrolyzer has a higher flexibility regarding the timing of operation and thus buying energy in the day-ahead market. The yearly revenue for plant variation H20 was lower than the revenue of the base plant Huntorf, but plant variations H120 and H470 showed higher yearly revenues than the Huntorf plant and variation C+. The retrofit plant variations CP+R and CP+RH showed considerably higher yearly revenues than the rest of the plant variations. For the current natural gas and carbon emission prices, the fossil retrofit yielded higher revenues on average than the emission-free hydrogen production and combustion of the retrofit CP+RH.
The yearly revenue varied through the years for every plant variation. This is due to the fact that the day-ahead market prices are dependent on various circumstances such as residual load, renewable energy generation capacity, and the prices of fossil resources. High average energy prices and a high variation lead to higher yearly revenues. The lowest average price (EUR 29.00/) and low variation (50% of the prices ranged between EUR 22.32/ and EUR 34.97/, which is a difference of only EUR 12.65/) caused the lowest yearly revenue in 2016. In 2018, the average price was EUR 44.47/, and 50% of the hourly price values ranged between EUR 34.45/ and EUR 54.87/ (difference of EUR 20.42/). The yearly revenue was highest for 2018 for all plant variations without electrolysis.
For 2016, the revenue of the retrofit with hydrogen (CP+RH) was higher than the revenue of the fossil retrofit (CP+R) because the average day-ahead market price was lower, which means that energy for the electrolyzer, which is bought in the day-ahead market, was cheaper. For 2018, the revenue of the fossil retrofit was notably higher than the revenue of CP+RH. The average of the day ahead market prices was higher, and therefore, the energy for the electrolyzer was more expensive.
In 2020, the average day-ahead market prices were low (EUR 30.96/) and the variation was high (50% of values in range of EUR 18.51/) [25]. It is suspected that the yearly revenue will be lower than for 2018, but higher than for 2016 and that the retrofit with hydrogen will yield a higher revenue than the fossil retrofit.
Figure 4 shows the revenue shares for use case DA for 2019. The resulting revenue, which is shown in Figure 3, is the sum of the positive bars minus the sum of the negative bars. The costs for natural gas and carbon dioxide emissions were the biggest cost factors. For plant variations with recuperation (R and CP+R), the fuel efficiency resulted in lower costs for natural gas and carbon emissions, which resulted moreover in higher costs on the day-ahead market because of the higher operating hours in charging mode. For plant variation H470, the high rated power of the electrolyzer resulted in high flexibility, which led to the electrolyzer operating mostly during times with negative day-ahead market prices. This resulted in positive day-ahead market proceeds for the operation of the electrolyzer. The costs for startups were insignificantly low with only 0.7% to 4.1% of the yearly revenue.
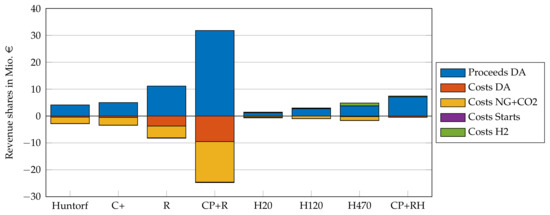
Figure 4.
Revenue shares of use case DA (2019).
The previous results were based on a natural gas price of EUR 20/ and a carbon price of EUR 25/t, which represent the current circumstances (base scenario). The MILP optimization was also performed for two other scenarios shown in Table 3. The second scenario represents the predicted prices by 2025 based on the German Fuel Emissions Trading Act. The third scenario represents the price predictions by 2040 based on the Fuel Emissions Trading Act and the findings by the International Energy Agency [28].

Table 3.
Natural gas and carbon dioxide emission prices for different scenarios.
Figure 5 shows the average revenue for years 2015 to 2019 for these three scenarios. For all plant variations except the retrofit with hydrogen, the revenue declined significantly when the natural gas and carbon prices rose. For the natural-gas-fueled plant variations, the revenue in 2025 was one third less on average than for the base scenario, and the revenue in 2040 was only 20% of the base scenario. For plant variations that use hydrogen in the high-pressure combustion chamber, the impact of the natural gas and carbon prices on the yearly revenue was less severe. For plant variation CP+RH, the revenue was constant because the plant did not use any natural gas in the combustion process. When both retrofit plant variations were compared, the revenue of the fossil one in 2025 was lower than the revenue of the one with hydrogen combustion in the same scenario. In 2040, the revenue of plant variation CP+R was only a quarter of the revenue of CP+RH.
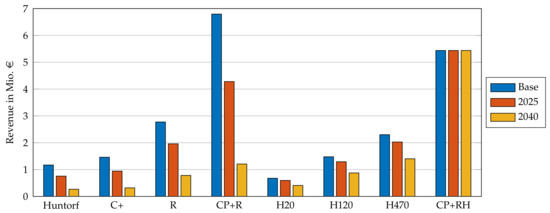
Figure 5.
Yearly revenue of use case DA with varying natural gas and carbon prices (average per year from 2015 to 2019).Yearly revenue of use case DA with varying natural gas and carbon prices.
Figure 6 compares the yearly revenue for the four implemented use cases: participation in the day-ahead market with and without forecast uncertainty (DA and DAF) and additional participation in the minute-reserve market (MR and MRF) with a natural gas price of EUR 20/ and a carbon price of EUR 25/t. Revenues for use case MR were the highest, and revenues for use case DAF were the lowest. The lowest yearly revenue with EUR 0.48 Mio was recorded for use case DAF and plant variation H20. The fossil retrofit CP+R showed the highest yearly revenue with EUR 6.96 Mio when participating in the day-ahead market, as well as the minute-reserve market with perfect forecasting (use case MR).
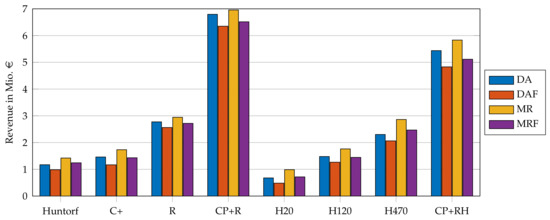
Figure 6.
Yearly revenue of use cases DA and DAF (average per year from 2015 to 2019) and use cases MR and MRF (average per year from 2015 to 2018).Yearly revenue of use cases DA, DAF, MR and MRF.
The revenues for the use cases that include participation in the minute-reserve market were between 2% and 48% higher than the revenues for use cases DA and DAF. The forecast uncertainty resulted in a decrease of revenue between 6% and 29%. The highest differences among the use cases were recorded for plant variation H20. The fossil retrofit CP+R showed the lowest differences among the use cases. This led to the conclusion that higher absolute revenues result in lower deviations among use cases.
3.2. Operation Parameters
The feasibility and plausibility of the previously presented use cases can be assessed and compared with criteria representing the operation parameters: operating hours, utilization, number of starts, and carbon emissions.
Figure 7 shows the average operating hours per year in charging mode (compressor) and discharging mode and of the electrolyzer when participating in the day-ahead market (use case DA). The operating hours in charging mode ranged between 138 h and 3730 h. Since the natural gas and carbon emission costs were the biggest factor of the revenue, the increase of fuel efficiency resulted in more opportunities to discharge and thus in more operating hours in charging mode. Additionally, the fossil retrofit (CP+R) offered more flexibility due to the increased storage capacity, which resulted in four-times higher operating hours than for the current Huntorf plant. For the plant variations with electrolysis, the operating hours in charging mode depended mainly on the rated power of the electrolyzer. The operating hours in charging mode for plant variation H20 were the lowest because with only 20 MW of electrolysis; the charging duration of the hydrogen storage was much higher than the charging duration of the compressed air storage. When comparing the retrofit plant variations with and without hydrogen combustion, it became obvious that the operating hours of the fossil retrofit were significantly higher than those of the retrofit with hydrogen combustion, even though the revenue was only slightly higher.
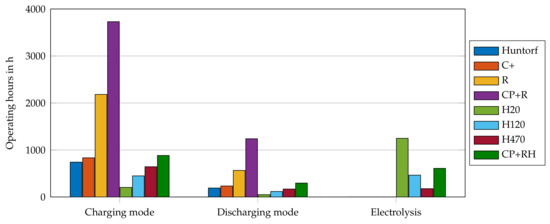
Figure 7.
Operating hours in charging mode (compressor) and discharging mode (turbine) and of the electrolyzer for use case DA (average per year from 2015 to 2019).
The operating hours in discharging mode ranged between 45 h and 1239 h and were significantly lower than in charging mode because the full cycle discharging duration was only a quarter of the charging duration (amount of time needed to fully discharge/charge the storage). The operating hours in discharging mode showed the same differences among plant variations as the operating hours in charging mode.
The operating hours of the electrolyzer ranged between 151 h and 1330 h per year. Even though plant variation H20 showed high operating hours of the electrolyzer, the operating hours in charging and discharging mode were very low. This was due to the fact that the rated power of the electrolyzer was only 20 MW and it took 150 h to fully charge the hydrogen storage. The rated power of the electrolyzer of the retrofit CP+RH was only 30 MW higher than the rated power of plant variation H470, but the operating hours of the electrolyzer were significantly higher. This was based on the recuperation of the retrofit, which resulted in a higher fuel efficiency and more opportunities to both discharge and charge.
When the plant participated additionally in the minute-reserve market (use case MR), the operating hours in both charging mode and discharging mode, as well as of the electrolyzer were slightly lower for all plant variations, but the decrease was less than 15%. When providing minute-reserve power, the plant increased revenue by being in standby. Plant variations with lower operating hours (Huntorf, C+, R, H20, H120, H470, and CP+RH) showed slightly higher operating hours if the forecast uncertainty was implemented with the rolling horizon approach. However, plant variations with high operating hours (R and CP+R) showed a decrease in operating hours for use cases DAF and MRF.
The utilization of a component can be assessed with the ratio of full load hours divided by operating hours. The compressor of the CAES plant operates always at rated power, which resulted in the utilization of one. Even though the power in discharging mode can be adjusted between 100 MW and 321 MW, the turbine almost always operated with rated power in all market-orientated use cases (utilization > 95%). The power of the electrolyzer offers more flexibility than the turbine and can be adjusted between 5% and 100% of the rated power. However, the utilization was greater than 85% for every use case.
The number of starts was minimized in all use cases by adding the startup cost component to the objective function. Figure 8 shows the average number of starts per year in charging mode (compressor) and discharging mode (turbine) and of the electrolyzer for use case DA (participation in the day-ahead market). With around 4800 h in operation in charging mode for the fossil retrofit and over 400 starts, the average duration the plant operated in charging mode was around 12 h at a time, which was less than half of the amount of time it took for the compressed air energy storage to be fully charged. For the retrofit with hydrogen combustion, the average operating time for one charging cycle was around 7 h. In conclusion, fewer operating hours resulted in a shorter average charging duration each start.
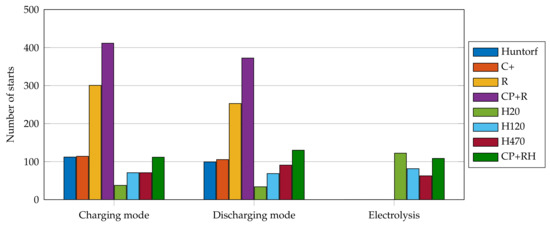
Figure 8.
Number of starts in charging mode (compressor) and discharging mode (turbine) and of the electrolyzer for use case DA (average per year from 2015 to 2019).
The number of starts in discharging mode was almost the same as the number of starts in charging mode. The average discharging cycle duration for the current Huntorf plant was 2 h and for the fossil retrofit 3.5 h. This was due to the higher storage capacity of the retrofit. The number of starts of the electrolyzer ranged between 60 and 130 starts. The higher rated power of the electrolyzer resulted in a lower number of starts. The average charging cycle duration was 10.2 h for the smallest electrolyzer (H20) and 2.6 h for the biggest electrolyzer (H470).
If the plant participated additionally in the minute-reserve market, the number of starts decreased. This was due to the fact that the plant could realize revenue when being in standby and providing minute-reserve power. For most plant variations, the number of starts increased when considering the forecast uncertainty. The average duration of one charging or discharging cycle was shorter because the plant may have to stop operating if the forecast changes.
An often discussed disadvantage of diabatic CAES is the carbon emissions. Carbon emissions are proportional to the operating hours in discharging mode and additionally depend on the type of fuel used. The current Huntorf plant and plant variations C+, R, and CP+R use natural gas in both combustion chambers. Hydrogen is used in the high-pressure combustion chamber, while natural gas is used on the low-pressure combustion chamber in plant variations H20, H120, and H470. For plant variation CP+RH, the carbon emissions are zero because hydrogen is burned both in the high-pressure and the low-pressure combustion chamber. The minimization of carbon emissions was an objective of the optimization since the carbon price was included in the fuel costs.
Figure 9 shows the average amount of carbon emissions per year for all use cases. Emissions ranged between 0 t and 105,710 t per year. Plant variations H20, H120, and H470 showed low carbon emissions with less than 10,000 t per year because of the hydrogen combustion. The difference between the amount of carbon emissions of the plant variation with increased storage capacity (C+) and recuperation (R) was small, even though the operating hours in discharging mode of plant variation R were twice as high as for plant variation C+. This was due to the increased fuel efficiency. Carbon emissions for the fossil retrofit were significantly higher than those of the other plant variations because of the high operating hours and combustion of natural gas in both combustion chambers.
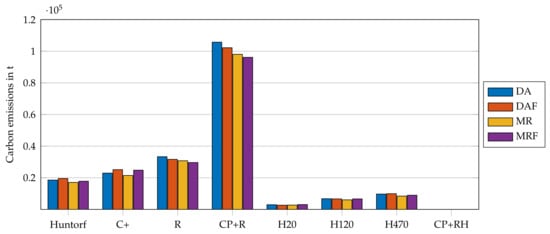
Figure 9.
Carbon emissions of all use cases (average per year from 2015 to 2019 for use cases DA and DAF and from 2015 to 2018 for use cases MR and MRF).Carbon emissions of all use cases.
3.3. Summary
The retrofit of the Huntorf CAES plant with increased storage capacity, rated charging and discharging power, and recuperation and with natural gas combustion showed the highest yearly revenue. The yearly revenue could be improved by 480% with this retrofit in comparison to the current Huntorf plant. The improvement of fuel consumption due to recuperation had a higher impact on the revenue than the increase in storage capacity and power, because the costs for natural gas and carbon dioxide emissions were the driving factors of the revenue. The yearly revenue of the plant variations including electrolysis depended on the rated power of the electrolyzer: higher rated powers resulted in higher revenues (investment costs were omitted). If the retrofit was fueled with hydrogen, the revenue could be improved by 365%. Revenues for the use cases with a rolling horizon optimization considering forecast uncertainty were only slightly less than the revenues for use cases with perfect forecasts. The yearly revenue of any plant variation increased slightly if the plant participated in the minute-reserve market in addition to the day-ahead market.
For the current natural gas and carbon emission prices, the proposed fossil retrofit with natural gas combustion yielded higher revenues on average than the emission-free retrofit with hydrogen production and combustion. For the natural-gas-fueled plant variations, the revenue was one third less on average by 2025 than for the base scenario, and by 2040, the revenue was only 20% of the base scenario due to rising natural gas and carbon emission prices. If carbon prices rose to EUR 55/ and higher, the CO2-emission-free retrofit with hydrogen would be more profitable than the retrofit with natural gas combustion.
High revenues did not necessarily lead to high operating hours or a high number of starts. Operating hours varied broadly depending on the plant variation. The hydrogen retrofit showed significantly lower operating hours than the fossil retrofit, even though the difference in revenue was small.
4. Conclusions
The economic benefits of the Huntorf compressed air energy storage power plant were analyzed using a mixed-integer linear programming model with various plant variations participating in the day-head market, as well as the minute-reserve market. The eight plant variations represented plant enhancements such as increased storage capacity, increased charging and discharging power, recuperation, and hydrogen combustion.
The results showed that a retrofit of the storage plant with increased storage capacity, fuel efficiency, and charging and discharging power yielded the highest yearly revenue. However, the usage of natural gas resulted in a significant dependency on natural gas and carbon emission prices. Both prices are expected to rise in the future, which would lead to the conclusion that the fossil retrofit would become less economical. The carbon-emission-free retrofit (fueled by hydrogen) is independent of these prices. Therefore, the hydrogen retrofit would likely be the better choice in the future.
However, the prediction of day-ahead-market prices for the future is very complex. It is often discussed that the future energy market design has to be adapted to incorporate the increasing share of renewable energies [36]. It is to be expected that future energy markets will provide further economic use cases for storage technologies, including compressed air energy storage plants.
The operating hours of both the CAES plant and the electrolyzer were not satisfying. They can be improved if the plant participates in additional markets (i.e., over-the-counter energy trading) or provides ancillary services such as leveling the residual load. The operating hours of the electrolyzer will be improved when the share of renewable energies in the energy generation is increased and day-ahead market prices decrease on average. To further improve utilization, the electrolyzer can also produce hydrogen for additional different consumer sectors, such as transportation and industry.
The presented MILP model can be adapted for various applications. Besides the economic use cases presented in this paper, the CAES plant can also operate grid-orientated by, for example, leveling the residual load, preventing grid bottlenecks, or storing excess renewable energy that would otherwise be curtailed. With the presented plant model and a different objective function, these use cases or a combination of use cases can be analyzed with regard to the future energy market and flexibility demands. Furthermore, the model can be adapted to analyze the economic benefits of other energy storage technologies such as hydrogen storage, pumped hydro storage, and hybrid storage solutions.
Author Contributions
Conceptualization, methodology, software, validation, visualization, and writing: A.-K.K. Funding acquisition, project administration, and supervision: H.-P.B. All authors have read and agreed to the published version of the manuscript.
Funding
The results presented in this paper were generated within the research project Huntorf 2020—Technologieentwicklung und Effizienzgewinn durch Neu-Konzipierung des Gesamtprozesses Druckluftspeicherkraftwerk Huntorf mit regenerativ erzeugtem Wasserstoff. It was a three-year project funded by the German Federal Ministry of Economic Affairs and Energy (Reference No. 03ET6139A). The project partners were Uniper Kraftwerke GmbH and the Forschungszentrum Energiespeichertechnolgien (EST) of Clausthal University of Technology, the latter representing both the Institute of Electrical Power Engineering and Energy Systems (IEE) and the Institute for Energy Process Engineering and Fuel Technology (IEVB). Further information is provided in [37].
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Please contact the authors.
Acknowledgments
The project was funded by the German Federal Ministry of Economic Affairs and Energy on a basis of a decision of the German Bundestag. We also acknowledge the support of the Open Access Publishing Fund of Clausthal University of Technology.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Indices used in the MILP model.
Table A1.
Indices used in the MILP model.
| Index | Description |
|---|---|
| t | time-dependent variable |
| r | rated |
| C | charging mode |
| D | discharging mode |
| A | compressed air |
| H | electrolysis/hydrogen |

Table A2.
Decision variables of the MILP model.
Table A2.
Decision variables of the MILP model.
| Symbol | Description |
|---|---|
| state of charge of the compressed air storage | |
| power in charging mode | |
| power in discharging mode | |
| binary variable: charging mode | |
| binary variable: discharging mode | |
| binary variable: startup charging mode | |
| binary variable: startup discharging mode | |
| State of charge of the hydrogen storage | |
| power of electrolysis | |
| binary variable: electrolysis | |
| binary variable: startup electrolysis | |
| reserved power for negative minute reserve | |
| reserved power for positive minute reserve | |
| called energy for negative minute reserve | |
| called energy for positive minute reserve | |
| binary variable: power reserved for negative minute reserve | |
| binary variable: power reserved for positive minute reserve |

Table A3.
Parameters of the MILP model. 1 Values given by the plant operator within the research project; 2 values estimated by the research partners within the research project; 3 values determined by considering the research objectives; 4 estimated values.
Table A3.
Parameters of the MILP model. 1 Values given by the plant operator within the research project; 2 values estimated by the research partners within the research project; 3 values determined by considering the research objectives; 4 estimated values.
| Symbol | Description |
|---|---|
| day-ahead market prices [25] | |
| fuel price (natural gas and carbon dioxide emissions) 1 | |
| startup costs: charging 1 | |
| startup costs: discharging 1 | |
| startup costs: electrolysis 1 | |
| tendered capacity price 4 () | |
| tendered energy price 4 () | |
| rated storage capacity of compressed air storage 1 | |
| rated power in charging mode 1 | |
| minimal power in discharging mode 1 | |
| rated power in discharging mode 1 | |
| efficiency in discharging mode 4 | |
| minimal power in discharging mode (partial load) 2 | |
| rated power in discharging mode (partial load) 2 | |
| fuel consumption at minimal discharging power 2 () | |
| fuel consumption constant 2 () | |
| rated storage capacity of H2 storage 4 | |
| minimal power of electrolyzer 3 | |
| rated power of electrolyzer 3 | |
| efficiency of electrolyzer 3 | |
| time step 3 |
References
- Prognos; Öko-Institut; Wuppertal-Institut. Towards a Climate-Neutral Germany by 2045. How Germany Can Reach Its Climate Targets before 2050. 2021. Executive Summary conducted for Stiftung Klimaneutralität, Agora Energiewende and Agora Verkehrswende. Available online: https://www.agora-energiewende.de/en/publications/towards-a-climate-neutral-germany-executive-summary/ (accessed on 10 September 2021).
- Fürstenwerth, D.; Waldmann, L. Electricity Storage in the German Energy Transition. 2014. Study by Agora Energywende. Available online: https://www.agora-energiewende.de/en/publications/electricity-storage-in-the-german-energy-transition/ (accessed on 10 September 2021).
- Succar, S.; Williams, R. Compressed Air Energy Storage: Theory, Resources, and Applications for Wind Power; Princeton Environmental Institute, Energy Systems Analysis Group: Princeton, NJ, USA, 2008. [Google Scholar]
- Eckroad, S.; Gyuk, I.; Mears, L.; Gotschall, H.; Kamath, H. EPRI-DOE Handbook of Energy Storage for Transmission and Distribution Applications. 2003. Available online: https://www.epri.com/research/products/1001834 (accessed on 10 September 2021).
- Moreno, R.; Moreira, R.; Strbac, G. A MILP model for optimising multi-service portfolios of distributed energy storage. Appl. Energy 2015, 137, 554–566. [Google Scholar] [CrossRef] [Green Version]
- Gu, Y.; Mccalley, J.; Ni, M.; Bo, R. Economic Modeling of Compressed Air Energy Storage. Energies 2013, 6, 2221–2241. [Google Scholar] [CrossRef]
- Nikolakakis, T.; Fthenakis, V. CAES models for energy arbitrage and ancillary services: Comparison using mixed-integer programming optimization with market data from the Irish power grid. Energy Technol. 2017, 6, 1290–1301. [Google Scholar] [CrossRef]
- Wolf, D.; Kanngießer, A.; Budt, M.; Doetsch, C. Adiabatic Compressed Air Energy Storage co-located with wind energy—multifunctional storage commitment optimization for the German market using GOMES. Energy Syst. 2012, 3, 181–208. [Google Scholar] [CrossRef]
- Nikolakakis, T.; Fthenakis, V. The Value of Compressed-Air Energy Storage for Enhancing Variable-Renewable-Energy Integration: The Case of Ireland. Energy Technol. 2017, 5, 2026–2038. [Google Scholar] [CrossRef]
- Ghalelou, A.N.; Fakhri, A.P.; Nojavan, S.; Majidi, M.; Hatami, H. A stochastic self-scheduling program for compressed air energy storage (CAES) of renewable energy sources (RESs) based on a demand response mechanism. Energy Convers. Manag. 2016, 120, 388–396. [Google Scholar] [CrossRef]
- Kaiser, F.; Weber, R.; Krueger, U. Thermodynamic Steady-State Analysis and Comparison of Compressed Air Energy Storage (CAES) Concepts. Int. J. Thermodyn. 2018, 21, 144–156. [Google Scholar] [CrossRef]
- Budt, M.; Wolf, D.; Span, R.; Yan, J. A review on compressed air energy storage: Basic principles, past milestones and recent developments. Appl. Energy 2016, 170, 250–268. [Google Scholar] [CrossRef]
- Kaiser, F.; Krueger, U. Exergy analysis and assessment of performance criteria for compressed air energy storage concepts. Int. J. Exergy 2019, 28, 274–291. [Google Scholar] [CrossRef]
- Crotogino, F.; Mohmeyer, K.U.; Scharf, R. Huntorf CAES: More than 20 Years of Successful Operation: Report Spring 2001 Meeting, Orlando. In Proceedings of the Spring 2001 Meeting, Orlando, FL, USA, 15–18 April 2001. [Google Scholar]
- Lund, H.; Salgi, G.; Elmegaard, B.; Andersen, A.N. Optimal operation strategies of compressed air energy storage (CAES) on electricity spot markets with fluctuating prices. Appl. Therm. Eng. 2009, 29, 799–806. [Google Scholar] [CrossRef] [Green Version]
- Bullough, C.; Gatzen, C.; Jakiel, C.; Koller, M.; Nowi, A.; Zunft, S. Advanced adiabatic compressed air energy storage for the Integration of wind energy. In Proceedings of the European Wind Energy Conference, EWEC 2004, London, UK, 22–25 November 2004. [Google Scholar]
- Denholm, P.; Sioshansi, R. The value of compressed air energy storage with wind in transmission-constrained electric power systems. Energy Policy 2009, 37, 3149–3158. [Google Scholar] [CrossRef]
- Nabil, I.; Khairat Dawood, M.M.; Nabil, T. Review of Energy Storage Technologies for Compressed-Air Energy Storage. Am. J. Mod. Energy 2021, 4, 51–60. [Google Scholar] [CrossRef]
- Drury, E.; Denholm, P.; Sioshansi, R. The value of compressed air energy storage in energy and reserve markets. Fuel Energy Abstr. 2011, 36, 4959–4973. [Google Scholar] [CrossRef]
- Nasouri Gilvaei, M.; Hosseini Imani, M.; Jabbari Ghadi, M.; Li, L.; Golrang, A. Profit-Based Unit Commitment for a GENCO Equipped with Compressed Air Energy Storage and Concentrating Solar Power Units. Energies 2021, 14, 576. [Google Scholar] [CrossRef]
- Jakiel, C.; Zunft, S.; Nowi, A. Adiabatic compressed air energy storage plants for efficient peak load power supply from wind energy: The European project AA-CAES. Int. J. Energy Technol. Policy 2007, 5, 296–306. [Google Scholar] [CrossRef]
- Zunft, S.; Dreißigacker, V.; Bieber, M.; Banach, A.; Klabunde, C.; Warweg, O. Electricity storage with adiabatic compressed air energy storage: Results of the BMWi-project ADELE-ING. In Proceedings of the International ETG Congress 2017, Bonn, Germany, 28–29 November 2017. [Google Scholar]
- Barbour, E.R.; Pottie, D.L.; Eames, P. Why is adiabatic compressed air energy storage yet to become a viable energy storage option? iScience 2021, 24, 102440. [Google Scholar] [CrossRef]
- Hamedi, K.; Sadeghi, S.; Esfandi, S.; Azimian, M.; Golmohamadi, H. Eco-Emission Analysis of Multi-Carrier Microgrid Integrated with Compressed Air and Power-to-Gas Energy Storage Technologies. Sustainability 2021, 13, 4681. [Google Scholar] [CrossRef]
- Bundesnetzagentur. Electricity Market Data. 2020. Available online: www.smard.de (accessed on 10 September 2021).
- 50Hertz Transmission GmbH; Amprion GmbH; TenneT TSO GmbH; TransnetBW GmbH. Regelleistung.net—Internet Platform for the Allocation of Control Power. 2020. Available online: https://www.regelleistung.net/ext/static/mrl (accessed on 10 September 2021).
- Quaschning, V. Specific Carbon Dioxide Emissions of Various Fuels. 2021. Available online: https://www.volker-quaschning.de/datserv/CO2-spez/index_e.php (accessed on 10 September 2021).
- International Energy Agency. World Energy Outlook 2017. 2017. Available online: https://www.iea.org/reports/world-energy-outlook-2017 (accessed on 10 September 2021).
- Hu, L.; Taylor, G.; Wan, H.B.; Irving, M. A Review of Short-Term Electricity Price Forecasting Techniques in Deregulated Electricity Markets. In Proceedings of the 2009 44th International Universities Power Engineering Conference (UPEC), Glasgow, UK, 1–4 September 2009; pp. 1–5. [Google Scholar]
- Aggarwal, S.; Saini, L.; Kumar, A. Electricity price forecasting in deregulated markets: A review and evaluation. Int. J. Electr. Power Energy Syst. 2009, 31, 13–22. [Google Scholar] [CrossRef]
- Ugurlu, U.; Tas, O.; Kaya, A.; Oksuz, I. The Financial Effect of the Electricity Price Forecasts’ Inaccuracy on a Hydro-Based Generation Company. Energies 2018, 11, 2093. [Google Scholar] [CrossRef] [Green Version]
- Delarue, E.; van den Bosch, P.; D’haeseleer, W. Effect of the accuracy of price forecasting on profit in a Price Based Unit Commitment. Electr. Power Syst. Res. 2010, 80, 1306–1313. [Google Scholar] [CrossRef]
- Lago, J.; de Ridder, F.; de Schutter, B. Forecasting spot electricity prices: Deep learning approaches and empirical comparison of traditional algorithms. Appl. Energy 2018, 221, 386–405. [Google Scholar] [CrossRef]
- Kopanos, G.M.; Pistikopoulos, E.N. Reactive Scheduling by a Multiparametric Programming Rolling Horizon Framework: A Case of a Network of Combined Heat and Power Units. Ind. Eng. Chem. Res. 2014, 53, 4366–4386. [Google Scholar] [CrossRef]
- Bischi, A.; Taccari, L.; Martelli, E.; Amaldi, E.; Manzolini, G.; Silva, P.; Campanari, S.; Macchi, E. A rolling-horizon optimization algorithm for the long term operational scheduling of cogeneration systems. Energy 2019, 184, 73–90. [Google Scholar] [CrossRef]
- Ashour Novirdoust, A.; Bicherl, M.; Bojung, C.; Buhl, H.U.; Fridgen, G.; Getschko, V.; Hanny, L.; Knörr, J.; Maldonado, F.; Neuhoff, K.; et al. Electricity Spot Market Design 2030–2050; Fraunhofer FIT: Sankt Augustin, Germany, 2020. [Google Scholar] [CrossRef]
- Fries, A.K.; Kaiser, F.; Beck, H.P.; Weber, R. Huntorf 2020—Improvement of Flexibility and Efficiency of a Compressed Air Energy Storage Plant based on Synthetic Hydrogen. In Proceedings of the NEIS 2018 Conference on Sustainable Energy Supply and Energy Storage Systems, Hamburg, Germany, 20–21 September 2018; pp. 1–5. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).