Characterization of the Effects of Ingested Bodies on the Rotor–Stator Interaction of Hydraulic Turbines
Abstract
:1. Introduction
2. Methodology
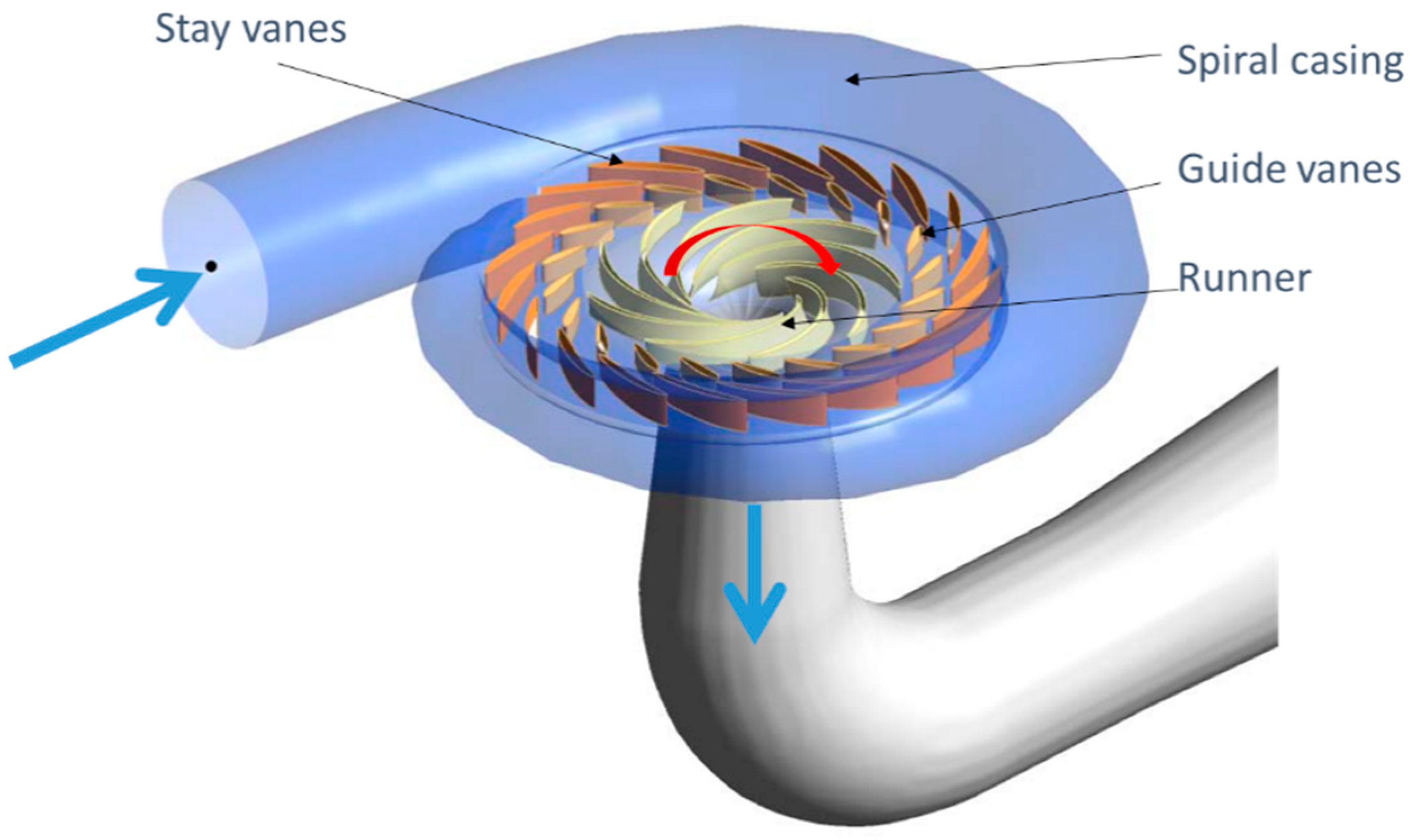
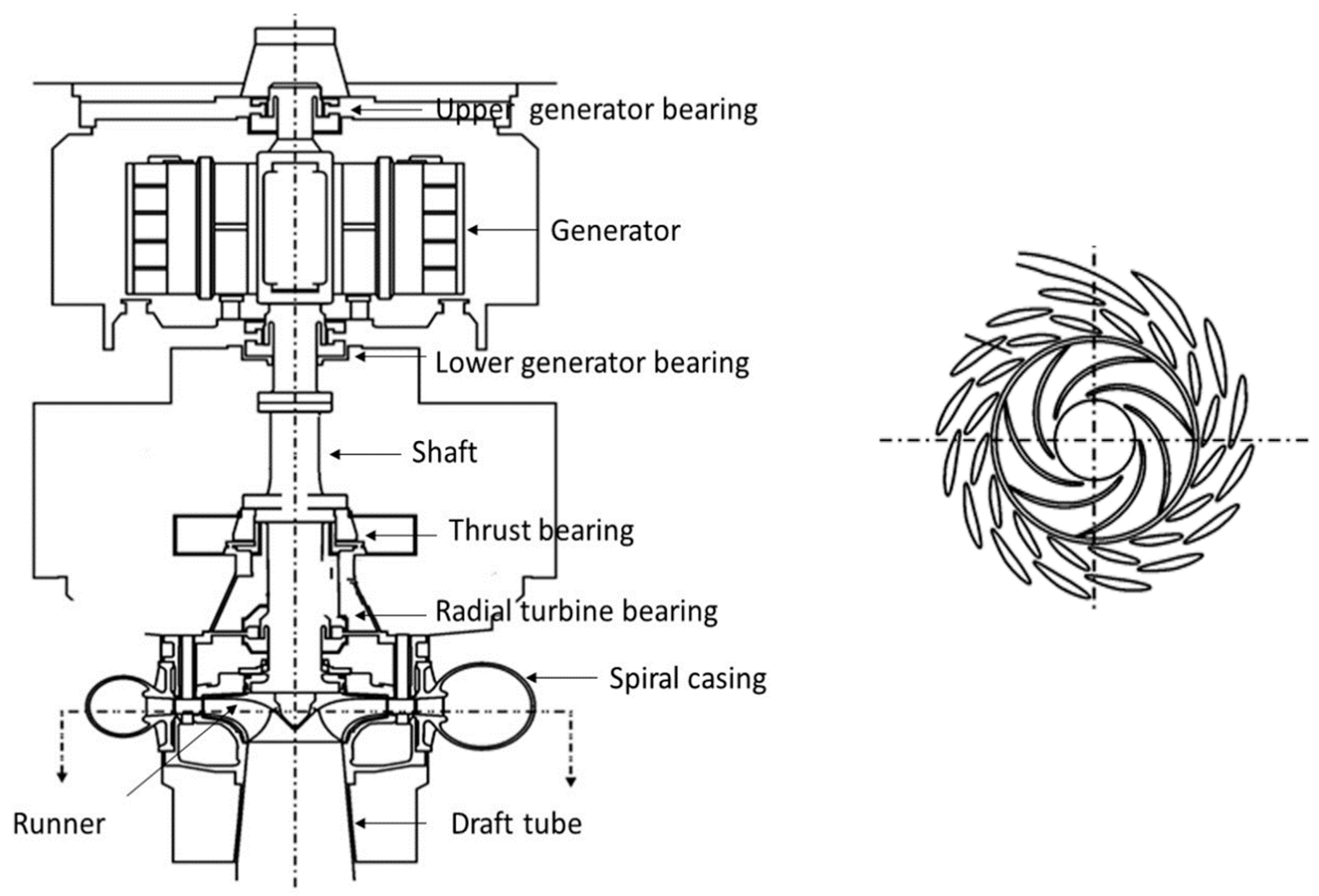
2.1. Case Study
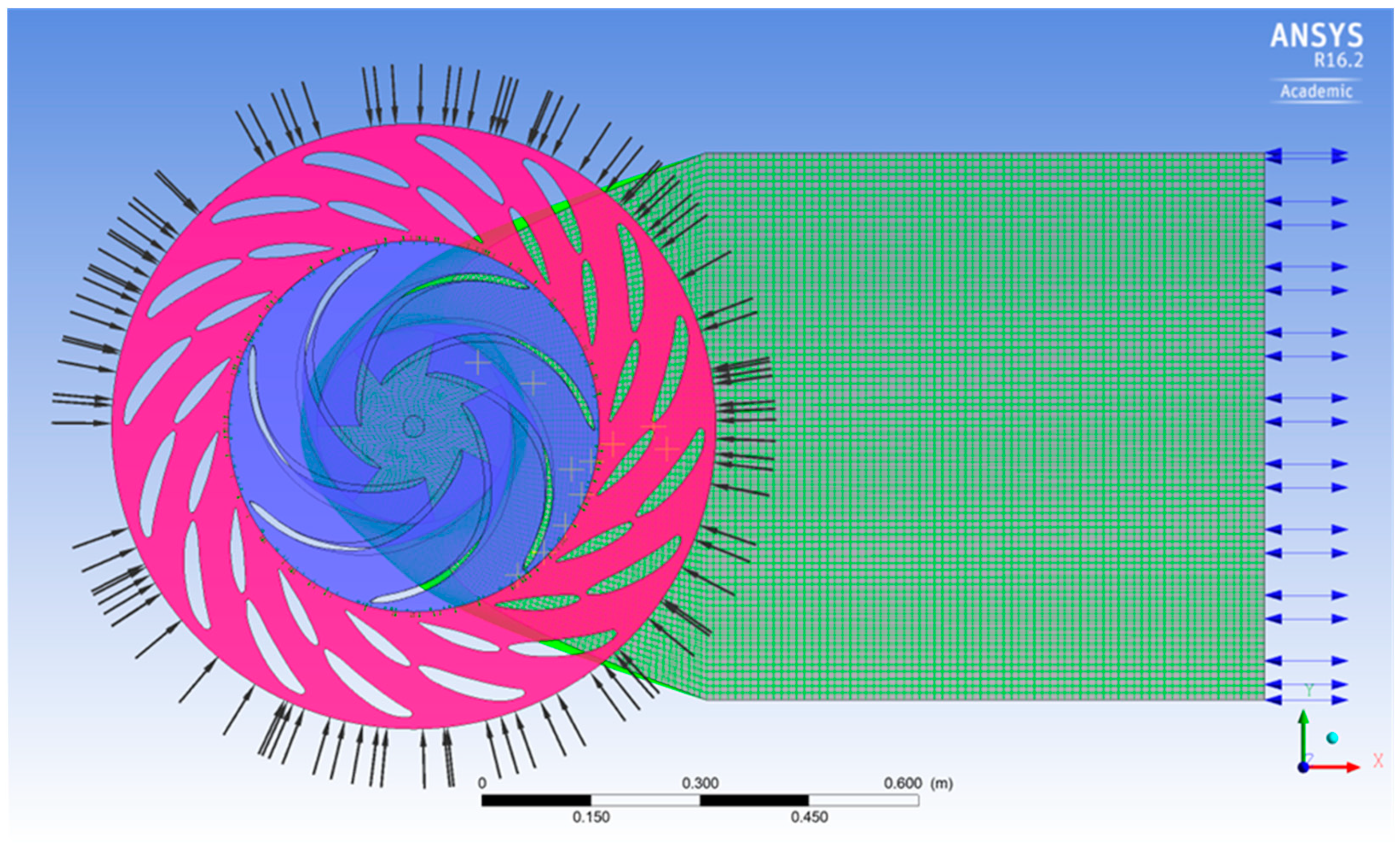
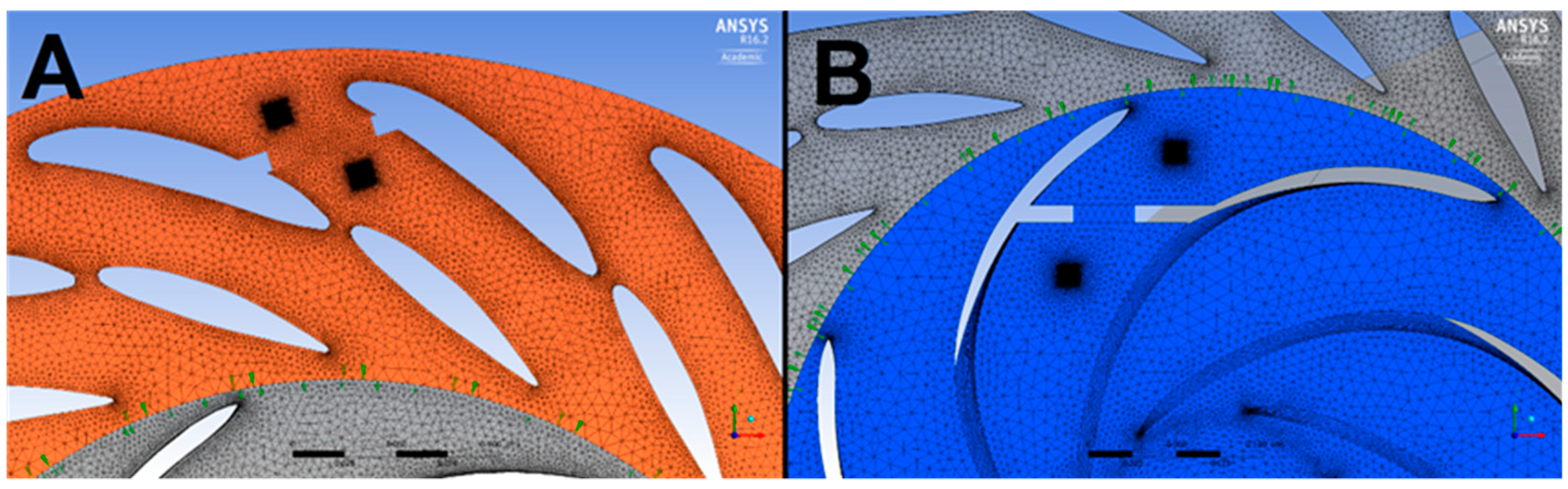
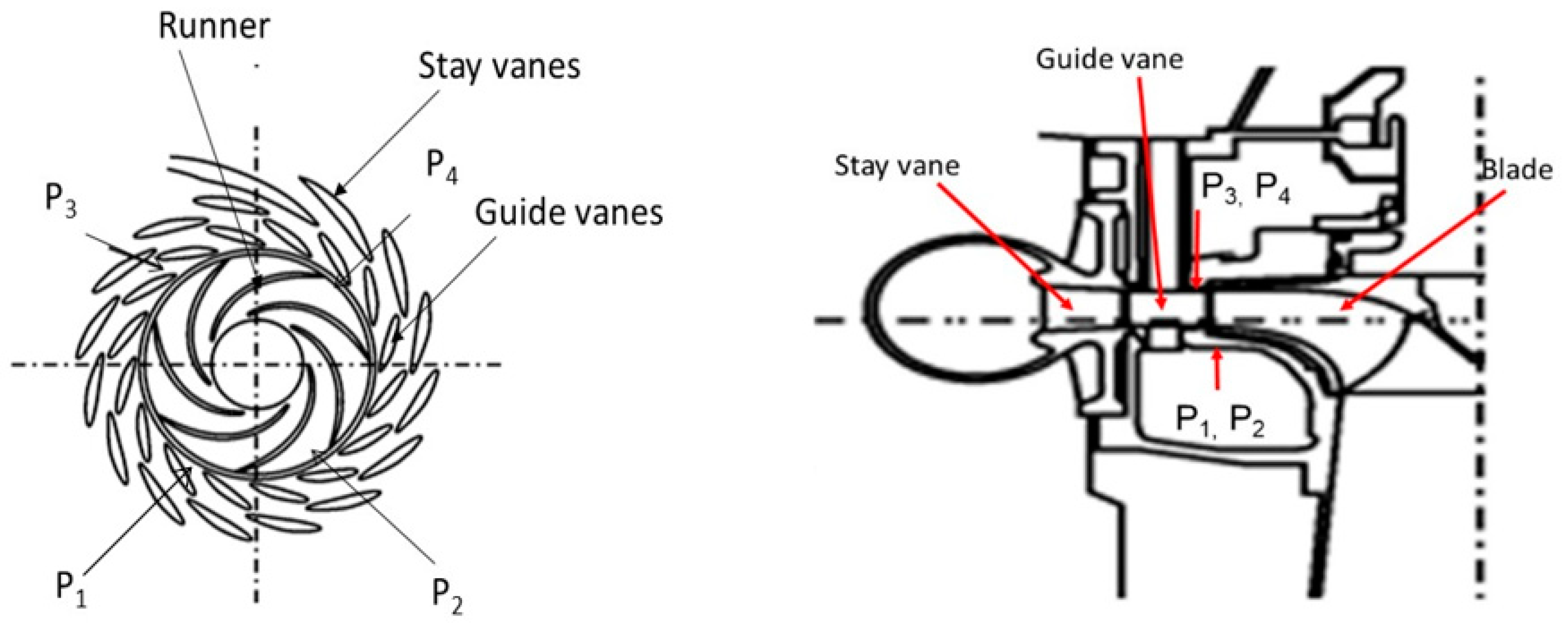
2.2. Geometry and Mesh
2.3. Numerical Procedure
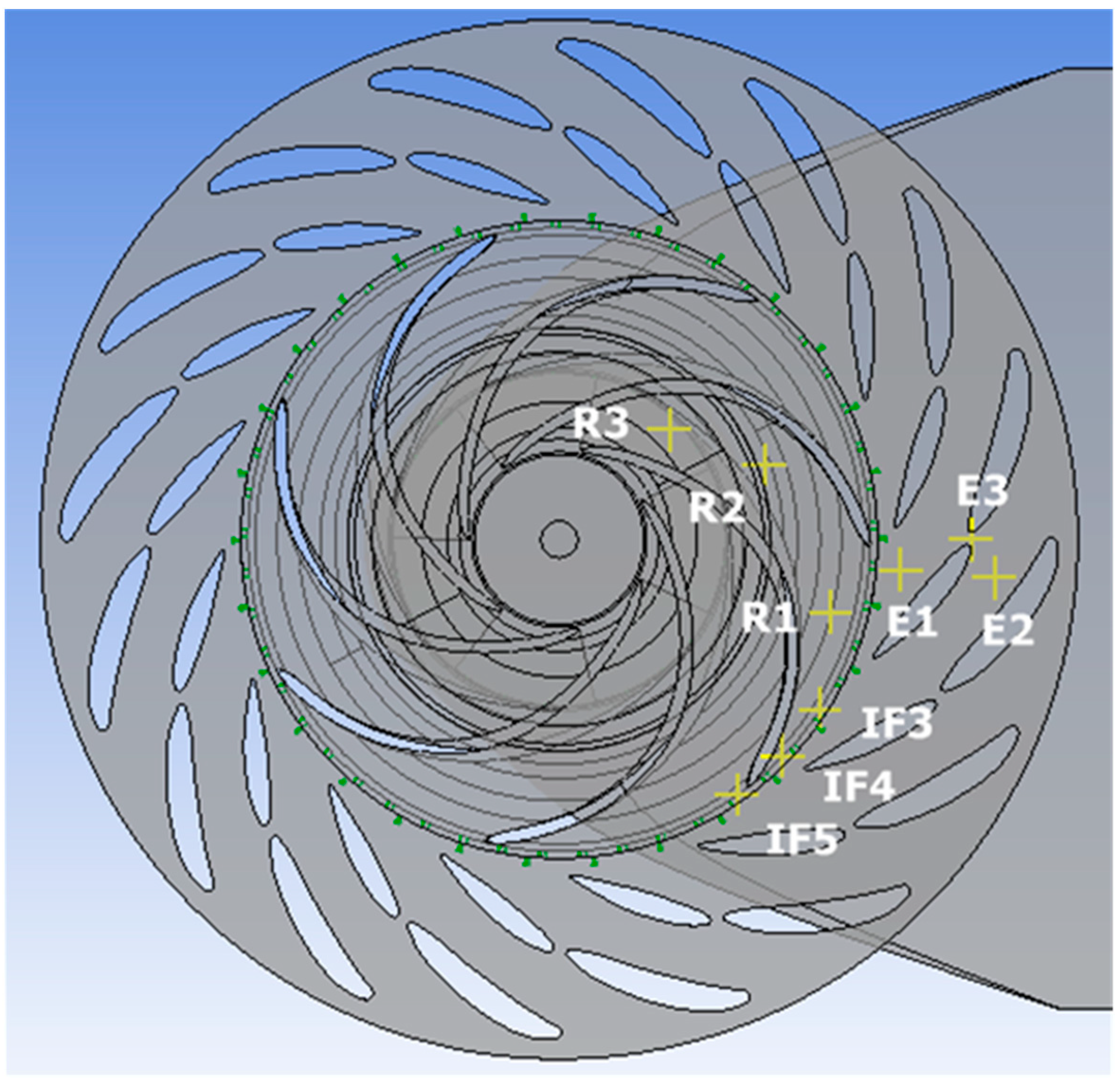
2.4. Post-Processing and Data Analysis
3. Results and Discussion
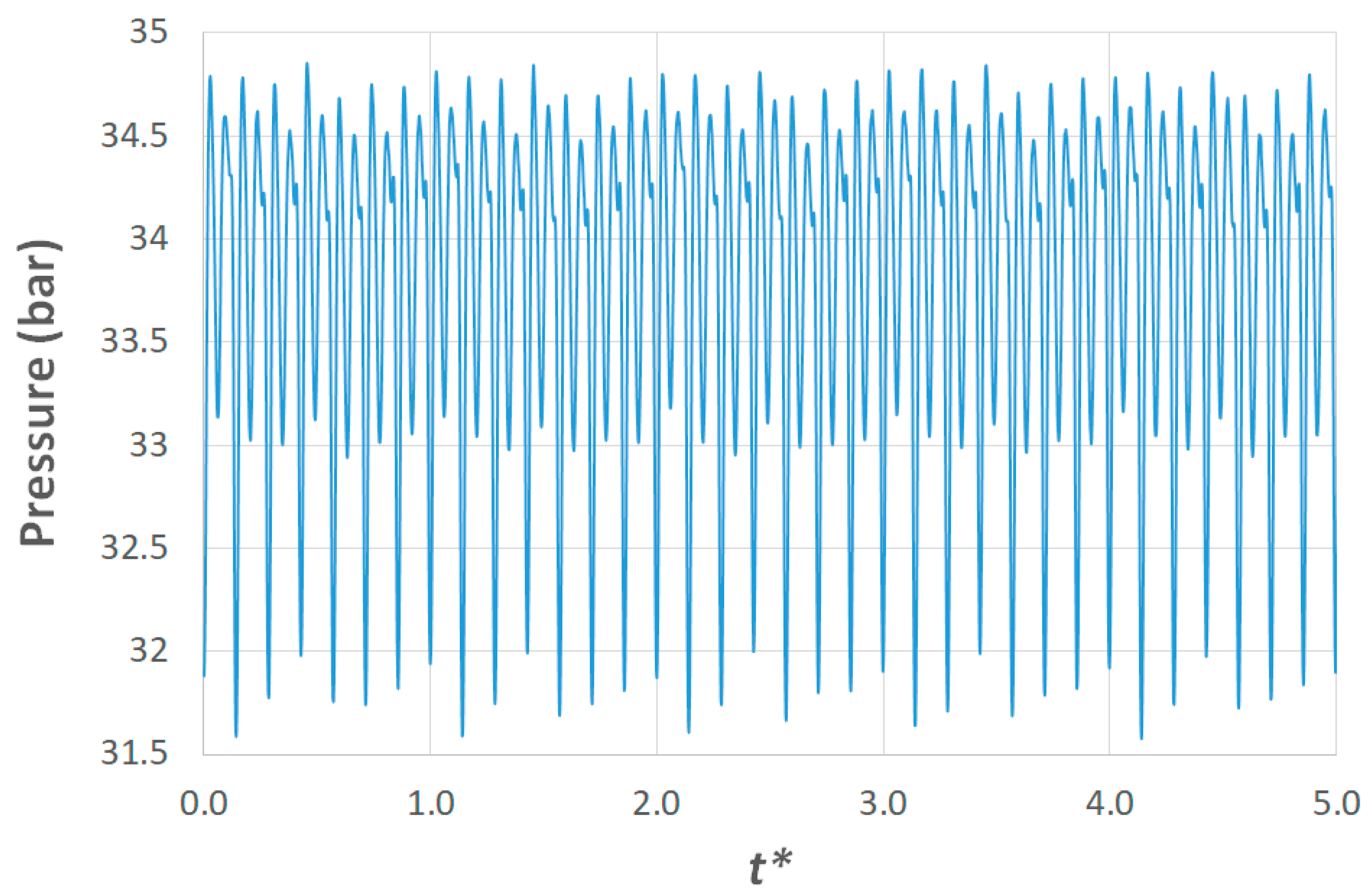
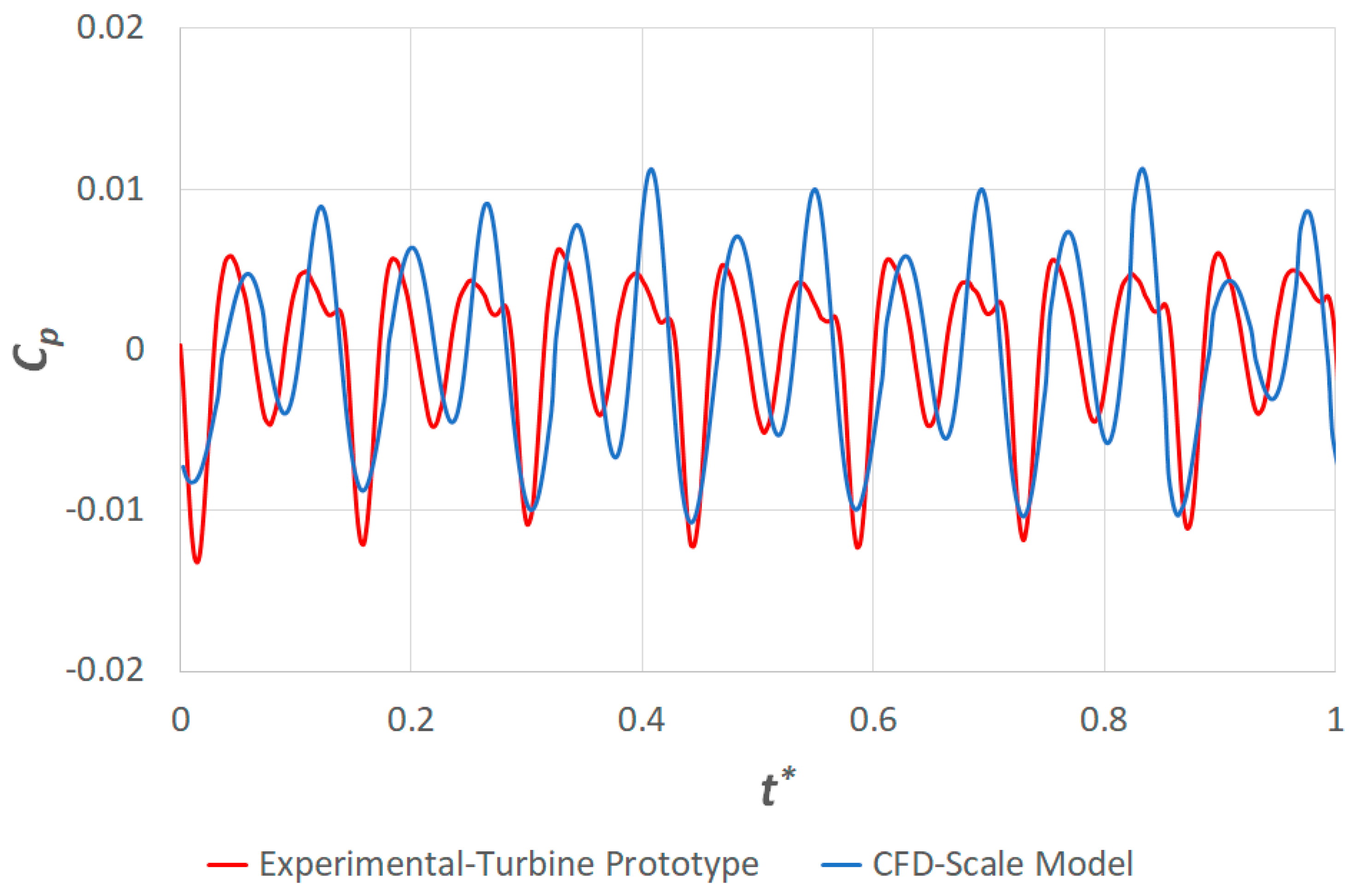
3.1. Validation of the Numerical Simulations
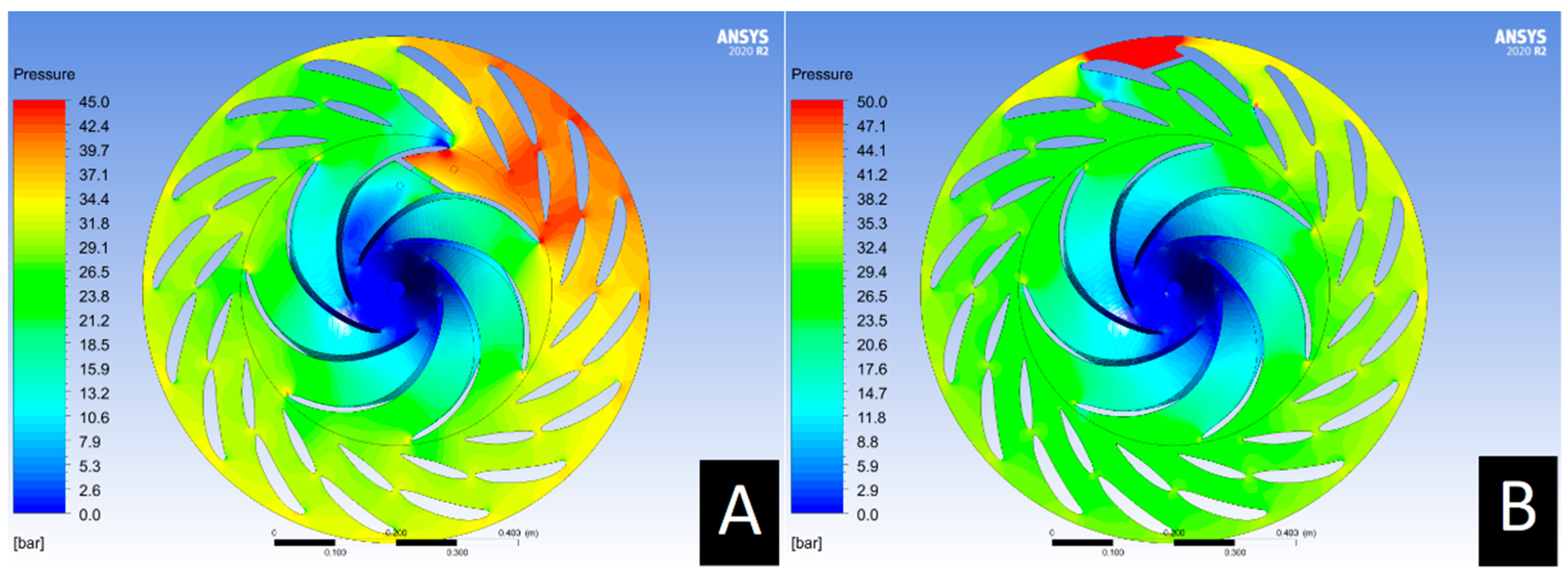
3.2. Pressure/Velocity Plots for Blockage Cases
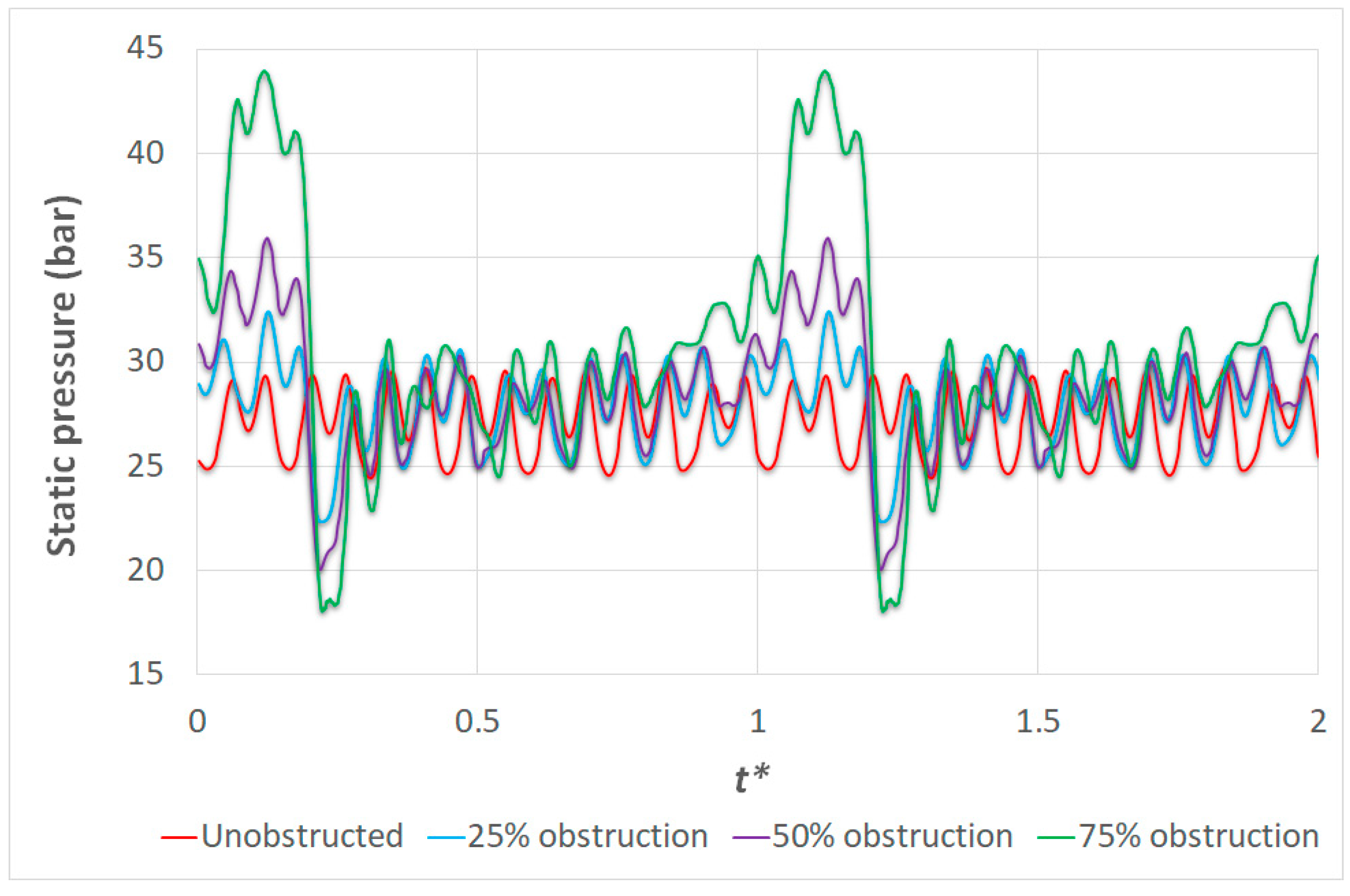
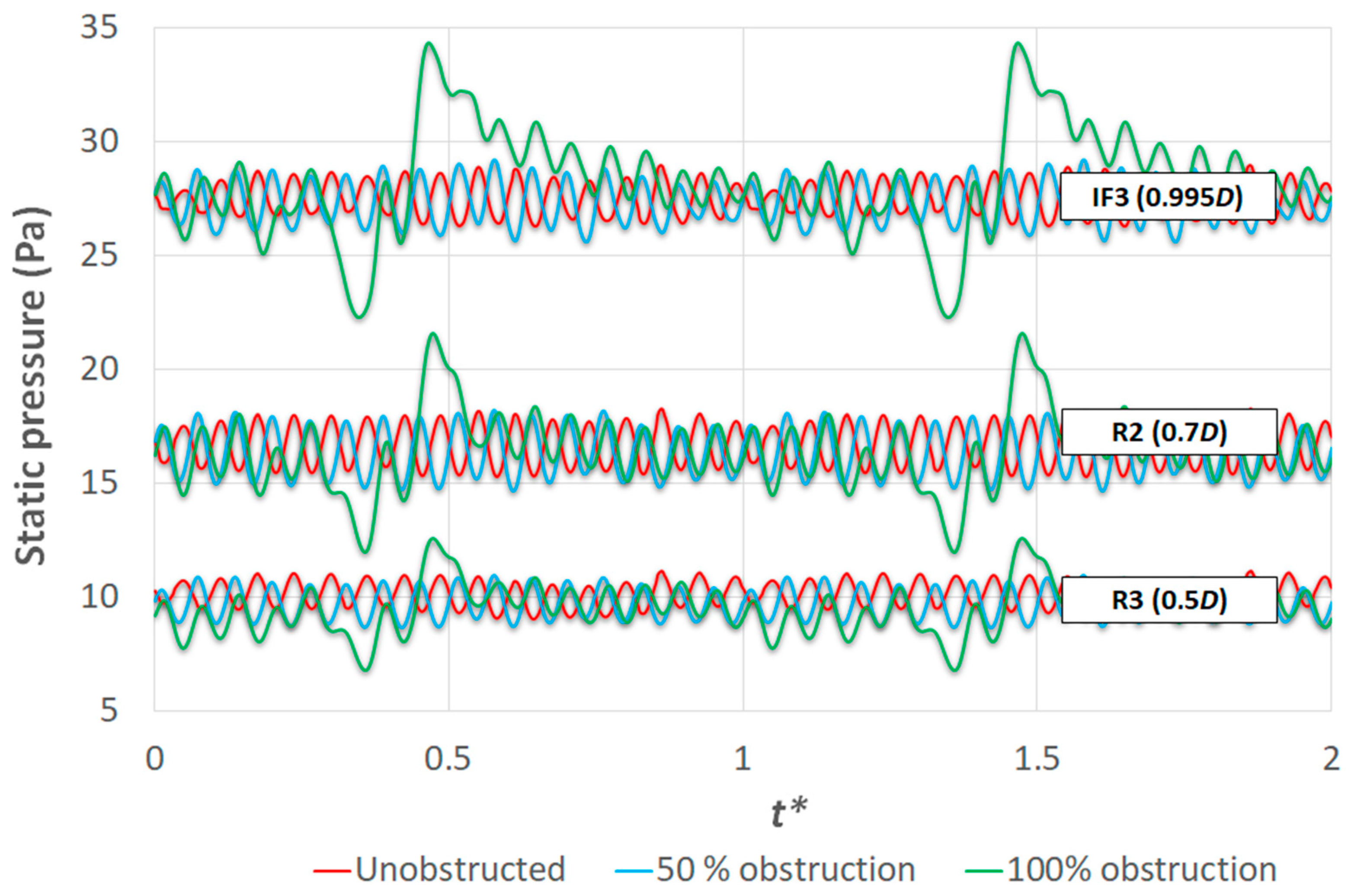
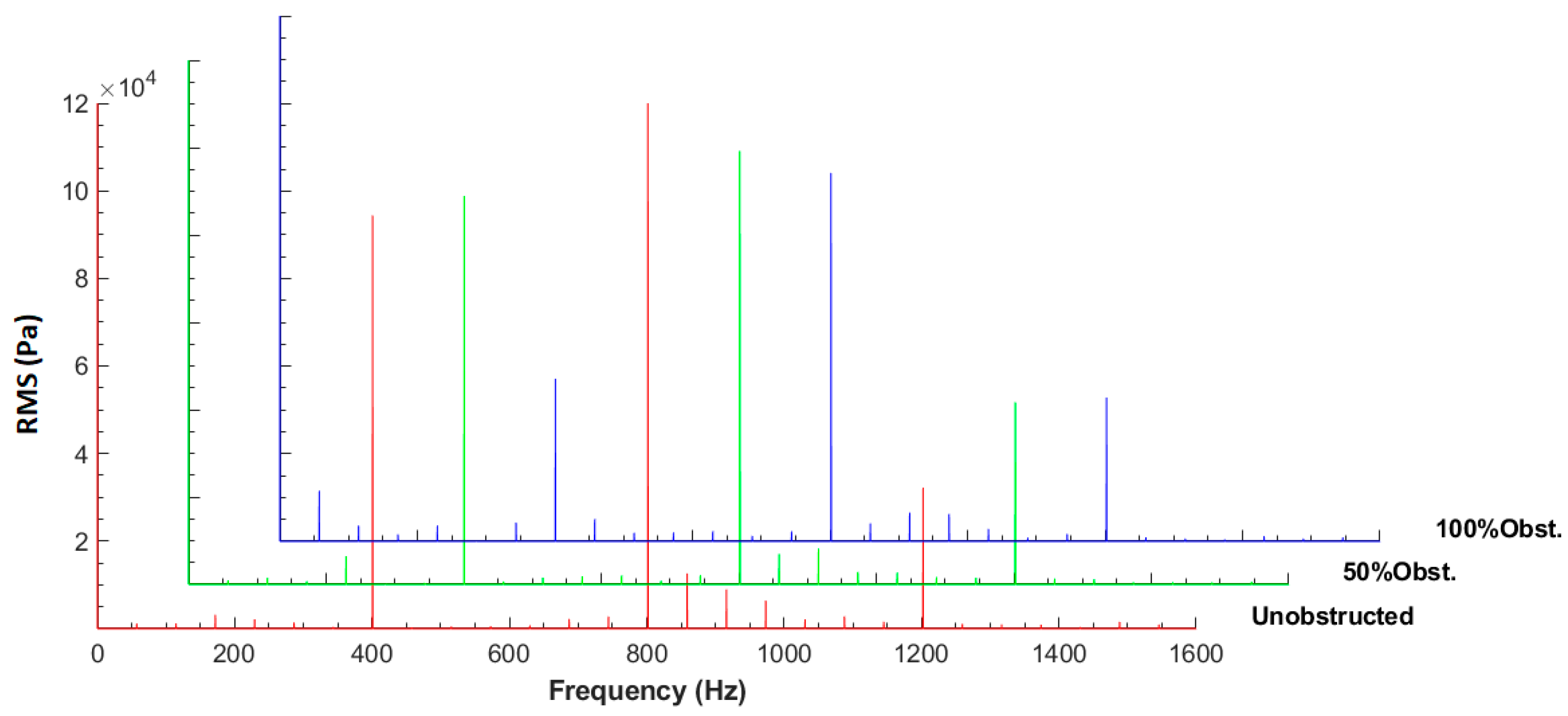
3.3. Obstructed Rotor Analysis
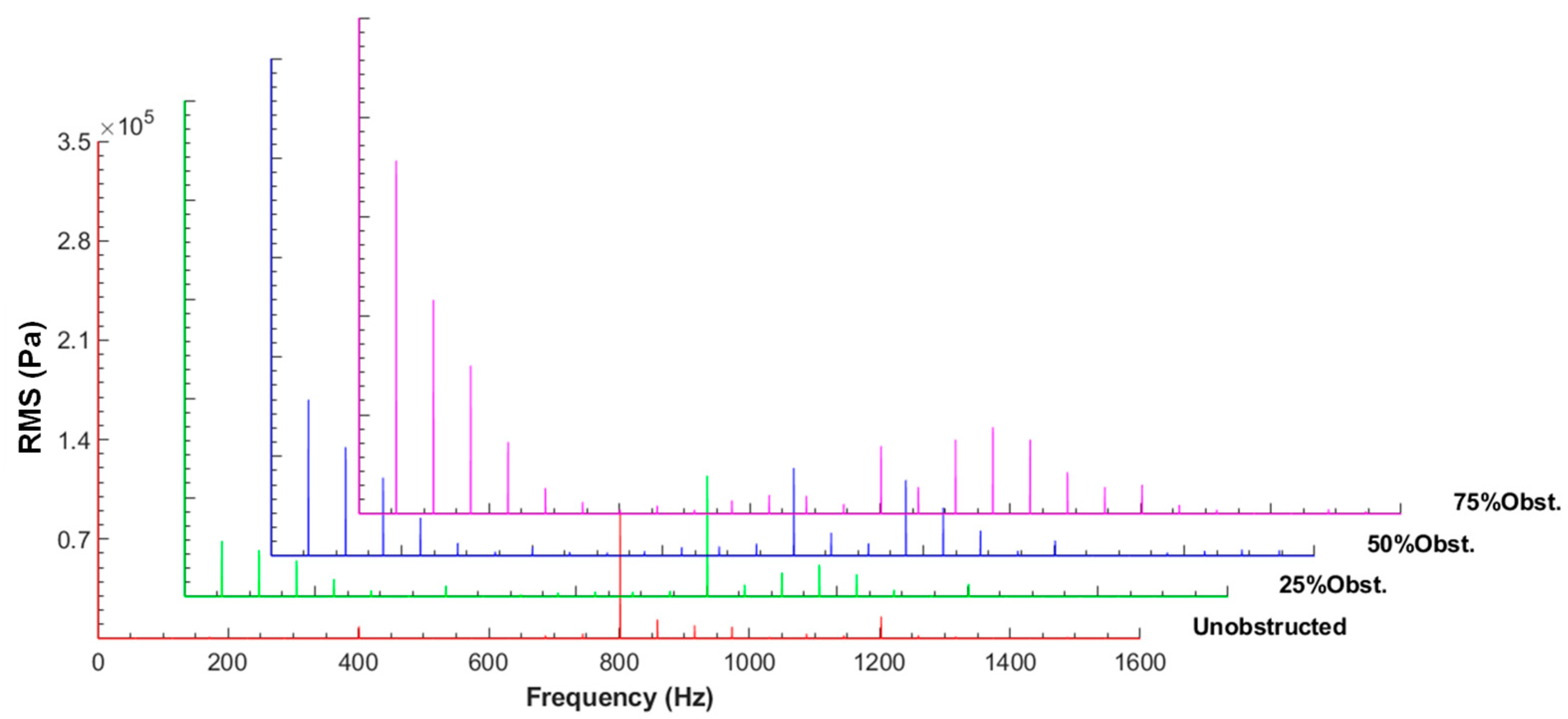
3.3.1. Effect of the Blockage Size
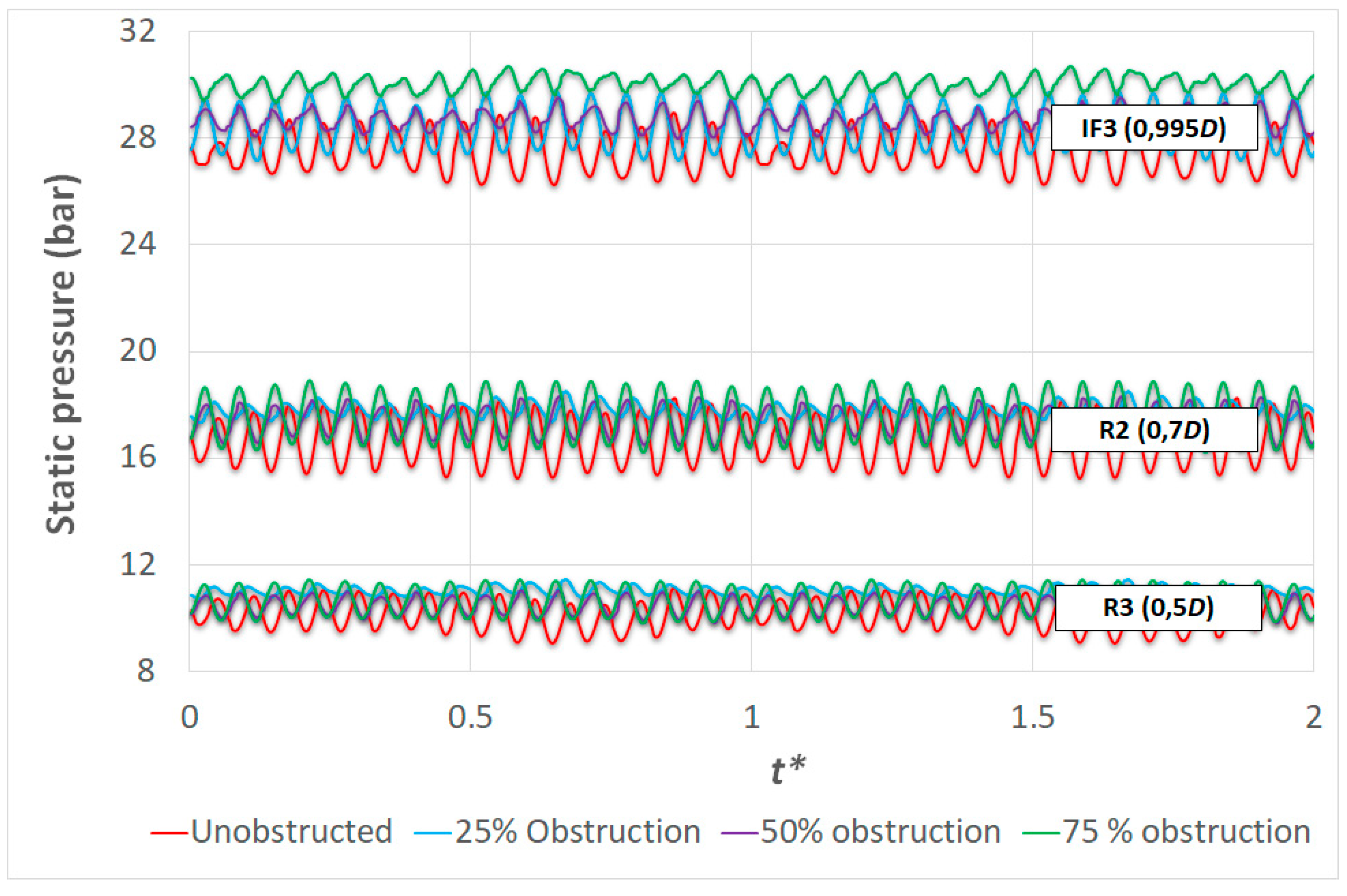
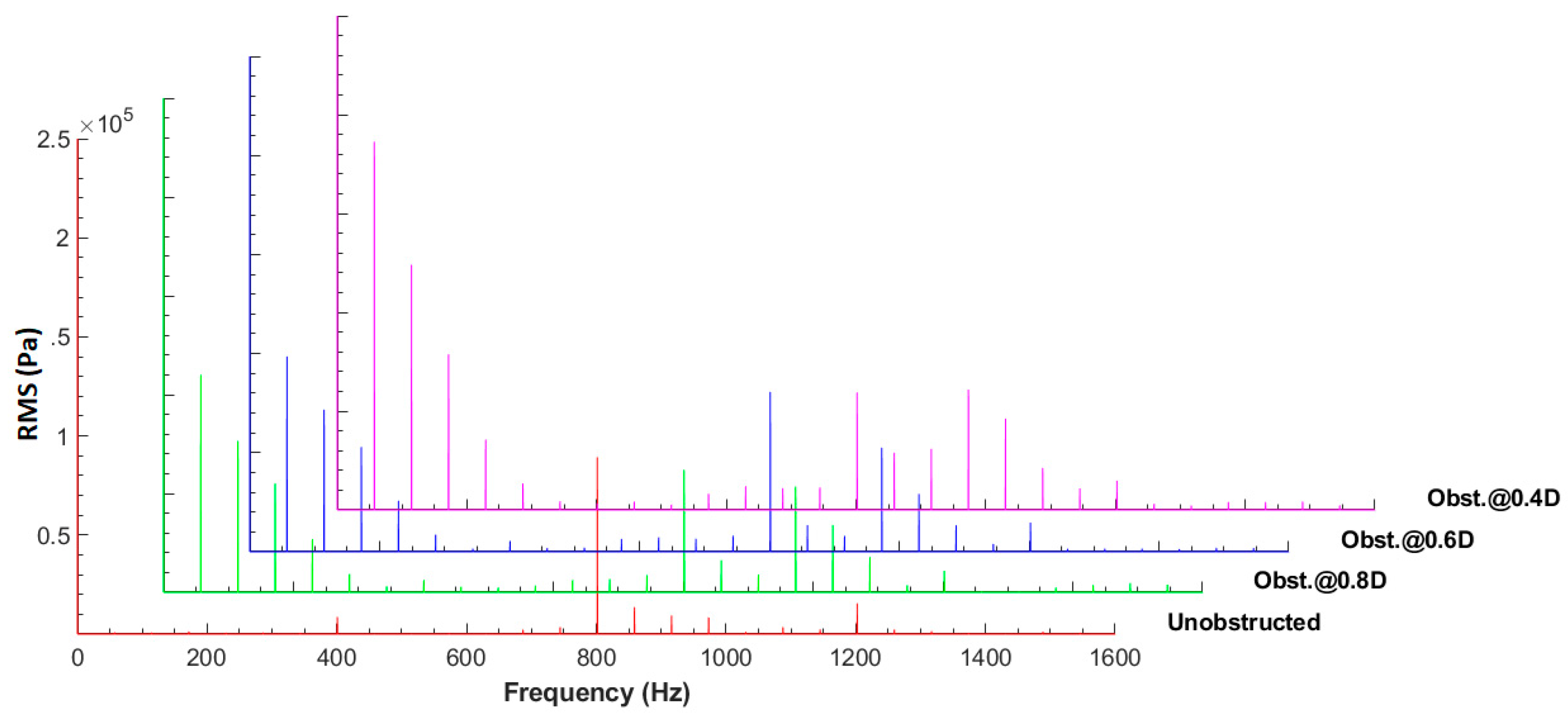
3.3.2. Effect of Blockage Position
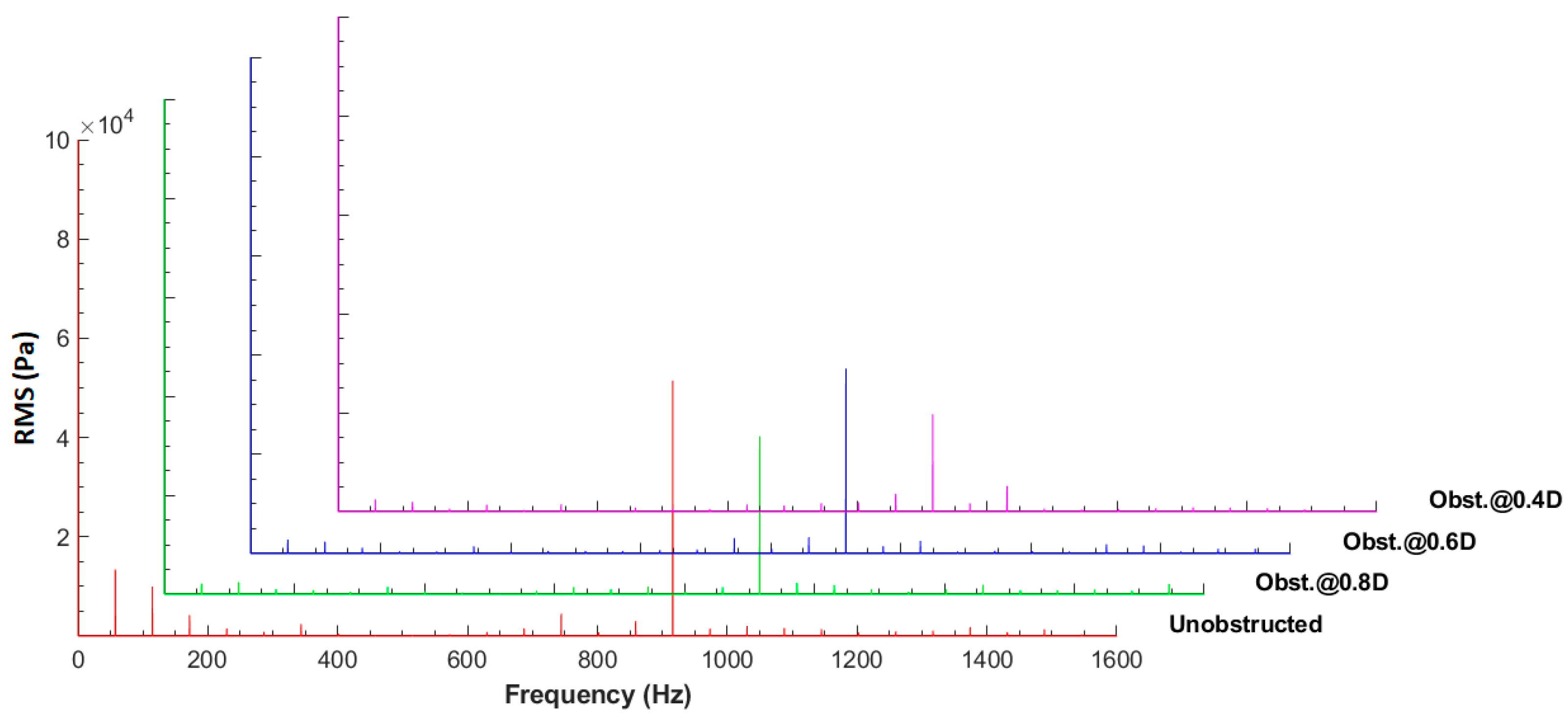
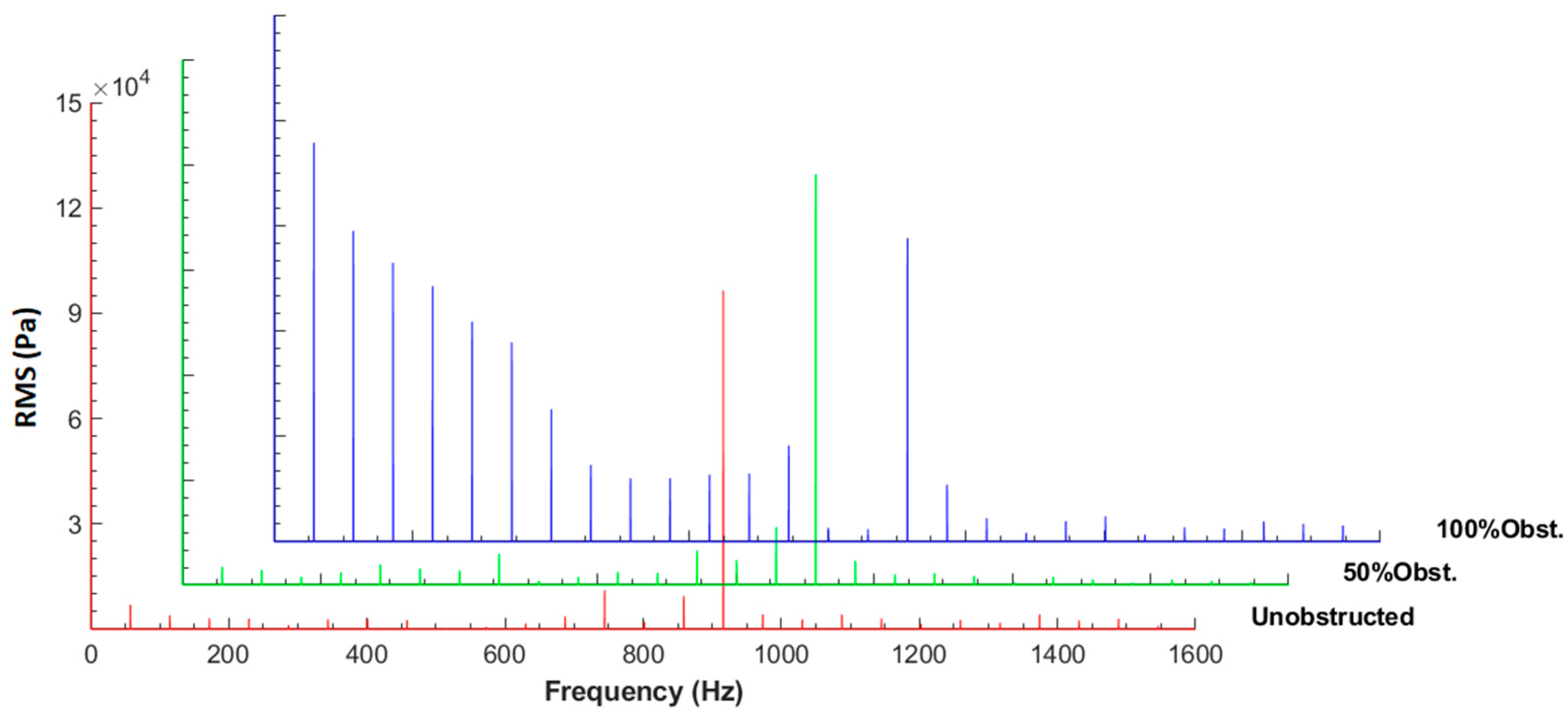
3.4. Obstructed Distributor Analysis
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Coefficient of pressure | ||
| Runner diameter | m | |
| Runner blade passing frequency | Hz | |
| Runner rotation frequency | Hz | |
| Distributor vane passing frequency | Hz | |
| Standard gravity | ||
| Pump turbine net head | m | |
| Runner rotation speed | rpm | |
| Dimensionless runner specific speed | ||
| Pressure | Pa | |
| Dimensionless time | ||
| Time | s | |
| Time of 1 runner revolution | s | |
| Volumetric flow rate | ||
| Dimensionless wall distance | ||
| Number of runner blades | - | |
| Number of distributor vanes | - | |
| Greek letters | ||
| Density | ||
| Runner rotation speed | ||
| Acronyms | ||
| AMG | Algebraic multigrid | |
| BEP | Best efficiency point | |
| CFD | Computational fluid dynamics | |
| FFT | Fast Fourier transform | |
| RMS | Root mean square | |
| RSI | Rotor–stator interaction | |
References
- Gaudard, L.; Romerio, F. The future of hydropower in Europe: Interconnecting climate, markets and policies. Environ. Sci. Policy 2014, 37, 172–181. [Google Scholar] [CrossRef]
- Dorji, U.; Ghomashchi, R. Hydro turbine failure mechanism: An overview. Eng. Fail. Anal. 2014, 44, 136–147. [Google Scholar] [CrossRef]
- Frunzǎverde, D.; Muntean, S.; Mǎrginean, G.; Câmpian, V.; Marşavina, L.; Terzi, R.; Şerban, V. Failure analysis of a Francis turbine runner. IOP Conf. Ser. Earth Environ. Sci. 2010, 12, 012115. [Google Scholar] [CrossRef]
- Egusquiza, E.; Valero, C.; Huang, X.; Jou, E.; Guardo, A.; Rodríguez, C. Failure investigation of a large pump-turbine runner. Eng. Fail. Anal. 2012, 23, 27–34. [Google Scholar] [CrossRef] [Green Version]
- Brekke, H. Performance and safety of hydraulic turbines. IOP Conf. Ser. Earth Environ. Sci. 2010, 12, 012061. [Google Scholar] [CrossRef]
- Liu, X.; Luo, Y.; Wang, Z. A review on fatigue damage mechanism in hydro turbines. Renew. Sustain. Energy Rev. 2016, 54, 1–14. [Google Scholar] [CrossRef]
- Liu, X.; Luo, Y.; Presas, A.; Wang, Z.; Zhou, L. Cavitation effects on the structural resonance of hydraulic turbines: Failure analysis in a real Francis turbine runner. Energies 2018, 11, 2320. [Google Scholar] [CrossRef] [Green Version]
- Thapa, B.S.; Dahlhaug, O.G.; Thapa, B. Sediment erosion in hydro turbines and its effect on the flow around guide vanes of Francis turbine. Renew. Sustain. Energy Rev. 2015, 49, 1100–1113. [Google Scholar] [CrossRef]
- Kjølle, A. Hydropower in Norway. Mechanical Equipment. Trondheim: Norwegian University of Science and Technology. 2001. Available online: https://www.ntnu.no/documents/381182060/641036380/Mechanical+Equipment+Kjolle+ny.pdf/ (accessed on 1 October 2021).
- Simoneau, R. The optimum protection of hydraulic turbines against cavitation erosion. In Proceedings of the 12th IAHR Symposium, Stirling, UK, 27–30 August 1984. [Google Scholar]
- Padhy, M.K.; Saini, R.P. A review on silt erosion in hydro turbines. Renew. Sustain. Energy Rev. 2007, 12, 1975–1986. [Google Scholar] [CrossRef]
- Neopane, H.P. Sediment Erosion in Hydro Turbines. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2010. [Google Scholar]
- Neopane, H.P.; Sujakhu, S.; Shrestha, S.; Subedi, K.; Basnet, A. Study of sediment erosion in hydraulic turbine using rotating disc apparatus. In Proceedings of the 2nd International Conference on the Developments in Renewable Energy Technology (ICDRET 2012), Dhaka, Bangladesh, 5–7 January 2012; pp. 1–4. [Google Scholar]
- Huang, X.; Valero, C.; Egusquiza, E.; Presas, A.; Guardo, A. Numerical and experimental análisis of the Dynamic response of large submerged trash-racks. Comput. Fluids 2013, 71, 54–64. [Google Scholar] [CrossRef]
- Egusquiza, E.; Valero, C.; Estévez, A.; Guardo, A.; Coussirat, M. Failures due to ingested bodies in hydraulic turbines. Eng. Fail. Anal. 2011, 18, 464–473. [Google Scholar] [CrossRef]
- Rodriguez, C.G.; Egusquiza, E.; Santos, I.F. Frequencies in the vibration induced by the rotor stator interaction in a centrifugal pump turbine. J. Fluids Eng. 2007, 129, 1428–1435. [Google Scholar] [CrossRef] [Green Version]
- Mathur, S.R. Unsteady flow simulations using unstructured sliding meshes. In Proceedings of the Fluid Dynamics Conference, Colorado Springs, CO, USA, 20–23 June 1994; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1994. [Google Scholar] [CrossRef]
- Nicolle, J.; Giroux, A.M.; Morissette, J.F. CFD configurations for hydraulic turbine startup. IOP Conf. Ser. Earth Environ. Sci. 2014, 22, 032021. [Google Scholar] [CrossRef]
- Simpson, A.T.; Spence, S.W.T.; Watterson, J.K. A comparison of the flow structures and losses within vaned and vaneless stators for radial turbines. J. Turbomach. 2009, 131, 031010. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Cooley, J.W.; Lewis, P.A.W.; Welch, P.D. Historical notes on the fast Fourier transform. IEEE Trans. Audio Electroacoust. 1967, 15, 76–79. [Google Scholar] [CrossRef]
- Welch, P.D. The use of fast Fourier transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms. IEEE Trans. Audio Electroacoust. 1967, 15, 70–73. [Google Scholar] [CrossRef] [Green Version]
- Trivedi, C.; Cervantes, M.J.; Dahlhaug, O.G. Numerical techniques applied to hydraulic turbines: A perspective review. Appl. Mech. Rev. 2016, 68, 010802. [Google Scholar] [CrossRef]
- Rodríguez, C.G.; Mateos-Prieto, B.; Egusquiza, E. Monitoring of rotor-stator interaction in pump-turbine using vibrations measured with on-board sensors rotating with shaft. Shock Vib. 2014, 2014, 276796. [Google Scholar] [CrossRef] [Green Version]
- WIKA Alexander Wiegand SE & Co. KG, High-Quality Pressure Transmitters—Model S-10. Available online: https://en.wika.com/s_10_en_co.WIKA (accessed on 7 August 2021).
- Brüel & Kjær A/S, 16-Channel CCLD Signal Conditioner|Type 2694-A|. Available online: https://www.bksv.com/en/transducers/signal-conditioning/ccld/2694-a (accessed on 7 August 2021).
- Sony Presicion Technology Inc., Portable DAT Instrumentation Recorder PC200Ax Series. Available online: https://www.daqlog-systems.co.uk/support/obsolete-systems/item/16-pc200-series (accessed on 7 August 2021).
- Egusquiza, E.; Valero, C.; Valentín, D.; Presas, A.; Rodriguez, C.G. Condition monitoring of pump-turbines. New challenges. Measurement 2015, 67, 151–163. [Google Scholar] [CrossRef] [Green Version]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guardo, A.; Fontanals, A.; Egusquiza, M.; Valero, C.; Egusquiza, E. Characterization of the Effects of Ingested Bodies on the Rotor–Stator Interaction of Hydraulic Turbines. Energies 2021, 14, 6669. https://doi.org/10.3390/en14206669
Guardo A, Fontanals A, Egusquiza M, Valero C, Egusquiza E. Characterization of the Effects of Ingested Bodies on the Rotor–Stator Interaction of Hydraulic Turbines. Energies. 2021; 14(20):6669. https://doi.org/10.3390/en14206669
Chicago/Turabian StyleGuardo, Alfredo, Alfred Fontanals, Mònica Egusquiza, Carme Valero, and Eduard Egusquiza. 2021. "Characterization of the Effects of Ingested Bodies on the Rotor–Stator Interaction of Hydraulic Turbines" Energies 14, no. 20: 6669. https://doi.org/10.3390/en14206669
APA StyleGuardo, A., Fontanals, A., Egusquiza, M., Valero, C., & Egusquiza, E. (2021). Characterization of the Effects of Ingested Bodies on the Rotor–Stator Interaction of Hydraulic Turbines. Energies, 14(20), 6669. https://doi.org/10.3390/en14206669






