Effective Permutation Encoding for Evolutionary Optimization of the Electric Vehicle Routing Problem
Abstract
:1. Introduction
1.1. Background
1.2. Literature Review
- Each customer is visited exactly once (2n repetitions of the constrain test, where n is the number of customers visited);
- All customer demands are satisfied (n repetitions of the constrain test);
- The load and capacity of vehicles are consistent;
- Goods travel routes are synchronized with vehicles’ routes (n2—n repetitions of constrain test);
- Number of vehicles dispatched and provided in the depot are consistent;
- The route is not disconnected.
- Non-negative level of fuel in vehicles;
- Sufficient fuel to continue the journey at each point of the route; and
- The amount of replenishment at stations.
1.3. Contribution of this Paper
- Every customer will be visited;
- There are no returns to a previously visited customer;
- The route is continuous.
- The need to recharge the battery while travelling a route;
- Supervision of the range of a vehicle—preventing it from “getting stuck” on the route;
- Selecting a charging station and taking into account the additional distance that the vehicle has to travel.
2. Problem Formulation
2.1. Assumptions
- A fleet of identical EV is waiting in the depot to set off to customers and deliver to each of them a certain quantity of goods that they ordered;
- All EVs set off from the depot with 100%-charged batteries, which allows covering the established distance;
- The carrying capacity of a single EV is limited by a fixed value which may not be exceeded;
- No customer requests more than the maximum capacity of one vehicle;
- In the area handled by the vehicle fleet there are charging stations allowing the batteries to be recharged in an acceptable time to level 80%;
- Each charging station can handle multiple vehicles at the same time;
- The route plan for each vehicle must include any need to replenish energy and return to the depot after the goods have been delivered;
- Between points on the map (depot, charging stations, and customers), the route distances that the vehicle must cover are given;
- The distance of a route between any two points is affected by the existing road infrastructure and is determined from empirical data or navigation. The route distances can be expressed in km, or in time units, which will allow the inclusion of additional aspects related to speed limitations on certain roads and delays due to traffic lights and periodic traffic congestion. Obviously, time data is more susceptible to variability than distance expressed in units of length.
2.2. Mathematical Model
| s = 1, 2, …, S | numbering of charging stations, |
| c = 1, 2, …, C | numbering of customers, |
| P | the total number of nodes considered in the planning (the depot, CSs and customers), |
| b, b1, b2 = 1, 2, …, B | numbering of elements in the solution vector y, |
| z = (z1, z2, …, zC) | vector of orders, |
| Lmax | carrying capacity of a single EV, |
| Rmax | range of EV with fully-charged batteries, |
| R80 | range of EV with 80%-charged batteries—after visiting CS, |
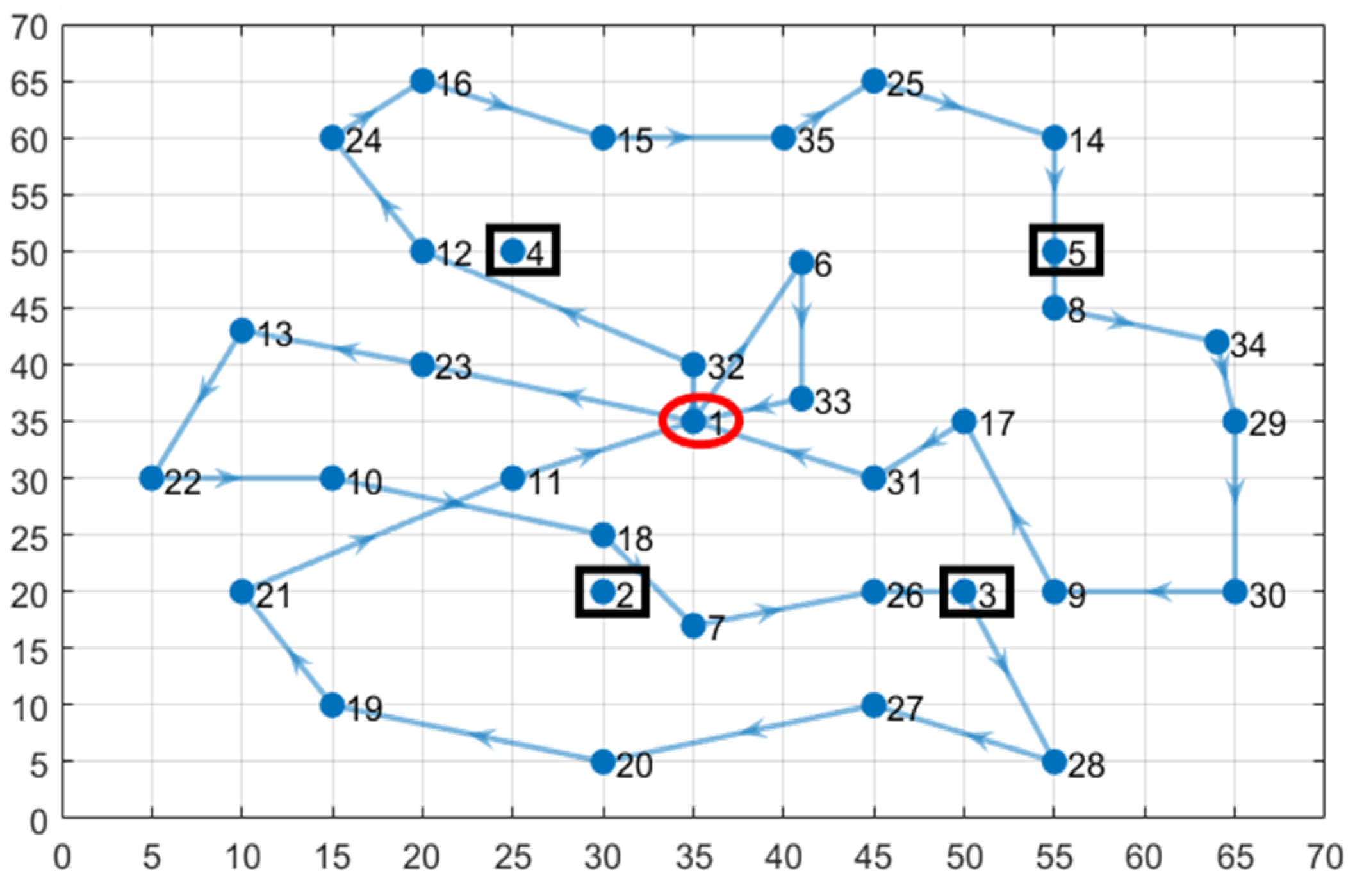
| D = (di,j)P × P | the distance matrix, with rows and columns correspond to nodes, as shown in the Figure 1. |
2.3. Permutation Encoding of Solution
∀c, c1, c2 = 1, 2, …, C: xc∈[S+2, P], xc1 ≠ xc2
- The maximum reach of the vehicle is 10;
- The maximum payload of the vehicle is 1;
- The charging station replenishes energy up to level 0.8;
- The encoded solution of the problem is a vector x = (7, 5, 4, 6, 8).
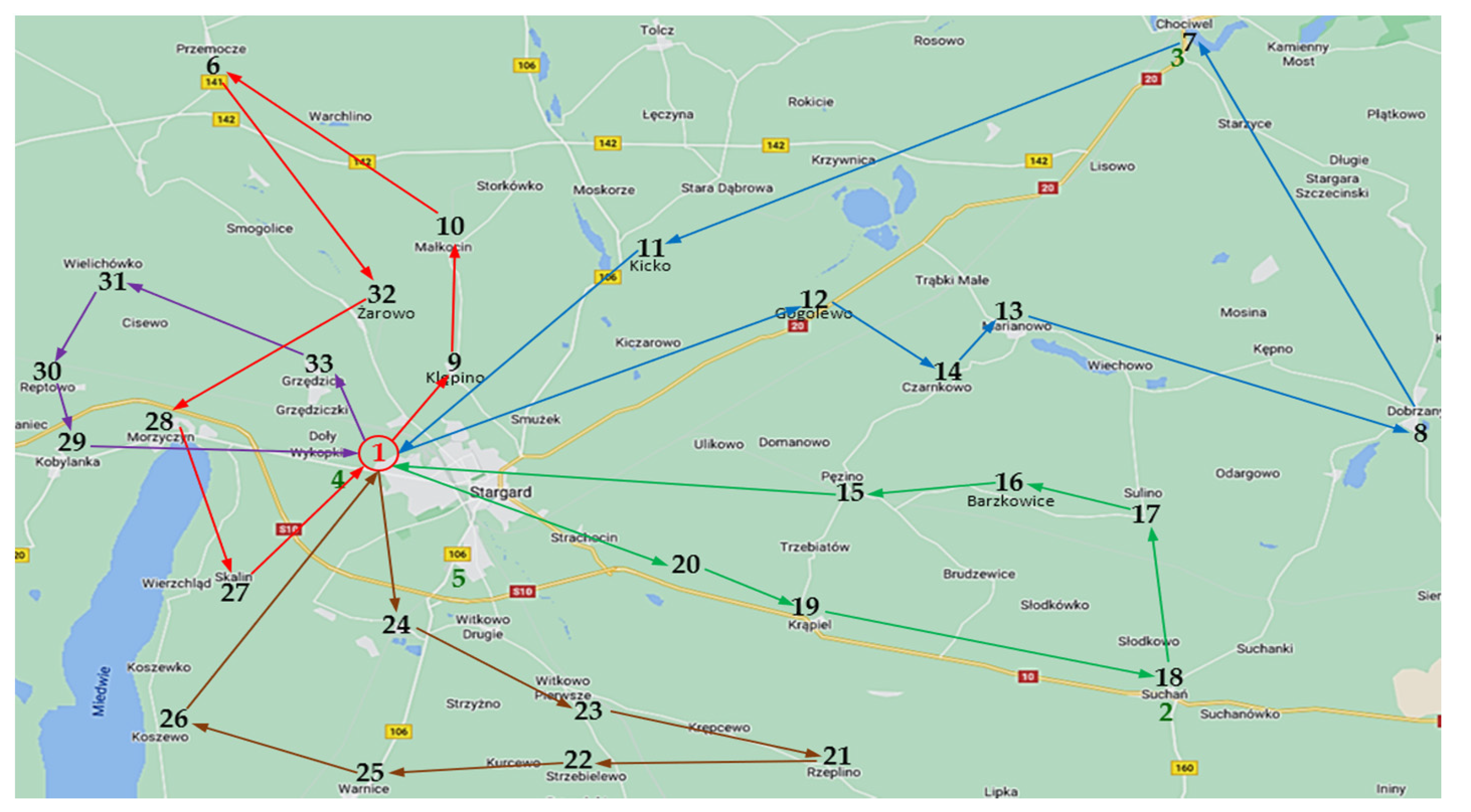
3. Example Study
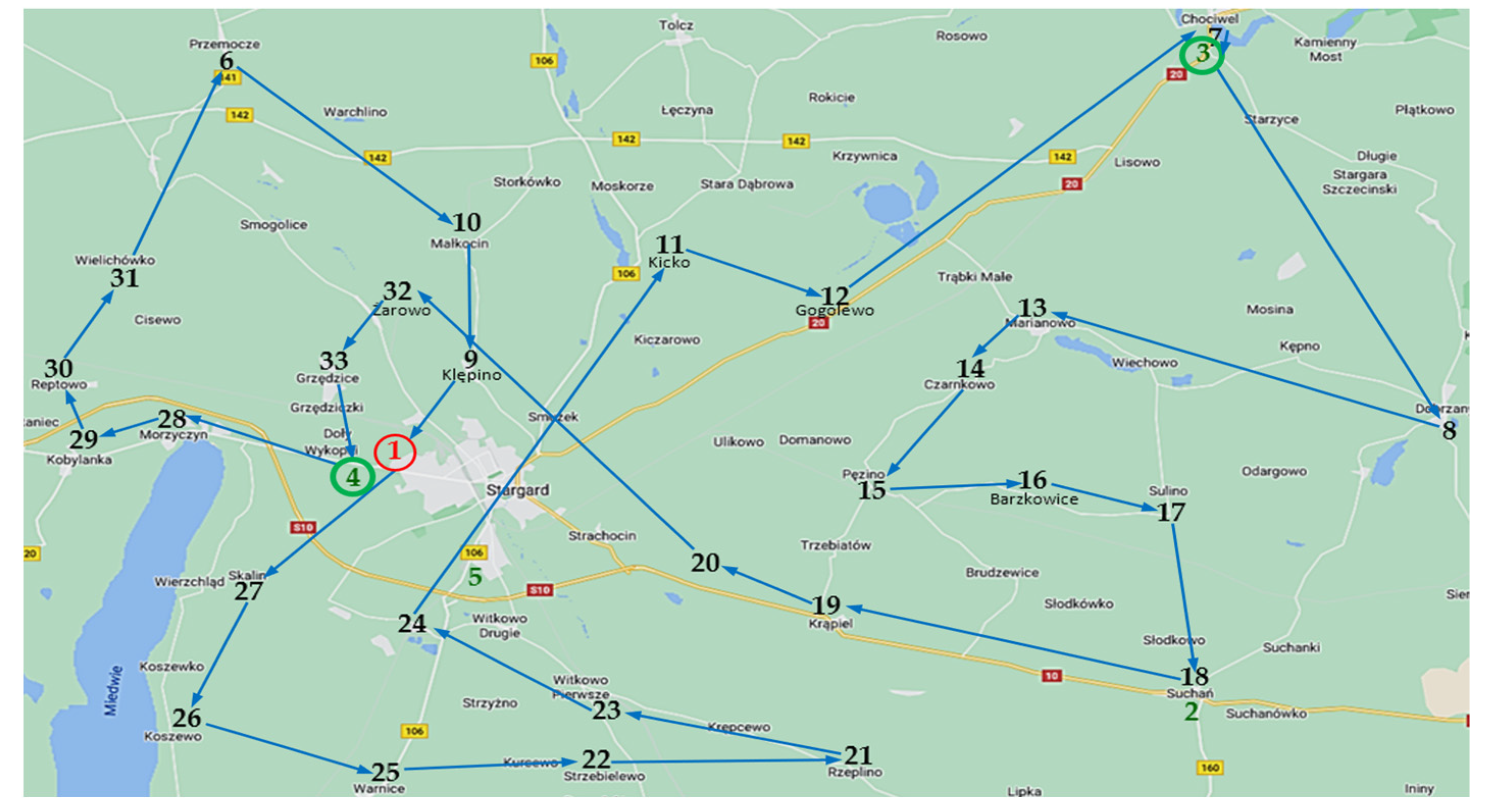
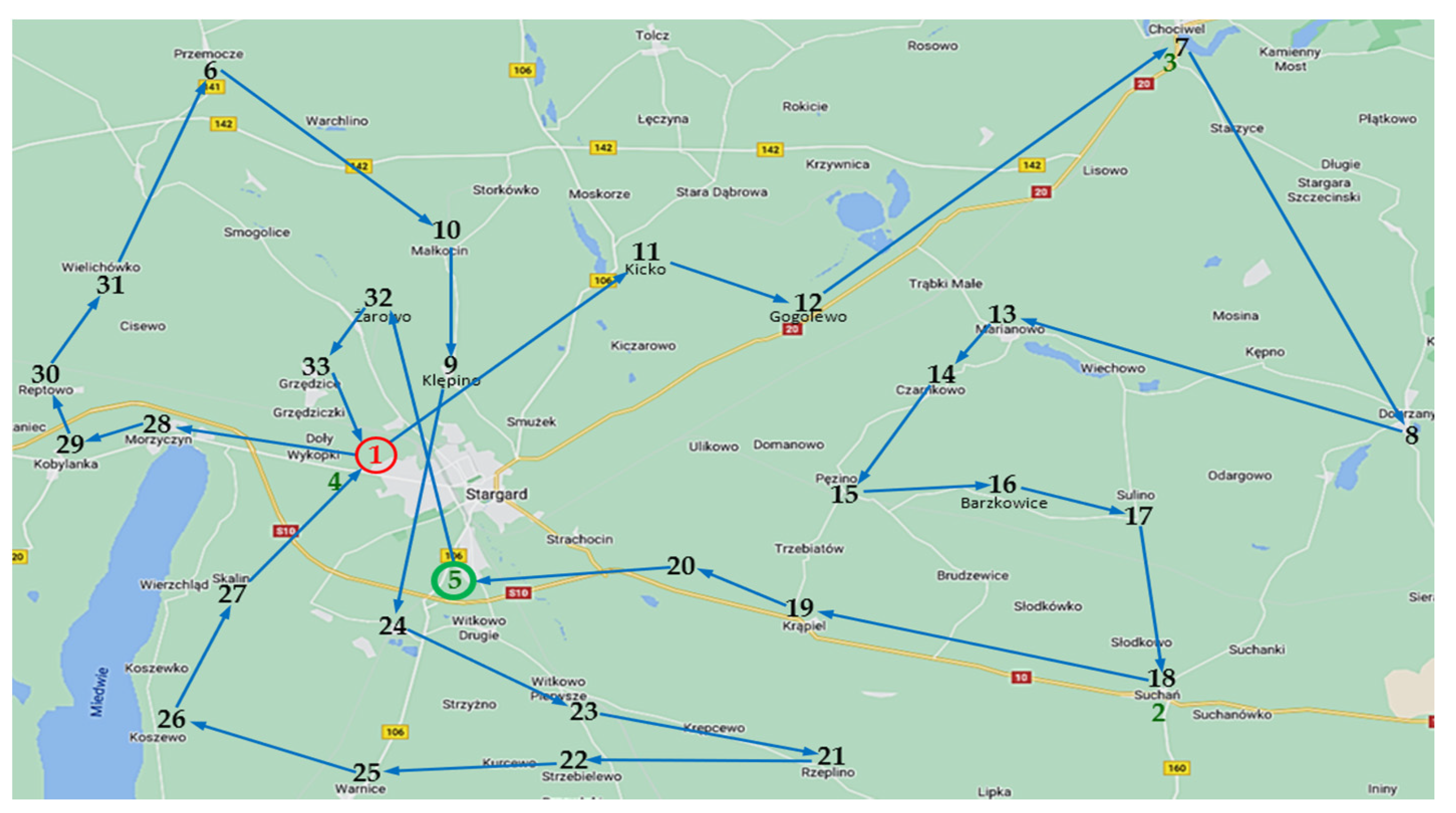
- Point 1—the depot—Stargard City located in north-western Poland;
- Points 2, 3, 4, 5—charging stations—located in the small cities of Suchań, Chociwel and on the outskirts of Stargard;
- Points 6, 7, …, 33—customers located in the vicinity of Stargard.
- The maximum payload of the vehicle is Lmax = 1700 kg;
- The maximum reach of the vehicle is Rmax = 120 km.
- Scenario 1: Each customer needs 60 kg of goods, so the demand vector is z = (60, 60, …, 60)1 × 28. In this scenario the total demand of the customers equals: 28 × 60 = 1680 kg, which is within the payload of one EV. The evolutionary algorithm is expected to look for a solution where a vehicle returns to the depot only after visiting all customers.
- Scenario 2: Each customer needs 121 kg of goods, so the demand vector z = (121, 121, …, 121)1 × 28. The total demand of the customers equals: 28 × 121 = 3388, which is within the carrying capacity of two EVs.
- Scenario 3: Each customer’s demand is a random number from interval [100,1700]. Ten different demand vectors were generated. It was analysed how the sum of the customers’ demands affects the delivery plan.
- Population size: G = 40;
- Number of elite individuals: E = 2;
- Mutation probability: P = 0.3;
- Number of populations: 20,000.
- Departure from the depot;
- Supplying the customers: 27, 26, 25, 22, 21, 23, 24, 11, 12, 7;
- Charging the battery in point 3 (Chociwel);
- Supplying the customers: 8, 13, 14, 15, 16, 17, 18, 19, 20, 32, 33;
- Charging the battery in point 4 (Shopping centre—Lipnik);
- Supplying the customers: 28, 29, 30, 31, 6, 10, 9;
- Return to the depot.
- Two EVs leave the depot;
- The first EV supplies the customers: 11, 12, 7, 8, 13, 14, 15, 16, 17, 18, 19, 20;
- The first EV charges the battery in point 5;
- The first EV supplies the customers: 32, 33;
- The second EV supplies the customers: 28, 29, 30, 31, 6, 10, 9, 24, 23, 21, 22, 25, 26, 27;
- Both EVs return to the depot.
4. Assessment of the Performance of the Proposed Algorithm
5. Discussion and Conclusions
Funding
Conflicts of Interest
Appendix A
| Base | Charging Points | Customers | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | |
| 1 | 0 | 25.1 | 30.4 | 3.3 | 6.2 | 20.8 | 30.4 | 35.6 | 6.5 | 10.6 | 14.7 | 14.5 | 23.4 | 20.3 | 17.5 | 26.2 | 29.9 |
| 2 | 24.5 | 0 | 29.2 | 26.6 | 21.6 | 40.2 | 29.2 | 13.4 | 24.1 | 28.2 | 28.8 | 24.6 | 14.4 | 16.9 | 12.6 | 10.9 | 7.4 |
| 3 | 30.4 | 29.3 | 0 | 32.5 | 28.4 | 33.1 | 0 | 17.2 | 27.1 | 25 | 21.8 | 15.6 | 14.8 | 19.7 | 23.9 | 19.9 | 21.8 |
| 4 | 1.2 | 24.8 | 30.2 | 0 | 6 | 20.8 | 30.2 | 35.4 | 6.5 | 10.6 | 14.5 | 14.6 | 23.5 | 20.1 | 17.3 | 23.5 | 29.7 |
| 5 | 6.2 | 22.5 | 28.4 | 8.3 | 0 | 22.6 | 28.4 | 33.5 | 8 | 12.1 | 12.7 | 12.8 | 21.7 | 18.3 | 15.5 | 21.7 | 27.4 |
| 6 | 21 | 45.1 | 33.1 | 19.8 | 22.4 | 0 | 33.1 | 42.6 | 16.1 | 12 | 18.1 | 27.6 | 30.7 | 33.1 | 30.3 | 35.8 | 37.7 |
| 7 | 30.4 | 29.3 | 0 | 32.5 | 28.4 | 33.1 | 0 | 17.2 | 27.1 | 25 | 21.8 | 15.6 | 14.8 | 19.7 | 23.9 | 19.9 | 21.8 |
| 8 | 35.6 | 13.4 | 15.9 | 37.7 | 33.6 | 42.6 | 15.9 | 0 | 32.3 | 34.6 | 31.3 | 20.8 | 11.9 | 15.6 | 19.8 | 16.7 | 11.4 |
| 9 | 6.5 | 24.6 | 27.1 | 8.8 | 7.9 | 16.1 | 27.1 | 32.3 | 0 | 4.1 | 11.4 | 11.5 | 20.4 | 17 | 14.2 | 20.5 | 27.4 |
| 10 | 10.6 | 28.7 | 25 | 12.9 | 12 | 12 | 25 | 34.7 | 4.1 | 0 | 10.1 | 15.6 | 22.7 | 21.1 | 18.3 | 24.6 | 28.3 |
| 11 | 14.6 | 29.1 | 21.8 | 16.9 | 12.7 | 18.3 | 21.8 | 31.4 | 11.3 | 10.3 | 0 | 8.5 | 19.5 | 17.1 | 11.2 | 20.5 | 24.3 |
| 12 | 14.8 | 24.6 | 15.6 | 16.9 | 12.8 | 27.6 | 15.6 | 20.8 | 11.5 | 15.6 | 8.5 | 0 | 8.9 | 5.5 | 9.7 | 13.3 | 15.9 |
| 13 | 23.8 | 14.4 | 14.9 | 25.9 | 21.8 | 30.8 | 14.9 | 11.9 | 20.5 | 22.7 | 19.5 | 9 | 0 | 3.7 | 7.9 | 5.1 | 7 |
| 14 | 20.3 | 16.9 | 19.7 | 22.4 | 18.4 | 33.1 | 19.7 | 15.6 | 17 | 21.1 | 17.1 | 5.5 | 3.7 | 0 | 4.2 | 7.8 | 10.7 |
| 15 | 17.5 | 12.6 | 23.9 | 19.6 | 15.5 | 30.3 | 23.9 | 19.8 | 14.2 | 18.3 | 11.2 | 9.7 | 8 | 4.2 | 0 | 6.3 | 10 |
| 16 | 23.8 | 11.1 | 19.9 | 25.9 | 21.8 | 35.8 | 19.9 | 16.7 | 20.4 | 24.5 | 20.5 | 13.2 | 5.2 | 7.8 | 6.3 | 0 | 5.3 |
| 17 | 29.4 | 7.4 | 20 | 32.8 | 25.8 | 37.7 | 20 | 11.4 | 24.2 | 28.3 | 24.3 | 15.9 | 7 | 10.7 | 10 | 5.3 | 0 |
| 18 | 24.5 | 0 | 29.2 | 26.6 | 21.6 | 40.2 | 29.2 | 13.4 | 24.1 | 28.2 | 28.8 | 24.6 | 14.4 | 16.9 | 12.6 | 10.9 | 7.4 |
| 19 | 14.5 | 10 | 34.5 | 16.6 | 11.6 | 30.2 | 34.5 | 23.4 | 14.1 | 18.2 | 18.8 | 14.6 | 12.8 | 9.1 | 4.9 | 10.4 | 14.1 |
| 20 | 8.2 | 16.9 | 28.1 | 10.3 | 6.2 | 23.6 | 28.1 | 30.3 | 7.8 | 11.8 | 12.5 | 12.5 | 19.7 | 16 | 11.8 | 18 | 21.7 |
| 21 | 18.6 | 17.1 | 40.8 | 20.7 | 13.4 | 35 | 40.8 | 29.2 | 20.4 | 24.5 | 25.1 | 25.2 | 30.2 | 30.7 | 27.9 | 26.7 | 23.2 |
| 22 | 14.3 | 24.8 | 36.5 | 16.4 | 9.1 | 30.7 | 36.5 | 36.9 | 16.1 | 20.2 | 20.8 | 20.9 | 29.8 | 26.4 | 23.6 | 30.8 | 30.9 |
| 23 | 10.6 | 25.1 | 32.8 | 12.7 | 5.4 | 27 | 32.8 | 37.2 | 12.4 | 16.5 | 17.1 | 17.2 | 26.1 | 22.7 | 19.9 | 26.1 | 30.8 |
| 24 | 9.9 | 22.8 | 32 | 12 | 3.8 | 25.8 | 32 | 35.8 | 11.6 | 15.7 | 16.4 | 16.4 | 25.3 | 21.9 | 17.6 | 23.9 | 27.6 |
| 25 | 13.8 | 26.7 | 36 | 15.9 | 8.2 | 30.2 | 36 | 40.1 | 14.6 | 19.7 | 20.3 | 20.4 | 29.2 | 25.8 | 21.6 | 27.8 | 31.6 |
| 26 | 14.5 | 33.3 | 41 | 13.3 | 14.7 | 30.9 | 41 | 46.1 | 19.8 | 23.9 | 25.3 | 25.4 | 34.3 | 30.9 | 28.1 | 34.3 | 38.1 |
| 27 | 9.2 | 26.7 | 34.4 | 8 | 8.2 | 25.6 | 34.4 | 39.6 | 12.8 | 18.2 | 18.8 | 18.9 | 27.7 | 24.4 | 21.5 | 27.8 | 31.6 |
| 28 | 6.5 | 30 | 35.1 | 4.9 | 10.9 | 22.5 | 35.1 | 40.3 | 11.4 | 15.5 | 19.4 | 19.5 | 28.4 | 25 | 22.2 | 28.4 | 34.9 |
| 29 | 9.7 | 33.2 | 38.3 | 8.1 | 14 | 25.7 | 38.3 | 43.4 | 14.6 | 18.7 | 22.6 | 22.7 | 31.6 | 28.2 | 25.4 | 31.6 | 38.1 |
| 30 | 11.7 | 35.3 | 40.6 | 10.4 | 16.4 | 24.7 | 40.6 | 50.9 | 17 | 21.1 | 25 | 25 | 40.3 | 36.6 | 30.4 | 38.6 | 42.3 |
| 31 | 17.5 | 37.6 | 36.5 | 16.7 | 19.4 | 8.3 | 36.5 | 46 | 18.4 | 14.2 | 21.5 | 26.3 | 34.1 | 31.9 | 29 | 39.2 | 41.1 |
| 32 | 7.2 | 27.3 | 31.6 | 6.5 | 9.1 | 13.3 | 31.6 | 36.8 | 8.1 | 12.2 | 16 | 16 | 24.9 | 21.6 | 18.7 | 25 | 31.9 |
| 33 | 5.1 | 28.6 | 33 | 3.8 | 9.8 | 16 | 33 | 38.2 | 9.5 | 13.6 | 17.4 | 17.4 | 26.3 | 23 | 20.1 | 26.4 | 33.3 |
| Customers | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | |
| 1 | 25.1 | 15.1 | 8.2 | 18.7 | 14.4 | 10.6 | 9.8 | 13.8 | 14.4 | 9.1 | 6.5 | 9.7 | 11.6 | 17.5 | 7.2 | 4.9 |
| 2 | 0 | 10 | 16.3 | 17 | 24.8 | 25.1 | 23.3 | 27.3 | 33.7 | 27.2 | 29.3 | 32.5 | 37.3 | 36.9 | 26.7 | 28 |
| 3 | 29.3 | 28.8 | 28.3 | 40.9 | 36.6 | 32.9 | 32 | 36 | 41 | 34.5 | 35.2 | 38.4 | 46.8 | 36.5 | 31.7 | 33.1 |
| 4 | 24.8 | 14.8 | 8 | 18.4 | 14.1 | 10.4 | 9.5 | 13.5 | 14.4 | 9.1 | 6 | 9.2 | 11.6 | 17.8 | 7.5 | 4.9 |
| 5 | 22.5 | 12.5 | 6.2 | 13.4 | 9.1 | 5.4 | 3.8 | 8.1 | 14.6 | 8 | 12.2 | 15.3 | 18.9 | 19.6 | 9.3 | 9.8 |
| 6 | 45.1 | 30.7 | 23.7 | 34.9 | 30.6 | 26.8 | 26 | 30 | 30.8 | 25.6 | 22.5 | 25.6 | 29.7 | 8.3 | 13.3 | 16 |
| 7 | 29.3 | 28.8 | 28.3 | 40.9 | 36.6 | 32.9 | 32 | 36 | 41 | 34.5 | 35.2 | 38.4 | 46.8 | 36.5 | 31.7 | 33.1 |
| 8 | 13.4 | 23.4 | 29.7 | 29.1 | 36.9 | 37.2 | 36.7 | 40.7 | 46.2 | 39.6 | 40.4 | 43.6 | 50.7 | 45.9 | 36.9 | 38.3 |
| 9 | 24.6 | 14.6 | 7.8 | 20.4 | 16.1 | 12.3 | 10.8 | 15.5 | 19.8 | 12.8 | 11.5 | 14.7 | 18.7 | 18.4 | 8.1 | 9.5 |
| 10 | 28.7 | 18.7 | 11.9 | 24.5 | 20.2 | 16.4 | 14.9 | 19.6 | 23.9 | 16.9 | 15.6 | 18.8 | 22.8 | 15.3 | 12.2 | 13.6 |
| 11 | 29.1 | 19.1 | 12.6 | 25.1 | 20.8 | 17.1 | 16.3 | 20.2 | 25.2 | 18.7 | 19.4 | 22.6 | 26.6 | 21.7 | 15.9 | 17.3 |
| 12 | 24.6 | 14.6 | 12.7 | 25.3 | 21 | 17.3 | 16.4 | 20.4 | 25.4 | 18.9 | 19.6 | 22.8 | 26.8 | 26.4 | 16.1 | 17.5 |
| 13 | 14.4 | 12.8 | 19.2 | 30.2 | 30 | 26.3 | 25.4 | 29.4 | 34.4 | 27.8 | 28.6 | 31.8 | 40.1 | 34.1 | 25.1 | 26.5 |
| 14 | 16.9 | 9.1 | 15.5 | 30.8 | 26.5 | 22.8 | 21.9 | 25.9 | 30.9 | 24.4 | 25.1 | 28.3 | 36.4 | 31.9 | 21.6 | 23 |
| 15 | 12.6 | 4.9 | 11.2 | 28 | 23.7 | 20 | 18.2 | 22.2 | 28.1 | 21.5 | 22.3 | 25.5 | 31 | 29.1 | 18.8 | 20.2 |
| 16 | 11.1 | 10.4 | 16.7 | 28.1 | 30.2 | 26.2 | 23.3 | 27.7 | 34.1 | 27.6 | 30.4 | 37.2 | 37.7 | 38 | 27.7 | 26.4 |
| 17 | 7.4 | 14.8 | 21.2 | 23.1 | 30.9 | 30.7 | 27.1 | 31.4 | 37.9 | 31.3 | 34.2 | 40.9 | 41.4 | 41 | 31.5 | 33.4 |
| 18 | 0 | 10 | 16.3 | 17 | 24.8 | 25.1 | 23.3 | 27.3 | 33.7 | 27.2 | 29.3 | 32.5 | 37.3 | 36.9 | 26.7 | 28 |
| 19 | 10 | 0 | 6.4 | 24.6 | 19.2 | 16.5 | 13.3 | 17.3 | 23.7 | 17.2 | 19.3 | 26.8 | 27.3 | 27 | 16.7 | 18.1 |
| 20 | 16.9 | 6.9 | 0 | 18.7 | 14.4 | 10.6 | 8.9 | 12.9 | 18.8 | 12.2 | 13 | 16.2 | 21.7 | 20.6 | 10.3 | 11.7 |
| 21 | 17.1 | 24 | 18.6 | 0 | 7.7 | 8 | 13.6 | 16.4 | 22.9 | 19.6 | 23.4 | 26.6 | 30.6 | 32.1 | 21.8 | 22.3 |
| 22 | 24.8 | 19.7 | 14.3 | 7.7 | 0 | 3.7 | 7.8 | 8.7 | 15.2 | 13 | 19.5 | 22.7 | 25.1 | 27.8 | 17.5 | 18 |
| 23 | 25.1 | 16 | 10.6 | 8 | 3.7 | 0 | 5.6 | 9.9 | 17.1 | 11.6 | 17 | 20.2 | 23.7 | 24 | 13.7 | 14.2 |
| 24 | 22.8 | 12.8 | 8.5 | 13.6 | 7.8 | 5.6 | 0 | 5.9 | 11.7 | 5.2 | 11.7 | 14.9 | 17.2 | 23.5 | 13 | 13.5 |
| 25 | 26.7 | 16.7 | 12.5 | 16.4 | 8.7 | 9.9 | 5.9 | 0 | 7.1 | 11.2 | 17.6 | 20.8 | 23.2 | 27.2 | 16.9 | 17.4 |
| 26 | 33.3 | 23.3 | 18.8 | 22.9 | 15.1 | 17.1 | 11.8 | 7.1 | 0 | 6.5 | 11.7 | 14.9 | 17.3 | 23.6 | 17.6 | 14.9 |
| 27 | 26.7 | 16.8 | 12.2 | 19.7 | 14.3 | 11.7 | 5.2 | 12.4 | 6.5 | 0 | 6.5 | 9.7 | 12 | 18.3 | 12.3 | 9.6 |
| 28 | 30 | 19.7 | 15.8 | 23.3 | 18.5 | 15.3 | 11.7 | 16.6 | 11.7 | 6.5 | 0 | 3.2 | 5.5 | 11.8 | 9.2 | 6.5 |
| 29 | 33.2 | 23.2 | 19 | 26.5 | 21.7 | 18.5 | 14.9 | 19.8 | 14.9 | 9.7 | 3.2 | 0 | 2.7 | 9 | 12.4 | 9.7 |
| 30 | 35.3 | 27.5 | 21.3 | 29.4 | 24 | 21.4 | 17.3 | 22.1 | 17.3 | 12 | 5.5 | 2.7 | 0 | 6.3 | 14.8 | 12.1 |
| 31 | 37.6 | 27.6 | 20.7 | 31.9 | 27.6 | 23.8 | 23 | 27 | 23.6 | 18.3 | 11.8 | 9 | 6.3 | 0 | 10.3 | 7.6 |
| 32 | 27.3 | 17.3 | 10.5 | 21.6 | 17.3 | 13.5 | 12.7 | 16.7 | 17.5 | 12.3 | 9.2 | 12.4 | 16.4 | 10.3 | 0 | 2.7 |
| 33 | 28.6 | 18.7 | 11.8 | 22.2 | 17.9 | 14.2 | 13.4 | 17.3 | 14.8 | 9.6 | 6.5 | 9.7 | 13.7 | 7.6 | 2.7 | 0 |
References
- Ghorbani, E.; Alinaghian, M.; Gharehpetian, G.B.; Mohammadi, S.; Perboli, G. A Survey on Environmentally Friendly Vehicle Routing Problem and a Proposal of Its Classification. Sustainability 2020, 12, 9079. [Google Scholar] [CrossRef]
- Wang, L.Y.; Song, Y.B. Multiple Charging Station Location-Routing Problem with Time Window of Electric Vehicle. J. Eng. Sci. Technol. Rev. 2015, 8, 190–201. [Google Scholar] [CrossRef]
- Erdelić, T.; Carić, T. A Survey on the Electric Vehicle Routing Problem: Variants and Solution Approaches. J. Adv. Transp. 2019, 2019, 5075671. [Google Scholar] [CrossRef]
- Erdoğan, S.; Miller-Hooks, E. A green vehicle routing problem. Transp. Res. Part E Logist. Transp. Rev. 2012, 48, 100–114. [Google Scholar] [CrossRef]
- Montoya, A.; Guéret, C.; Mendoza, J.E.; Villegas, J. The electric vehicle routing problem with nonlinear charging function. Transp. Res. Part B Methodol. 2017, 103, 87–110. [Google Scholar] [CrossRef] [Green Version]
- Kullman, N.; Goodson, J.; Mendoza, J.E. Electric Vehicle Routing with Public Charging Stations. Transp. Sci. 2021, 55, 3. [Google Scholar] [CrossRef]
- Zuo, X.; Xiao, Y.; You, M.; Kaku, I.; Xu, Y. A new formulation of the electric vehicle routing problem with time windows considering concave nonlinear charging function. J. Clean. Prod. 2019, 236, 117687. [Google Scholar] [CrossRef]
- Koç, Ç.; Jabali, O.; Mendoza, J.E.; Laporte, G. The electric vehicle routing problem with shared charging stations. Int. Trans. Oper. Res. 2019, 26, 1211–1243. [Google Scholar] [CrossRef]
- Lee, C. An exact algorithm for the electric-vehicle routing problem with nonlinear charging time. J. Oper. Res. Soc. 2020, 1–24. [Google Scholar] [CrossRef]
- Kancharla, S.R.; Ramadurai, G. Electric Vehicle Routing Problem with Non-Linear Charging and Load-Dependent Discharging. Expert Syst. Appl. 2020, 113714. [Google Scholar] [CrossRef]
- Gheysens, F.; Golden, B.; Assad, A. A comparison of techniques for solving the fleet size and mix vehicle routing problem. OR Spektrum 1984, 6, 207–216. [Google Scholar] [CrossRef]
- Bula, G.A.; Gonzalez, F.A.; Prodhon, C.; Afsar, H.M.; Velasco, N.M. Mixed Integer Linear Programming Model for Vehicle Routing Problem for Hazardous Materials. IFAC-PapersOnLine 2016, 49, 538–543. [Google Scholar] [CrossRef]
- Madankumar, S.; Rajendran, C. A mixed integer linear programming model for the vehicle routing problem with simultaneous delivery and pickup by heterogeneous vehicles, and constrained by time windows. Sādhanā 2019, 44, 39. [Google Scholar] [CrossRef] [Green Version]
- Xiang, X.; Tian, Y.; Zhang, X.; Xiao, J.; Jin, Y. A Pairwise Proximity Learning-Based Ant Colony Algorithm for Dynamic Vehicle Routing Problems. IEEE Trans. Intell. Transp. Syst. 2021. [Google Scholar] [CrossRef]
- Shao, S.; Guan, W.; Ran, B.; He, Z.; Bi, J. Electric Vehicle Routing Problem with Charging Time and Variable Travel Time. Math. Probl. Eng. 2017, 2017, 5098183. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Gao, S.; Wang, K.; Li, T.; Li, L.; Chen, Z. Time-Dependent Electric Vehicle Routing Problem with Time Windows and Path Flexibility. J. Adv. Transp. 2020, 2020, 3030197. [Google Scholar] [CrossRef]
- Froger, A.; Mendoza, J.E.; Jabali, O.; Laporte, G. Improved formulations and algorithmic components for the electric vehicle routing problem with nonlinear charging functions. Comput. Oper. Res. 2019, 104, 256–294. [Google Scholar] [CrossRef] [Green Version]
- Flood, M.M. The Traveling-Salesman Problem. Oper. Res. 1956, 4, 61–75. [Google Scholar] [CrossRef]
- Abdoun, O.; Abouchabaka, J. A Comparative Study of Adaptive Crossover Operators for Genetic Algorithms to Resolve the Traveling Salesman Problem. Int. J. Comp. App. 2011, 31, 49–57. [Google Scholar] [CrossRef]
- Iwańkowicz, R.; Sekulski, Z. Solving of vehicle routing problem by evolutionary algorithm. Adv. Sci. Technol. Res. J. 2016, 10, 123–134. [Google Scholar] [CrossRef]
- Malhotra, R.; Singh, N.; Singh, Y. Genetic Algorithms: Concepts, Design for Optimization of Process Controllers. Comput. Inf. Sci. 2011, 4. [Google Scholar] [CrossRef]
- Chieng, H.H.; Wahid, N. A Performance Comparison of Genetic Algorithm’s Mutation Operators in n-Cities Open Loop Travelling Salesman Problem. In Recent Advances on Soft Computing and Data Mining; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar] [CrossRef]
- Wang, Q.; Peng, S.; Liu, S. Optimization of Electric Vehicle Routing Problem Using Tabu Search. In Proceedings of the 2020 Chinese Control and Decision Conference, Hefei, China, 22–24 August 2020. [Google Scholar] [CrossRef]

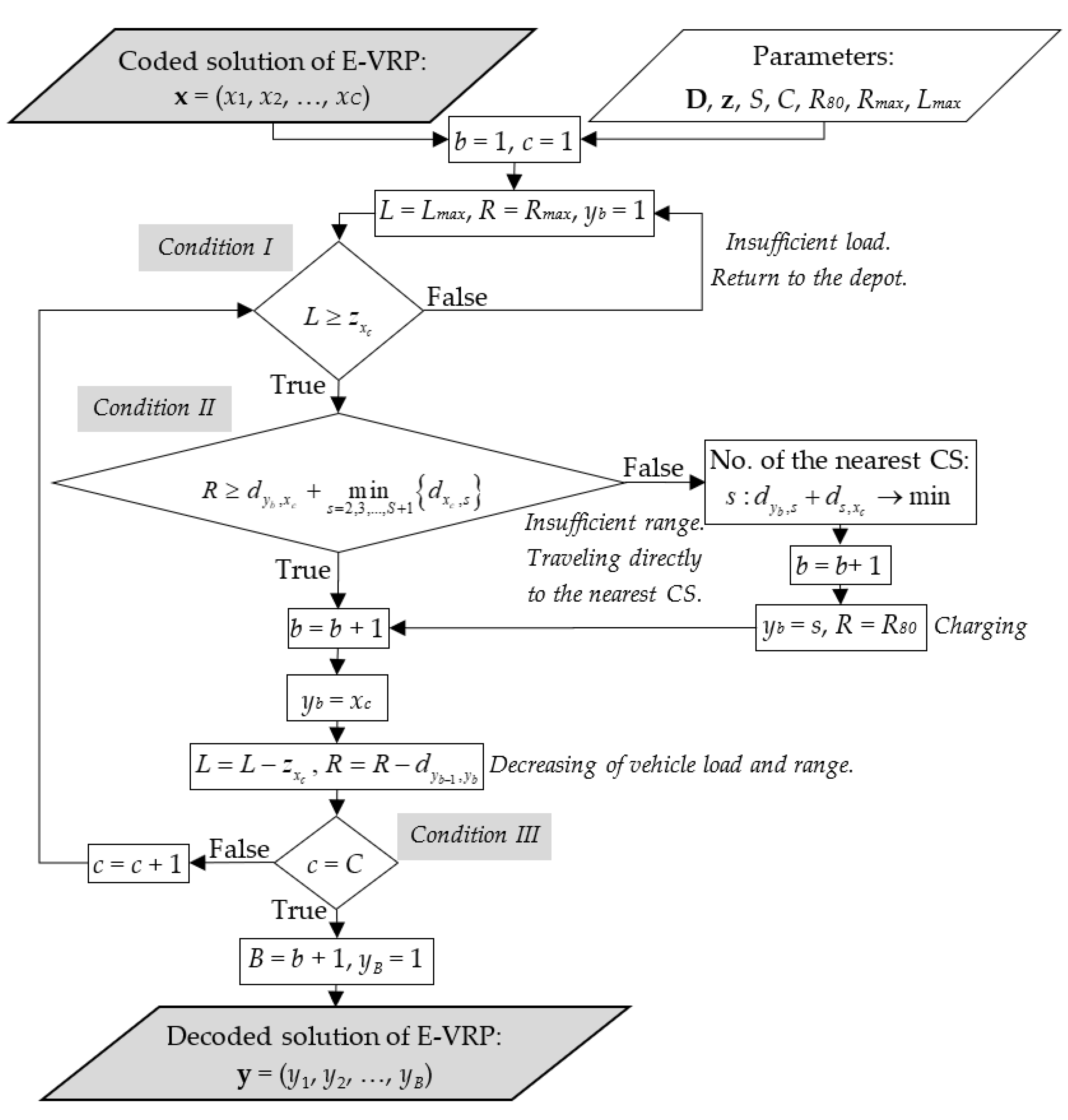


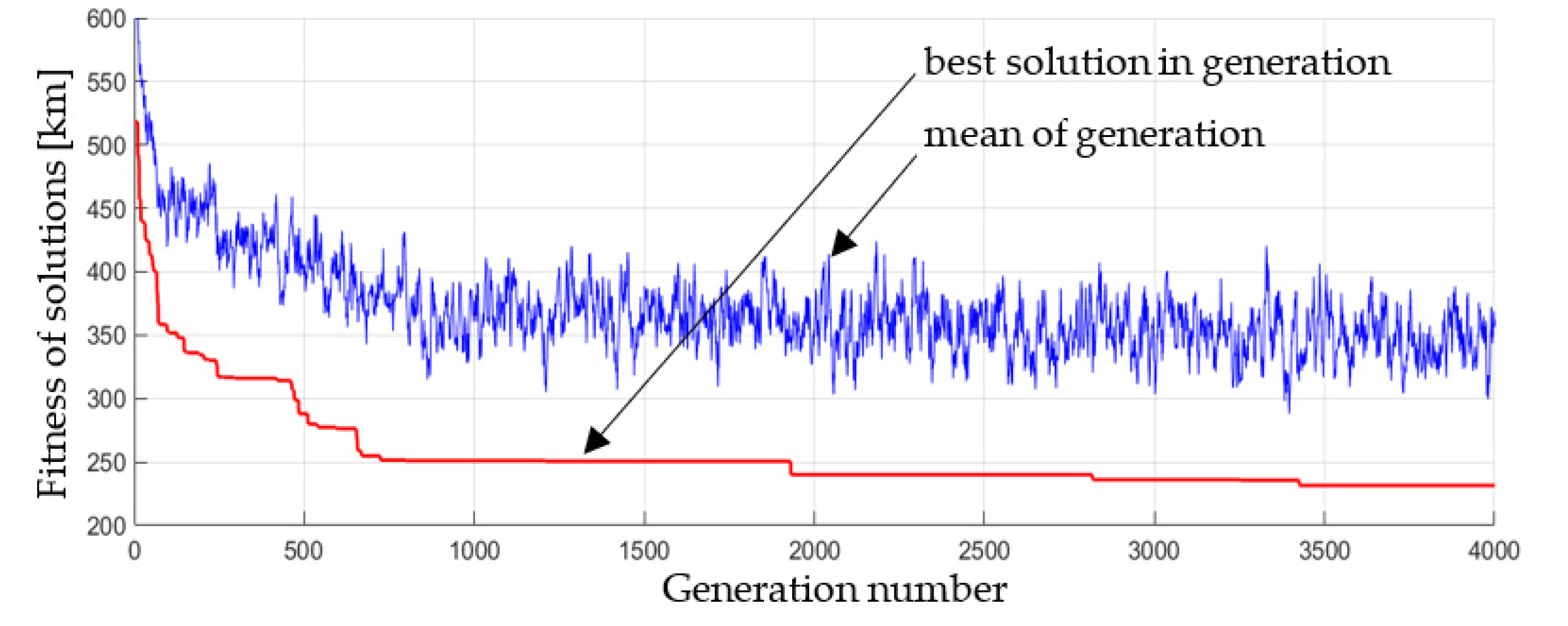


| b | Vehicle Location yi | Vehicle Reach R | Vehicle Load L | c | Next Customer xc | Step Results |
|---|---|---|---|---|---|---|
| 1 | 1 | 10 | 1 | 1 | 7 | Conditions I and II—met. Travelling from 1 (the depot) to 7. |
| 2 | 7 | 9 | 0.7 | 2 | 5 | Conditions I and II—met. Travelling from 7 to 5. |
| 3 | 5 | 6 | 0.5 | 3 | 4 | Condition II—not met. Travelling to 3 (the nearest CS). |
| 4 | 3 | 8 | 0.5 | 3 | 4 | Conditions I and II—met. Travelling to 4. |
| 5 | 4 | 5 | 0.1 | 4 | 6 | Condition I—not met. Travelling to 1 (the depot). |
| 6 | 1 | 10 | 1 | 4 | 6 | Conditions I and II—met. Travelling from 1 (the depot) to 6. |
| 7 | 6 | 6 | 0.8 | 5 | 8 | Conditions I and II—met. Travelling from 6 to 8. |
| 8 | 8 | 4 | 0.3 | - | - | Condition III—met. End of route, return to 1. |
| 9 | 1 | - | - | - | - |
| Random Problem No. | Demand Sum [kg] | Minimum Number of EVs | Solution Distance [km] | Used EVs |
|---|---|---|---|---|
| 1 | 3358 | 2 | 304 | 2 |
| 2 | 7109 | 5 | 303 | 5 |
| 3 | 10,271 | 7 | 357 | 7 |
| 4 | 14990 | 9 | 454 | 10 |
| 5 | 19,992 | 12 | 542 | 13 |
| 6 | 22,814 | 14 | 611 | 15 |
| 7 | 37,251 | 22 | 891 | 28 |
| 8 | 14,475 | 9 | 428 | 9 |
| 9 | 15,155 | 9 | 432 | 10 |
| 10 | 15,589 | 10 | 446 | 10 |
| Method | Node Number | Result [km] | Time [s] | Reference |
|---|---|---|---|---|
| MILP encoding + Tabu search | 20 | 247 | 5 | [23] |
| 30 | 422.56 | 5 | ||
| MILP encoding + CPLEX | 20 | 247 | 49 | [23] |
| 30 | 422.56 | 358 | ||
| Permutation encoding + Evolutionary optimisation | 20 | 247 | 4.8 | proposed method |
| 30 | 394.76 | 7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iwańkowicz, R. Effective Permutation Encoding for Evolutionary Optimization of the Electric Vehicle Routing Problem. Energies 2021, 14, 6651. https://doi.org/10.3390/en14206651
Iwańkowicz R. Effective Permutation Encoding for Evolutionary Optimization of the Electric Vehicle Routing Problem. Energies. 2021; 14(20):6651. https://doi.org/10.3390/en14206651
Chicago/Turabian StyleIwańkowicz, Remigiusz. 2021. "Effective Permutation Encoding for Evolutionary Optimization of the Electric Vehicle Routing Problem" Energies 14, no. 20: 6651. https://doi.org/10.3390/en14206651
APA StyleIwańkowicz, R. (2021). Effective Permutation Encoding for Evolutionary Optimization of the Electric Vehicle Routing Problem. Energies, 14(20), 6651. https://doi.org/10.3390/en14206651






