Definition of Residential Power Load Profiles Clusters Using Machine Learning and Spatial Analysis
Abstract
:1. Introduction
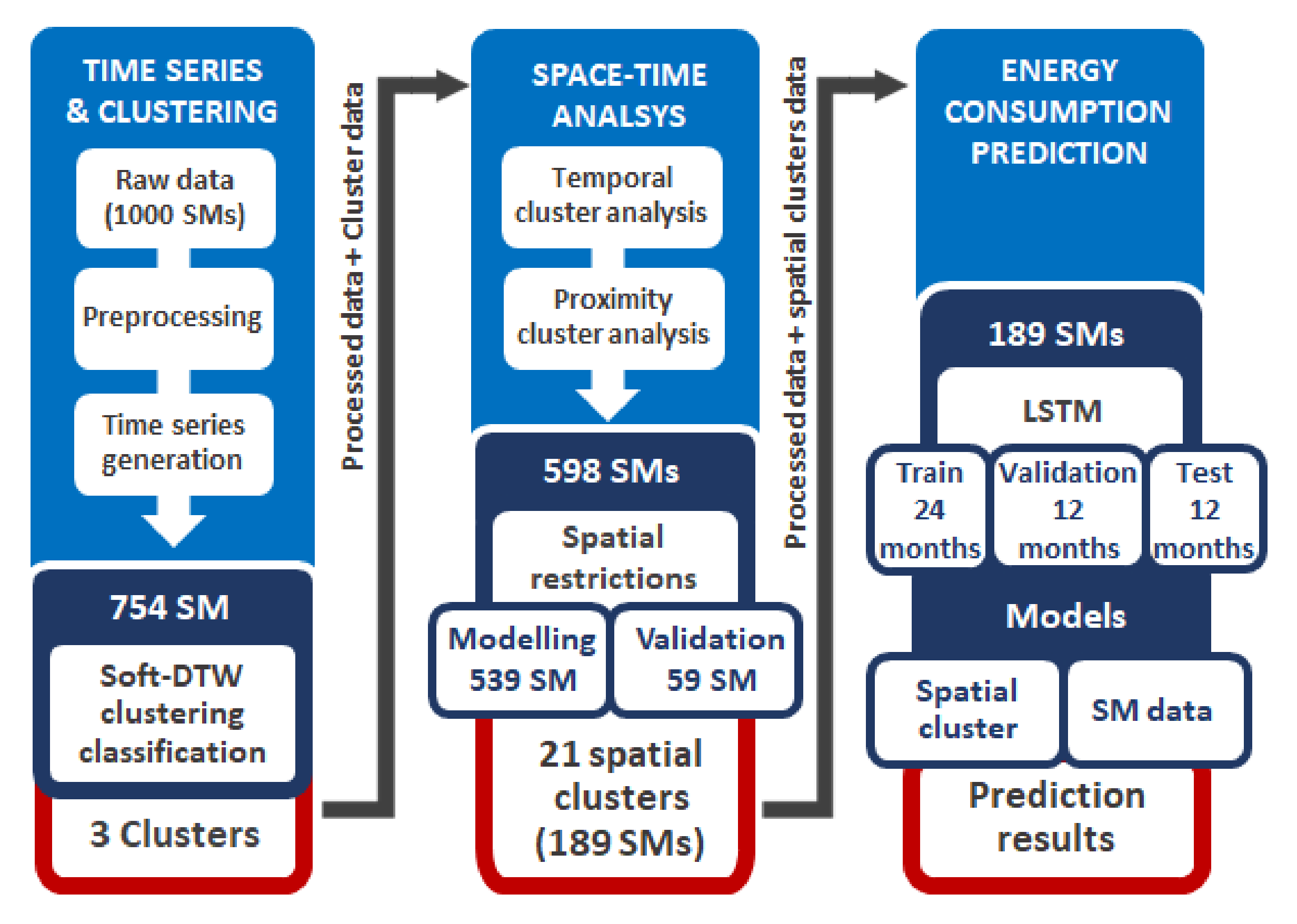
2. Materials and Methods
- Data collection, pre-processing and time series generation,
- Clustering time series generation,
- Spatial-temporal analysis, and
- Applications for energy consumption forecasting.
2.1. Data Pre-Processing and Time Series Generation
- Geographic position of the SMs,
- Timestamp with the date and time of measurement,
- Customer code to identify the client (anonymised data), and
- Active power (kW).
2.2. Time Series Clustering
2.3. Spatial-Temporal Analysis
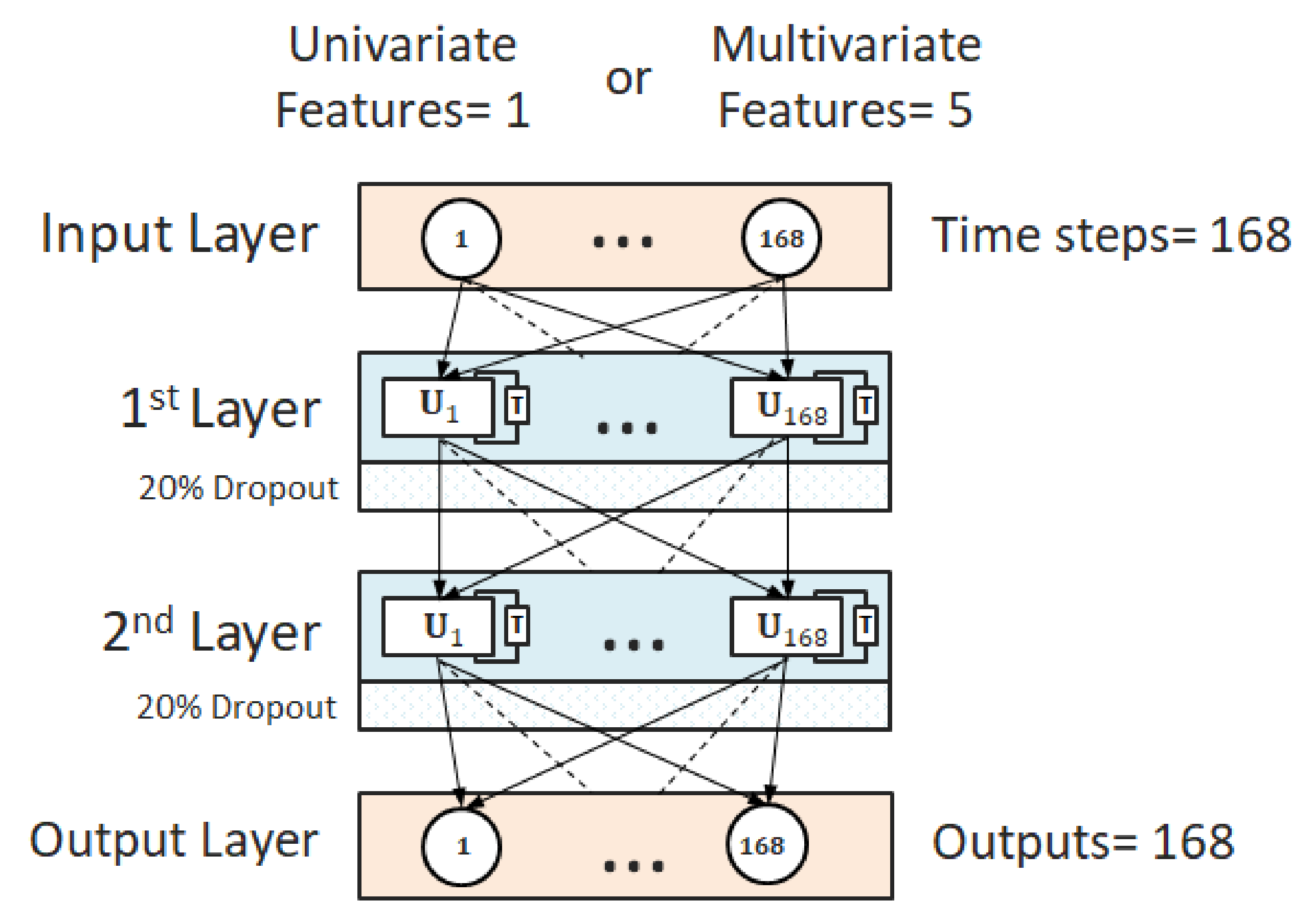
2.4. Forecasting of Energy Consumption
3. Results
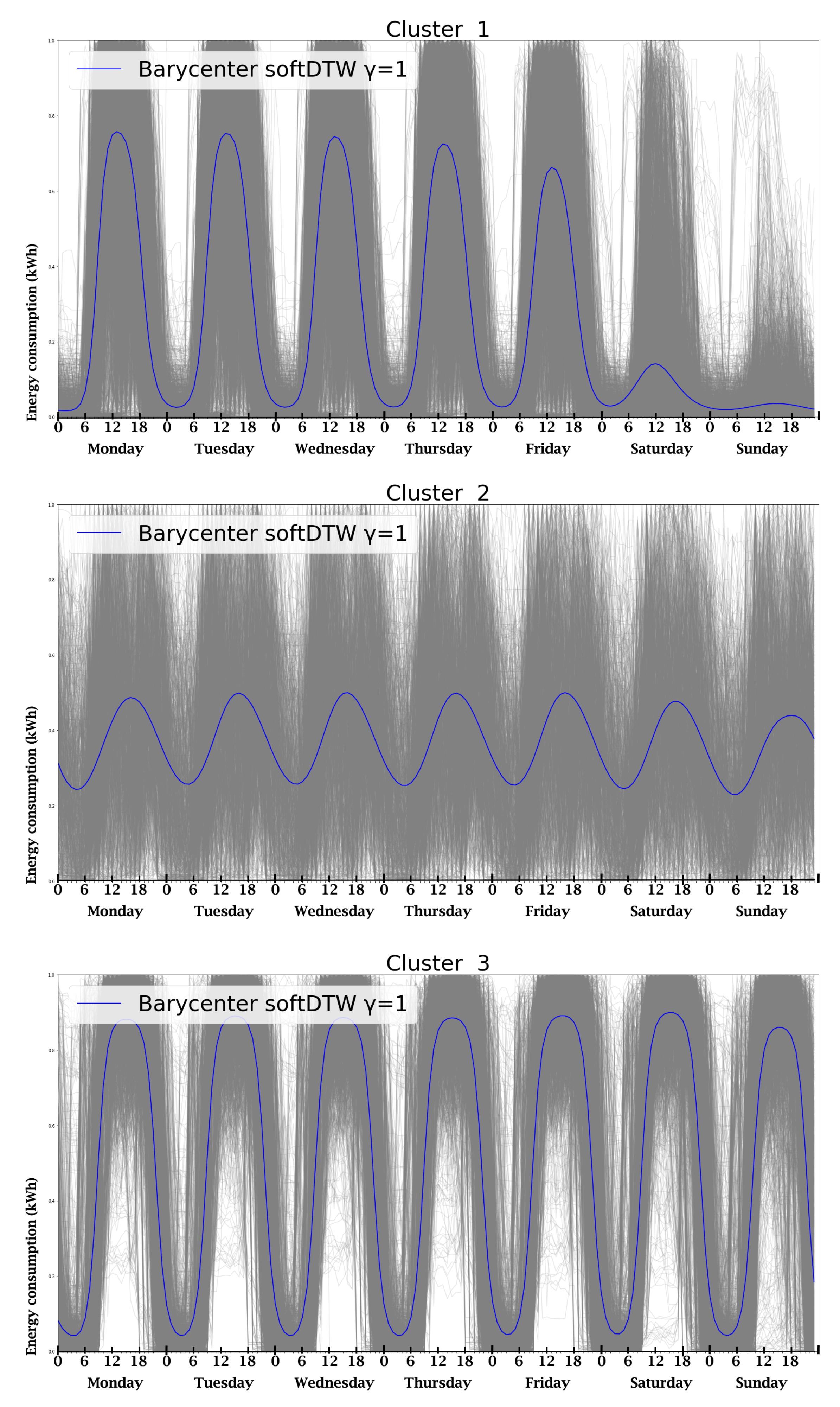
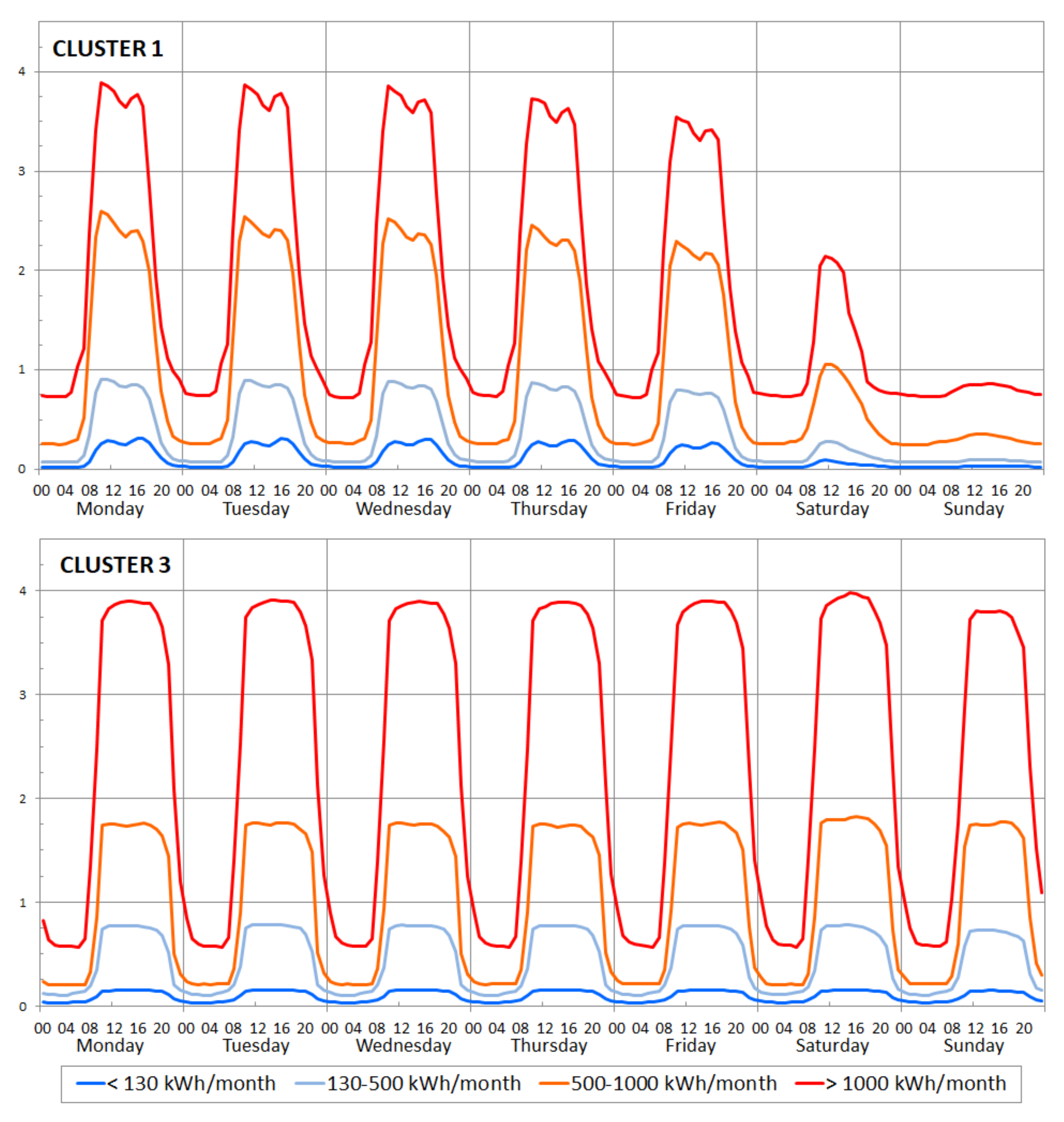
3.1. Time Series Clustering
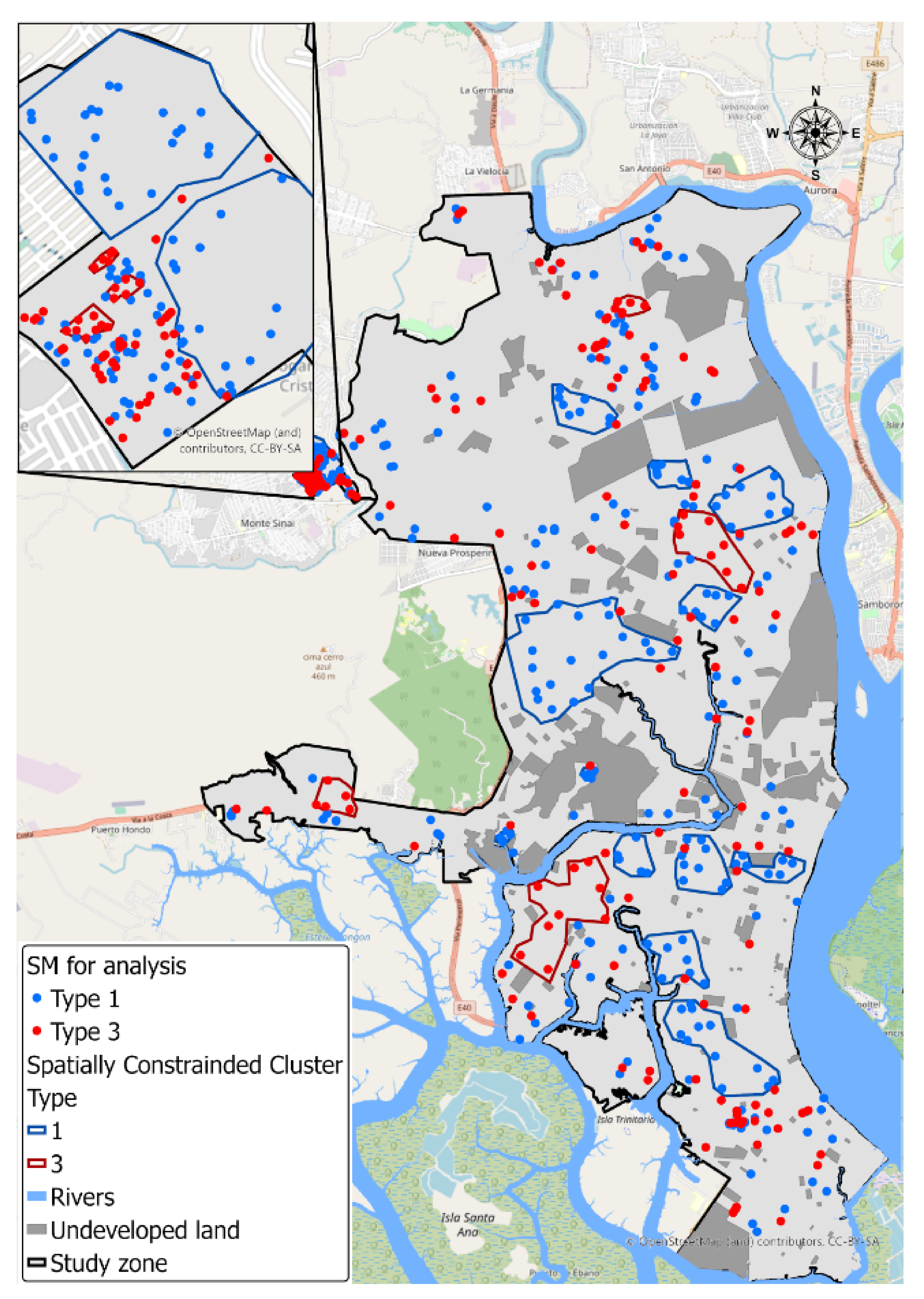
3.2. Spatial and Temporal Analysis
3.3. Forecasting of Energy Consumption
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AMI | Advanced metering infrastructure |
| ANN | Artificial neural networks |
| DTW | Dynamic time warping |
| GIS | Geographic Information System |
| LSTM | Long short-term memory |
| RMSE | Root mean squared error |
| RNN | Recurrent neural network |
| SM | Smart meter |
| sMAPE | Symmetric mean absolute percentage error |
References
- Hsiao, Y.H. Household electricity demand forecast based on context information and user daily schedule analysis from meter data. IEEE Trans. Ind. Inform. 2014, 11, 33–43. [Google Scholar] [CrossRef]
- Zhou, K.; Yang, C.; Shen, J. Discovering residential electricity consumption patterns through smart-meter data mining: A case study from China. Util. Policy 2017, 44, 73–84. [Google Scholar] [CrossRef]
- Lavin, A.; Klabjan, D. Clustering time-series energy data from smart meters. Energy Effic. 2015, 8, 681–689. [Google Scholar] [CrossRef] [Green Version]
- Gouveia, J.P.; Seixas, J. Unraveling electricity consumption profiles in households through clusters: Combining smart meters and door-to-door surveys. Energy Build. 2016, 116, 666–676. [Google Scholar] [CrossRef]
- Viegas, J.L.; Vieira, S.M.; Melício, R.; Mendes, V.; Sousa, J.M. Classification of new electricity customers based on surveys and smart metering data. Energy 2016, 107, 804–817. [Google Scholar] [CrossRef]
- Kwac, J.; Flora, J.; Rajagopal, R. Household energy consumption segmentation using hourly data. IEEE Trans. Smart Grid 2014, 5, 420–430. [Google Scholar] [CrossRef]
- Abreu, J.M.; Pereira, F.C.; Ferrão, P. Using pattern recognition to identify habitual behavior in residential electricity consumption. Energy Build. 2012, 49, 479–487. [Google Scholar] [CrossRef]
- Tascikaraoglu, A.; Sanandaji, B.M. Short-term residential electric load forecasting: A compressive spatio-temporal approach. Energy Build. 2016, 111, 380–392. [Google Scholar] [CrossRef]
- Xu, J.; Yue, M.; Katramatos, D.; Yoo, S. Spatial-temporal load forecasting using AMI data. In Proceedings of the 2016 IEEE International Conference on Smart Grid Communications (SmartGridComm), Sydney, NSW, Australia, 6–9 November 2016; pp. 612–618. [Google Scholar]
- Melo, J.D.; Carreno, E.M.; Padilha-Feltrin, A. Multi-agent simulation of urban social dynamics for spatial load forecasting. IEEE Trans. Power Syst. 2012, 27, 1870–1878. [Google Scholar] [CrossRef]
- Zhang, L.; Feng, J.; Jian, X. Model of energy alternative in spatial load forecasting. In Proceedings of the 2016 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Xi’an, China, 25–28 October 2016; pp. 2106–2110. [Google Scholar]
- Melo, J.; Padilha-Feltrin, A.; Carreno, E. Spatial pattern recognition of urban sprawl using a geographically weighted regression for spatial electric load forecasting. In Proceedings of the 2015 18th International Conference on Intelligent System Application to Power Systems (ISAP), Porto, Portugal, 11–16 September 2015; pp. 1–5. [Google Scholar]
- Wijaya, T.K.; Vasirani, M.; Humeau, S.; Aberer, K. Cluster-based aggregate forecasting for residential electricity demand using smart meter data. In Proceedings of the 2015 IEEE International Conference on Big Data (Big Data), Santa Clara, CA, USA, 29 October–1 November 2015; pp. 879–887. [Google Scholar]
- Sevlian, R.; Rajagopal, R. Short term electricity load forecasting on varying levels of aggregation. arXiv 2014, arXiv:1404.0058. [Google Scholar]
- Shahzadeh, A.; Khosravi, A.; Nahavandi, S. Improving load forecast accuracy by clustering consumers using smart meter data. In Proceedings of the 2015 International Joint Conference on Neural Networks (IJCNN), Killarney, Ireland, 12–17 July 2015; pp. 1–7. [Google Scholar]
- Ilic, D.; Karnouskos, S.; Da Silva, P.G. Improving load forecast in prosumer clusters by varying energy storage size. In Proceedings of the IEEE Grenoble PowerTech, Grenoble, France, 16–20 June 2013. [Google Scholar]
- Biswas, M.R.; Robinson, M.D.; Fumo, N. Prediction of residential building energy consumption: A neural network approach. Energy 2016, 117, 84–92. [Google Scholar] [CrossRef]
- Marino, D.L.; Amarasinghe, K.; Manic, M. Building energy load forecasting using deep neural networks. In Proceedings of the IECON 2016-42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; pp. 7046–7051. [Google Scholar]
- Mocanu, E.; Nguyen, P.H.; Gibescu, M.; Kling, W.L. Deep learning for estimating building energy consumption. Sustain. Energy Grids Netw. 2016, 6, 91–99. [Google Scholar] [CrossRef]
- Ryu, S.; Noh, J.; Kim, H. Deep neural network based demand side short term load forecasting. Energies 2017, 10, 3. [Google Scholar] [CrossRef]
- Cuturi, M.; Blondel, M. Soft-DTW: A differentiable loss function for time-series. arXiv 2017, arXiv:1703.01541. [Google Scholar]
- Cano, E.L.; Groissböck, M.; Moguerza, J.M.; Stadler, M. A strategic optimization model for energy systems planning. Energy Build. 2014, 81, 416–423. [Google Scholar] [CrossRef]
- Esther, B.P.; Kumar, K.S. A survey on residential demand side management architecture, approaches, optimization models and methods. Renew. Sustain. Energy Rev. 2016, 59, 342–351. [Google Scholar] [CrossRef]
- Mahmoudi-Kohan, N.; Moghaddam, M.P.; Sheikh-El-Eslami, M. An annual framework for clustering-based pricing for an electricity retailer. Electr. Power Syst. Res. 2010, 80, 1042–1048. [Google Scholar] [CrossRef]
- Rhodes, J.D.; Cole, W.J.; Upshaw, C.R.; Edgar, T.F.; Webber, M.E. Clustering analysis of residential electricity demand profiles. Appl. Energy 2014, 135, 461–471. [Google Scholar] [CrossRef] [Green Version]
- Beaudin, M.; Zareipour, H. Home energy management systems: A review of modelling and complexity. Renew. Sustain. Energy Rev. 2015, 45, 318–335. [Google Scholar] [CrossRef]
- Subramanian, A.S.R.; Gundersen, T.; Adams, T.A. Modeling and simulation of energy systems: A review. Processes 2018, 6, 238. [Google Scholar] [CrossRef] [Green Version]
- Lilla, S.; Orozco, C.; Borgethhi, A.; Napolitano, F.; Tossani, F. Day-ahead scheduling of a local energy community: An alternating direction method of multipliers approach. IEEE Trans. Power Syst. 2020, 35, 1132–1142. [Google Scholar] [CrossRef]
- E-LAND Horizon H2020. Available online: https://elandh2020.eu (accessed on 1 October 2021).
- Chicco, G. Overview and performance assessment of the clustering methods for electrical load pattern grouping. Energy 2012, 42, 68–80. [Google Scholar] [CrossRef]
- Hino, H.; Shen, H.; Murata, N.; Wakao, S.; Hayashi, Y. A versatile clustering method for electricity consumption pattern analysis in households. IEEE Trans. Smart Grid 2013, 4, 1048–1057. [Google Scholar] [CrossRef]
- Paparrizos, J.; Gravano, L. k-shape: Efficient and accurate clustering of time series. In Proceedings of the 2015 ACM SIGMOD International Conference on Management of Data, Melbourne, VIC, Australia, 31 May–4 June 2015; pp. 1855–1870. [Google Scholar]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef] [Green Version]
- Assunção, R.M.; Neves, M.C.; Câmara, G.; da Costa Freitas, C. Efficient regionalization techniques for socio-economic geographical units using minimum spanning trees. Int. J. Geogr. Inf. Sci. 2006, 20, 797–811. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Medsker, L.R.; Jain, L. Recurrent neural networks. Des. Appl. 2001, 5, 64–67. [Google Scholar]
- Hochreiter, S.; Bengio, Y.; Frasconi, P.; Schmidhuber, J. Gradient Flow in Recurrent Nets: The Difficulty of Learning Long-Term Dependencies. In A Field Guide to Dynamical Recurrent Networks; Kolen, J.F., Kremer, S.C., Eds.; IEEE Press: New York, NY, USA, 2001; pp. 237–244. [Google Scholar]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef]
- Chen, Z.; Yang, Y. Assessing Forecast Accuracy Measures. 2004. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.69.1016&rep=rep1&type=pdf (accessed on 1 October 2021).
- Tavenard, R.; Faouzi, J.; Vandewiele, G.; Divo, F.; Androz, G.; Holtz, C.; Payne, M.; Yurchak, R.; Rußwurm, M.; Kolar, K.; et al. Tslearn, A Machine Learning Toolkit for Time Series Data. J. Mach. Learn. Res. 2020, 21, 1–6. [Google Scholar]
- Average Weather in Guayaquil. 2018. Available online: weatherspark.com (accessed on 1 July 2021).

| Cluster Method | k | Silhouette Index |
|---|---|---|
| Soft-DTW () | 3 | 0.5775 |
| Soft-DTW () | 3 | 0.5297 |
| Soft-DTW () | 4 | 0.5280 |
| DTW | 3 | 0.5234 |
| K-Shape | 3 | 0.5213 |
| Soft-DTW () | 4 | 0.5187 |
| Euclidean | 3 | 0.5132 |
| K-Shape | 5 | 0.5119 |
| Soft-DTW () | 3 | 0.5083 |
| K-Shape | 4 | 0.4907 |
| Soft-DTW () | 5 | 0.4479 |
| DTW | 4 | 0.4235 |
| Soft-DTW () | 5 | 0.3714 |
| Soft-DTW () | 5 | 0.3675 |
| Soft-DTW () | 4 | 0.3617 |
| Euclidean | 4 | 0.3341 |
| Euclidean | 5 | 0.3023 |
| DTW | 5 | 0.2755 |
| Months with Complete Information per Year (2014–2017) | Behaviour Type | SMs | SMs (%) |
|---|---|---|---|
| 12 months | constant | 594 | 78.78 |
| 10–11 months | constant | 82 | 10.88 |
| 10–12 months | variable | 78 | 10.34 |
| Total | 754 | 100.00 |
| Cluster | SMs | >1 km | <1 km |
|---|---|---|---|
| Type 1 | 370 | 2 | 368 |
| Type 2 | 74 | 16 | 58 |
| Type 3 | 232 | 2 | 230 |
| Total | 676 | 20 | 656 |
| Cluster | RMSE | sMAPE | SMs | SMs |
|---|---|---|---|---|
| Type 1 | 0.5541 | 45.78 | 368 | 56.10% |
| Type 2 | 1.5594 | 63.25 | 58 | 8.84% |
| Type 3 | 0.6078 | 40.82 | 230 | 35.06% |
| Total: | 656 | 100.00% |
| Behaviour Type | SMs | Assigned SMs in Spatial Cluster | Number of Spatial Clusters |
|---|---|---|---|
| Type 1 | 332 | 143 | 14 |
| Type 3 | 207 | 46 | 7 |
| Total | 539 | 189 | 21 |
| Metric | Total (%) |
|---|---|
| Specificity | 90.32 |
| Precision | 86.96 |
| Recall | 95.24 |
| F-Score | 90.91 |
| Type | Univariate (%) | Multivariate (%) | Increment (%) |
|---|---|---|---|
| Type 1 | 19.72 | 16.84 | 2.88 |
| Type 3 | 14.70 | 12.65 | 2.05 |
| Total | 17.21 | 14.75 | 2.46 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Flor, M.; Herraiz, S.; Contreras, I. Definition of Residential Power Load Profiles Clusters Using Machine Learning and Spatial Analysis. Energies 2021, 14, 6565. https://doi.org/10.3390/en14206565
Flor M, Herraiz S, Contreras I. Definition of Residential Power Load Profiles Clusters Using Machine Learning and Spatial Analysis. Energies. 2021; 14(20):6565. https://doi.org/10.3390/en14206565
Chicago/Turabian StyleFlor, Mario, Sergio Herraiz, and Ivan Contreras. 2021. "Definition of Residential Power Load Profiles Clusters Using Machine Learning and Spatial Analysis" Energies 14, no. 20: 6565. https://doi.org/10.3390/en14206565
APA StyleFlor, M., Herraiz, S., & Contreras, I. (2021). Definition of Residential Power Load Profiles Clusters Using Machine Learning and Spatial Analysis. Energies, 14(20), 6565. https://doi.org/10.3390/en14206565







