The Multi-Advective Water Mixing Approach for Transport through Heterogeneous Media
Abstract
:1. Introduction
2. Governing Equations
3. Solution Method
3.1. Water Parcel Method
3.2. Random Walk Method
3.3. Algebra of Mixing Matrices
4. Applications
4.1. Transition Matrix Validation with Markovian Models
4.2. Comparison between RW and WP in Transport through Heterogeneous Porous Media
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Solute concentration | |
| Porosity | |
| Velocity | |
| Time | |
| Exchanged water diffusion flux associated to the water molecular diffusion coefficient (see [15]) | |
| Advective correlation length | |
| Probability density of a velocity transition after covering a step in space | |
| Probability density per unit time of diffusive transitions between velocity states | |
| Water volume of a parcel | |
| Water volumetric flux diffused | |
| Time step | |
| Water mixing ratio (see [15]) | |
| Transition matrix that expresses the probability of the solute to transit between velocity classes in a space step considering both advection and diffusion | |
| considering only advection | |
| Transition matrix that expresses the probability of the solute to transit between velocity classes in a time step considering only diffusion | |
| Solute probability | |
| Total mass in domain | |
| Storage matrix | |
| Probability transition matrix. It may have dimension of space (numerical targets) or velocity (classes) | |
| Concentration transition matrix. It may have dimension of space or velocity | |
| Volumetric water exchanged matrix. It may have dimension of space or velocity | |
| Water transition matrix | |
| Peclet number | |
| Water molecular diffusion coefficient | |
| Initial concentration reference | |
| Mean spatial position | |
| Standard deviation of spatial solute distribution | |
| G | Global mixing in space domain |
| G′ | Global mixing in velocity domain |
References
- Gjetvaj, F.; Russian, A.; Gouze, P.; Dentz, M. Dual control of flow field heterogeneity and immobile porosity on non-Fickian transport in Berea sandstone. Water Resour. Res. 2015, 51, 8273–8293. [Google Scholar] [CrossRef] [Green Version]
- Le Borgne, T.; Gouze, P. Non-Fickian dispersion in porous media: 2. Model validation from measurements at different scales. Water Resour. Res. 2008, 44, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Willmann, M.; Carrera, J.; Sánchez-Vila, X. Transport upscaling in heterogeneous aquifers: What physical parameters control memory functions? Water Resour. Res. 2008, 44, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Gelhar, L.W.; Mantoglou, A.; Welty, C.; Rehfeldt, K.R. A Review of Field-Scale Physical Solute Transport Processes in Saturated and Unsaturated Porous Media. EPRI Report EA-4190. 1985. Available online: https://books.google.ro/books?id=iS33BwAAQBAJ&pg=PA296&lpg=PA296&dq=4.+Gelhar,+L.W.;+Mantoglou,+A.;+Welty,+C.;+Rehfeldt,+K.R.+A+Review+of+Field-Scale+Physical+Solute+Transport+Processes+in+Saturated+and+Unsaturated+Porous+Media;+EPRI+Report+EA-4190;+1985.&source=bl&ots=eQFqb2KYx6&sig=ACfU3U3Wm3zSPmLxECV8U0Q8szdKsqEppQ&hl=en&sa=X&ved=2ahUKEwim_b_S7sTzAhX2_7sIHUgkB-QQ6AF6BAgCEAM#v=onepage&q=4.%20Gelhar%2C%20L.W.%3B%20Mantoglou%2C%20A.%3B%20Welty%2C%20C.%3B%20Rehfeldt%2C%20K.R.%20A%20Review%20of%20Field-Scale%20Physical%20Solute%20Transport%20Processes%20in%20Saturated%20and%20Unsaturated%20Porous%20Media%3B%20EPRI%20Report%20EA-4190%3B%201985.&f=false (accessed on 15 September 2021).
- Neuman, S.P. Universal scaling of hydraulic conductivities and dispersivities in geologic media. Water Resour. Res. 1990, 26, 1749–1758. [Google Scholar] [CrossRef]
- Vogel, H.-J.; Cousin, I.; Ippisch, O.; Bastian, P. The dominant role of structure for solute transport in soil: Experimental evidence and modelling of structure and transport in a field experiment. Hydrol. Earth Syst. Sci. 2006, 10, 495–506. [Google Scholar] [CrossRef] [Green Version]
- Alcolea, A.; Carrera, J.; Medina, A. Regularized pilot points method for reproducing the effect of small scale variability: Application to simulations of contaminant transport. J. Hydrol. 2008, 355, 76–90. [Google Scholar] [CrossRef]
- Valocchi, A.J. Validity of the Local Equilibrium Assumption for Modeling Sorbing Solute Transport Through Homogeneous Soils. Water Resour. Res. 1985, 21, 808–820. [Google Scholar] [CrossRef]
- Carrera, J. An overview of uncertainties in modelling groundwater solute transport. J. Contam. Hydrol. 1993, 13, 23–48. [Google Scholar] [CrossRef]
- Soler-Sagarra, J.; Luquot, L.; Martínez-Pérez, L.; Saaltink, M.W.; De Gaspari, F.; Carrera, J. Simulation of chemical reaction localization using a multi-porosity reactive transport approach. Int. J. Greenh. Gas Control. 2016, 48, 59–68. [Google Scholar] [CrossRef]
- Battiato, I.; Tartakovsky, D.; Scheibe, T. On breakdown of macroscopic models of mixing-controlled heterogeneous reactions in porous media. Adv. Water Resour. 2009, 32, 1664–1673. [Google Scholar] [CrossRef]
- Sadhukhan, S.; Gouze, P.; Dutta, T. A simulation study of reactive flow in 2-D involving dissolution and precipitation in sedimentary rocks. J. Hydrol. 2014, 519, 2101–2110. [Google Scholar] [CrossRef]
- Scheibe, T.D.; Schuchardt, K.; Agarwal, K.; Chase, J.; Yang, X.; Palmer, B.J.; Tartakovsky, A.M.; Elsethagen, T.; Redden, G. Hybrid multiscale simulation of a mixing-controlled reaction. Adv. Water Resour. 2015, 83, 228–239. [Google Scholar] [CrossRef] [Green Version]
- Tartakovsky, A.; Tartakovsky, G.; Scheibe, T. Effects of incomplete mixing on multicomponent reactive transport. Adv. Water Resour. 2009, 32, 1674–1679. [Google Scholar] [CrossRef]
- Soler-Sagarra, J.; Saaltink, M.W.; Nardi, A.; De Gaspari, J.; Carrera, J. Water Mixing Approach (WMA) for Reactive Transport Modeling. 2021. submitted. Available online: http://blogs.uned.es/catedra-aquae/wp-content/uploads/sites/111/2021/06/Tesis-Joaquim-Soler.pdf (accessed on 15 September 2021).
- Seymour, J.D.; Gage, J.P.; Codd, S.L.; Gerlach, R. Anomalous Fluid Transport in Porous Media Induced by Biofilm Growth. Phys. Rev. Lett. 2004, 93, 198103. [Google Scholar] [CrossRef] [PubMed]
- Bijeljic, B.; Mostaghimi, P.; Blunt, M. Signature of Non-Fickian Solute Transport in Complex Heterogeneous Porous Media. Phys. Rev. Lett. 2011, 107, 204502. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kang, P.K.; de Anna, P.; Nunes, J.P.; Bijeljic, B.; Blunt, M.J.; Juanes, R. Pore-scale intermittent velocity structure underpinning anomalous transport through 3-D porous media. Geophys. Res. Lett. 2014, 41, 6184–6190. [Google Scholar] [CrossRef]
- Hatano, Y.; Hatano, N. Dispersive transport of ions in column experiments: An explanation of long-tailed profiles. Water Resour. Res. 1998, 34, 1027–1033. [Google Scholar] [CrossRef]
- Rinaldo, A.; Benettin, P.; Harman, C.J.; Hrachowitz, M.; McGuire, K.J.; van der Velde, Y.; Bertuzzo, E.; Botter, G. Solute transport in low-heterogeneity sandboxes: The role of correlation length and permeability variance. Water Resour. Res. 2015, 51, 4840–4847. [Google Scholar] [CrossRef] [Green Version]
- Garabedian, S.P.; LeBlanc, D.R. Large-Scale natural gradient tracer test in sand and gravel, Cape Cod, Massachusetts 2. Analysis of spatial moments for a nonreactive tracer. Water Resour. Res. 1991, 27, 911–924. [Google Scholar] [CrossRef]
- Becker, M.W.; Shapiro, A. Tracer transport in fractured crystalline rock: Evidence of nondiffusive breakthrough tailing. Water Resour. Res. 2000, 36, 1677–1686. [Google Scholar] [CrossRef] [Green Version]
- McKenna, S.A.; Meigs, L.C.; Haggerty, R. Tracer tests in a fractured dolomite: 3. Double-porosity, multiple-rate mass transfer processes in convergent flow tracer tests. Water Resour. Res. 2001, 37, 1143–1154. [Google Scholar] [CrossRef] [Green Version]
- Kang, P.K.; Le Borgne, T.; Dentz, M.; Bour, O.; Juanes, R. Impact of velocity correlation and distribution on transport in fractured media: Field evidence and theoretical model. Water Resour. Res. 2014, 51, 940–959. [Google Scholar] [CrossRef] [Green Version]
- Zech, A.; Attinger, S.; Cvetkovic, V.; Dagan, G.; Dietrich, P.; Fiori, A.; Rubin, Y.; Teutsch, G. Is unique scaling of aquifer macrodispersivity supported by field data? Water Resour. Res. 2015, 51, 7662–7679. [Google Scholar] [CrossRef] [Green Version]
- De Dreuzy, J.-R.; Carrera, J.; Dentz, M.; Le Borgne, T. Time evolution of mixing in heterogeneous porous media. Water Resour. Res. 2012, 48, W06511. [Google Scholar] [CrossRef] [Green Version]
- De Dreuzy, J.-R.; Carrera, J. On the validity of effective formulations for transport through heterogeneous porous media. Hydrol. Earth Syst. Sci. 2016, 20, 1319–1330. [Google Scholar] [CrossRef] [Green Version]
- Montroll, E.W.; Weiss, G.H. Random Walks on Lattices. II. J. Math. Phys. 1965, 6, 167–181. [Google Scholar] [CrossRef]
- Scher, H.; Lax, M. Stochastic Transport in a Disordered Solid. I. Theory. Phys. Rev. B 1973, 7, 4491–4502. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Berkowitz, B.; Cortis, A.; Dentz, M.; Scher, H. Modeling non-Fickian transport in geological formations as a continuous time random walk. Rev. Geophys. 2006, 44, 1–49. [Google Scholar] [CrossRef] [Green Version]
- Neuman, S.P.; Tartakovsky, D.M. Perspective on theories of non-Fickian transport in heterogeneous media. Adv. Water Resour. 2009, 32, 670–680. [Google Scholar] [CrossRef]
- Scher, H.; Montroll, E.W. Anomalous transit-time dispersion in amorphous solids. Phys. Rev. B 1975, 12, 2455–2477. [Google Scholar] [CrossRef]
- Klafter, J.; Silbey, R. Derivation of the Continuous-Time Random-Walk Equation. Phys. Rev. Lett. 1980, 44, 55–58. [Google Scholar] [CrossRef] [Green Version]
- Le Borgne, T.; Dentz, M.; Carrera, J. Spatial Markov processes for modeling Lagrangian particle dynamics in heterogeneous porous media. Phys. Rev. E 2008, 78, 026308. [Google Scholar] [CrossRef] [PubMed]
- Le Borgne, T.; Dentz, M.; Carrera, J. Lagrangian Statistical Model for Transport in Highly Heterogeneous Velocity Fields. Phys. Rev. Lett. 2008, 101, 090601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kang, P.; Dentz, M.; Le Borgne, T.; Juanes, R. Spatial Markov Model of Anomalous Transport Through Random Lattice Networks. Phys. Rev. Lett. 2011, 107, 180602. [Google Scholar] [CrossRef] [Green Version]
- Benke, R.; Painter, S. Modeling conservative tracer transport in fracture networks with a hybrid approach based on the Boltzmann transport equation. Water Resour. Res. 2003, 39, 1–11. [Google Scholar] [CrossRef]
- De Anna, P.; Le Borgne, T.; Dentz, M.; Tartakovsky, A.M.; Bolster, D.; Davy, P. Flow Intermittency, Dispersion, and Correlated Continuous Time Random Walks in Porous Media. Phys. Rev. Lett. 2013, 110, 184502. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kang, P.; Dentz, M.; Le Borgne, T.; Juanes, R. Anomalous transport on regular fracture networks: Impact of conductivity heterogeneity and mixing at fracture intersections. Phys. Rev. E 2015, 92, 022148. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kang, P.; Dentz, M.; Le Borgne, T.; Lee, S.; Juanes, R. Anomalous transport in disordered fracture networks: Spatial Markov model for dispersion with variable injection modes. Adv. Water Resour. 2017, 106, 80–94. [Google Scholar] [CrossRef] [Green Version]
- Cirpka, O.A.; Valocchi, A.J. Reply to comments on “Two-dimensional concentration distribution for mixing-controlled bioreactive transport in steady state” by H. Shao et al. Adv. Water Resour. 2009, 32, 298–301. [Google Scholar] [CrossRef]
- Rezaei, M.; Sanz, E.; Raeisi, E.; Ayora, C.; Vázquez-Suñé, E.; Carrera, J. Reactive transport modeling of calcite dissolution in the fresh-salt water mixing zone. J. Hydrol. 2005, 311, 282–298. [Google Scholar] [CrossRef]
- De Simoni, M.; Carrera, J.; Sanchez-Vila, X.; Guadagnini, A. A procedure for the solution of multicomponent reactive transport problems. Water Resour. Res. 2005, 41, 1–16. [Google Scholar] [CrossRef]
- De Simoni, M.; Sanchez-Vila, X.; Carrera, J.; Saaltink, M.W. A mixing ratios-based formulation for multicomponent reactive transport. Water Resour. Res. 2007, 43, 1–10. [Google Scholar] [CrossRef]
- Tartakovsky, A.M.; Redden, G.; Lichtner, P.C.; Scheibe, T.; Meakin, P. Mixing-induced precipitation: Experimental study and multiscale numerical analysis. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Fick, A. On liquid diffusion. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1855, 10, 30–39. [Google Scholar] [CrossRef]
- Einstein, A. Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. Ann. der Phys. 1905, 322, 549–560. [Google Scholar] [CrossRef] [Green Version]
- Soler-Sagarra, J. Mathematical Formulations of Water Mixing for Reactive Transport through Heterogeneous Media. Ph.D. Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2020. [Google Scholar]
- Kitanidis, P.K. Prediction by the method of moments of transport in a heterogeneous formation. J. Hydrol. 1988, 102, 453–473. [Google Scholar] [CrossRef]
- Kitanidis, P.K. The concept of the Dilution Index. Water Resour. Res. 1994, 30, 2011–2026. [Google Scholar] [CrossRef]
- Chiogna, G.; Cirpka, O.A.; Grathwohl, P.; Rolle, M. Transverse mixing of conservative and reactive tracers in porous media: Quantification through the concepts of flux-related and critical dilution indices. Water Resour. Res. 2011, 47, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Le Borgne, T.; Dentz, M.; Bolster, D.; Carrera, J.; de Dreuzy, J.-R.; Davy, P. Non-Fickian mixing: Temporal evolution of the scalar dissipation rate in heterogeneous porous media. Adv. Water Resour. 2010, 33, 1468–1475. [Google Scholar] [CrossRef]
- Rolle, M.; Eberhardt, C.; Chiogna, G.; Cirpka, O.A.; Grathwohl, P. Enhancement of dilution and transverse reactive mixing in porous media: Experiments and model-based interpretation. J. Contam. Hydrol. 2009, 110, 130–142. [Google Scholar] [CrossRef]
- Tartakovsky, A.M.; Tartakovsky, D.M.; Meakin, P. Stochastic Langevin Model for Flow and Transport in Porous Media. Phys. Rev. Lett. 2008, 101, 044502. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De Anna, P.; Jimenez-Martinez, J.; Tabuteau, H.; Turuban, R.; Le Borgne, T.; Derrien, M.; Méheust, Y. Mixing and Reaction Kinetics in Porous Media: An Experimental Pore Scale Quantification. Environ. Sci. Technol. 2014, 48, 508–516. [Google Scholar] [CrossRef] [PubMed]
- Jiménez-Martínez, J.; de Anna, P.; Tabuteau, H.; Turuban, R.; Le Borgne, T.; Méheust, Y. Pore-scale mechanisms for the enhancement of mixing in unsaturated porous media and implications for chemical reactions. Geophys. Res. Lett. 2015, 42, 5316–5324. [Google Scholar] [CrossRef] [Green Version]
- Le Borgne, T.; Dentz, M.; Villermaux, E. The lamellar description of mixing in porous media. J. Fluid Mech. 2015, 770, 458–498. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Benson, D.; Reeves, D.M. Time and space nonlocalities underlying fractional-derivative models: Distinction and literature review of field applications. Adv. Water Resour. 2009, 32, 561–581. [Google Scholar] [CrossRef]
- Frippiat, C.C.; Holeyman, A.E. A comparative review of upscaling methods for solute transport in heterogeneous porous media. J. Hydrol. 2008, 362, 150–176. [Google Scholar] [CrossRef]
- Berkowitz, B.; Scher, H. Anomalous Transport in Random Fracture Networks. Phys. Rev. Lett. 1997, 79, 4038–4041. [Google Scholar] [CrossRef]
- Dentz, M.; Cortis, A.; Scher, H.; Berkowitz, B. Time behavior of solute transport in heterogeneous media: Transition from anomalous to normal transport. Adv. Water Resour. 2004, 27, 155–173. [Google Scholar] [CrossRef]
- Geiger, S.; Cortis, A.; Birkholzer, J.T. Upscaling solute transport in naturally fractured porous media with the continuous time random walk method. Water Resour. Res. 2010, 46, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Selker, J.S.; Tyler, S.; van de Giesen, N. Comment on “Capabilities and limitations of tracing spatial temperature patterns by fiber-optic distributed temperature sensing” by Liliana Rose et al. Water Resour. Res. 2014, 50, 5372–5374. [Google Scholar] [CrossRef] [Green Version]
- Dentz, M.; Kang, P.; Le Borgne, T. Continuous time random walks for non-local radial solute transport. Adv. Water Resour. 2015, 82, 16–26. [Google Scholar] [CrossRef] [Green Version]
- Edery, Y.; Guadagnini, A.; Scher, H.; Berkowitz, B. Origins of anomalous transport in heterogeneous media: Structural and dynamic controls. Water Resour. Res. 2014, 50, 1490–1505. [Google Scholar] [CrossRef]
- Aquino, T.; Dentz, M. Chemical Continuous Time Random Walks. Phys. Rev. Lett. 2017, 119, 230601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cushman, J.H.; Ginn, T.R. Fractional advection-dispersion equation: A classical mass balance with convolution-Fickian Flux. Water Resour. Res. 2000, 36, 3763–3766. [Google Scholar] [CrossRef]
- Benson, D.; Wheatcraft, S.W.; Meerschaert, M.M. Application of a fractional advection-dispersion equation. Water Resour. Res. 2000, 36, 1403–1412. [Google Scholar] [CrossRef] [Green Version]
- Becker, M.W.; Shapiro, A. Interpreting tracer breakthrough tailing from different forced-gradient tracer experiment configurations in fractured bedrock. Water Resour. Res. 2003, 39, 1024. [Google Scholar] [CrossRef] [Green Version]
- Babey, T.; de Dreuzy, J.-R.; Casenave, C. Multi-Rate Mass Transfer (MRMT) models for general diffusive porosity structures. Adv. Water Resour. 2015, 76, 146–156. [Google Scholar] [CrossRef]
- Carrera, J.; Sanchez-Vila, X.; Benet, I.; Medina, A.; Galarza, G.; Guimerà, J. On matrix diffusion: Formulations, solution methods and qualitative effects. Hydrogeol. J. 1998, 6, 178–190. [Google Scholar] [CrossRef]
- de Dreuzy, J.-R.; Rapaport, A.; Babey, T.; Harmand, J. Influence of porosity structures on mixing-induced reactivity at chemical equilibrium in mobile/immobile Multi-Rate Mass Transfer (MRMT) and Multiple INteracting Continua (MINC) models. Water Resour. Res. 2013, 49, 8511–8530. [Google Scholar] [CrossRef] [Green Version]
- Haggerty, R.; Gorelick, S.M. Multiple-Rate Mass Transfer for Modeling Diffusion and Surface Reactions in Media with Pore-Scale Heterogeneity. Water Resour. Res. 1995, 31, 2383–2400. [Google Scholar] [CrossRef]
- Fernandez-Garcia, D.; Sanchez-Vila, X. Mathematical equivalence between time-dependent single-rate and multiratemass transfer models. Water Resour. Res. 2015, 51, 3166–3180. [Google Scholar] [CrossRef] [Green Version]
- Steefel, C.; DePaolo, D.; Lichtner, P. Reactive transport modeling: An essential tool and a new research approach for the Earth sciences. Earth Planet. Sci. Lett. 2005, 240, 539–558. [Google Scholar] [CrossRef]
- Benzi, R.; Succi, S.; Vergassola, M. The lattice Boltzmann equation: Theory and applications. Phys. Rep. 1992, 222, 145–197. [Google Scholar] [CrossRef]
- Chen, S.; Doolen, G.D. Lattice Boltzmann Method for fluids flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef] [Green Version]
- Kang, Q.; Lichtner, P.C.; Zhang, D. Lattice Boltzmann pore-scale model for multicomponent reactive transport in porous media. J. Geophys. Res. Space Phys. 2006, 111. [Google Scholar] [CrossRef]
- Acharya, R.C.; Valocchi, A.J.; Werth, C.; Willingham, T.W. Pore-scale simulation of dispersion and reaction along a transverse mixing zone in two-dimensional porous media. Water Resour. Res. 2007, 43, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Willingham, T.W.; Werth, C.J.; Valocchi, A.J. Evaluation of the Effects of Porous Media Structure on Mixing-Controlled Reactions Using Pore-Scale Modeling and Micromodel Experiments. Environ. Sci. Technol. 2008, 42, 3185–3193. [Google Scholar] [CrossRef] [PubMed]
- Tartakovsky, A.M.; Meakin, P.; Scheibe, T.D.; West, R.M.E. Simulations of reactive transport and precipitation with smoothed particle hydrodynamics. J. Comput. Phys. 2007, 222, 654–672. [Google Scholar] [CrossRef]
- Tartakovsky, A.M.; Trask, N.; Pan, K.; Jones, B.; Pan, W.; Williams, J.R. Smoothed particle hydrodynamics and its applications for multiphase flow and reactive transport in porous media. Comput. Geosci. 2016, 20, 807–834. [Google Scholar] [CrossRef] [Green Version]
- Liu, M.B.; Liu, G.R. Smoothed Particle Hydrodynamics (SPH): An Overview and Recent Developments. Arch. Comput. Methods Eng. 2010, 17, 25–76. [Google Scholar] [CrossRef] [Green Version]
- Meile, C.; Tuncay, K. Scale dependence of reaction rates in porous media. Adv. Water Resour. 2006, 29, 62–71. [Google Scholar] [CrossRef]
- Li, L.; Peters, C.; Celia, M.A. Upscaling geochemical reaction rates using pore-scale network modeling. Adv. Water Resour. 2006, 29, 1351–1370. [Google Scholar] [CrossRef]
- Blunt, M.J. Flow in porous media—Pore-network models and multiphase flow. Curr. Opin. Colloid Interface Sci. 2001, 6, 197–207. [Google Scholar] [CrossRef]
- Blunt, M.; Jackson, M.; Piri, M.; Valvatne, P.H. Detailed physics, predictive capabilities and macroscopic consequences for pore-network models of multiphase flow. Adv. Water Resour. 2002, 25, 1069–1089. [Google Scholar] [CrossRef]
- Raoof, A.; Hassanizadeh, S.M.; Leijnse, A. Upscaling transport of adsorbing solutes in porous media: Pore-network modeling. Vadose Zo. J. 2010, 9, 624–636. [Google Scholar] [CrossRef]
- Raoof, A.; Hassanizadeh, S.M. A new formulation for pore-network modeling of two-phase flow. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Varloteaux, C. Modélisation Multi-Echelles des Mécanismes de Transport Réactif. Implact sur les Propriétés Pétrophysiques des Roches Lors du Stockage de CO2. Ph.D. Thesis, Université Pierre et Marie Curie, Paris, France, 2013. [Google Scholar]
- Sole-Mari, G.; Bolster, D.; Fernàndez-Garcia, D.; Sanchez-Vila, X. Particle density estimation with grid-projected and boundary-corrected adaptive kernels. Adv. Water Resour. 2019, 131. [Google Scholar] [CrossRef] [Green Version]
- Schmidt, M.J.; Pankavich, S.; Benson, D.A. A Kernel-based Lagrangian method for imperfectly-mixed chemical reactions. J. Comput. Phys. 2017, 336, 288–307. [Google Scholar] [CrossRef] [Green Version]
- Battiato, I.; Tartakovsky, D.M.; Tartakovsky, A.M.; Scheibe, T. Hybrid models of reactive transport in porous and fractured media. Adv. Water Resour. 2011, 34, 1140–1150. [Google Scholar] [CrossRef]
- Tartakovsky, A.M.; Tartakovsky, D.M.; Scheibe, T.D.; Meakin, P. Hybrid simulations of reaction-diffusion systems in porous media. SIAM J. Comput. 2008, 30, 2799–2816. [Google Scholar] [CrossRef]
- Van Leemput, P.; Vandekerckhove, C.; Vanroose, W.; Roose, D. Accuracy of Hybrid Lattice Boltzmann/Finite Difference Schemes for Reaction-Diffusion Systems. Multiscale Model. Simul. 2007, 6, 838–857. [Google Scholar] [CrossRef]
- Soler-Sagarra, J.; Bonet, E.; Roig, C.; Becker, P.; Carrera, J. Modeling Mixing in Stratified Heterogeneous Media: The Role of Water Velocity Discretization in Phase Space Formulation. 2021. Available online: http://hdl.handle.net/10261/218842 (accessed on 15 September 2021). [CrossRef]
- Dentz, M.; Kang, P.; Comolli, A.; Le Borgne, T.; Lester, D. Continuous time random walks for the evolution of Lagrangian velocities. Phys. Rev. Fluids 2016, 1, 074004. [Google Scholar] [CrossRef]
- Hakoun, V.; Comolli, A.; Dentz, M. Upscaling and Prediction of Lagrangian Velocity Dynamics in Heterogeneous Porous Media. Water Resour. Res. 2019, 55, 3976–3996. [Google Scholar] [CrossRef]
- Schlather, M.; Malinowski, A.; Menck, P.J.; Oesting, M.; Strokorb, K. Analysis, Simulation and Prediction of Multivariate Random Fields with Package RandomFields. J. Stat. Softw. 2015, 63, 1–25. [Google Scholar] [CrossRef] [Green Version]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2015. [Google Scholar]
- Pollock, D.W. Semianalytical Computation of Path Lines for Finite-Difference Models. Groundwater 1988, 26, 743–750. [Google Scholar] [CrossRef]
- Hoteit, H.; Mose, R.; Younes, A.; Lehmann, F.; Ackerer, P. Three-Dimensional Modeling of Mass Transfer in Porous Media Using the Mixed Hybrid Finite Elements and the Random-Walk Methods. Math. Geol. 2002, 34, 435–456. [Google Scholar] [CrossRef]
- Pool, M.; Carrera, J.; Alcolea, A.; Bocanegra, E. A comparison of deterministic and stochastic approaches for regional scale inverse modeling on the Mar del Plata aquifer. J. Hydrol. 2015, 531, 214–229. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000; p. 771. [Google Scholar]
- Risken, H. The Fokker-Planck Equation; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Perez, L.; Hidalgo, J.J.; Dentz, M. Upscaling of Mixing-Limited Bimolecular Chemical Reactions in Poiseuille Flow. Water Resour. Res. 2019, 55, 249–269. [Google Scholar] [CrossRef] [Green Version]
- Comolli, A.; Dentz, M. Anomalous dispersion in correlated porous media: A coupled continuous time random walk approach. Eur. Phys. J. B 2017, 90, 35–40. [Google Scholar] [CrossRef] [Green Version]
- Le Borgne, T.; Ginn, T.R.; Dentz, M. Impact of fluid deformation on mixing-induced chemical reactions in heterogeneous flows. Geophys. Res. Lett. 2014, 41, 7898–7906. [Google Scholar] [CrossRef] [Green Version]
- Gramling, C.M.; Harvey, C.; Meigs, L.C. Reactive Transport in Porous Media: A Comparison of Model Prediction with Laboratory Visualization. Environ. Sci. Technol. 2002, 36, 2508–2514. [Google Scholar] [CrossRef] [PubMed]
- Le Borgne, T.; Dentz, M.; Davy, P.; Bolster, D.; Carrera, J.; De Dreuzy, J.-R.; Bour, O. Persistence of incomplete mixing: A key to anomalous transport. Phys. Rev. E 2011, 84, 015301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
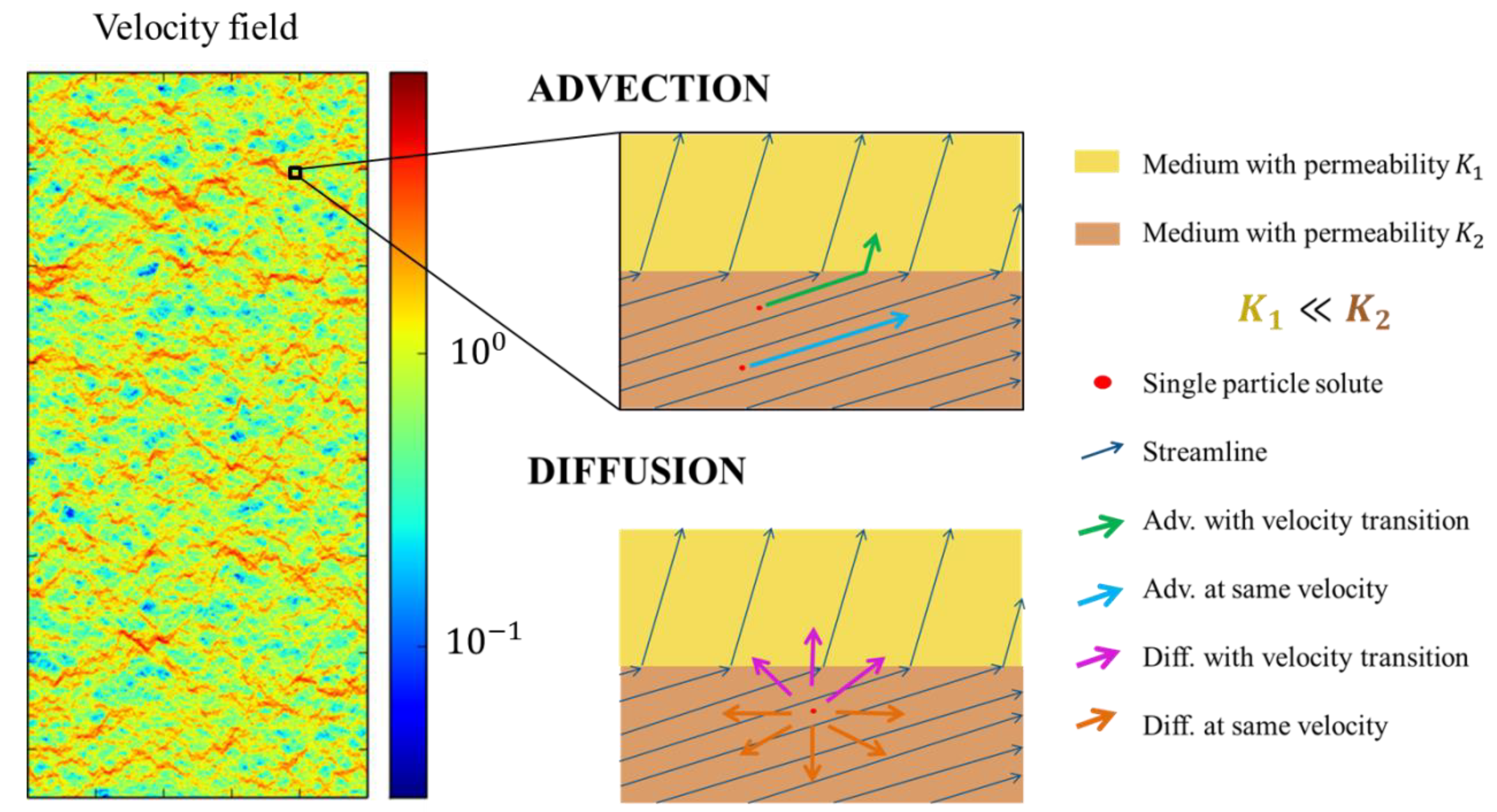


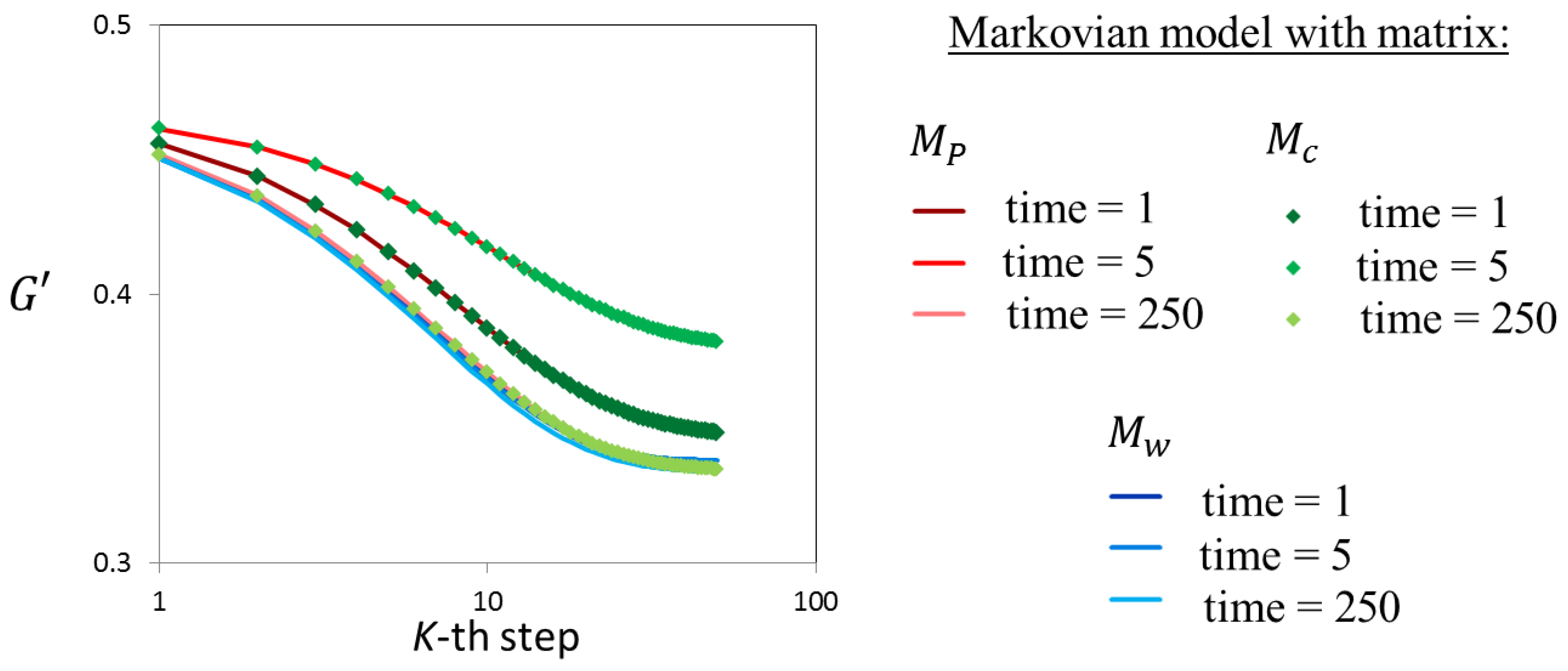
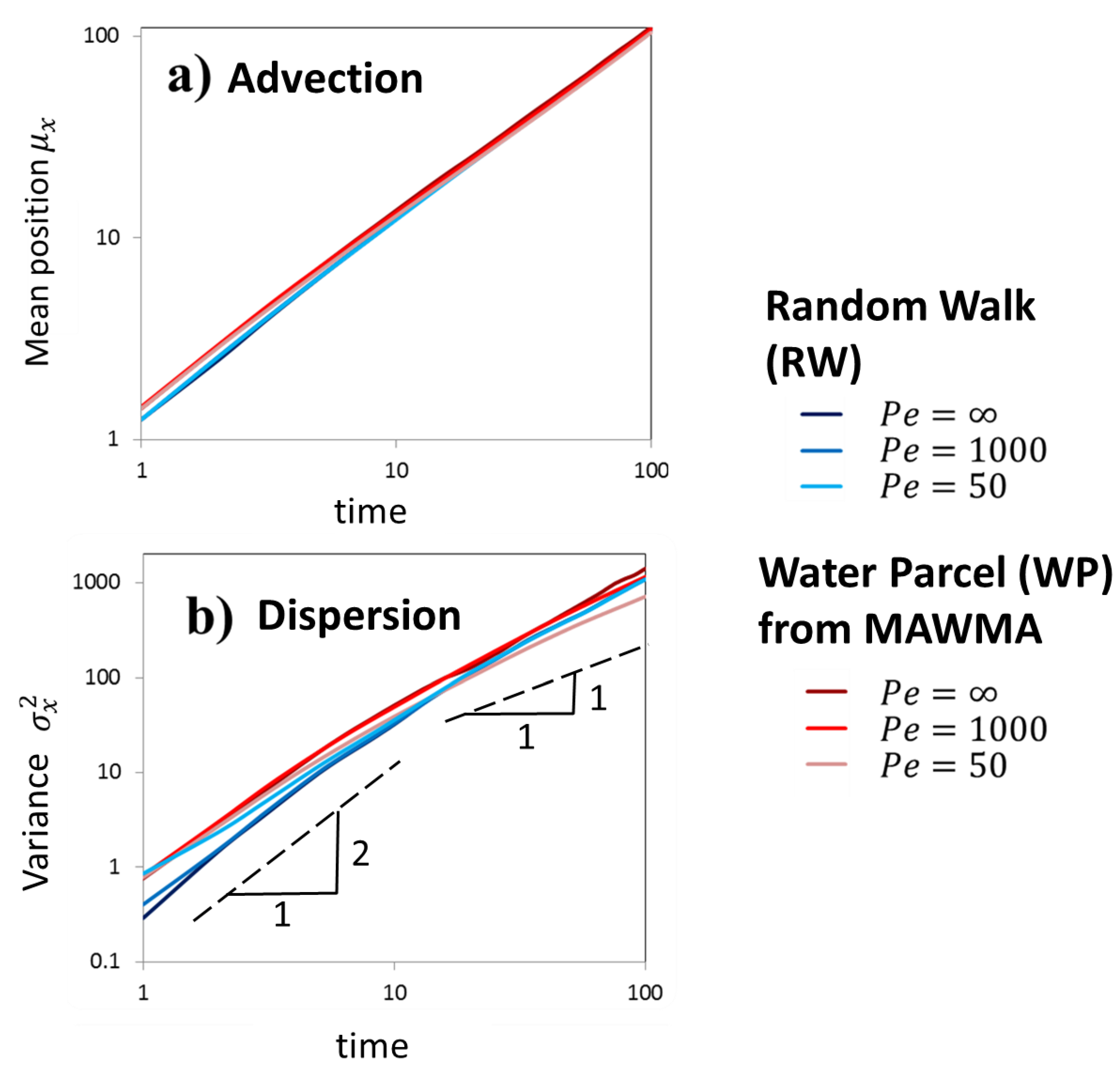

| Flow | Transport | ||||
|---|---|---|---|---|---|
| λ (m) | 10 | Num. time steps | 100 | (kg/m3) | 1 |
| 600λ | 0.3 | Δt (s) | 1 | ||
| 150λ | RW | Cases | |||
| Δx, Δy | λ/10 | 2.25 × 106 | Peclet | ||
| 0 | WP | 0 | |||
| 1 | 30 | 10−2 | 103 | ||
| 1.44 × 105 | 0.2 | 50 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soler-Sagarra, J.; Hakoun, V.; Dentz, M.; Carrera, J. The Multi-Advective Water Mixing Approach for Transport through Heterogeneous Media. Energies 2021, 14, 6562. https://doi.org/10.3390/en14206562
Soler-Sagarra J, Hakoun V, Dentz M, Carrera J. The Multi-Advective Water Mixing Approach for Transport through Heterogeneous Media. Energies. 2021; 14(20):6562. https://doi.org/10.3390/en14206562
Chicago/Turabian StyleSoler-Sagarra, Joaquim, Vivien Hakoun, Marco Dentz, and Jesus Carrera. 2021. "The Multi-Advective Water Mixing Approach for Transport through Heterogeneous Media" Energies 14, no. 20: 6562. https://doi.org/10.3390/en14206562
APA StyleSoler-Sagarra, J., Hakoun, V., Dentz, M., & Carrera, J. (2021). The Multi-Advective Water Mixing Approach for Transport through Heterogeneous Media. Energies, 14(20), 6562. https://doi.org/10.3390/en14206562






