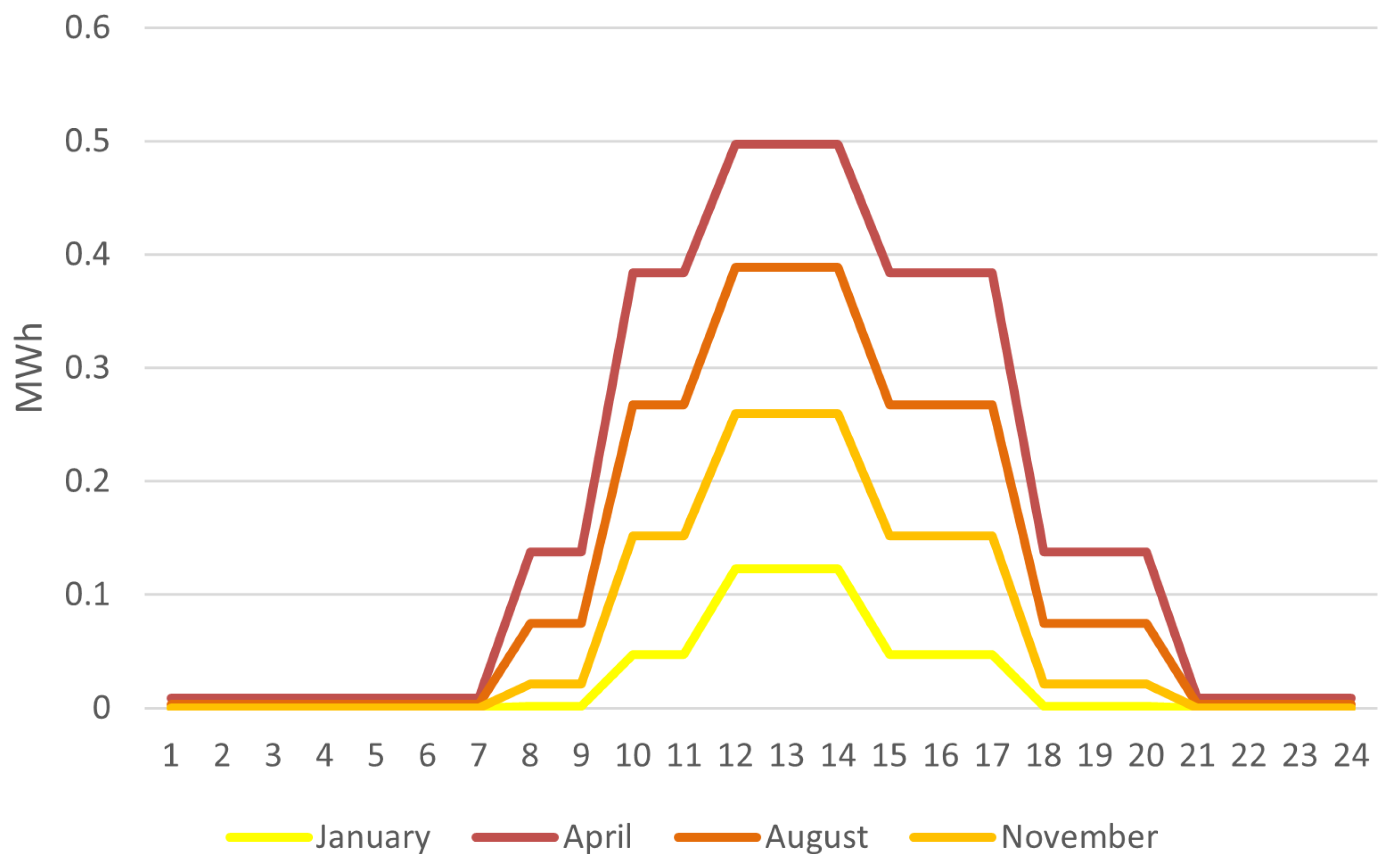
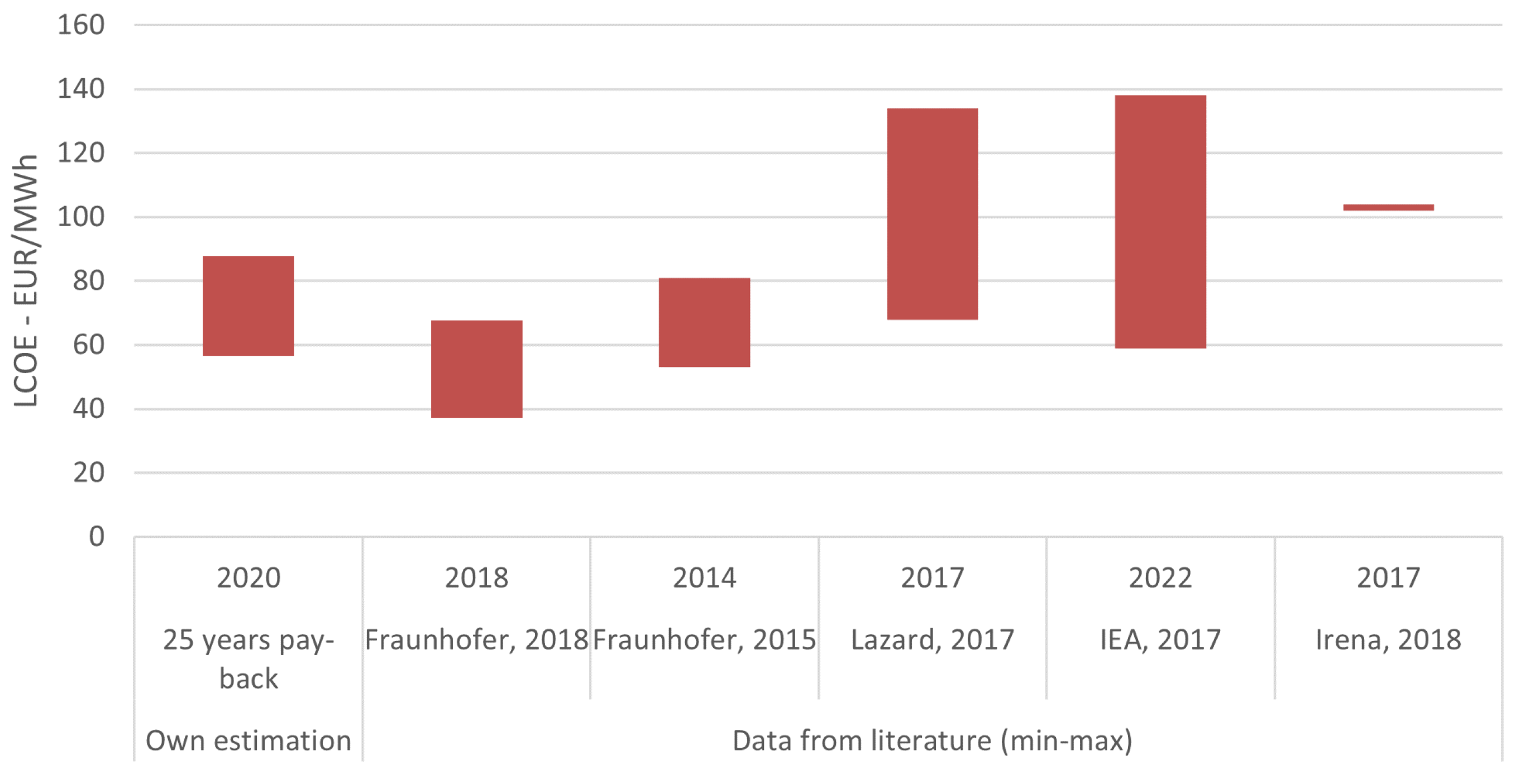
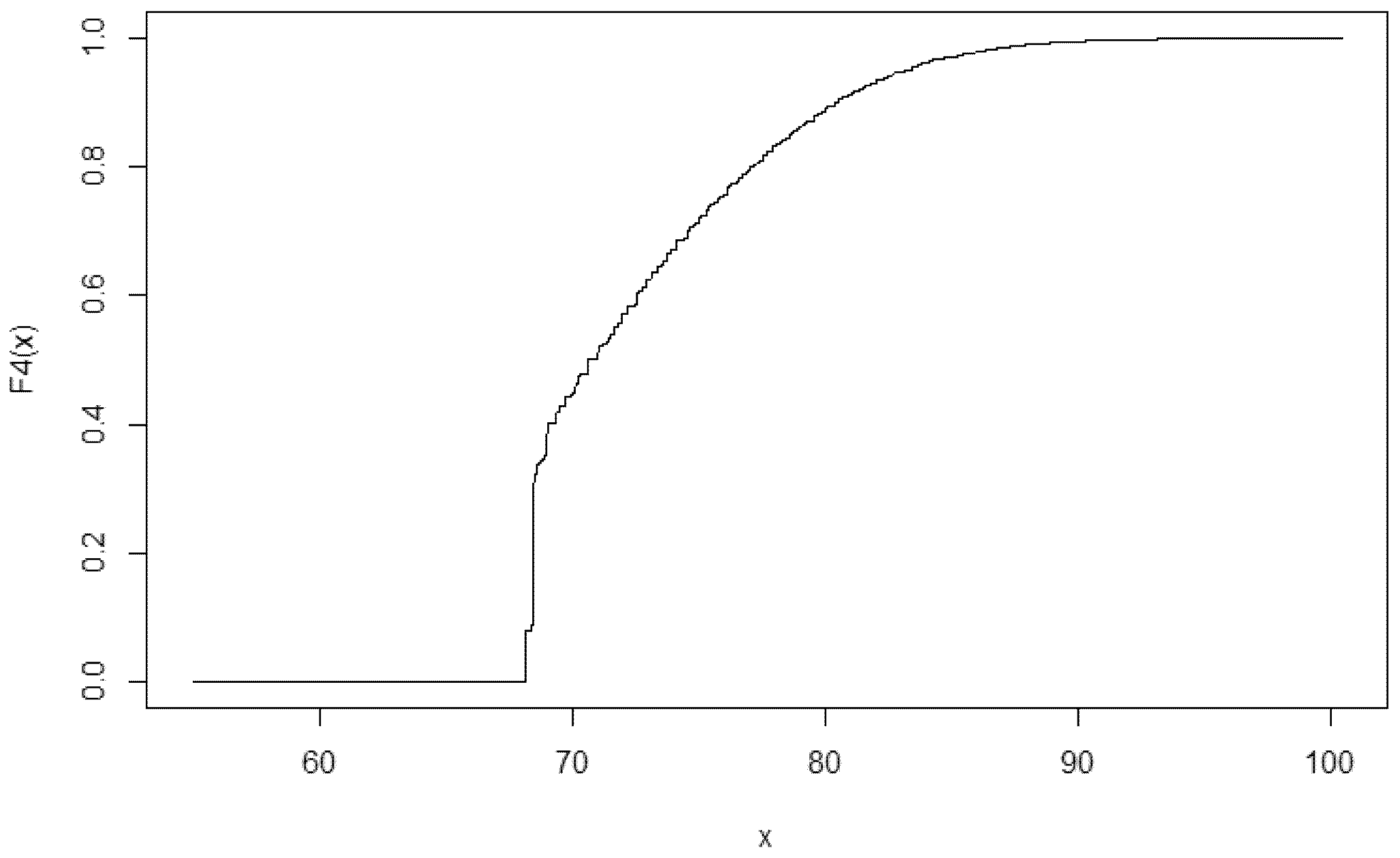3.1. Modified Lcoe Calculation
After all the above inputs are in place the values can be calculated. First, the is calculated using an 800 €/kW investment cost, arriving to 70.38 €/MWh.
It is worth noting that for the “simple” LCOE value, the support period was set equal to the lifetime of the project, so this value should be lower than the 20-year lifetime simple LCOE while somewhat higher, than the 25-year lifetime (and support period!) simple LCOE. The difference, however, is rather small, because in the last 5 years the wholesale market prices are close to the outcome, and in the first 20 years there is some—but not much—additional income from the higher than wholesale prices.
The value of this small additional income can be quantified assuming a FiT system (or a two-sided FiP) for 20 years—the period which producers receive a fixed price, and then 5 additional years on the wholesale market. The under these assumptions is 70.42 €/MWh. This means, that the “value” of the possibility to keep the difference between market prices and the strike price (if the first one is higher) accounts for 70.42 − 70.38 = 0.04 €/MWh.
Another very important quality of this modified calculation is that the income side includes several items, not only the income from the support. This way it is possible for the project to turn profitable without any support. If the investment cost is low enough and the electricity price high enough, the value can be 0.
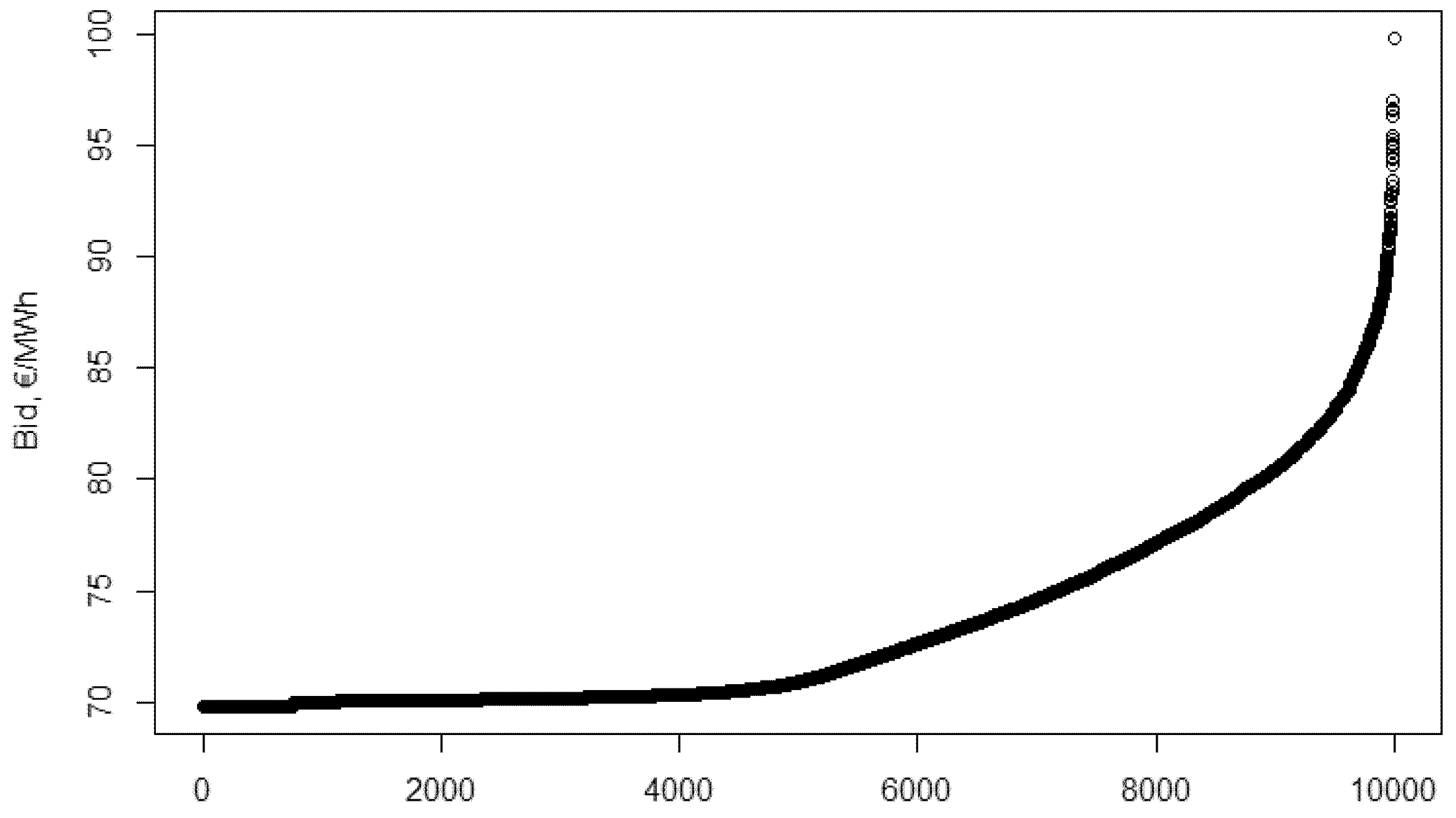
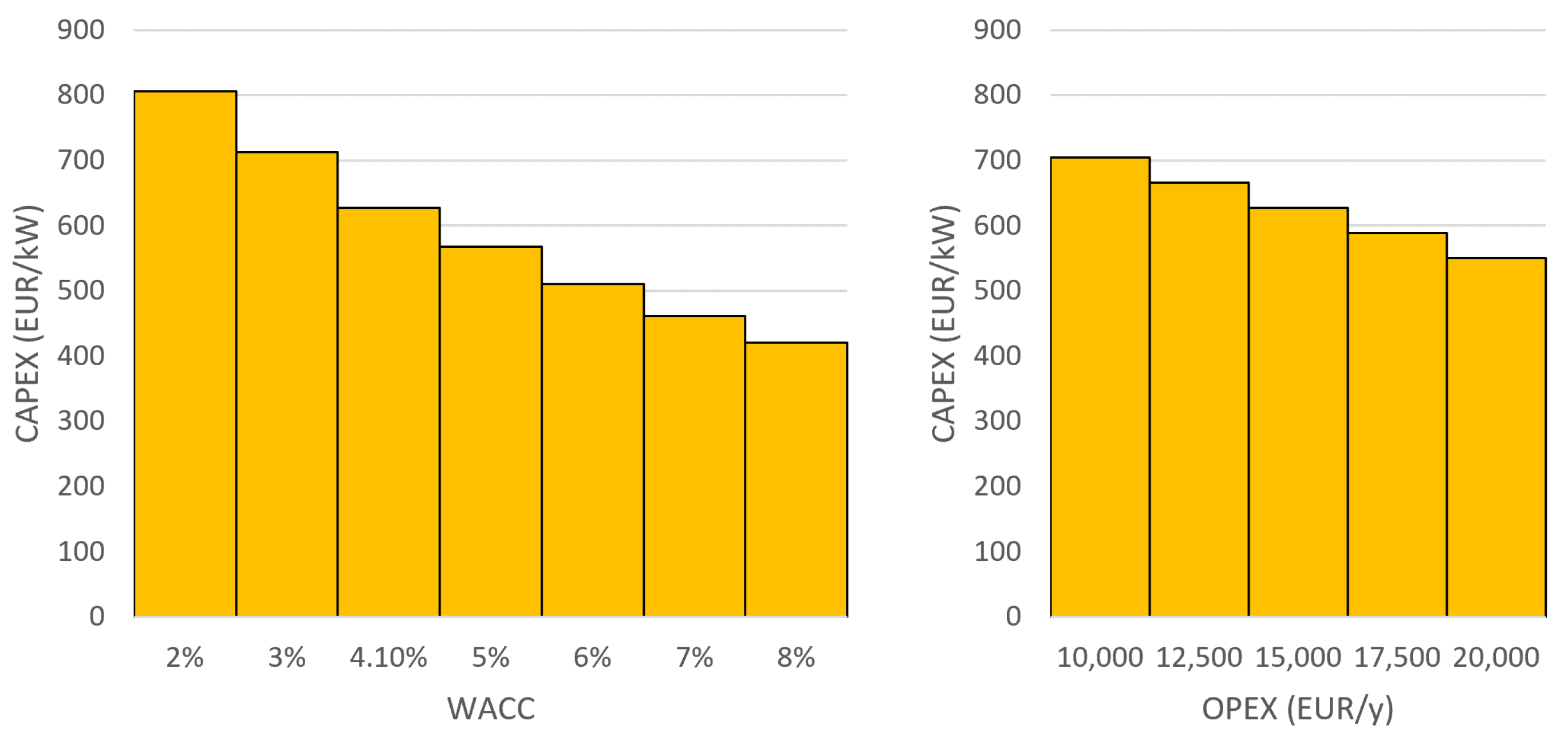
This way, the “critical investment cost” (if all other inputs are fixed) can be calculated: which is the investment cost level to make the project profitable without any support. Put another way, this is the investment cost that makes the NPV of incomes and costs equal without any support. For a critical investment cost, the
will be exactly 0. This value can be calculated with different inputs: as shown on
Figure 4, changing
wacc (weighted average cost of capital) values and different
opex (operation and maintenance) costs result in different critical investment costs.
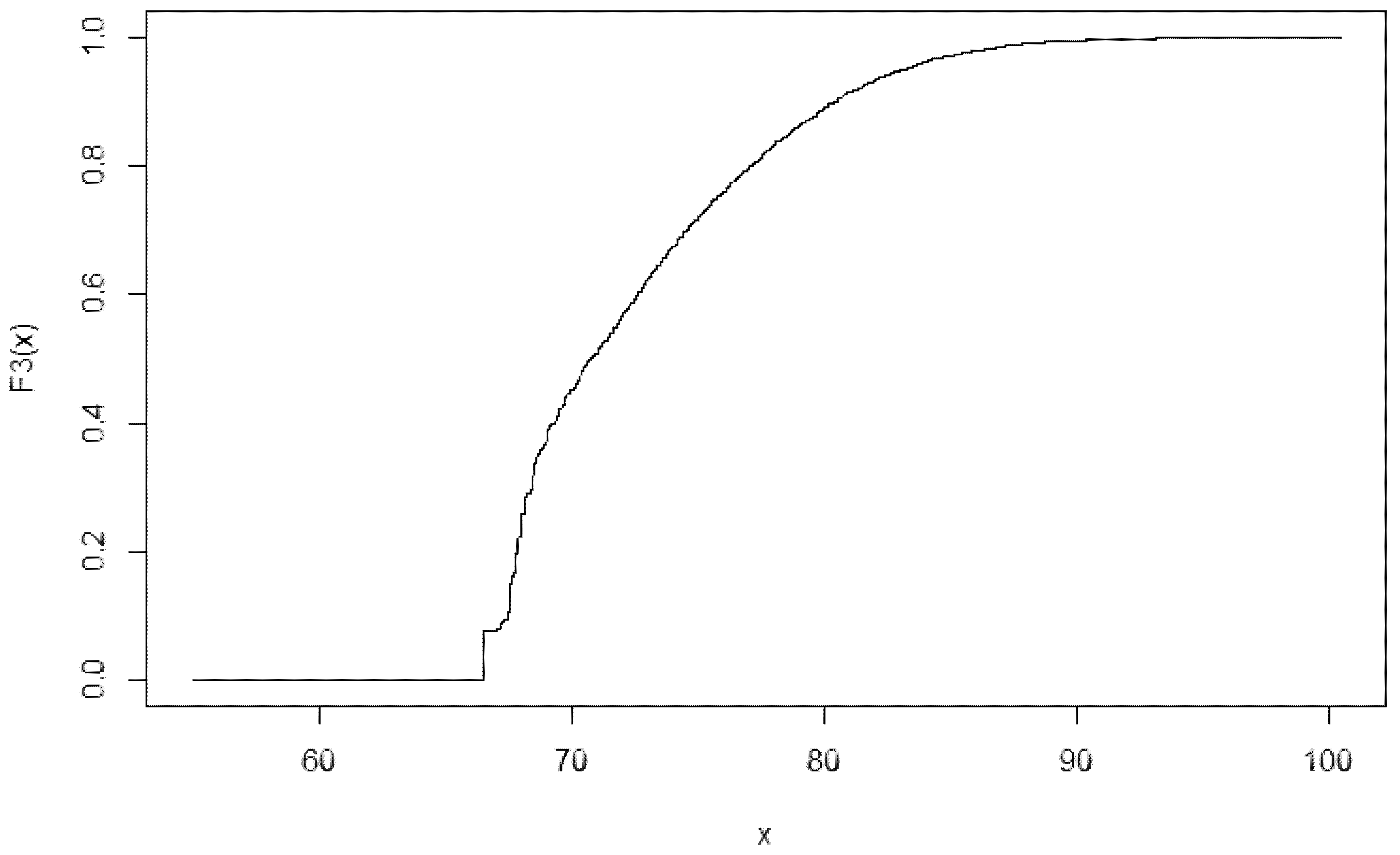
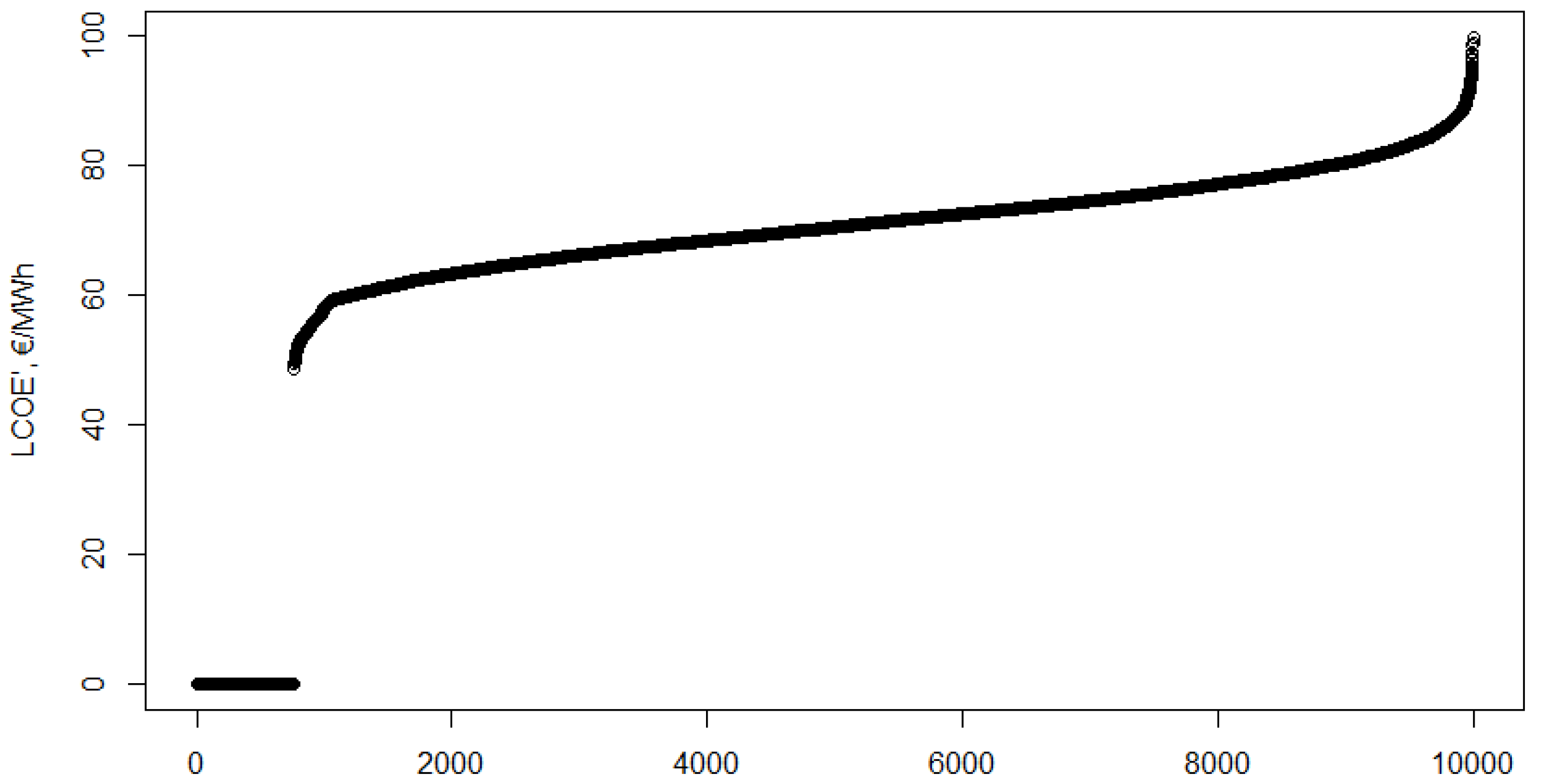
After calculating the value with different fixed investment costs the distribution of has to be calculated, based on the assumed distribution of the investment cost. As stated above, the calculation is an optimisation: 10,000 investment cost values are simulated using the assumed distribution to calculate the values. This provides an empirical distribution of the value. For investment costs lower than the “critical investment cost”, 0 support is needed this is the minimum, since no one would ask for a negative support.
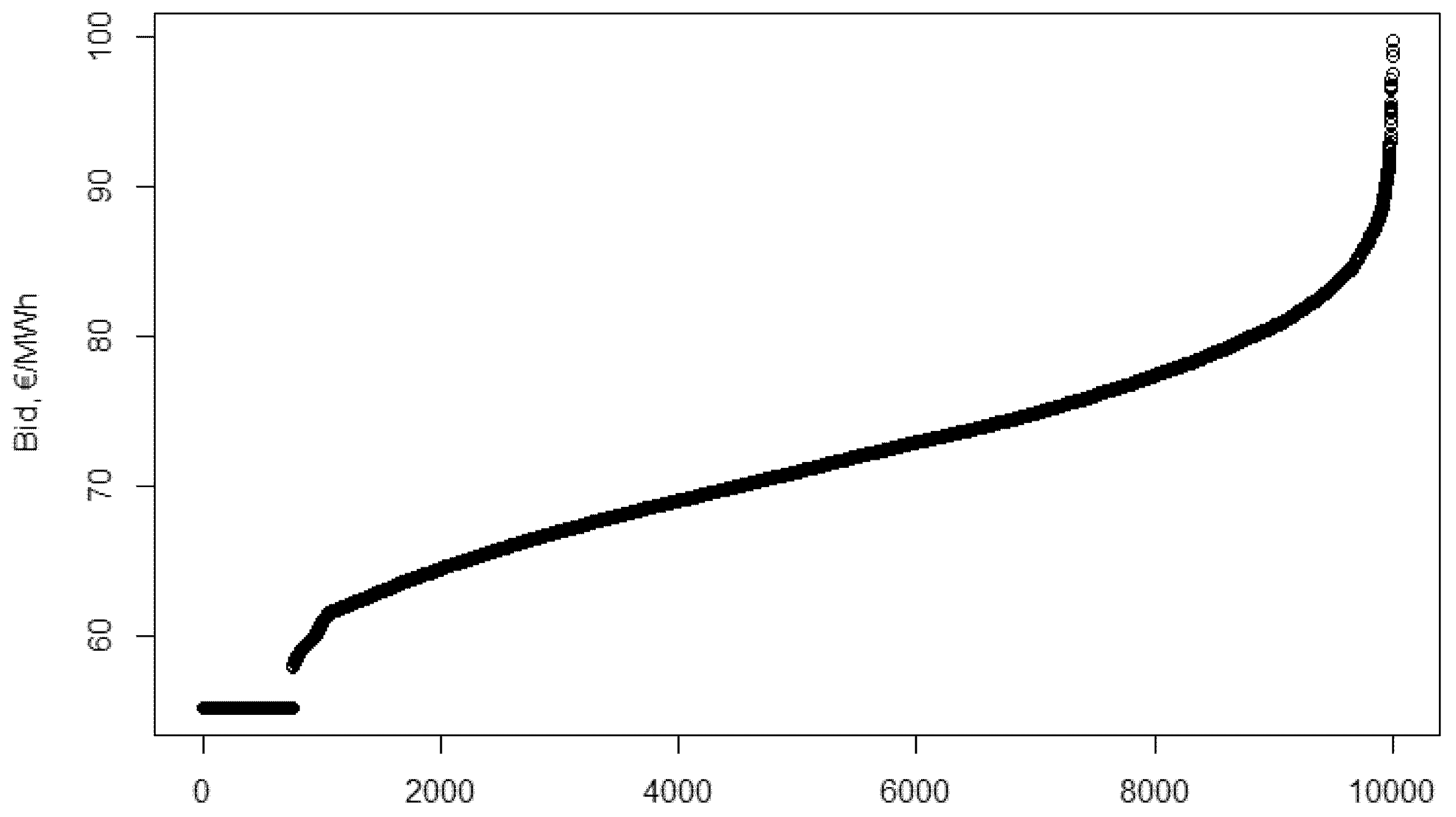
The sorted
values are presented in
Figure 5. The first 759 elements are 0, meaning out of 10,000 investment cost simulations 759 are lower than the critical investment cost. For these projects it is assumed that project developers will take part in the auction, since they can make their investment more profitable by winning. This model does not put a cost on participation, so participation is incentivised.
3.2. Nash-Equilibrium Bid Function in Case of the Pay-as-Bid Auction
In the following subsection the algorithm is explained, and results summerised. More details of the calculation, including the code and the data are available as
Supplementary Materials.
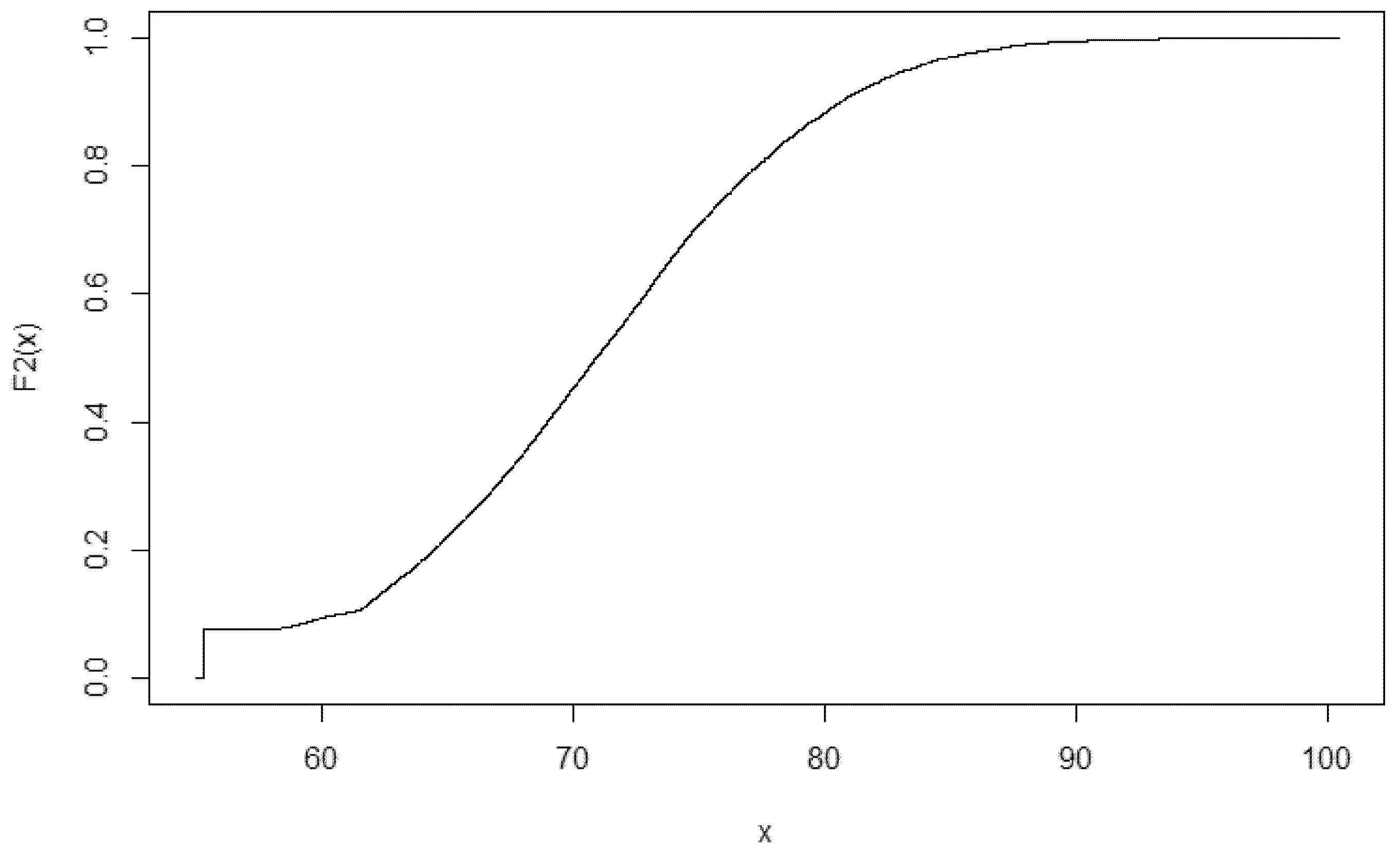
The first step of the iteration assumes a normal distribution for the bids of others, with the mean and variance of the simulated 10,000 value, of which the cumulative distribution function is .
Next the optimal bids are calculated for all 10,000 different simulated values. This way I get 10,000 bids. From the point of view of another participant each of them is equally possible to be the optimal one, as he does not know the exact , just the possible 10,000 valuations or the valuation distribution.
If this bid distribution is equal to the original, this signals a Nash-equilibrium—though not necessarily the only one—because if all participants assume this bid distribution, then the best response will lead to the assumed distribution making every participants’ bid function the best response to others’. If the two distributions are different, then the optimal bid function—assuming this new distribution—has to be tested in the next step of the iteration.
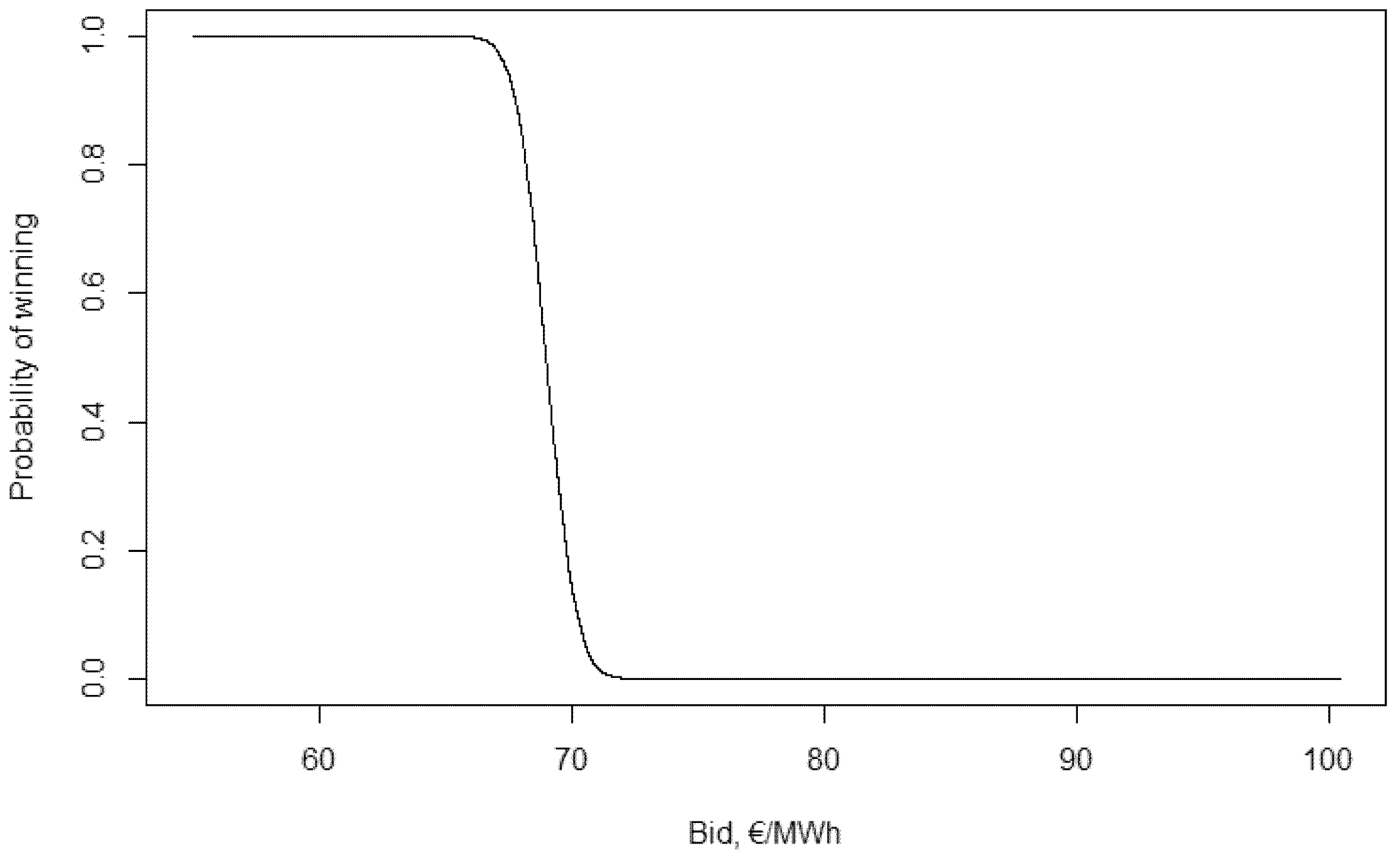
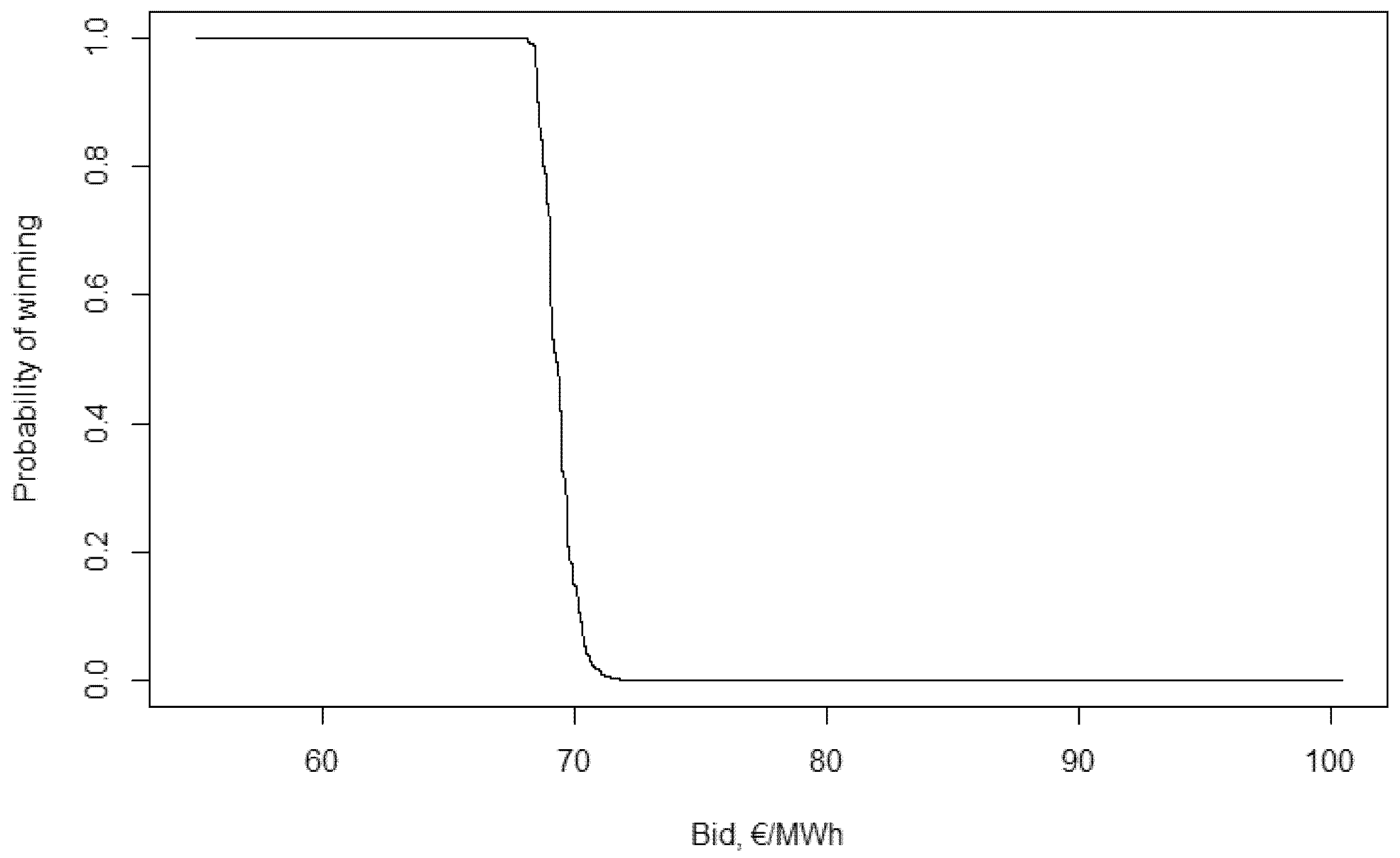
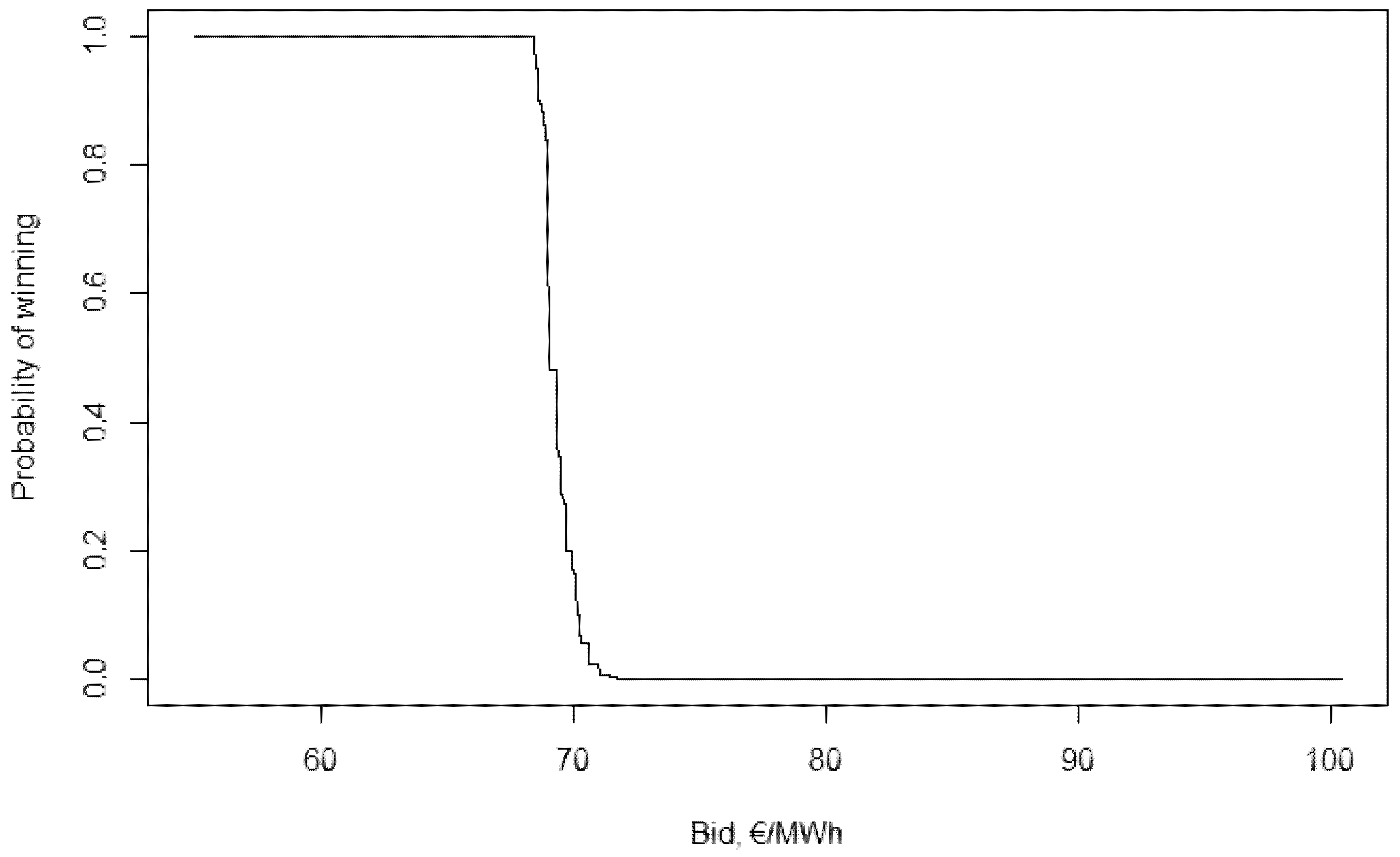
To calculate the optimal bids the probability of winning needs to be calculated for the different bids first. This is shown by figures in
Appendix A.
There is a clear range of bids that are “in the game”: with a bid of 50 €/MWh the probability of winning is over 0.9999, while a bid of 70 €/MWh has a probability of winning less than . The optimal bid can be calculated for all valuations using these probabilities (for this step I used the command “optimize” of the program R).
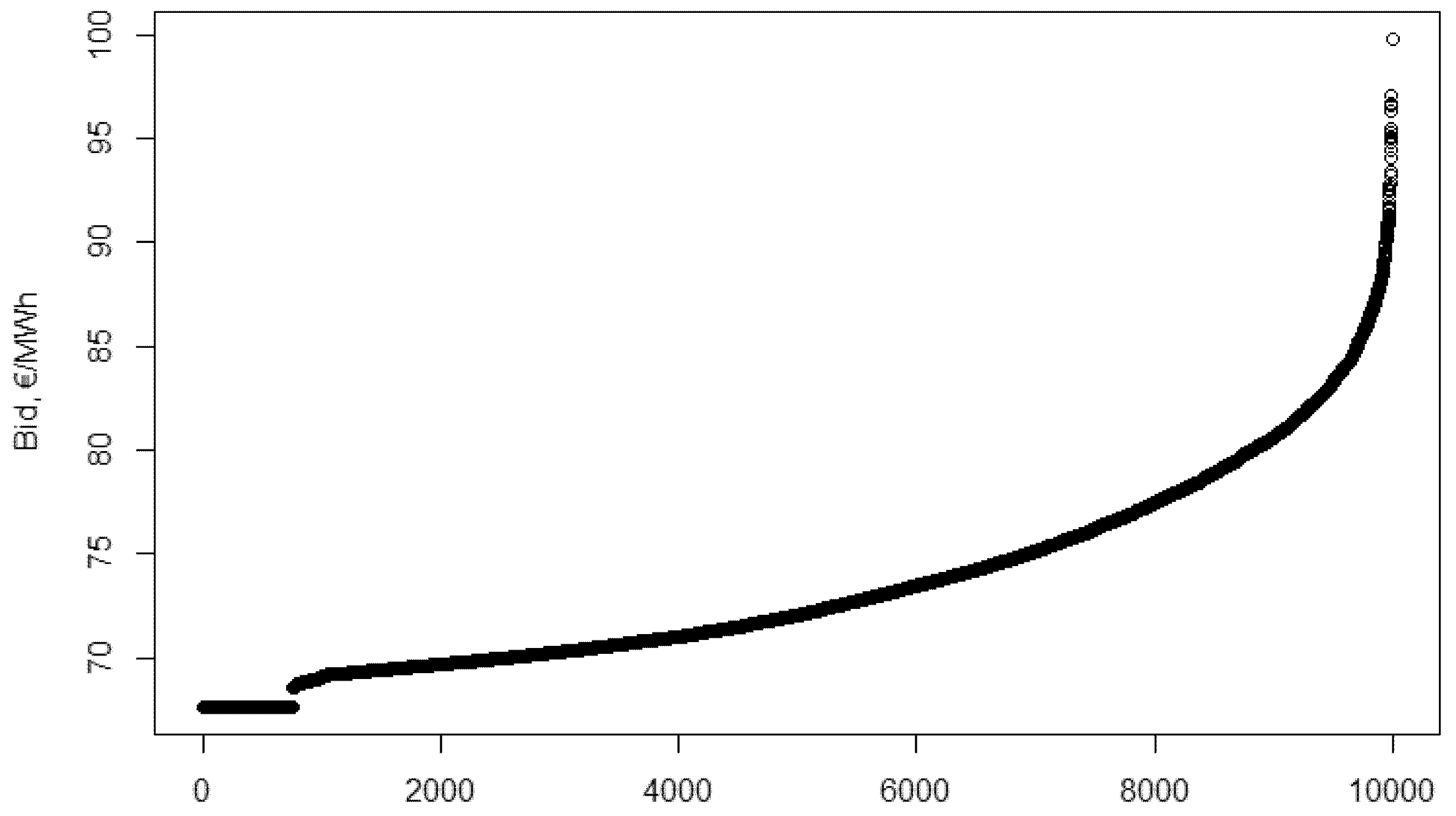
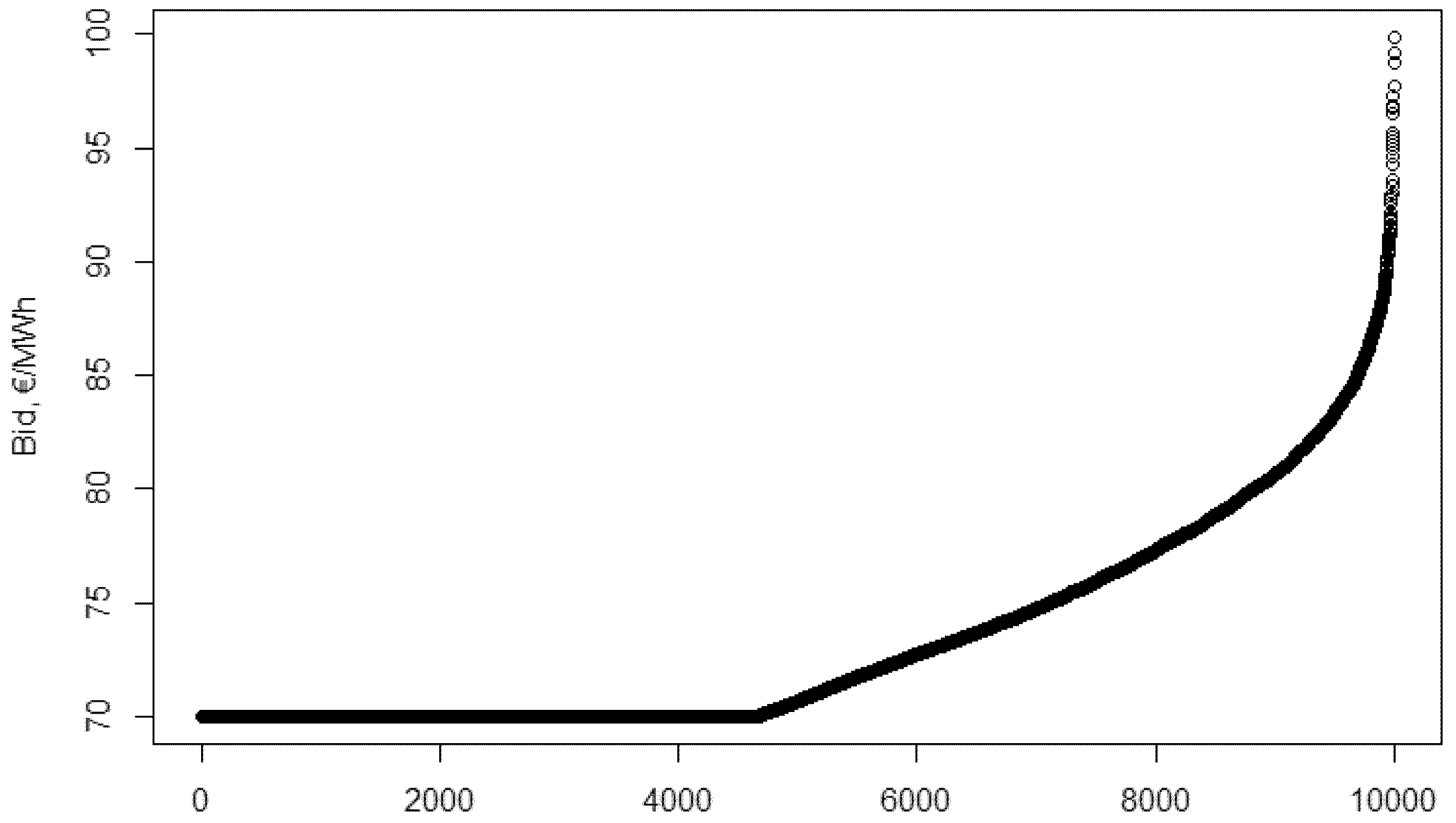
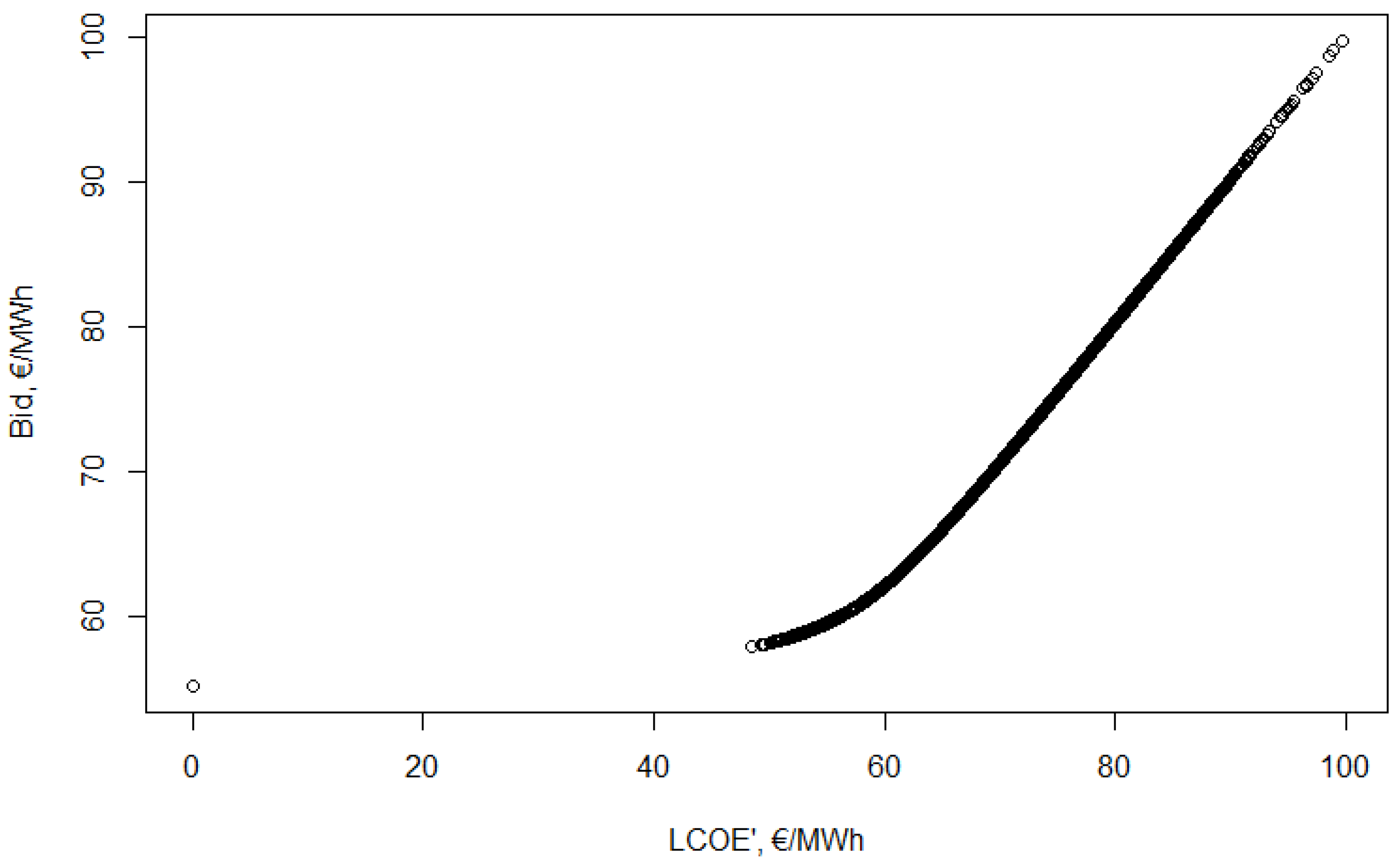
In
Figure 6, the optimal bids (
y axis) and valuations (
x axis) are shown. There is no need to have the exact formula of the bid function at this point, the difference between them is visible from the figures. These are not actual functions at this point—here, the valuation–bid pairs are presented.
To proceed the new bid distribution, has to be specified. If the optimal bid for all 10,000 possible valuations leads to a distribution , then it is a Nash-equilibrium. If not, further analysis is needed. It is possible, that the best response would be the same when assuming as in case of , but it would mean, the normal bid distribution leads to Nash-equilibrium. Furthermore, as it is shown later, this is not the case.
In order to specify 10,000 optimal bid–valuation pairs had to be fitted. The first step is sorting the optimal bids and depicting them on a graph. We can interpret this graph as the probability of a bid smaller than the y coordinate of a given point is the x coordinate of the given point divided by 10,000. Thus, because of the sorting, the probability of receiving a bid (from this distribution) smaller than the 500th bid is , while the probability of receiving a bid smaller than the largest bid would be 1 (1 = ).
This way, with some small modifications the inverse of the depicted function will be the cumulative distribution function (from now on referred to as the distribution function). The first modification is that instead of the sequence number (the x coordinate) the ten thousandth of the number is used, to get probabilities.
The first part of the function represented by the horizontal line can not be inverted. The probability of having a bid below the minimum is 0, while the value of the distribution function for bids larger than the minimum bid would also be larger than the one ten thousandth of the highest sequence number of minimum bids (in this case the value of the distribution function will be larger or equal than for bids larger or equal than the minimum bid, reflecting 759 bids with the minimum value).
The form of this bid distribution comes from the 759 cases out of 10,000 simulated when the was 0, and without any support the project would be profitable (meaning the expected return can be realised).
The formulas of the distribution functions are included in
Appendix A. The distribution function defined above satisfies all conditions to be a distribution function:
Having the new assumption for the bid distribution () the optimal bids can be calculated again. The new optimal bid function then can be compared to the one from Step 1, when assuming . If these are not equal, then it is not a Nash-equilibrium, as the best response for the others’ assumed optimal bidding strategy is different from the assumed.
As a first step, the probability of winning is calculated for different bids. The new probabilities are “shifted”: with a bid of 65 €/MWh the probability of winning is larger than 0.9999, while it goes down under 1% only at around 76 €/MWh.
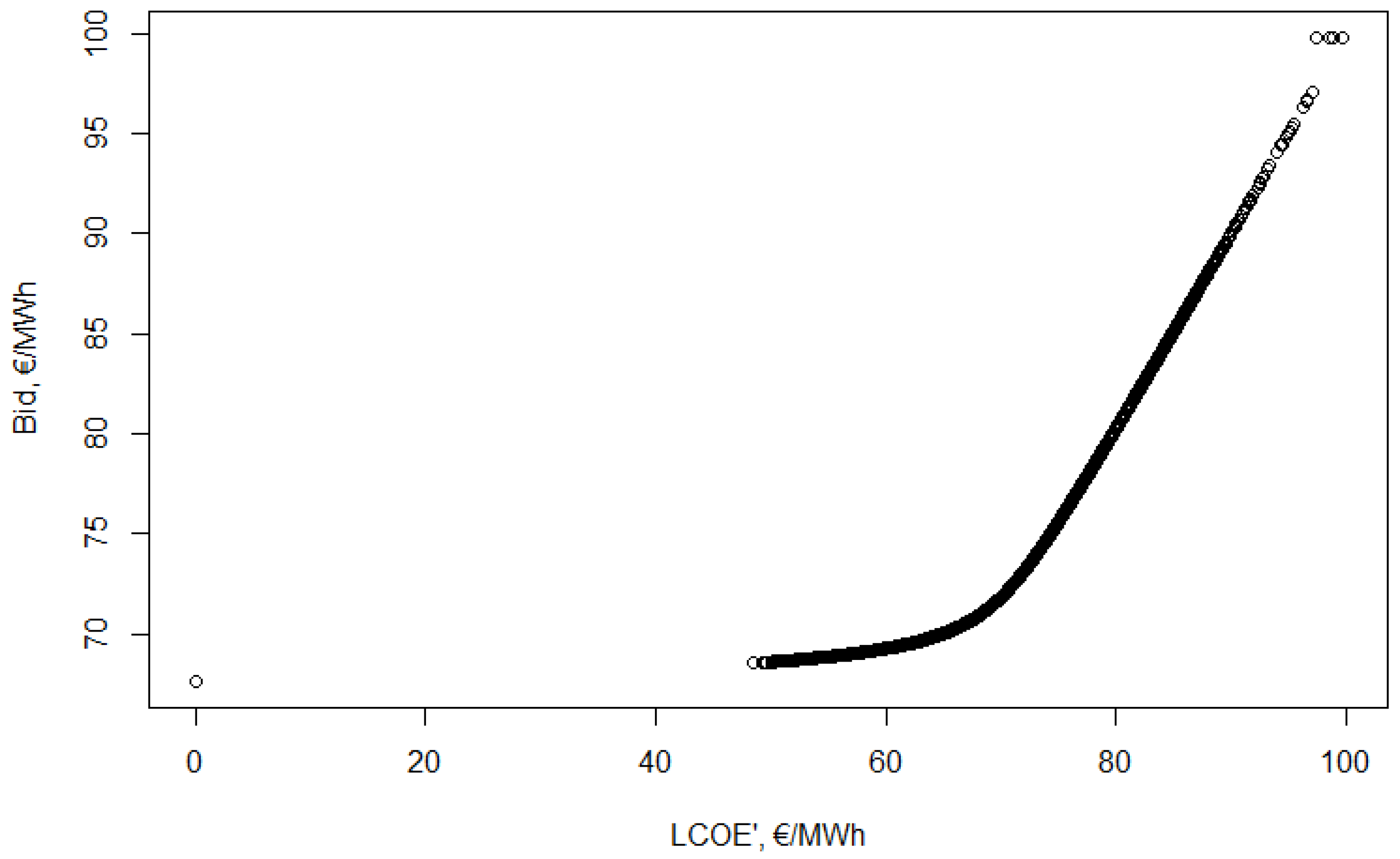
Using these results the optimal bid for the 10,000 different simulated valuations is calculated. The bid function presented on
Figure 7 shows a different bid function, so there is another step in the iteration.
The two parts of the function are more distinguishable, with the first part being flatter, then the function becomes steeper. Many participants have the minimum bid, however, this minimum bid is larger than before.
To sum up, the two optimal bid functions are quite different, thus the iteration has to continue, until reaching the Nash-equilibrium.
Next the bid distribution has to be calculated with the help of the bid function, sorting the 10,000 optimal bids for the generated 10,000 valuations. Bids are on average higher than last time, including the maximum bid, and there is a shorter distance between the minimum bid and the next smallest bid. The new bid distribution function,
is presented in
Appendix A.
Then the probability of winning for different bids assuming bid distribution for other participants’ bids is calculated. From this, optimal bids for all 10,000 valuations can be determined.
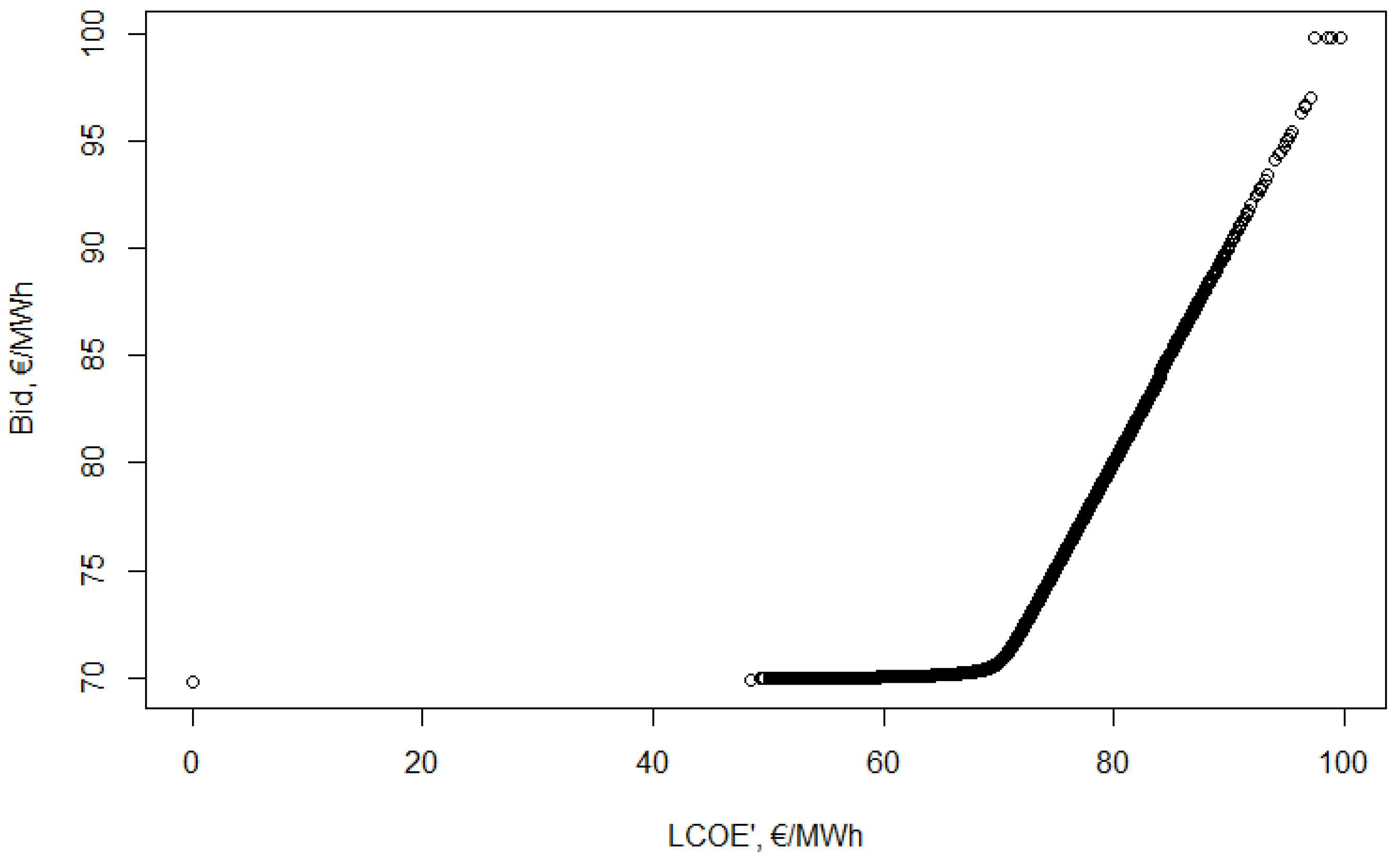
The first part of the bid function is even flatter, though, still not entirely horizontal, and most bids are very close to 70 €/MWh. The point of inflecion is even clearer before the function turns into a steep, linear trajectory (see details on
Figure 8).
After sorting the optimal bids it is clear, that there is no longer a jump between the participants with a 0 valuation and a larger valuation—their bids will be very close to each other. From these sorted bids the new, bid distribution can be calculated.
The probability of winning shows that the range, in which the probability is clearly higher than 0 and smaller than 1 gets very narrow. The bid function is quite similar to the one from in Step 3, with only minor differences (see
Figure 9). The minimum bids increase from 69.81 to 70.01 €/MWh.
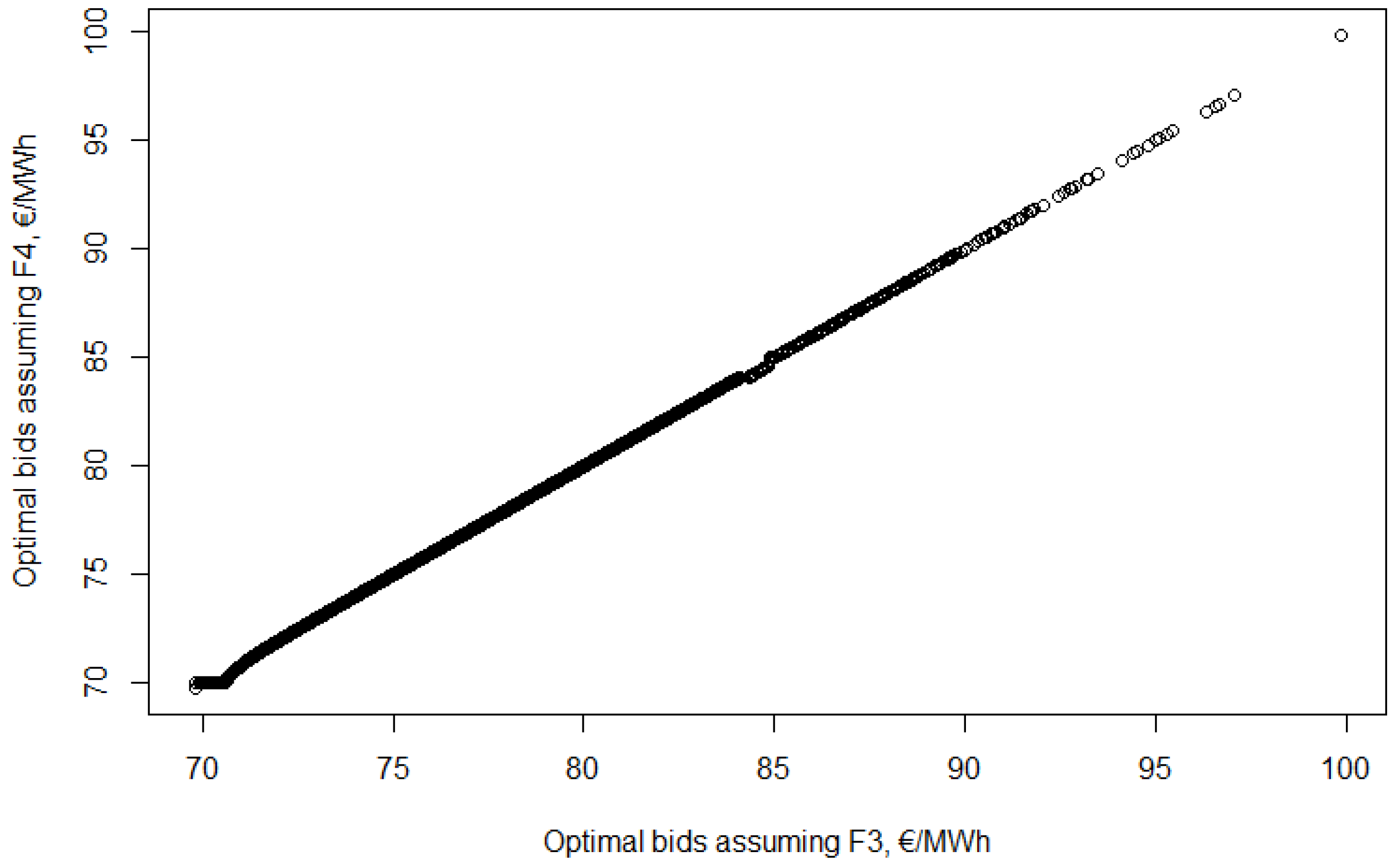
It is likely that this is very close to the Nash-equilibrium. In
Figure 10 the magnitude of the difference between the two bid functions is represented. Each valuation is one point, for which the x coordinate is the optimal bid assuming
while the y coordinate is the optimal bid assuming
.
This shows that the two functions are very close to each other and the difference can be found using the Root Mean Square Error (RMSE) value. For the 10,000-item-long series the RMSE value is 0.17 €/MWh. The Normalised Root Mean Square Error (NRMSE) compares this to the mean of the data set—that is 73.39 and 73.45 €/MWh respectively. The NRMSE is less than 0.25% which can be considered rather low. It is close to the point where the iteration stops (0.2%), but it is still higher than that.
The two bid functions are close enough that it could almost be considered that it is Nash-equilibrium. However, in each step it becomes clear, that the bid functions are getting closer to a specific form: from entirely horizontal to a steepness of around 45 degree.
The following conjecture can be stated: the optimal bid function in a Nash-equilibrium is the following. Under a valuation of 69.706 €/MWh the optimal bid is 70.007 €/MWh, above that the optimal bid is 0.457 €/MWh higher than the 99.78% of the valuation. The exact function form is the following:
The last step is checking whether this is a Nash-equilibrium bidding strategy: assuming this bidding strategy for others would lead to the same optimal bidding strategy.
The first task is calculating the optimal bids assuming
bid function for all 10,000 valuations, and sorting them. This is presented on
Figure A11 in
Appendix A.
This shows that these bids are very close to the ones from Step 4—as the definition of the bid function came from these outputs.
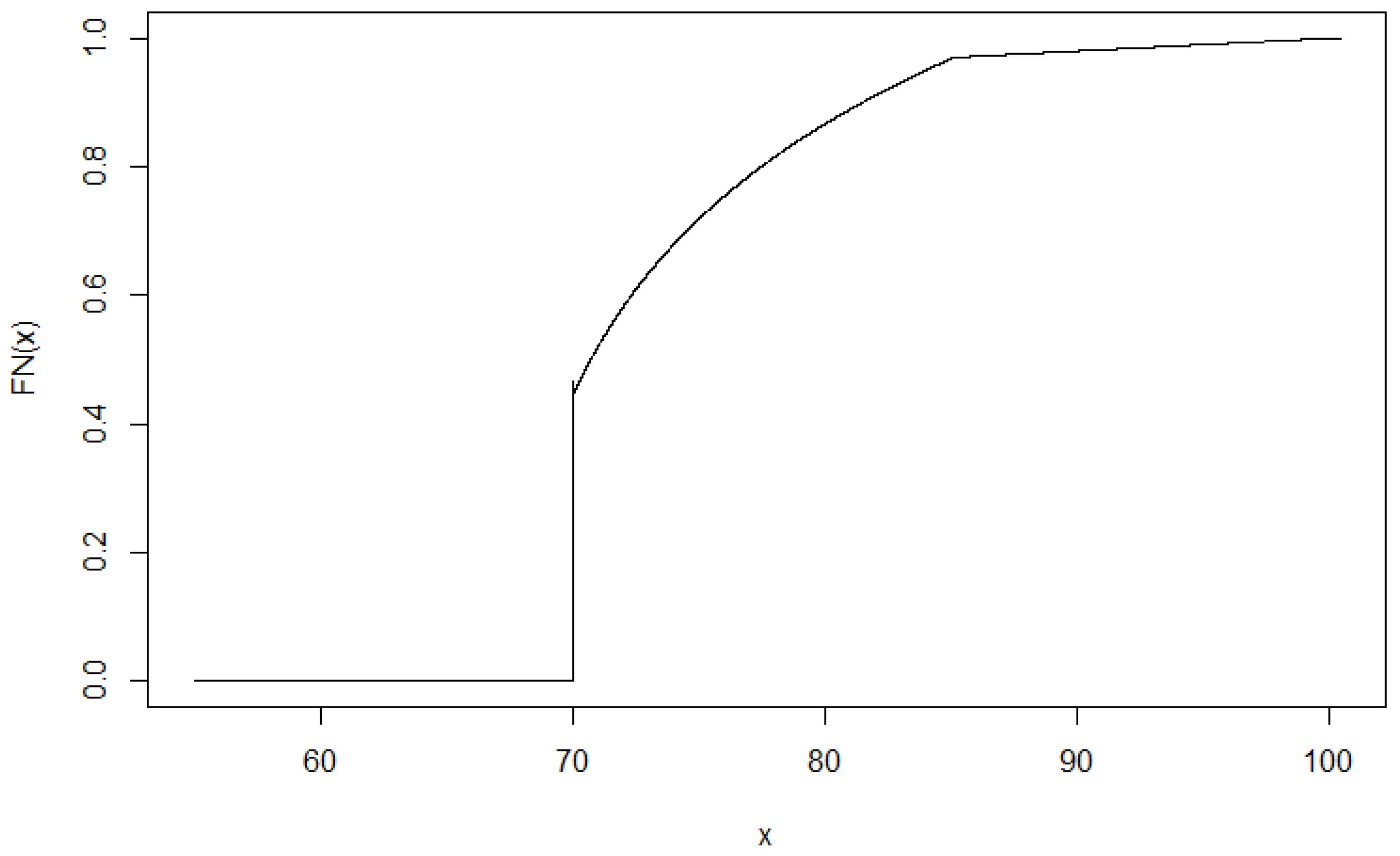
The first part of the function consists of the first 4672 bids: all of them are equal to 70.007 €/MWh. This part of the function can not be inverted, but it is easy to interpret: the probability of other participants’ bids to be less than 70.007 €/MWh is 0, thus for all . The probability of a bid 70.007 €/MWh is exactly , so when , then .
The next section of the function starts from the 4672th smallest bid. Exponential and linear fitting is applied for the rest of the function (the RMSE of the fitted and the original curve is 0.8934. Compared to the mean of the data sets (NRMSE—Normalised Root Mean Square Error) the value is 1.2%). In this step it is rather important to have a precise fitting method when the bid distribution that comes from the assumed bid function is defined. A possible future extension of this work would be to apply a more automatic fitting procedure, that can guarantee to have a well-fitted distribution function in all steps. The new bid distribution can be calculated from the fitted curve. The distribution function
is presented in
Figure 11.
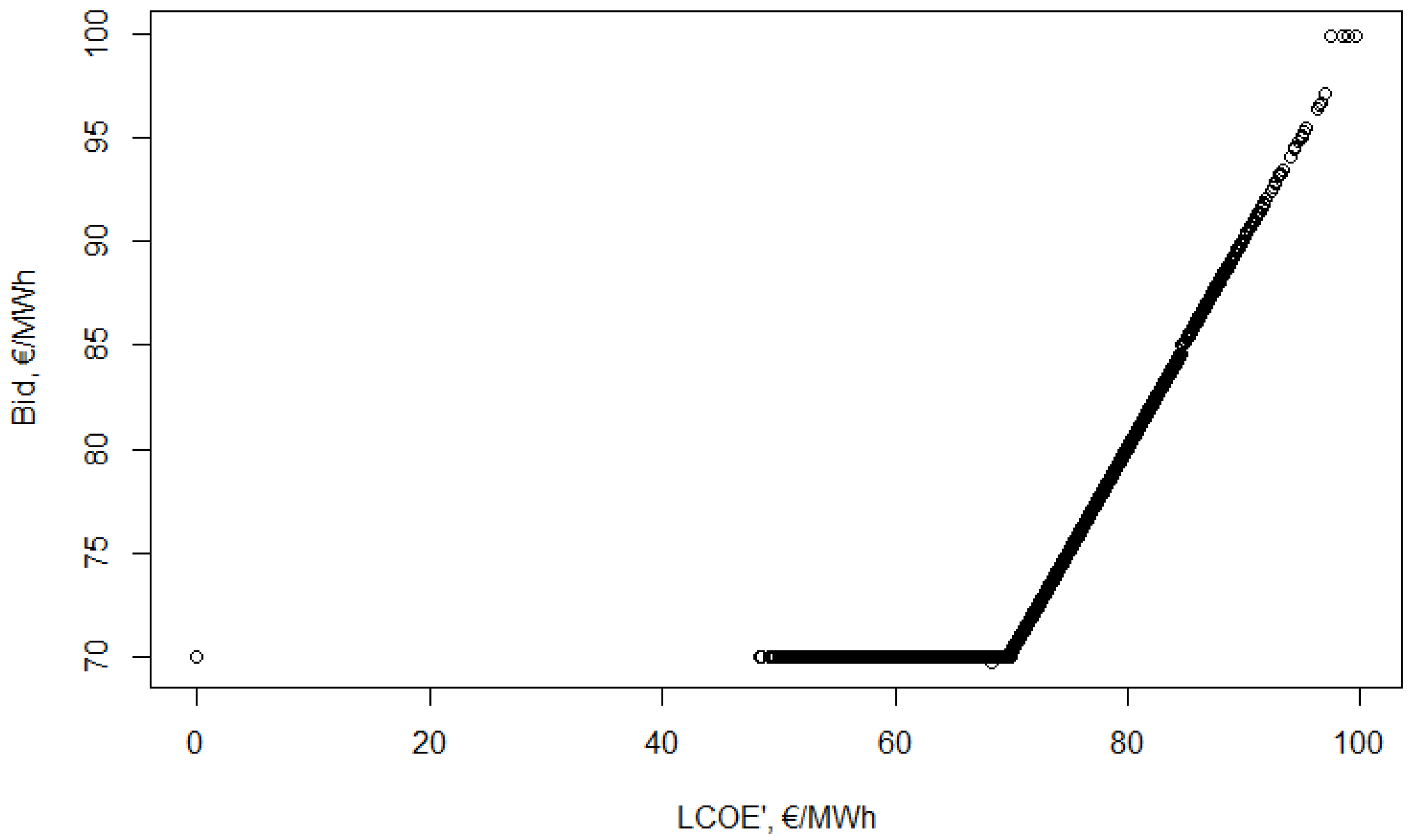
Using this bid distribution the probability of winning and the optimal bids for all valuations can be derived like before. The optimal bid function—assuming the bidding strategy
for other participants—is presented in
Figure 12.
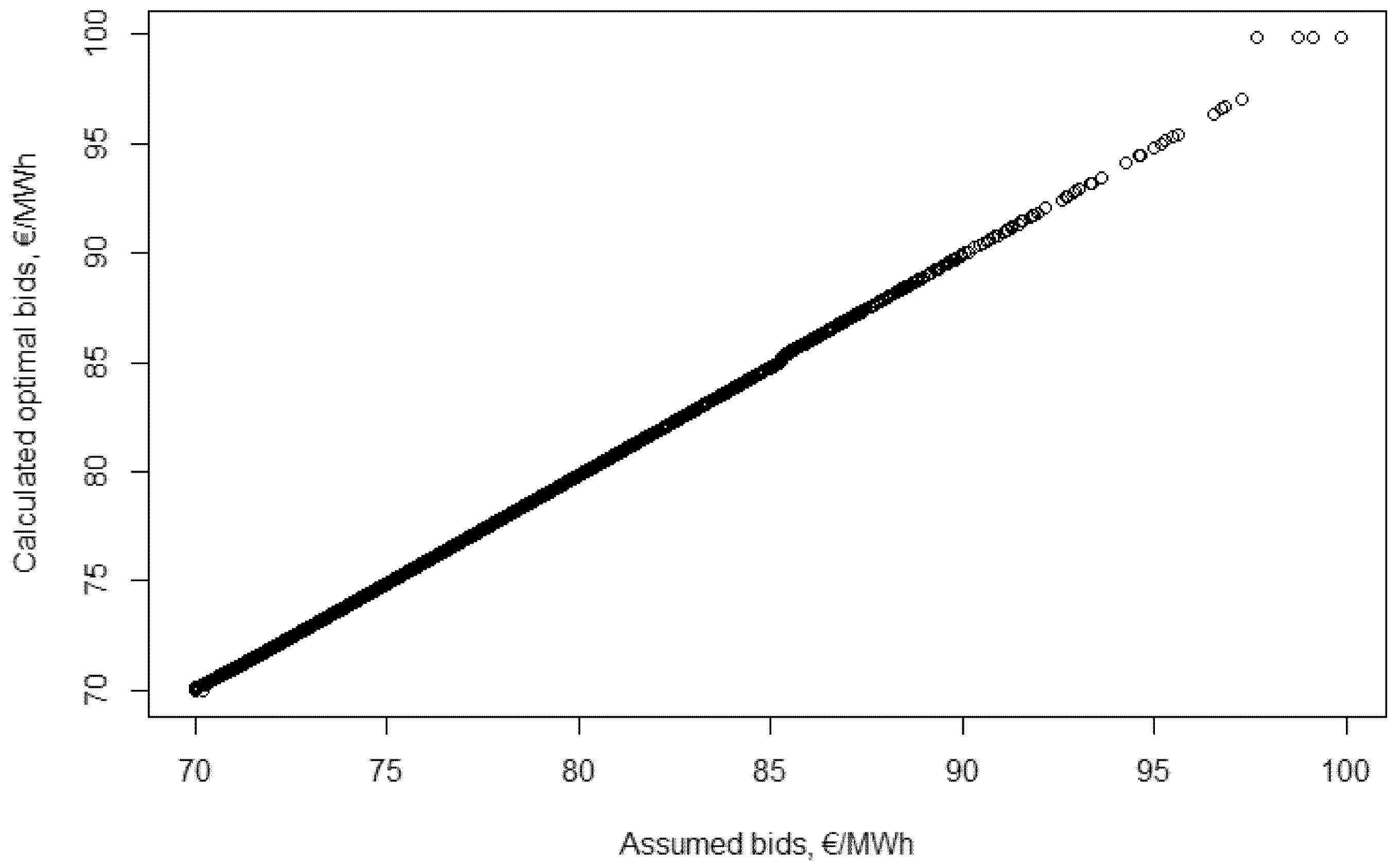
The graph illustrates that the assumed bid function is correct. The assumed and optimal bids for all 10,000 valuations are presented in
Figure 13.
To check that the assumed and optimal bidding strategies are the same the (N)RMSE value can be applied: RMSE is 0.10, while NRMSE is 0.15% (mean values are 73.39 and 73.45). This is lower than the pre-defined stopping criterion 0.2%. This means that the two bid functions are very close to each other. From this it can be concluded that the assumed bid function, is a Nash-equilibrium bidding strategy: when every other player bids according to this function, then the best response is this function, thus when all players use this bid function it is a Nash-equilibrium.
3.3. Auction Results with the Applied Nash-Equilibrium Bid Functions
In this section the results of the simulation of 100 uniform price and 100 pay-as-bid auctions are presented. To make results more comparable the same 100 × 100 valuations will be used throughout the simulations.
The first step is the simulation of the valuation for all 100 participants. Then, assuming all participants use the Nash-equilibrium bid function all 100 bids can be calculated. The smallest 40 bids are chosen as winners. In case of a tie, winners are chosen randomly. Then the strike price for each winner can be specified, and the total support paid out (or the net present value of it) can be calculated. This again uses own forecast for the electricity prices (the same as assumed when the is calculated), as this is the best available information.
The results from the two different rules (uniform price and pay-as-bid) are compared according to the smallest and largest winning bid and the total support. They are also compared to the former German PV auctions, taking into account that not all rules could be implemented into this modelling. Since most of the data used for the calculation is from before 2019, it should be compared with the results from 2017, 2018 and 2019.
As shown on page 12, the Nash-equilibrium bidding strategy is bidding the true valuation under the uniform price rule. Thus, only results of the auction simulation are summarised: the minimum and maximum strike price, and the net present value of the total support.
For each simulation round a valuation “draw” is taken for each of the 100 valuations, using the distribution (see details above). As these valuations are the bids themselves, they are sorted, then the 40 smallest are selected. The strike price is the 41th smallest bid, this will be received by all winners.
The lowest strike price from the 100 auctions is 65.19 €/MWh, and the highest is 70.86 €/MWh. The mean value of the strike prices is 68.33 €/MWh. These values can be the starting point for comparison to determine how much it costs for the state not to incentivise participants to “tell the truth” about their valuations.
The net present value of the total support to be paid in the next 20 years is calculated using the strike price, the monthly average forecasted (and PV generation weighted) electricity prices and the assumed total generation.
For every month the total support consists of the difference between the strike price and the PV generation weighted average wholesale electricity price (in €/MWh), multiplied by the total generation (in MWh). If it is negative, the total support for that month is 0. The assumed symmetry and uniform price rule lead to all 40 winners receiving the same amount of support, meaning the calculation is only needed for 1 participant, and then multiplied by 40 to arrive at the total support. The net present value of the total support to be paid is the following:
where,
is the PV generation weighted average monthly electricity price in year t and month m, and
r is the assumed discount rate.
The minimum support (from the 100 different auction outcomes) is 4.48 million €, and the maximum is 7.16 million €. Out of the 100 auction outcomes the average net present value of support over the next 20 year period is 5.93 million € under the uniform price rule.
For the pay-as-bid auction the most important result is the Nash-equilibrium bid function. According to the literature [
1] the participants typically do not tell their true valuations, and ask for more support (or offer less when participants want to buy something on the auction) than their true valuations, which is confirmed by this model.
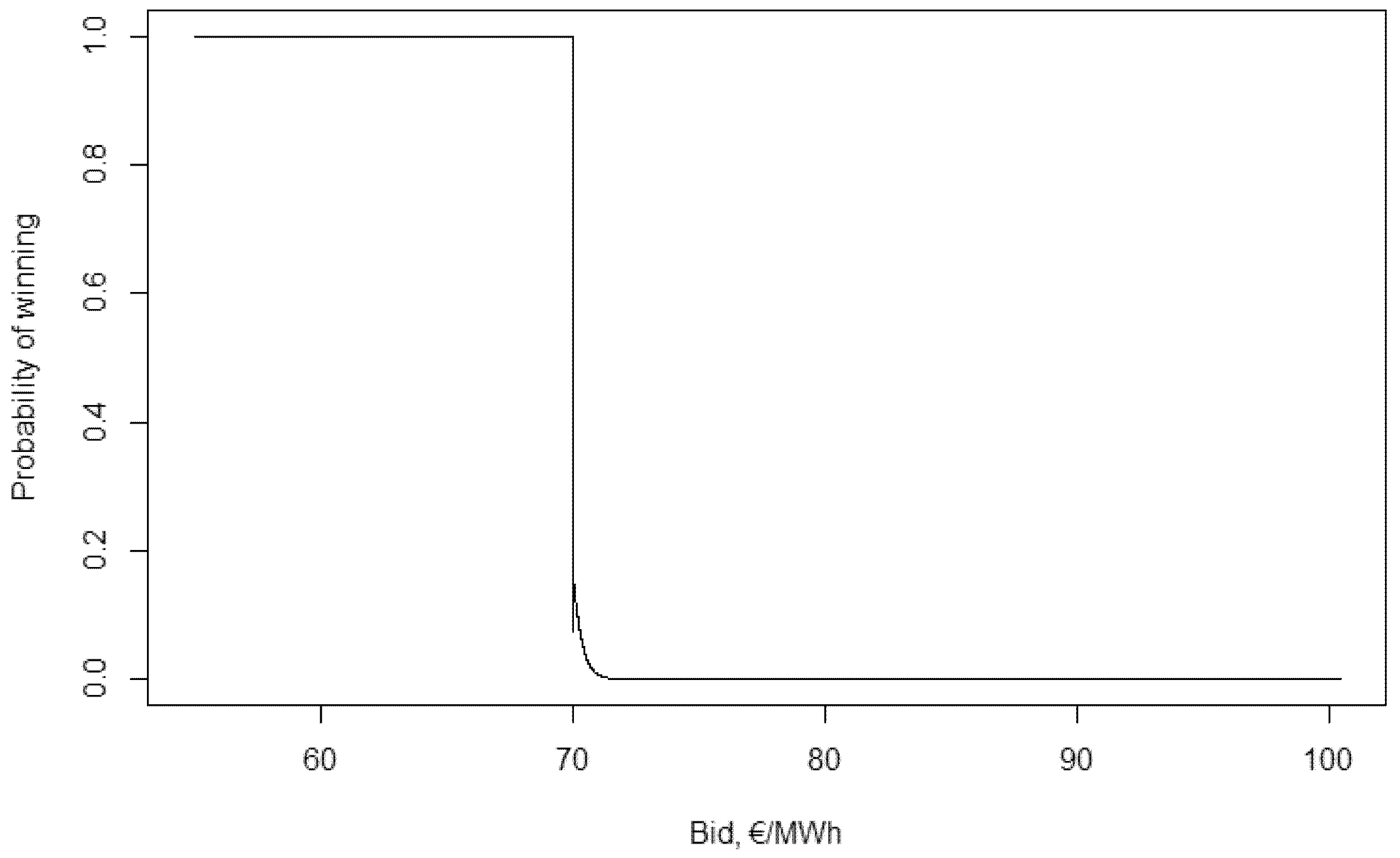
Figure 12 shows that the participants always bid a higher value than their valuation. With a valuation under 69.706 €/MWh their bid will be 70.007 €/MWh, no matter how much lower their valuation is. This is the Nash-equilibrium bid for players with a valuation of 0 as well. Above that, the optimal bid is 0.457 €/MWh higher than the 99.78% of their valuation.
Several bid values were 70.007 €/MWh, which is surprising considering the mean of the valuations is 65.84 €/MWh (calculating from the 10,000 simulated values). There are only 18 cases, with a higher strike price than that in the 100 simulated auction rounds together.
To compare the resulting strike prices and support needs with the uniform price case the calculation slightly differs. Each auction has 40 strike prices, where the support level must also be calculated for all 40 winners separately (for all 100 auctions).
The mean of the support requirement is 6.74 million euros, while the most and least expensive auctions have a cost of 6.75 and 6.74 million euros. This means auction results are quite stable and, more importantly, in most, but not all of the cases, more expensive than the uniform price auctions. The results are summarised in
Table 6.
This is an important message for policy makers: according to this model when a group of participants have a 0 valuation (no support is needed for them), and we consider monotone (but not strictly monotone) bid functions, then the uniform price rule (on average) leads to lower support requirements than the pay-as-bid rule, by incentivising participants to bid according to their true valuations. Eventhough this is a special case considering all of the limitations of the model, it is still an interesting and relevant result.
In case of the ordinary auction theory models (assuming bid functions that have an inverse) normally the revenue equivalence theorem stands in most of the cases (see [
1]). This means that this work covers a specific different case. Similar results are included in [
48], where authors analyse discrete bids and valuations, and arrive to different bid functions compared to the theoretical continuous situation. It is not stated explicitly, but conceivable based on the results, that the revenue equivalence theorem no longer stands in their case neither.
As most of the former models include very different assumptions here the results are compared to the actual German PV auction outcomes. The minimum and maximum strike prices are compared in
Table 7.
The results indicate, that the modelled strike prices are rather high comparatively, the only higher prices are observable from the larger (500 MW) auction in March 2019, which can be explained by several factors. It could be a result of own cost calculation not being reflecting precise actual costs. Furthermore, the bid ceiling was not introduced here for the sake of simplicity.
Participants in real life may not calculate the Nash-equilibrium strategies and bid according to them. This is an important limitation of this work, when it comes to policy decisions. However, eventhough the calculation in this specific case is rather complicated, it still can be assumed, that in case of such a large investment the participants are willing to bid according to their best interest.
Unfortunately, we can not compare the difference between the real valuations and the bids, since the information is not publicly available for exact costs of bidders. Only realisation rates of the projects for the first two auctions in 2017 are known, ending up near 100%: 98.85% and 96.74%. This means that the strike price in these auctions were at least as high as the valuation of the bidders.
It should also be emphasised, that in the modelling a typical auction was considered: with 100 participants and 200 MW capacity. The real auctions have similar but not identical attributes. Changing these parameters can also bring some uncertainty regarding the results, a possible future research could answer how robust are them when it comes to different number of participants and winners.
In this model it is a novelty, that investors with 0 support participate in the auctions. With PV cost reduction still underway this can happen in the near future. It is evident, that this situation reveals different bidding behaviour, making the findings of this work important for policy makers. The biggest takeaway is the following: uniform pricing rules might lead to more cost efficient support allocation compared to the pay-as-bid pricing mechanism, through incentivising participants to bid according to their true valuations.