Optimal Operation Scheduling Considering Cycle Aging of Battery Energy Storage Systems on Stochastic Unit Commitments in Microgrids
Abstract
1. Introduction
1.1. Background
1.2. Literature Review
1.3. Contributions and Paper Organization
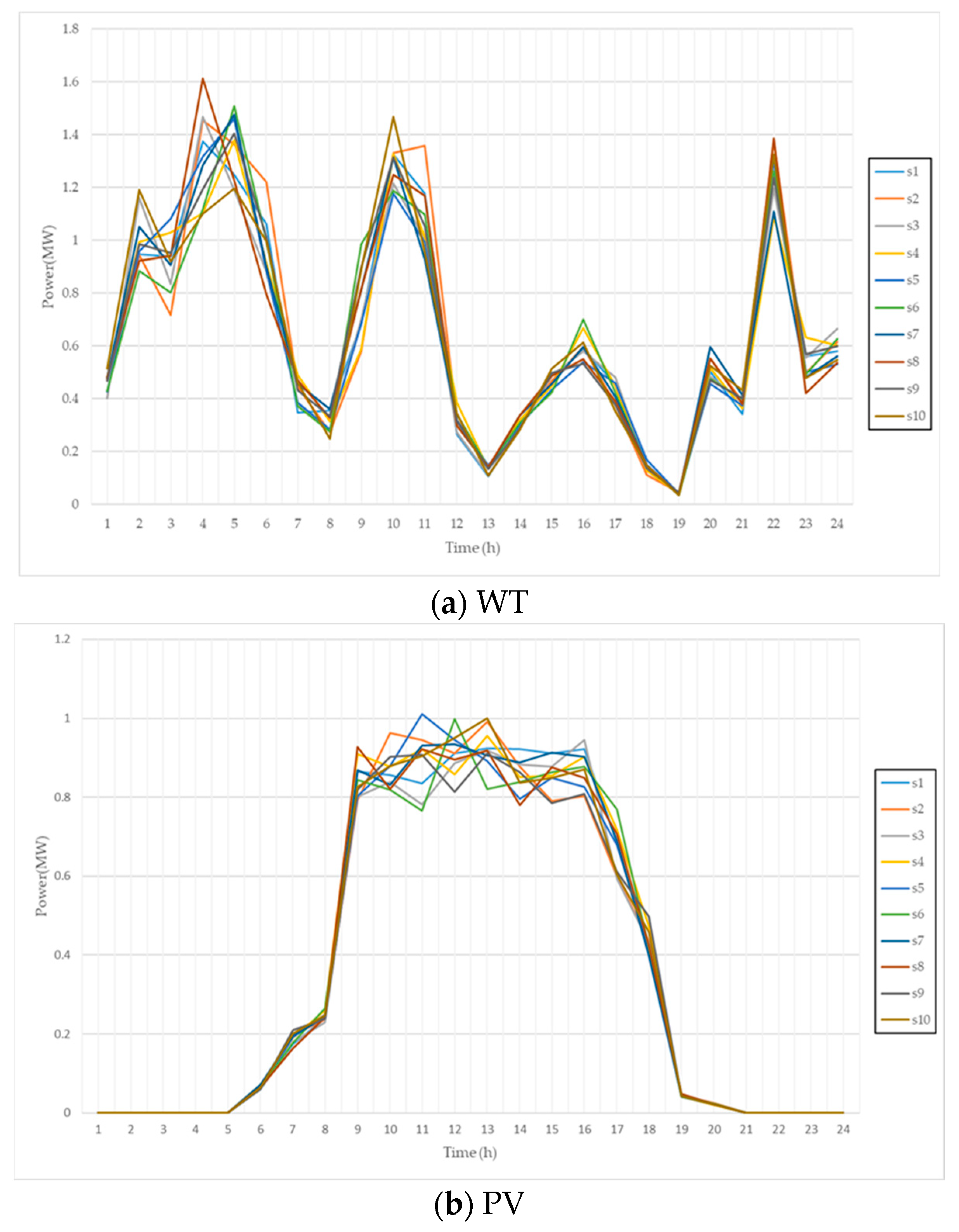
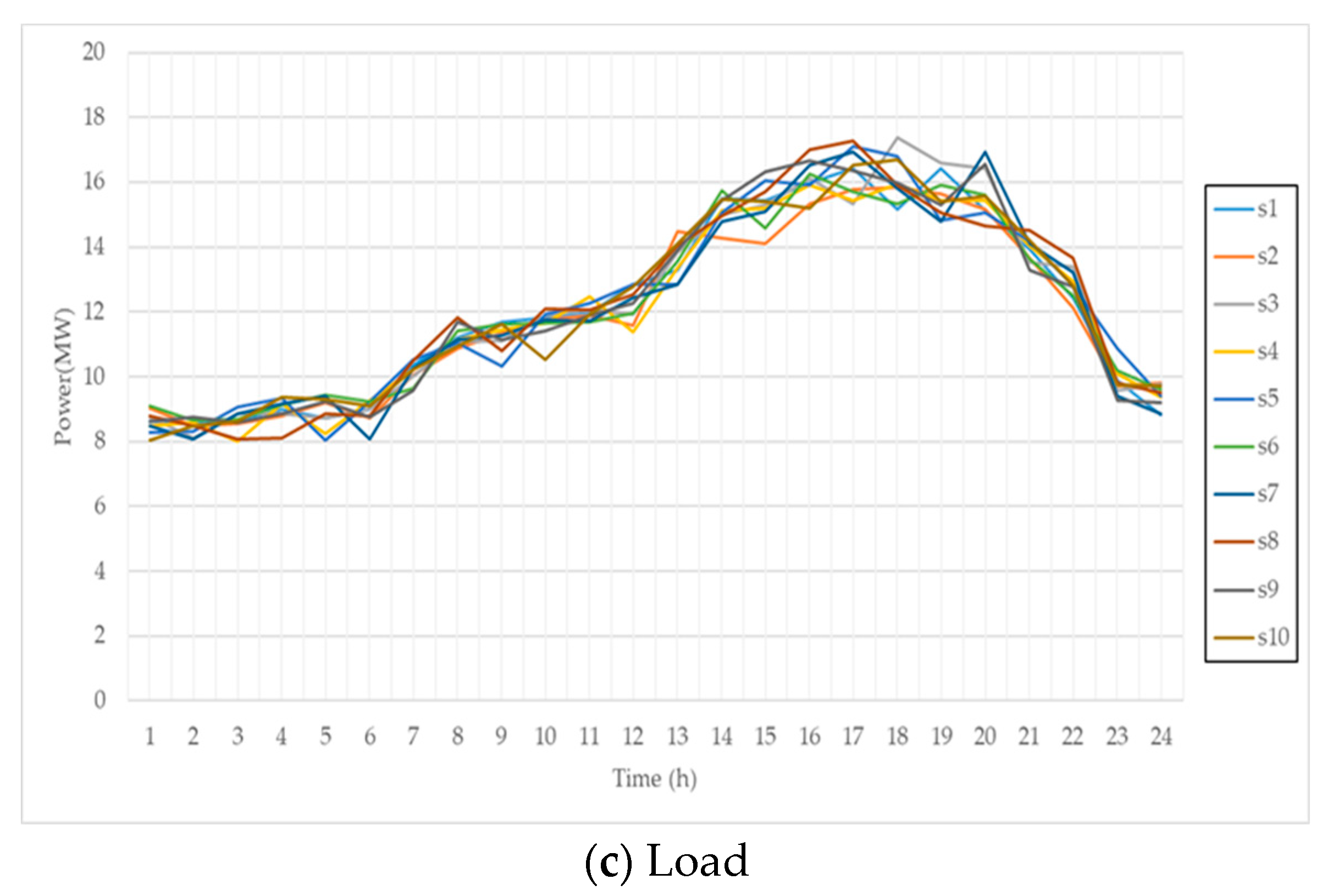
- Considering the uncertain characteristics of WTs, PVs, and load, historical data are generated through MCS based on the distribution function of each uncertain variable. The generated scenarios are reduced to cluster scenarios with a similar dense distribution through K-means clustering.
- Using the rainflow-counting algorithm, the SOC profile of the BESS is expressed as a charging/discharging cycle. By partially linearizing the nonlinear cycle aging stress function through linear approximation, the DOD cycle aging is formulated in the SUC problem.
- Using Benders decomposition (BD), the proposed optimal BESS scheduling is formulated as a master problem and a set of subproblems via parallel processing. In BD, the master problem solves SUC only through MILP without considering the BESS. The subproblem set derives the optimal operation scheduling considering the cycle aging of the BESS.
- The superiority of the proposed optimal BESS operation scheduling is shown by comparison with other cases. The simulation results confirm that the proposed scheduling is more effective at reducing the TOC and LCC simultaneously, while the life cycle of the BESS also increases significantly. Furthermore, by implementing BD, the convergence speed of the optimization process is improved in comparison with the cases without BD.
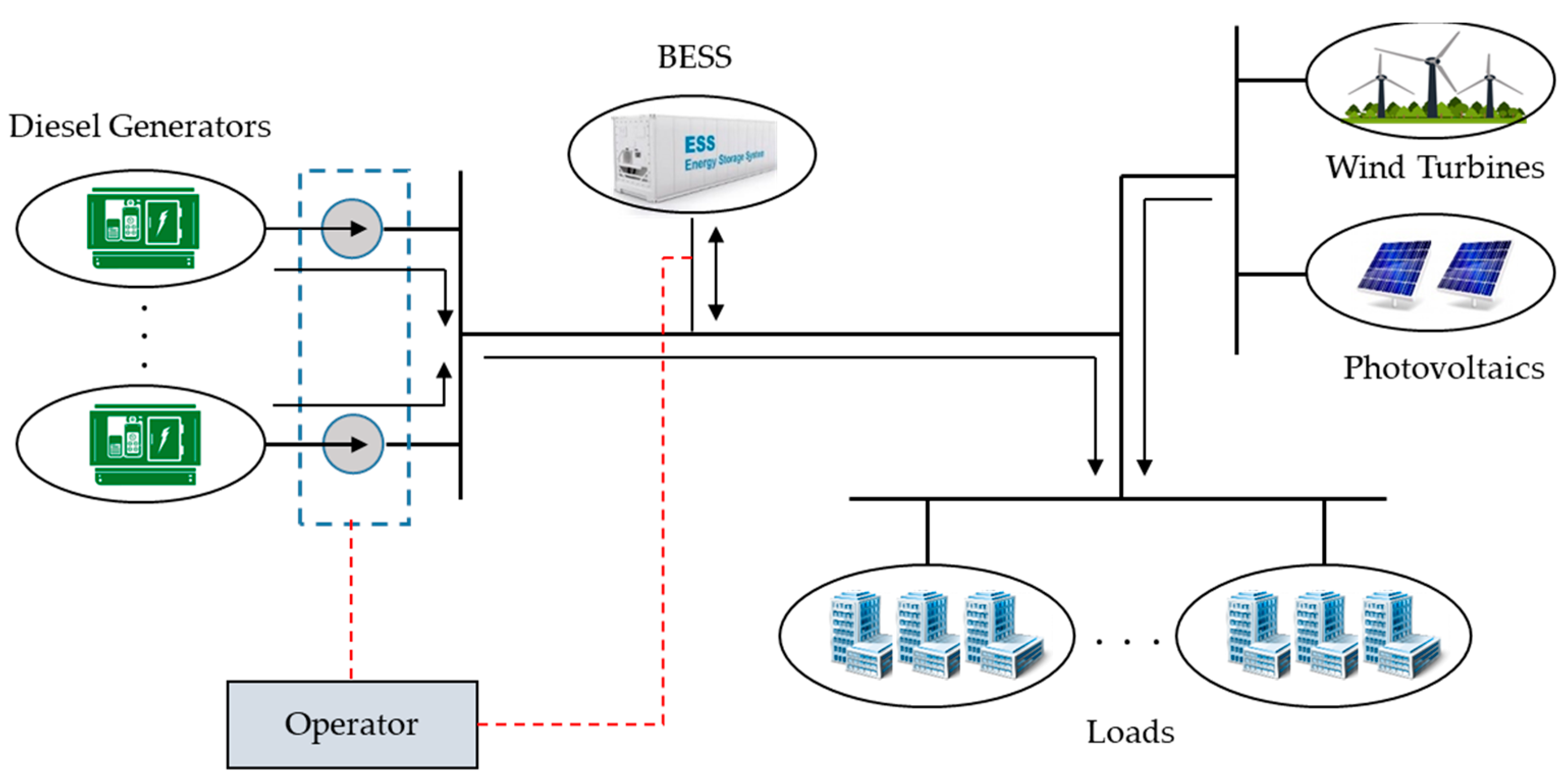
2. MG Modeling
2.1. Renewable Energy Sources Modeling
2.1.1. WT
2.1.2. PV
2.1.3. Load
2.2. Uncertainty Analysis Model
3. BESS Modeling
3.1. Operation Model
3.2. Life Cycle Aging Model
3.2.1. Rainflow-Counting Algorithm
- The procedure starts from and involves the calculation of and ;
- If and , a full cycle of depth is confirmed. Thereafter, are removed from the profile, and step (2) is repeated using points …;
- If a cycle is not confirmed, the confirmation is shifted forward, and step (2) is repeated using points …;
- The confirmation is repeated until no more full cycles can be confirmed throughout the remaining profile.
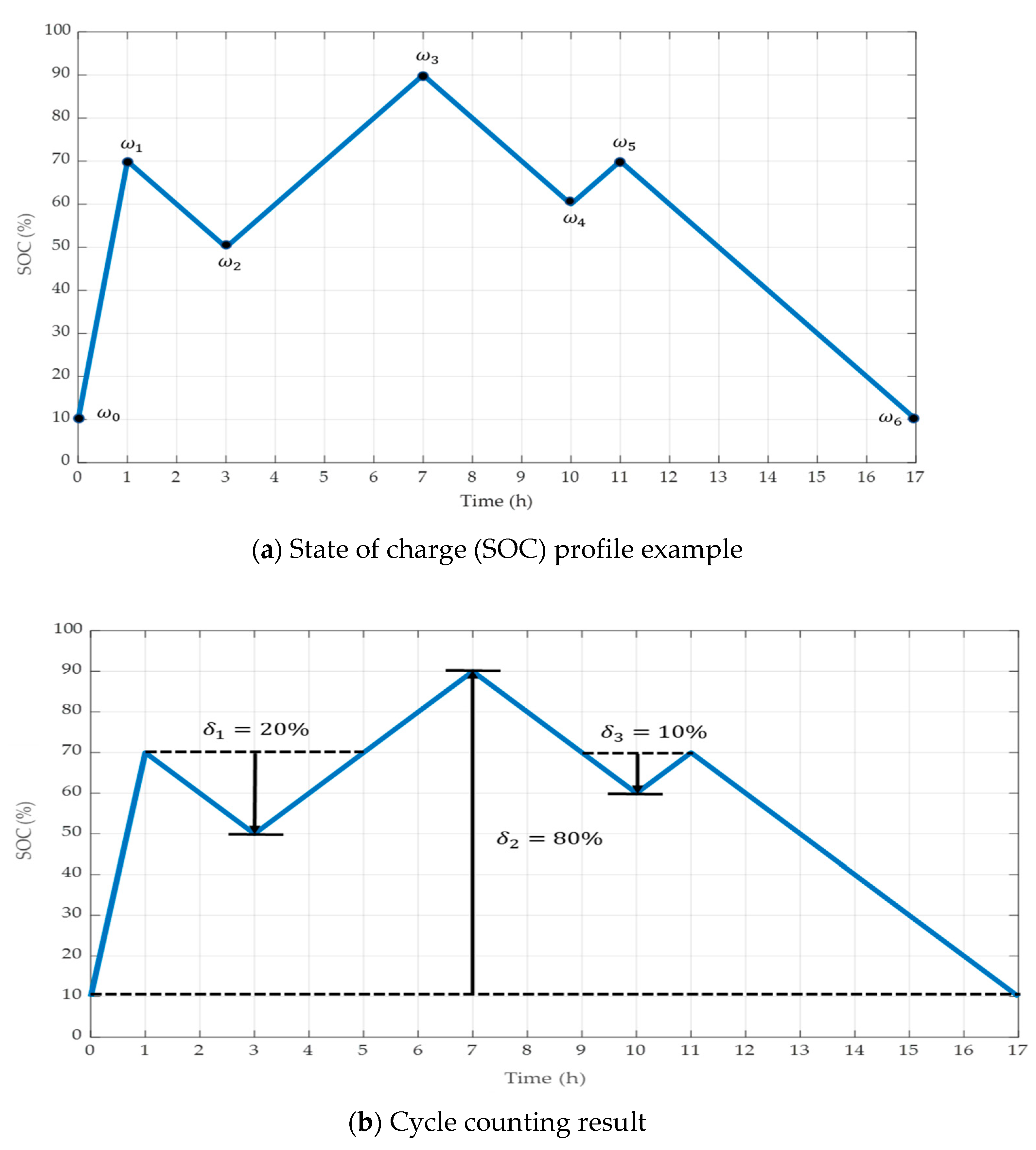
3.2.2. LCC
4. Proposed SUC Optimization
4.1. Objective Function
4.2. System Constraints
4.2.1. Balancing Constraints
4.2.2. DG Constraints
4.2.3. RES Constraints
4.2.4. BESS Constraints
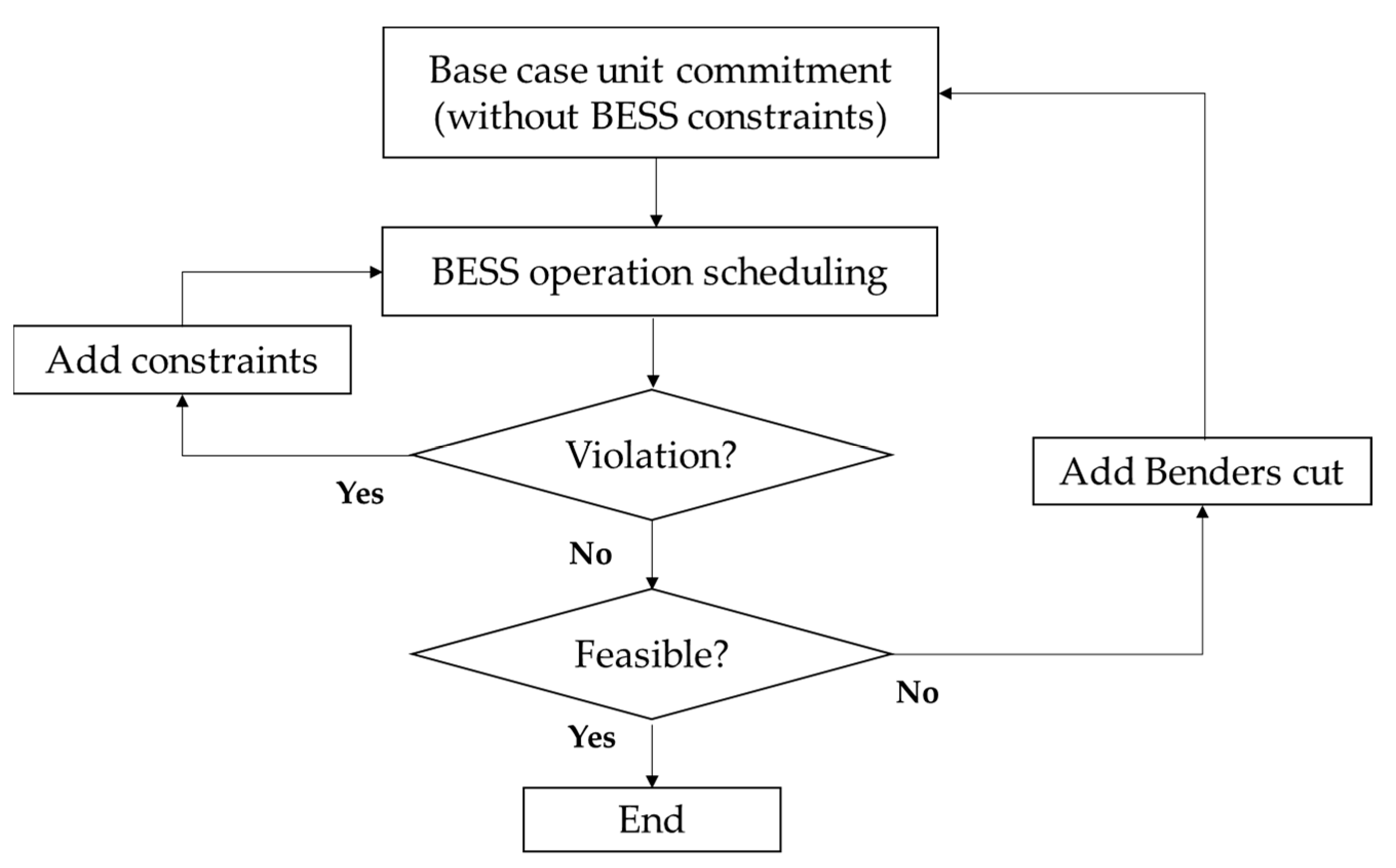
4.3. Benders Decomposition
4.3.1. Subproblem
4.3.2. Master Problem
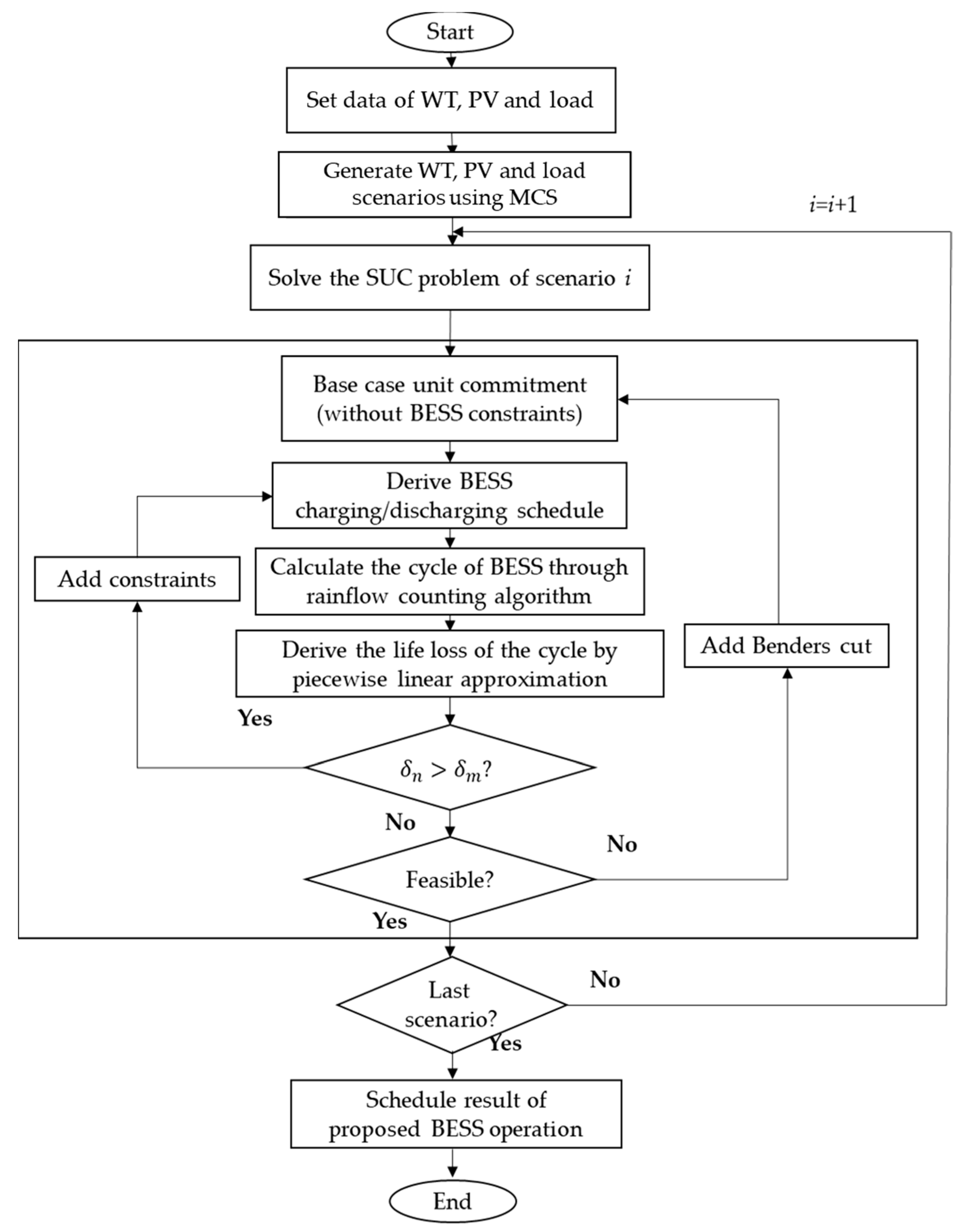
4.4. Solution Procedure
- Step 1:
- Set the DG, PV, WT, load, and BESS data;
- Step 2:
- Following the error of elements, generate each WT, PV, and load scenario using MCS and obtain the representative scenarios according to K-means clustering;
- Step 3:
- Solve the SUC problem by implementing BD.
- (a)
- Compute the base case of the SUC problem (master problem), which does not consider the BESS constraints, through MILP.
- (b)
- Apply BESS to maximize the MG revenue.
- (b1)
- Configure the BESS charging/discharging schedule according to generating volumes and power generation (subproblem).
- (b2)
- Calculate the LCC of the BESS using the rainflow-counting algorithm and linear approximation.
- (b3)
- Derive the LCC of the BESS.
- (b4)
- Add Benders cut to the master problem according to the DOD.
- Step 4:
- Return to Step 3 until the last scenario is solved.
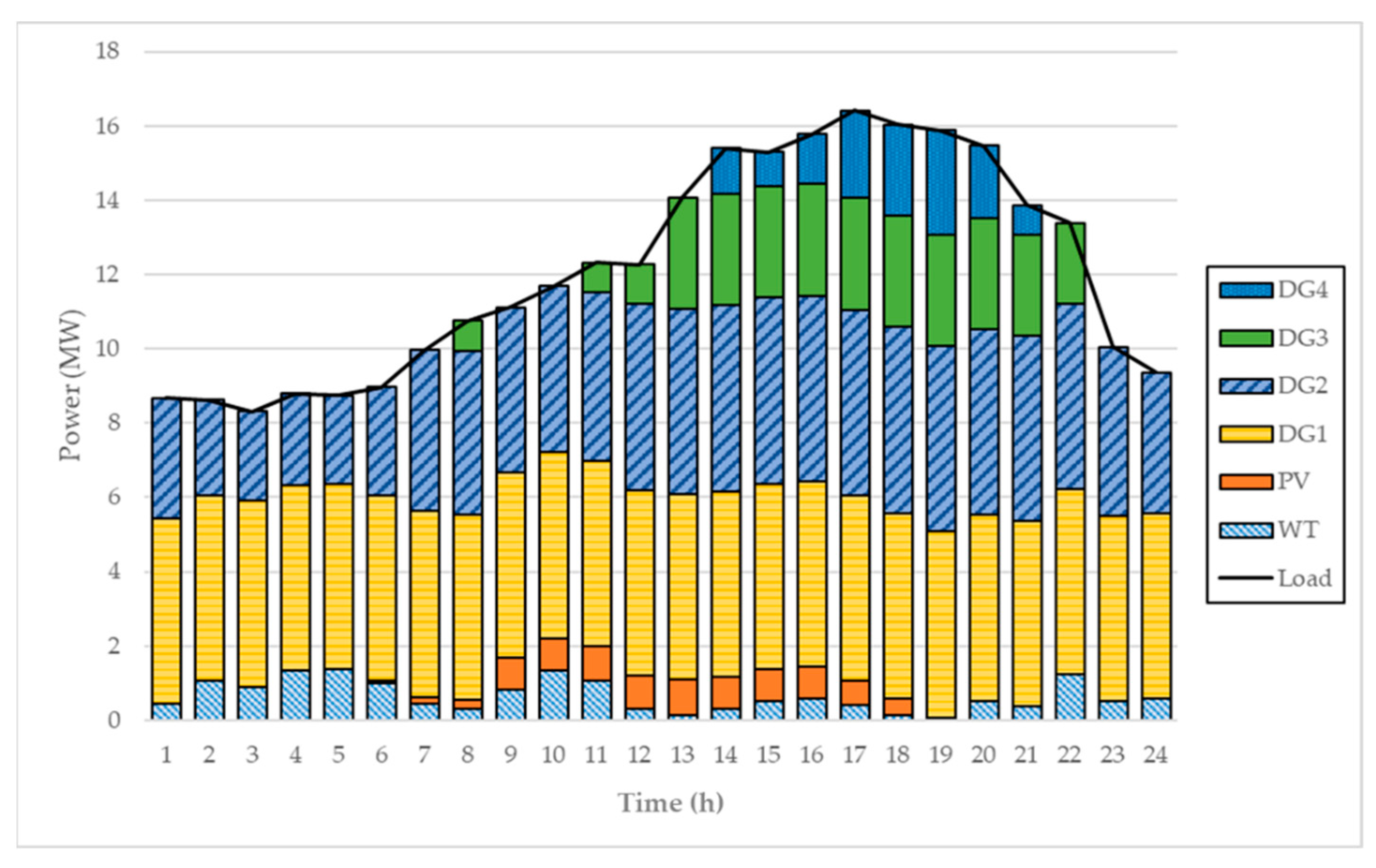
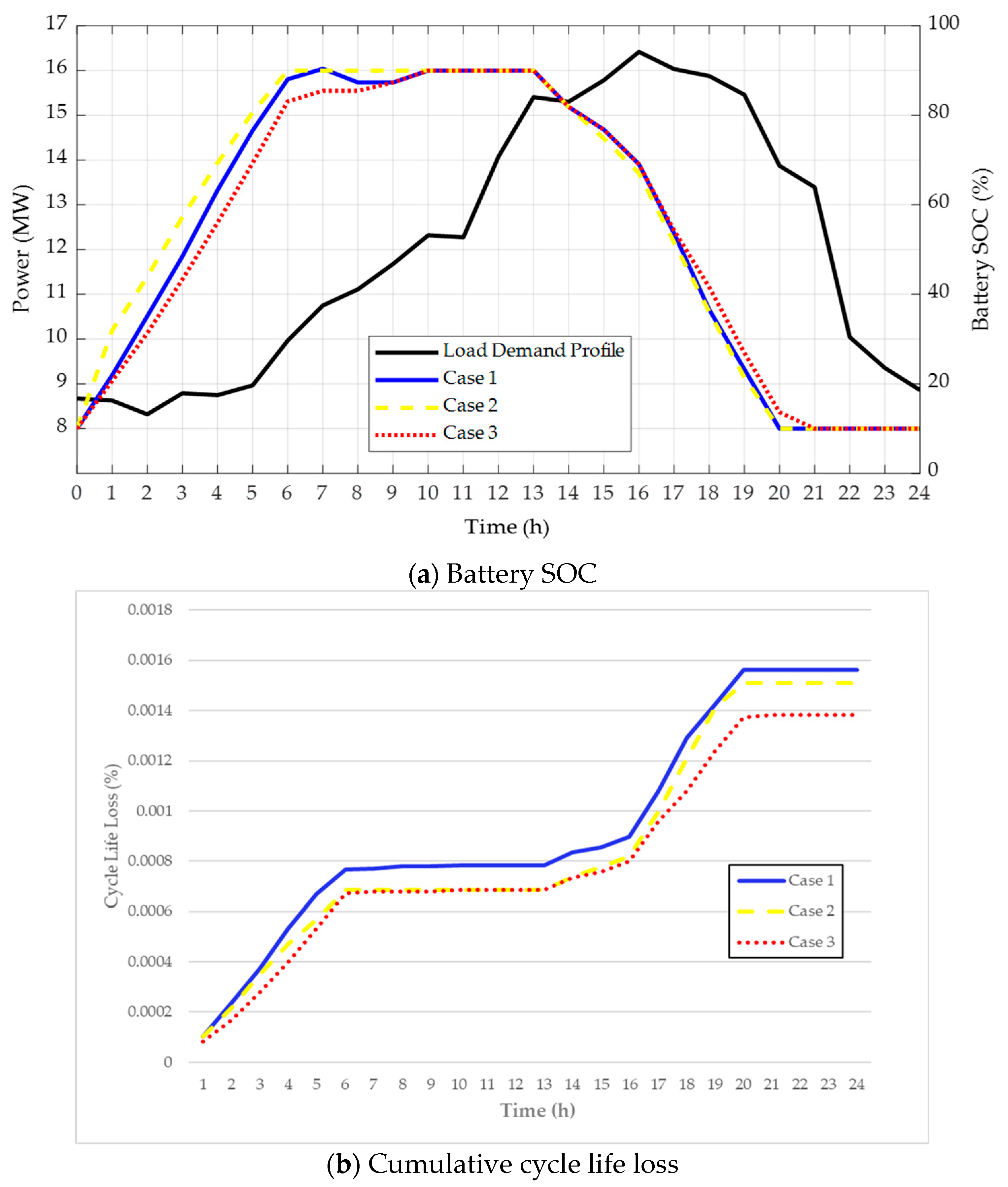
5. Case Studies
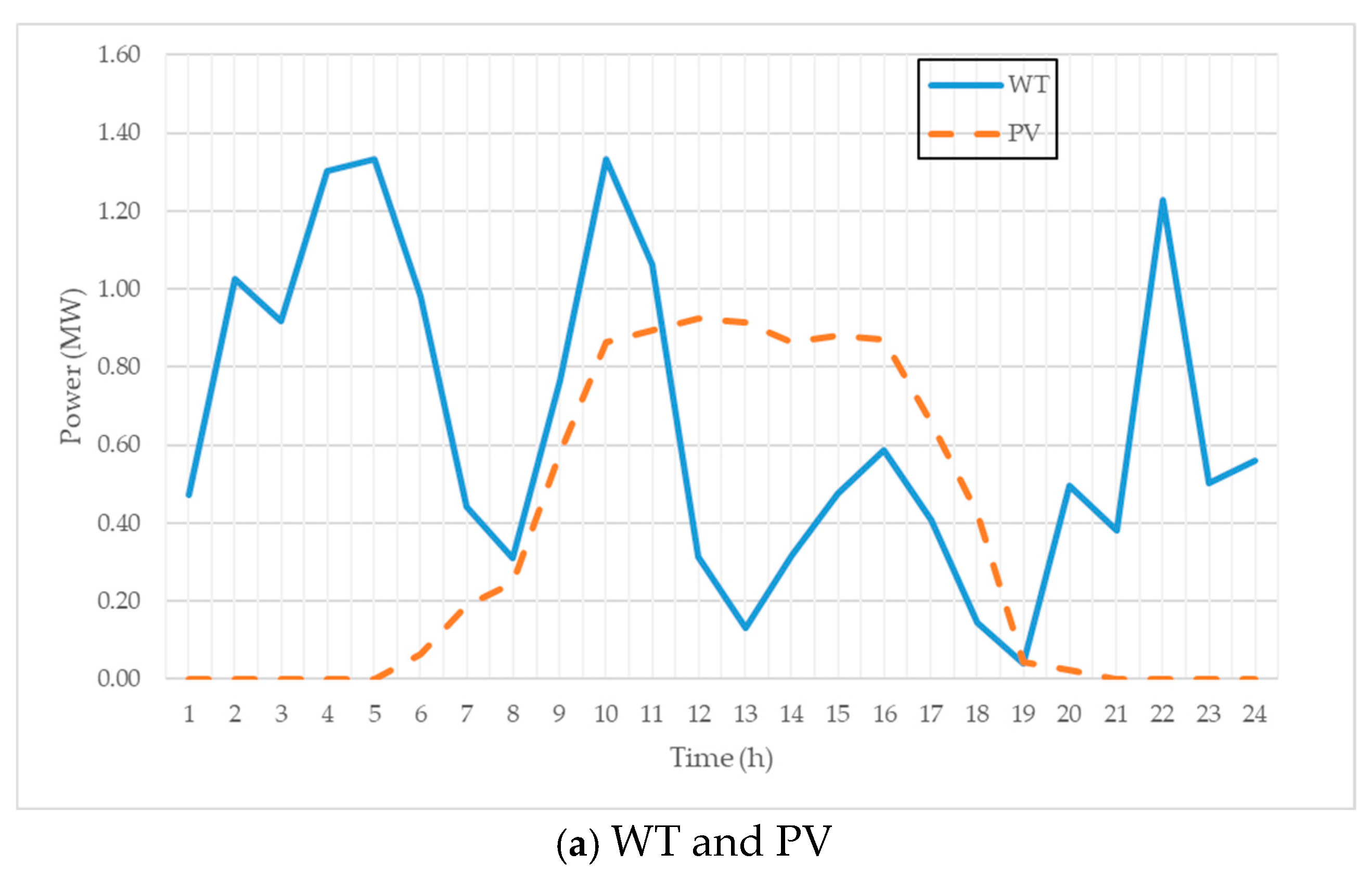
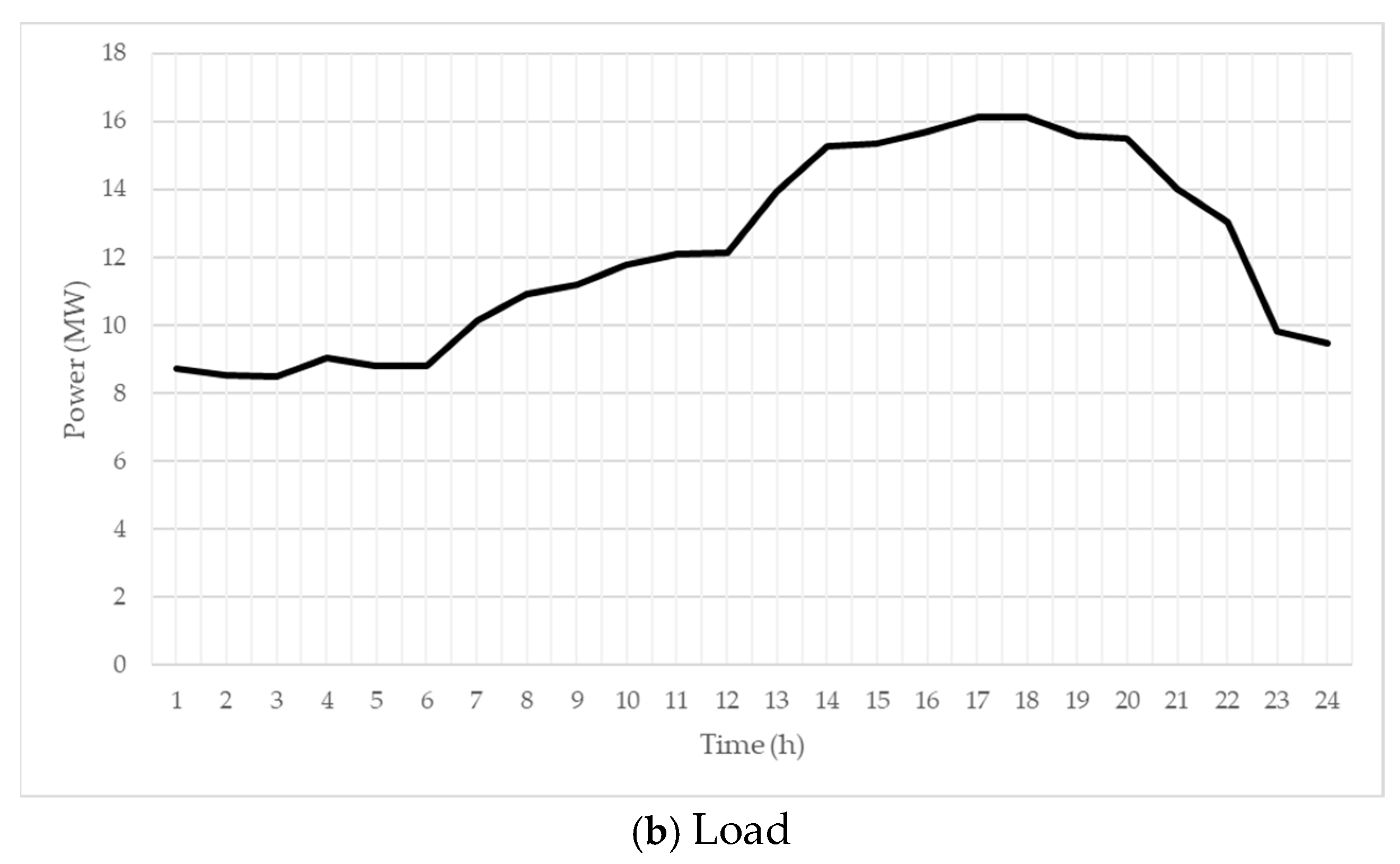
Dataset of MG
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Soshinskaya, M.; Crijns-Graus, W.H.; Guerrero, J.M.; Vasquez, J.C. Microgrids: Experiences, barriers and success factors. Renew. Sustain. Energy Rev. 2014, 40, 659–672. [Google Scholar] [CrossRef]
- Wang, J.; Xu, Y.; Lv, M. Modeling and Simulation Analysis of Hybrid Energy Storage System Based on Wind Power Generation System. In Proceedings of the 2018 International Conference on Control, Automation and Information Sciences (ICCAIS), Hangzhou, China, 24–27 October 2018; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2018; pp. 422–427. [Google Scholar]
- Divya, K.; Østergaard, J. Battery energy storage technology for power systems—An overview. Electr. Power Syst. Res. 2009, 79, 511–520. [Google Scholar] [CrossRef]
- Oudalov, A.; Cherkaoui, R.; Beguin, A. Sizing and Optimal Operation of Battery Energy Storage System for Peak Shaving Application. In 2007 IEEE Lausanne Power Tech; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2007; pp. 621–625. [Google Scholar]
- Zhao, B.; Zhang, X.; Chen, J.; Wang, C.; Guo, L. Operation Optimization of Standalone Microgrids Considering Lifetime Characteristics of Battery Energy Storage System. IEEE Trans. Sustain. Energy 2013, 4, 934–943. [Google Scholar] [CrossRef]
- Sheble, G.B.; Fahd, G.N. Unit commitment literature synopsis. IEEE Trans. Power Syst. 1994, 9, 128–135. [Google Scholar] [CrossRef]
- Jabbari-Sabet, R.; Moghaddas-Tafreshi, S.-M.; Mirhoseini, S.-S. Microgrid operation and management using probabilistic reconfiguration and unit commitment. Int. J. Electr. Power Energy Syst. 2016, 75, 328–336. [Google Scholar] [CrossRef]
- Siahkali, H.; Vakilian, M. Stochastic unit commitment of wind farms integrated in power system. Electr. Power Syst. Res. 2010, 80, 1006–1017. [Google Scholar] [CrossRef]
- Jo, K.-H.; Kim, M. Stochastic Unit Commitment Based on Multi-Scenario Tree Method Considering Uncertainty. Energies 2018, 11, 740. [Google Scholar] [CrossRef]
- Kim, H.; Kim, M.; Lee, J. A two-stage stochastic p-robust optimal energy trading management in microgrid operation considering uncertainty with hybrid demand response. Int. J. Electr. Power Energy Syst. 2021, 124, 106422. [Google Scholar] [CrossRef]
- Bruninx, K.; Delarue, E. Scenario reduction techniques and solution stability for stochastic unit commitment problems. In Proceedings of the 2016 IEEE International Energy Conference (ENERGYCON), Leuven, Belgium, 4–8 April 2016; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2016; pp. 1–7. [Google Scholar]
- Olivares, D.E.; Canizares, C.A.; Kazerani, M. A Centralized Energy Management System for Isolated Microgrids. IEEE Trans. Smart Grid 2014, 5, 1864–1875. [Google Scholar] [CrossRef]
- Farhadi, M.; Mohammed, O. Energy Storage Technologies for High-Power Applications. IEEE Trans. Ind. Appl. 2016, 52, 1953–1961. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, J.; Wang, X. An improved charging/discharging strategy of lithium batteries considering depreciation cost in day-ahead microgrid scheduling. Energy Convers. Manag. 2015, 105, 675–684. [Google Scholar]
- Kim, R.-K.; Glick, M.B.; Olson, K.R.; Kim, Y.-S. MILP-PSO Combined Optimization Algorithm for an Islanded Microgrid Scheduling with Detailed Battery ESS Efficiency Model and Policy Considerations. Energies 2020, 13, 1898. [Google Scholar] [CrossRef]
- Alvarado-Barrios, L.; Del Nozal, Á.R.; Valerino, J.B.; Vera, I.G.; Martínez-Ramos, J.L. Stochastic unit commitment in microgrids: Influence of the load forecasting error and the availability of energy storage. Renew. Energy 2020, 146, 2060–2069. [Google Scholar] [CrossRef]
- He, G.; Chen, Q.; Kang, C.; Pinson, P.; Xia, Q. Optimal Bidding Strategy of Battery Storage in Power Markets Considering Performance-Based Regulation and Battery Cycle Life. IEEE Trans. Smart Grid 2016, 7, 2359–2367. [Google Scholar] [CrossRef]
- Dong, X.; Yuying, Z.; Tong, Z. Planning-operation co-optimization model of active distribution network with energy storage considering the lifetime of batteries. IEEE Access 2018, 6, 59822–59832. [Google Scholar] [CrossRef]
- Xu, B.; Oudalov, A.; Ulbig, A.; Andersson, G.; Kirschen, D.S. Modeling of Lithium-Ion Battery Degradation for Cell Life Assessment. IEEE Trans. Smart Grid 2018, 9, 1131–1140. [Google Scholar] [CrossRef]
- Motapon, S.N.; Lachance, E.; Dessaint, L.A.; Al-Haddad, K. A Generic Cycle Life Model for Lithium-Ion Batteries Based on Fatigue Theory and Equivalent Cycle Counting. IEEE Open J. Ind. Electron. Soc. 2020, 1, 207–217. [Google Scholar] [CrossRef]
- Alam, M.J.E.; Saha, T.K. Cycle-life degradation assessment of Battery Energy Storage Systems caused by solar PV variability. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2016; pp. 1–5. [Google Scholar]
- Eom, J.-K.; Noh, Y.-S.; Lee, S.-R.; Choi, B.-Y.; Won, C.-Y. ESS operation algorithm for economics considering battery degradation properties. In Proceedings of the 2014 IEEE Conference and Expo Transportation Electrification Asia-Pacific (ITEC Asia-Pacific), Beijing, China, 31 August–3 September 2014; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2014; pp. 1–5. [Google Scholar]
- Choi, Y.; Kim, H. Optimal Scheduling of Energy Storage System for Self-Sustainable Base Station Operation Considering Battery Wear-Out Cost. Energies 2016, 9, 462. [Google Scholar] [CrossRef]
- Kim, H.; Kim, M. Optimal generation rescheduling for meshed AC/HIS grids with multi-terminal voltage source converter high voltage direct current and battery energy storage system. Energy 2017, 119, 309–321. [Google Scholar] [CrossRef]
- Fan, H.; Yuan, Q.; Cheng, H. Multi-Objective Stochastic Optimal Operation of a Grid-Connected Microgrid Considering an Energy Storage System. Appl. Sci. 2018, 8, 2560. [Google Scholar] [CrossRef]
- Uddin, M.; Romlie, M.F.; Abdullah, M.; Tan, C.; Shafiullah, G.; Bakar, A. A novel peak shaving algorithm for islanded microgrid using battery energy storage system. Energy 2020, 196, 117084. [Google Scholar] [CrossRef]
- Alamri, A.; AlOwaifeer, M.; Meliopoulos, A.P.S. Multi-Objective Unit Commitment Economic Dispatch for Power Systems Reliability Assessment. In Proceedings of the 2020 International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), Liege, Belgium, 18–21 August 2020; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar]
- Vatanpour, M.; Yazdankhah, A.S. The impact of energy storage modeling in coordination with wind farm and thermal units on security and reliability in a stochastic unit commitment. Energy 2018, 162, 476–490. [Google Scholar] [CrossRef]
- Eisenhut, C.; Krug, F.; Schram, C.; Klckl, B. Wind-Turbine Model for System Simulations Near Cut-In Wind Speed. IEEE Trans. Energy Convers. 2007, 22, 414–420. [Google Scholar] [CrossRef]
- Tsai, H.L.; Tu, C.S.; Su, Y.J. Development of generalized photovoltaic model using MATLAB/SIMULINK. In Proceedings of the World Congress on Engineering and Computer Science, San Francisco, CA, USA, 22–24 October 2008; Volume 2008. [Google Scholar]
- He, S.; Yang, S.; Cao, X.; Lu, Z.; Zhang, H.; Wei, Z. Short-term Power Load Probability Density Forecasting Based on PCA-QRF. In Proceedings of the 2018 2nd IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 20–22 October 2018; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2018; pp. 1–5. [Google Scholar]
- Ryu, H.-S.; Kim, M. Two-Stage Optimal Microgrid Operation with a Risk-Based Hybrid Demand Response Program Considering Uncertainty. Energies 2020, 13, 6052. [Google Scholar] [CrossRef]
- Sarker, M.R.; Murbach, M.D.; Schwartz, D.T.; Ortega-Vazquez, M.A. Optimal operation of a battery energy storage system: Trade-off between grid economics and storage health. Electr. Power Syst. Res. 2017, 152, 342–349. [Google Scholar] [CrossRef]
- Ecker, M.; Nieto, N.; Käbitz, S.; Schmalstieg, J.; Blanke, H.; Warnecke, A.; Sauer, D.U. Calendar and cycle life study of Li (NiMnCo) O2-based 18650 lithium-ion batteries. J. Power Sources 2014, 248, 839–851. [Google Scholar] [CrossRef]
- Musallam, M.; Johnson, C.M. An Efficient Implementation of the Rainflow Counting Algorithm for Life Consumption Estimation. IEEE Trans. Reliab. 2012, 61, 978–986. [Google Scholar] [CrossRef]
- Lee, Y.L.; Barkey, M.E.; Kang, H.T. Metal Fatigue Analysis Handbook: Practical Problem-Solving Techniques for Computer-Aided Engineering; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Xu, B.; Zhao, J.; Zheng, T.; Litvinov, E.; Kirschen, D.S. Factoring the cycle aging cost of batteries participating in electricity markets. IEEE Trans. Power Syst. 2017, 33, 2248–2259. [Google Scholar]
- Weitzel, T.; Schneider, M.; Glock, C.H.; Löber, F.; Rinderknecht, S. Operating a storage-augmented hybrid microgrid considering battery aging costs. J. Clean. Prod. 2018, 188, 638–654. [Google Scholar] [CrossRef]
- Khodaei, A. Microgrid Optimal Scheduling With Multi-Period Islanding Constraints. IEEE Trans. Power Syst. 2013, 29, 1383–1392. [Google Scholar] [CrossRef]


| Sources | Cost Coefficient (USD/MWh) | Minimum Up/Down Time (h) | ||||
|---|---|---|---|---|---|---|
| DG 1 | 27.7 | 1 | 5 | 2.5 | 2.5 | 3 |
| DG 2 | 39.1 | 1 | 5 | 2.5 | 2.5 | 3 |
| DG 3 | 61.3 | 0.8 | 3 | 3 | 3 | 1 |
| DG 4 | 65.6 | 0.8 | 3 | 3 | 3 | 1 |
| WT | 0 | 0 | 1.5 | - | - | - |
| PV | 0 | 0 | 1 | - | - | - |
| BESS Parameters | Value |
|---|---|
| Charging and discharging power rating | 3 MW |
| Energy capacity | 15 MWh |
| Charging and discharging efficiency | 95% |
| Maximum SOC | 90% |
| Minimum SOC | 10% |
| Battery replacement cost | 300,000 USD/MWh |
| Case | Generating Cost (USD) | LCC (USD) | TOC (USD) | Lifetime (Days) | Savings (%) |
|---|---|---|---|---|---|
| Base | 10,072 | 0 | 10,072 | - | 0 |
| 1 | 9736.7 | 328.6 | 10,065.3 | 2880 | 0.067 |
| 2 | 9783.5 | 272.8 | 10,056.3 | 2930 | 0.156 |
| 3 | 9722.9 | 256.7 | 9979.6 | 3260 | 0.918 |
| Case | Iterations (w/o BD) | Iterations (with BD) | Ratio |
|---|---|---|---|
| 1 | 17 | 14 | 0.82 |
| 2 | 16 | 13 | 0.84 |
| 3 | 25 | 16 | 0.64 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, Y.-R.; Kim, H.-J.; Kim, M.-K. Optimal Operation Scheduling Considering Cycle Aging of Battery Energy Storage Systems on Stochastic Unit Commitments in Microgrids. Energies 2021, 14, 470. https://doi.org/10.3390/en14020470
Lee Y-R, Kim H-J, Kim M-K. Optimal Operation Scheduling Considering Cycle Aging of Battery Energy Storage Systems on Stochastic Unit Commitments in Microgrids. Energies. 2021; 14(2):470. https://doi.org/10.3390/en14020470
Chicago/Turabian StyleLee, Yong-Rae, Hyung-Joon Kim, and Mun-Kyeom Kim. 2021. "Optimal Operation Scheduling Considering Cycle Aging of Battery Energy Storage Systems on Stochastic Unit Commitments in Microgrids" Energies 14, no. 2: 470. https://doi.org/10.3390/en14020470
APA StyleLee, Y.-R., Kim, H.-J., & Kim, M.-K. (2021). Optimal Operation Scheduling Considering Cycle Aging of Battery Energy Storage Systems on Stochastic Unit Commitments in Microgrids. Energies, 14(2), 470. https://doi.org/10.3390/en14020470






