Development of a Resolver-to-Digital Converter Based on Second-Order Difference Generalized Predictive Control †
Abstract
1. Introduction
2. Theoretical Foundations
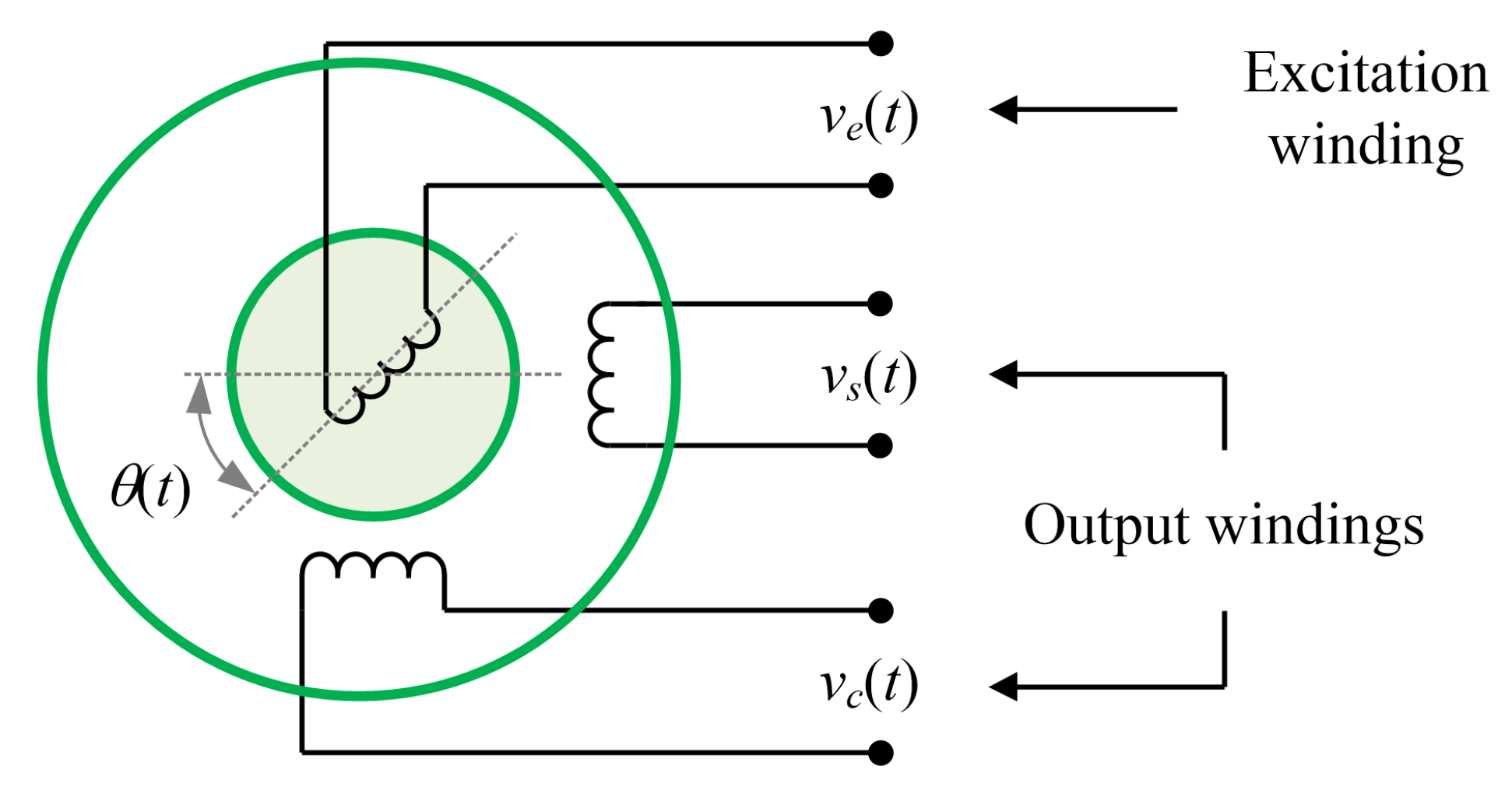
2.1. Resolver
2.2. Difference Operation
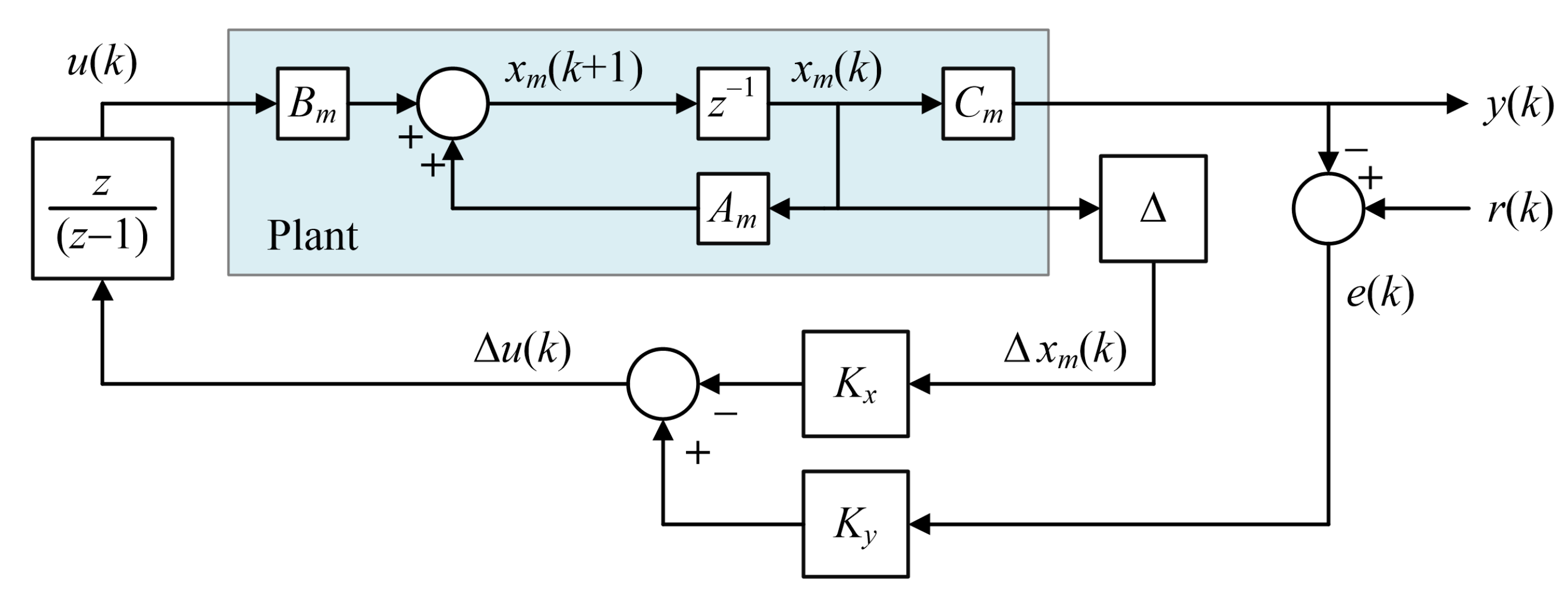
2.3. Conventional GPC
3. Proposed RDC System Based on SOD-GPC
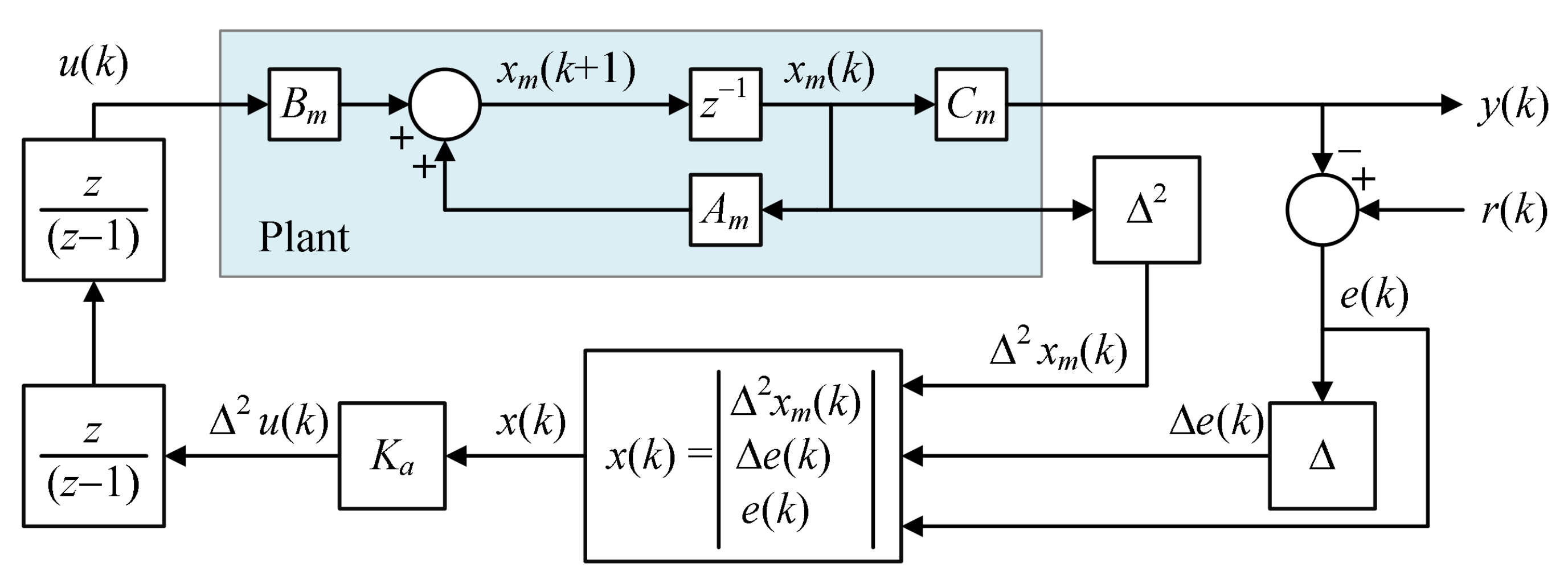
3.1. Second-Order Difference GPC
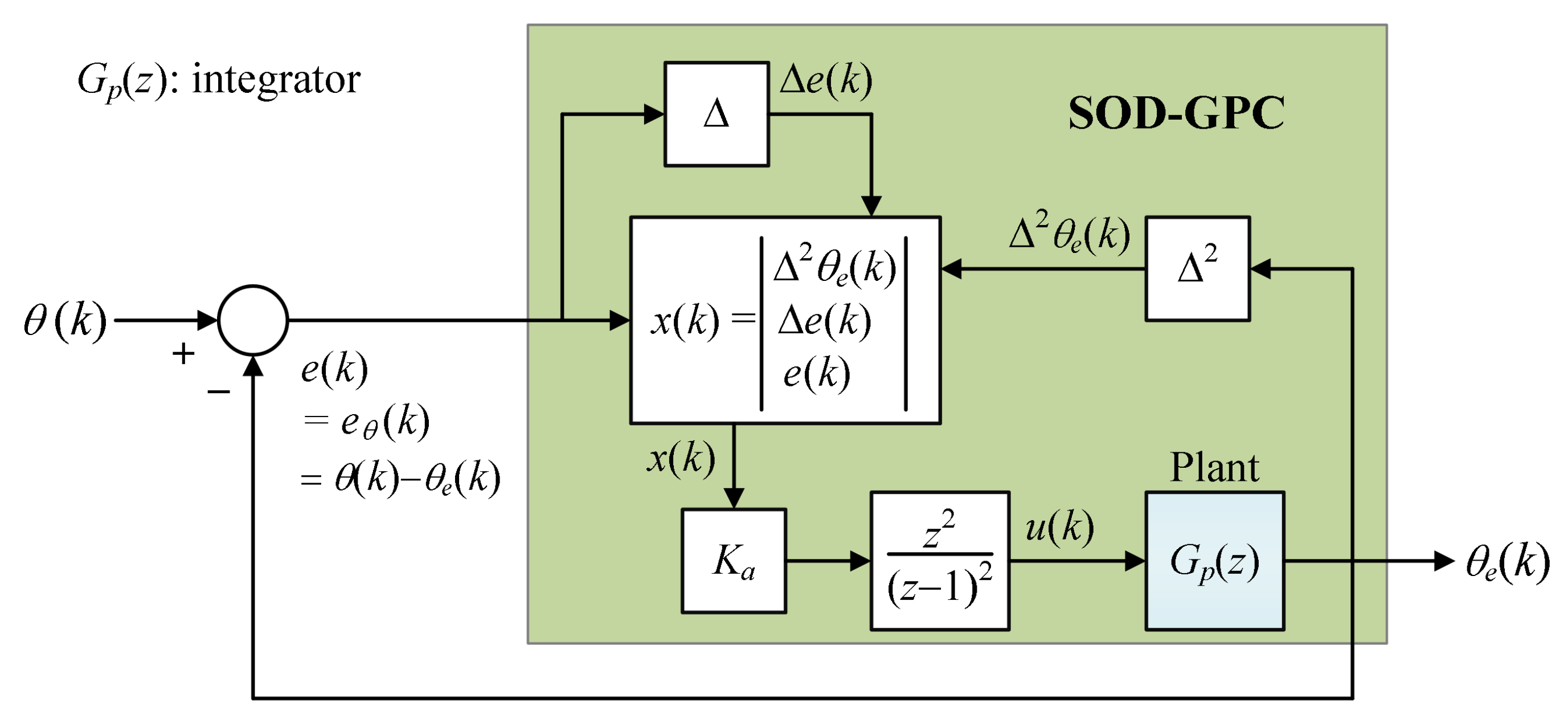
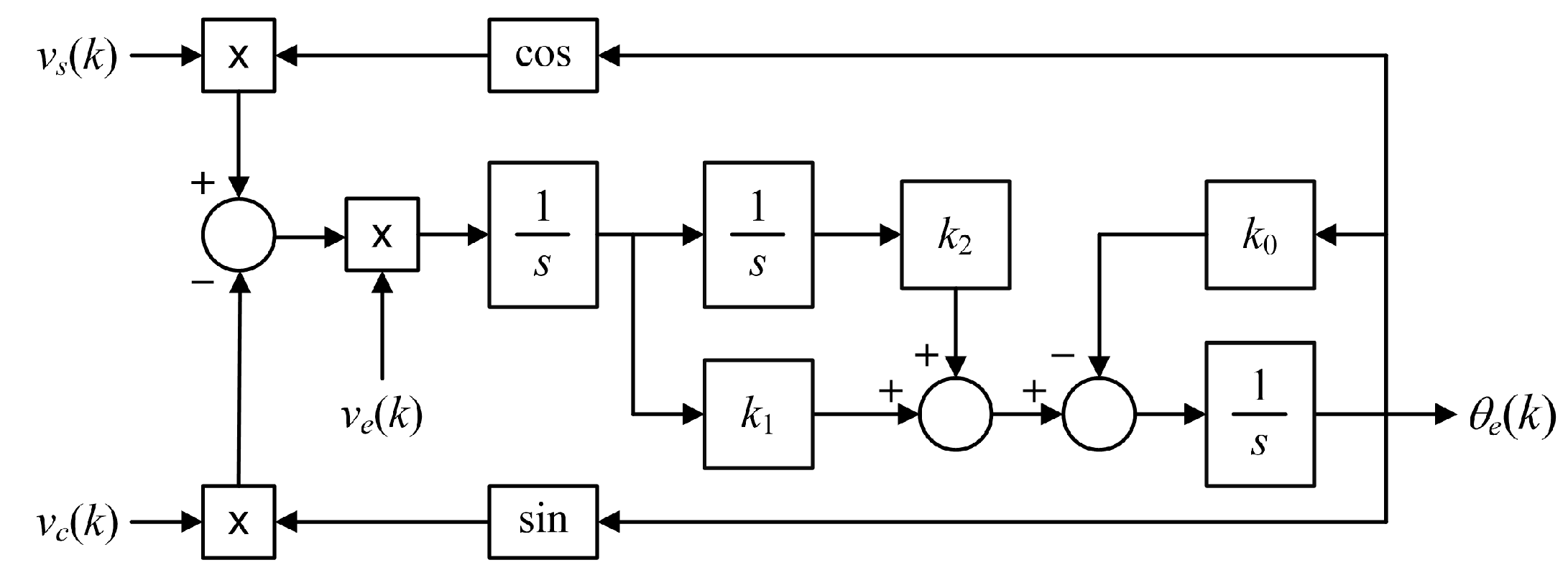
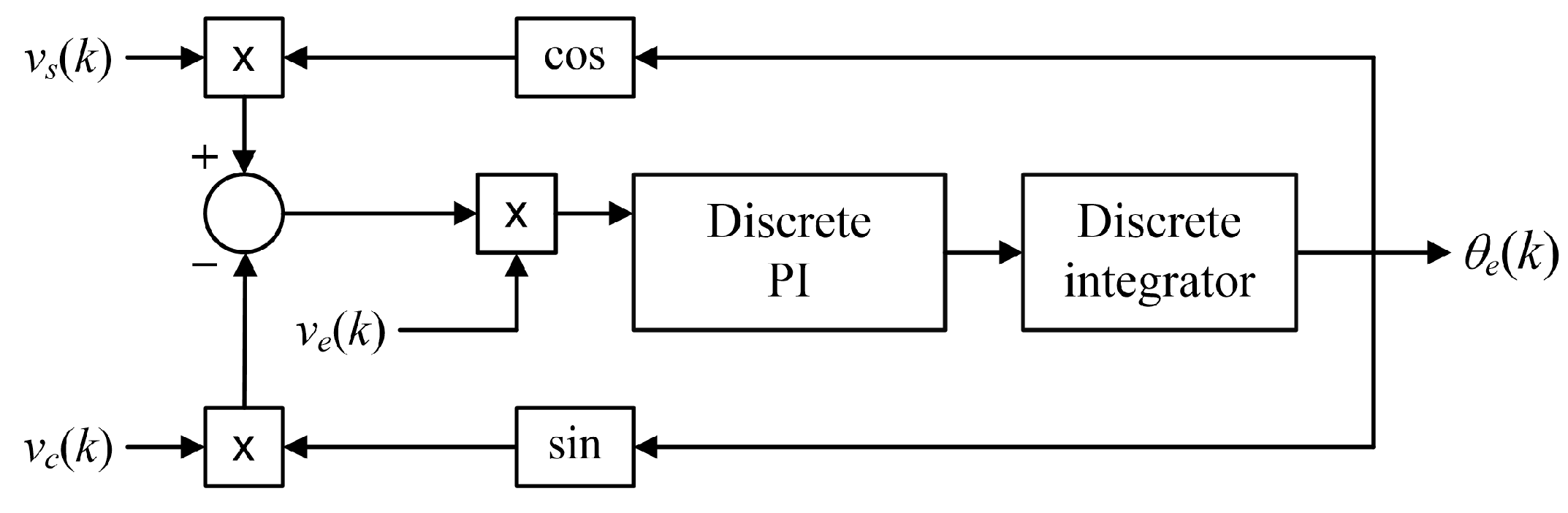
3.2. Proposed GPC-Based ATO
3.3. Effect of Resolver Parameter Variations in the Angle Estimation
- Amplitude imbalance: amplitude difference between the resolver outputs.
- Imperfect quadrature: spatial misalignment between the two resolver phases.
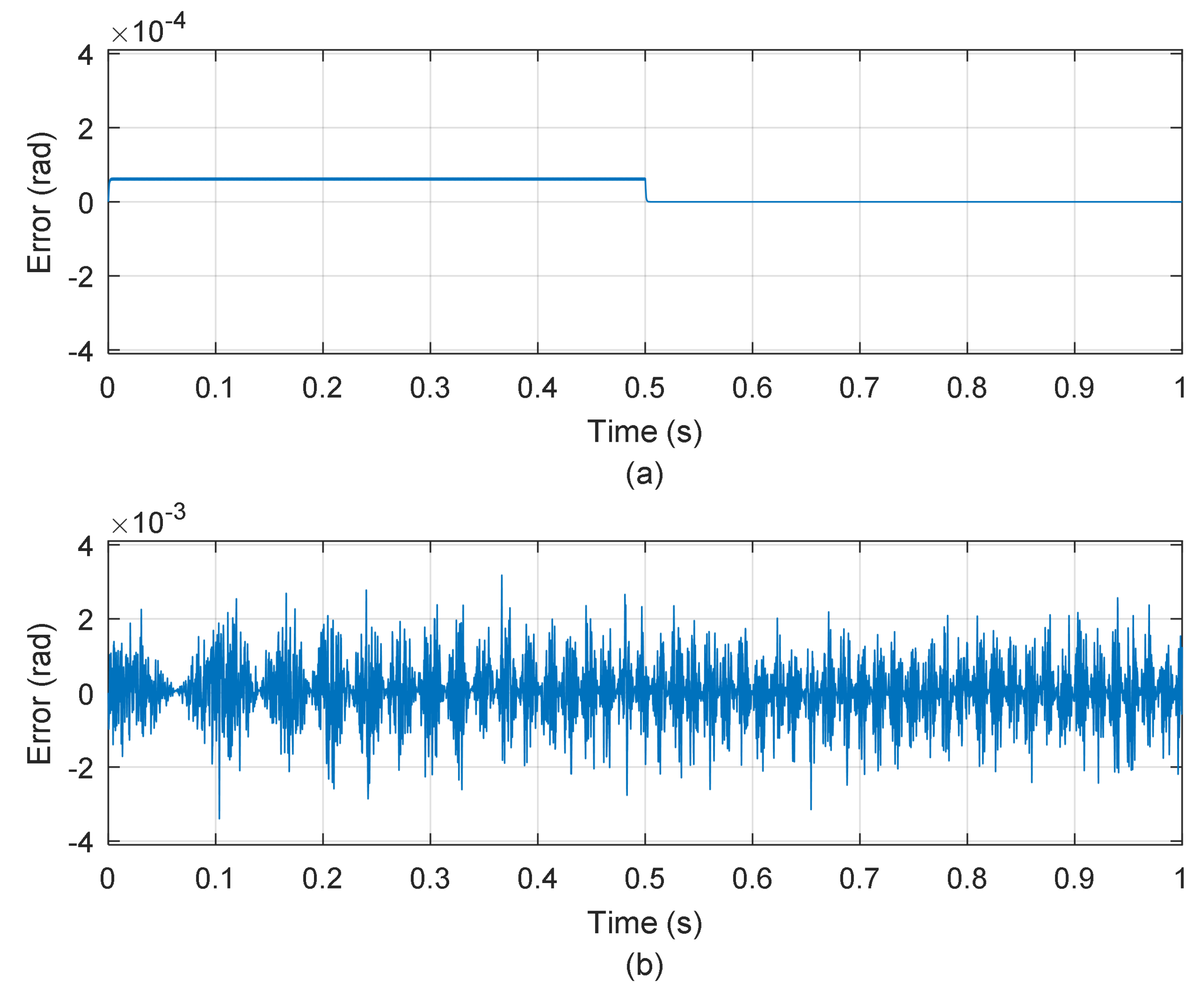
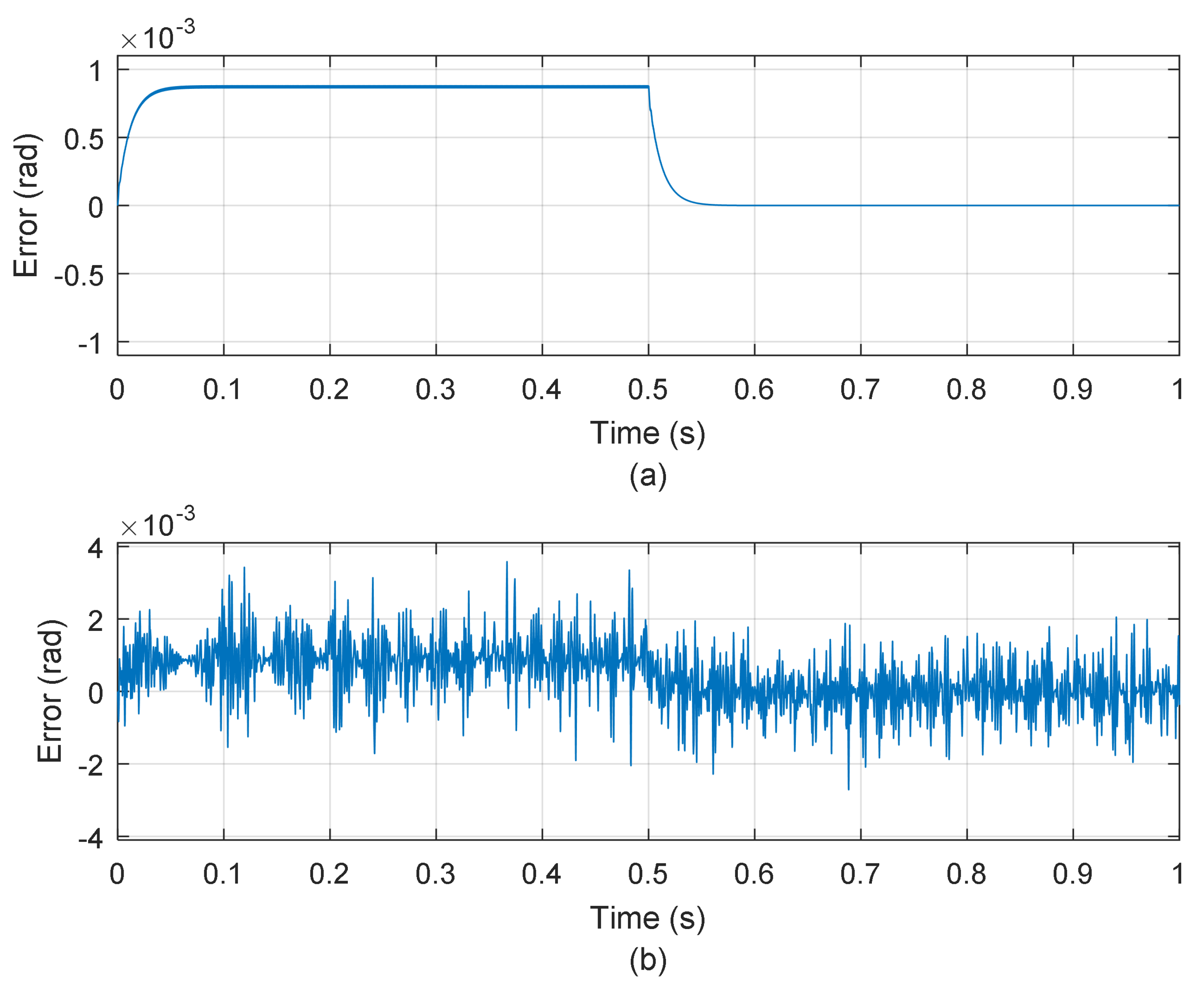
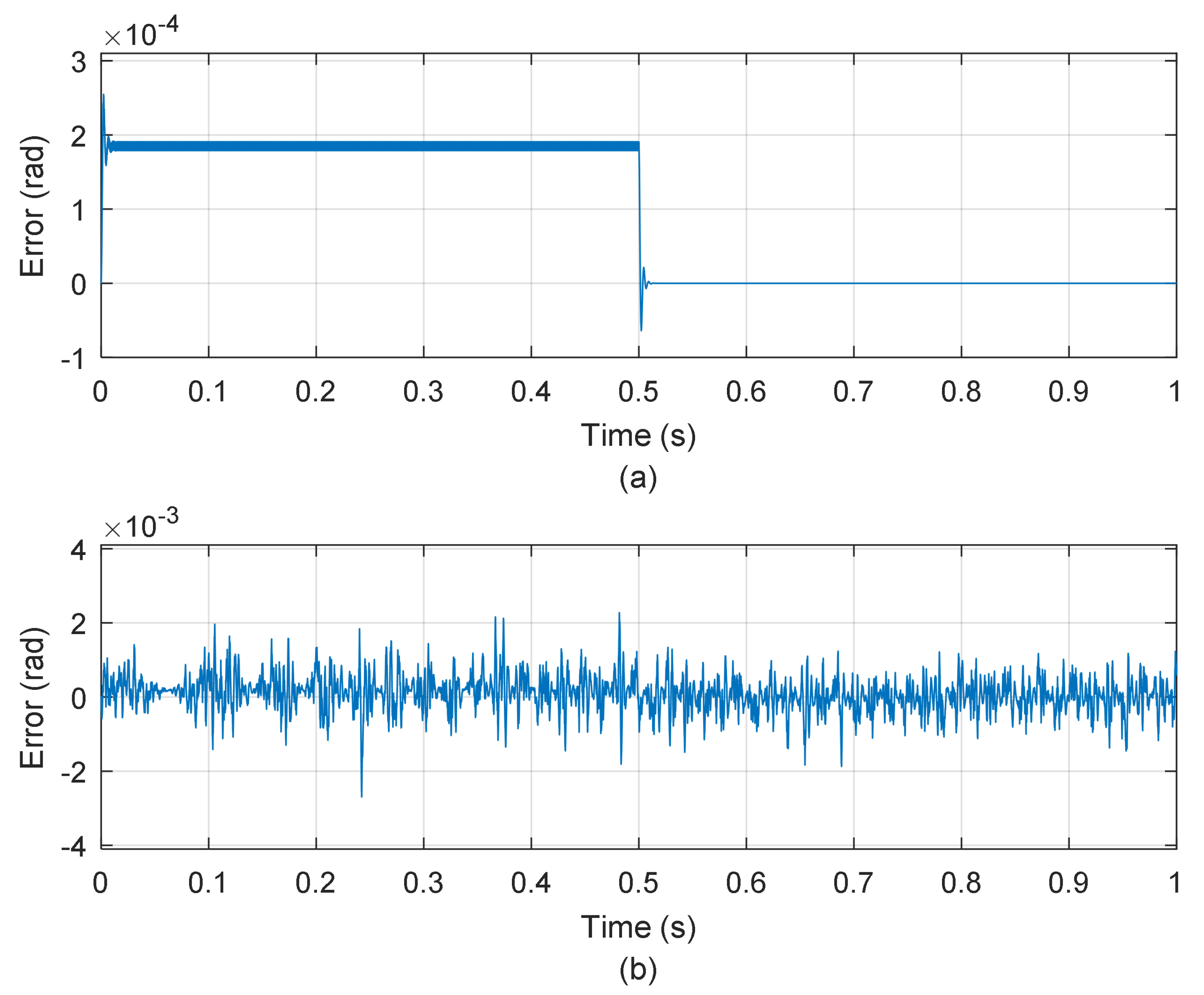
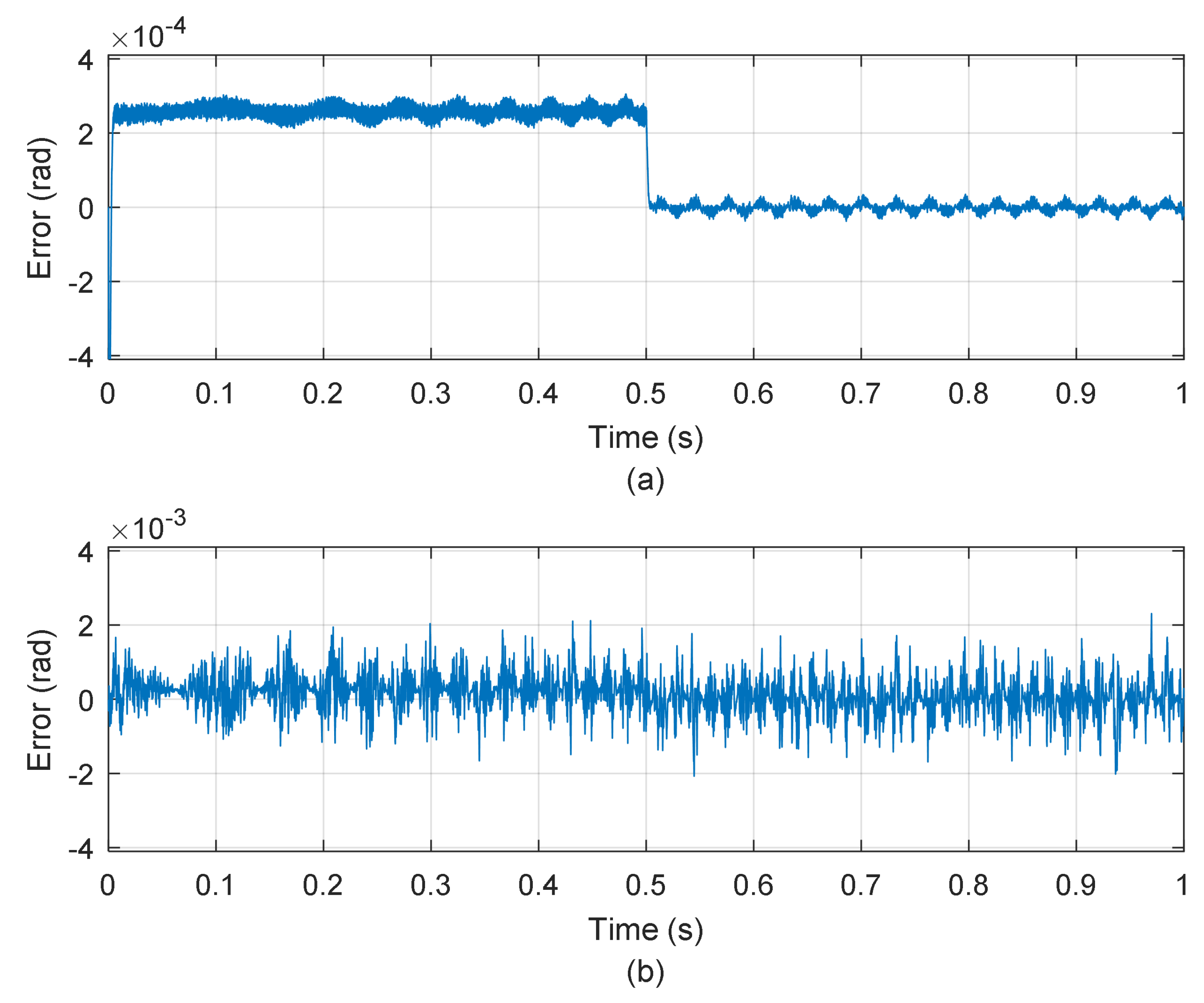
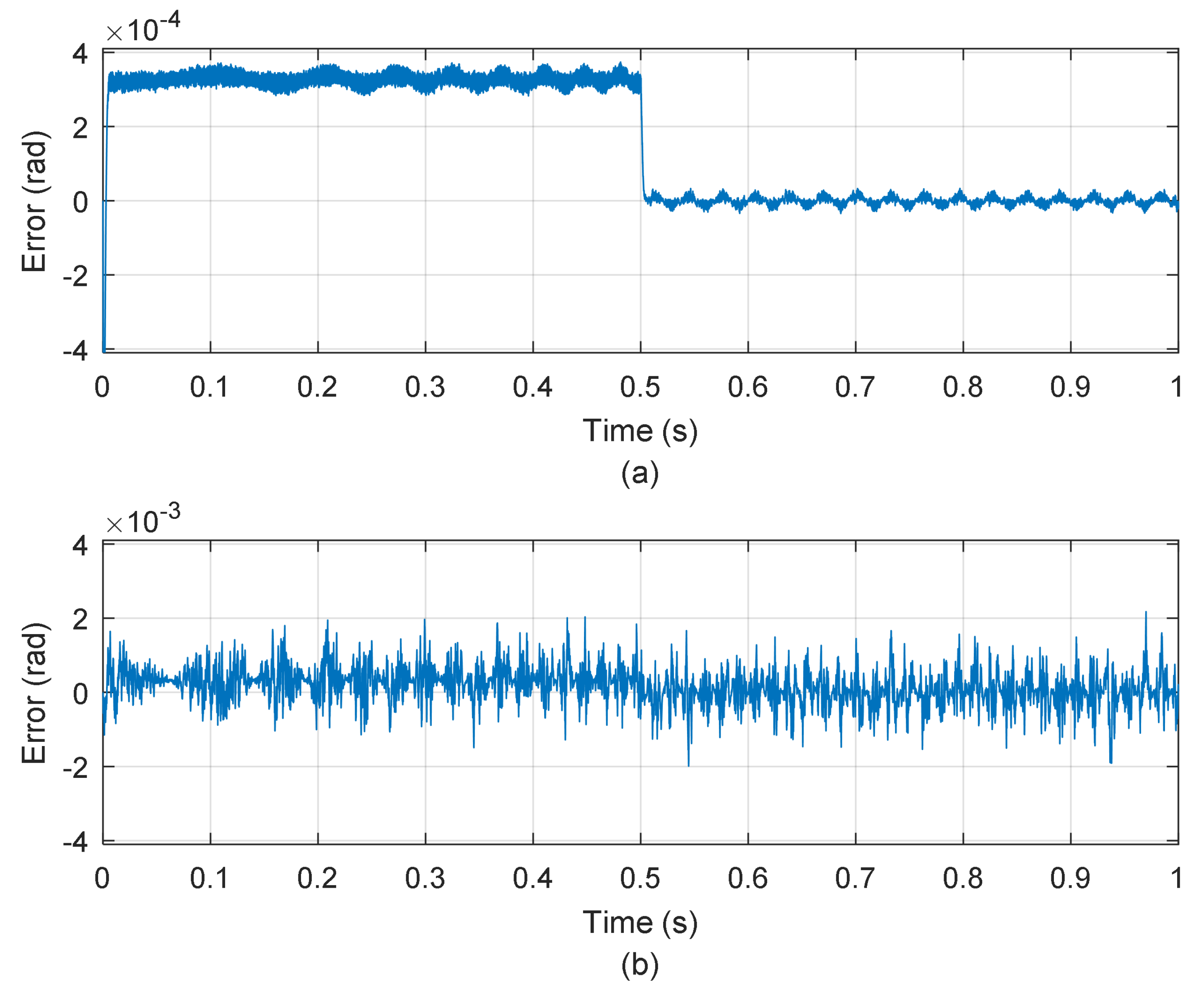
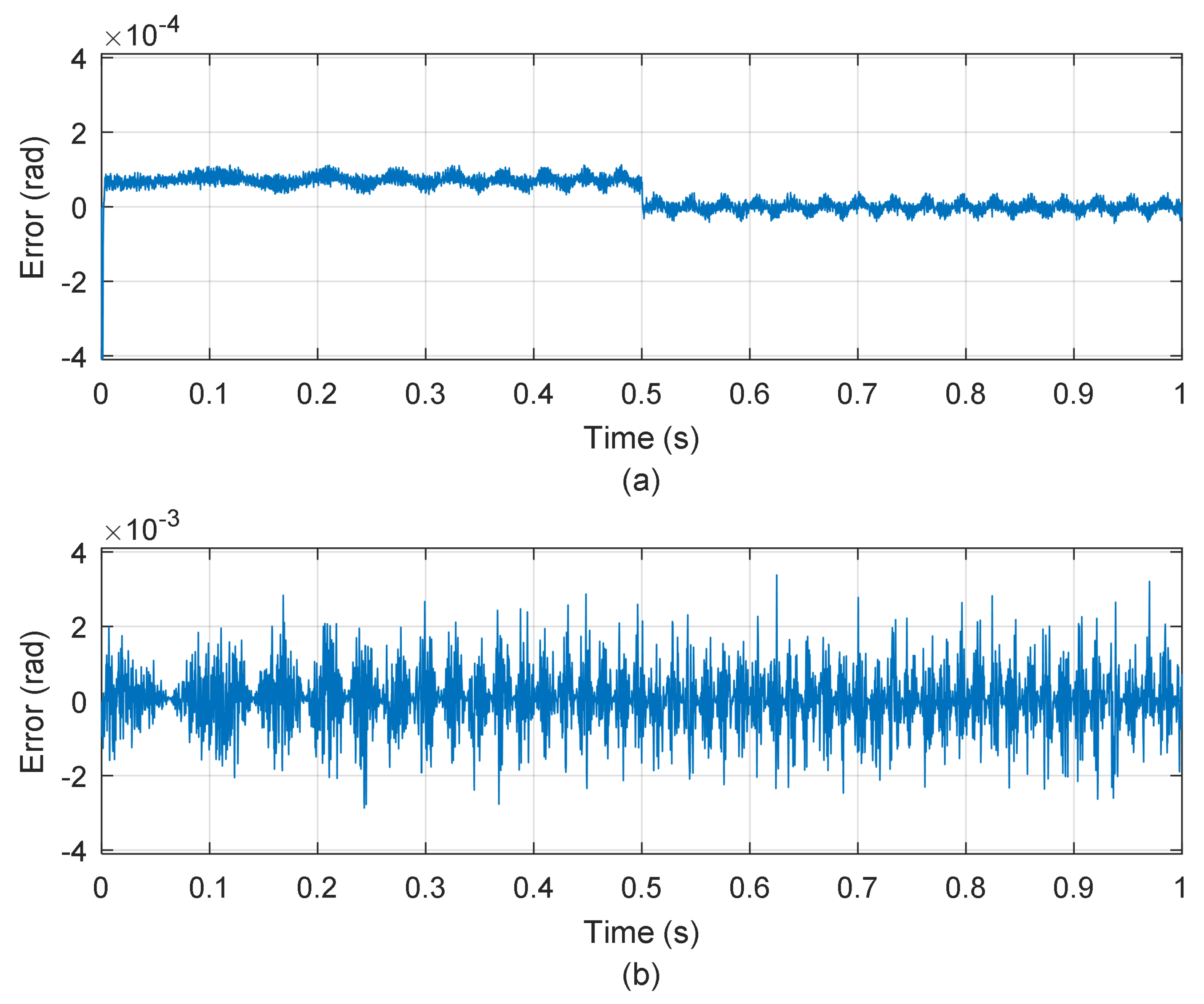
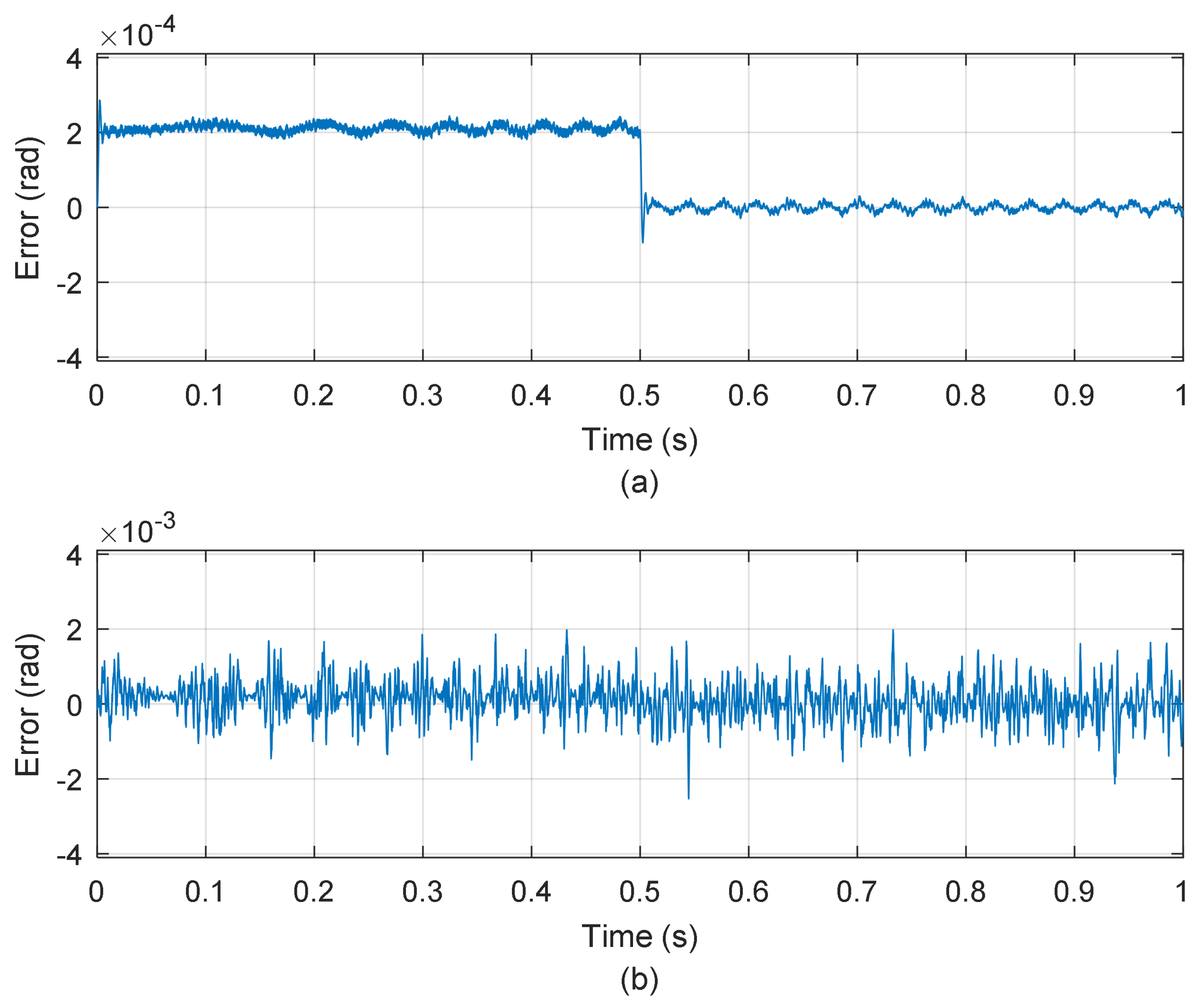
4. Results
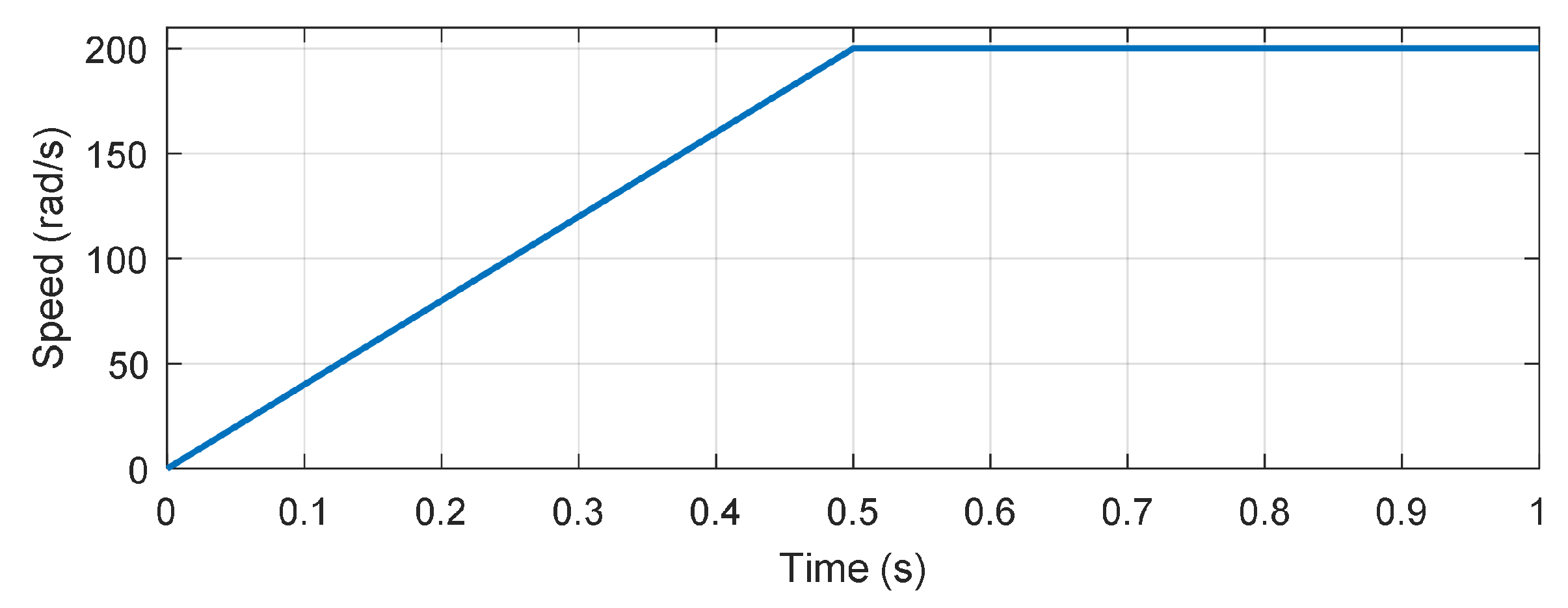
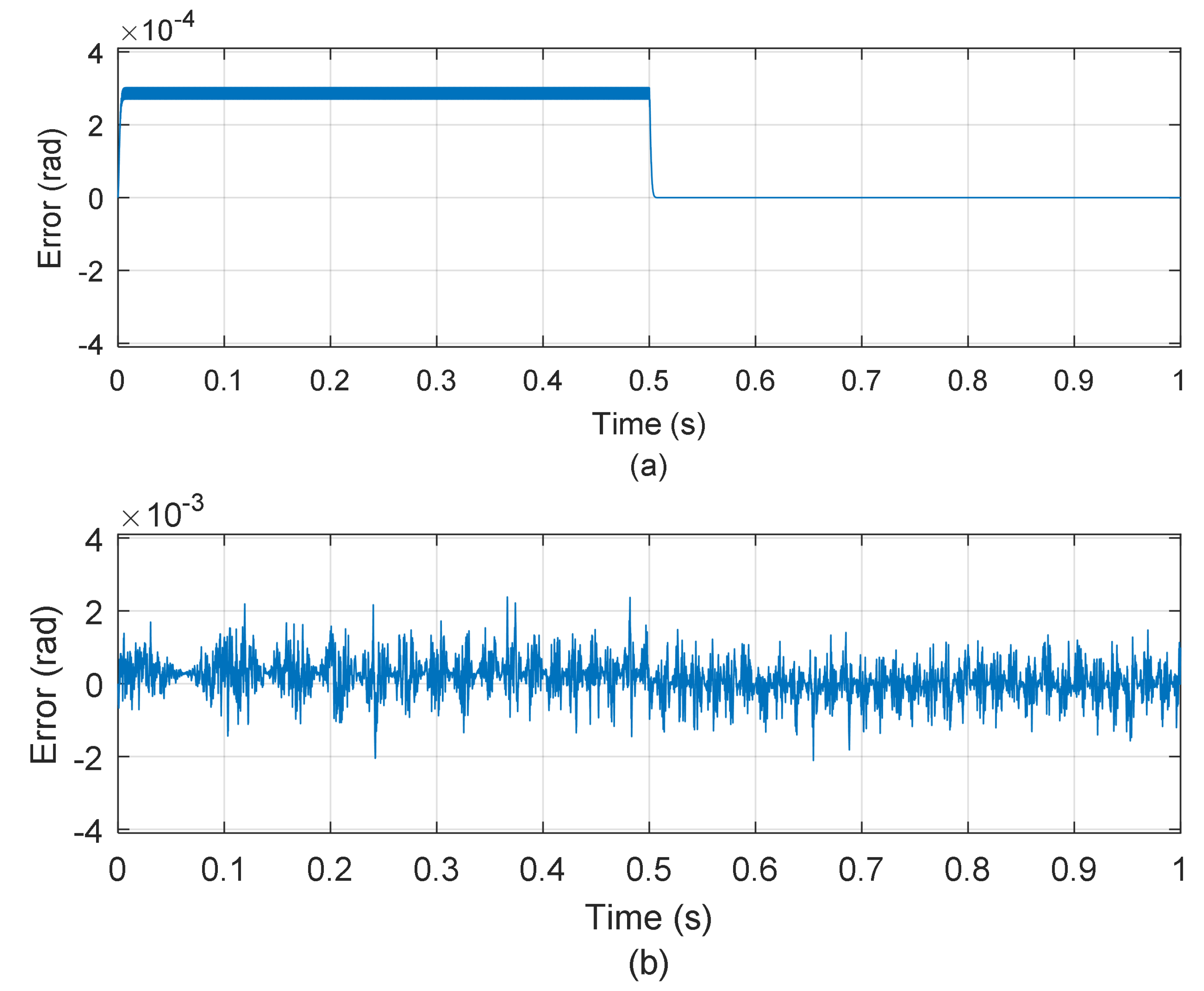
4.1. Simulation Results
- Configuration 1: ,
- Configuration 2: ,
- Configuration 3: .
4.2. Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| resolver excitation amplitude (V) | |
| resolver excitation frequency (Hz) | |
| transformation ratio | |
| control horizon | |
| prediction horizon | |
| tuning coefficient | |
| I | identity matrix |
| first-order difference operator | |
| second-order difference operator | |
| resolver excitation frequency (rad/s) | |
| eigenvalue | |
| angular position (rad) | |
| estimated angular position (rad) | |
| ATO | angle tracking observer |
| DSP | digital signal processor |
| FPGA | field programmable gate array |
| RDC | resolver-to-digital converter |
References
- Datlinger, C.; Hirz, M. An Extended Approach for Validation and Optimization of Position Sensor Signal Processing in Electric Drive Trains. Electronics 2019, 8, 77. [Google Scholar] [CrossRef]
- Luo, P.; Tang, Q.; Jing, H.; Chen, X. Design and development of a self-calibration-based inductive absolute angular position sensor. IEEE Sens. J. 2019, 19, 135–142. [Google Scholar] [CrossRef]
- Jeon, N.; Lee, H. Integrated fault diagnosis algorithm for motor sensors of in-wheel independent drive electric vehicles. Sensors 2016, 16, 2106. [Google Scholar] [CrossRef]
- Mok, H.S.; Kim, S.H.; Cho, Y.H. Reduction of PMSM torque ripple caused by resolver position error. Electron. Lett. 2007, 43, 646–647. [Google Scholar] [CrossRef]
- Kovacs, I.; Iosub, A.; Ţopa, M.; Buzo, A.; Pelz, G. On the influence of angle sensor nonidealities on the torque ripple in PMSM systems—An analytical approach. In Proceedings of the 2016 13th International Conference on Synthesis, Modeling, Analysis and Simulation Methods and Applications to Circuit Design (SMACD), Lisbon, Portugal, 27–30 June 2016. [Google Scholar]
- Hwang, M.-H.; Lee, H.-S.; Cha, H.-R. Analysis of Torque Ripple and Cogging Torque Reduction in Electric Vehicle Traction Platform Applying Rotor Notched Design. Energies 2018, 11, 3053. [Google Scholar] [CrossRef]
- Liu, Y.; Fang, J.; Tan, K.; Huang, B.; He, W. Sliding Mode Observer with Adaptive Parameter Estimation for Sensorless Control of IPMSM. Energies 2020, 13, 5991. [Google Scholar] [CrossRef]
- Wachowiak, D. Genetic Algorithm Approach for Gains Selection of Induction Machine Extended Speed Observer. Energies 2020, 13, 4632. [Google Scholar] [CrossRef]
- Liu, T.-H.; Ahmad, S.; Mubarok, M.S.; Chen, J.-Y. Simulation and Implementation of Predictive Speed Controller and Position Observer for Sensorless Synchronous Reluctance Motors. Energies 2020, 13, 2712. [Google Scholar] [CrossRef]
- Woldegiorgis, A.T.; Ge, X.; Li, S.; Hassa, M. Extended sliding mode disturbance observer-based sensorless control of IPMSM for medium and high-speed range considering railway application. IEEE Access 2019, 7, 175302–175312. [Google Scholar] [CrossRef]
- Chen, S.; Zhao, Y.; Qiu, H.; Ren, X. High-precision rotor position correction strategy for high-speed permanent magnet synchronous motor based on resolver. IEEE Trans. Power Electron. 2020, 35, 9716–9726. [Google Scholar] [CrossRef]
- Datlinger, C.; Hirz, M. Benchmark of Rotor Position Sensor Technologies for Application in Automotive Electric Drive Trains. Electronics 2020, 9, 1063. [Google Scholar] [CrossRef]
- Saneie, H.; Nasiri-Gheidari, Z.; Tootoonchian, F. Accuracy improvement in variable reluctance resolvers. IEEE Energy Convers. 2019, 34, 1563–1571. [Google Scholar] [CrossRef]
- Hou, B.; Zhou, B.; Song, M.; Lin, Z.; Zhang, R. A Novel Single-Excitation Capacitive Angular Position Sensor Design. Sensors 2020, 16, 1196. [Google Scholar] [CrossRef]
- Tang, T.; Chen, S.; Huang, X.; Yang, T.; Qi, B. Combining load and motor encoders to compensate nonlinear disturbances for high precision tracking control of gear-driven gimbal. Sensors 2018, 18, 754. [Google Scholar] [CrossRef]
- Ni, Q.; Yang, M.; Odhano, S.A.; Tang, M.; Zanchetta, P.; Liu, X.; Xu, D. A new position and speed estimation scheme for position control of PMSM drives using low-resolution position sensors. IEEE Trans. Ind. Appl. 2019, 55, 3747–3758. [Google Scholar] [CrossRef]
- Xiao, L.; Li, Z.; Bi, C. An optimization approach to variable reluctance resolver. IEEE Trans. Magn. 2020, 56, 7509005. [Google Scholar] [CrossRef]
- Hajmohammadi, S.; Alipour-Sarabi, R.; Nasiri-Gheidari, Z.; Tootoonchian, F. Influence of different installation configurations on the position error of a multiturn wound-rotor resolver. IEEE Sens. J. 2020, 20, 5785–5792. [Google Scholar] [CrossRef]
- Sun, L.; Taylor, J.; Dorneles Callegaro, A.; Emadi, A. Stator-pm-based variable reluctance resolver with advantage of motional back-emf. IEEE Trans. Ind. Electron. 2020, 67, 9790–9801. [Google Scholar] [CrossRef]
- Bahari, M.; Davoodi, A.; Saneie, H.; Tootoonchian, F.; Nasiri-Gheidari, Z. A new variable reluctance pm-resolver. IEEE Sens. J. 2020, 1, 125–142. [Google Scholar] [CrossRef]
- Wang, K.; Wu, Z. Hardware-based synchronous envelope detection strategy for resolver supplied with external excitation generator. IEEE Access 2019, 7, 20801–20810. [Google Scholar] [CrossRef]
- Wang, S.; Kang, J.; Degano, M.; Buticchi, G. A resolver-to-digital conversion method based on third-order rational fraction polynomial approximation for PMSM control. IEEE Trans. Ind. Electron. 2019, 66, 6383–6392. [Google Scholar] [CrossRef]
- Bennamar, M.; Gonzales, A.S.P. A Novel PLL resolver angle position indicator. IEEE Trans. Instrum. Meas. 2016, 65, 123–131. [Google Scholar] [CrossRef]
- Staebler, M.; Verma, A. TMS320F240 DSP Solution for Obtaining Resolver Angular Position and Speed; Texas Instrument Inc.: Dallas, TX, USA, 2017. [Google Scholar]
- Abou Qamar, N.; Hatziadoniu, C.J.; Wang, H. Speed error mitigation for a DSP-based resolver-to-digital converter using autotuning filters. IEEE Trans. Ind. Electron. 2015, 62, 1134–1139. [Google Scholar] [CrossRef]
- Kaewjinda, W.; Konghirun, M.A. DSP—based vector control of pmsm servo drive using resolver sensor. In Proceedings of the 2006 IEEE Region 10 Conference (TENCON), Hong Kong, China, 14–17 November 2006; pp. 1–4. [Google Scholar]
- Idkhajine, L.; Monmasson, E.; Naouar, M.W.; Prata, A.; Boullaga, K. Fully integrated FPGA-based controller for synchronous motor drive. IEEE Trans. Ind. Electron. 2009, 56, 4006–4017. [Google Scholar] [CrossRef]
- Garcia, R.C.; Pinto, J.O.P.; Suemitsu, W.I.; Soares, J.O. Improved demultiplexing algorithm for hardware simplification of sensored vector control through frequency-domain multiplexing. IEEE Trans. Ind. Electron. 2017, 64, 6538–6548. [Google Scholar] [CrossRef]
- Smidl, V.; Janous, S.; Peroutka, Z.; Adam, L. Time-optimal current trajectory for predictive speed control of PMSM drive. In Proceedings of the 2017 IEEE International Symposium on Predictive Control of Electrical Drives and Power Electronics (PRECEDE), Pilsen, Czech Republic, 4–6 September 2017; pp. 83–88. [Google Scholar]
- Moreno, J.C.; Espi Huerta, J.M.; Gil, R.G.; Gonzalez, S.A. A robust predictive current control for three-phase grid-connected inverters. IEEE Trans. Ind. Electron. 2009, 56, 1993–2004. [Google Scholar] [CrossRef]
- Camacho, E.F.; Bordons, C. Model Predictive Control, 2nd ed.; Springer: London, UK, 2004; pp. 13–124. [Google Scholar]
- Wang, L. Model Predictive Control System Design and Implementation Using Matlab®; Springer: London, UK, 2009; pp. 1–20. [Google Scholar]
- Ruchika, N.R. Model predictive control: History and development. Int. J. Eng. Trends Technol. 2013, 4, 2600–2602. [Google Scholar]
- Qin, S.J.; Badgwell, T.A. A survey of industrial model predictive control technology. In Proceedings of the 2016 European Control Conference (ECC), Aalborg, Denmark, 29 June–1 July 2016; pp. 733–764. [Google Scholar]
- Clarke, D.W.; Mohtadi, C.; Tuffs, P.S. Generalized predictive control—Part I. the basic algorithm. Automatica 1987, 23, 137–148. [Google Scholar] [CrossRef]
- Clarke, D.W.; Mohtadi, C.; Tuffs, P.S. Generalized Predictive Control—Part II. Extensions and Interpretations. Automatica 1987, 23, 149–160. [Google Scholar] [CrossRef]
- Prajwowski, K.; Golebiewski, W.; Lisowski, M.; Abramek, K.F.; Galdynski, D. Modeling of working machines synergy in the process of the hybrid electric vehicle acceleration. Energies 2020, 13, 5818. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, Z.; Mei, X.; Rodríguez, J.; Kennel, R. Advanced control strategies of induction machine: Field oriented control, direct torque control and model predictive control. Energies 2018, 11, 120. [Google Scholar] [CrossRef]
- Gonçalves, P.; Cruz, S.; Mendes, A. Finite control set model predictive control of six-phase asymmetrical machines—An overview. Energies 2019, 12, 4693. [Google Scholar] [CrossRef]
- Nguyen, T.-T.; Yoo, H.-J.; Kim, H.-M.; Nguyen-Duc, H. Direct phase angle and voltage amplitude model predictive control of a power converter for microgrid applications. Energies 2018, 11, 2254. [Google Scholar] [CrossRef]
- Jin, N.; Pan, C.; Li, Y.; Hu, S.; Fang, J. Model predictive control for virtual synchronous generator with improved vector selection and reconstructed current. Energies 2020, 13, 5435. [Google Scholar] [CrossRef]
- Abdelrahem, M.; Hackl, C.M.; Rodríguez, J.; Kennel, R. Model reference adaptive system with finite-set for encoderless control of PMSGs in micro-grid systems. Energies 2020, 13, 4844. [Google Scholar] [CrossRef]
- Turley, C.; Jacoby, M.; Pavlak, G.; Henze, G. Development and evaluation of occupancy-aware hvac control for residential building energy efficiency and occupant comfort. Energies 2020, 13, 5396. [Google Scholar] [CrossRef]
- Bahramnia, P.; Hosseini Rostami, S.M.; Wang, J.; Kim, G.-J. Modeling and controlling of temperature and humidity in building heating, ventilating, and air conditioning system using model predictive control. Energies 2019, 12, 4805. [Google Scholar] [CrossRef]
- Estrabis, T.; Cordero, R.; Batista, E.; Andrea, C.; Grassi, M.A.S. Application of model predictive control in a resolver-to-digital converter. In Proceedings of the 2019 IEEE 15th Brazilian Power Electronics Conference and 5th IEEE Southern Power Electronics Conference (COBEP/SPEC), Santos, Brazil, 1–4 December 2019; pp. 1–6. [Google Scholar]
- Dorf, R.C.; Bishop, R.H. Modern Control Systems, 8th ed.; Addison Wesley Longman, Inc.: Menlo Park, CA, USA, 1998; pp. 662–666. [Google Scholar]
- Belda, K.; Vosmik, D. Explicit generalized predictive control of speed and position of PMSM drives. IEEE Trans. Ind. Electron. 2016, 63, 3889–3896. [Google Scholar] [CrossRef]
- Maeder, U.; Morari, M. Offset-free reference tracking with model predictive control. Automatica 2010, 46, 1469–1476. [Google Scholar] [CrossRef]
- Cordero, R.; Estrabis, T.; Batista, E.A.; Andrea, C.Q.; Gentil, G. Ramp-tracking generalized predictive control system based on second-order difference. IEEE Trans. Circuits Syst. II Exp. Briefs 2020. to be published. [Google Scholar] [CrossRef]
- Jerry, A.J. Difference Equations with Discrete Transform Methods; Springer Science+Business Media: Dordrecht, The Netherlands, 1996; pp. 1–22. [Google Scholar]
- Proakis, J.C.; Manolakis, D.G. Digital Signal Processing: Principles, Algorithms and Applications, 3rd ed.; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Wu, Z.; Li, Y. High-accuracy automatic calibration of resolver signals via two-step gradient estimators. IEEE Sens. J. 2018, 18, 2883–2891. [Google Scholar] [CrossRef]
- Sarma, S.; Venkateswaralu, A. Systematic error cancellations and fault detection of resolver angular sensors using a DSP based system. Mechatronics 2009, 19, 1303–1312. [Google Scholar] [CrossRef]
- Noori, N.; Khaburi, D.A. Diagnosis and compensation of amplitude imbalance, imperfect quadrant and offset in resolver signals. In Proceedings of the 2016 7th Power Electronics and Drive Systems Technologies Conference (PEDSTC), Tehran, Iran, 16–18 February 2016; pp. 76–81. [Google Scholar]
- Gao, Z.; Zhou, B.; Hou, B.; Li, C.; Wei, Q.; Zhang, R. Self-calibration of nonlinear signal model for angular position sensors by model-based automatic search algorithm. Sensors 2019, 19, 2760. [Google Scholar] [CrossRef]
- Cordero, R.; Pinto, J.O.P.; Ono, I.E.; Fahed, H.D.S.; Brito, M. Simplification of the acquisition system for sensored vector control using resolver sensor based on fdm and current synchronous sampling. In Proceedings of the 2018 IEEE 4th Southern Power Electronics Conference (SPEC), Singapore, 10–13 December 2018; pp. 1–4. [Google Scholar]



| Parameters | Values |
|---|---|
| Excitation amplitude () | 8 V |
| Excitation frequency () | 2.5 kHz |
| Transformation ratio () | 0.5 |
| ATO | Sum (+) | Multiplication (×) |
|---|---|---|
| SOD-GPC-based ATO | 9 | 8 |
| ATO in [56] | 6 | 9 |
| PI-based ATO | 3 | 6 |
| Configuration | RMSE (without Noise) | RMSE (with Noise) | Settling Time (s) |
|---|---|---|---|
| ATO in [56] | |||
| PI-based ATO |
| Configuration | RMSE (without Noise) | RMSE (with Noise) | Settling Time (s) |
|---|---|---|---|
| PI-based ATO |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Estrabis, T.; Gentil, G.; Cordero, R. Development of a Resolver-to-Digital Converter Based on Second-Order Difference Generalized Predictive Control. Energies 2021, 14, 459. https://doi.org/10.3390/en14020459
Estrabis T, Gentil G, Cordero R. Development of a Resolver-to-Digital Converter Based on Second-Order Difference Generalized Predictive Control. Energies. 2021; 14(2):459. https://doi.org/10.3390/en14020459
Chicago/Turabian StyleEstrabis, Thyago, Gabriel Gentil, and Raymundo Cordero. 2021. "Development of a Resolver-to-Digital Converter Based on Second-Order Difference Generalized Predictive Control" Energies 14, no. 2: 459. https://doi.org/10.3390/en14020459
APA StyleEstrabis, T., Gentil, G., & Cordero, R. (2021). Development of a Resolver-to-Digital Converter Based on Second-Order Difference Generalized Predictive Control. Energies, 14(2), 459. https://doi.org/10.3390/en14020459






