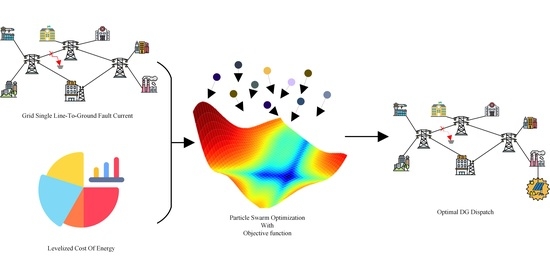
The Optimal Allocation of Distributed Generators Considering Fault Current and Levelized Cost of Energy Using the Particle Swarm Optimization Method
Abstract
1. Introduction
2. Problem Statement
3. Distributed Generators and Their Fault Analysis
3.1. Distributed Generators
- Rotational DGs such as wind power and gas turbines;
- Stationary DGs using inverters such as solar power and variable-speed wind power.
3.2. Distribution Generator Modeling Method
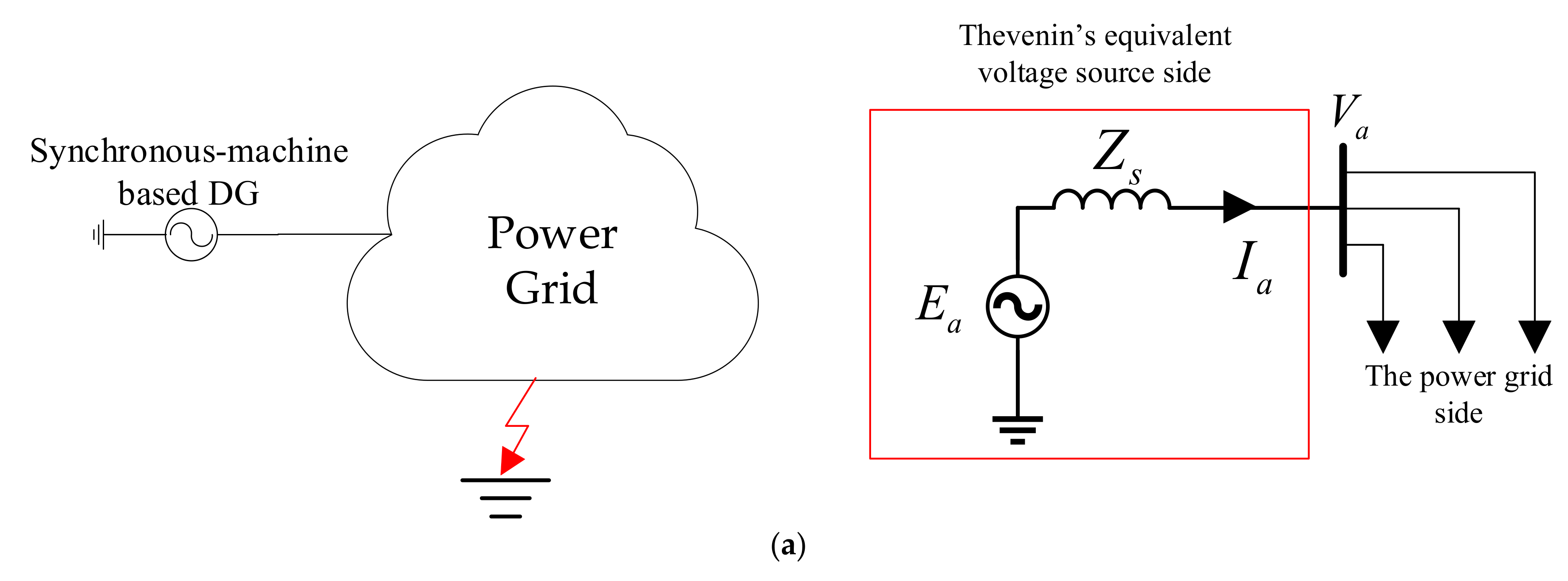
3.2.1. Voltage Source
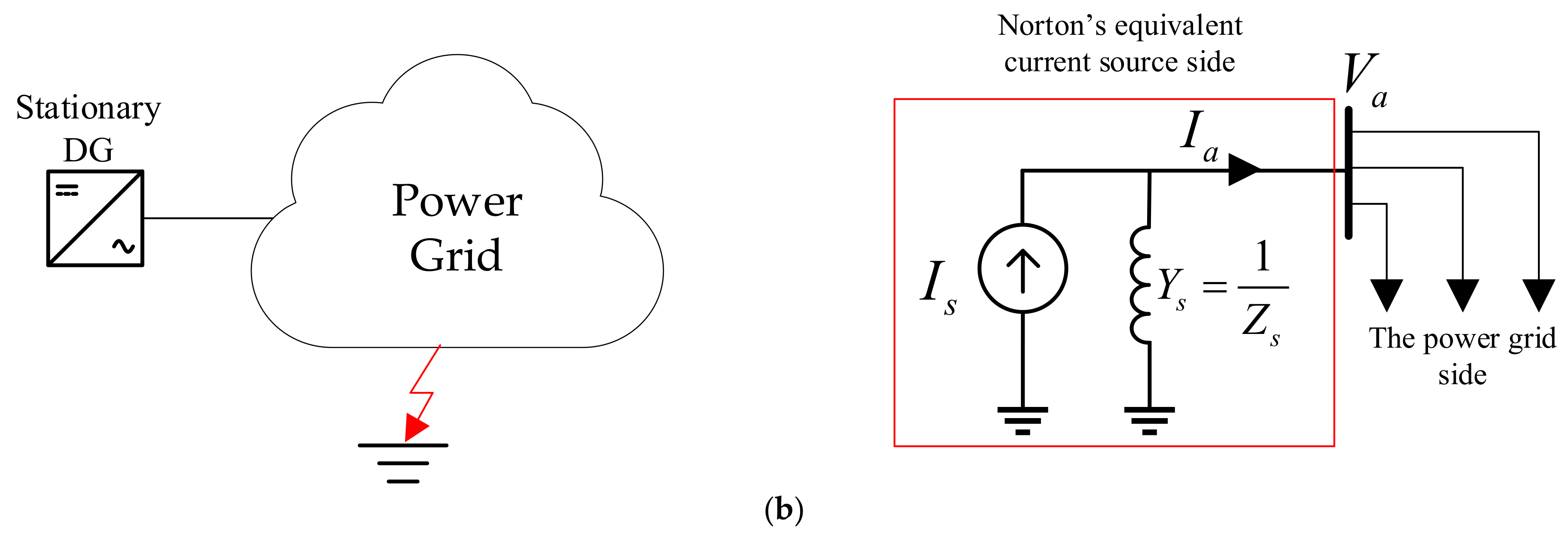
3.2.2. Current Source
3.3. Fault Analysis
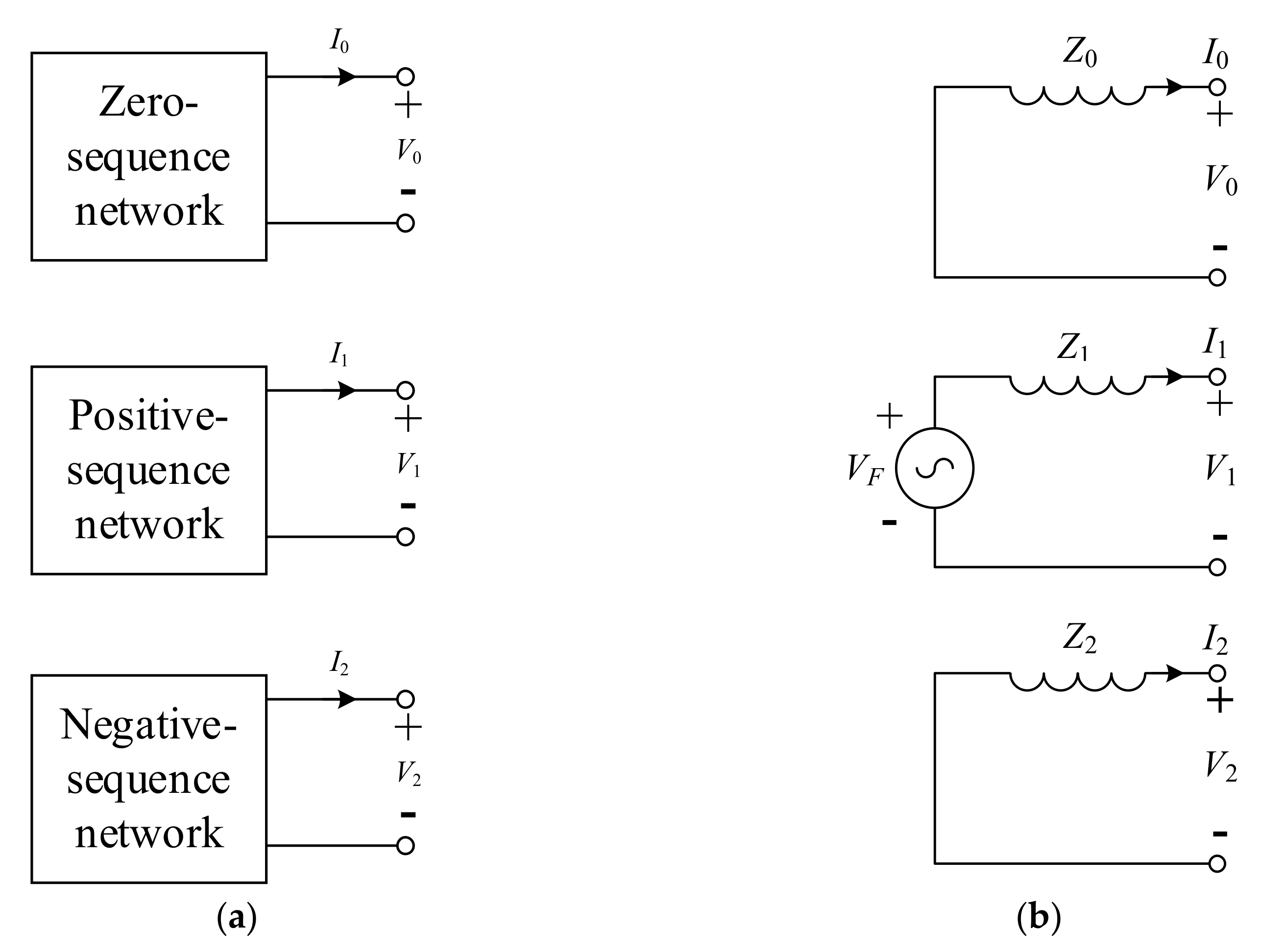
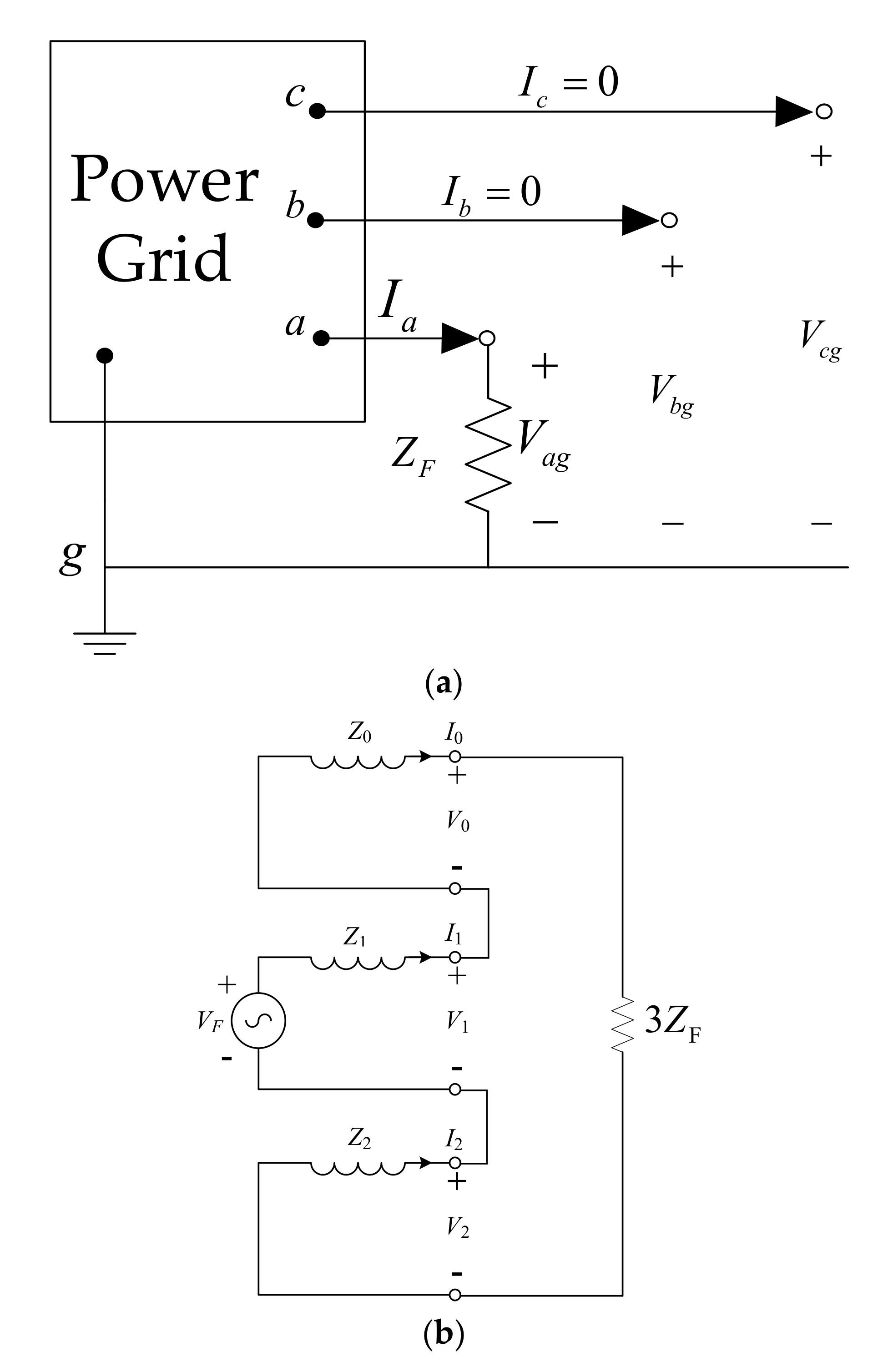
3.3.1. Unsymmetrical Electrical Fault
3.3.2. General Analysis Method of Single Line-to-Ground Fault
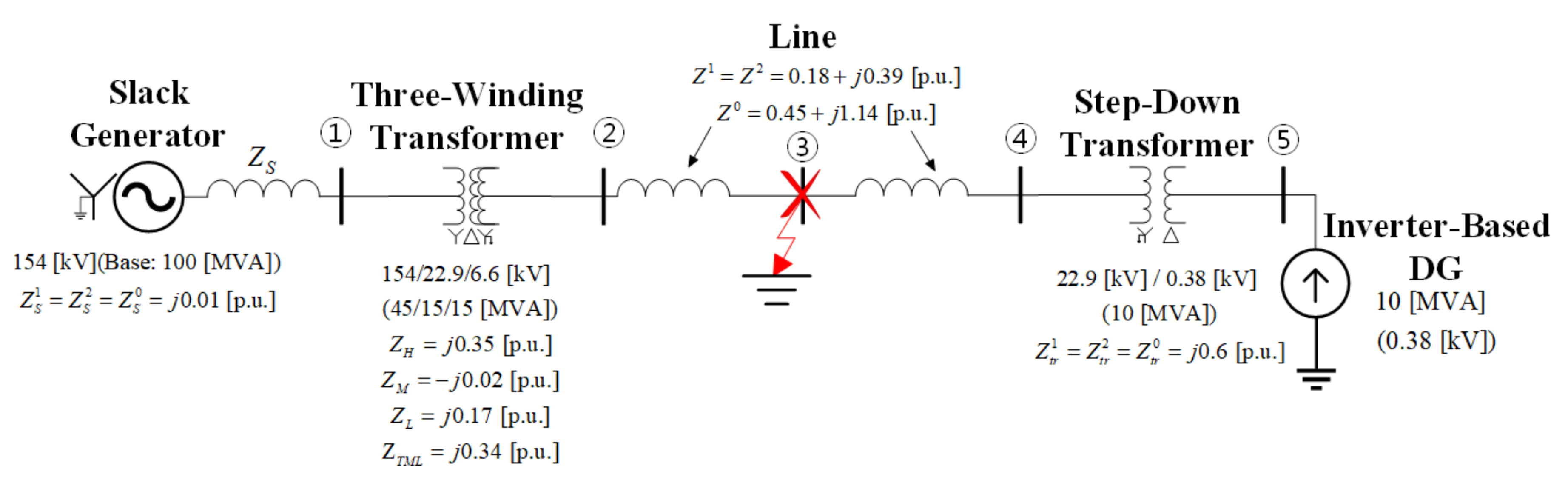
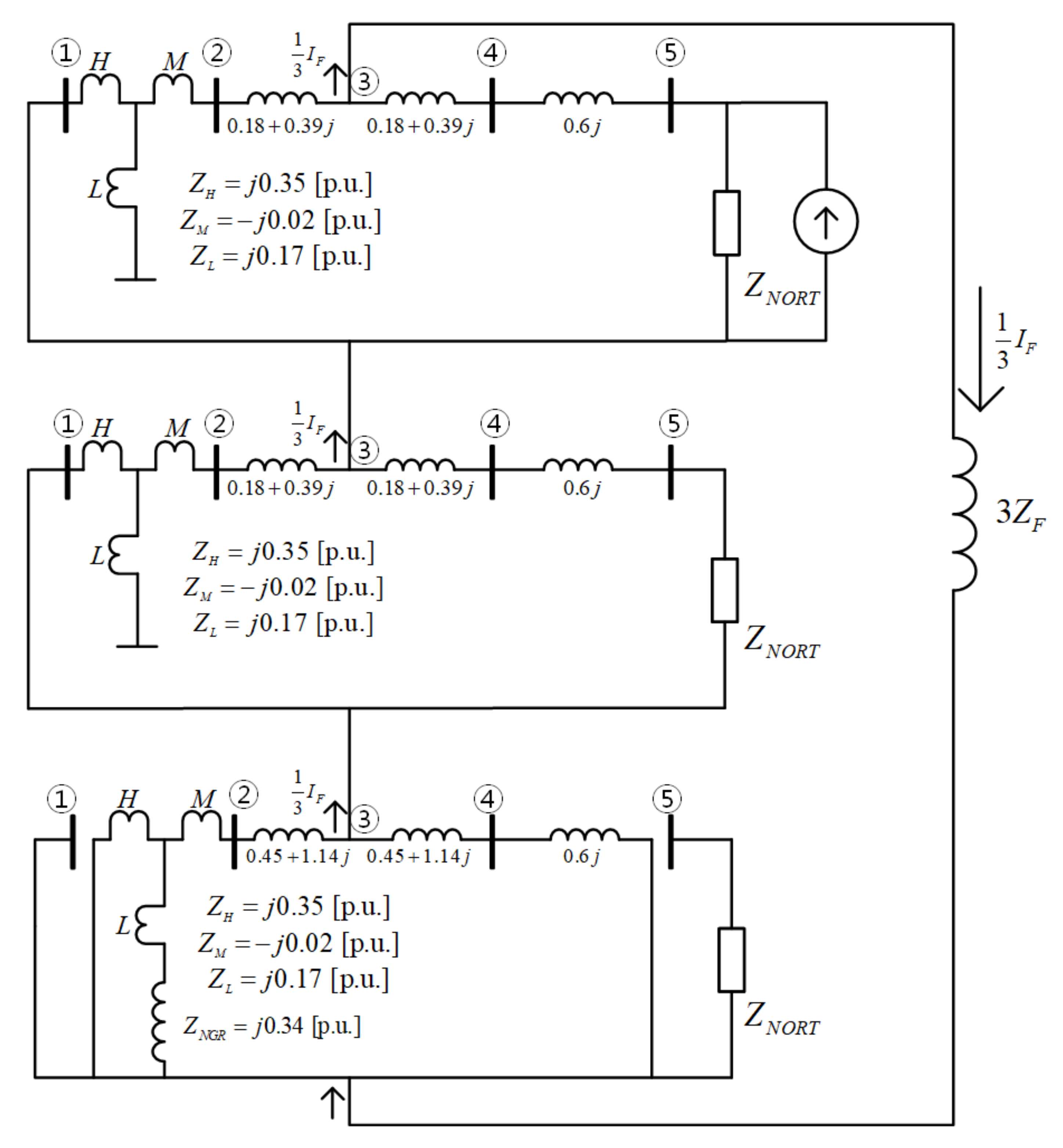
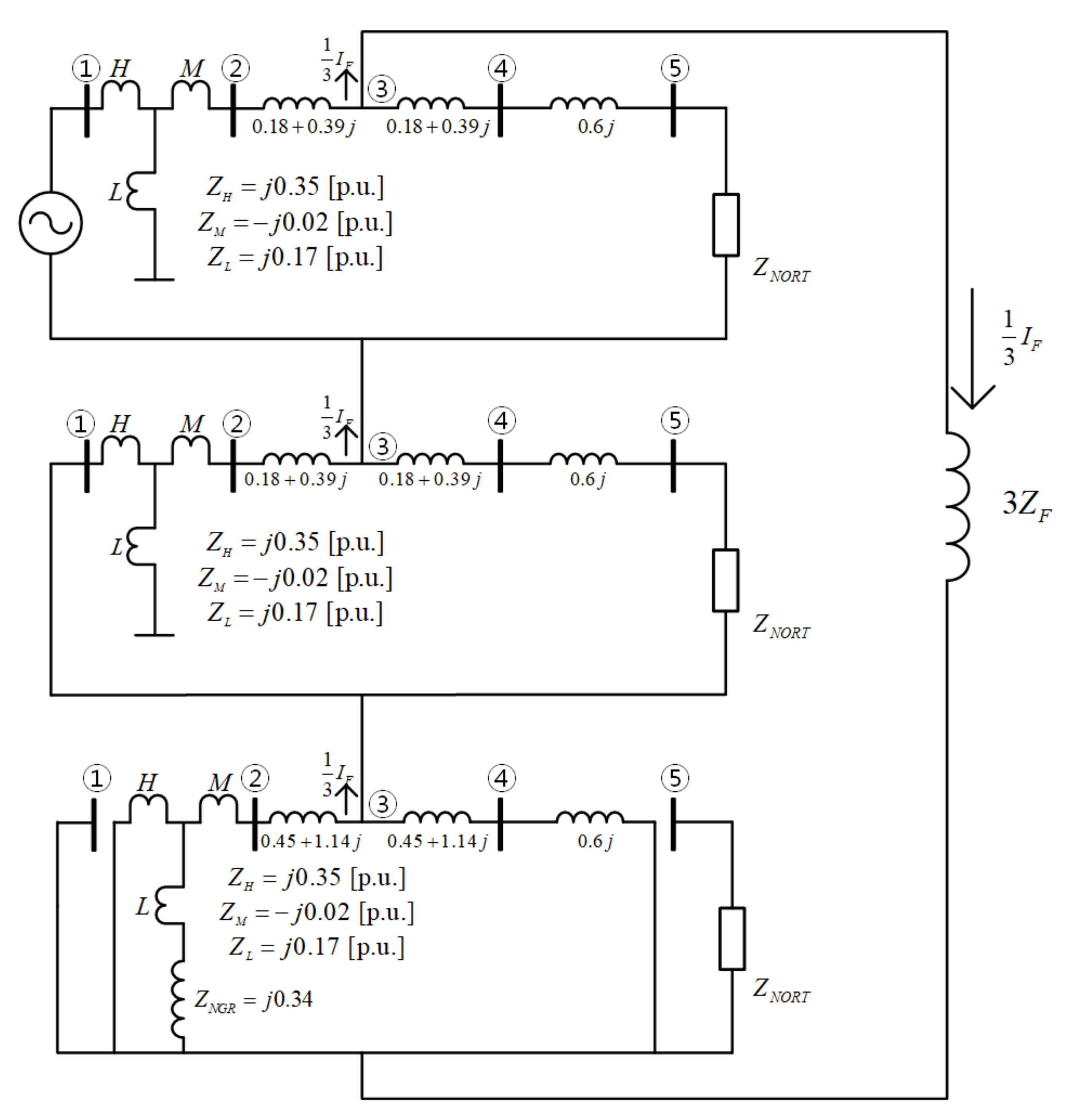
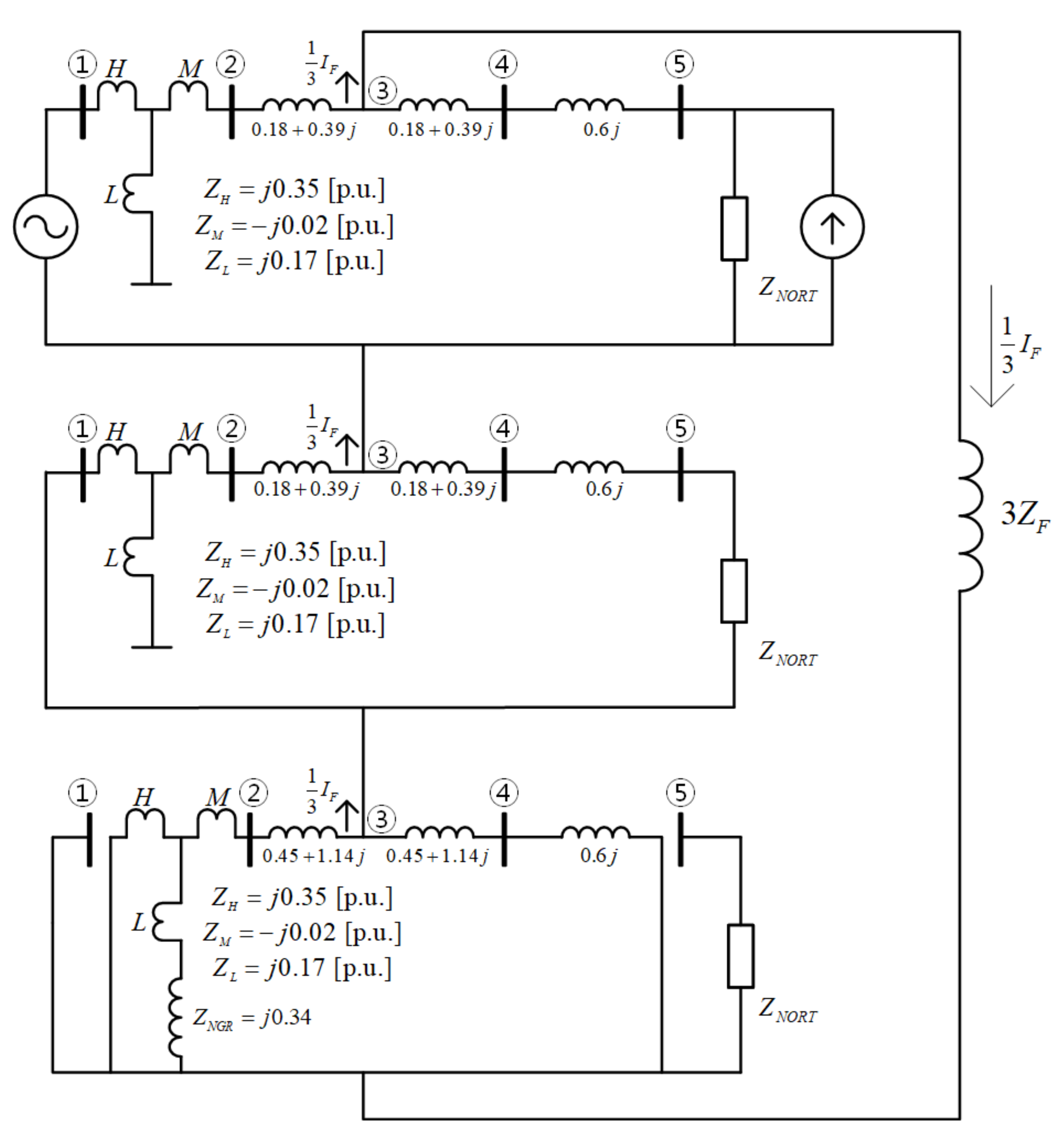
3.4. Short-Circuit Current Calculation Example
3.4.1. Fault Current Contributed by a Voltage Source
3.4.2. Current Injection Method
3.4.3. Effect of Current Source
4. Proposed Methods
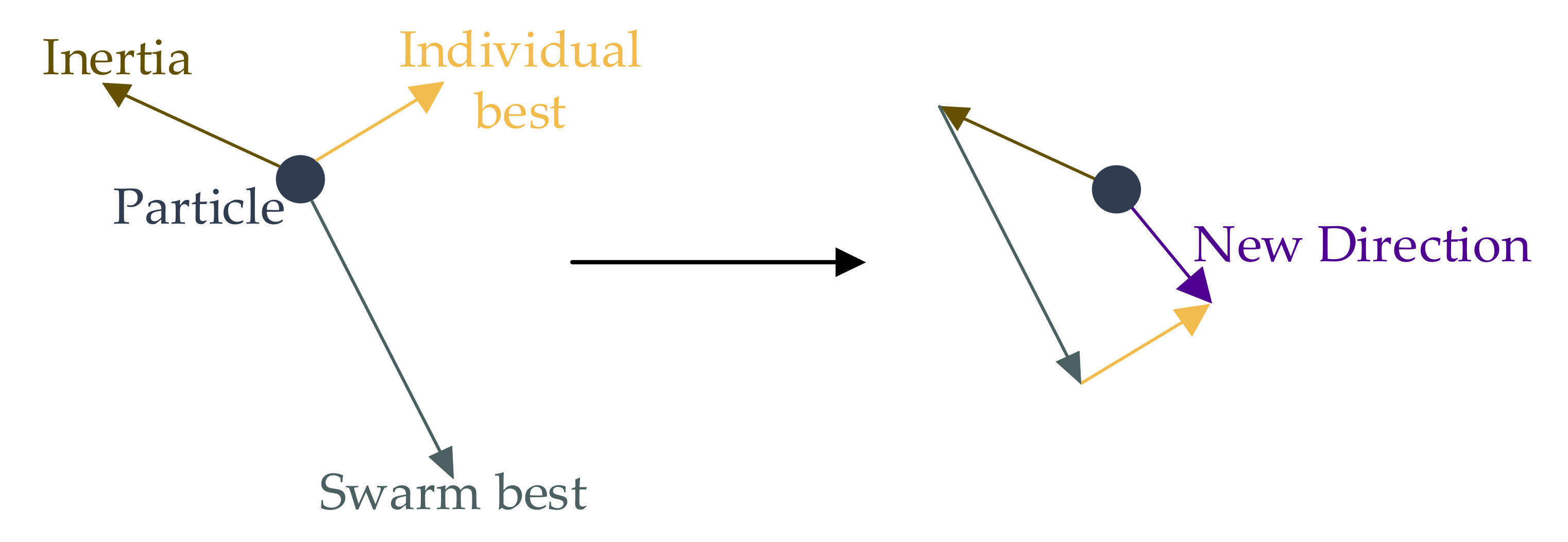
4.1. Particle Swarm Optimization
- Inertia: the velocity of particles at the previous step.
- Cognitive force: the distance from the known best position of each particle, which is also called the individual best.
- Social force: the distance from the known best position of the swarm, which is also called swarm best.
- = velocity in jth step
- = weight of inertia
- = acceleration
- = random number
- = individual best position
- = swarm best position
- = position of each particles in jth step
- = cognitive component (i.e., individual best, cognitive force)
- = social component (i.e., swarm best, social force)
4.2. Mathematical Optimization Problem
4.2.1. Fault Current and Levelized Cost of Energy
4.2.2. Objective Function
4.2.3. Variable Normalization
5. Optimization and Results
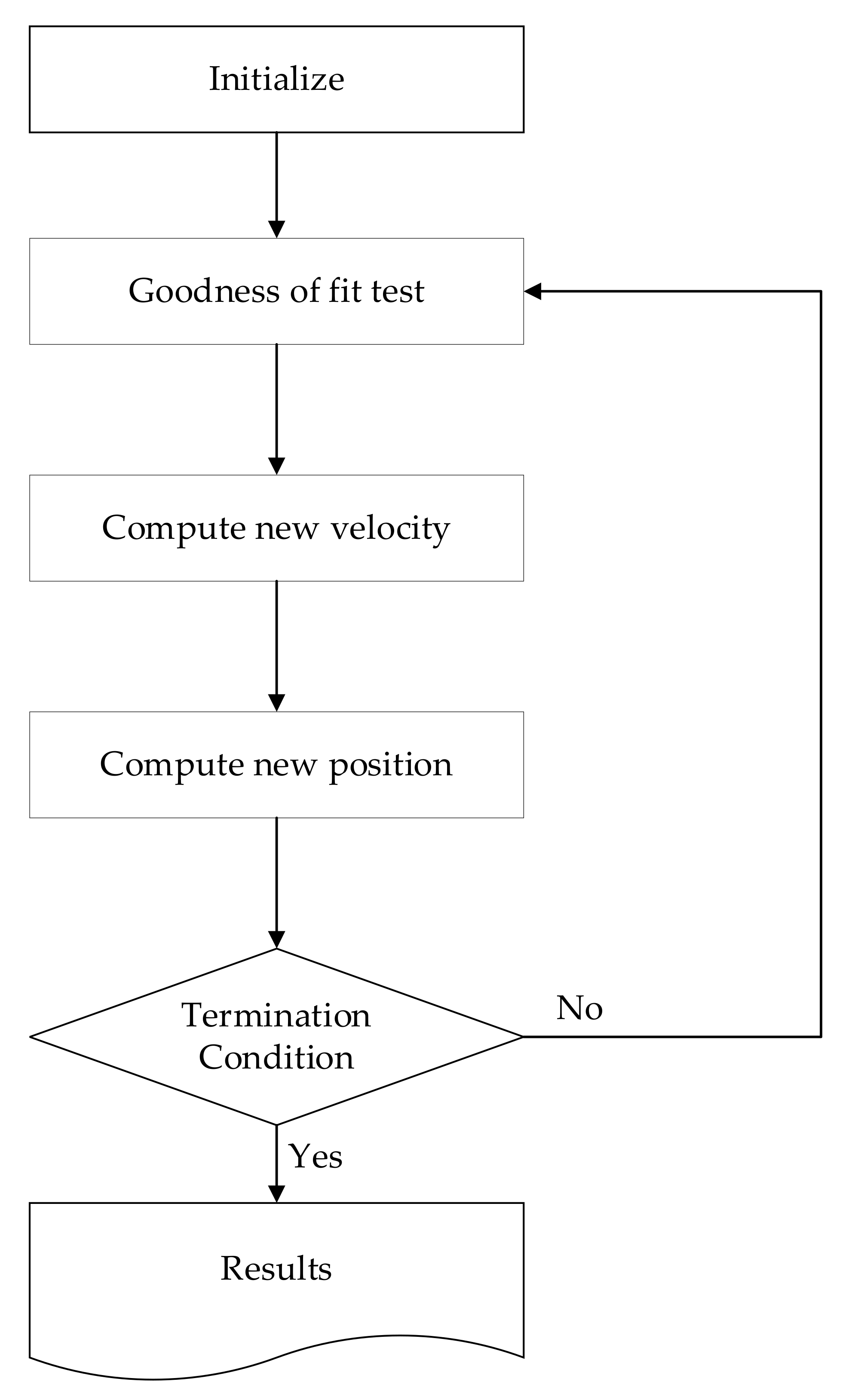
5.1. Conducting PSO in Detail
| Algorithm 1 PSO Algorithm | |
| 1: | Set up PSO parameters |
| 2: | Initialize position of particles and velocity |
| 3: | Set iteration counter |
| 4: | For each particle do |
| 5: | Calculate initial fitness of particle |
| 6: | End |
| 7: | Find index of the best particle of population and best fitness |
| 8: | Select and |
| 9: | While current iteration maximum iterations do |
| 10: | Calculate inertial weight |
| 11: | For each particle do |
| 12: | For each dimension do |
| 13: | Pick random numbers and |
| 14: | Update the particle’s velocity |
| 15: | Update the particle’s position |
| 16: | End |
| 17: | Evaluate fitness of particles |
| 18: | If then |
| 19: | Update of population |
| 20: | Update best fitness |
| 21: | End |
| 22: | End |
| 23: | Find index of the best particle and best fitness |
| 24: | If then |
| 25: | Update of population |
| 26: | Update best particle |
| 27: | Update best fitness |
| 28: | End |
| 29: | Increase iteration counter |
| 30: | End |
| 31: | Print out index of best particle and |
GA Details
- (a)
- The production of initial population members,
- (b)
- The evaluation of the fitness function of each individual member,
- (c)
- Selection,
- (d)
- Crossover,
- (e)
- Mutation.
- (a)
- A time limit is reached;
- (b)
- A fixed number of generations is reached;
- (c)
- Sufficient fitness is achieved, or;
- (d)
- A combination of these conditions [42].
5.2. Results
5.2.1. Simulation Results
5.2.2. Index for Objective Function Selection and DG Installation Property
(a) Voltage Profile Index (IVD)
(b) Fault Current Level Index (FCI)
(c) Real and Reactive Power Losses (ILP and ILQ)
5.2.3. Index Results by Function
5.2.4. Evaluation of Swarm Intelligence
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| DG | distributed generator |
| DLG | double line-to-ground |
| IBDG | inverter based distributed generator |
| GA | genetic algorithm |
| LL | line-to-line |
| PSO | particle swarm optimization |
| SCADA | supervisory control and data acquisition |
| SLG | single line-to-ground |
| LCOE | levelized cost of energy |
| Thevenin’s equivalent voltage source | |
| Thevenin’s equivalent impedance | |
| Norton’s equivalent current source | |
| Norton’s equivalent admittance | |
| zero-, positive-, and negative-sequence fault voltages | |
| zero-, positive-, and negative-sequence fault currents | |
| zero-, positive-, and negative-sequence fault impedances | |
| pre-fault voltage source | |
| fault impedance | |
| line-to-ground voltage of phases a, b, and c | |
| zero-, positive-, negative-sequence impedances connected to the slack bus | |
| three-winding transformer impedances | |
| neutral grounding resistors | |
| zero-, positive-, negative-sequence transformer impedances | |
| Norton’s equivalent impedance | |
| fault current caused by the voltage source | |
| fault current caused by the current source | |
| velocity in the jth step | |
| weight of inertia | |
| acceleration | |
| random number | |
| individual best position | |
| swarm best position | |
| position of each particles in the jth step |
References
- Kimbark, E.W. Power System Stability II; John Wiley: Hoboken, NJ, USA, 1948. [Google Scholar]
- Anderson, R. Analysis of Faulted Power Systems; The Iowa State University Press: Ames, IA, USA, 1973. [Google Scholar]
- Kundur, P. Power System Stability and Control; Mc Grow Hill Inc.: New York, NY, USA, 1994. [Google Scholar]
- Gao, Z.; Cecati, C.; Ding, S.X. A Survey of Fault Diagnosis and Fault-Tolerant Techniques—Part I: Fault Diagnosis With Model-Based and Signal-Based Approaches. IEEE Trans. Ind. Electron. 2015, 62, 3757–3767. [Google Scholar] [CrossRef]
- Kim, I.; Harley, R.G.; Regassa, R.; Del Valle, Y. The effect of the volt/var control of photovoltaic systems on the time-series steady-state analysis of a distribution network. In Proceedings of the 2015 Clemson University Power Systems Conference (PSC), Clemson, SC, USA, 10–13 March 2015; pp. 1–6. [Google Scholar]
- Guo, L.; Lei, Y.; Xing, S.; Yan, T.; Li, N. Deep Convolutional Transfer Learning Network: A New Method for Intelligent Fault Diagnosis of Machines with Unlabeled Data. IEEE Trans. Ind. Electron. 2019, 66, 7316–7325. [Google Scholar] [CrossRef]
- Chien, C.-F.; Chen, S.-L.; Lin, Y.-S. Using Bayesian network for fault location on distribution feeder. IEEE Trans. Power Deliv. 2002, 17, 785–793. [Google Scholar] [CrossRef]
- Thukaram, D.; Khincha, H.P.; Vijaynarasimha, H. Artificial Neural Network and Support Vector Machine Approach for Locating Faults in Radial Distribution Systems. IEEE Trans. Power Deliv. 2005, 20, 710–721. [Google Scholar] [CrossRef]
- Kanchev, H.; Colas, F.; Lazarov, V.; Francois, B. Emission Reduction and Economical Optimization of an Urban Microgrid Operation Including Dispatched PV-Based Active Generators. IEEE Trans. Sustain. Energy 2014, 5, 1397–1405. [Google Scholar] [CrossRef]
- Currie, R.; Ault, G.; McDonald, J. Methodology for determination of economic connection capacity for renewable generator connections to distribution networks optimised by active power flow management. IEE Proc. Gener. Transm. Distrib. 2006, 153, 456. [Google Scholar] [CrossRef]
- IEEE Guide for Monitoring, Information Exchange, and Control of Distributed Resources Interconnected with Electric Power Systems; IEEE Std.: Piscataway, NJ, USA, 2008; pp. 1–160. [CrossRef]
- Sörensen, K.; Glover, F. Metaheuristics. In Encyclopedia of Operations Research and Management Science; Springer: New York, NY, USA, 2013; pp. 960–970. [Google Scholar]
- Gandomi, A.H.; Yang, X.-S.; Talatahari, S.; Alavi, A.H. Metaheuristic Algorithms in Modeling and Optimization. In Metaheuristic Applications in Structures and Infrastructures; Elsevier: Amsterdam, The Netherlands, 2013; pp. 1–24. [Google Scholar] [CrossRef]
- Beheshti, Z.; Shamsuddin, S.M. A review of population-based meta-heuristic algorithm. Int. J. Adv. Soft Comput. Appl. 2013, 5, 1–35. [Google Scholar]
- Mareddy, P.; Reddy, V.C.V.; Vyza, U. Optimal DG placement for minimum real power loss in radial distribution systems using PSO. J. Theor. Appl. Inf. Technol. 2010, 13, 107–116. [Google Scholar]
- Singh, D.; Singh, D.; Verma, K. GA based energy loss minimization approach for optimal sizing & placement of distributed generation. Int. J. Knowl.-Based Intell. Eng. Syst. 2008, 12, 147–156. [Google Scholar] [CrossRef]
- Bouzguenda, M.; Samadi, A.; Rajamohamed, S. Optimal placement of distributed generation in electric distribution networks. In Proceedings of the 2017 IEEE International Conference on Intelligent Techniques in Control, Optimization and Signal Processing (INCOS) 2017, Srivilliputhur, India, 23–25 March 2017; Volume 2018, pp. 1–5. [Google Scholar] [CrossRef]
- Popović, D.; Greatbanks, J.; Begović, M.; Pregelj, A. Placement of distributed generators and reclosers for distribution network security and reliability. Int. J. Electr. Power Energy Syst. 2005, 27, 398–408. [Google Scholar] [CrossRef]
- Abdmouleh, Z.; Gastli, A.; Ben-Brahim, L.; Haouari, M.; Al-Emadi, N. Review of optimization techniques applied for the integration of distributed generation from renewable energy sources. Renew. Energy 2017, 113, 266–280. [Google Scholar] [CrossRef]
- Viral, R.; Khatod, D. Optimal planning of distributed generation systems in distribution system: A review. Renew. Sustain. Energy Rev. 2012, 16, 5146–5165. [Google Scholar] [CrossRef]
- La Scala, M.; Bruno, S.; Nucci, C.A.; Lamonaca, S.; Stecchi, U. From Smart Grids to Smart Cities, 1st ed.; Wiley-ISTE: Somerset, NJ, USA, 2017. [Google Scholar]
- Yun, S.; Jung, J.; Cho, N. Analyzing the Single-Line to Ground Fault Current Contribution by the Type of Transformer and Distributed Generator. In Proceedings of the IEEE Region 10 Annual International Conference, Proceedings/TENCON, Jeju, Korea, 28–31 October 2018; pp. 751–761. [Google Scholar]
- Irwin, J.D.; Nelms, R.M. Basic Engineering Circuit Analysis, 11th ed.; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]
- Duncan, G.; Duncan, J. Power System Analysis and Design, 6th ed.; Cengage Learning: Boston, MA, USA, 2016. [Google Scholar]
- Pazos, F.J.; Navarro, E. Field experience of power frequency overvoltages in wide-scale photovoltaic systems. In Proceedings of the 2009 CIGRE/IEEE PES Joint Symposium Integration of Wide-Scale Renewable Resources into the Power Delivery System, Calgary, AB, Canada, 29–31 July 2009; p. 1. [Google Scholar]
- Bravo, R.J.; Salas, R.; Yinger, R.; Robles, S.; Salas, R. Solar photovoltaic inverters transient over-voltages. In Proceedings of the 2013 IEEE Power & Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013. [Google Scholar] [CrossRef]
- Bravo, R.J.; Yinger, R.; Robles, S.; Tamae, W. Solar PV inverter testing for model validation. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011. [Google Scholar] [CrossRef]
- Ropp, M.; Hoke, A.; Chakraborty, S.; Schutz, D.; Mouw, C.; Nelson, A.; Mccarty, M.; Wang, T.; Sorenson, A. Ground Fault Overvoltage With Inverter-Interfaced Distributed Energy Resources. IEEE Trans. Power Deliv. 2017, 32, 890–899. [Google Scholar] [CrossRef]
- Wieserman, L.; McDermott, T. Fault current and overvoltage calculations for inverter-based generation using symmetrical components. In Proceedings of the 2014 IEEE Energy Conversion Congress and Exposition (ECCE), Pittsburgh, PA, USA, 14–18 September 2014; pp. 2619–2624. [Google Scholar]
- Kim, I. Short-Circuit Analysis Models for Unbalanced Inverter-Based Distributed Generation Sources and Loads. IEEE Trans. Power Syst. 2019, 34, 3515–3526. [Google Scholar] [CrossRef]
- Kim, I. A calculation method for the short-circuit current contribution of current-control inverter-based distributed generation sources at balanced conditions. Electr. Power Syst. Res. 2021, 190, 106839. [Google Scholar] [CrossRef]
- Kim, I. Steady-state short-circuit current calculation for internally limited inverter-based distributed generation sources connected as current sources using the sequence method. Int. Trans. Electr. Energy Syst. 2019, 29. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Clerc, M. Particle Swarm Optimization; ISTE: Newport Beach, CA, USA, 2006. [Google Scholar]
- IRENA. Renewable Power Generation Costs in 2019, Abu Dhabi. 2020. Available online: https://www.irena.org/publications/2020/Jun/Renewable-Power-Costs-in-2019 (accessed on 5 August 2020).
- Mishra, S.K. Some New Test Functions for Global Optimization and Performance of Repulsive Particle Swarm Method. SSRN Electron. J. 2006. [Google Scholar] [CrossRef]
- Appendix I: Test Functions. In Practical Genetic Algorithms; John Wiley & Sons: Hoboken, NJ, USA, 2003; pp. 205–209.
- Bäck, T. Evolutionary Algorithms in Theory and Practice: Evolution Strategies, Evolutionary Programming, Genetic Algorithms; Oxford University Press: New York, NY, USA, 1996. [Google Scholar]
- Rosenbrock, H.H. An Automatic Method for Finding the Greatest or Least Value of a Function. Comput. J. 1960, 3, 175–184. [Google Scholar] [CrossRef]
- Alam, M.N. Particle Swarm Optimization: Algorithm and Its Codes in MATLAB. 2016. Available online: https://search.datacite.org/works/10.13140/rg.2.1.4985.3206 (accessed on 20 August 2020).
- Deb, K. Multi-Objective Optimization Using Evolutionary Algorithms: An Introduction Multi-Objective Optimization Using Evolutionary Algorithms: An Introduction; Indian Institute of Technology Kanpur: Kanpur, India, 2001. [Google Scholar]
- Kumar, M.; Husain, M.; Upreti, N.; Gupta, D. Genetic Algorithm: Review and Application. SSRN Electron. J. 2010. [Google Scholar] [CrossRef]
- Ochoa, L.F.; Padilha-Feltrin, A.; Harrison, G.P. Evaluating Distributed Generation Impacts with a Multiobjective Index. IEEE Trans. Power Deliv. 2006, 21, 1452–1458. [Google Scholar] [CrossRef]
- Elnashar, M.M.; El Shatshat, R.; Salama, M.M. Optimum siting and sizing of a large distributed generator in a mesh connected system. Electr. Power Syst. Res. 2010, 80, 690–697. [Google Scholar] [CrossRef]
- Aziz, N.A.A.; Mubin, M.; Ibrahim, Z.; Nawawi, S.W. Statistical Analysis for Swarm Intelligence–Simplified. Int. J. Futur. Comput. Commun. 2015, 4, 193–197. [Google Scholar] [CrossRef]
| Rosenbrock Function | Himmelblau Function | Beale Function | |||
|---|---|---|---|---|---|
| Bus No. | Capacity (MVA) | Bus No. | Capacity (MVA) | Bus No. | Capacity (MVA) |
| 8 | 54 | 1 | 100 | 2 | 37 |
| 9 | 16 | 3 | 100 | 3 | 100 |
| 12 | 83 | 4 | 100 | 4 | 18 |
| 13 | 28 | 17 | 100 | 5 | 44 |
| 22 | 48 | 18 | 100 | 9 | 22 |
| 26 | 74 | 21 | 100 | 14 | 26 |
| Goldstein-Price Function | Ackley Function | ||
|---|---|---|---|
| Bus No. | Capacity (MVA) | Bus No. | Capacity (MVA) |
| 6 | 22 | 9 | 1 |
| 16 | 20 | 18 | 1 |
| 21 | 1 | 20 | 1 |
| 26 | 1 | 26 | 1 |
| Rosenbrock Function | Himmelblau Function | Beale Function | |||
|---|---|---|---|---|---|
| Bus No. | Capacity (MVA) | Bus No. | Capacity (MVA) | Bus No. | Capacity (MVA) |
| 2 | 100 | 1 | 100 | 2 | 50 |
| 5 | 90 | 4 | 100 | 12 | 50 |
| 13 | 99 | 5 | 100 | 15 | 50 |
| 15 | 100 | 6 | 100 | 16 | 50 |
| 28 | 100 | 10 | 100 | 22 | 50 |
| 29 | 78 | 13 | 100 | 24 | 51 |
| Goldstein-Price Function | Ackley Function | ||
|---|---|---|---|
| Bus No. | Capacity (MVA) | Bus No. | Capacity (MVA) |
| 2 | 20 | 1 | 0 |
| 7 | 16 | 2 | 0 |
| 11 | 20 | - | - |
| 13 | 17 | - | - |
| Bus No./Capacity | IVD | FCI | ILP | ILQ |
|---|---|---|---|---|
| Bus 8/54 MVA | 0 | 0.017 | 0.67 | 0.40 |
| Bus 9/16 MVA | 0 | 0.004 | 0.88 | 0.75 |
| Bus 12/83 MVA | 0 | 0.024 | 0.65 | 0.1 |
| Bus 13/28 MVA | 0 | 0.001 | 0.84 | 0.61 |
| Bus 22/48 MVA | 0 | 0.014 | 0.71 | 0.29 |
| Bus 26/74 MVA | 0 | 0.019 | 1.09 | 1.23 |
| Bus No./Capacity | IVD | FCI | ILP | ILQ |
|---|---|---|---|---|
| Bus 6/22 MVA | 0 | 0.007 | 0.99 | 0.98 |
| Bus 16/20 MVA | 0 | 0.005 | 1.00 | 0.98 |
| Bus 21/1 MVA | 0 | 0.004 | 0.99 | 0.99 |
| Bus 26/1 MVA | 0 | 0.000 | 0.99 | 0.99 |
| Bus No./Capacity | IVD | FCI | ILP | ILQ |
|---|---|---|---|---|
| Bus 2/100 MVA | 0.008 | 0.027 | 1.00 | 1.00 |
| Bus 5/90 MVA | 0.007 | 0.014 | 1.00 | 0.99 |
| Bus 13/99 MVA | 0.002 | 0.007 | 0.99 | 0.99 |
| Bus 15/100 MVA | 0 | 0.007 | 1.16 | 1.21 |
| Bus 28/100 MVA | 0 | 0.032 | 1.07 | 1.07 |
| Bus 29/78 MVA | 0 | 0.025 | 1.40 | 1.56 |
| Bus No./Capacity | IVD | FCI | ILP | ILQ |
|---|---|---|---|---|
| Bus 2/20 MVA | 0.008 | 0.019 | 1.00 | 1.00 |
| Bus 7/16 MVA | 0.006 | 0.005 | 1.00 | 0.98 |
| Bus 11/20 MVA | 0.003 | 0.005 | 1.00 | 1.00 |
| Bus 13/17 MVA | 0.002 | 0.005 | 1.00 | 0.99 |
| Goldstein-Price Function | Rosenbrock Function | |
|---|---|---|
| p-value |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, B.; Rusetskii, N.; Jo, H.; Kim, I. The Optimal Allocation of Distributed Generators Considering Fault Current and Levelized Cost of Energy Using the Particle Swarm Optimization Method. Energies 2021, 14, 418. https://doi.org/10.3390/en14020418
Kim B, Rusetskii N, Jo H, Kim I. The Optimal Allocation of Distributed Generators Considering Fault Current and Levelized Cost of Energy Using the Particle Swarm Optimization Method. Energies. 2021; 14(2):418. https://doi.org/10.3390/en14020418
Chicago/Turabian StyleKim, Beopsoo, Nikita Rusetskii, Haesung Jo, and Insu Kim. 2021. "The Optimal Allocation of Distributed Generators Considering Fault Current and Levelized Cost of Energy Using the Particle Swarm Optimization Method" Energies 14, no. 2: 418. https://doi.org/10.3390/en14020418
APA StyleKim, B., Rusetskii, N., Jo, H., & Kim, I. (2021). The Optimal Allocation of Distributed Generators Considering Fault Current and Levelized Cost of Energy Using the Particle Swarm Optimization Method. Energies, 14(2), 418. https://doi.org/10.3390/en14020418