Abstract
To investigate the evolution process of LNG (Liquefied Natural Gas) liquid pool and gas cloud diffusion, the Realizable k-ε model and Eluerian model were used to numerically simulate the liquid phase leakage and diffusion process of LNG storage tanks. The experimental results showed that some LNG flashed and vaporized rapidly to form a combustible cloud during the continuous leakage. The diffusion of the explosive cloud was divided into heavy gas accumulation, entrainment heat transfer, and light gas drift. The vapor cloud gradually separated into two parts from the whole “fan leaf shape”. One part was a heavy gas cloud; the other part was a light gas cloud that spread with the wind in the downwind direction. The change of leakage aperture had a greater impact on the whole spill and dispersion process of the storage tank. The increasing leakage aperture would lead to 10.3 times increase in liquid pool area, 78.5% increase in downwind dispersion of methane concentration at 0.5 LFL, 22.6% increase in crosswind dispersion of methane concentration at 0.5 LFL, and 249% increase in flammable vapor cloud volume. Within the variation range of the leakage aperture, the trend of the gas cloud diffusion remained consistent, but the time for the liquid pool to keep stable and the gas cloud to enter the next diffusion stage was delayed. The low-pressure cavity area within 200 m of the leeward surface of the storage tank would accumulate heavy gas for a long time, forming a local high concentration area, which should be an area of focus for alert prediction.
1. Introduction
LNG is mostly methane with small amounts of ethane, propane, butane and nitrogen, which is expected to be the second-largest energy source in energy composition in 2030 [1]. However, there may be a leak of liquefied natural gas (LNG) in the presence of an ignition source that will cause a fire or explosion in a fully or partially hazardous environment [2].
In view of this, several studies have been published on storage tank accidents [3,4,5,6]. Scholars in China and overseas have conducted many studies on the prediction of possible hazards associated with LNG vapor dispersion. Koopman et al. [7] carried out the Burro series of tests in 1980 to observe the diffusion of LNG vapor clouds under different conditions after LNG leaked to the water surface. It was found that the leakage mode of LNG has a certain influence on the vapor cloud diffusion. In 1983, the Coyote series of tests [8] were conducted to study the ignition and flash evaporation processes of LNG, and the rapid phase transition, vapor cloud diffusion and pool fire were all observed in this test. Brown et al. [9] carried out Falcon series of experiments to study the leakage and diffusion of LNG under obstacles. They accurately evaluated the effectiveness of the fence so as to mitigate the harm of LNG gas cloud diffusion.
In addition, several mathematical models have been developed to simulate heavy gas diffusion based on experimental data, such as DEGADIS, SLAB [10], FEM3 [11,12], etc. First of all, field tests can reproduce the actual situation of LNG leakage and diffusion; in addition, the cycle was too long and the repeatability was poor. Therefore, CFD simulation was used as a promising alternative to calculate the diffusion distance of LNG. Giannissi et al. [13] simulated the LNG diffusion under an open and obstructed condition based on Falcon series experiments. It was proved that the leak source model greatly affected LNG diffusion, and the best case to simulate the leakage source was to model the source as having two phases. Vílchez et al. [14] used the DEGADIS model to predict the explosive distances of vapor clouds after LNG leakage and they defined the diffusion safety factor (DSF) to estimate these distances. Li et al. [15] evaluated the effect of safety clearance on the diffusion of cylindrical floating LNG with FLACS software. The results demonstrated that the safety gap increased the size of the gas cloud far from the cylindrical FLNG release position but decreased the size of the gas cloud near the release position.
Zhang et al. [16] studied the process of LNG leakage and diffusion in different wind directions. The results showed that the LNG spread farthest along the horizontal downwind direction. Marsegan et al. [17] carried out a numerical simulation of LNG diffusion under active and passive barriers and found that the active barrier effectively reduced the diffusion area of LNG by accelerating the entrainment between air and gas. Nguyen et al. [18] conducted a liquid pool evaporation experiment with different leak rates on the water surface. They proposed a model to express the function relationship between evaporation rate, leakage rate and time based on the experimental results and one-dimensional heat conduction model. Gopalaswami et al. [19] developed a transient three-dimensional multiphase model in CFX based on the comprehensive test data and numerical simulation data, which was found that wind affected the evaporation and diffusion of LNG by carrying additional heat and unsaturation. Ikealumba et al. [20] studied the effects of atmospheric and ocean stability on LNG diffusion where they found that the instability caused by the waves would aggravate the leakage hazard of LNG ships. Luo et al. [21] proposed an integrated multiphase CFD model to simulate the complete process of LNG leakage on the water surface, concluding that water storage would shorten the horizontal diffusion distance of the gas cloud. Dasgotra et al. [22] simulated the diffusion of heavy gas in natural gas storage facilities. They found that the average diameter of the gas cloud ranged from 0 to 500 m under relatively stable weather conditions. Giannissi et al. [23] investigated the effect of environmental humidity on the diffusion of LNG, and concluded that in the case of high environmental humidity, the explosion distance of gas cloud would be reduced.
The above studies mainly focus on the potential hazards which are associated with LNG leakage and the influence degree of external environmental factors on the dispersion effect of LNG leakage. However, few considerations have been given to phase change. Therefore, in this study, the effect of phase change on dispersion during LNG release is studied to analyze the behavior characteristics of LNG liquid pool expansion and gas cloud diffusion, and the effect of the leaking aperture on the gas cloud diffusion process is also studied.
2. Materials and Methods
2.1. Numerical Model
The homogeneous Eulerian multiphase model [24,25] was adopted to model the phase change process after LNG leaked to the ground. The realizable k-ε model had higher accuracy in concentration distribution than the standard k-ε model by simulating Thorney’s heavy gas diffusion (Freon-12) field test [26]. Therefore, the realizable k-ε model was selected for gas diffusion turbulence.
At present, the k-ε model is the most widely used turbulence model for the turbulence simulations of wind fields in large structures such as storage tanks. The standard k-ε model proposed by Launder and Spalding greatly improves the zero-equation model and one equation model, so it is widely used in engineering flow field calculation and has been well verified in practice. However, the applicability of the standard k-ε model for each component of Reynolds stress is not strong. For example, it is assumed that the turbulent viscosity coefficient is isotropic, while the turbulence is anisotropic in the case of curved wall flow, curved streamline flow, or strong swirling flow. Therefore, it is not recommended to use the standard k-ε model to calculate the wind field of a storage tank with curved wall flow; otherwise, it will produce a certain degree of distortion in calculation.
The equation of turbulent kinetic energy k and dissipation rate ε of the standard k-ε model is described as follows.
In the above equation, Gk represents the turbulent kinetic energy generated due to the average velocity gradient; Gb refers to the turbulent kinetic energy caused by buoyancy; YM refers to the effect of compressible turbulent pulsating expansion on the total dissipation rate.
The coefficient of turbulence viscosity is:
In FLUENT, these three parameters , , are the default constant, = 1.4, = 1.92, and = 0.09. The turbulent Prandt numbers of turbulent kinetic energy k and dissipation rate ε are respectively 1.0 and 1.3.
The transport equation of turbulent kinetic energy k and dissipation rate ε is described as follows.
The equation k:
The equation :
where,
In the above equation, k is the kinetic energy of turbulence pulsation; ε is the dissipation rate of the turbulent pulsation kinetic energy; Gk is the turbulent kinetic energy caused by the average velocity gradient; Gb is the turbulent kinetic energy caused by buoyancy; YM is the effect of compressible turbulent pulsating expansion on the total dissipation rate. and are constant; and is turbulent Prandt numbers of turbulent kinetic energy and dissipation rate, respectively.
In Fluent,
2.2. Parameter Setting
A 16 × 104 m3 large cylindrical LNG storage tank was chosen for numerical simulation, and its structural dimension are shown in Figure 1. The outer diameter of the tank was 82 m and the height was 50 m. The normal operating pressure of the storage tank was 25 kPa, and the maximum liquid level in the tank was 34.6 m. The origin of the computational domain was located at the center of the bottom of the tank. The coordinate of the leakage hole center point was (41, 10, 0), which was located on the leeward side of the tank. The leakage hole sizes were, respectively, 0.1 m × 0.1 m, 0.13 m × 0.13 m, 0.15 m × 0.15 m, 0.18 m × 0.18 m and 0.2 m × 0.2 m. Considering the calculation accuracy, the computational domain was determined to be 1000 m × 250 m × 500 m in the x, y, and z directions, and the tank that has a blocking rate of 2.78% was placed at a distance of 200 m downwind. The whole computational domain was discretized by the structured grid, and the specific grid division is shown in Figure 2a. In order to adapt to the change of flow field and ensure the accuracy of the solution, the grid around the leakage hole was encrypted by the block method. The independence of the grid and time step had been verified. The total number of cells in the calculation domain was finally determined to be 1,865,345, and the simulation time step was set to 0.1 s.
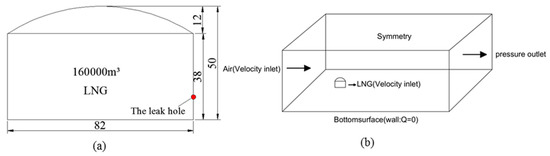
Figure 1.
The settings of the large-scale LNG storage tank. (a) Geometric schematic of the tank; (b) the boundary settings of the tank.
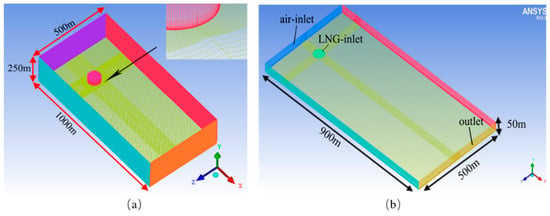
Figure 2.
Mesh division in this study. (a) The meshing of the computational watershed; (b) the meshing of LNG leakage diffusion experiment.
In order to represent the node coordinates more accurately and ensure the convergence of calculation, a double-precision solver and implicit method were used in the calculation. Figure 2b shows the meshing of the LNG leakage diffusion experiment. The calculation domain was established with a size of 900 m × 500 m × 50 m on the x-axis, y-axis, and z-axis, respectively. The x–z plane was placed on the ground, and the y-direction was the vertical height. Furthermore, the wind direction remained unchanged throughout the calculation domain. The boundary conditions on the left and right sides of the calculation domain were the velocity–inlet and the pressure–outlet, respectively. Hexahedral mesh units were used for mesh generation, while the area around the pond was divided into fine meshes. A total of 803,287 cells were used for subsequent simulations.
2.3. Model Validation
In this paper, data from the Burro eight-spill test [27], which was conducted in 1980, was used as the basis of the validation analysis. In the test, LNG was released onto the water surface of a round pond, with 25 gas concentration monitors placed at different heights in the downwind. In addition, the water pond had an average diameter of 58 m, with an average water level about 1.5 m below the surrounding ground level. Based on the Burro series tests, the reliability of the multiphase model was evaluated by comparing the numerical results with the experimental results based on the diffusion range and concentration change of methane.
Figure 3 and Figure 4 show the contour distribution of methane volume fraction after LNG spill 80 s on the x = 57 m and y = 1 m planes, respectively. In Figure 3a,b and Figure 4a,b, the distribution areas of methane with different volume fractions on the horizontal and vertical planes are basically consistent with the experimental data. Figure 3c and Figure 4c show the comparison of the coverage areas of dispersion clouds with different volume concentrations. There is a very good quantitative agreement between the simulation results and the experimental data. Besides, Table 1 shows that the comparison between the calculated and experimental values of maximum volume fraction of methane at different distances in downwind direction. It shows that the calculated maximum volume fraction of methane is lower than that of the experiment; however, in the area away from the leakage source, the calculated maximum volume fraction of methane is higher than that of the experiment. The reason is that the coupled heat transfer between the ground and the LNG vapor cloud is assumed to be constant in the simulation; in fact, the heat produced by ground heat transfer and solar radiation is variable. The error analysis method of the heavy gas diffusion model proposed by Emark et al. [28] is used to analyze the deviation between the simulation result and the test value. The method includes relative deviation (FB), geometric mean deviation (MG), geometric mean-variance (VG), relative mean square error (MRSE), relative mean square error (FAC2) and normalized mean square error (NMSE), which can be used to judge the validity of the numerical model. The deviation between numerical simulation and experimental values is shown in Table 2. It can be seen that all the deviations were within the allowable range of the evaluation parameters. Therefore, the multiphase model is suitable for the study of LNG leakage and diffusion.

Figure 3.
Comparison of experimental and simulated values of methane volume concentration at a vertical height of 1 m. (a) Burro eight-test measured value. (b) Fluent simulation results. (c) Comparison of test and simulation.

Figure 4.
Comparison between experimental and simulated values of methane volume concentration at 57 m in downwind direction. (a) Burro-eight test measured value. (b) Fluent simulation results. (c) Comparison of test and simulation.

Table 1.
Experimental and simulated values of maximum volume fraction of methane at different distances in downwind direction.

Table 2.
The error comparison of simulation results.
3. Results and Discussions
3.1. The Influence of Wind Field on Leakage and Diffusion of LNG Storage Tank
3.1.1. Numerical Simulation of Wind Field of LNG Storage Tank
The LNG storage tank will obstruct the flow of wind speed and thus affect the diffusion of LNG. In this study, the average wind speed at the height of 10 m is 4 m/s, and the wind speed of the inflow profile is implemented in a user-defined function (UDF) which is embedded in the numerical model as a boundary condition. Figure 5 shows the wind speed distribution in different planes of the calculation domain. As shown in Figure 5a, the wind speed at the boundary of the entire wind field is evenly distributed in the vertical plane of 0 m. The wind speed varied with height, forming gradient wind, which is the same as the wind field distribution law of the real atmospheric environment.
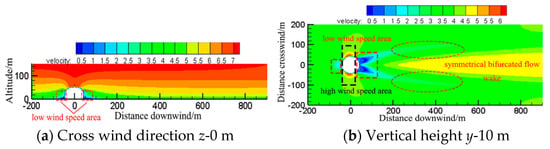
Figure 5.
The wind speed in the calculation area.
However, the atmospheric flow near the storage tank is affected by various factors, resulting in changes in wind speed and direction. When the wind flows from the top and both sides of the storage tank, it causes a high wind speed zone with a speed of 7 m/s on top of the storage tank (shown in the black box, Figure 5 and a low wind speed zone with a speed of less than 1 m/s on both sides of the storage tank (shown in the red box, Figure 5). In Figure 5b, in the area away from the storage tank, the wind keeps up to 4 m/s; however, in the area near the storage tank, the wind speed is reduced because of obstruction. A detention zone is formed on the windward side of the tank due to the obstruction of the tank, so the wind speed decreases sharply. When the wind bypasses both sides of the tank, a certain length of a symmetrical bifurcated flow wake is formed downstream of the tank (shown in the red circle).
Figure 6 shows the distribution of the wind speed streamline near the storage tank. It shows that there are obvious vortices on the windward and leeward sides of the tank. In addition, two symmetrical vortices are formed at 70 m in the x-axis behind the horizontal of the tank after the atmosphere bypasses the tank (Figure 6a). In the process of the wind flowing downstream along both sides of the tank, the wind speed decreases continuously and the wind direction changes, thus producing backflow. When the wind reaches the central axis of the storage tank, the wind speed is close to zero, and a small cavity zone is formed on the back of the storage tank (Figure 6b). However, the vortex and low wind speed areas are very close to the storage tank. When the wind is away from the storage tank, the streamline returns to normal and the wind movement also stabilizes.
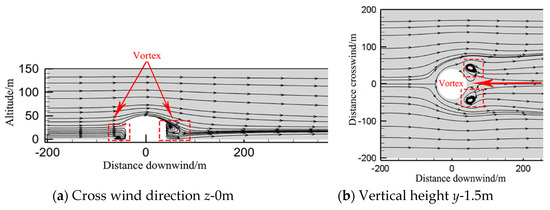
Figure 6.
The distribution of wind speed streamlines near the storage tank.
3.1.2. Leakage and Diffusion Process of LNG Storage Tank under Wind Field
The average wind speed was assumed to be 4 m/s, and at the same time LNG was assumed to leak at a rate of 105.5 kg/s for 400 s. The expansion of LNG after leakage is shown in Figure 7. It can be seen that the pressure difference between the inside and outside of the tank causes the LNG to continue to spray from the leakage port to the ground in a parabolic form. The amount of LNG leakage is large, but the heat of the surrounding environment is limited, which makes it difficult to provide enough heat for the entire LNG to vaporize. Therefore, some LNG absorbs heat from the surrounding environment and then evaporates into a low-temperature gas cloud, and others form a liquid pool on the ground. During the landing process, some of the atomized LNG droplets absorb heat from the air and then evaporates into a gas state, resulting in a higher concentration of LNG leaking from the leakage hole and a lower concentration of LNG in the surface liquid pool (Figure 7c). Under the action of initial kinetic energy and gravity, the liquid LNG diffuses around the landing point, which is 7 m away from the storage tank and thus forming a thin “round” liquid pool (Figure 7b).
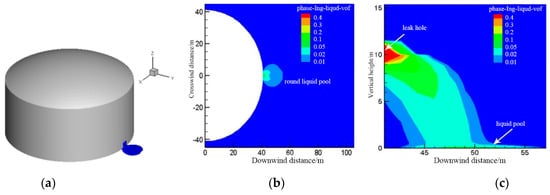
Figure 7.
The distribution of LNG liquid pool. (a) Three-dimensional view of the liquid pool; (b) expansion of liquid pool at y = 0 m; (c) LNG injection at z = 0 m.
Figure 8 is a three-dimensional perspective view of gas clouds, which shows different methane volume fractions at different leakage moments, clearly showing the movement and diffusion process of low-temperature steam cloud containing leaking LNG. At the initial stage of leakage, the density of the low-temperature vapor cloud formed by flash evaporation is greater than that of the surrounding air, resulting in the extremely low gas cloud with methane volume fractions greater than 1%, 5%, and 15%. This phenomenon is also due to gravitational settling. As the leakage time increases to 120 s, the gas cloud with a volume fraction greater than 15% is still close to the ground with a “hole” inside, while the gas cloud with a volume fraction greater than 1% and 5% rises slightly. When the leakage time reaches 320 s, the whole gas cloud presents the phenomenon of “leaf-like bifurcation” on both sides. However, the height of gas clouds with 15% and more than 5% volume fraction is lower, while the height of gas cloud with volume fraction above 1% is relatively high, with a large amount of light methane floating over the tank (shown in the red box). The whole diffusion process fully reflects that LNG accumulates in the form of heavy gas cloud after leakage, mixes with air to absorb and transfer heat, resulting in the gradual narrowing of the difference between gas cloud density and air density. Finally, heavy methane turns into light methane in the periphery of the gas cloud.

Figure 8.
Three-dimensional perspectives of gas clouds with different methane volume concentrations at different leakage moments. (a) Three-dimensional image of the vapor cloud with volume fraction of methane in excess of 15%(upper flammability limit, UFL); (b) Three-dimensional image of vapor cloud with volume fraction of methane in excess of 5%(lower flammability limit, LFL); (c) Three-dimensional image of vapor cloud with methane fraction in excess of 1%.
In order to reveal the spatial distribution characteristics of the LNG vapor cloud near the storage tank, methane concentration contours are selected from the x-y plane, x-z plane, and y-z plane for analysis. Considering that the low height of the gas cloud and bifurcated gas cloud along the z-axis on both sides of the tank, x = 57 m, z = 30 m and y = 0.5 m are selected as the observation surface. Figure 9 shows that the distribution of methane gas cloud concentration is in different planes. As shown in Figure 9a, at the plane y = 0.5 m, the overall shape of the gas cloud is “fan-shaped” (shown in white box), accompanied by a cavity with a radius of about 17 m on the back. A high concentration of methane is deposited on both sides of the cloud, while a low concentration of methane is distributed in the middle of the cloud. As the leakage time increases, the low concentration methane in the middle is preferentially diluted by air, resulting in a “hole” in the middle of the gas cloud (shown in white box). As the leak continues for some time, the “hole” area expands from the middle to the tail, and the gas cloud splits into two parts. One part is a heavy gas cloud, which is stacked behind the storage tank in the form of “leaf-like bifurcation” (shown in white box), and the other part is a light gas cloud (shown in a white round frame), spreading further with the wind. During the whole leakage process, the gas cloud gradually develops from a complete “fan shape” to a front-end “leaf-shaped” bifurcation. Due to the disturbance effect of the storage tank on the atmospheric movement, the detention zone and low wind speed region behind the storage tank restrains the downwind expansion in the middle of the gas cloud in some sense. When the low-temperature LNG vapor mixes with the atmosphere, the movement of the vapor cloud also diverges laterally along the streamline development at the back of the tank, resulting in a large amount of methane accumulation on both sides and thus forming a leaf-shaped bifurcation.
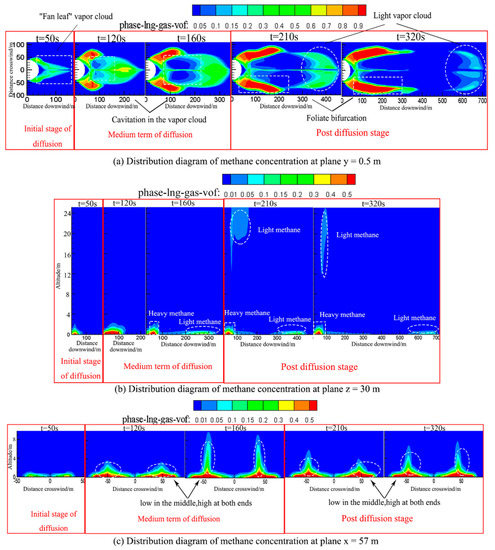
Figure 9.
Distribution of methane concentration in different planes. (a) Distribution diagram of methane concentration at plane y = 0.5 m; (b) Distribution diagram of methane concentration at plane z = 30 m; (c) Distribution diagram of methane concentration at plane x = 57 m.
In Figure 9b, it can be seen that the gas cloud is divided into different concentration layers along the vertical direction z = 30 m, and the methane volume fraction decreases with height. Among them, the methane concentration is high near the ground (shown in white box), and low far away from the ground (shown in white round frame). The reason is that a large amount of highly concentrated methane accumulates near the storage tank during the leakage process, which makes it difficult to dilute and dissipate. However, the heavy methane in the outermost part of the gas cloud continuously absorbs and transfers heat with air in order to form light methane with low concentration and then to spread to higher and farther places. In Figure 9c, the gas cloud after leakage is symmetrically distributed behind the storage tank at 57 m on the x-direction. As the leak progresses, the width and height of the vapor cloud in this area increase slightly. The vapor cloud appears as “low in the middle and high at both ends” (shown in a white circle).
According to the results of numerical simulation and relevant heavy gas diffusion theory [29], the macroscopic diffusion behavior of the LNG vapor cloud could be roughly divided into three stages according to the continuous leakage of the LNG tank studied in this paper.
(1) Initial stage of diffusion (heavy gas accumulation): This stage is a period of heavy gas accumulation and diffusion. As shown in Figure 9, from the beginning of the leakage to 50 s, the vapor cloud is in the shape of “fan leaf”, and its internal concentration of the vapor cloud is in an unstable state.
(2) Mid-stage of diffusion (Transitional levitation): This stage is the period of heavy gas transiting to light gas. From 120 s to 160 s, the development of gas cloud is in a neutral state, and the whole gas cloud is still in a “fan leaf shape”. The methane concentration inside the gas cloud increases to a peak.
(3) Post-diffusion stage (Light gas drift): this stage is the light gas into passive diffusion. After 210 s of leakage, the development of the vapor cloud is in a stable state, in which case the width of the gas cloud remains unchanged, but the length and height of the vapor cloud slowly increases. As the “hole” area inside the vapor cloud continues to expand, the contact area between the gas cloud and the surrounding air increases, which lead to the rise of temperature and the decrease of methane density at the tail of the gas cloud. Under the influence of wind, methane in the outermost part of the cloud is diluted the fastest. As a result, the cloud still behaves as “low in the middle and high at both ends”.
3.2. Influence of Leakage Aperture on LNG Vapor Cloud Diffusion
Figure 10 shows the change in the morphology of LNG vapor cloud with time at 0.5 m on the y-axis under five leakage apertures. When the leakage lasts for 60 s, which belongs to the initial stage of diffusion, the vapor cloud is in the shape of “fan leaf” with a similar downwind diffusion speed under different leakage aperture. As the leakage aperture increases, the volume concentration of methane in the gas cloud keeps rising, and the width of the gas cloud increases slightly. Compared with the situation at 60 s, the gas cloud has different degrees of holes inside at 180 s, which is at the middle stage of diffusion. However, the area of the hole in the gas cloud decreases with the leakage aperture increasing (shown in the white box). When the leak lasts for 320 s, it reaches the late stage of diffusion, the heavy gas in the vapor cloud is accumulated behind the storage tank in the form of “leaf-like bifurcation”, while the light gas at the tail of the vapor cloud is diluted with the wind. With the increase of the leakage aperture, the width of the heavy gas cloud becomes larger, and the methane volume concentration of the light gas in the tail increases (shown in white round frame), which makes it more difficult to be diluted. According to the LNG gas cloud diffusion under different leakage conditions, it could be demonstrated that the trend of the LNG vapor diffusion under different leakage apertures has similar characteristics. The change of the leakage aperture size will affect the coverage and concentration of the gas cloud, thus delaying the development of the gas cloud to the next diffusion stage. The motion trajectory of the vapor cloud is still determined by the wind field behind the tank.

Figure 10.
Variation of gas cloud concentration distribution at y = 0.5 m plane under different leakage apertures.
Figure 11 shows the furthest length, maximum width and height of the gas cloud diffusion with 1/2 LFL concentration under different leakage apertures. The increase of the leakage aperture will promote the diffusion speed of the vapor cloud in the downwind direction. As the leakage aperture increases, the maximum explosion range of methane and the volume of flammable clouds increases rapidly. For example, when the leakage aperture increases from 0.1 m to 0.2 m, the maximum diffusion distance of methane 0.5 LFL in Figure 11a increases by 78.5% from 531 m to 948 m, and the volume of flammable vapor cloud in Figure 11c enlarges from 13,563.44 m3 to 53,642.89 m3, with a growth rate of 295%. However, there is some difference, as shown in Figure 11b. When the leakage aperture is 0.1 m, the gas cloud with a concentration of 0.5 LFL has the largest width on the z-axis at 243 m. When the leakage aperture increases from 0.13 m to 0.2 m, the largest width of methane 0.5 LFL increases by 22.6% from 194.6 m to 238.6 m. This was because that when the leakage pore size is 0.1 m, due to the small leakage volume, the methane density in the late stage of diffusion is close to the air and the gas cloud diffuses faster in the horizontal direction, resulting in the farthest diffusion distance of the gas cloud along the z-axis. As leakage aperture increases, the leakage and vaporization of LNG increases, and a larger volume of combustible gas clouds increases too. However, the dilution ability of air is limited, and the gas cloud rapidly accumulates and diffuses along the downwind distance, resulting in a larger diffusion distance along the x-axes and z-axes. Therefore, after the LNG leaks, the leakage source should be cut off or blocked in time to reduce the amount of LNG leakage.
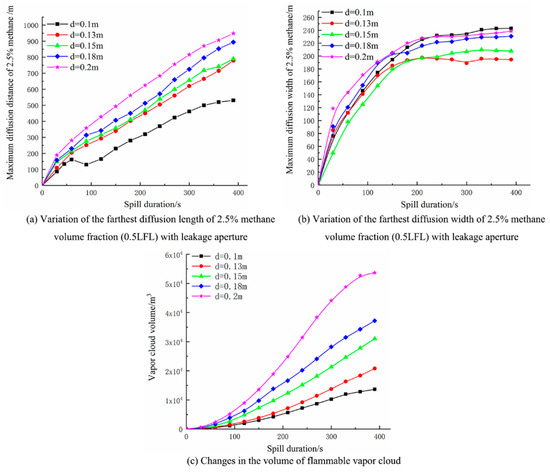
Figure 11.
Variation of the farthest moving distance and volume of flammable vapor clouds with leakage time under different leakage apertures. (a) Variation of the farthest diffusion length of 2.5% methane volume fraction (0.5 LFL) with leakage aperture; (b) Variation of the farthest diffusion width of 2.5% methane volume fraction (0.5 LFL) with leakage aperture; (c) Changes in the volume of flammable vapor cloud.
4. Conclusions
With the integrated use of the realizable k-ε turbulence model and the Eluerian model, numerical simulation of the leakage and diffusion process of the LNG storage tank was conducted. The conclusions were drawn as follows.
- (a)
- After the storage tank leaked, LNG was sprayed to the ground to form a circular liquid pool and then continuously exchanged heat with air to evaporate into low-temperature steam. The diameter of the liquid pool increased first and then remained unchanged with the leakage time, and the gas cloud diffusion state was divided into three stages due to the cylindrical turbulence of the tank. In these three stages, the LNG gas cloud experienced heavy gas accumulation, entrainment heat transfer and light gas drift, with the shape gradually developing from a complete “fan blade” to a “leaf bifurcation” of heavy methane at the front end.
- (b)
- The leakage aperture greatly affected the heat transfer between LNG and the surrounding environment. It delayed the development of the liquid pool and gas cloud to a stable state. The increase of leakage aperture quantitatively affected the distribution of vapor clouds across LNG dispersion routes. The liquid pool area was increased by 10.3 times, while the length, width, and volume of the flammable vapor cloud increased by 78.5%, 22.6%, and 249%, respectively. In addition, within the variation range of leakage aperture, there would always be a local high concentration area within 200 m downstream of the storage tank. In the field near the storage tank, the clouds settled and accumulated towards the ground in the state of gas–liquid two-phase flow, and the density of the cloud was gradually lower than the air in the far-field, manifesting as light gas diffusion. This area was characterized by high concentration and long duration of methane, which should be the focus area of alarm prediction.
Author Contributions
Conceptualization, X.L. (Xue Li) and N.Z.; methodology, X.L. (Xuanya Liu); validation, W.H.; formal analysis, Q.Z.; resources, B.C.; data curation, L.K.; writing—original draft preparation, X.L. (Xue Li); writing—review and editing, X.L. (Xue Li), N.Z. and V.R.; project administration, N.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by National Key R&D Program of China [No. 2017YFC0805100]; The Natural Science Research Project of Higher Education Institutions of Jiangsu Province [No. 20KJB620004]; Scientific Research Project “Fire Risk Analysis of Petrochemical Enterprises” of Fire Department of Ministry of Public Security [No. 2016JSYJD04]; Tianjin Science and Technology Project [No. 2016ZXCXSF0080]; Major projects supported by the Natural Science Research of Jiangsu Higher Education Institutions [No. 17KJA440001]; Open Project of Jiangsu Key Laboratory of Oil and Gas Storage and Transportation Technology [No. CDYQCY202104].
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors of this study have no conflict of interests or competing interests.
References
- Eser, P.; Chokani, N.; Abhari, R. Impact of Nord Stream 2 and LNG on gas trade and security of supply in the European gas network of 2030. Appl. Energy 2019, 238, 816–830. [Google Scholar] [CrossRef]
- Zerouali, B.; Hamaidi, B. Predictive analysis for risk of fire and explosion of LNG storage tanks by fuzzy Bayesian network. Life Cycle Reliab. Saf. Eng. 2020, 9, 319–328. [Google Scholar] [CrossRef]
- Zhang, M.; Song, W.; Chen, Z.; Wang, J. Risk assessment for fire and explosion accidents of steel oil tanks using improved AHP based on FTA. Process Saf. Prog. 2017, 35, 260–269. [Google Scholar] [CrossRef]
- Schmidt, M.S. Atmospheric tank failures: Mechanisms and an unexpected case study. Process Saf. Prog. 2017, 36, 353–361. [Google Scholar] [CrossRef]
- Choi, I.H.; Chang, D. Reliability and availability assessment of seabed storage tanks using fault tree analysis. Ocean Eng. 2016, 120, 1–14. [Google Scholar] [CrossRef]
- Necci, A.; Argenti, F.; Landucci, G.; Cozzani, V. Accident scenarios triggered by lightning strike on atmospheric storage tanks. Reliab. Eng. Syst. Saf. 2014, 127, 30–46. [Google Scholar] [CrossRef]
- Koopman, R.P.; Baker, J.; Cederwall, R.T.; Goldwire, H.C., Jr.; Hogan, W.J.; Kamppinen, L.M.; Kiefer, R.D.; McClure, J.W.; McRae, T.G.; Morgan, D.L. Burro Series Data Report LLNL/NWC 1980 LNG Spill Tests. UCID-19075; Lawrence Livermore National Laboratory: Livermore, CA, USA, 1982. [Google Scholar]
- Ermak, D.L.; Chapman, R.; Goldwire, H.C.; Gouveia, F.J.; Rodean, H.C. Heavy Gas Dispersion Test Summary Report. ESL-TR-88-22; Lawrence Livermore National Laboratory: Livermore, CA, USA, 1989. [Google Scholar]
- Brown, T.C.; Cederwall, R.T.; Chan, S.T.; Ermak, D.L.; Koopman, R.P.; Lamson, K.C.; McClure, J.W.; Morris, L.K. Falcon Series Data Report: 1987 LNG Vapor Barrier Verification Field; Gas Research Institute Report: Chicago, IL, USA, 1990. [Google Scholar]
- Siuta, D.; Markowski, A.S.; Mannan, M.S. Uncertainty techniques in liquefied natural gas (LNG) dispersion calculations. J. Loss Prev. Process. Ind. 2013, 26, 418–426. [Google Scholar] [CrossRef]
- Chan, S.T. Numerical simulations of LNG vapor dispersion from a fenced storage area. J. Hazard. Mater. 1992, 30, 195–224. [Google Scholar] [CrossRef]
- Chan, S.T. Three-Dimensional Model for Simulating Atmospheric Dispersion of Heavy-Gases over Complex Terrain. UCRL-JC-127475; Lawrence Livermore National Laboratory: Livermore, CA, USA, 1997.
- Giannissi, S.G.; Venetsanos, A.G.; Markatos, N.; Bartzis, J.G. Numerical simulation of LNG dispersion under two-phase release conditions. J. Loss Prev. Process Ind. 2013, 26, 245–254. [Google Scholar] [CrossRef]
- VílchezJuan, A.; Villafane, D.; Casal, J. A dispersion safety factor for LNG vapor clouds. J. Hazard. Mater. 2013, 246–247, 181–188. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Ma, G.; Abdel-Jawad, M.; Huang, Z. Gas dispersion risk analysis of safety gap effect on the innovating FLNG vessel with a cylindrical platform. J. Loss Prev. Process Ind. 2016, 40, 304–316. [Google Scholar] [CrossRef]
- Zhang, Q.X.; Liang, D. Numerical simulations of LNG vapor dispersion from LNG jetting in different directions. Procedia Eng. 2016, 135, 316–321. [Google Scholar] [CrossRef][Green Version]
- Marsegan, C.; Busini, V.; Rota, R. Influence of active mitigation barriers on LNG dispersion. J. Loss Prev. Process Ind. 2016, 44, 380–389. [Google Scholar] [CrossRef]
- Nguyen, L.D.; Kim, M.; Choi, B. An experimental investigation of the evaporation of cryogenic-liquid-pool spreading on concrete ground. Appl. Therm. Eng. 2017, 123, 196–204. [Google Scholar] [CrossRef]
- Gopalaswami, N.; Kakosimos, K.; Zhang, B.; Liu, Z.; Mentzer, R.; Mannan, M.S. Experimental and numerical study of liquefied natural gas (LNG) pool spreading and vaporization on water. J. Hazard. Mater. 2017, 334, 244–255. [Google Scholar] [CrossRef] [PubMed]
- Ikealumba, W.C.; Wu, H. Effect of atmospheric and sea stability on liquefied natural gas (LNG) dispersion: Implications to Australian LNG marine transport. Fuel 2017, 197, 8–19. [Google Scholar] [CrossRef]
- Luo, T.P.; Yu, C.C.; Liu, R.M.; Li, M. Numerical simulation of LNG release and dispersion using a multiphase CFD model. J. Loss Prev. Process Ind. 2018, 56, 316–327. [Google Scholar] [CrossRef]
- Dasgotra, A.; Varun Teja, G.V.V.; Sharma, A.; Mishra, K.B. CFD modeling of large-scale flammable cloud dispersion using FLACS. J. Loss Prev. Process Ind. 2018, 56, 531–536. [Google Scholar] [CrossRef]
- Giannissi, S.G.; Venetsanos, A.G. A comparative CFD assessment study of cryogenic hydrogen and LNG dispersion. Int. J. Hydrogen Energy 2018, 44, 9018–9030. [Google Scholar] [CrossRef]
- Urióstegui-Hernández, A.; Garnica-González, P.; Ramos-Banderas, J.N.; Hernández-Bocanegra, C.A.; Solorio-Díaz, G. Multiphasic Study of Fluid-Dynamics and the Thermal Behavior of a Steel Ladle during Bottom Gas Injection Using the Eulerian Model. Metals 2021, 11, 1082. [Google Scholar] [CrossRef]
- Gallot-Lavallée, S.; Jones, W.P.; Marquis, A.J. Large Eddy Simulation of an Ethanol Spray Flame with Secondary Droplet Breakup. Flow Turbul. Combust. 2021, 107, 709–743. [Google Scholar] [CrossRef]
- Tauseef, S.M.; Rashtchian, D.; Abbasi, S.A. CFD-based simulation of dense gas dispersion in presence of obstacles. J. Loss Prev. Process Ind. 2011, 24, 371–376. [Google Scholar] [CrossRef]
- Kovalets, I.V.; Maderich, V.S. Numerical Simulation of Interaction of the Heavy Gas Cloud with the Atmospheric Surface Layer. Environ. Fluid Mech. 2006, 6, 313–340. [Google Scholar] [CrossRef]
- Sklavounos, S.; Rigas, F. Simulation of coyote series trials-Part I: CFD estimation of non-isothermal LNG releases and comparison with box-model predictions. Chem. Eng. Sci. 2006, 61, 1434–1443. [Google Scholar] [CrossRef]
- Duijm, N.J.; Carissimo, B.; Mercer, A. Development and test of an evaluation protocol for heavy gas dispersion models. J. Hazard. Mater. 1997, 56, 273–285. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).