Forecasting for Battery Storage: Choosing the Error Metric

Abstract

We describe our approach to the Western Power Distribution (WPD) Presumed Open Data (POD) 6 MWh battery storage capacity forecasting competition, in which we finished second. The competition entails two distinct forecasting aims to maximise the daily evening peak reduction and using as much solar photovoltaic energy as possible. For the latter, we combine a Bayesian (MCMC) linear regression model with an average generation distribution. For the former, we introduce a new error metric that allows even a simple weighted average combined with a simple linear regression model to score very well using the competition performance metric.

1. Introduction

The Western Power Distribution (WPD) Presumed Open Data (POD) 6MWh battery storage capacity forecasting competition ran from 28 January 2021 through 18 March 2021. The competition entails prescribing battery charging and discharging profiles for the upcoming week:

1

battery charging profile—For each half hour before 3:30 pm for each day of the upcoming week, prescribe how much charge the battery will take (up to a maximum of 2.5 MW over that half hour); and

2

a battery discharging profile—For each half hour from 3:30 pm until 9 pm for each day of the upcoming week, prescribe how much the battery will discharge (up to a maximum of 2.5 MW over that half hour).

The battery can charge up to a maximum of 6MWh in total. To optimise their score, the entrant needs to align the charging profile as much as possible with electricity generation from a solar farm; and align the discharging profile so that the peak demand from the substation (after 3:30 pm) each day is minimised.

The motivation behind the competition is to help understand the role batteries can play in improving efficiency and reliability of the electricity grid and prevent expensive network reinforcement. Firstly to determine how well batteries can use energy generation from solar farms rather than that energy being directly fed into the grid (less efficient) and the batteries charging from the grid (extra demand on the grid). Secondly to determine how much peak energy reduction can be made on the substation by discharging a battery at pre-scheduled times.

Competition Details

The Western Power Distribution Presumed Open Data (WPD-POD) challenge was launched on 12 February 2021 with four competition phases—submission deadlines of 25 February 2021, 4 March 2021, 11 March 2021, and 18 March 2021. Over those periods, more-and-more of the full dataset was gradually released to entrants. In each phase, entrants had to produce charging and discharging profiles for the battery for the week after the end of the latest dataset release. The first forecast week was the week beginning 16 October 2018 and data was provided from 3 November 2017 up to 15 October 2018. The second forecast week was the week beginning 10 March 2019. The third was for the pre-Christmas week of 18 December 2019 through 24 December 2019. The final forecasting week with the most amount of available data to train on was the week beginning 3 July 2020, during which time the UK was in lockdown due to the Covid-19 pandemic with the UK having entered lockdown on 26 March 2020. During this time people were restricted from going out of their homes without valid reasons.

These same four weeks are used in this paper to illustrate the results from our approach and compared to several relevant benchmark approaches.

Competition entrants were allowed to charge the battery any time up to 3:30 pm UTC, producing a charging profile for the 31 half-hours from midnight, up to a maximum of 6 MWh charged per day. The charge had to be consumed (discharged after 3:30 pm) in the day so that the next day the battery started empty again. The charging profile is rewarded if it coincides with solar radiation, so that as much of the battery charge comes from solar as possible. The charging score for day d, $P_d$ is given by the fraction of the charging specified that could be achieved by solar:

$$P_d=\frac{\sum {}_{t=1}^{t=31}min\{P_{d,t},B_{d,t}\}}{\sum {}_{t=1}^{t=31}{B}_{d,t}}$$

(1)

where $B_{d,t}$ is the charging profile specified at the half-hour time period t and $P_{d,t}$ is the total power generated by solar over the time period t.

For discharging, entrants were asked to produce a profile over the 11 half-hours from 3:30 pm UTC onwards until 9 pm UTC. The sum of the discharge over those 11 half-hours needs to match the sum of the charge, typically the maximum allowed value of 6 MWh. The battery then theoretically discharges to the consumers alleviating demand on the substation. The aim is to produce a discharge profile from the battery to reduce the late-afternoon/early-evening peak demand on the substation as much as possible. The discharging score for day d, is given by the percentage peak reduction after 3:30 pm:

$$R_d=100\times \left(\frac{\underset{t\in \{32,\dots ,42\}}{max}\left(S_{d,t}\right)-\underset{t\in \{32,\dots ,42\}}{max}(S_{d,t}-B_{d,t})}{\underset{t\in \{32,\dots ,42\}}{max}\left(S_{d,t}\right)}\right)$$

(2)

where $B_{d,t}$ is the discharging profile and $S_{d,t}$ is the substation demand at time t on day d.

The overall competition score for day d is given by:

$${\nu }_d=R_d\times (2P_d+1)$$

(3)

and then this is averaged over the forecast week to produce the score for that phase.

The competition data is real-world. There are the usual missing values, spurious values, and adjustments for British Summer Time, school holidays, to consider. Along with this, weather forecasts are hourly from multiple weather stations while charging/discharging profiles need to be half-hourly. In addition, one of the forecast weeks was the lead-up to Christmas. Another was forecasting during the COVID-19 induced lockdown. These are real-world scenarios that need addressing. While handling these are not the focus of this paper, it is worth pointing out that simpler, open methods, such as the ones presented here, make it easier to adjust for a lack of historical data, such as what to do when Christmas day is on a Wednesday for the first time in years, or when a pandemic strikes.

There were 55 teams in the competition from 72 different organisations across 15 countries including 30 universities. We finished second overall in the competition based largely on the approach discussed here, finishing 4th, 6th, 5th and 4th respectively in Task Weeks 1, 2, 3 and 4.

2. Data Provided

Data from around the town of Plymouth in Devon, United Kingdom, were released periodically over the course of the competition. This included electricity consumption data from 3rd November 2017 through to the day before the date of the task week (when the battery profiles are for), with the last competition task to provide charging and discharging profiles for the week commencing 3 July 2020. It also included data (irradiance, power output and panel temperature) from a solar site near the substation from 3 November 2017 up to the day before the date of the task week. In addition, weather reanalysis data (temperature and solar luminosity) at 6 close-by locations were provided from 1 January 2015 through to the end of the task week. Other well-published data, such as school and bank holidays, dates of Covid-19-related lockdowns were also permitted to be used. The data can be obtained from: https://doi.org/10.5281/zenodo.5500457 (accessed on 1 October 2021) and used under the Western Power Distribution Open Data License therein.

3. Materials and Methods

3.1. Approach

Given the independence of the charging and discharging profile times and scoring, we treat each separately. The four forecasting weeks from the competition will serve as a benchmark for the method described here. Here we describe the methods both for providing a charging profile for the battery and a discharge profile. These are treated as two completely separate challenges. Note that the Task 4 challenge week had the most available data and this is the week that is generally illustrated in the description here. However, the method is equally applied to all previous challenge weeks albeit with less data to calibrate.

3.2. Forecasting Battery Charging Profiles

The aim here is to schedule a battery charging profile to align with photovoltaic (PV) generation at a local 5MW solar farm. Depending on the time of year, there may be insufficient energy from the solar farm to fully charge the battery and therefore additional charge will be required from the grid. For the purposes of the competition, the charging schedule needs to be pre-defined. Although, the option was left open, it proved always beneficial to fully charge the battery whether using solar or charging from the grid. Thus between the hours of midnight and 3:30 pm, we needed to fully charge the 6 MWh battery.

There are two primary sources of data for producing the charging profiles. First there are the historic PV data (irradiance, power and panel temperature). Secondly, there are the weather reanalsyis (akin to weather forecast) that includes forecast solar luminosity and temperature at the site, both historically and for the forecast task week. With this in mind, we took two approaches. One was to directly use the historic data to make an estimate. The second was to use the forecast solar luminosity to produce an estimate. The former has the advantage that it is not affected by inaccuracies in the forecast; while the latter has the advantage of likely being more accurate due to being based on a forecast.

There are two possible regimes. One is where we expect there to be sufficient solar radiation to fully charge the battery from solar. In which case, the challenge becomes minimising the risk that we ask for more energy to charge the battery at any given half-hour than is provided by PV. The second is when we expect PV to be insufficient to fully charge the battery and the challenge becomes maximising the available solar—that is, providing a charging profile that, for each half-hour, is always at least as much as the available solar. Throughout the competition it was generally obvious which regime the task fell under given the solar forecast. For example, for Task 3 (w/c 18 December 2019) there was never enough solar to fully charge the battery in a day on solar energy alone. While for Task 4 (w/c 3 July 2020) solar energy was plentiful. For Tasks 1 and 2 it depended on the individual day and the solar forecast over the course of that day.

The first step was to combine the six weather station solar luminosity forecasts into a single estimate $L_t$. We did this by optimising the combination that minimises the standard error of a single linear regression fit, forced through the origin, between $L_t$ and $P_t$ across all available training data points, where $P_t$ is the solar output of the farm. For the Task 4 week (with maximum data), this provides a prior estimate of the regression fit: $P_t=(0.00968\pm 0.0000165)L_t$ with standard error 0.407. Allowing the fit to cross the axis provides a fit of $P_t=(0.009612\pm 0.000096)L_t+(0.0137\pm 0.00223)$ and standard error of 0.406. We then extracted the periods around the same time of year as the forecast week (3 July 2020–9 July 2020) when the position of the sun in the sky will be roughly similar. For this we used the 3 weeks from 26 June through till 16 July from both 2018 and 2019 and the week prior to the forecast (26 June 2020–2 July 2020). Thus we had 49 days of data. For other challenge weeks we chose suitable sets of 49 days of data that were around the same time of year as the challenge week. For each half-hour of the day we ran a Bayesian linear regression [1] using Markov Chain Monte Carlo (MCMC) [2] for 10,000 steps with a beta distribution prior(for Task 4) of $\alpha \sim \mathcal{N}(0,0.00223)$ and $\beta \sim \mathcal{N}(0.00968,0.0000165)$. As an example, the first 500 steps across all half-hours produced the distribution of intercepts and slopes values in Figure 1.

As an example, Figure 2 shows how the value of the slope changes over each step of the MCMC algorithm starting at its prior value. This results in the fits shown in Figure 3. As can be seen, there is a spread in the fits.

Depending on whether we expect to exceed the 6 MWh full capacity of the battery, either the minimum or maximum slope estimated value for each half hour was chosen to provide the MCMC estimates of the PV generation. For the forecast week in Task 4 in the UK summer solar energy is plentiful and therefore the minimum values were chosen. For Task 3 in the UK winter there is never sufficient solar energy to fully charge the battery in a day and the maximal possible estimate from the solar forecast fit was used. The secondary solar generation model took, for each half hour of the day, a simple mean of the 49 data points to provide a 49-point average energy output and a 49-point average (reanalysed forecasted) solar luminosity. The two models were combined by taking the 49-point average energy output result and then applying an adjustment based on the difference between the forecast solar luminosity and the average solar luminosity (from the 49 data points). If we expected to have plentiful solar over the day (e.g., Task 4) then the adjustment could only be downwards. Where there was expected to be insufficient solar (e.g., Task 3), the adjustment could only be upwards. The adjustment made is to multiple the MCMC slope (either minimum or maximum) by the difference in forecasted solar luminosity and the 49-point average solar luminosity. The forecast energy outputs over the charging period were then normalised to sum to 12 MW.

Three other models are compared. One is the 49-point average energy output. Another is a simple linear regression fit of the energy output to the solar luminosity forecast and the third is the competition benchmark which was to take the current week actual energy output as forecast for the following week. Each of these are normalised so the output over the charging period sums to 12 MW.

3.3. Forecasting Battery Discharge Profiles

A common quote in problem-solving classes, often misattributed to Einstein is “If I had only one hour to solve a problem, I would spend up to two-thirds of that hour in attempting to define what the problem is.” All too often, however, we forget these wise words and march straight in with attempting to find the “optimal” forecast without taking the time to define what we mean by optimal. So while others, such as [3], who finished a very respectable third, took a more traditional approach to forecasting attempting to optimise standard error metrics, such as Root-Mean-Squared-Error (RMSE) and Mean-Absolute-Percentage-Error (MAPE), we first focused on choosing the appropriate error metric for the problem.

3.3.1. Example Motivation

Consider the two forecasts in Figure 4. The forecast in the left panel does a better job of matching the actual electricrity demand and consequently produces smaller standard error metrics. The forecast in the right panel, however, does a better job of matching the shape of the actual demand profile during the late afternoon-evening peaks even though it consistently under-forecasts during that period by exactly 0.5MW each half-hour. As a result of this, the corresponding battery discharge profile results in a better average peak reduction. Remember that this is the goal of forecasting here—to maximise the average daily peak reduction. See

Table 1. Error metrics from Forecast 1 and Forecast 2. RMSE and ADPR units are in MW and MAPE is a percentage. ADPR is the Average Daily Peak Reduction.

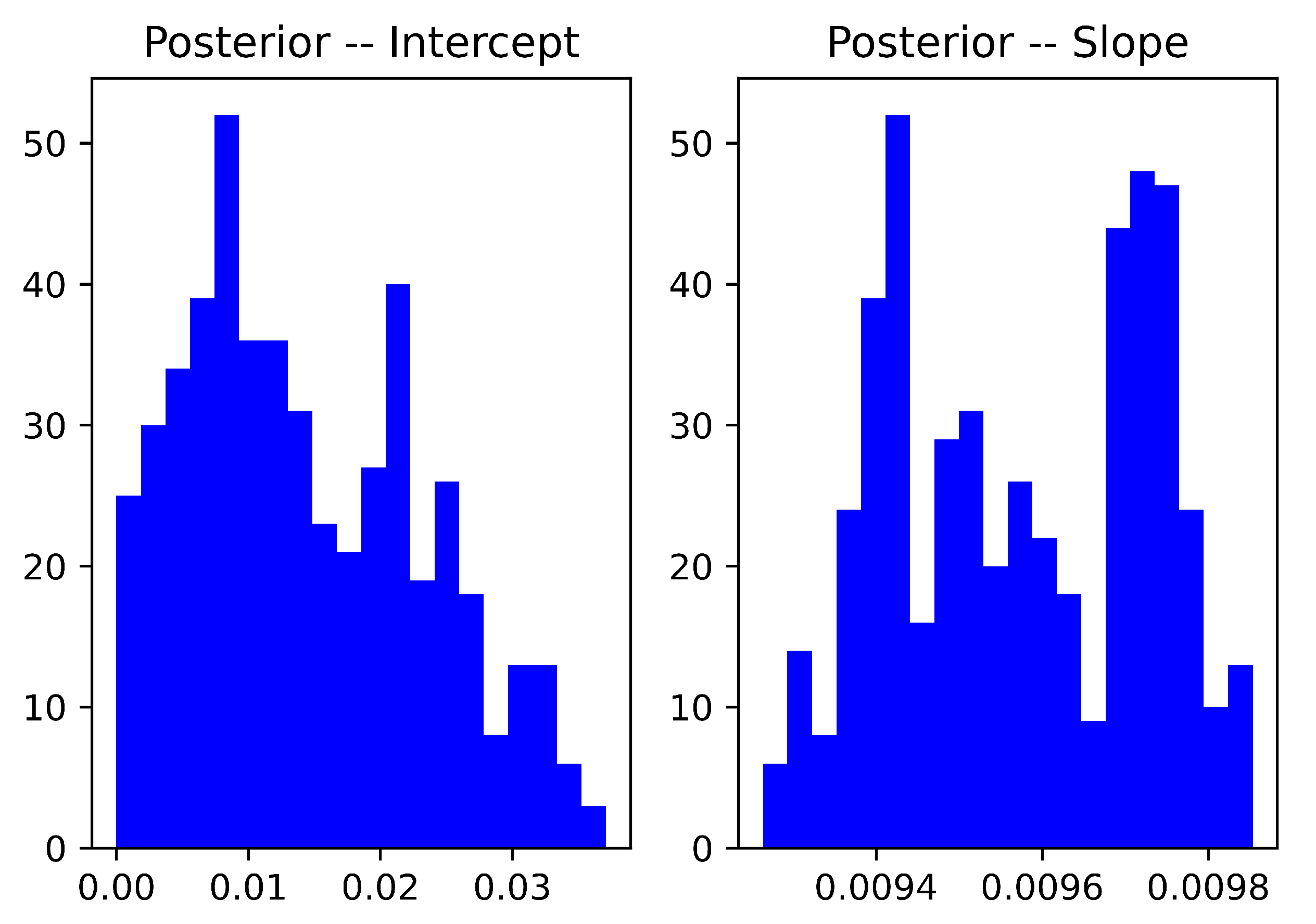
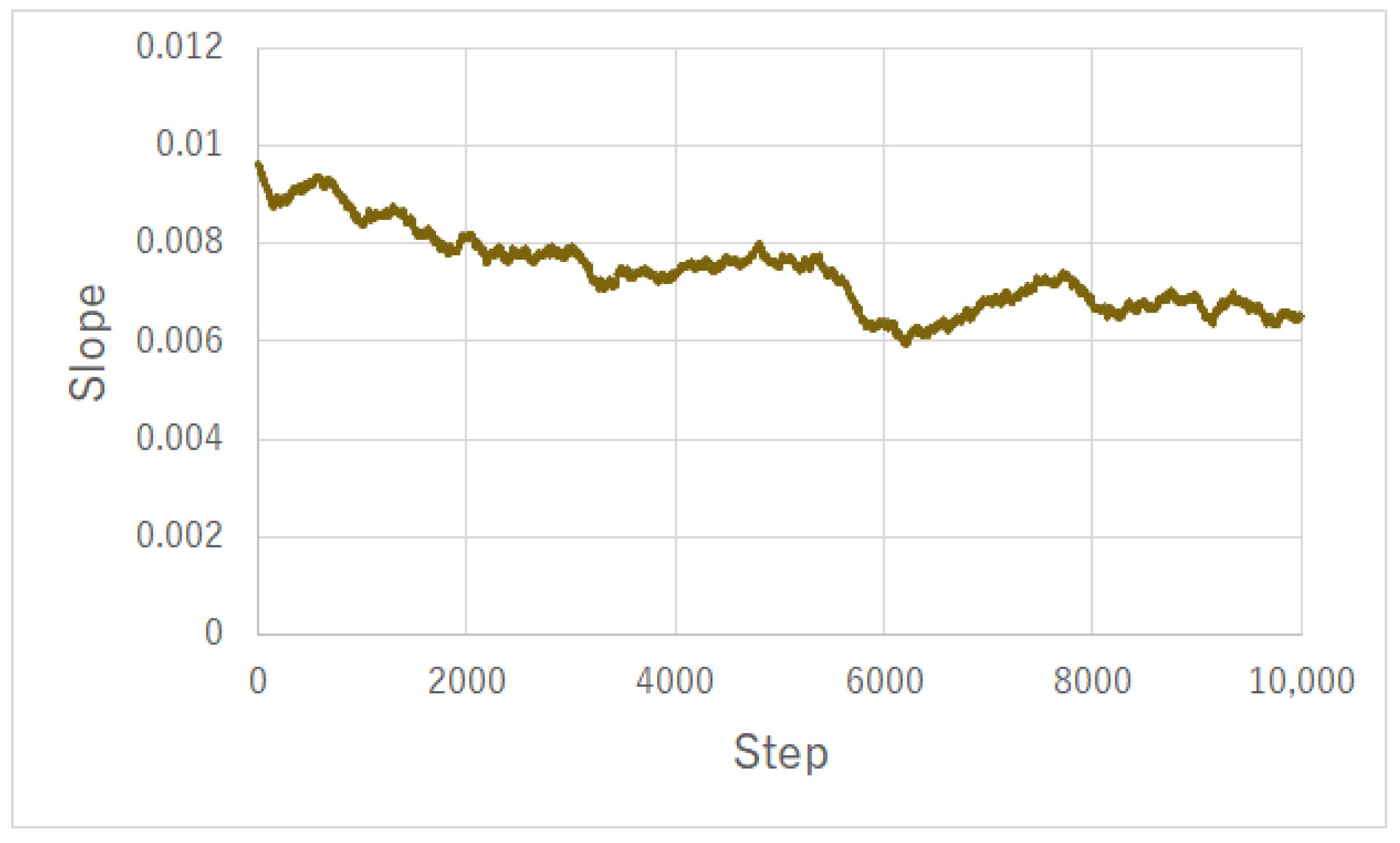
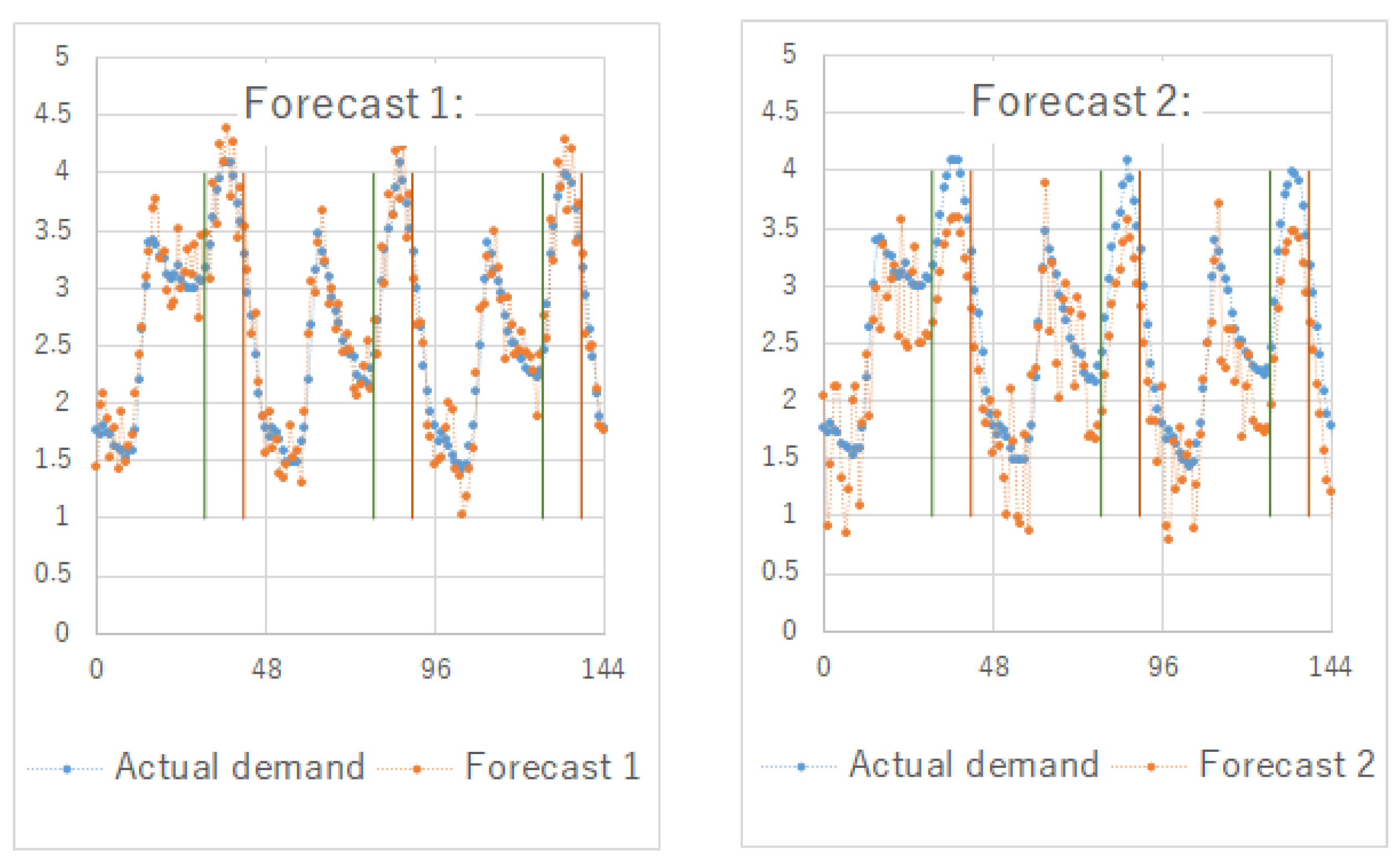
Error Metric	Forecast 1	Forecast 2	Optimal
RMSE—lower is better	0.24	0.47	0
MAPE—lower is better	8.58	17.12	0
ADPR—higher is better	1.21	1.56	1.56

.

The idea of using an error metric that befits the problem is not new and others have introduced their own metrics for various other problems being studied [4,5,6,7,8,9,10,11]. However, the field is still dominated by the top four metrics of RMSE, MAPE, MAE and MSE [12,13].

Here we do not propose to displace any of the standard error measures, but simply to point out, and emphasise, that the error measure being used needs to suit the problem being addressed. For the problem specified here, an improvement to the forecast translates as an improvement to the battery discharge profile and thus increased average daily peak reduction.

3.3.2. Deriving the Optimal Discharge Profile

The aim is to produce a discharge profile for each day—a distribution over the 11 discharge half-hour periods that sums to the capacity of the battery. The capacity of the battery is 6MWh which equates to 12 MW per half-hour. Provided all 11 periods are sufficiently close in forecast demand then it is trivial to produce an optimal discharge profile for that forecast. Indeed, the forecasted optimal post-discharge peak (maximum substation demand), $\widehat{M}$ can be derived by:

$$\widehat{M}=F_{avg}-\frac{12}{11}$$

(4)

where

$$F_{avg}=\frac{\sum {}_{t=32}^{t=42}{F}_t}{11}$$

(5)

and where $F_t$ is the forecast for half-hour period t in the day with $t=32$ corresponding to 3:30 pm and $t=42$ corresponding to 9 pm. This gives the evening peak period we are tasked with reducing. The optimal discharge for this forecast to associate with each half-hour is therefore given by

$$B_t=F_t-\widehat{M}$$

(6)

which will bring the forecast grid consumption (original demand minus battery discharge) down to $\widehat{M}$ for all half hours between 3:30 pm and 9 pm. Where the forecast demands are not sufficiently close, this may result in an invalid negative discharge amount. In which case, a short iterative routine can exclude those periods that would become negative and the 11 in the above equations is replaced by the number of qualifying periods to ensure $B_t\ge 0$. The actual peak that occurs is then given by

$$M=\underset{t\in \{32,\dots ,42\}}{max}(A_t-B_t)$$

(7)

where $A_t$ is the actual demand that would have occurred before any discharging. It is M that we are trying to minimise.

3.3.3. Error Metric

We therefore need $(A_t-B_t)$ to be consistent across t, taking the same value so as not to waste any discharge energy that could be used to reduce the peak further. This means that a necessary and sufficient condition for optimal discharge is:

$$A_t-F_t=C-F_{avg}$$

(8)

for any constant C. Therefore the discharge profile is optimised not only when $F_t=A_t$ but any time where $A_t-F_t$ take the same value across the 11 half-hour periods. Thus it is the error relative to each other across the 11 half-hour periods that governs optimality rather than any absolute error. That is to say, if a forecast is exactly some constant too high or too low across all 11 periods then the forecast still belongs to the equivalence class of optimal solutions. Moreover, the accuracy of the forecast outside those 11 periods is irrelevant. We can now see why Forecast 2 in Figure 4 provides optimal peak reduction despite being inaccurate in the traditional sense. This motivates us to target a timeseries shape error given by:

$${ϵ}_0={\left(\frac{{\sum }_t{[(F_t-F_{37})-(A_t-A_{37})]}^2}{11}\right)}^{1/2}$$

(9)

where the sum runs over $t\in [32,42]$. This is the RMSE of the error defined by the difference between the forecast difference at time t and at 6 pm ($t=37$) and the actual difference at time t and at 6 pm. Note that the actual time of 6 pm chosen to relate to is arbitrary and any of the 11 times could be used. 6pm was chosen because the actual original peak frequently occurs at 6pm. This is not the only error metric that could be chosen of course. For example, the mean absolute timeseries shape error could be used. That is the MAPE version of Equation (9) instead of the RMSE version. See [14] for a comparison of RMSE and MAE errors. Targeting just this error would result in attempting just to fit forecasts over the peak period. In practise, however, to help optimise fitting parameters and provide realistic forecasts, it is useful to also fit an actual estimate in the more usual way since this provide significantly more data points to fit. The actual error we use is:

$$ϵ=\sum _t{\mathsf{\Omega }}_t\left(\mathsf{\Psi }{[(F_t-F_{37})-(A_t-A_{37})]}^2+{\left[(F_t-A_t)\right]}^2\right)$$

(10)

where $\mathsf{\Psi }$ is the relative weight to apply to the timeseries shape error relative to the conventional error. $ϵ$ is a combination of the timeseries shape error metric introduced in Equation (9) combined with a traditional mean-squared error. We arbitrarily set $\mathsf{\Psi }=10$ to give dominance to the timeseries shape error. ${\mathsf{\Omega }}_t$ is the weight to apply for half-hour time t and we choose ${\mathsf{\Omega }}_t=10$ when it is inside the peak period $t\in [32,42]$ and 1 everywhere else. There are 11 periods inside the peak and 37 outside, thus this choice of 10 effectively means there is ≈3 times the emphasis on the peak periods than non-peak. The choise is arbitrary but could be chosen by cross-validation techniques. Different weights could be placed for the shape error and for the conventional error parts. However, whichever metric is chosen, it is important that it penalises shape error. For more discussion on this, please see the Discussion section at the end.

3.3.4. Forecasting

Having defined the error metric we now use a relatively simple forecasting technique. The point here is to demonstrate the improvements that can be made by choosing an appropriate error metric and choosing an approach (parameters) appropriate to that metric. Given that even this simple approach allowed us to finish second in the competition, it shows the importance of choosing an appropriate error metric. It is expected that more sophisticated forecasting techniques aimed at optimising Equation (10) would produce even better results. For completeness, the technique we used involves taking a weighted average of the actual demand over the previous 6 weeks and adjusting for temperature T and day d number. The parameters to optimise are: (i) the 6 weights ${\omega }_w$ for previous weeks w, a temperature coefficient $c_t$ for each of the 11 half-hour periods plus a single temperature coefficient $c_0$ outside those periods, and a coefficient $\alpha$ of the day number for 2 separate time periods (${\alpha }_1$ for the early part of the week $t<37$ and ${\alpha }_2$ for the late part $t\ge 37$) and a separate day coefficient ${\alpha }_0$ for outside that period. The idea is that because we wanted to optimise the timeseries shape error, we wanted as much flexibility in the relative half-hour forecast thus having separate temperature coefficients for each half-hour. We used only three coefficients for the day number because of low sensitivity to the parameter which may have resulted in over-fitting if more had been used. Thus our forecast for time period t on day d is gven by:

$$F_{d,t}=\left\{\begin{array}{cc}\sum _{w=-6}^{-1}{\omega }_w{A}_{d+7w,t}+c_t(T_{d,t}-T_{d+7w,t})+{\alpha }_1{X}_1\left(t\right)+{\alpha }_2{X}_2\left(t\right)\hfill & \mathrm{for}t\in [32,42]\hfill \\ \sum _{w=-6}^{-1}{\omega }_w{A}_{d+7w,t}+c_0(T_{d,t}-T_{d+7w,t})+{\alpha }_0\hfill & \mathrm{for}t\notin [32,42]\hfill \end{array}\right.$$

(11)

Here, $X_1\left(t\right)=1$ if $t\in [32,36]$ and 0 otherwise. $X_2\left(t\right)=1$ if $t\in [37,42]$ and 0 otherwise. $T_{d,t}$ is the forecast or reanalysis forecast temperature on day d and time t.

The parameters are then optimised to minimise Equation (10) using generalised reduced gradient v2 [15], although any reasonable optimiser would be suitable. In practise, we did not have a single temperature estimate and therefore needed to generate one from 6 local weather stations. We produced a linear combination of these as the estimate for the temperature with the coefficients summing to unity. Thus there were 5 parameters to determine temperature. To reduce the number of parameters we assumed the weekly weights ${\omega }_w$ form a simple power law ${\omega }_w={(7+w)}^r$, for $w\in \{-1,-2,-3,-4,-5,-6\}$ where r is an index to be fitted. The actual weights applied to the previous weeks are normalised by the sum of the weights. Thus we ended up with 5 weather station temperature coefficients +1 weekly weight index +12 temperature coefficients per half-hour +3 day coefficients = 21 parameters. We compare our results to three models. The first “RMSE Multiple Parameters (RMSE-MP)” has the same parameters, borrowing the ideas behind optimising the relative demand with the parameters to optimise differences over the discharge period. However, instead of optimising to minimise Equation (10) during the calibration period, it is optimised to minimise the standard RMSE error during the calibration period. The second “RMSE Simple (RMSE-S)” comparison model has a single temperature coefficient and a single day coefficient applied to all times. Both these comparison models are optimised for standard RMSE. The final model “Benchmark model” is simply forecasting the next week as the actual demand from the current week. This was the benchmark used in the competition.

4. Results

4.1. Charging Profiles

As can be seen in

Table 2. Percentage charge dervied from PV based on charging profiles from four different models. Our model is based on combining an average for the time of year with a Bayesian regression of the forecast solar luminosity.

W/c	Our Model	49-pt Average	Regression	Benchmark
16 October 2018	89.89%	89.81%	88.12%	86.95%
10 March 2019	77.36%	76.05%	78.01%	71.03%
18 December 2019	43.24%	43.28%	42.60%	40.10%
3 July 2020	96.73%	96.69%	96.08%	94.32%
Average	76.80%	76.46%	76.20%	73.10%

, our model performs the best out of those considered, which we believe is due to taking account of both uncertainty in the solar luminosity as well as uncertainty in the relationship between luminosity forecast and solar panel energy output. What is also interesting is how well the 49-point average model performs outperforming a regression model. The 49-point average model simply takes an average of historic solar panel energy output around the time of year. It ignores any solar luminosity forecasts. This suggests that either the solar luminosity forecasts are quite poor and/or that they have to be used with a great deal of caution.

4.2. Discharging Profiles

From

Table 3. The average daily peak reduction in MW achieved by the four forecast models. The greater the peak reduction the better. Presented are the results for each of the 4 task weeks averaged over the 7 days in those task weeks. In addition, the average result across those 4 task weeks is provided. Also presented are the “In-sample” calibration model peak reduction averaged over the 35 days closest to the task week and while some of those days are quite distant from the task week and are in-sample they do provide an average result across more days and so are more robust.

Task Week	W/c	Our Model	RMSE-MP	RMSE-S	Benchmark
In-sample	last 35 days	1.511	1.507	1.504	1.492
1	16 October 2018	1.478	1.376	1.359	1.436
2	10 March 2019	1.440	1.438	1.455	1.406
3	18 December 2019	1.366	1.360	1.331	1.305
4	3 July 2020	1.303	1.299	1.273	1.259
Average	all 4 weeks	1.397	1.368	1.354	1.351

, we can see that our model that aims to minimise $ϵ$ outperforms all three other models considered in all cases apart from one occurrence in Task 2 where the RMSE-S model performs best. There are considerable fluctuations in demand at this granularity and so it is always possible for one model to outperform another on an individual week just by chance. The RMSE-MP model that minimises the RMSE error but has the same parameters to fit as our model also performs well except in the Task 1 week. This suggests choosing the appropriate parameters to optimise is important. However, it is consistently outperformed by our model suggesting choosing the best metric to optimise is also important, particularly when it comes to squeezing the last piece of available accuracy.

5. Discussion

Forecasting PV generation in the unpredictable UK weather is clearly challenging and at least in the forecast week here, a simple average over similar times of year outperforms a regression model based on the forecast luminosity. This suggests that the forecast luminosity cannot be completely relied upon when producing forecasts of PV generation. The discharge results show the importance of choosing an appropriate error metric. Once the error metric is established, choosing an appropriate model (e.g., parameters) to optimise the solution becomes more apparent. In this case, having defined the error metric, we then designed the forecast model choosing parameters that can most influence the error metric value. Had we approached the problem with a traditional error metric, then we would not have chosen the parameters we did. Thus specifying an appropriate error metric not only helps approximate optimal solutions directly but it also helps in defining the model to use to approximate those optimal solutions and to optimise that model. There is considerable freedom in choosing the exact nature of the error metric to use. For example, we use a weighted RMSE-style combination of the timeseries shape error and conventional error. However, a MAPE equivalent could also have been used and/or with different weightings. One option would be to use cross-validation to identify an optimal choice of weighting and metric form over the calibration period. Such an approach is not without dangers though given the relatively limited amount of data to fit, the already large number of parameters used and the fact that the forecasting period is not the same as the calibration period and therefore one would expect different customer behaviour. The aim of this paper was to draw the reader’s attention to the benefits of choosing a suitable error metric rather than necessarily finding the absolute best charging/discharging profile possible. For that, there are more sophisticated techniques that could be employed.

6. Conclusions

We believe that employing two key methods helped generate our excellent competition performance. First, the combination of a Bayesian Linear Regression with an historical average gave us an edge on the charging profile. Second, the introduction of a new error metric designed to help forecasts for battery discharge allowed us to better optimise the discharging profile. We recommend that once a forecasting problem is understood, considerable effort should be made deciding the most appropriate error metric. The fact that our approach is easy to understand makes it easier to make adjustments for festive periods and previously unknown events such as lockdowns. Were a blackbox technique employed, it may be difficult to know what and how much of the effects of, say the lockdown, have already been accounted for.

The benefits to the power systems community are really two-fold.

One is the direct application of such forecasting techniques to deriving charging and discharging profiles for large batteries that could be placed on the grid to reduce the strain on substations by allowing customers to feed off the battery instead. The amount of peak reduction that can be achieved is quite substantial and could substantially increase the life expectancy of network assets. In addition, by using solar energy to charge batteries and reducing peak demand reduces the amount of time that non-renewable resources need to be used to fill the demand gap.

The second benefit is the challenge to the status quo of error metrics. That by reading this paper, forecasters may start to think more about whether the error metric they are trying to reduce is really the appropriate one for their particular problem. Perhaps more effort needs to be placed on forecasting the peak; or perhaps it is about forecasting the amount of peak demand rather than the exact timing. Either of these scenarios as well as battery discharging profiles, could benefit from non-standard error metrics.

For simplicity the competition did not concern itself with the potential for additional peak load in the morning. This allowed the battery charging and discharging challenges to be completely separated. In practise, with the current setup the afternoon/evening peak could easily be reduced to below the morning peak. Furthermore, charging the battery in the morning, could result in even higher morning peaks. For a practical solution, the charging and discharging profiles need to be considered together. It would be easy to extend the demand forecasting methods here to be for any period, even non-adjacent ones, that might generate a peak rather than being restricted to just those 11 half-hours between 3:30 pm and 9 pm. This becomes easier if the battery is charged outside those hours, perhaps by wind energy. It becomes much more complex if for some half-hours the battery is allowed to either charge or discharge and it would be necessary to understand the relative importance of reducing peak demand versus capturing solar energy for storage.

Finally, the competition was also setup so that the charging/discharging profiles had to be produced for the full week ahead. In practise, it should be possible to get daily updates and therefore more reliable/up-to-date solar and temperature forecasts. It may even be possible to have intraday updates to the charging/discharging profiles in which case feedback from the current demand on the network and solar output could play a significant role in providing even more effective profiles. By laying the solid groundwork with an appropriate error metric allows various techniques to be explored in the most relevant and practical way.