Influence of the Variability of Compressed Air Temperature on Selected Parameters of the Deformation-Stress State of the Rock Mass Around a CAES Salt Cavern
Abstract
1. Introduction
- Cooling of the rock mass during leaching which is caused by the fact that the temperature of the water used for leaching is lower than the temperature of the rock mass;
- Thermo-hydrodynamic changes in the air injected into the cavern;
- Heat exchange between the stored medium, the rock mass and the pipes used for exploitation;
- Heat propagation in the rock mass due to thermal conductivity;
- Heat convection in the cavern.
2. Thermo-Mechanical Properties of Salt
2.1. Thermodynamic Model
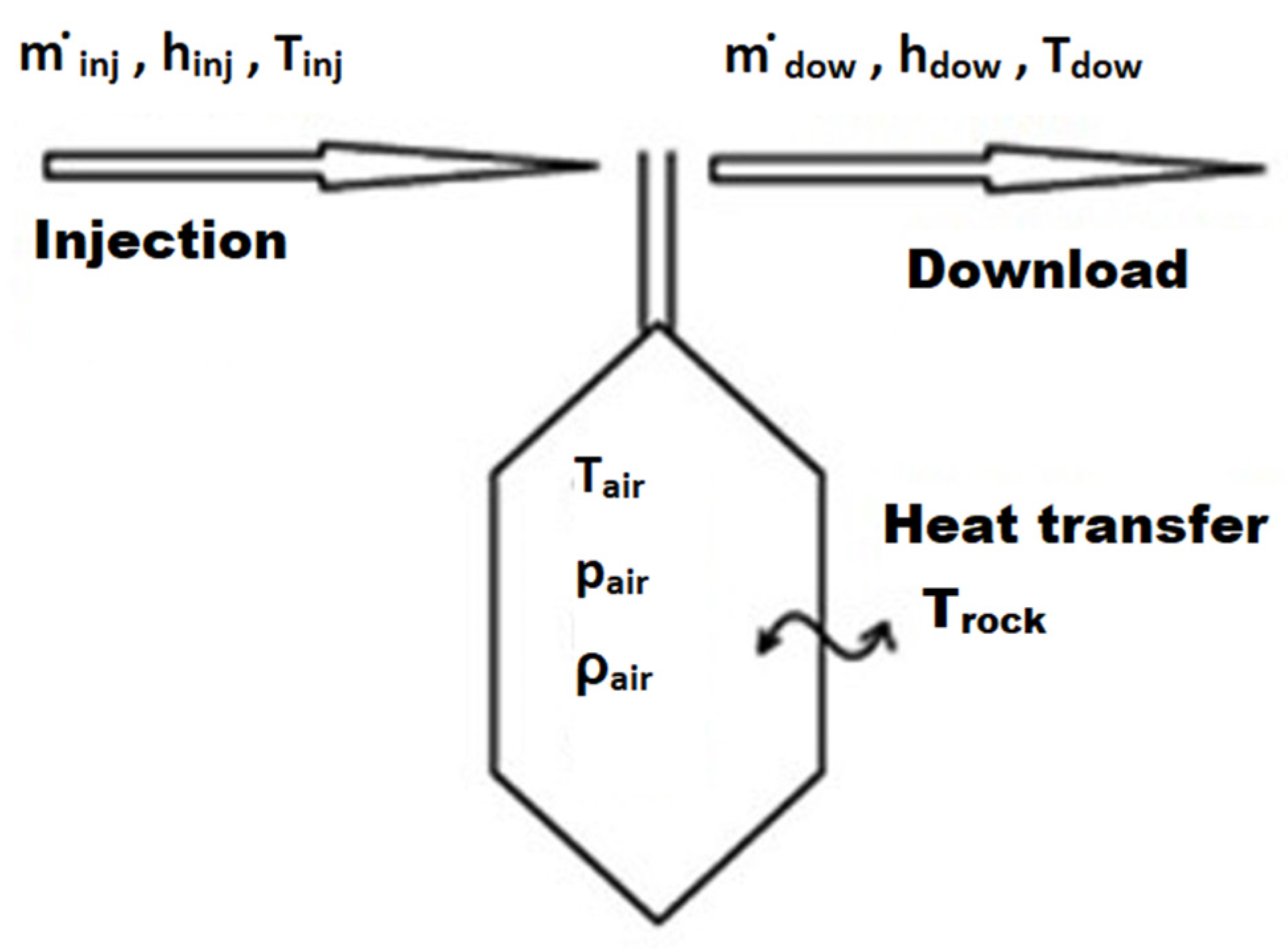
- For thermodynamic problems, the cavern is considered as one volume (Figure 1);
- The compressibility of rock salt is very low compared to the compressibility of gas; therefore, it is assumed that the cavern volume is constant throughout the simulation (the change in cavern volume is much smaller than the total volume, therefore its influence on temperature and air pressure is negligible) [12]. When formulating the mass and energy balance equations in the first stage of the analysis, a constant volume V for the cavern is assumed. In the second stage of the analysis, in which the cavity stability is tested, the volumetric convergence is calculated to ensure that the applied thermo-mechanical loads meet the design requirements and stability is maintained;
- Injection and download air characteristics (temperature, enthalpy, and mass flow rate) are controlled by the CAES installation operator. Therefore, it can be assumed that the air properties are known during the injection and download processes to and from the cavern;
- Air is considered an ideal gas—this assumption is true for the pressure and temperature inside the CAES storage cavern [10].
2.2. Cavern Operating Parameters
2.2.1. Balance of Mass and Energy in the Cavern for Steady-State Conditions
2.2.2. PVT Equation for the State of Gas in a Cavern
2.2.3. Heat Exchange between Cavern and Rock Mass (Macroscopic Balance)
2.2.4. Temperature Changes in the Salt Rock Mass—Thermal Conductivity
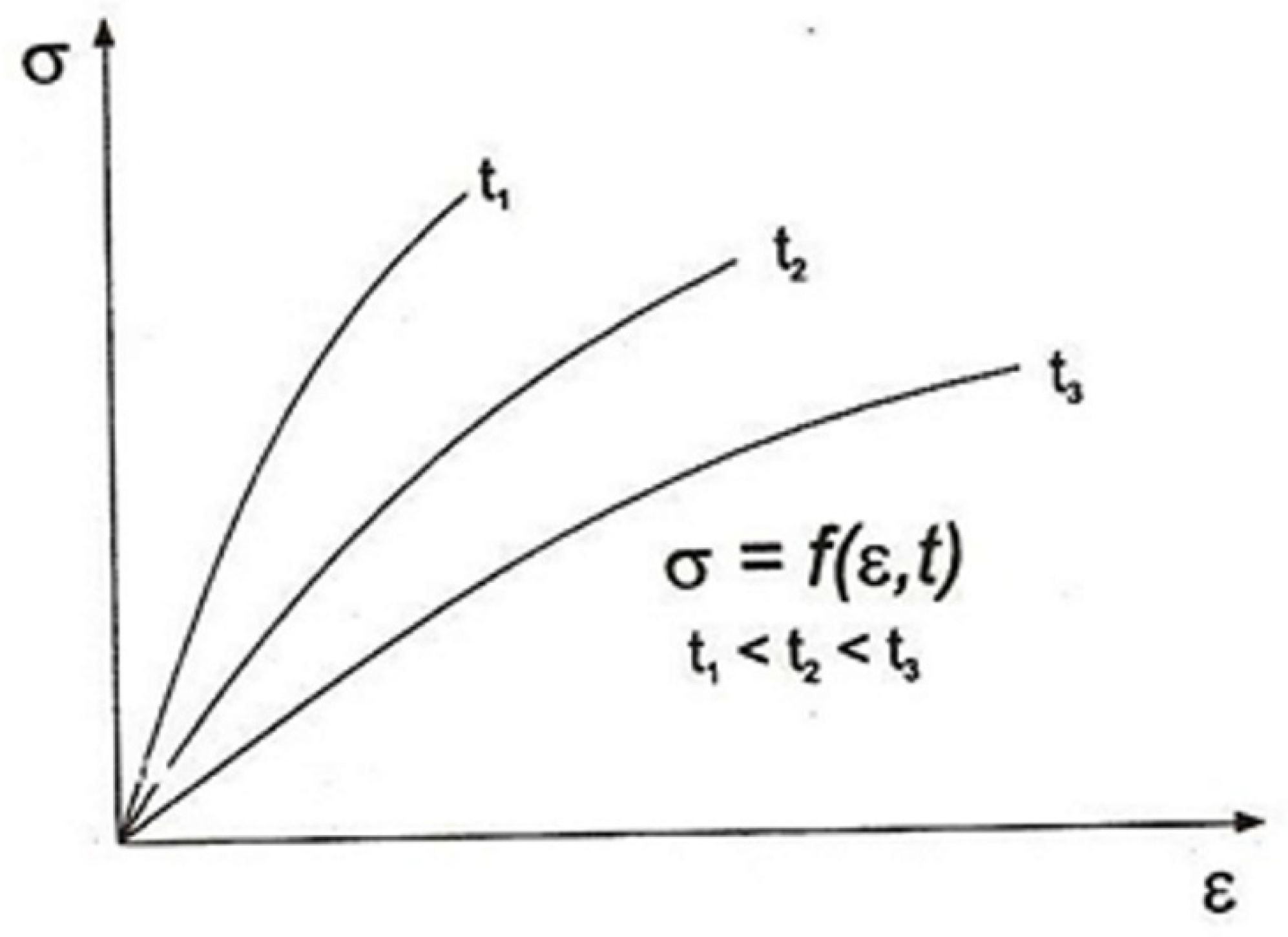
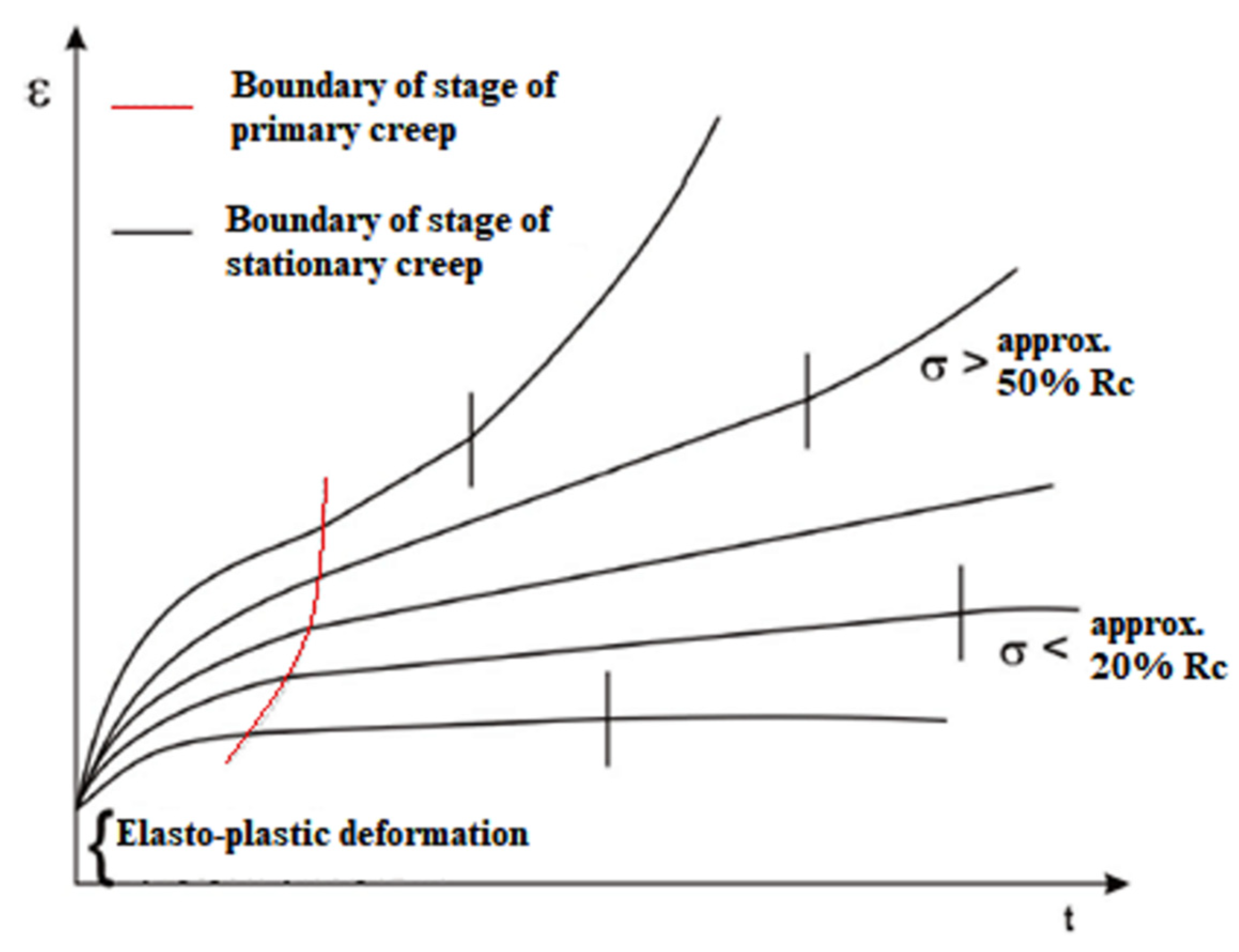
2.3. The Constitutive Equation of Rock Salt
- The initial deformation phase occurs so quickly that time is usually omitted in its description;
- Primary creep, when creep speed decreases;
- Stationary creep, characterized by a constant increase in strain over time. This phase has the greatest impact on the strain-stress state of the rock mass around the cavern;
- Final phase. Under the influence of stresses, creep accelerates rapidly, which leads to material destruction [7].
2.4. Cavern Stability Parameters
2.4.1. Local Stability of the Cavern
- Lack of tensile stresses. This criterion results from the very low tear strength of the salt, which means that in the evaluation of the stress state it is assumed to be zero. If this criterion is met, an appropriate vault is created during the leaching of the cavern.
- Long-term durability is not exceeded. This is one of the most discussed criteria in geomechanics. In the case of rock salt, it is unacceptable for the rock mass to enter the third phase of creep because this leads to rapid destruction. In order to determine the permissible stress state, strength hypotheses and rock mass effort are introduced as these determine the value of the analyzed stress state in relation to the short-term strength. The allowable values of the effort are determined subjectively depending on the required level of security.
- The permissible deformations are not exceeded. Taking into account the ambiguity of the stress and deformation states and the variable pressure inside the working storage cavern, it is necessary to determine the permissible effective deformation state. This criterion determines the allowable increase in effective deformation during pressure reduction and at minimum pressure, as well as the allowable rate of effective deformations.
2.4.2. Global Cavern Stability
2.4.3. The Tightness of the Cavern
2.4.4. Cavern Capacity Changes during Storage Operations
- The cavern remains at pressure pmin for duration ∆tmin;
- The cavern is filled to pressure pmax for duration ∆tinj;
- The cavern remains filled to pressure pmax for duration ∆tmax;
- The cavern is emptied to pressure pmin for duration ∆tdow.
2.4.5. Protection of the Site Surface
3. Assumptions for the Assessment of the Influence of Temperature Variability on the Deformation-Stress State of Salt Rock
3.1. Analysis of the Injection and Download Cycles of the Cavern
3.2. Preferred Range of Operating Pressure
3.3. Temperature Variation Range
- Daily cyclic emptying and filling—1 daily cycle consists of two hours of emptying the cavern (download); 6 h of resting the cavern at the minimum pressure, 8 h of filling (injection); and 8 h of resting the cavern at the maximum pressure.
- With these assumptions, a thermodynamic simulation of CAES cavern operation was carried out. On this basis, the temperature distribution in the cavern was obtained. Then, the temperature distribution in the cavern was included in the further geomechanical calculations using a modified version of the GEOSOLK program, which considers the thermo-mechanical effects, including the temperature distribution around the storage cavern.
- For proper simulation in the GEOSOLK program, it was assumed that after the leaching process was completed, the cooling of the rock mass would stabilize the temperature in the cavern at 36.0 °C.
- For the thermodynamic simulations, the minimum temperature in the cavern (in the first emptying to 46 bar) was 12.28 °C. After 365 daily operating cycles, it dropped to the minimum value: 11.19 °C.
- The maximum temperature in the cavern after filling to the maximum pressure was 41.54 °C at the beginning of the simulation (after the first filling); it stabilized at 40.23 °C after filling and the simulation was complete after 365 daily work cycles.
4. Numerical Model of CAES Salt Cavern Operation
- (1)
- Constant primary temperature on the vertical edge of the model;
- (2)
- The heat flux resulting from the geothermal gradient on the horizontal edge.
4.1. Strength Criteria Adopted for Salt
4.2. The Condition of Viscoelasticity–the Creep Law
4.3. Thermal Properties of Salt
4.4. The Adopted Calculation Scenario and Model Parameters
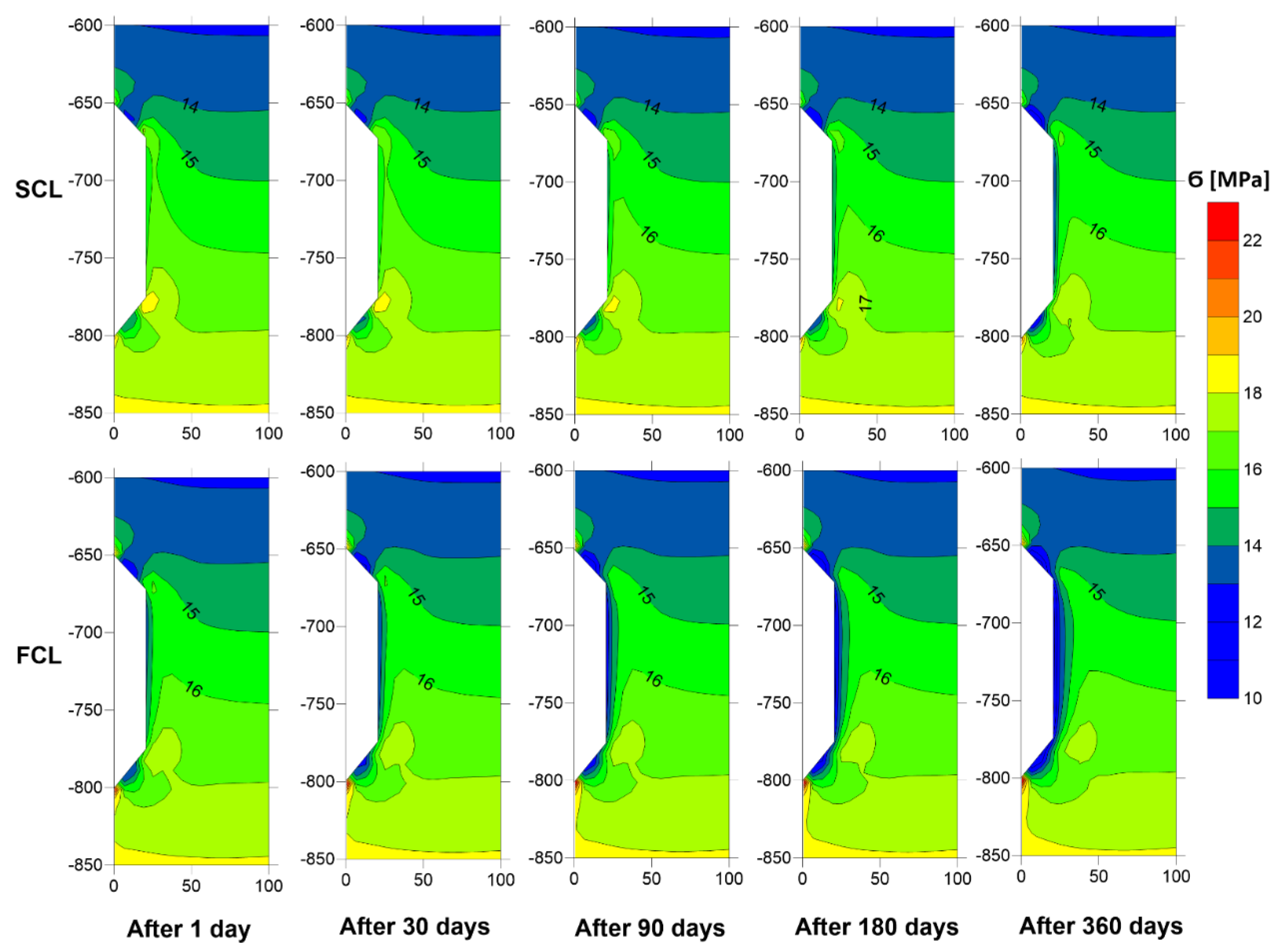
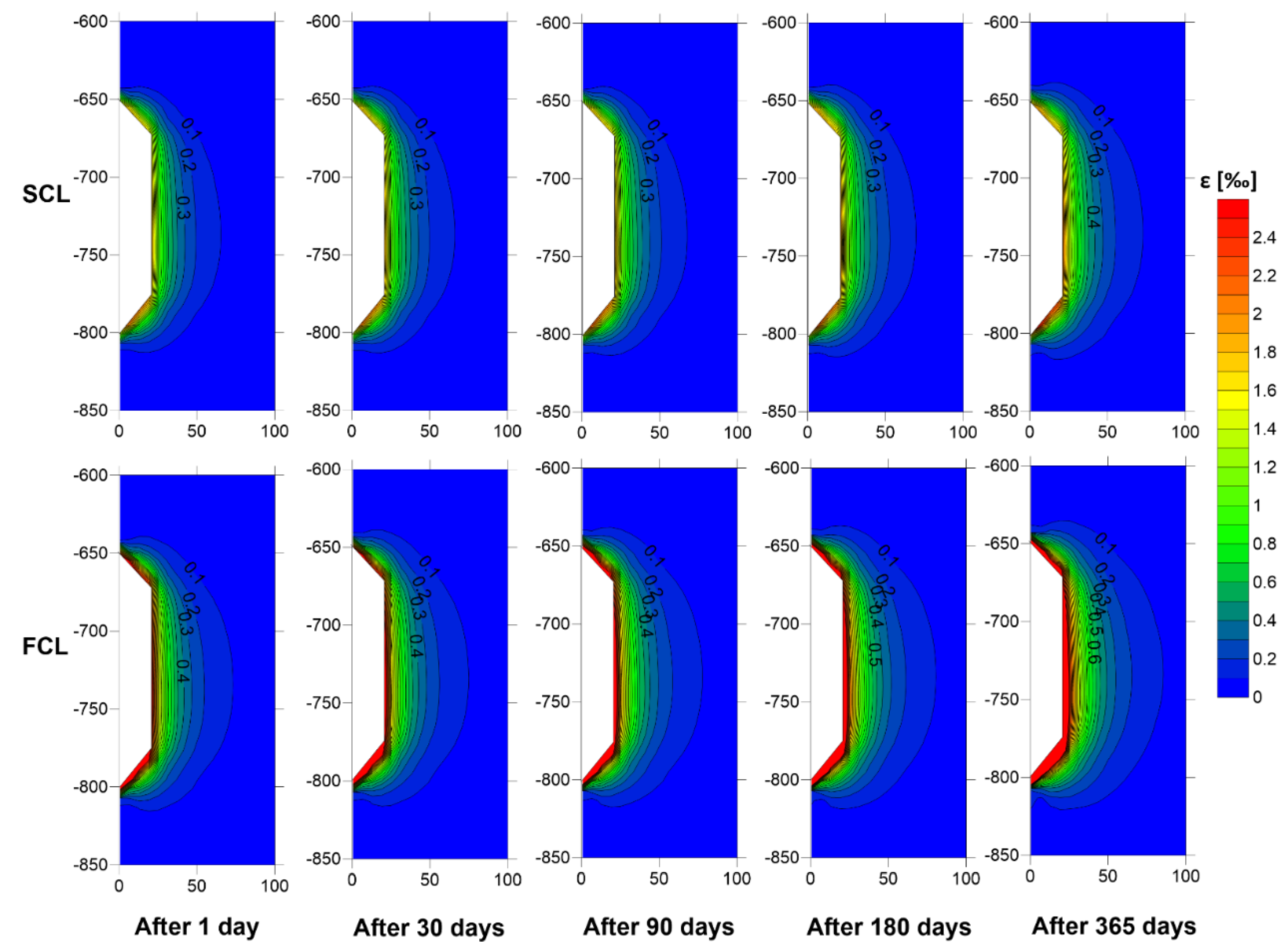
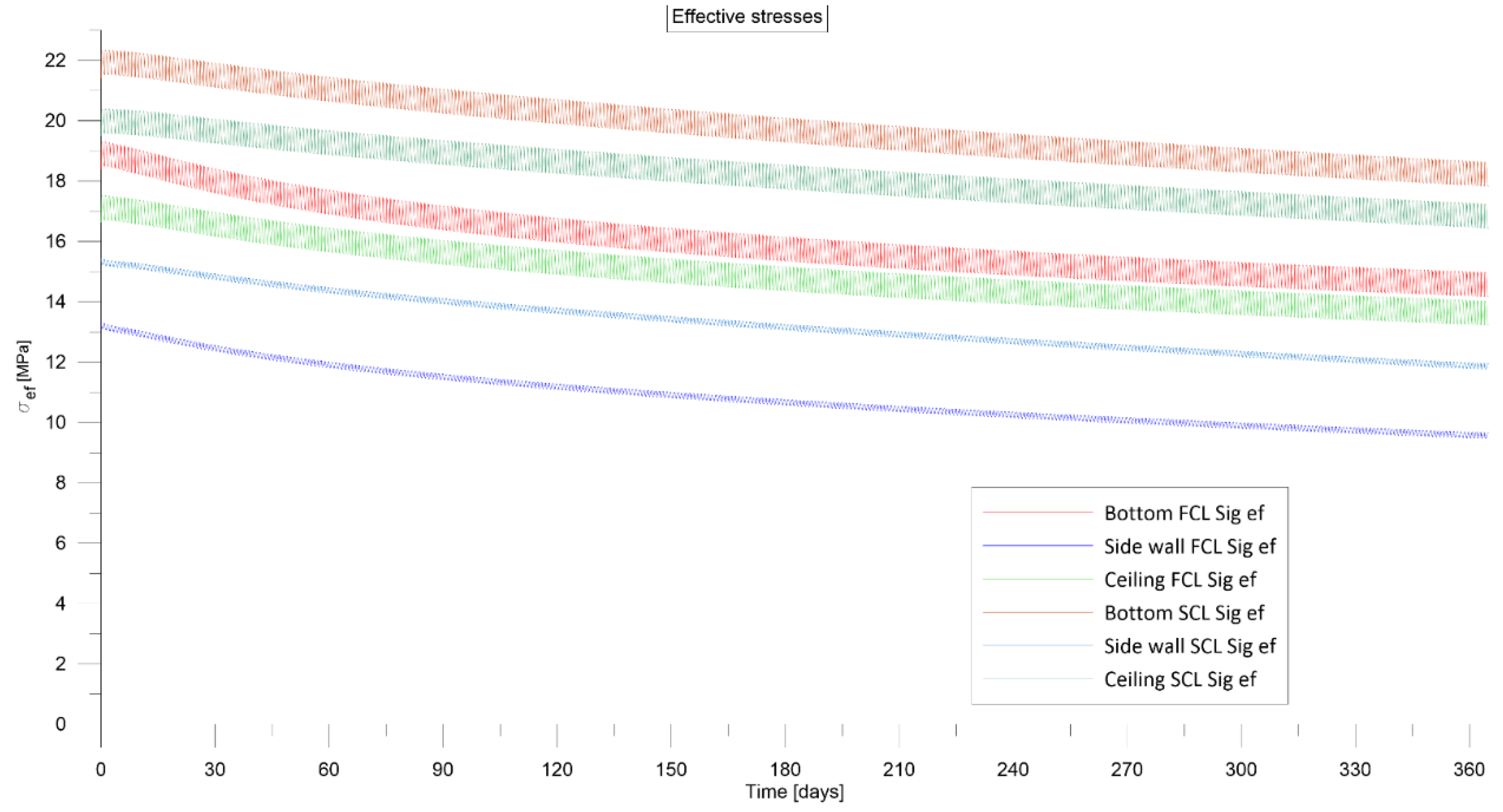
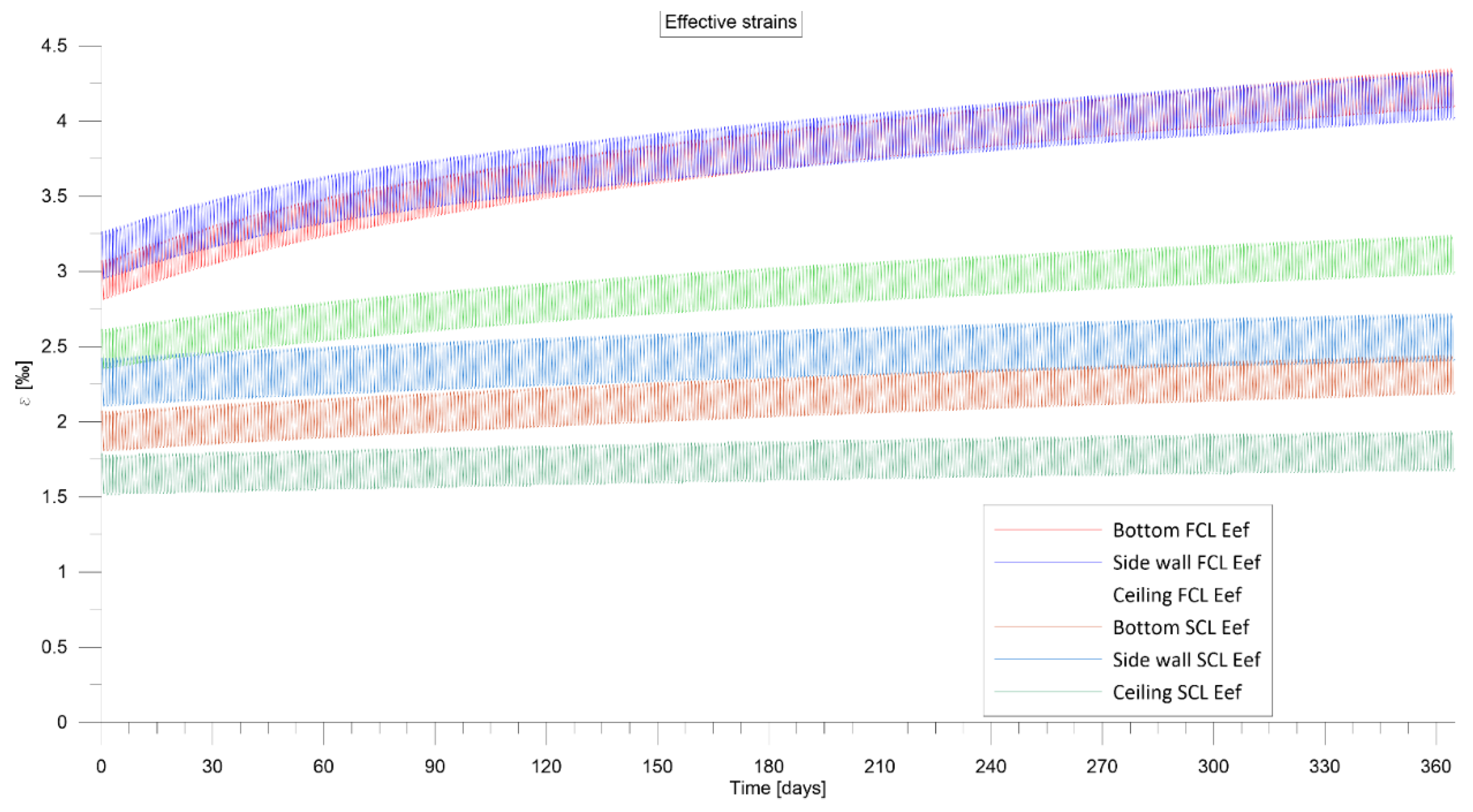
4.5. The Influence of Creep Law on the Deformation-Stress State in the Rock Mass Around the CAES Cavern
5. Influence of Temperature and Salt-Creep Speed on the Stability of the CAES Cavern
5.1. Strength Criteria and Rock Mass Effort
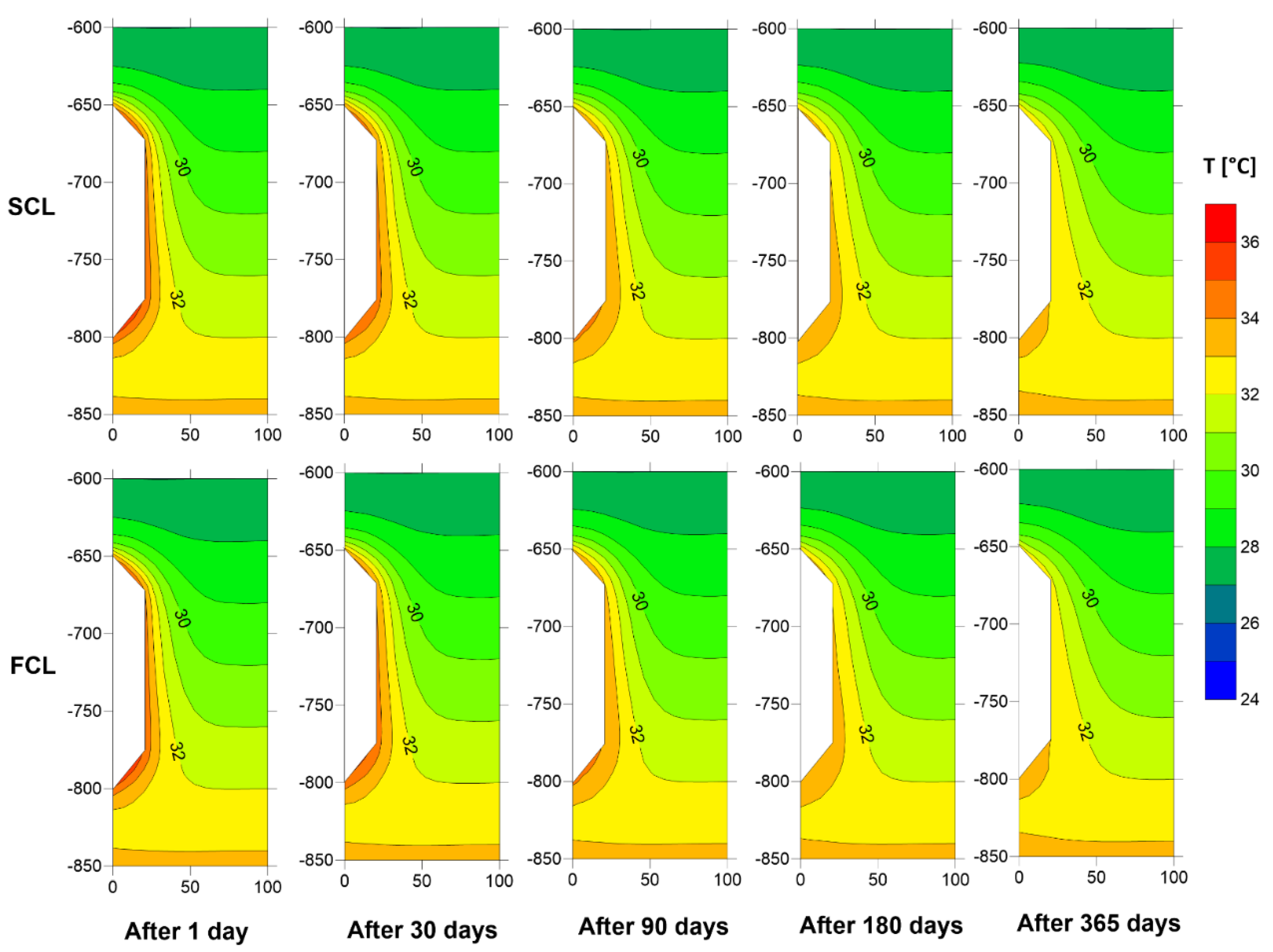
5.2. Temperature Distribution in the Rock Mass Around CAES Cavern
6. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Time (Days) | Cavern Pressure (MPa) | Model Type | Ceiling | Side Wall | Bottom | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 4.45 | SCL | 0.14 | 0.22 | 0.15 | 0.35 | 0.20 | 0.28 | 0.24 | 0.50 | 0.15 | 0.23 | 0.18 | 0.37 |
| FCL | 0.12 | 0.20 | 0.12 | 0.32 | 0.17 | 0.25 | 0.19 | 0.46 | 0.13 | 0.21 | 0.14 | 0.34 | ||
| 30 | 4.45 | SCL | 0.14 | 0.22 | 0.15 | 0.34 | 0.19 | 0.27 | 0.23 | 0.49 | 0.15 | 0.23 | 0.17 | 0.36 |
| FCL | 0.12 | 0.19 | 0.11 | 0.31 | 0.15 | 0.23 | 0.17 | 0.44 | 0.13 | 0.20 | 0.13 | 0.33 | ||
| 90 | 4.42 | SCL | 0.13 | 0.21 | 0.14 | 0.33 | 0.18 | 0.26 | 0.21 | 0.48 | 0.14 | 0.22 | 0.16 | 0.35 |
| FCL | 0.11 | 0.19 | 0.11 | 0.30 | 0.14 | 0.22 | 0.15 | 0.42 | 0.12 | 0.20 | 0.12 | 0.31 | ||
| 180 | 4.38 | SCL | 0.13 | 0.21 | 0.13 | 0.33 | 0.17 | 0.25 | 0.19 | 0.47 | 0.14 | 0.22 | 0.15 | 0.35 |
| FCL | 0.11 | 0.18 | 0.10 | 0.29 | 0.13 | 0.21 | 0.13 | 0.41 | 0.11 | 0.19 | 0.11 | 0.30 | ||
| 365 | 4.31 | SCL | 0.12 | 0.20 | 0.12 | 0.32 | 0.16 | 0.24 | 0.17 | 0.46 | 0.13 | 0.21 | 0.14 | 0.34 |
| FCL | 0.10 | 0.17 | 0.09 | 0.28 | 0.12 | 0.20 | 0.12 | 0.41 | 0.11 | 0.18 | 0.10 | 0.29 | ||
| Time (Days) | Cavern Pressure (MPa) | Model Type | Ceiling | Side Wall | Bottom | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 4.67 | SCL | 0.13 | 0.22 | 0.15 | 0.35 | 0.19 | 0.27 | 0.23 | 0.49 | 0.15 | 0.23 | 0.17 | 0.36 |
| FCL | 0.12 | 0.20 | 0.12 | 0.31 | 0.16 | 0.24 | 0.18 | 0.45 | 0.13 | 0.21 | 0.14 | 0.33 | ||
| 30 | 4.67 | SCL | 0.13 | 0.21 | 0.14 | 0.33 | 0.18 | 0.27 | 0.21 | 0.48 | 0.14 | 0.23 | 0.16 | 0.35 |
| FCL | 0.11 | 0.19 | 0.11 | 0.30 | 0.15 | 0.23 | 0.16 | 0.42 | 0.12 | 0.20 | 0.12 | 0.32 | ||
| 90 | 4.64 | SCL | 0.13 | 0.21 | 0.13 | 0.33 | 0.17 | 0.26 | 0.20 | 0.47 | 0.14 | 0.22 | 0.15 | 0.35 |
| FCL | 0.11 | 0.18 | 0.10 | 0.29 | 0.13 | 0.21 | 0.14 | 0.40 | 0.11 | 0.19 | 0.11 | 0.30 | ||
| 180 | 4.60 | SCL | 0.12 | 0.20 | 0.13 | 0.32 | 0.16 | 0.24 | 0.18 | 0.46 | 0.13 | 0.21 | 0.15 | 0.34 |
| FCL | 0.10 | 0.18 | 0.09 | 0.28 | 0.12 | 0.20 | 0.13 | 0.40 | 0.11 | 0.19 | 0.10 | 0.29 | ||
| 365 | 4.52 | SCL | 0.12 | 0.20 | 0.12 | 0.31 | 0.15 | 0.23 | 0.16 | 0.44 | 0.13 | 0.21 | 0.13 | 0.33 |
| FCL | 0.10 | 0.17 | 0.08 | 0.27 | 0.12 | 0.19 | 0.11 | 0.39 | 0.10 | 0.18 | 0.09 | 0.28 | ||
| Time (Days) | Cavern Pressure (MPa) | Model Type | Ceiling | Side Wall | Bottom | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 6.73 | SCL | 0.10 | 0.19 | 0.10 | 0.28 | 0.13 | 0.22 | 0.14 | 0.38 | 0.11 | 0.20 | 0.12 | 0.30 |
| FCL | 0.08 | 0.17 | 0.07 | 0.24 | 0.10 | 0.19 | 0.10 | 0.33 | 0.09 | 0.18 | 0.09 | 0.26 | ||
| 30 | 6.73 | SCL | 0.10 | 0.19 | 0.09 | 0.27 | 0.13 | 0.21 | 0.13 | 0.37 | 0.11 | 0.20 | 0.11 | 0.29 |
| FCL | 0.08 | 0.17 | 0.06 | 0.23 | 0.09 | 0.18 | 0.08 | 0.30 | 0.09 | 0.18 | 0.08 | 0.25 | ||
| 90 | 6.69 | SCL | 0.09 | 0.18 | 0.08 | 0.26 | 0.12 | 0.21 | 0.12 | 0.35 | 0.10 | 0.19 | 0.10 | 0.29 |
| FCL | 0.07 | 0.16 | 0.06 | 0.22 | 0.08 | 0.17 | 0.07 | 0.28 | 0.08 | 0.17 | 0.07 | 0.23 | ||
| 180 | 6.65 | SCL | 0.09 | 0.18 | 0.08 | 0.25 | 0.11 | 0.20 | 0.10 | 0.34 | 0.10 | 0.19 | 0.10 | 0.28 |
| FCL | 0.07 | 0.15 | 0.05 | 0.20 | 0.07 | 0.16 | 0.06 | 0.26 | 0.08 | 0.16 | 0.06 | 0.22 | ||
| 365 | 6.57 | SCL | 0.08 | 0.17 | 0.07 | 0.24 | 0.10 | 0.18 | 0.09 | 0.32 | 0.09 | 0.18 | 0.08 | 0.26 |
| FCL | 0.06 | 0.14 | 0.04 | 0.19 | 0.07 | 0.15 | 0.05 | 0.26 | 0.07 | 0.15 | 0.05 | 0.21 | ||
| Time (Days) | Cavern Pressure (MPa) | Model Type | Ceiling | Side Wall | Bottom | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 6.63 | SCL | 0.10 | 0.19 | 0.10 | 0.28 | 0.13 | 0.22 | 0.14 | 0.39 | 0.11 | 0.20 | 0.12 | 0.30 |
| FCL | 0.08 | 0.17 | 0.07 | 0.24 | 0.11 | 0.19 | 0.10 | 0.33 | 0.10 | 0.18 | 0.09 | 0.27 | ||
| 30 | 6.62 | SCL | 0.10 | 0.19 | 0.09 | 0.27 | 0.13 | 0.22 | 0.14 | 0.38 | 0.11 | 0.20 | 0.11 | 0.30 |
| FCL | 0.08 | 0.17 | 0.07 | 0.23 | 0.09 | 0.18 | 0.08 | 0.31 | 0.09 | 0.18 | 0.08 | 0.25 | ||
| 90 | 6.58 | SCL | 0.10 | 0.18 | 0.09 | 0.27 | 0.12 | 0.21 | 0.12 | 0.36 | 0.11 | 0.20 | 0.11 | 0.29 |
| FCL | 0.07 | 0.16 | 0.06 | 0.22 | 0.08 | 0.17 | 0.07 | 0.28 | 0.08 | 0.17 | 0.07 | 0.24 | ||
| 180 | 6.54 | SCL | 0.09 | 0.18 | 0.08 | 0.26 | 0.11 | 0.20 | 0.11 | 0.35 | 0.10 | 0.19 | 0.10 | 0.28 |
| FCL | 0.07 | 0.15 | 0.05 | 0.21 | 0.08 | 0.16 | 0.06 | 0.27 | 0.08 | 0.16 | 0.06 | 0.23 | ||
| 365 | 6.46 | SCL | 0.09 | 0.17 | 0.07 | 0.24 | 0.10 | 0.18 | 0.09 | 0.33 | 0.10 | 0.18 | 0.09 | 0.27 |
| FCL | 0.06 | 0.15 | 0.04 | 0.20 | 0.07 | 0.15 | 0.05 | 0.26 | 0.07 | 0.15 | 0.05 | 0.21 | ||
References
- Ślizowski, J.; Urbańczyk, K. Możliwości Magazynowania Gazu Ziemnego w Polskich Złożach Soli Kamiennej w Zależności od Warunków Geologiczno-Górniczych; IGSMiE PAN: Kraków, Poland, 2011. [Google Scholar]
- Crotogino, F. Compressed Air Storage. In Proceedings of the First International Renewable Energy Storage (IRES I) Conference, Gelsenkirchen, Germany, 30–31 October 2006. [Google Scholar]
- Robb, D. The CAES for wind. Renew. Energy Focus 2011, 12, 18–19. [Google Scholar] [CrossRef]
- Ślizowski, J.; Urbańczyk, K.; Lankof, L.; Serbin, K. Selection of Possible Locations of Underground Storage Tanks for Energy Storage in the Form of Compressed Air from the Point of View ot the Use Underground Geological Structures in the Indicated Areas of Poland—Wytypowanie Możliwych Lokalizacji Podziemnych Zbiorników do Magazynowania Energii w Postaci Sprężonego Powietrza z Punktu Widzenia Wykorzystania Podziemnych Struktur Geologicznych we Wskazanych Obszarach Polski; IGSMiE PAN: Cracow, Poland, 2011; unpublished. [Google Scholar]
- Khaledi, K.; Mahmoudi, E.; Datcheva, M.; Schanz, T. Analysis of compressed air storage caverns in rock salt considering thermo-mechanical cyclic loading. Environ. Earth Sci. 2016, 75, 1–17. [Google Scholar] [CrossRef]
- Perazzelli, P.; Anagnostou, G. Design issues for compressed air energy storage in sealed underground cavities. J. Rock Mech. Geotech. Eng. 2016, 8, 314–328. [Google Scholar] [CrossRef]
- Ślizowski, J. Geomechaniczne Podstawy Projektowania Komór Magazynowych Gazu Ziemnego w Złożach Soli Kamiennej; Wydawnictwo IGSMiE PAN: Kraków, Poland, 2006. [Google Scholar]
- Polański, K. Numerical calculations of main stress in the rock massif around salt cavern for compressed air storage. IOP Conf. Ser. Earth Environ. Sci. 2019, 214, 012079. [Google Scholar] [CrossRef]
- Kushnir, R.; Dayan, A.; Ullmann, A. Temperature and pressure variations within compressed air energy storage caverns. Int. J. Heat Mass Transf. 2012, 55, 5616–5630. [Google Scholar] [CrossRef]
- Raju, M.; Khaitan, S.K. Modeling and simulation of compressed air storage in caverns: A case study of the Huntorf plant. Appl. Energy 2012, 89, 474–481. [Google Scholar] [CrossRef]
- Xia, C.; Zhou, Y.; Zhou, S.; Zhang, P.; Wang, F. A simplified and unified analytical solution for temperature and pressure variations in compressed air energy storage caverns. Renew Energy 2015, 74, 718–726. [Google Scholar] [CrossRef]
- Berest, P.; Djizanne, H.; Brouard, B.; Hevin, G. Rapid depressurization: Can they lead to irreversible damage? In Proceedings of the SMRI Conference, Regina, SK, Canada, 23–24 April 2012. [Google Scholar]
- Berest, P.; Brouard, B.; Djakeun-Djizanne, H.; Hevin, G. Thermomechanical effects of a rapid depressurization in a gas cavern. Acta Geotech. 2013, 9, 181–186. [Google Scholar] [CrossRef]
- Berest, P.; Brouard, B.; Jafari, M.K.; Sambeek, L.V. Thermomechanical aspects of high frequency cyclic in salt storage caverns. In Proceedings of the International Gas Union Research Conference, Seoul, Korea, 19–21 October 2011. [Google Scholar]
- Skorek, J.; Banasiak, K. Thermodynamic Analysis of the Compressed Air Energy Systems operation. Inżynieria Chem. Proces. 2007, 27, 187–200. [Google Scholar]
- He, W.; Luo, X.; Evans, D.; Busby, J.; Garvey, S.; Parkes, D.; Wang, J. Exergy storage of compressed air in cavern and cavern volume estimation of the large-scale compressed air energy storage system. Appl. Energy 2017, 208, 745–757. [Google Scholar] [CrossRef]
- Serbin, K. Wpływ Parametrów Termodynamicznych Procesu Magazynowania Gazu na Pojemność Kawerny w Złożu Soli Kamiennej. Ph.D. Thesis, AGH-UST, Kraków, Poland, 2013. [Google Scholar]
- Lux, K.-H.; Hou, Z.; Düsterloh, U. Some New Aspects in Modelling of Cavern Behavior and Safety Analysis. In Proceedings of the SMRI Meeting, Rome, Italy, 4–7 October 1998. [Google Scholar]
- Ślizowski, J.; Serbin, K. Wpływ Zmienności Temperatury na Stan Deformacyjno-Naprężeniowy Górotworu w Otoczeniu Komory Magazynowej Gazu; Statutory work of IGSMiE PAN: Cracow, Poland, 2012; unpublished. [Google Scholar]
- Urbańczyk, K.; Ślizowski, J. An attempt to asses suitability of middle-Poland salt domes for natural gas storage. Arch. Min. Sci. 2012, 57, 335–349. [Google Scholar]
- Wang, S.Y.; Wu, J.L. Optimal sizing of the CAES system in a power system with high wind power penetration. Int. J. Electr. Power Energy Syst. 2012, 37, 117–125. [Google Scholar] [CrossRef]
- Dzierżanowski, Ł. Elektrownie CAES. Energia Elektryczna—nr 2-3/2011; Oficyna Wydawnicza Energia [Stowarzyszenie Elektryków Polskich - COSiW]: Warsaw, Poland, 2011. [Google Scholar]
- Kuczyński, S.; Skokowski, D.H.; Włodek, T.; Polański, K. Compressed air energy storage as backup generation capacity combined with wind energy sector in Poland implementation possibilities. AGH Drill. Oil Gas 2015, 32, 23–32. [Google Scholar] [CrossRef][Green Version]
- Samotyj, M. Złapać Wiatr i Pod Ziemię! Materiały Problemowe Cire; Centrum Informacji o Rynku Energii: Warsaw, Poland, 2012. [Google Scholar]
- Hunshe, U. True Triaxial Failure Tests on Cubic Rock Salt Samples—Experimental Methods and Results. In Proceedings of the IUTAM-Symposium—Hannover; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Hunshe, U. Uniaxial and Triaxial Creep and Failure Tests on Rock: Experimental Technique and Interpretation. In Uniaxial and Triaxial Creep and Failure Tests on Rock: Experimental Technique and Interpretation; Cristescu, N.D., Gioda, G., Eds.; Springer: Vienn, Austria, 1994; Volume 350. [Google Scholar]
- Ślizowski, J.; Urbańczyk, K. Influence of Depth on Rock Salt Effort around the Single Chamber; IGSMiE: Cracow, Poland, 2004. [Google Scholar]

| Model | A (‰) | Q/R (K) | N | dε/dt * (‰/day) |
|---|---|---|---|---|
| Slow-creep Law (SCL) | 219.65 | 6500 | 4 | 0.004 |
| Fast-Creep Law (FCL) | 175.72 | 6500 | 5 | 0.032 |
| Thermal conductivity of the salt rock mass (W/m⋅K) | 6.5 |
| Thermal diffusivity of the rock mass (m2/s) | 0.45⋅10−5 |
| Salt density (kg/m3) | 2155 |
| Heat transfer in salt (W/m2⋅K) | 50 |
| Temperature gradient αrock (K/m) | 0.025 |
| Factor β | 298 |
| The considered interval (m) | 0–2000 |
| Download | Injection | |
|---|---|---|
| Temperature at the wellhead (°C) | 15.2 | 35 |
| Pressure at the wellhead (bar) | 64.75 | 70 |
| Air density (kg/m3) | 80.128 | 80.239 |
| Download | Injection | |
|---|---|---|
| Air flow (kg/s) | 417 | 108 |
| Air flow (kg/h) | 1,501,200 | 388,800 |
| Air flow (Nm3/h) | 1,164,932 | 301,709 |
| Pressure change (in the cavern) (MPa/h) | 1 | 0.25 |
| Time of step (h) | 2 | 8 |
| Ceiling depth (m) | 650 |
| Bottom depth (m) | 800 |
| Cavern radius (m) | 17.841 |
| Volume (m3) | 149,996 |
| Internal diameter of the exploitation pipes (m) | 0.508 (20″) |
| Heat transfer in the well (W/m2K) | 15 |
| Heat transfer in the rock mass (W/m2K) | 50 |
| Time (Days) | Pressure in Cavern (MPa) | Model Type | Ceiling | Side Wall | Bottom | |||
|---|---|---|---|---|---|---|---|---|
(MPa) | (‰) | (MPa) | (‰) | (MPa) | (‰) | |||
| 1 | 4.45 | SCL | 20.39 | 1.79 | 15.30 | 2.43 | 22.33 | 2.07 |
| FCL | 17.53 | 2.62 | 13.18 | 3.26 | 19.32 | 3.07 | ||
| 30 | 4.45 | SCL | 20.08 | 1.80 | 14.81 | 2.46 | 21.94 | 2.11 |
| FCL | 17.00 | 2.71 | 12.44 | 3.47 | 18.45 | 3.30 | ||
| 90 | 4.42 | SCL | 19.37 | 1.83 | 13.99 | 2.53 | 21.07 | 2.19 |
| FCL | 16.07 | 2.86 | 11.48 | 3.74 | 17.21 | 3.63 | ||
| 180 | 4.38 | SCL | 18.56 | 1.87 | 13.13 | 2.61 | 20.11 | 2.29 |
| FCL | 15.18 | 3.02 | 10.64 | 3.99 | 16.17 | 3.93 | ||
| 365 | 4.31 | SCL | 17.25 | 1.94 | 11.82 | 2.72 | 18.64 | 2.45 |
| FCL | 14.04 | 3.24 | 9.52 | 4.33 | 14.99 | 4.35 | ||
| Time (Days) | Pressure in Cavern (MPa) | Model Type | Ceiling | Side Wall | Bottom | |||
|---|---|---|---|---|---|---|---|---|
(MPa) | (‰) | (MPa) | (‰) | (MPa) | (‰) | |||
| 1 | 4.67 | SCL | 20.35 | 1.75 | 15.22 | 2.39 | 22.30 | 2.04 |
| FCL | 17.48 | 2.59 | 13.10 | 3.23 | 19.27 | 3.04 | ||
| 30 | 4.67 | SCL | 20.02 | 1.77 | 14.74 | 2.43 | 21.88 | 2.08 |
| FCL | 16.94 | 2.69 | 12.37 | 3.44 | 18.38 | 3.27 | ||
| 90 | 4.64 | SCL | 19.31 | 1.80 | 13.92 | 2.49 | 21.02 | 2.16 |
| FCL | 16.01 | 2.83 | 11.41 | 3.71 | 17.15 | 3.60 | ||
| 180 | 4.60 | SCL | 18.50 | 1.84 | 13.06 | 2.57 | 20.05 | 2.26 |
| FCL | 15.12 | 2.99 | 10.57 | 3.96 | 16.11 | 3.90 | ||
| 365 | 4.52 | SCL | 17.20 | 1.91 | 11.75 | 2.69 | 18.58 | 2.42 |
| FCL | 13.99 | 3.21 | 9.46 | 4.29 | 14.93 | 4.32 | ||
| Time (Days) | Pressure in Cavern (MPa) | Model Type | Ceiling | Side Wall | Bottom | |||
|---|---|---|---|---|---|---|---|---|
(MPa) | (‰) | (MPa) | (‰) | (MPa) | (‰) | |||
| 1 | 6.73 | SCL | 19.62 | 1.52 | 15.39 | 2.10 | 21.57 | 1.80 |
| FCL | 16.75 | 2.35 | 13.27 | 2.95 | 18.53 | 2.81 | ||
| 30 | 6.73 | SCL | 19.29 | 1.53 | 14.92 | 2.14 | 21.14 | 1.85 |
| FCL | 16.20 | 2.45 | 12.55 | 3.15 | 17.64 | 3.04 | ||
| 90 | 6.69 | SCL | 18.58 | 1.56 | 14.10 | 2.21 | 20.28 | 1.93 |
| FCL | 15.27 | 2.60 | 11.60 | 3.43 | 16.41 | 3.37 | ||
| 180 | 6.65 | SCL | 17.77 | 1.61 | 13.25 | 2.29 | 19.32 | 2.03 |
| FCL | 14.39 | 2.76 | 10.75 | 3.67 | 15.38 | 3.67 | ||
| 365 | 6.57 | SCL | 16.47 | 1.67 | 11.94 | 2.40 | 17.86 | 2.18 |
| FCL | 13.26 | 2.98 | 9.65 | 4.01 | 14.20 | 4.09 | ||
| Time (Days) | Pressure in Cavern(MPa) | Model Type | Ceiling | Side Wall | Bottom | |||
|---|---|---|---|---|---|---|---|---|
(MPa) | (‰) | (MPa) | (‰) | (MPa) | (‰) | |||
| 1 | 6.63 | SCL | 19.58 | 1.53 | 15.40 | 2.12 | 21.53 | 1.82 |
| FCL | 16.71 | 2.37 | 13.27 | 2.96 | 18.50 | 2.82 | ||
| 30 | 6.62 | SCL | 19.25 | 1.54 | 14.93 | 2.16 | 21.10 | 1.86 |
| FCL | 16.16 | 2.47 | 12.56 | 3.17 | 17.60 | 3.06 | ||
| 90 | 6.58 | SCL | 18.54 | 1.58 | 14.12 | 2.22 | 20.24 | 1.94 |
| FCL | 15.24 | 2.62 | 11.61 | 3.44 | 16.38 | 3.38 | ||
| 180 | 6.54 | SCL | 17.73 | 1.62 | 13.26 | 2.30 | 19.29 | 2.04 |
| FCL | 14.36 | 2.77 | 10.77 | 3.69 | 15.35 | 3.69 | ||
| 365 | 6.46 | SCL | 16.44 | 1.69 | 11.95 | 2.42 | 17.82 | 2.20 |
| FCL | 13.22 | 2.99 | 9.66 | 4.02 | 14.17 | 4.10 | ||
| Model | Increase in Strain (‰/year) (State at the End of the Work Cycle) | ||
|---|---|---|---|
| Ceiling | Side Wall | Bottom | |
| Slow-creep Law | 0.16 | 0.30 | 0.38 |
| Fast-creep Law | 0.62 | 1.06 | 1.28 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Polański, K. Influence of the Variability of Compressed Air Temperature on Selected Parameters of the Deformation-Stress State of the Rock Mass Around a CAES Salt Cavern. Energies 2021, 14, 6197. https://doi.org/10.3390/en14196197
Polański K. Influence of the Variability of Compressed Air Temperature on Selected Parameters of the Deformation-Stress State of the Rock Mass Around a CAES Salt Cavern. Energies. 2021; 14(19):6197. https://doi.org/10.3390/en14196197
Chicago/Turabian StylePolański, Krzysztof. 2021. "Influence of the Variability of Compressed Air Temperature on Selected Parameters of the Deformation-Stress State of the Rock Mass Around a CAES Salt Cavern" Energies 14, no. 19: 6197. https://doi.org/10.3390/en14196197
APA StylePolański, K. (2021). Influence of the Variability of Compressed Air Temperature on Selected Parameters of the Deformation-Stress State of the Rock Mass Around a CAES Salt Cavern. Energies, 14(19), 6197. https://doi.org/10.3390/en14196197






