Understanding the Reasons behind the Energy Performance Gap of an Energy-Efficient Building, through a Probabilistic Approach and On-Site Measurements
Abstract
:Highlights
- The energy performance gap of a new multi-family Minergie® building was identified by comparing the measured and the calculated heating demand.
- The comparisons between the measured and the calculated heating demand showed that the latter underestimates the real heating demand, by a factor of 2.
- Commonly used hypotheses in the Swiss building practice, considering the climate conditions of the building, the indoor temperature and the electricity consumption, as causes of the increased performance gap, were not justified for this case study.
- A probabilistic framework was then proposed, so as to include the different uncertainties of the parameters of the heating demand, as an attempt to reduce the performance gap.
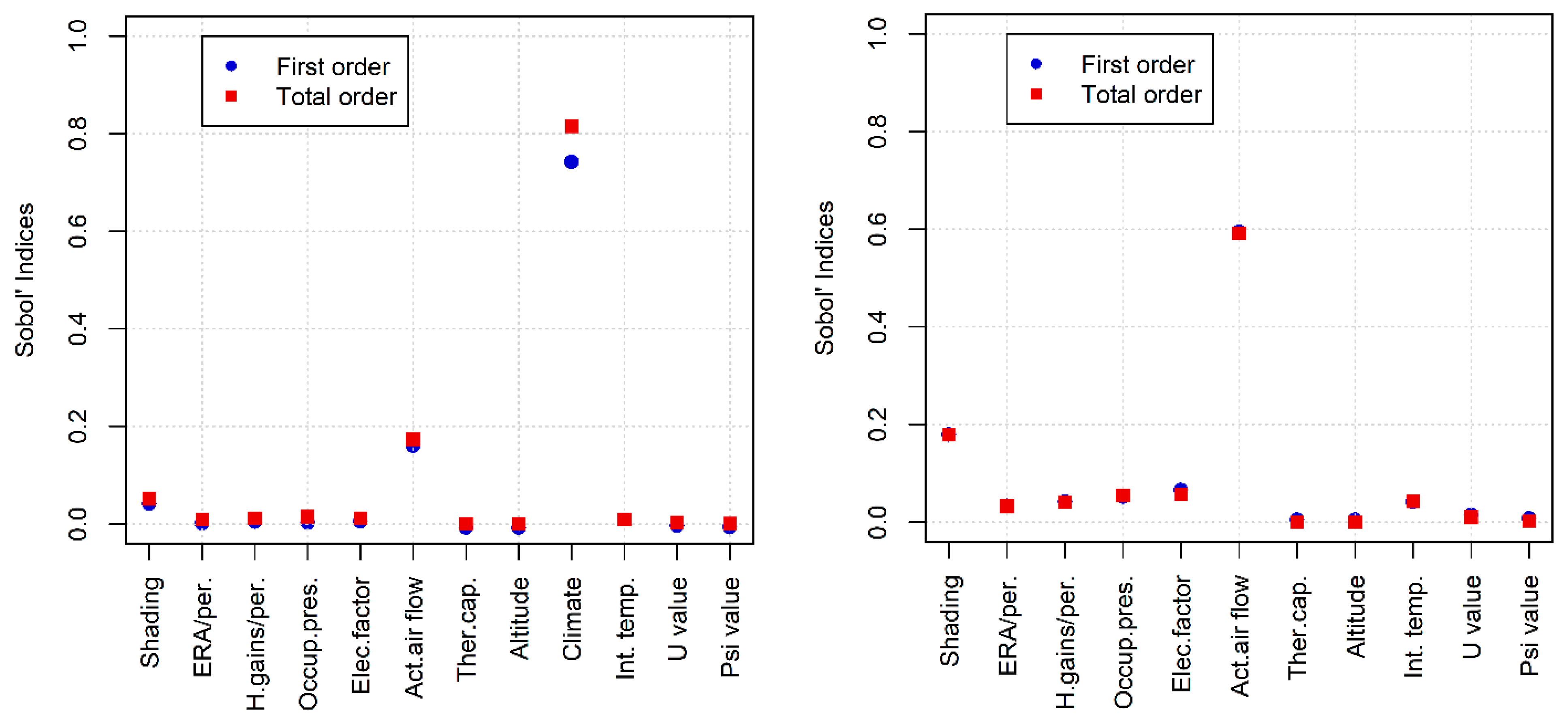
- A sensitivity analysis showed that the shading factor and the active heat flow were identified as being the most influential on the uncertainty of the heating demand. Correction measures were finally proposed, based on these results.
1. Introduction
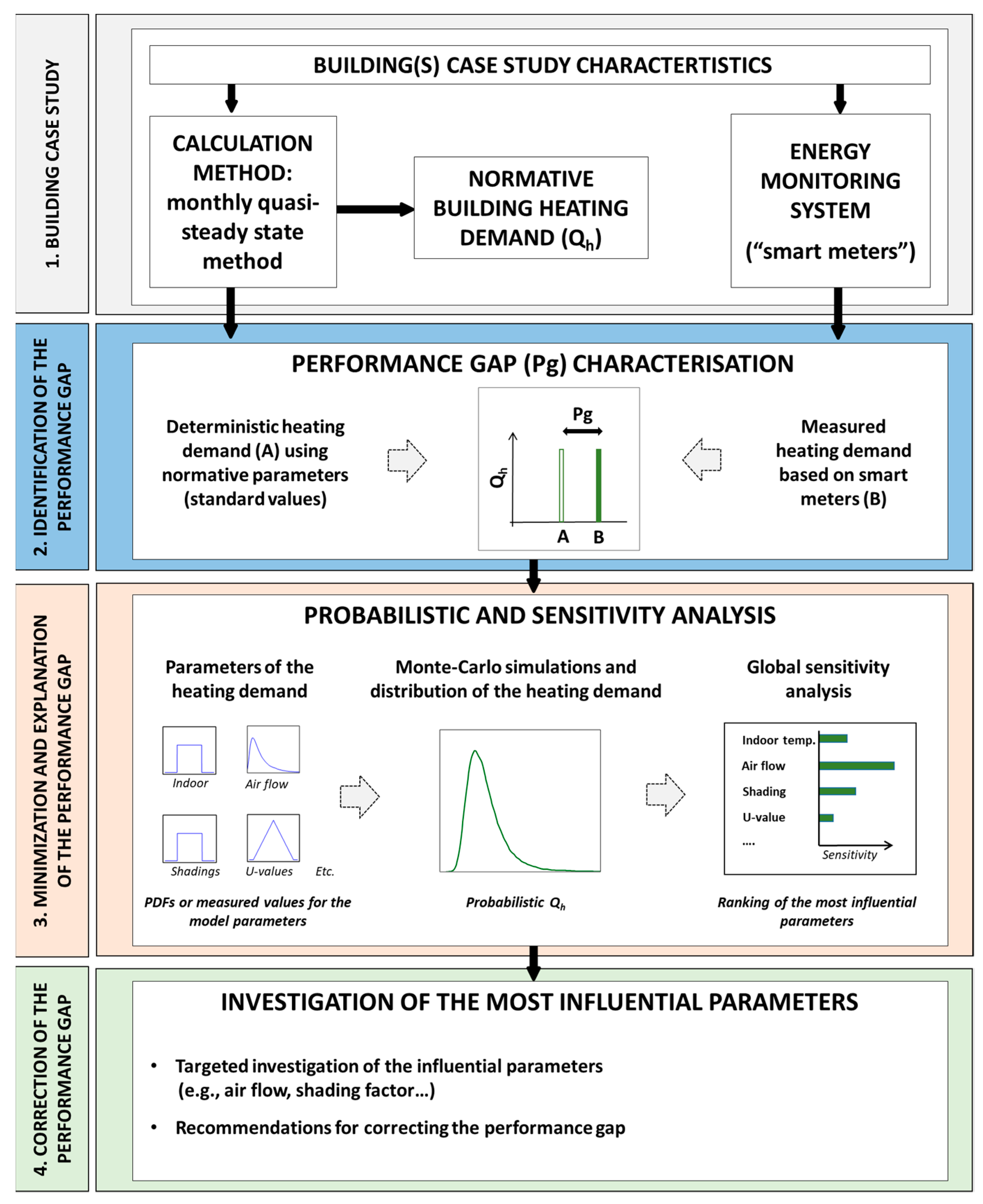
2. Materials and Methods
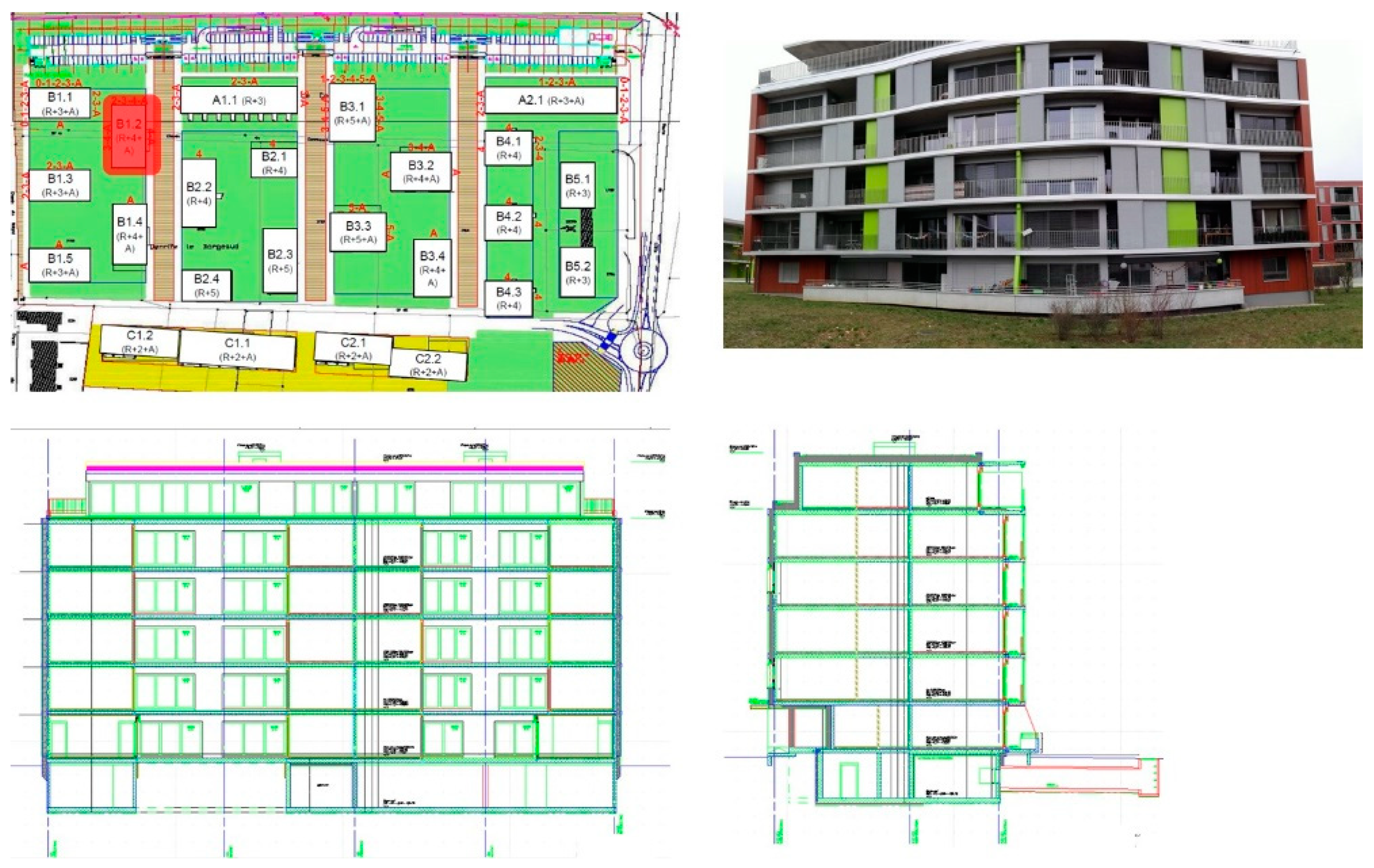
2.1. Building Case Study and Monitoring System, Real and Normative Heating Demand
2.2. Minimization and Explanation of the Performance Gap through Uncertainty and Sensitivity Analyses
3. Results
3.1. Identifying the Energy Performance Gap
3.2. Explaining the Performance Gap by Comparing the Model Assumptions and the Measured Data
3.3. Reducing the Performance Gap, Using a Probabilistic Approach
3.4. Explaining the Performance Gap, Using a Global Sensitivity Analysis
4. Discussion
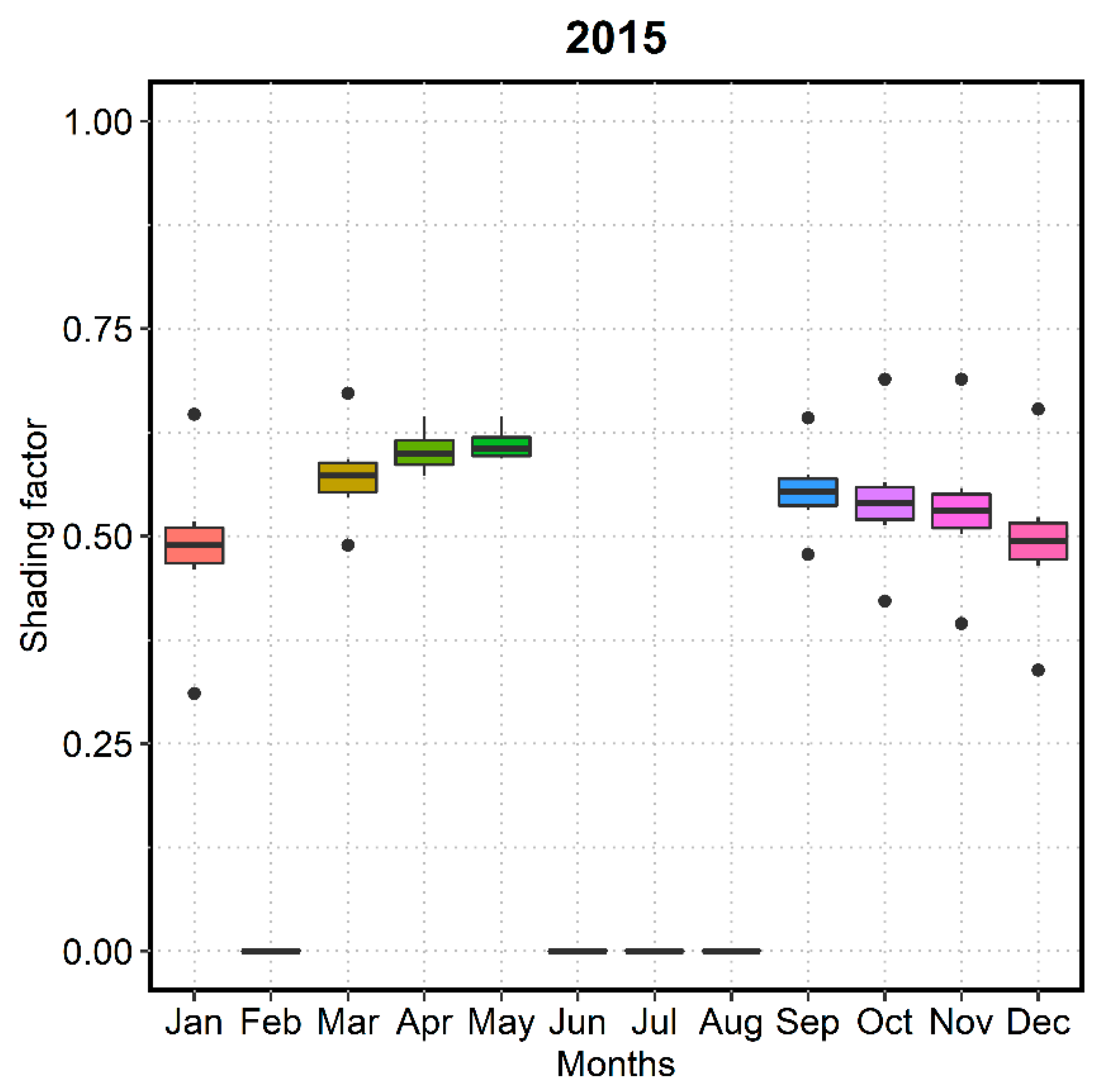
4.1. Further Reduction of the Performance Gap by Adjusting the Shading Factor
4.2. Limitations of the Current Approach
5. Conclusions
- (a)
- Among the reasons explaining the performance gap, we can find the overestimation of the solar and internal gains in the heating demand calculations, errors of the measurement system, wrong configurations of the technical system, the non-representativeness of the normative values included in the simulations, regarding the real conditions of the building or the uncertainty of the parameters controlled by the occupants.
- (b)
- The probabilistic analysis can be an efficient method for minimizing the performance gap both in ex-post and ex-ante evaluations, while the sensitivity analysis proved to be a straightforward method for the identification of the parameters that explained the variance of the probabilistic heating demand. This step allows a targeted investigation of these parameters, regarding their adjustment in the simulation or in the real construction and gives hints about the causes of the performance gap as well as solutions for its correction.
- (c)
- The results of the sensitivity analysis cannot be generalized since only one residential case study was analyzed. However, the analysis showed that increasing the percentage of the shading factor in the Minergie® simulations for this specific case study can lead to the minimization of the gap between the measurements and the simulation. Further studies are now needed that also includes the use of a more accurate building heating demand model using a dynamic calculation and more measurement data in sensitive parameters (e.g., shading factor).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- De Wilde, P. The gap between predicted and measured energy performance of buildings: A framework for investigation. Autom. Constr. 2014, 41, 40–49. [Google Scholar] [CrossRef]
- Shi, X.; Si, B.; Zhao, J.; Tian, Z.; Wang, C.; Jin, X.; Zhou, X. Magnitude, causes, and solutions of the performance gap of buildings: A review. Sustainability 2019, 11, 937. [Google Scholar] [CrossRef] [Green Version]
- Van Dronkelaar, C.; Dowson, M.; Spataru, C.; Mumovic, D. A review of the regulatory energy performance gap and its underlying causes in non-domestic buildings. Front. Mech. Eng. 2016, 1, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Fokaides, P.A.; Maxoulis, C.N.; Panayiotou, G.P.; Neophytou, M.K.-A.; Kalogirou, S.A. Comparison between measured and calculated energy performance for dwellings in a summer dominant environment. Energy Build. 2011, 43, 3099–3105. [Google Scholar] [CrossRef]
- Menezes, A.C.; Cripps, A.; Bouchlaghem, D.; Buswell, R. Predicted vs. actual energy performance of non-domestic buildings: Using post-occupancy evaluation data to reduce the performance gap. Appl. Energy 2012, 97, 355–364. [Google Scholar] [CrossRef] [Green Version]
- Newsham, G.R.; Mancini, S.; Birt, B.J. Do LEED-certified buildings save energy? Yes, but…. Energy Build. 2009, 41, 897–905. [Google Scholar] [CrossRef]
- Haldi, F.; Robinson, D. On the behaviour and adaptation of office occupants. Build. Environ. 2008, 43, 2163–2177. [Google Scholar] [CrossRef]
- Korjenic, A.; Bednar, T. Validation and evaluation of total energy use in office buildings: A case study. Autom. Constr. 2012, 23, 64–70. [Google Scholar] [CrossRef]
- Niu, S.; Pan, W.; Zhao, Y. A virtual reality integrated design approach to improving occupancy information integrity for closing the building energy performance gap. Sustain. Cities Soc. 2016, 27, 275–286. [Google Scholar] [CrossRef]
- Miller, C.; Nagy, Z.; Schlueter, A. Automated daily pattern filtering of measured building performance data. Autom. Constr. 2015, 49, 1–17. [Google Scholar] [CrossRef]
- Yuming, S. Closing the Building Energy Performance Gap by Improving Our Predictions; Georgia Institute of Technology: Atlanta, GA, USA, 2014. [Google Scholar]
- Walker, W.; Harremoës, P.; Rotmans, J.; van der Sluijs, J.P.; Van Asselt, M.; Janssen, P.; Von Krauss, M.K. Defining Uncertainty: A Conceptual Basis for Uncertainty Management in Model-Based Decision Support. Integr. Assess. 2003, 4, 5–17. [Google Scholar] [CrossRef] [Green Version]
- Björklund, A.E. Survey of approaches to improve reliability in lca. Int. J. Life Cycle Assess. 2002, 7, 64–72. [Google Scholar] [CrossRef]
- Calì, D.; Andersen, R.K.; Müller, D.; Olesen, B.W. Analysis of occupants’ behavior related to the use of windows in German households. Build. Environ. 2016, 103, 54–69. [Google Scholar] [CrossRef] [Green Version]
- Tagliabue, L.C.; Manfren, M.; Ciribini, A.L.C.; DE Angelis, E. Probabilistic behavioural modeling in building performance simulation—The Brescia eLUX lab. Energy Build. 2016, 128, 119–131. [Google Scholar] [CrossRef]
- Cecconi, F.R.; Manfren, M.; Tagliabue, L.C.; Ciribini, A.L.C.; De Angelis, E. Probabilistic behavioral modeling in building performance simulation: A Monte Carlo approach. Energy Build. 2017, 148, 128–141. [Google Scholar] [CrossRef]
- Branco, G.; Lachal, B.; Gallinelli, P.; Weber, W. Predicted versus observed heat consumption of a low energy multifamily complex in Switzerland based on long-term experimental data. Energy Build. 2004, 36, 543–555. [Google Scholar] [CrossRef]
- Cozza, S.; Chambers, J.; Patel, M.K. Measuring the thermal energy performance gap of labelled residential buildings in Switzerland. Energy Policy 2020, 137, 111085. [Google Scholar] [CrossRef]
- Reimann, W.; Lehmann, M.; Bühlmann, E.; Bade, S.; Krämer, S.; Ott, W.; Montanari, D.; Ménard, M. Erfolgskontrolle Gebäudeenergiestandards 2014–2015, Schlussbericht; Swiss Federal Office for Energy: Bern, Switzerland, 2016. [Google Scholar]
- Minergie. Available online: https://www.minergie.ch/fr/ (accessed on 1 September 2021).
- Padey, P.; Wagner, G.; Périsset, B.; Lasvaux, S. Usergap, Partie HEIG-VD: Analyse de L’écart de Performance Lié à la Demande de Chauffage du Bâtiment B1.2 de L’éco-Quartier Eikenott à Gland (VD), Rapport Intermédiaire; Swiss Federal Office for Energy: Bern, Switzerland, 2019. [Google Scholar]
- eSmart Technologies, SA. Available online: https://www.myesmart.com/ (accessed on 6 January 2021).
- SIA 380/1. Besoins de Chaleur pour le Chauffage; Schweizerischer Ingenieur- und Architektenverein: Zürich, Switzerland, 2016. [Google Scholar]
- E4Tech. Lesosai Software webpage. Available online: https://lesosai.com/ (accessed on 1 September 2021).
- The R Project for Statistical Computing. Available online: https://www.r-project.org/ (accessed on 1 September 2021).
- Kucherenko, S.; Song, S. Different numerical estimators for main effect global sensitivity indices. Reliab. Eng. Syst. Saf. 2017, 165, 222–238. [Google Scholar] [CrossRef] [Green Version]
- Sobol, I.M.; Kucherenko, S.S. Global sensitivity indices for nonlinear mathematical models. Review. Wilmott 2005, 2005, 56–61. [Google Scholar] [CrossRef]
- Saltelli, A. Sensitivity Analysis in Practice: A Guide to Assessing Scientific Models; Wiley: New York, NY, USA, 2004. [Google Scholar]

| Parameter | Deterministic Assessment | Probabilistic Assessment | ||
|---|---|---|---|---|
| Normative Value According to the Minergie® Standard | Range of the Parameter | Comments on the Sampling Type | ||
| Parameters (normative values and PDFs) | Shading factor | 0% | [0, 100] % | For each window of the building (total: 43), a random uniform sampling is performed |
| Energy reference area per person | 40 m2/person | [30, 50] m2/user | Uniform | |
| Internal heat gains per person | 70 W/person | [50, 90] W/user | Uniform | |
| Occupant presence per day | 12 h/day | [8, 16] h/day | Uniform | |
| Reduction factor for the electricity heating needs | 70% | [70, 100] % | Uniform | |
| Active thermal air flow rate 1 | 0.33 m3/(m2ERA∙h) | [0.3, 0.7] m3/(m2ERA∙h) | Uniform | |
| Thermal capacity of the envelope | 0.50 MJ/(m2∙K) | [0.45, 0.555] MJ/(m2∙K) | Uniform | |
| U-value of the components of the thermal envelope | According to the normative assumptions for the layers of construction materials | ±10% of the calculated U-value in the normative heating demand (Qh) | A U-value is sampled for each building component of the thermal envelope (total: 68 for each simulation) | |
| ψ value of the thermal bridges | According to the normative assumptions for the ψ value between building components | ±10% of the calculated ψ value in the normative heating demand (Qh) | A ψ value is sampled for each thermal bridge (total: 7 for each simulation) | |
| Mean air flow | 2400 m3/h | - | - | |
| Infiltration rate | 0.15 m3/(h. m2ERA) | - | ||
| Efficiency of the heat recovery | 80% | - | - | |
| Others parameters 1 (normative and measured values) | Electricity consumption (other domestic uses excluding DHW) | 100 MJ/(m2ERA.an) | Average monthly real electricity consumption | - |
| External temperature | Normative weather station (Payerne, Switzerland) | Local weather station (Gland, Switzerland) | ||
| Solar irradiation | Normative weather station (Payerne, Switzerland) | Local weather station (Gland, Switzerland) | ||
| Internal temperature | Monthly average temperatures in each flat of the building taken from the smart meters | Average monthly real internal temperature | ||
| 2014 | 2015 | 2016 | 2017 | ||
|---|---|---|---|---|---|
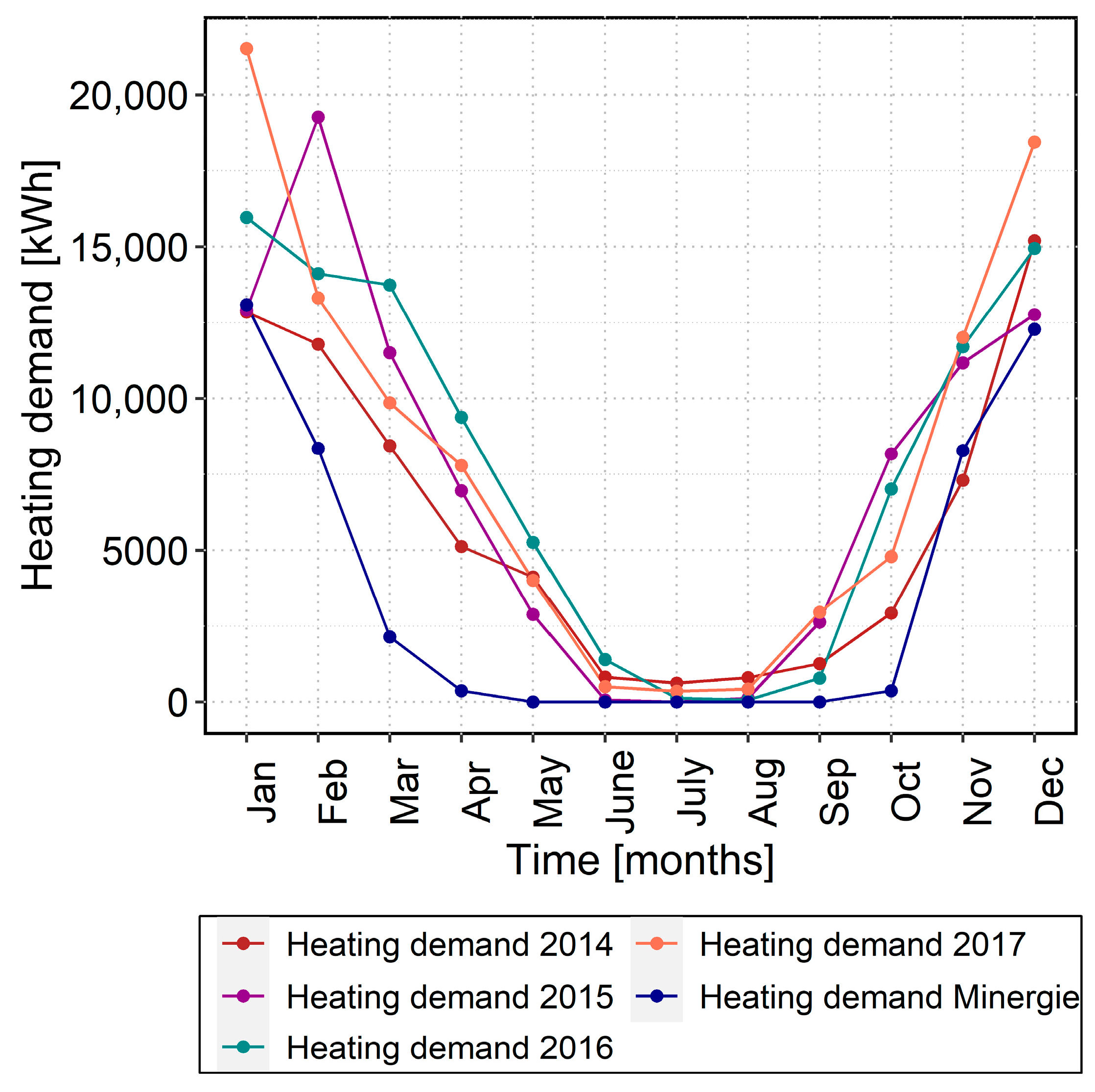
| Deterministic normative heating demand (Qh) according to the Minergie® label | [kWhuseful] | 44,899 | 44,899 | 44,899 | 44,899 |
| Measured heating demand (Qh) | [kWhuseful] | 71,273 | 88,477 | 94,509 | 95,999 |
| Relative difference between the deterministic and the measured heating demand | [%] | +59 | +97 | +111 | +114 |
| Measurements | Normative Values (SIA 380/1) | |
|---|---|---|
| External temperature | Climate data of the station in Gland, close to the building. | Default climate data: station of Payerne |
| Internal temperature | Mean temperature of the apartments (during the heating season): 21–23 °C | 20 °C |
| Electricity consumption | 23 kWh/m2 ERA sd = 1.10 kWh/m2 ERA | 27.8 kWh/m2 ERA |
| Energy signature | 1.67 kW/K | 1.55 kW/K |
| Measured Parameters Integrated in the Energy Simulation | 2014 | 2015 | 2016 | 2017 | |
|---|---|---|---|---|---|
| Real climate data | [%] | +227 | +239 | +250 | +213 |
| Real climate data + measured indoor temperature | [%] | +158 | +159 | +136 | +146 |
| Real climate data + measured indoor temperature + electricity consumption | [%] | +104 | +116 | +96 | +112 |
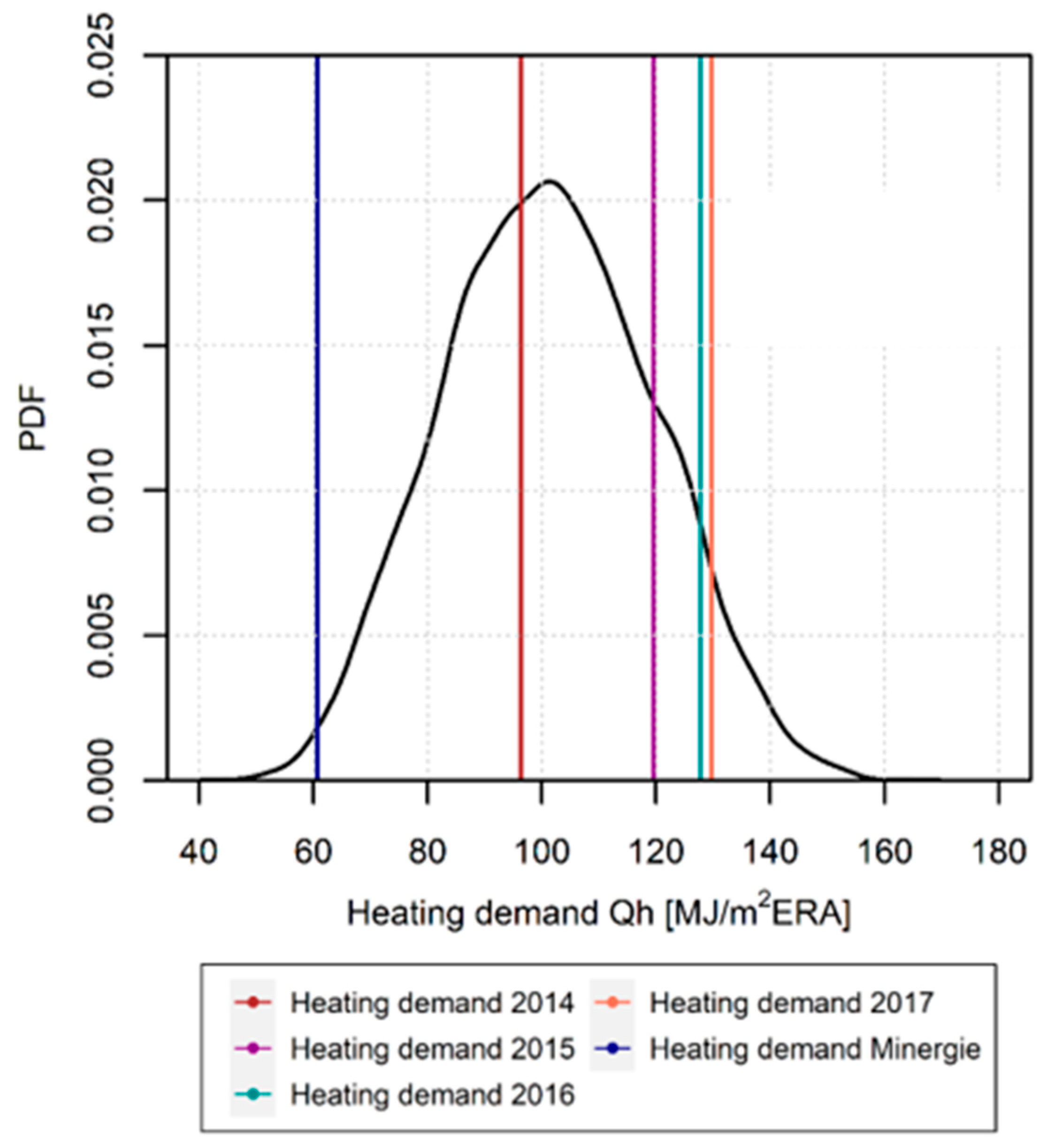
| 2014 | 2015 | 2016 | 2017 | |
|---|---|---|---|---|
| Energy performance gap between measurements and the mean value of the probabilistic Qh [%] | +5% | +18% | +26% | +28% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Padey, P.; Goulouti, K.; Wagner, G.; Périsset, B.; Lasvaux, S. Understanding the Reasons behind the Energy Performance Gap of an Energy-Efficient Building, through a Probabilistic Approach and On-Site Measurements. Energies 2021, 14, 6178. https://doi.org/10.3390/en14196178
Padey P, Goulouti K, Wagner G, Périsset B, Lasvaux S. Understanding the Reasons behind the Energy Performance Gap of an Energy-Efficient Building, through a Probabilistic Approach and On-Site Measurements. Energies. 2021; 14(19):6178. https://doi.org/10.3390/en14196178
Chicago/Turabian StylePadey, Pierryves, Kyriaki Goulouti, Guy Wagner, Blaise Périsset, and Sébastien Lasvaux. 2021. "Understanding the Reasons behind the Energy Performance Gap of an Energy-Efficient Building, through a Probabilistic Approach and On-Site Measurements" Energies 14, no. 19: 6178. https://doi.org/10.3390/en14196178
APA StylePadey, P., Goulouti, K., Wagner, G., Périsset, B., & Lasvaux, S. (2021). Understanding the Reasons behind the Energy Performance Gap of an Energy-Efficient Building, through a Probabilistic Approach and On-Site Measurements. Energies, 14(19), 6178. https://doi.org/10.3390/en14196178





