Abstract
Uncertainty quantification in LIB manufacturing has received interest in order to improve the reliability of LIB. The uncertainty generated during the manufacturing causes variations in the performance of LIBs, thereby increasing capacity degradation and leading to failure. In this study, a reliability-based design optimization (RBDO) of LIBs is conducted to reduce performance failure while maximizing the specific energy. The design variables with uncertainty are the thickness, porosity, and particle size of the anode and cathode. The specific energy is defined as the objective function in the optimization design problem. To maintain the specific power in the initial design of the LIB, it is defined as the constraint function. Reliability is evaluated as the probability that the battery satisfies the performance of the required design. The results indicate that the design optimized through RBDO increases the specific energy by 42.4% in comparison with that of the initial design while reducing the failure rate to 1.53%. Unlike the conventional deterministic design optimization method (DDO), which exhibits 55.09% reliability, the proposed RBDO method ensures 98.47% reliability. It is shown that the proposed RBDO approach is an effective design method to reduce the failure rate while maximizing the specific energy.
1. Introduction
Strict reinforcement of environmental regulations has increased the use of lithium-ion batteries (LIBs), which can be charged and discharged conveniently, as energy storage devices for eco-friendly electric vehicles [1,2]. LIB is an energy storage device that converts chemical energy directly into electrical energy and exhibits several advantages, such as high energy, power, voltage, and long lifespan. Although it is essential to develop a new material to increase the energy and power of LIB, another effective method is optimizing the design variables of currently used LIB cells. Several studies have been conducted to improve the energy and power of LIBs through the optimization of design variables [3,4,5,6]. However, the effect of manufacturing uncertainty on battery performance is not considered thus far. As manufacturing uncertainty may cause variation in the performance of LIBs and affect the safety of battery packs [7,8,9], manufacturing uncertainty must be considered during the design process.
LIBs have been optimized using numerical analysis to improve the performance by applying design variables as deterministic values. The numerical model for the LIB was developed by Newman and Doyle as a mathematical modeling method for chemical reactions during charging and discharging [10,11,12]. Kim et al. optimized the particle size, porosity, and thickness to maximize the energy density using the Newman model. Additionally, the design variables of the cathode, anode, and separator were used to increase the specific energy by 60% while maintaining the specific power density of the initial design [3]. Xue et al. conducted a study to maximize the specific energy of LIBs using 12 design variables, such as C-rates, diffusivity, conductivity, thickness, particle size, and porosity. Optimization was performed using a gradient-based algorithm to maximize the specific energy, wherein the results verified that the positive particle size and separator thickness must be maintained low, and the diffusivities and conductivities should be high [4]. Liu and Liu performed multi-objective design optimization using design variables of porosity, thickness, particle size, and conductivity of an LIB to maximize the specific energy and specific power and minimize the capacity reduction caused by charging and discharging. The genetic algorithm was used to improve the LIB capacity [5]. Kim et al. determined the design factor affecting the specific energy using design variables of the cathode, anode, and separator of an LIB based on the design of experiment and analysis of variation methods. They reported an increase of 56.8% in the specific energy using the progressive quadratic response surface method for the design variables of electrode porosity and thickness [6]. However, these studies on optimization do not consider manufacturing uncertainties that affect the performance variation and cause the failure of LIBs.
Distribution of design variables due to manufacturing uncertainty affects variations in the performance of LIBs [13,14,15]. Schmidt et al. confirmed that the distribution of design variables is caused by the manufacturing uncertainty through simulations of the electrode manufacturing system. Additionally, the distribution of electrode thickness and porosity can fluctuate the specific energy of LIBs [13]. Santhanagopalan and White applied particle size distribution to a numerical modeling of electrochemical and analyzed the effect of distribution of design variables on the performance of LIBs. They confirmed that the distribution of particle size causes voltage variation during battery discharge [14]. DuBeshter et al. measured the porosity and tortuosity of the electrodes made of the same material. Furthermore, the distribution of porosity affected the lithium-ion transport during the chemical reaction of LIBs [15]. These studies reported that distribution of design variables caused by manufacturing uncertainty induces variations in the performance of LIBs that can lead to performance failure.
The capacity variation of LIBs reduces the life and safety of the battery pack and increase the risk of failures [16,17,18]. Baumhöfer et al. performed an experiment, wherein 48 identical LIBs were charged and discharged over 1800 cycles. They reported that the capacity and lifespan variations existed even in mass production lines for LIBs. As the number of charging and discharging cycles increases, the lifespan and capacity variation of LIBs increased [16]. Harris et al. used 24 commercial LIBs and statistically analyzed the capacity reduction in an experiment with 600 cycles of charging and discharging. They reported that the distribution of capacity becomes very wide as the battery is used and proposed that a method for evaluating the failure based on capacity [17]. Shin et al. used the LIB equivalent circuit model and verified that the capacity variation between cells reduces the capacity of the battery pack. They determined that assembling the modules by minimizing the capacity variation between modules during the manufacturing of a battery pack can increase the capacity of the pack [18]. These studies reported that the distribution of design variables causes variations in the performance of LIBs by reducing the capacity, lifespan, and reliability of battery packs. Thus, reducing the failure rate by considering the distribution of design variables that occur owing to manufacturing uncertainties in the design process of LIBs must be investigated.
To reduce the failure rate, process control may reduce the impact of manufacturing uncertainty and solve the failure problem of LIBs. Mohanty et al. measured the magnitude of the deviation caused by the manufacturing uncertainty of the electrode using a laser displacement sensor. They reported that the distribution of design variables was caused by manufacturing uncertainty, and the quality control method can reduce the failure rate of the product [19]. However, although process control can reduce the impact of manufacturing uncertainty, it cannot be eliminated completely [20].
Design methods that consider the manufacturing uncertainty can also reduce the failure rate. The reliability-based design optimization (RBDO) is used in engineering design to find the optimal solution and methodology that consider the distribution of design variables. Typically, RBDO is performed with probabilistic constraints for each iteration to determine an optimal solution. It has been used as an optimization method in various engineering fields, wherein design processes with uncertainties exist [21,22,23,24,25]. However, it has not been applied to LIB design yet. The studies of LIB have so far not considered the uncertainty caused by manufacturing uncertainty in the process. Furthermore, the effect of manufacturing uncertainty on battery performance is not considered. Applying the RBDO method to the LIB improves the performance and reduces the performance failure. The RBDO is highly efficient optimization method because it reduces the variability of the performance.
In this paper, the RBDO is proposed to maximize the specific energy of LIBs while reducing the failure rate based on the distribution of design variables caused by the manufacturing uncertainty of LIBs. The specific energy and specific power were calculated by using LIB electrochemical model. Maximizing the specific energy is defined as the objective function in the optimization design problem. The design variables are the thickness, porosity, and particle size of the anode and cathode. The probability distribution was applied to design variables due to manufacturing uncertainty. To maintain the specific power of the initial design, the constraint function is the specific power. The failure rate is evaluated as the probability that the battery satisfies the performance of the required design in the reliability analysis. In addition, the failure is the probability that the performance of the required design is not satisfied. The reliability of the proposed RBDO method is compared with the reliability of the deterministic design optimization (DDO). It is shown that the proposed RBDO approach is an effective design method to maximize the specific energy while lowering the failure rate.
2. Electrochemical Model-Based on Manufacturing Uncertainty
2.1. Electrochemical Model for LIBs
The LIB is a sandwich structure composed of a porous anode, a porous cathode, and a separator. Figure 1 depicts the LIB comprising a current collector, an electrode, and a separator. The pseudo-two-dimensional (P2D) model was used as the numerical modeling of electrochemical. The P2D model developed by Newman and Doyle as a numerical model for LIBs combines the porous electrode theory and concentrated solution theory [10,11,12]. Equations (1)–(5) represent the governing equations for approximating the electrochemical reaction in the model. Equations (1) indicate the electronic charge balance in the electrode where is solid-phase electrical potential. Equation (2) indicates the ionic charge balance in the electrolyte where is the average molar activity coefficient and is the electronic conductivity. Equation (3) denotes Fick’s second law, which defines the diffusion of lithium in the active material where is the lithium concentration of solid-phase and is radial distance from the center of active particle. Equation (4) represents the ionic charge transport of lithium ions in the electrolyte where is the effective diffusivity of the liquid-phase and is the porosity of the electrolyte. Equation (5) indicates the reaction kinetics defined by Li+ flux and the Butler–Volmer equation on the surface of the active material where is the exchange current density and is local surface overpotential.
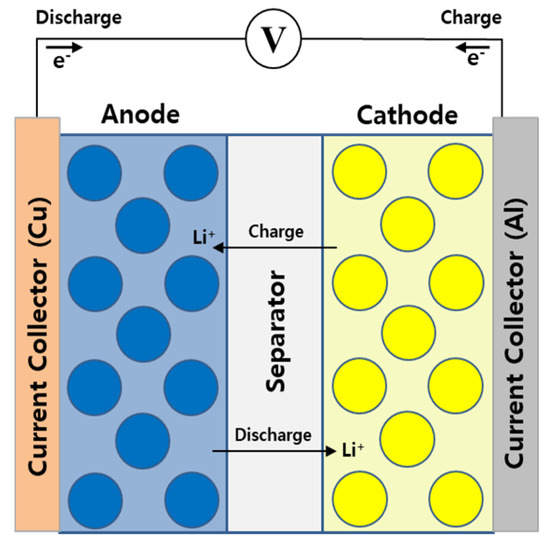
Figure 1.
Schematic of the Li-ion battery.
These equations calculate the electrochemical reactions of lithium-ion battery. In the diffusion mechanism of lithium ion, lithium is ionized through an electrochemical reaction during the charge and discharge of LIB and transferred from anode to cathode through electrolyte. This occurs due to the difference in concentration and transfer of charges generated by ionization of lithium. The lithium-ion concentration in the cathode gradually increases through the transfer of lithium ion. The energy and power performance of the LIB in charging and discharging can be accurately predicted through the governing equations.
In this study, a graphite/LMO pouch-type LIB was used, and the parameters of a previous study [11] served as the design variables of the LIB. Figure 2 illustrates that the predicted battery capacity based on the P2D model, and the actual battery capacity are identical. The LIB is discharged from 4.2 V to a cut-off voltage of 3 V. Equation (6) indicates the mass of LIB as the sum of the separator, electrode, and current collector. The mass of LIB is calculated by multiplying the volume of the separator, cathode, anode, and electrolyte by the density. Equations (7) and (8) represent the specific power and specific energy of the LIB, respectively, in terms of current, voltage, discharge time, and mass. Table 1 presents the specific energy and specific power of initial design when the LIB is discharged at a 1C rate. The current density of the 1C rate was 25 A/m2.
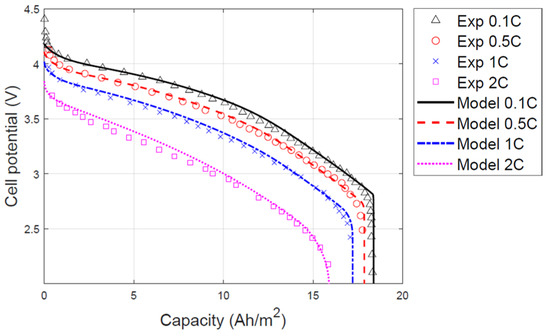
Figure 2.
Comparison of simulation results of working voltage and experimental data during different discharge rates [12].

Table 1.
Properties and performance of lithium-ion batteries in the initial design.
2.2. Manufacturing Uncertainties of LIBs
The cathode and anode are materials that determine the performance of LIBs, and both are manufactured through coating and calendaring processes. During manufacturing, uncertainty exists in each process owing to the tolerance in the accuracy and precision of manufacturing facility. The tolerance that occurs in the continuous process causes the distribution of design variables, which in turn results in variations in the performance of LIB. As the battery system expands in units of modules and packs, the variation in performance of LIBs caused by the uncertainty in the manufacturing process degrades the capacity, lifespan, and safety [18].
Manufacturing uncertainty that causes variations in performance of LIBs can be expressed using a probability density function (PDF), which represents the probability that a random variable exists in the probability space. Equation (9) indicates a Gaussian distribution, which is a type of PDF, where μ and σ denote the mean and standard deviation, respectively. The Gaussian distribution represents a random variable using the mean and standard deviation. Figure 3 depicts the random uncertainty in design variables using the Gaussian distribution.
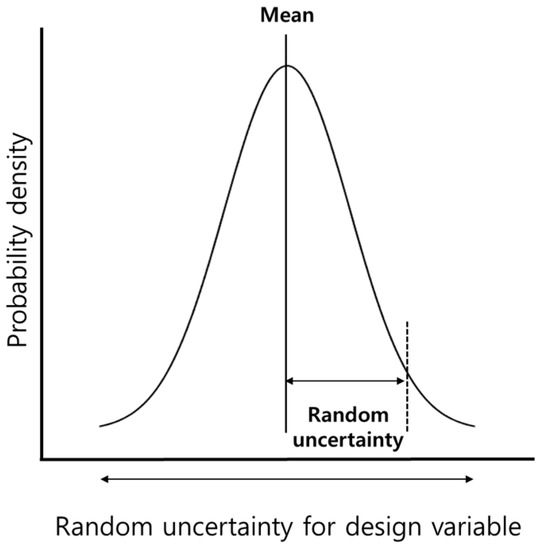
Figure 3.
Random uncertainty in design variables.
3. Reliability-Based Design Optimization of LIB
3.1. Reliability Analysis
Reliability analysis is required in the RBDO because the probability of failure is applied as the constraint function. Reliability is evaluated as the probability that the battery satisfies the performance of the required design under various sources of uncertainty. Reliability analysis evaluates the probability of the performance not satisfying the constraint function, which represents the probability of failure. Equation (10) can be used to calculate the reliability R, where g(xi) and f(xi) represent the constraint function and PDF of the design variable (xi), respectively. When g(xi) < 0, the performance of the system satisfies the constraint function, and g(xi) ≥ 0 implies that the system performance does not satisfy the constraint function. Reliability analysis aims to determine the probability of system failure occurrence. The probability of failure is defined as the event when g(xi) ≥ 0. As it is difficult to calculate the integral in Equation (10) analytically, the Monte Carlo simulation is used to calculate an approximation of R [26,27]. Equations (11) and (12) are used to calculate the mean and standard deviation of the specific energy and specific power in the system, respectively.
3.2. Design Variables
The coating and calendaring processes that manufacture electrodes are essential in determining the performance of LIBs [13]. The electrodes of a lithium-ion battery determine the quantity and speed of lithium storage, directly affecting the capacity, the specific power, and the specific energy of the battery. In the coating process, a slurry of a certain thickness is coated on the substrate function as the positive electrode and the negative electrode. In the subsequent calendaring process, heat is applied to compress the slurry and manufacture the electrode with a uniform density and thickness. Manufacturing uncertainty may result in the distribution of design variables rather than a constant value within a probability distribution. Distribution of design variables that occur during the manufacturing process make variation the electrode thickness, porosity, and particle size. The particle size, porosity, and thickness have high impact on the specific energy and are highly dependent on the manufacturing process [13,28].
The design variables with uncertainty are defined for the cathode and anode in terms of particle size, porosity, and thickness. Table 2 summarizes the design space and standard deviation of all design variables [14,15,19]. The anode particle size ranges from 5 μm to 50 μm, whereas the cathode particle size ranges from 2 μm to 20 μm. The porosity and thickness range from 0.2 to 0.6 and 40 μm to 250 μm, respectively, for both the cathode and anode.

Table 2.
Probabilistic distribution of design variables [14,15,19].
3.3. Formulation of Reliability-Base Desgin Optimization (RBDO)
Several studies on optimizing the design variables of LIBs were conducted using deterministic design optimization (DDO) [9,10,11,12], which is conventional optimization method that maximizes or minimizes the objective function while satisfying the constraint function. The DDO method involves applying a safety factor to consider the design variables with uncertainty. However, as the safety factor relies on the experience of the engineer, the product may be overdesigned with poor reliability. Figure 4 illustrates the difference between the RBDO and DDO methods. The RBDO method, which considers the probability, identifies a solution that minimizes or maximize the objective function while satisfying the target reliability for the performance of the system based on the design variables with uncertainty. Conversely, the DDO cannot consider the uncertainty of the design variables, resulting in low reliability.
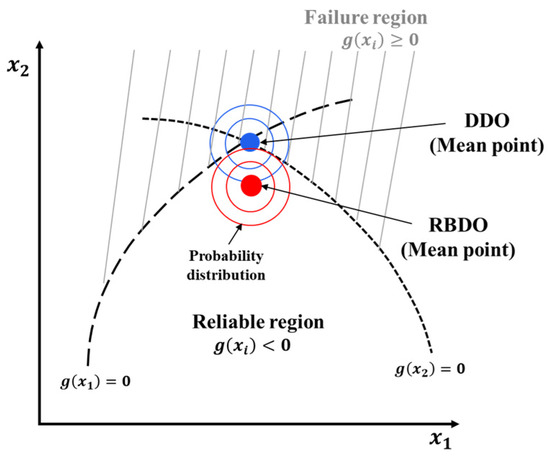
Figure 4.
Schematic comparison between the reliability-based design optimization (RBDO) and deterministic design optimization (DDO).
To maximize the specific energy of the LIB by applying the RBDO, the objective function is the mean of the specific energy (μi). The design variables are the anode particle size (x1), the cathode particle size (x2), the anode porosity (x3), the cathode porosity (x4), the anode thickness (x5), and the cathode thickness (x6). Lithium-ion cells are optimized for either high specific energy or high specific power. Since the objective function is defined as specific energy, the constraint function is defined. To maintain the specific power of cell, the constraint function is defined as ±2% of 139.7 W/kg, which was the specific power of the initial model, allowing the power performance to not change even after optimization for high capacity. The target reliability that satisfies the constraint function is defined as 99%. Equation (13) represents the formulation of the RBDO problem. The system reliability optimization was used as an RBDO algorithm [29,30]. Figure 5 depicts the flowchart of the RBDO process.
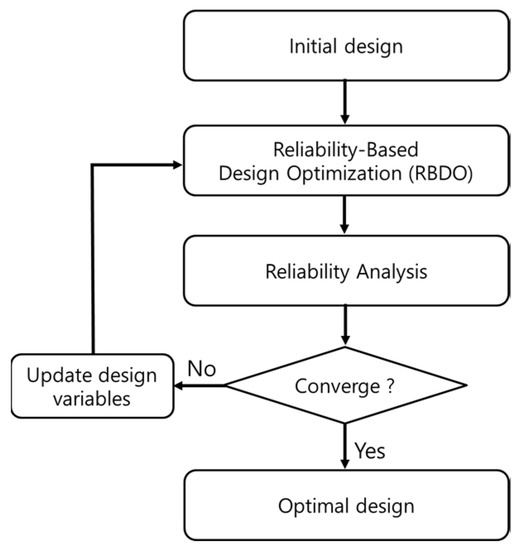
Figure 5.
Flowchart of the reliability-based design optimization process.
4. Discussion
4.1. RBDO Results
In the RBDO results, the anode and cathode particle sizes decreased from 12.5 μm to 5.17 μm and 8.5 μm to 3.05 μm, respectively. The small particle size increases the interfacial surface area of the cathode and decreases the length of the diffusion path for lithium ions, which maximize the specific energy [31]. The porosity of the anode and cathode decreased to 0.246 and 0.201, respectively, which increased the amount of active material and specific energy [32]. The anode thickness increased from 100 μm to 126 μm, whereas the cathode thickness decreased from 174 μm to 130 μm. An increase in the thickness of the electrode increases the capacity of the LIB [33]. Table 3 summarizes the initial design variables, the design variables optimized by the RBDO process, and the rate of change.

Table 3.
Comparison of design variables and probability of failure between the initial and optimized designs.
To maximize the specific energy, the particle size and porosity must converge to the lowest value in the design space [4]. However, this phenomenon was not observed in the design optimized through RBDO because the target reliability needs to be satisfied. If the particle size and porosity have the smallest values in the design space, the target reliability cannot be satisfied as the constraint function is violated when considering the design variables with uncertainty. Figure 6 illustrates the PDFs of the specific energy and specific power of the initial design and the design optimized by the RBDO process. In the optimized design, the mean of the specific power is shifted to a smaller value than that of the initial design to satisfy the constraint function.
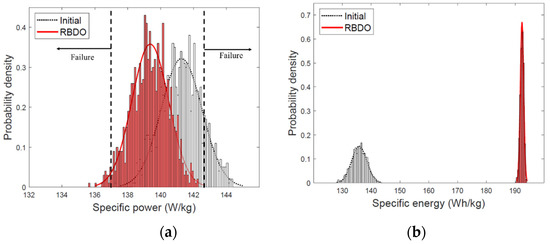
Figure 6.
Probability distribution of the initial design and design optimized through the reliability-based design optimization (RBDO) (a) specific power; (b) specific energy.
The capacity balancing of the negative electrode (NE) and positive electrode (PE) in LIBs has been considered to be a crucial point considering lifetime and safe operation of cell design. The N/P ratio is defined as the ratio of areal reversible capacity of NE and PE. The N/P ratio is generally controlled between 1.05 and 1.2 in commercial LIBs [34]. In the initial design, the cathode thickness is thicker than the anode. The changes in the thickness ratio of the anode and cathode improved the specific energy by improving the N/P ratio to 1.2. As the thickness of the anode increases and the thickness of the cathode decreases, the RBDO design balances the capacity ratio of the anode and the cathode. The lithium-ion concentration of the cathode in the optimized design increased in comparison with that of the initial design. The lithium-ion concentration in the cathode was measured when RBDO and the initial design was applied to the P2D model and discharged at a 1C rate. Figure 7 depicts the change in the lithium-ion concentration in the initial and optimized designs during discharge in solid phase of the cathode.
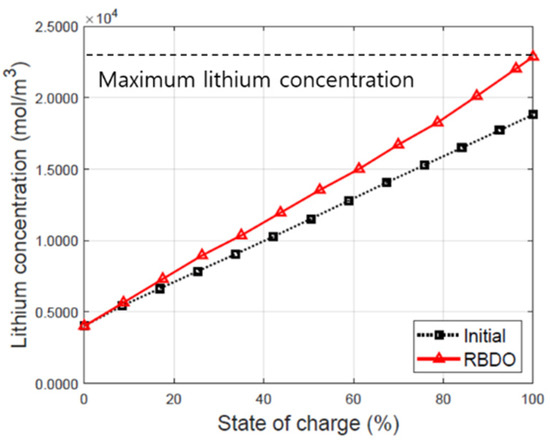
Figure 7.
Lithium concentration of the cathode in the initial and optimized designs during discharge.
The small particle size can shorten the diffusion pathway for lithium ions, which reduces the internal resistance of the LIB [35]. Therefore, it is possible to maximize the usable energy of the LIB by reducing the energy lost during charging and discharging. The hybrid pulse power characterization (HPPC) test was performed to calculate the polarization and internal resistance of the LIB [36]. The LIB was discharged and recharged at a 10C rate for 10 s after 10 s of relaxation. Figure 8 illustrates the HPPC test results of the initial and optimized designs. The internal resistance and voltage loss is measured in the solid phase of the cathode. The internal resistance was calculated by dividing the total polarization by the applied current. In the optimized design, the internal resistance decreased by 13.43% in comparison with that of the initial design.
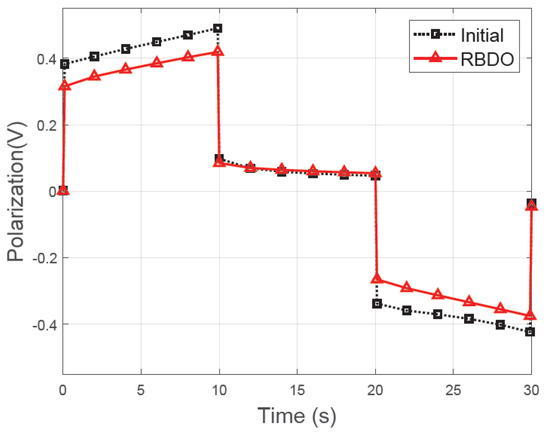
Figure 8.
Comparison of total polarization between the initial and optimized designs in the hybrid pulse power characterization (HPPC) test.
In the design optimized through RBDO, the mean and standard deviation of the specific energy are 193.39 Wh/kg and 0.5958 Wh/kg, respectively. The mean of the specific energy increased by 42.4% compared to that of the initial design. The LIB to which the RBDO and DDO designs are applied was discharged at a 1C rate until the cut-off voltage. Figure 9 illustrates that the discharge time increased by 59.8% in the optimized design owing to the increase in the specific energy. Furthermore, the mean and standard deviation of the specific power are 139.37 W/kg and 1.1142 W/kg, respectively. The mean of the specific power decreased by 1.37% in comparison with that of the initial design without violating the constraint function. Consequently, the magnitude of the deviation in both specific power and the specific energy was reduced, and the failure rate decreased to 1.53%. In summary, the design optimized through the RBDO verifies that, if 100 LIBs are produced, less than two products that do not satisfy the specific power criteria may fail. Thus, the RBDO method considering the design variables with uncertainty can effectively improve the reliability and performance of LIBs.
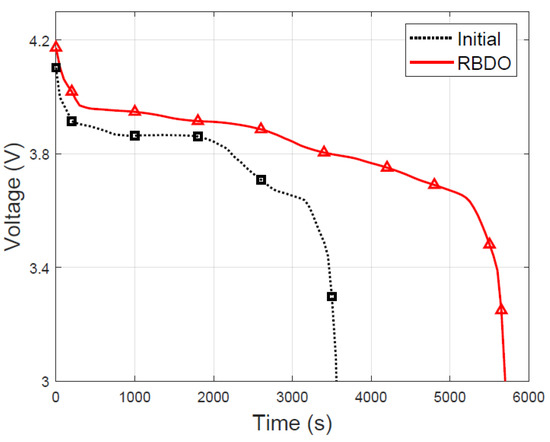
Figure 9.
Comparison of discharge voltage between the initial and optimized designs.
4.2. Comparison between RBDO and DDO Results
The DDO was performed by applying the same objective and constraint functions as those of the RBDO. Table 4 presents the formulation of the RBDO and DDO problems. The DDO considers the design variables as deterministic values in the optimization. The DDO applied the sequential quadratic programming algorithm, which is used in non-linear optimization problems with the constraint function. Table 5 summarizes the design variables used in the RBDO and DDO.

Table 4.
Formulation of the reliability-based design optimization (RBDO) and deterministic design optimization (DDO) problems.

Table 5.
Comparison of design variables and probability of failure between the reliability-based design optimization (RBDO) and deterministic design optimization (DDO).
In the design optimized through DDO, the mean and standard deviation of the specific power are 137.02 W/kg and 1.0988 W/kg, respectively; the mean and standard deviation of the specific energy are 193.58 Wh/kg and 0.5557 Wh/kg, respectively. The standard deviation of the specific energy and mean of the specific power are smaller than those of the design optimized using RBDO. Moreover, the mean of the specific energy is larger than that observed in the design optimized through RBDO. The particle size of the DDO design is smaller than the RBDO design. The small particle size improves the specific energy of LIB. However, there exists a trade-off between the specific energy and specific power. In general, the higher the specific energy, the lower would be the specific power. Figure 10 illustrates the PDFs exhibiting the specific power and specific energy of the designs optimized through RBDO and DDO methods.
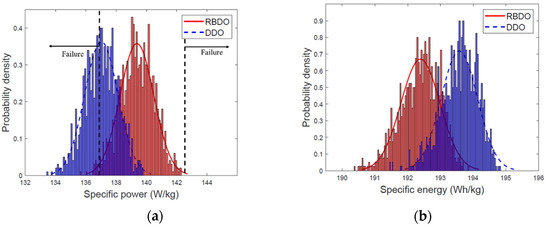
Figure 10.
Probability distributions of designs optimized through reliability-based design optimization (RBDO) and deterministic design optimization (DDO) (a) specific power; (b) specific energy.
Based on the comparison of only the mean and standard deviation of the specific energy, the DDO provides a better optimization solution than the RBDO. However, as the DDO considers the constraint function as a deterministic value, the optimization is obtained at a position close to the upper and lower bounds of the design space. Therefore, considering the design variables with uncertainty, the failure rate is nearly half. The DDO is a low-reliability optimization method owing to the high risk of product failure caused by performance variation.
To resolve this issue, the RBDO is an optimization method that considers the design variables with uncertainty. The difference between the specific power and specific energy of the RBDO and DDO is within 2%. Although the difference in performance is not large, the difference in the failure rate exceeds 40%. The RBDO method maximizes the specific energy by more than 40% in comparison with that of the initial design while lowering the failure rate to less than 2%. Figure 11 depicts the optimization convergence graph of the RBDO and DDO methods, which were able to identify the optimal solution through 21 and 23 iterations, respectively.
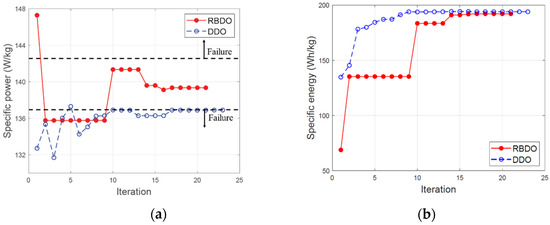
Figure 11.
Convergence histories of the reliability-based design optimization (RBDO) and deterministic design optimization (DDO) (a) specific power; (b) specific energy.
Figure 12 illustrates a graph of the specific power and specific energy for the initial designs and the designs optimized through RBDO and DDO methods. Both RBDO and DDO methods maximized the specific energy significantly in comparison with that of the initial design. Although the specific power and specific energy of the two optimization designs are similar, the difference in failure rate is significant. Several studies using the DDO for the LIB design can improve battery performance, but the DDO does not consider manufacturing uncertainties, so there is a risk of high failure rate. Therefore, when designing an LIB, the RBDO is needed to consider the manufacturing uncertainty.
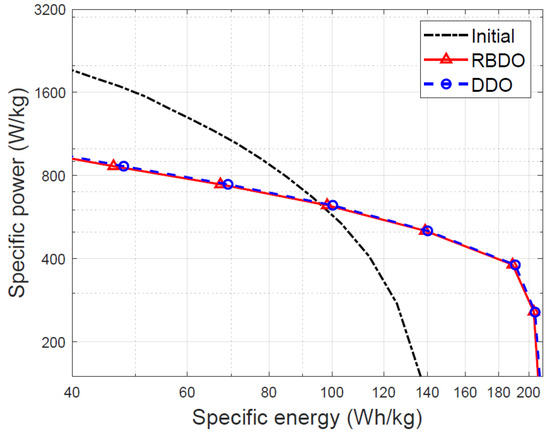
Figure 12.
The Ragone plot comparing the initial design with the designs optimized through reliability-based design optimization (RBDO) and deterministic design optimization (DDO) methods.
5. Conclusions
The uncertainty generated during the manufacturing of LIBs causes variations in the performance, thereby increasing capacity degradation and leading to failure. In this study, the reliability-based design optimization (RBDO) is conducted to reduce the performance failure while maximizing the specific energy of LIBs by considering the manufacturing uncertainty. The specific energy and specific power were evaluated by using the electrochemical model. In the formulation of the RBDO problem, the objective function is to maximize the specific energy, and the constraint function is the specific power. The design variables are defined as the thickness, porosity, and particle size of the cathode and anode. Reliability is evaluated as the probability that the battery satisfies the performance of the required design, and the failure is the probability that the performance of the required design is not satisfied. The design optimized through the RBDO increased the specific energy by 42.4% in comparison with that of the initial design while satisfying the target reliability. The mean of the specific energy conducted by the design optimized through the conventional DDO method was 193.58 Wh/kg. However, the failure rate was 44.91% in the case of DDO, which exhibits a problem of low reliability. By contrast, the mean of the specific energy in the design optimized using the RBDO was 193.39 Wh/kg, and the failure rate was reduced to 1.53%. Thus, the proposed RBDO approach can lower the performance failure while maximizing the energy capacity of LIBs by considering the uncertainties of the LIB manufacturing process. The proposed approach can be used as a cell design method in various types of battery and manufacturing environments. For example, optimization by applying the proposed RBDO process to NCM and LCO type batteries is also possible. However, to apply proposed design to commercial battery design, research is needed to quantitatively measure the uncertainty of the manufacturing process. Changes in battery performance, such as cycling safety and coulombic efficiency, caused by changes in design variables need to be considered in future studies.
Author Contributions
Conceptualization, D.Y.; investigation, D.Y. and J.P.; software, J.M.; validation, D.Y., J.P. and J.M.; methodology, C.K.; supervision, C.K.; Writing—Original draft preparation, D.Y.; Writing—Review and editing, D.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by National Research Foundation of Korea (NRF) grant funded by the Ministry of Science, ICT & Future Planning (No. 2019R1A2C1090228) and by the Technology Innovation Program (20004627) funded By the Ministry of Trade, Industry & Energy (MOTIE, Korea).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
List of Symbols
| mean of design variables | |
| deviation of design variables | |
| specific energy (Wh/kg) | |
| specific power (W/kg) | |
| mass of cell (kg) | |
| electric potential of cell | |
| discharge time | |
| design variable | |
| response at design variable | |
| mean of the response at sampling points | |
| deviation of the response at sampling points | |
| probability of reliability | |
| number of total points obtained from the metamodel | |
| probability constraint | |
| objective function | |
| constraint function | |
| ion number | |
| electrical potential (V) | |
| local surface overpotential (V) | |
| density (kg/m3) | |
| porosity | |
| significance level | |
| li concentration (mol/m3) | |
| diffusivity (m2/s) | |
| average molar activity coefficient | |
| Faraday’s constant, 96 487 (C /mol) | |
| exchange current density (A/m2) | |
| local current density (A/m2) | |
| electronic conductivity (S/m) | |
| li+ flux (mol/m2s) | |
| radial distance from the center of active particle (μm) | |
| gas constant, 8.314 (J/mol-K) | |
| transport number of Li+ | |
| absolute temperature (K) | |
| Subscripts and Superscripts | |
| applied | |
| effective value | |
| electrolyte | |
| current Collector | |
| lithium-ion battery | |
| negative electrode | |
| positive electrode | |
| separator | |
| solid phase | |
| liquid phase | |
| lower bounds | |
| upper bounds | |
References
- Curry, C. Lithium-Ion Battery Costs and Market, Bloomberg New Energy Finance 2017. Available online: https://data.bloomberglp.com/bnef/sites/14/2017/07/BNEF-Lithium-ion-battery-costs-and-market.pdf (accessed on 23 August 2021).
- Sun, X.; Hao, H.; Zhao, F.; Liu, Z. Global Lithium Flow 1994-2015: Implications for Improving Resource Efficiency and Security. Environ. Sci. Technol. 2018, 52, 2827–2834. [Google Scholar] [CrossRef]
- Kim, C.-W.; Yang, H.-I.; Lee, K.-J.; Lee, D.-C. Metamodel-Based Optimization of a Lithium-Ion Battery Cell for Maximization of Energy Density with Evolutionary Algorithm. J. Electrochem. Soc. 2019, 166, A211–A216. [Google Scholar] [CrossRef]
- Xue, N.; Du, W.; Gupta, A.; Shyy, W.; Marie Sastry, A.; Martins JR, R.A. Optimization of a Single Lithium-Ion Battery Cell with a Gradient-Based Algorithm. J. Electrochem. Soc. 2013, 160, A1071–A1078. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.; Liu, L. Optimal Design of Li-Ion Batteries through Multi-Physics Modeling and Multi-Objective Optimization. J. Electrochem. Soc. 2017, 164, E3254–E3264. [Google Scholar] [CrossRef]
- Kim, J.S.; Lee, D.C.; Lee, J.J.; Kim, C.W. Optimization for maximum specific energy density of a lithium-ion battery using progressive quadratic response surface method and design of experiments. Sci. Rep. 2020, 10, 1–11. [Google Scholar] [CrossRef]
- Omariba, Z.B.; Zhang, L.; Sun, D. Review of Battery Cell Balancing Methodologies for Optimizing Battery Pack Performance in Electric Vehicles. IEEE Access 2019, 7, 129335–129352. [Google Scholar] [CrossRef]
- Lenze, G.; Bockholt, H.; Schilcher, C.; Froböse, L.; Jansen, D.; Krewer, U.; Kwade, A. Impacts of Variations in Manufacturing Parameters on Performance of Lithium-Ion-Batteries. J. Electrochem. Soc. 2018, 165, A314–A322. [Google Scholar] [CrossRef]
- Kenney, B.; Darcovich, K.; MacNeil, D.D.; Davidson, I.J. Modelling the impact of variations in electrode manufacturing on lithium-ion battery modules. J. Electrochem. Soc. 2012, 213, 391–401. [Google Scholar] [CrossRef]
- Doyle, M.; Fuller, T.F.; Newman, J. Modeling of Galvanostatic Charge and Discharge of the Lithium/Polymer/Insertion Cell. J. Electrochem. Soc. 1993, 140, 1526–1533. [Google Scholar] [CrossRef]
- Doyle, M.; Newman, J.; Gozdz, A.S.; Schmutz, C.N.; Tarascon, J. Comparison of Modeling Predictions with Experimental Data from Plastic Lithium-Ion Cells. J. Electrochem. Soc. 1996, 143, 1890–1903. [Google Scholar] [CrossRef]
- Doyle, M. Design and Simulation of Lithium Rechargeable Batteries. Ph.D. Dissertation, University of California, Berkeley, CA, USA, 1 August 1995. [Google Scholar]
- Schmidt, O.; Thomitzek, M.; Röder, F.; Thiede, S.; Herrmann, C.; Krewer, U. Modeling the Impact of Manufacturing Uncertainties on Lithium-Ion Batteries. J. Electrochem. Soc. 2020, 167, 060501. [Google Scholar] [CrossRef]
- DuBeshter, T.; Sinha, P.K.; Sakars, A.; Fly, G.W.; Jorne, J. Measurement of Tortuosity and Porosity of Porous Battery Electrodes. J. Electrochem. Soc. 2014, 161, A599–A605. [Google Scholar] [CrossRef]
- Santhanagopalan, S.; White, R.E. Modeling Parametric Uncertainty Using Polynomial Chaos Theory. ECS Trans. 2019, 3, 243–256. [Google Scholar] [CrossRef]
- Baumhöfer, T.; Brühl, M.; Rothgang, S.; Sauer, D.U. Production caused variation in capacity aging trend and correlation to initial cell performance. J. Power Sources 2014, 247, 332–338. [Google Scholar] [CrossRef]
- Harris, S.J.; Harris, D.J.; Li, C. Failure statistics for commercial lithium-ion batteries: A study of 24 pouch cells. J. Power Sources 2017, 342, 589–597. [Google Scholar] [CrossRef] [Green Version]
- Shin, D.; Poncino, M.; Macii, E.; Chang, N. A statistical model-based cell-to-cell variability management of Li-ion battery pack. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2015, 34, 252–265. [Google Scholar] [CrossRef]
- Mohanty, D.; Li, J.; Born, R.; Maxey, L.C.; Dinwiddie, R.B.; Daniel, C.; Wood, D.L. Non-destructive evaluation of slot-die-coated lithium secondary battery electrodes by in-line laser caliper and IR thermography methods. Anal. Methods 2014, 6, 674–683. [Google Scholar] [CrossRef]
- Oliveira, L.; Pinho De Sousa, J.; Claro, J. Dealing with uncertainty in modern supply chains: Vulnerability and risk management. In Proceedings of the 24th Anual Production and Operations Management Conference, Denver, CO, USA, 3–6 May 2013. [Google Scholar]
- Li, H.; Cho, H.; Sugiyama, H.; Choi, K.K.; Gaul, N.J. Reliability-based design optimization of wind turbine drivetrain with integrated multibody gear dynamics simulation considering wind load uncertainty. Struct. Multidiscip. Optim. 2017, 56, 183–201. [Google Scholar] [CrossRef]
- Lee, Y.S.; Choi, B.L.; Lee, J.H.; Kim, S.Y.; Han, S. Reliability-based design optimization of monopile transition piece for offshore wind turbine system. Renew. Energy 2014, 71, 729–741. [Google Scholar] [CrossRef]
- Song, X.; Sun, G.; Li, Q. Sensitivity analysis and reliability-based design optimization for high-strength steel tailor welded thin-walled structures under crashworthiness. Thin-Walled Struct. 2016, 109, 132–142. [Google Scholar] [CrossRef]
- Hu, W.; Choi, K.K.; Cho, H. Reliability-based design optimization of wind turbine blades for fatigue life under dynamic wind load uncertainty. Struct. Multidiscip. Optim. 2016, 54, 953–970. [Google Scholar] [CrossRef]
- Wang, Z.; Almeida JH, S.; St-Pierre, L.; Wang, Z.; Castro SG, P. Reliability-based buckling optimization with an accelerated Kriging metamodel for filament-wound variable angle tow composite cylinders. Compos. Struct. 2020, 254, 112821. [Google Scholar] [CrossRef]
- Landau, D.P.; Binder, K. A Guide to Monte Carlo Simulations in Statisticalphysics, 2nd ed.; Cambridge University Press: New York, NY, USA, 2005. [Google Scholar]
- Helton, J.C.; Johnson, J.D.; Sallaberry, C.J.; Storlie, C.B. Survey of sampling-based methods for uncertainty and sensitivity analysis. Reliab. Eng. Syst. Saf. 2006, 91, 1175–1209. [Google Scholar] [CrossRef] [Green Version]
- Hadigol, M.; Maute, K.; Doostan, A. On uncertainty quantification of lithium-ion batteries: Application to an LiC6/LiCoO2 cell. J. Power Sources 2015, 300, 507–524. [Google Scholar] [CrossRef] [Green Version]
- Khorshidi, H.A.; Gunawan, I.; Ibrahim, M.Y. Investigation on system reliability optimization based on classification of criteria. In Proceedings of the IEEE International Conference on Industrial Technology (ICIT), Cape Town, South Africa, 25−28 February 2013; pp. 1706–1711. [Google Scholar]
- PIAnO Introduction. Available online: http://pidotech.com/en/product/piano.aspx (accessed on 22 September 2021).
- Drezen, T.; Kwon, N.H.; Bowen, P.; Teerlinck, I.; Isono, M.; Exnar, I. Effect of particle size on LiMnPO4 cathodes. J. Power Sources 2007, 174, 949–953. [Google Scholar] [CrossRef]
- Heubner, C.; Nickol, A.; Seeba, J.; Reuber, S.; Junker, N.; Wolter, M.; Schneider, M.; Michaelis, A. Understanding thickness and porosity effects on the electrochemical performance of LiNi0.6Co0.2Mn0.2O2-based cathodes for high energy Li-ion batteries. J. Power Sources 2019, 419, 119–126. [Google Scholar] [CrossRef]
- Zhao, R.; Liu, J.; Gu, J. The effects of electrode thickness on the electrochemical and thermal characteristics of lithium-ion battery. Appl. Energy 2015, 139, 220–229. [Google Scholar] [CrossRef]
- Wu, X.; Song, K.; Zhang, X.; Hu, N.; Li, L.; Li, W.; Zhang, L.; Zhang, H. Safety issues in lithium-ion batteries: Materials and cell design. Front. Energy Res. 2019, 7, 65. [Google Scholar] [CrossRef] [Green Version]
- Bischoff, C.; Fitz, O.; Schiller, C.; Gentischer, H.; Biro, D.; Henning, H. Investigating the Impact of Particle Size on the Performance and Internal Resistance of Aqueous Zinc Ion Batteries with a Manganese Sesquioxide Cathode. Batteries 2018, 3, 44. [Google Scholar] [CrossRef] [Green Version]
- Belt, J.R. Battery Test Manual for Plug-In Hybrid Electric Vehicles; Idaho National Engineering & Environmental Laboratory: Idaho Falls, ID, USA, 2010. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).