1. Introduction
A power system (PS) is considered an intricate structure that interconnects multiple networks of varying loads. In modern, large-scale interconnected PSs (IPS), automatic generation control (AGC) plays a critical role in delivering quality electrical power to customers with a reasonable degree of system protection. Sudden load requirements cause imbalance in generation and demand of interconnected areas, which is responsible for frequency deviation from their nominal values. These frequency variations due to load fluctuations can often lead to a complete blackout of the PS. To prevent such a scenario, AGC tries to sustain the system frequency and the inter area tie-line power flows very close to the nominal values using a control strategy sufficient to cope with these sudden load requirements [
1,
2]. Recently, the necessity for inexpensive energy storage device technologies raised in recent years due to the increased residential and commercial electrical demand. Therefore, Super Capacitors (SCs) are considered as the most effective sort of energy storage devices because of their widespread use in portable electronics, telecommunications, backup power systems, and transportation [
3,
4,
5].
Various control methods are employed in the AGC configuration to attain better dynamic efficiency. Among the different types of AGC controllers, simple traditional controllers are most frequently used in the industry due to their simpler structure, easy implementation, low cost, and strong design [
6]. In the AGC PS analysis, the proportional integral derivative (PID) controller and its various modified forms are mostly used in [
7]. The authors of [
8] used an Integral-Proportional Derivative controller (I-PD) controller for AGC of two area IPS with multi-generation units and they show its superiority over PID and PI controllers. The authors of [
9] used PID with a double derivative controller for an AGC system, comparing its output to that of I/PI/PID controllers. Additionally, traditional controllers are not guaranteed to have the superior transient response under realistically limited conditions, such as GRC, GDZ, TD, and BD. The basic approaches of conventional controllers are not successful in accomplishing good dynamic output considering a large variation in step load magnitude. Further, various research works focused on AGC employing Artificial Neural Network (ANN) and Fuzzy Logic Controller (FLC) [
10]. The FLC-based AGC system relies on choice of rule base, membership feature selection, scaling factor, and method of defuzzification to better optimize the outputs of the system, compared with traditional controllers. However, FLC and ANN require considerable computational time to analyze and train the database.
Non-integer or fractional-order controller (FOC) are now gaining attention in AGC systems due to its added versatility, disturbance rejection ability, and design methodology [
11]. Similarly, the AGC system response is improved using a FO controller with a Fuzzy system [
12]. The tilt integral derivative (TID) controller has a structure similar to that of a PID controller with a proportional gain in non-integer power. The authors of [
13] demonstrated the efficacy of the TID controller on the system performance in respect of improved disturbance rejection capability, precise tuning, robustness, and minimization of parameter uncertainties, compared to the PID controller. In [
14], the authors used a TID controller with derivative filter for AGC of two-area IPS considering GRC and GDB nonlinearities. The authors of [
15] employed a modified form of TID controller for LFC of IPS and compared the performance of the proposed controller with TID and PID controllers. In [
16], the authors used a fuzzy-based TIDF controller for AGC of two area IPS with multi-generation units. The literature study states that FO with I-TD controller is not employed for AGC system. Therefore, this study proposes FO with I-TD controller for the enhanced operation of AGC system.
Meta-heuristic algorithm for optimizing PS problems has gained remarkable attention in the field of engineering over the last couple of decades. For instance, a fractional-order PID controller [
17] used Differential Evolution (DE) for a three-area single-source reheat-thermal unit of the LFC problem considering various constraints, such as BD, GRC, and GDZ. In [
18], the authors proposed a salp swarm-based PID controller for LFC of two area IPS incorporating communication delay (CD), GDB, and GDZ as a nonlinear constrained. The authors of [
19] proposed a cascaded-based fuzzy fractional-order integral-derivative filter (CF-FOIDF) tuned with Imperialist Competitive Algorithm (ICA), considering the effect of electric vehicles on LFC of multi-area hydrothermal- and thermal-connected PS. Other heuristic computational methods were also employed to solve the AGC problem for interconnected power areas, such as PID controller tuned with Symbiotic Organism Search (SOS) [
20], Improved Fitness-Dependent Optimizer (I-FDO)-based FO PID controller [
21], Improved Ant Colony Optimization (IACO)-based fuzzy PID controller [
22], fuzzy-based DE optimized PID controller [
23], Improved PSO (IPSO)-based optimized TID and FOPID controller [
24], Grey Wolf Optimizer tuned with fuzzy PID controller [
25], FO type-2 fuzzy-based PID controller optimized with Improved Grey Wolf Optimization (IGWO) algorithm [
26], FO controller optimized with Volleyball Premier League (VPL) [
27], Hybrid DE with SSA-based two-degree-of-freedom (2DOF) TID controller [
28], PSO hybrid with Gravitational Search Algorithm (GSA) [
29], I-TD controller optimized with Water Cycle Algorithm (WCA) [
30], Path Finder Algorithm (FPA)-based FOTID controller [
31], hybrid improved TLBO with DE algorithm-based (hITLBO-DE) cascaded PID controller [
32], PI controller optimized with a hybrid chemical reaction (HCR)-based PSO [
33], and backtracking search algorithm (BSA)-based PI controller [
34].
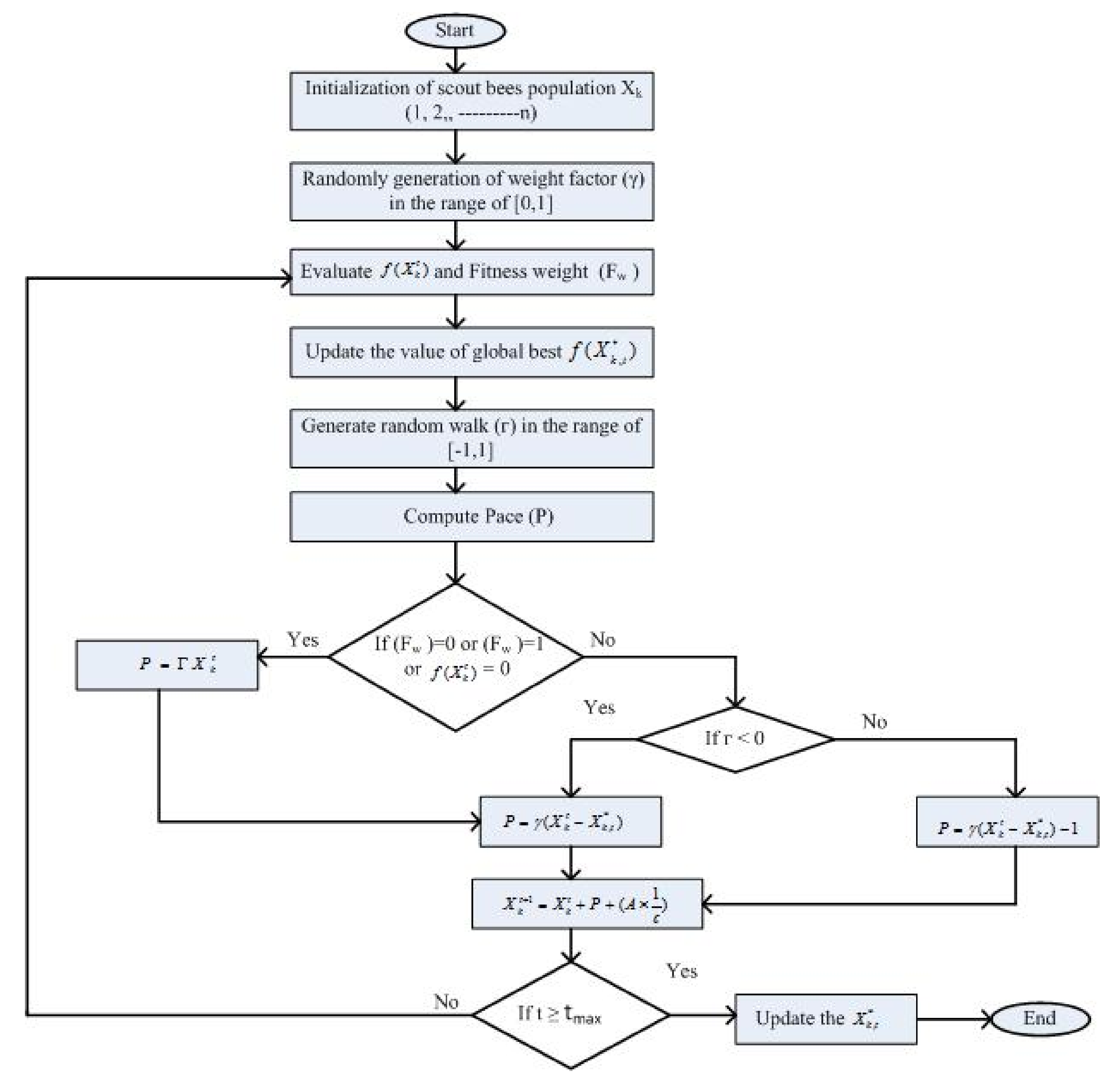
In view of the omnipresent problems of high dimensionality, diversity, and multi-modality, it is still a very difficult and crucial challenge to attain the global maxima of optimization problem efficiently and effectively. Recently, an improved version of FDO method has been employed to effectively solve the AGC problem. A FDO algorithm has been suggested based on swarming behavior of bees comprised of queen bees, scout bees, and worker bees. Whereas queen bees are responsible for reproduction and decision-making, scout bees explore the surroundings and exploit the suitable target, while worker bees work under the supervision of queen bees. The advantages of the I-FDO algorithm are rapid convergence, easy implementation and modification due to few parameters, greater performance, possibility of finding optimal, and effective exploration and extraction globally.
By properly constructing the control structure and implementing intelligent optimization approaches, the performance of AGC can be improved. As a result, for a multigeneration two-field AGC issue with numerous nonlinearities, such as BD, GRC, GDZ, and TD, a novel and unique modified FOTID controller denoted as FOI-TD controller is proposed in this paper. The gains of the proposed controller are optimized via developed improved-FDO. To show the efficacy of the proposed I-FDO algorithm, this study also compares the performance of the proposed method with benchmark approaches, such as FDO, PSO, and TLBO. Further, the FOI-TD controller’s efficiency is compared with benchmark controllers, namely, FOTID, PID, and I-TD. Additionally, the FOI-TD controller’s resilience is tested by altering the AGC’s parameters over a range of  ± 50%. The nomenclature is represented in
Table 1.
This paper is organized as follows.
Section 2 presents the PS model, while
Section 3 describes the formulation of the objective function and controller configuration.
Section 4 describes the optimization techniques accompanied by the I-FDO and FDO algorithms.
Section 5 presents the implementation and results of the proposed approach. Finally, concluding remarks and future directions are included in
Section 6.
2. Power System Model
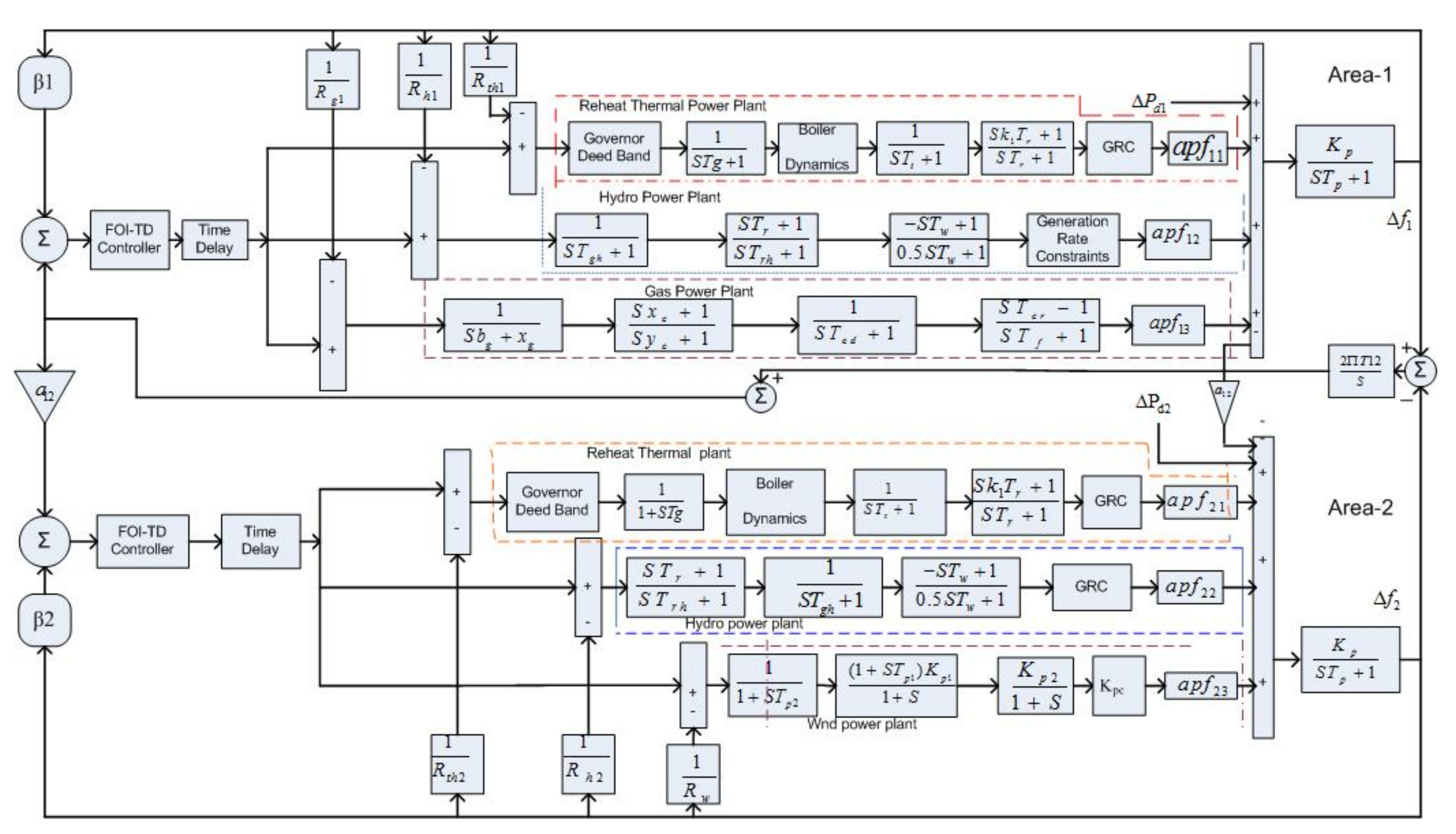
The system considered for investigation is a two-area integrated PS model consisting of multigeneration units such as reheat-thermal, hydro, wind, and gas, as shown in
Figure 1. For more realistic analysis, various constraints, such as TD, GDZ, GRC, and BD, having nonlinear features are incorporated in the specified system. The rate of power variation is limited by GRC to a quantifiable value. The GRC limits are  ± 3 percent per minute for thermal units, while for the hydro-system, the limits are 270 percent and 360 percent per minute for generation increase and decrease, respectively. The GDB specifies no adjustment in the location of valve even if it has a particular variation in the magnitude of the speed. This is due to the concept of Coulomb friction and backlash in multiple controller connections and valve overlaps in hydraulic relays. For hydro units, the GDB limit of 0.02 percent is contemplated, while for the thermal system, the GDB consequences are included in the governor’s transfer function (TF) as given in Equation (
1). Reheat thermal generation unit consist of sub-block of turbine, governor, re-heater unit with TF
,
, and
, respectively. The hydro-generation system comprised of sub-block of governor with TF (
), droop compensation with TF (
), and pen stock turbine with TF
. Similarly, the gas generation unit have comprised of valve position, compressor discharge, governor, and fuel combustion reaction having TF of
,
,
and
respectively. Wind generation unit consist of turbine blade and hydraulic pitch actuator with TF
, and
, respectively.
where
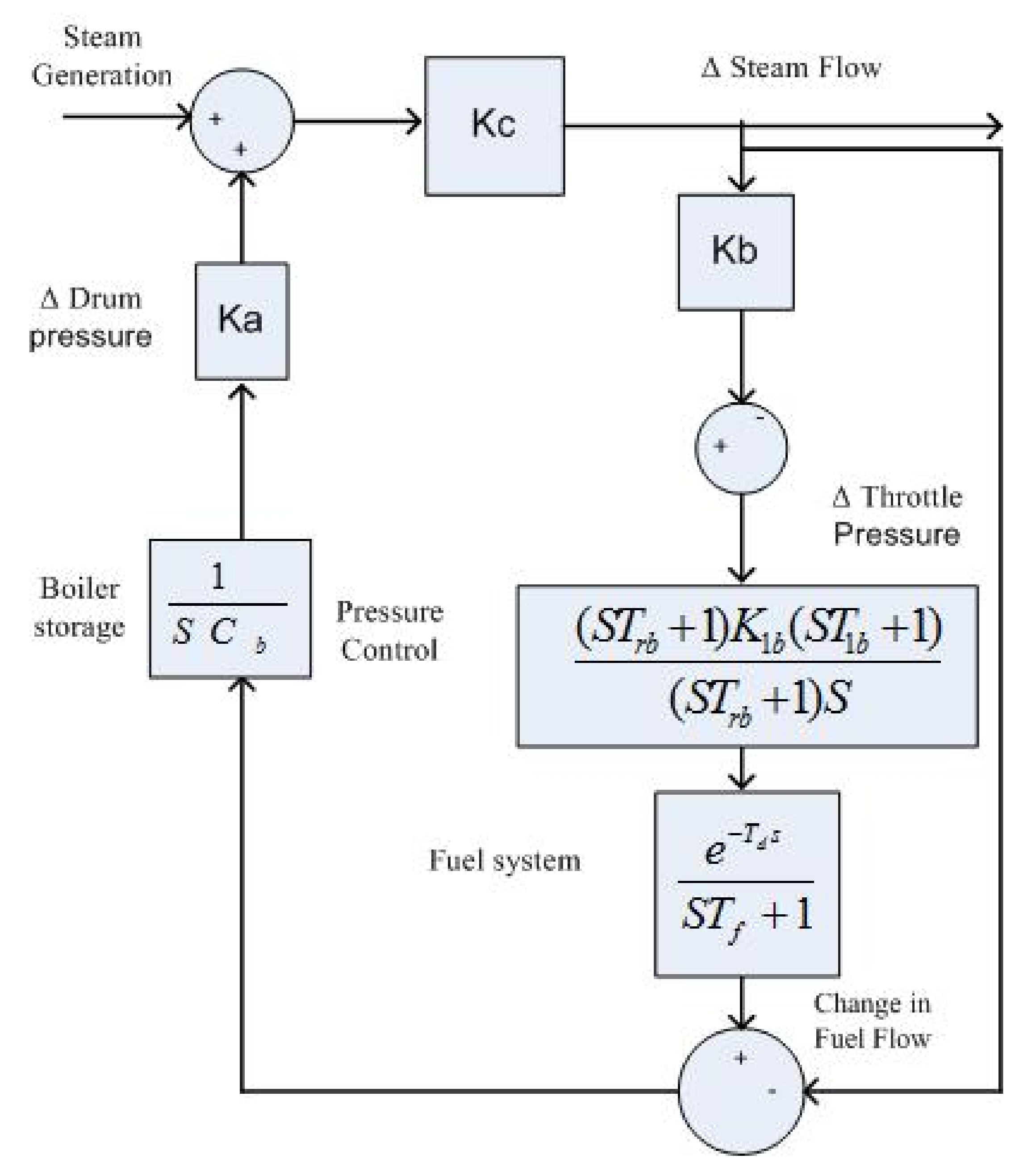
T is a time constant of speed governor. In this study, BD is considered in coal-fired system with fine-tuned controls for AGC performance evaluation. The block diagram model of BD is depicted in
Figure 2. The representation of the TF of the pressure control module
and the fuel system
may be indicated by below equations [
7,
8].
where
represents the integrator gain,
shows PI ratio gains,
is the lead lag compensator time,
shows delay time of fuel firing, and TF represents fuel system time constant. The AGC-related time delay influences the accomplishment of the system if it is not incorporated appropriately. However, in certain situations, the stability of the system can be affected. In this analysis, we used a TD of 2 seconds for the AGC model, which is used more practically [
8].
3. Controller Structure
Fractional-order or non-integer controller gained tremendous reputation in the performance of AGC systems due to its added versatility, disturbance rejection ability, and design methodology. TID and I-TD controllers are types of FO controllers that are analogs with PID and I-PD controllers, respectively, but are based on fractional calculus. TID and I-TD controllers have the same number of parameters but differ in structure, provided in
Figure 3a,b, respectively. The I-TD controller [
30] results in superior performance, compared to the TID controller. In compliance with the above concept, the FOI-TD controller is designed and developed, which is a modified form of the FOTID controller. The FOTID controller has a similar structure to the FOPID controller, but the only difference lies on proportional gain which is tilted and has TF of
. FOTID and FOI-TD controllers comprise six gains, namely, derivative (
), integral
, proportional (
), fractional integrator order (
), tilt nonzero real number (n), and fractional derivative order (
). In FOTID [
31], the coefficient blocks are connected in forward path; however, in the FOI-PD controller, the integral parameter
is connected in a forward path and the rest of the coefficient blocks are linked in feedback. The transfer function of FOTID and FOI-TD controllers is indicated by the below equations, respectively.
where U(s) denotes control signal, Y(s) represent system output, and E(s) denotes the error signal. The abrupt change in the FOTID controller’s input signal “R(s)” generates an abrupt change in U(s). The sudden change in the output is known as a derivative or proportional spike, and it causes a systematic problem by suddenly changing the control signal. The updated FOTID controller structure called as FOI-TD is implemented and develop to address these disadvantages. In the modified form of proposed controller, the integral term reacts on error signal E (s), while derivative and proportional terms respond on output signal which will not be affected by a momentary spike in the set point specification. The parameter of newly developed controller are optimized with the performance criteria including integral time multiplied quadratic error, Integral Absolute Error, integral time multiplied by Absolute Error and integral quadratic error and are, respectively, represented by the following equation:
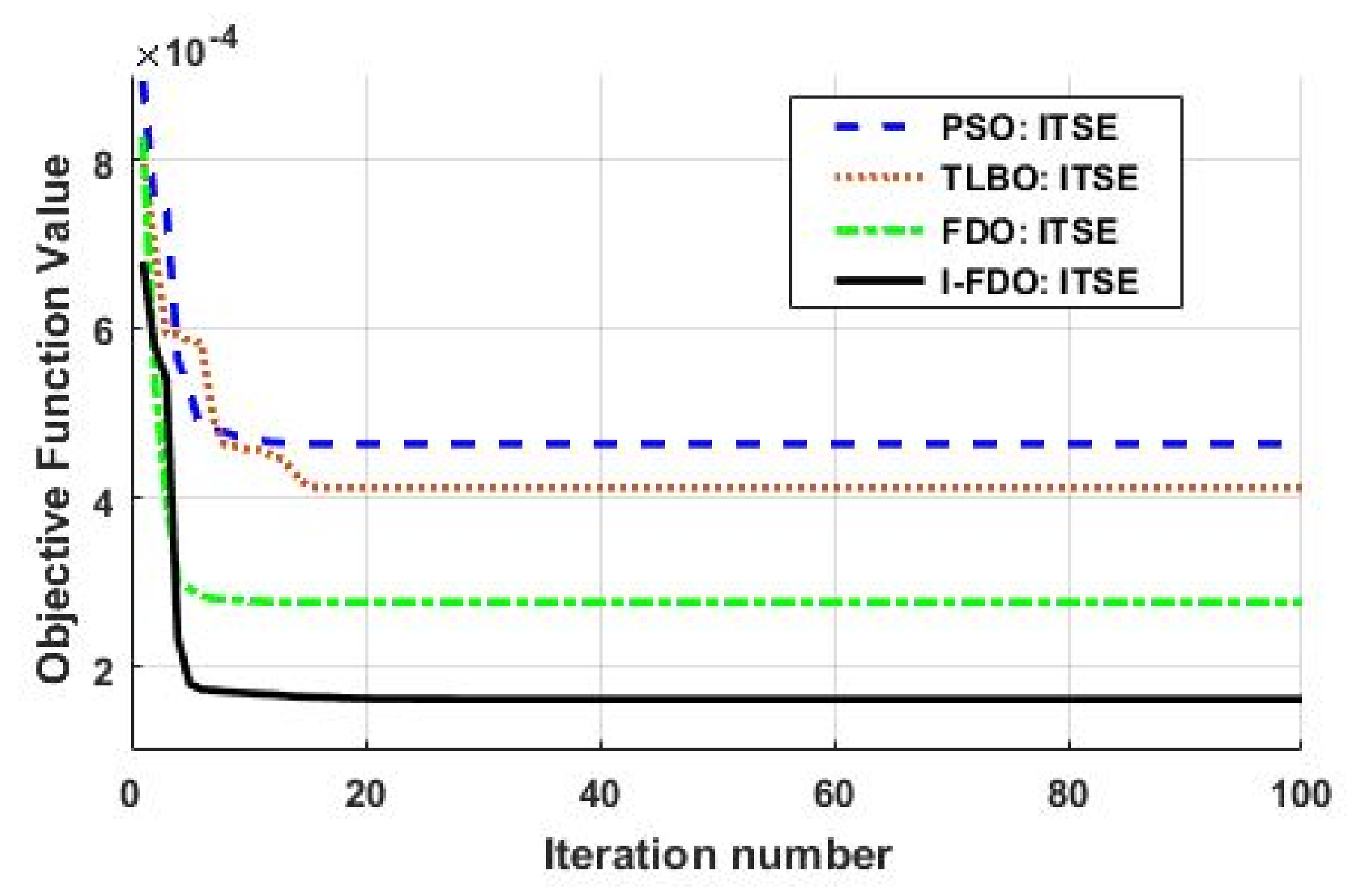
The convergence characteristics for different algorithms using FOI-TD controller minimized with the ITSE objective function are given in
Figure 4. The results provided in
Figure 4 and
Table 2 indicate that our proposed I-FDO-based algorithms converge quickly at cost function = 0.00003 as compared to other algorithms like FDO, PSO, and TLBO that converges at cost function of values 0.00012, 0.00029, and 0.00033, respectively. The minimum value of cost function represents the fast convergence which indicates the superiority of the proposed I-FDO algorithm.
5. Performance Validation
In this section, a diverse generation unit of the two-area interconnected system depicted in
Figure 1 is developed by using
Appendix A (
Table A1) in Matlab/Simulink environment via 1% step load disturbance (SLD) at t = 0 s. An I-FDO metaheuristic technique is applied optimizing the gains of proposed FOI-TD controller using ITSE criteria due to its better fitness values provided in
Table 2. The parameters of I-FDO given in
Appendix A (
Table A2) are utilized for the optimal gains of proposed controller after running the algorithm for 30 iteration and picked the best values among them is the final gains of the controller which is provided in
Table 3. In order to demonstrate the performance of AGC system of two area multi generation units has been validated with respect to two scenarios.
Scenario-1:
In this scenario, the I-FDO metaheuristic algorithm is compared with benchmark approaches like FDO, PSO, and TLBO to show the effectiveness of our proposed model. The convergence profile for different algorithms are provided in
Figure 4, indicating that our proposed I-FDO algorithm (ITSE = 0.00003) converges quickly, compared to TLBO (ITSE = 0.00029), FDO (ITSE = 0.00012), and PSO (ITSE = 0.00033).
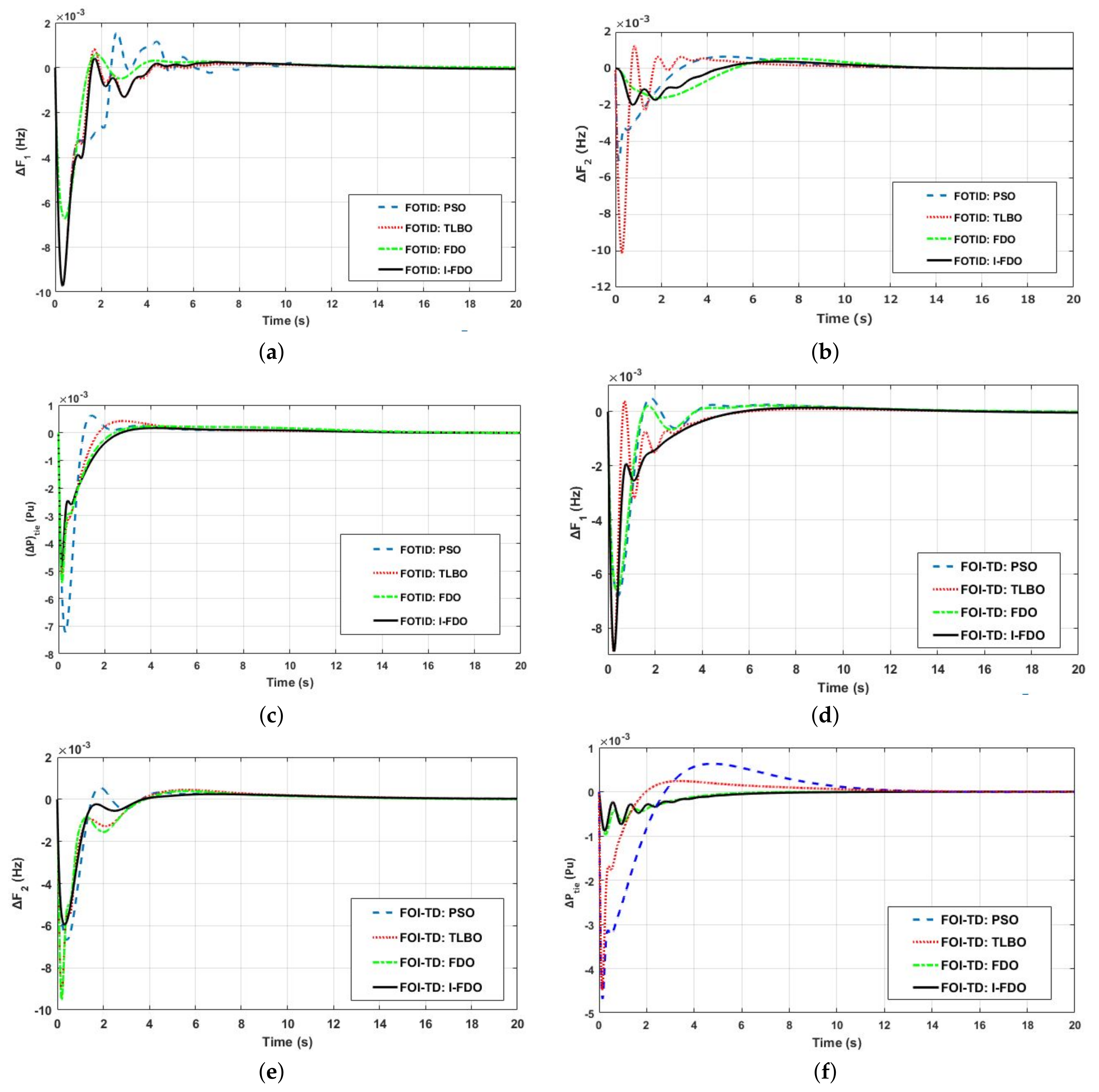
Figure 6a–f shows the dynamic transient response of AGC system with different techniques for frequency deviation in area 1 (
), area 2 (
), and tie-line power deviations (
).
Figure 6a–f shows that the I-FDO optimization-based FOTID and FOI-TD controllers rapidly suppressed oscillation and decreased peak overshoot and undershoot for
,
, and
. A comprehensive comparative result analysis for
,
, and
are given in
Table 4 for different algorithms in terms of Overshoot (Os), Undershoot (Us), and Settling time (Ts). I-FDO tuned FOI-TD controller increased settlement time by (46. 47%, 0.89% and 0.19%) and effectively decreased overshoot by (96.03%, 55.41%, and 0.39%) for
,
, and
, compared to FOI-TD controller optimized with PSO algorithms.
Table 4 shows that I-FDO-based tuned FOI-TD controller offers a substantial increase of 77.79%, 27.50% and 19.89 %, and compared to Pathfinder algorithm-based FOTID controller, thus effectively reducing peak overshoot of 96.95%, 84.90%, and 38.11% and undershoot of 5.93%, 69.98% and 74.12% for two areas and in tie-line power. Similarly, the FOI-TD-based I-FDO controller also offers an increase of 6.37%, 53.62%, and 4.96% in time settling for
,
, and
, respectively, compared to the WCA-based I-TD controller. It can be observed from
Figure 6d that the I-FDO-based optimized FOI-TD controller minimized overshoot time and decreased settling time as compared to FDO and PSO base tune algorithm at the cost of increasing undershoot of value (−0.0066) and (−0.0068) respectively.
Scenario-2:
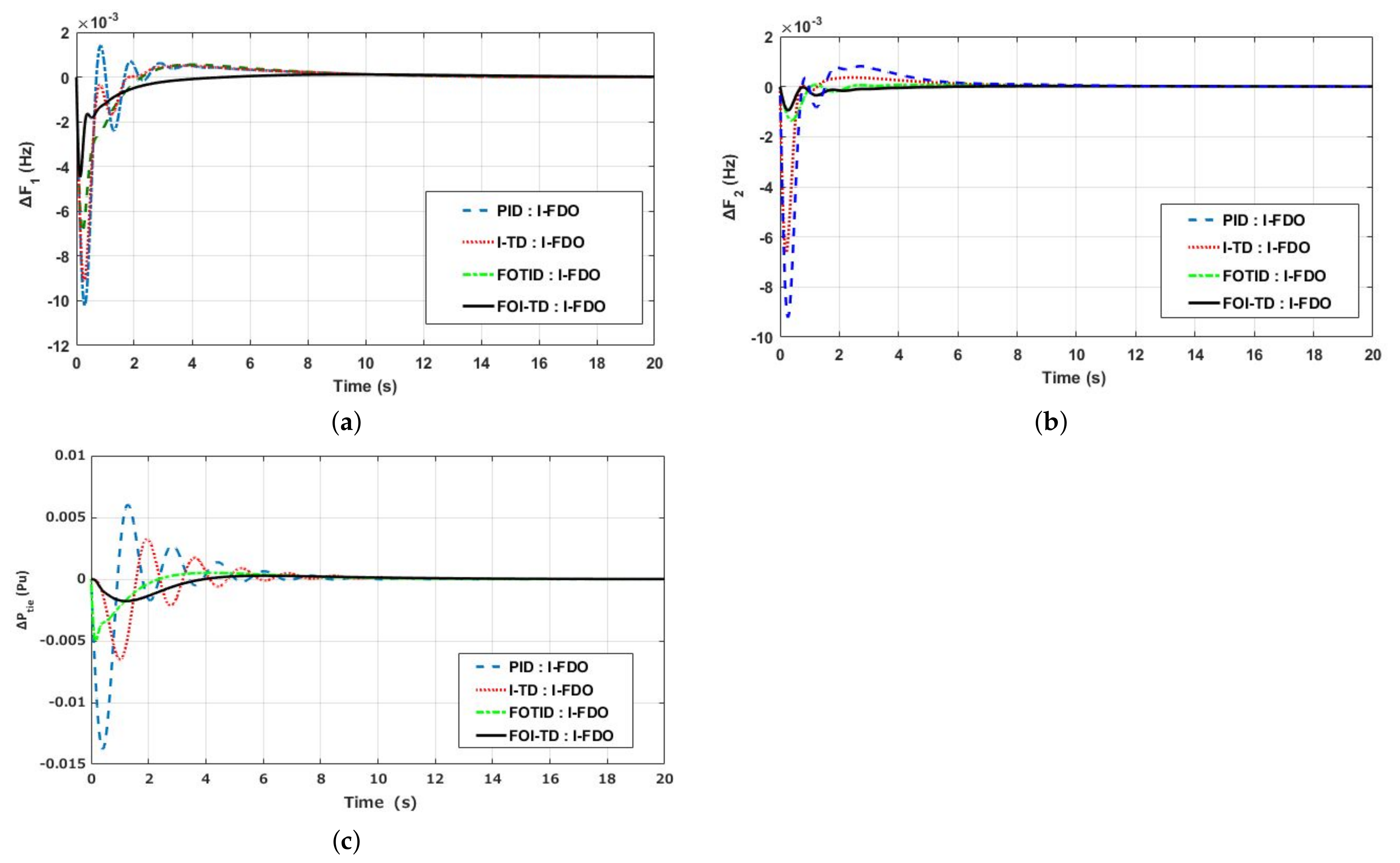
The effectiveness of the proposed FOI-TD controller tuned with I-FDO algorithm was compared with other type of controllers including FOTID, I-TD, and PID optimized with same algorithm for AGC problem of interconnected multigeneration PS.
Table 2 shows that the minimum value of the ITSE cost function with I-FDO-tuned FOI-TD controller is 0.000012, and the next position is occupied by the FOTID and I-TD controllers having ITSE values are 0.000068 and 0.00098, respectively, and also the I-FDO-tuned PID controller provides the maximum value of cost function that is 0.00765. Similarly, compared to FOTID, I-TD, and PID controllers, the transient response performances (peak overshoot, peak undershoot, and settling time) associated with frequency variations of the two areas and the power deviation in tie-lines are enhanced for FOI-TD controllers which is depicted in
Table 5 and
Figure 7a–c.
Table 5 and
Figure 7a–c revealed that that I-FDO based optimized FOI-TD controller effectively reduced overshoot (Osh) by (50.01%, 90.03%, and 94.9%), enhanced time settling by (43. 01%, 9.89%, and 19.97%), and reduced undershoot by (32.00%, 42.11%, and 86.86%) for
,
, and
respectively by comparing with I-FDO tuned PID controller.
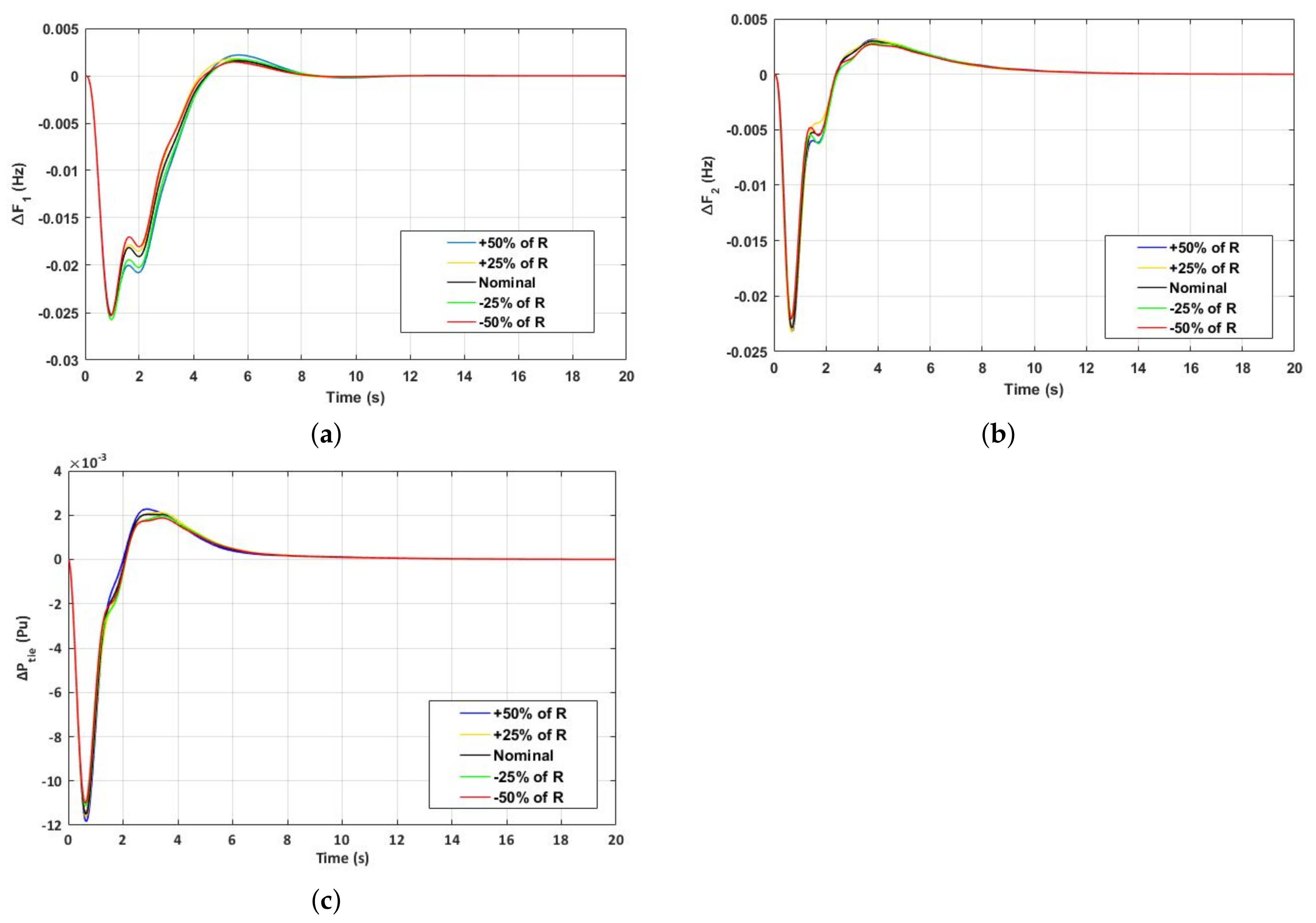
Sensitivity Analysis
This section is focused on checking the robust capabilities of the controller under the influence of large variations in the system parameters of AGC. In this study, the sensitivity analysis of the I-FDO-optimized FO-ITD controller is performed by varying the wind turbine
, turbine time constant
, governor constant
, and droop constant
R to  ± 50% of their nominal values, keeping the optimum parameters intact for the FOI-TD controller as listed in
Table 3. The transient performance in terms of
,
, and
affecting to varied system situations are shown in
Table 6. The results obtained in the range of  ± 50% by varying AGC parameters are depicted in
Figure 8. The transient response of the system parameters are almost identical to the nominal values, as shown in
Table 6 and
Figure 8, indicating the robustness of the proposed FOI-TD controllers. From this sensitivity test, it can be concluded that re-tuning of the controller settings for these large variations in system parameters from their nominal values is not necessary.
6. Conclusions and Future Directions
A FOI-TD controller is optimized for the AGC problem using a recent metaheuristic-based approach called the I-FDO algorithm. The performance of the proposed controller structure is validated considering two-area interconnected hydro, gas, thermal, and wind power plants. Various constraints were also considered for more realistic analysis, such as GRC, GDZ, TD, and BD having nonlinear characteristics that were assimilated in the specified AGC model. A comparative analysis of the proposed FOI-TD controller with FOTID, PID, and I-TD controllers is provided. Investigation on simulated outcomes show that I-FDO tuned FOI-TD controller effectively reduced overshoot (Os) by 50.01%, 90.03%, and 94.98%; enhanced time settling by 43.01%, 9.89%, and 19.97%; and reduced undershoot by 32.00%, 42.11%, and 86.86% for , and , respectively, compared with I-FDO tuned PID controller. Further, I-FDO-based tuned FOI-TD controller resulted in a substantial increase of 77.79%, 37.50%, and 19.89% , , and , respectively, compared with WCA-based I-TD controller. Further, the proposed FOI-TD controller also reduced peak overshoot of 96.95%, 84.90%, and 38.11% and undershoot of 5.93%, 69.98%, and 74.12% for both areas and tie-line power. Finally, the capability of the developed FOI-TD controller is confirmed by modifying the system’s parameters and load condition in the range of  ± 50% for the AGC problem.
In future, the same power system model can be analyzed by incorporating various energy storage devices like super capacitor’s, redox flow batteries, and superconducting magnets to enhance the dynamic response of the power systems.