Abstract
This study aimed to examine the energy and exergy indices of the rosemary drying process in a hybrid-solar dryer (HSD) and the effects of air-drying parameters on these thermodynamic indices. Drying experiments were carried out at four levels of air temperature (40, 50, 60, and 70 °C) and three levels of air velocity (1, 1.5, and 2 m/s). Energy and exergy were calculated by application of the first and second laws of thermodynamics. Based on the principal laws, energy efficiency, exergy losses, and exergetic improvement potential rate, were evaluated. The results showed that the energy utilization ratio (EUR) ranged from 0.246 to 0.502, and energy utilization (EU) ranged from 0.017 to 0.060 (kJ/s). Exergy loss and efficiency varied from 0.009 to 0.028 (kJ/s) and from 35.08% to 78.5%, respectively, and increased with increased temperature and air velocity. It was found that the exergy loss rate was affected by temperature and air velocity because the overall heat transfer coefficient was different under these conditions. By comparison, with increasing temperature and air velocity, the exergy efficiency increased. Because most energy is used to evaporate moisture, this behavior may be explained by improved energy utilization. The drying chamber sustainability index ranged from 0.0129 to 0.0293. This study provides insights into the optimization process of drying operations and operational parameters in solar hybrid dryers that reduce energy losses and consumption.
1. Introduction
The use of herbal medicines for treating an extensive range of diseases and/or modifying nonpathogenic conditions is increasing globally [1]. Rosmarinus officinalis L., known as rosemary, is a fragrant plant with needle-like leaves of the Lamiaceae family. Due to its anti-inflammatory and antioxidant properties attributed to ursolic acids and carnosol/carnosic, rosemary has been used mainly in traditional medicine, cosmetics, and pharmaceutical industries [2]. In traditional medicine, rosemary is applied as an oral medicine to alleviate muscle spasms, dysmenorrhea, and renal colic due to its medicinal properties. In addition, it has antioxidant, antiviral, antifungal, antibacterial, antitumor, antidepressant, analgesic, and anti-inflammatory properties [2]. In addition, the Mediterranean region plays an important role in providing a major proportion of the flavorings and spices for numerous uses in global food chains [3].
Rosemary is also found in dried form, and aromatic and medicinal plants are usually sold in pharmacies along with their oil. Overall, the primary drying process is a key parameter in the processing of herbs and spices, and is essential to the stabilization and preservation of the valuable ingredients of medicinal plants [3]. Sun-drying is the most common method for drying rosemary leaves, which are is exposed to sunlight in a thin layer. Despite being the least expensive method and requiring no additional energy, its effectiveness heavily depends on the air flow rate and temperature. In addition to the low drying rate, this method is subject to several kinds of interference, such as insects, wind, or dust. Several drying methods have been developed to address these problems, including solar dryers, which represent an inexpensive method that can be applied in many places without requiring a secondary power source [4,5,6].
To reduce the dependence of the drying process on sunlight, an electric heater element can be used in the dryer. This device is commonly known as an HSD [7,8]. Several researchers have investigated the utilization of HSDs in several products, such as starch [9], mushrooms [10], mint [11], chamomile [12], and corn [13]. Results showed that the HSD improved the drying rate compared to that of conventional solar dryers.
In modeling the drying process, the effective moisture diffusivity (Deff) is a significant transport characteristic in food and other materials. It also identifies the function of moisture content and temperature in materials. Physical and thermal characteristics of food products, for instance, the parameters of the moisture diffusion coefficient and activation energy, are needed for the ideal dryer design [4].
Energy analysis is often used to evaluate the dryer’s performance. Because the drying process needs a large amount of energy, exergy or the maximum power work, as another indicator of efficiency, can be measured using a specific reference environment and a composite system. This analysis identifies the cause, location, and extent of process inefficiency. Moreover, exergy analysis can be utilized as a criterion to determine whether an activity is valuable, because it can be used to assess energy quality and degradation via identification of the locations, types, and true magnitudes of losses [9].
Several studies have been undertaken using exergy and energy analysis of the drying processes of crops, such as potato slices in a continuous band dryer [14], rice in a convective dryer [15], mushroom slices in a hot air dryer [16], bananas in convective dryers [17,18], parboiled paddy rice in a LSU industrial dryer [19], drying corn in a new industrial dryer system [20], carrots in a convective dryer [21], onions in a convective dryer [22], turmeric in forced convection solar tunnel dryers [23,24], and carob pulp in a solar collector dryer [25].
To date, no attempts have been made in the relevant literature to examine the use of solar hybrid dryers to dry rosemary plants, and to undertake energy and exergy analysis. Therefore, this study aimed to investigate the thermodynamic performance of a solar hybrid dryer to dry rosemary leaves, by analyzing the moisture content, in addition to a comprehensive evaluation of the associated energy and exergy.
2. Materials and Methods
2.1. Sample Preparation
Rosemary (Rosmarinus officinalis L.) plants were harvested. The initial moisture determination of samples was performed using the oven method at 70 °C for 24 (h) until a constant weight was achieved [6]. As a result, the fresh rosemary samples had an initial moisture content of 81% (% d.b.).
2.2. Dryer Equipment
The laboratory-scale HSD used in this study includes a solar collector unit and a dryer chamber (Figure 1). The dryer represented in Figure 1 is equipped with a control system for the air temperature, velocity, and relative humidity. The dryer chamber contains two aluminum perforated trays. The top of the dryer chamber is equipped with an exhaust duct to allow the air to reach the external environment. The solar collector frame is made of aluminum, and a black aluminum sheet with air-conducting blades is used as a radiation absorber. A 1000 W electric element is incorporated inside the collector to heat the input air flowing into the dryer chamber, and is powered by batteries. The temperature and relative humidity of the air displacement were measured using five LM75 temperature sensors with a measuring range of −55 to 125 °C (±2 °C), and two HS1101 humidity sensors with an accuracy of ±2%, respectively. By adjusting the dryer fan, the air entry into the dryer chamber could be altered. The flow velocity of air translocation into the dryer chamber was measured using a vane velocity-meter (AVM-07 made in Taiwan, with an accuracy of 0.1 m/s).
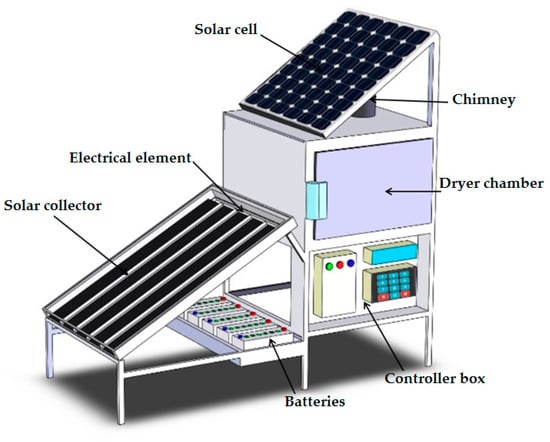
Figure 1.
Dryer diagram used.
2.3. Experimental Procedure
For each experiment of the drying process, a mass of 500 g of the fresh rosemary plant (including stems and leaves) was applied and uniformly dispersed on the thin film of the dryer tray. Prior to starting the drying process experiments, the dryer was turned on for at least 30 min to acquire steady-state conditions. However, to ensure the quality of the dried product, the experiments were performed at four temperatures of 40, 50, 60, and 70 °C, and three levels of air velocity of 1, 1.5, and 2 m/s, with three replications in a relative humidity of 32 %. The heated air flow entered the drying cabinet under the perforated trays and flowed upwards through the fresh samples.
Changes in the product weight during the drying process were recorded using a digital scale (GF-3000, AND, with ± 0.01 g accuracy). Instantaneous moisture content was calculated using the mass balance in Equation (1):
where M and W are instantaneous moisture content (based on fresh weight) and instantaneous mass (kg) of drying samples, respectively. M0 and W0 are initial humidity (% d.b.) and mass of fresh samples (kg), respectively. The rosemary samples were dried until the moisture content reached about 12% (% d.b.) based on fresh weight.
2.4. Data Analysis
2.4.1. Moisture Content Analysis
The two parameters of moisture ratio and drying rate during the drying process were calculated using Equations (2) and (3), respectively [26]:
where MR is the humidity ratio, Mt is the mass humidity (% d.b.), and Me is the equilibrium moisture. MC is the moisture content at t and t + dt. Due to the low value of Me compared to M0 and Mt, Equation (2) was simplified as MR = Mt/M.
2.4.2. Effective Moisture Diffusivity Coefficient (Deff)
It is well known that Fick’s 2nd law of diffusion is used to explain the penetration in the drying process of agricultural products [4]:
To determine the diffusivity coefficient after the expansion of Equation (4), and to account for the drying conditions over a long period, relationship (5) was obtained as follows [25]:
The effective diffusivity coefficient (Deff) was obtained from the slope (K) of the Ln(MR) diagram relative to time, as follows:
where Deff is the defined effective diffusivity coefficient (m2/s) and L is the semi-thickness of each sample.
2.4.3. Activation Energy
From the Arrhenius equation, the activation energy for different velocities and temperatures can be extracted using the relationship (7):
where Ea is activation energy (kJ/mol), Tabs is the temperature inside the dry chamber (k), Rg is the universal gas constant equal to 38.143 (kJ/mol.K), and D0 is the Arrhenius pre-exponential factor (m2/s) with a constant value. T is also the absolute air temperature. To obtain Ea, linear relation (8) was used:
By drawing the ln plot of (Deff) versus 1/Tabs, the slope of K2 was obtained as below:
2.4.4. Energy and Exergy Analysis
To analyze energy and exergy, the drying process of rosemary was considered to be a continuous flow process. Equation (10) was applied to calculate the energy use (EU) during the drying process of rosemary foliage [4]:
where is mass flow rate of dry air (Kg/s); ha,i and ha,o are input and output air enthalpy of the dryer (J/kg), respectively; and are mass flow rates of fresh and dried products (kg/s), respectively; hPF and hPD are enthalpy of fresh input and dried products (kJ/kg), respectively; and is the heat loss from the dryer body (kJ/s).
The following relationships can be used to calculate the input and output airflow of the dryer and air density:
where A is the cross-section of the dryer chamber (m3) and Va is the linear velocity of the input air flow to the dryer chamber (m/s). To calculate the dry air density of ρa (kg/m3), Equation (14) was used [27]:
where Ta is air temperature (°C). The input and output air enthalpy of the drying chamber is calculated using the following equation [28]:
where Ca is the specific heat of the air at constant pressure (kJ/kg °C) and T∞ is the temperature of the output air (°C), hfg is the latent heat of evaporation of water (kJ/kg), and w is the absolute humidity of the input or output air.
The heat transfer rate leading to evaporation of the water from the product inside the dryer was calculated through the following relationship:
The specific heat of the output or input product must be first calculated to estimate the enthalpy of the dried and fresh product; and then, the temperature of the output or input product, also the ambient temperature was measured using the thermometer:
where Cp is the specific heat of the input or output product (kJ/kg °C) and Tp is the temperature of the input or output product (°C). To specify the enthalpy of input or output air, Equation (18) is used:
Moreover, the amount of heat lost from the amount of heat loss and the output air from the dryer body can be calculated using Equations (19)–(21), respectively:
where Cai is the specific heat of the input air (kJ/kg °C); Tai and Tao, are the temperature of the input and output air (°C), respectively; Udef is the thermal degradation coefficient of the dryer body (Kw/m2 °C); Adef is the contact surface with the dryer body (m2); and Tmvdef is the average temperature at three points of the dryer body.
Finally, the energy utilization ratio (EUR) is calculated by Equation (22):
Exergy analysis is undertaken according to the 2nd law of thermodynamics, which accounts for quantity and quality. Using the 2nd law of thermodynamics, exergy values at the inlet of the dryer chamber (Exin), exergy at the outlet of the drying chamber (Exout), and exergy loss (Exloss) were calculated:
Moreover, exergy efficiency (Exeff) is defined as the ratio of outflow exergy to input exergy to the dryer chamber, and calculated by applying Equation (26):
The maximum improvement potential of exergy efficiency for the drying process is achieved when exergy loss or irreversibility is minimized. The exergetic improvement potential rate for the drying process is calculated by application of Equation (27) [15,29]:
The drying process sustainability index (SI) is indicated by Equation (28):
2.4.5. Specific Energy Consumption
The equations for calculating the specific energy consumption of the HSD for drying rosemary foliage at different temperatures and air input velocities are given in Equations (29)–(33), where U is voltage (volt), I is current (ampere), and t is drying time (seconds).
3. Results
3.1. Moisture Content
The moisture content of the rosemary foliage is shown versus time at four temperatures and three air velocities in Figure 2. As shown in this figure, the higher drying temperature dramatically reduced moisture content. The drying time of rosemary foliage using hot air varied from 240 to 500 min. The shortest drying time for rosemary was at 70 °C and a velocity of 2 m/s. Humidity in the air is lower at higher temperatures, which causes more water to be removed, more quickly, from the plant’s foliage. These results are consistent with other studies that used an HSD [4,9,11].
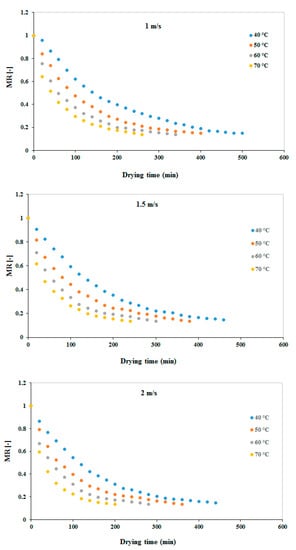
Figure 2.
The effect of air temperature on moisture ratio at different air velocities.
3.2. Drying Rate
Figure 3 illustrates drying rate changes (g water/g dry matter min) with drying time in solar drying of rosemary foliage at four temperatures and three air velocities. The drying rate is constantly reduced by decreasing MR or increasing drying time (Figure 3), indicating that drying rate is a function of the three parameters of time, temperature, and air velocity. Initially, all four temperatures resulted in the highest amount of drying of rosemary foliage, but over time, its drying rate decreased. Water available inside the samples moves to the surface at higher temperatures, which causes evaporation and a faster rate of drying. The drying rate curve also demonstrated an exponential decrease at all temperature levels.
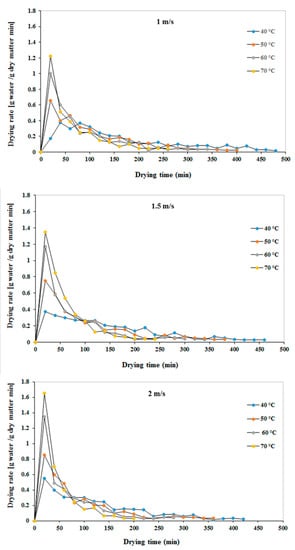
Figure 3.
Drying rate of rosemary in different drying conditions.
The high drying rate in the initial drying period can be attributed to the large difference between the rosemary moisture content and the equilibrium moisture content of dry air, causing the rapid evaporation of rosemary free moisture. During the drying process, the free moisture decreases and the bound moisture content in the inner tissue of rosemary evaporates. Compared to free moisture, the evaporation of bound moisture is more difficult. Accordingly, a higher amount of bound moisture evaporation decreases the drying rate. These results are consistent with the findings of other researchers using a solar hybrid dryer, including Kaveh, Karami and Jahanbakhshi [4] for pennyroyal, Karami, Lorestani and Tahvilian [5] for Thyme, Vijayan, Arjunan and Kumar [27] for bitter squash slices, and Suherman, Hadiyanto, Susanto, Utami and Ningrum [28] for sugar-palm vermicelli.
3.3. Determination of Deff
Table 1 presents Deff values for the drying of rosemary. Deff values range from 8−10 to 12−10 m2/s for foods and crops [30]. With increasing air velocity and temperature, effective moisture diffusivity coefficients increase. The maximum effective moisture diffusivity coefficient at 70 °C and an air velocity of 2 m/s was 1.57 × 10−9 m2/s. In addition, the lowest value (4.8 × 10−10 m2/s) was recorded at 40 °C and an air velocity of 1 m/s. Deff in the rosemary foliage occurred as a result of cell wall degradation caused by increased input air velocity and temperature. The range obtained for Deff has been confirmed by other researchers [25,27,31,32].

Table 1.
Variation of Deff (m2/s) with drying air temperature and velocity.
3.4. Activation Energy
Activation energy is the energy necessary to overcome the drying process barrier. Activation energy can be inferred via the reverse relationship between the logarithm of the effective emission and the temperature. For different input air velocities and temperatures, activation energy values for rosemary foliage in the HSD were 16.9 to 25.3 kJ/mol. The highest activation energy level, of 25.3 kJ/mol, was obtained at an air velocity of 1 m/s, with an R2 value of 0.994, whereas the lowest value of 16.9 kJ/mol occurred at 1.5 m/s, and the R2 value was 0.998. Similar results have been reported for apple slices and Chilean berry [33,34].
3.5. Energy Utilization Ratio (EUR)
EUR for the drying of rosemary samples was calculated using Equation (22), and its average values ranged from 0.246 to 0.502. Table 2 presents the average changes in EUR with temperature and air velocity. It was found that EUR increased as temperature increased from 40 to 70 °C at each air velocity. At 70 °C and the velocity of 2 m/s, the highest EUR was obtained, of 0.502, whereas the lowest, of 0.246, was observed at 40 °C and the velocity of 1 (m/s). Moreover, the EUR values increase as the air temperature rises. The evaporation rate of moisture from a product increases as the temperature increases. Conversely, at high temperatures, mass and heat transfer are high, causing excessive moisture loss. Moreover, according to the figure, EUR increases due to the increase in the air velocity from 1 to 2 m/s. Similar results have been reported by other researchers, including in studies of mint [4], mushrooms [16], green peas [26], and onions [35].

Table 2.
Variation of EU (kJ/s) and EUR (%) with air temperature and velocity.
3.6. Energy Utilization (EU)
The EU level at different temperatures and air velocities is presented in Table 2. The highest EU (0.060 kJ/s) was achieved at 70 °C and an air velocity of 2 m/s, whereas the lowest value, of 0.017 kJ/s, was obtained at 40 °C and an air velocity of 1 m/s. The results illustrate that, by increasing the temperature and air velocity, the EU increased. In addition, the increased EU can be explained by the direct relationship between energy consumption, EU, and energy utilization. Therefore, the greater the air velocity, the greater the mass transfer. This increase leads to enhanced energy utilization. Similar results were found for okra drying in a compulsory convection cabinet dryer [36], mushroom slices in convective drying [37], and cassava starch drying in a tray dryer [38], in which researchers reported that the greater the input air temperature, the greater the energy consumption.
3.7. Input Exergy, Output Exergy, and Exergy Loss
Exergy is the highest quantity of useful and possible energy in a drying process that equilibrates the system with the heat accumulated in the solar collector. The work loss or difference between the highest work and the actual work is referred to as the exergy loss. The results of exergy analysis of the drying process of rosemary samples under different input temperatures and air velocities to the drying chamber are indicated in Table 3. As shown, the mean output exergy and exergy losses ranged from 0.005 to 0.101 kJ/s, and 0.009 to 0.028 kJ/s, respectively. The highest amount of exergy loss was 0.028 kJ/s, obtained at 70 °C and an air velocity of 2 m/s. The exergy of a system (input and output) has a direct relationship with the temperature and mass flow intensity of air; thus, increases in these values increases the exergy [39]. Aviara, Onuoha, Falola and Igbeka [38] undertook exergy analysis of dry starch in a tray dryer. They found that increasing the dry air temperature from 40 to 60 °C increased input and output exergy from 0.399 to 686.2 J/s and 0.055 to 0.555 J/s, respectively. Fudholi et al. [40] calculated the minimum and maximum input and output exergies for drying chili peppers of 12.7 and 505.7 J/s, and 11.7 and 489.7 J/s), respectively.

Table 3.
The results of exergy analysis (kJ/s) for the drying process of rosemary plant.
Moreover, the lowest exergy loss was 0.009 kJ/s, obtained at 40 °C and an air velocity of 1 m/s. Exergy loss decreased with increasing drying time, which can be attributed to the decrease in the temperature during drying. As the input air velocity to the dryer chamber increases, the exergy loss also increases; thus, it not only increases the velocity of mass transfer, but also reduces the rosemary humidity content, in addition to decreasing the drying process time. Aviara, Onuoha, Falola and Igbeka [38] stated that the exergy loss of the dryer increases as the dry air temperatures increases. They identified that increasing dry air temperatures from 40 to 60 °C can increase the exergy loss from 0.344 to 2.131 J/s. These results demonstrate that the rates of exergy input, output, and loss increase with increasing temperature and air velocity. These results accord with others [17,19,20,41,42].
3.8. Exergy Efficiency
The average exergy efficiency of the drying process of rosemary under different conditions is displayed in Figure 4. The average exergy efficiency varied from 35.08% for an air temperature of 40 °C and an air velocity of 1 m/s, to 78.50% for an air temperature of 70 °C and an air velocity of 2 m/s. Increasing the temperature of the input air to the dryer increases the exergy loss, but this value is less than the enhanced exergy. As the temperature increased at different input air velocities, the exergy efficiency was enhanced. There was a direct relationship between exergy efficiency and dryer energy efficiency. Moreover, increasing the velocity of the input air increases the exergy efficiency, because the entropy and enthalpy of the input air to the dryer increases with increasing air velocity. This leads to an increase in exergy efficiency. As shown in Figure 4, the effect of the input air velocity on exergy efficiency at low temperatures is considerably higher than at high temperatures. Yogendrasasidhar and Pydi Setty [43] reported an increase in exergy efficiency as temperatures rose from 40 to 60 °C. Okunola, Adekanye and Idahosa [36] reported that increasing the temperature to 70 °C caused energy efficiency to increase from 26.59% to 68.24%.
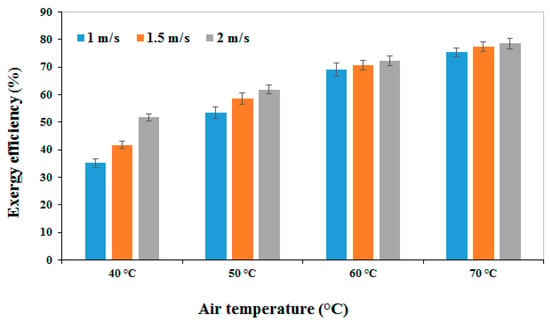
Figure 4.
Effect of air velocity and temperature on exergy efficiency.
3.9. Exergetic Improvement Potential Rate (IP)
IP represents an improvement in the drying process based on the solar dryer. By increasing the exergy loss, the dryer chamber IP increases. The average rate of IP was calculated using Equation (27), and the values obtained are shown in Figure 5. It can be observed that the minimum average value of IP is 0.321 kJ/s at 40 °C air temperature and 1 m/s air velocity, whereas the maximum IP, of 2.141 kJ/s, was observed at 70 °C air temperature and an air velocity of 2 m/s. In addition, it can be seen that increasing the temperature and air velocity increased the IP. Aviara, Onuoha, Falola and Igbeka [38] stated that the improvement potential linearly increases with the increase in the drying air temperature. They reported that increasing the drying air temperature from 40 to 60 °C increased the improvement potential from 0.2 to 1.6 J/s. Similarly, Fudholi, Sopian, Yazdi, Ruslan, Gabbasa and Kazem [40] reported a potential IP of between 0 and 135 J/s, with an average of 47 J/s. Vijayan, Arjunan and Kumar [27] also found that the average IP values vary from 3.75 to 6.58 J/s. Ndukwu et al. [44] reported that the range of IP values is between 0.036 and 20.6 J/s.
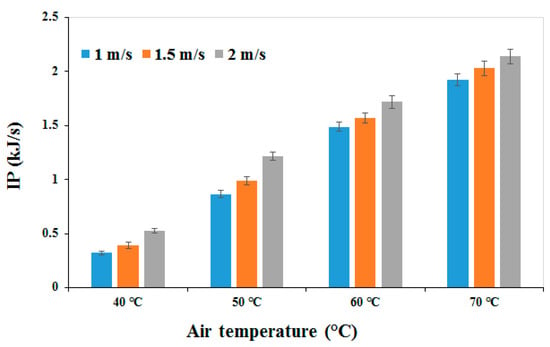
Figure 5.
Effect of air velocity and temperature on IP.
3.10. Sustainability Index (SI)
SI indirectly fits the exergy loss. SI describes the input exergy per unit of exergy loss in the dryer chamber; therefore, it has a reverse relationship with the exergy loss. The effect of air velocity and temperature on the SI of the dryer chamber is presented in Figure 6. The SI in the studied experimental conditions varies from 0.0129 to 0.0293, and its value has a reverse relationship with increased temperature and air velocity. As explained previously, due to higher exergy efficiency, the higher the sustainability index, the fewer the environmental impacts. Therefore, to reduce this effect, the efficiency of exergy must be improved. Okunola, Adekanye and Idahosa [36] obtained an SI between 2.14 and 2.77. They reported that this value varies under the experimental conditions, and its value is proportional to the load density and has an inverse relationship with increasing temperature. In addition, Beigi, Tohidi and Torki-Harchegani [15] obtained SI values for rice in a displacement dryer between 1.48 and 3.11. Kavak Akpinar [45] reported similar SI values ranging from 0.393 to 6.156. Mugi and Chandramohan [46] reported SI values between 1.19 and 17.05 W.
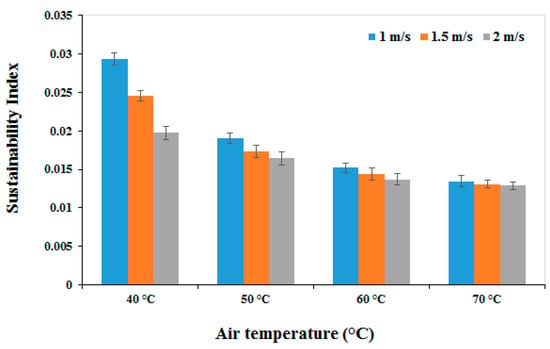
Figure 6.
Effect of air temperature and air velocity on SI.
3.11. Specific Energy Consumption (SEC)
The SEC indicates the amount of required energy per kg of moisture from dried products. The average SEC in the process of drying rosemary plants in different temperature and air velocity conditions ranged from 24.854 to 64.836 MJ/kg (Table 4). The highest SEC was related to 40 °C and 1 m/s, whereas the lowest was recorded at 70 °C and 2 m/s. This mechanism can affect the total energy consumption. The increased demand for dryer energy is caused by decreased temperature, which can be attributed to prolonged periods of drying at lower temperatures. In addition, the total energy consumption increased slightly by slowing down the drying air, showing the significant impact of the drying temperature compared to that of the air velocity on energy consumption. In different drying conditions (temperatures of 50–80 °C and air velocities of 0.09 and 0.18 m/s), Tagnamas, Lamsyehe, Moussaoui, Bahammou, Kouhila, Idlimam and Lamharrar [25] obtained SEC values between 0.15 and 0.25 kWh/kg for carob pulp. The results for our research work are consistent with the findings of others [47,48,49,50,51,52].

Table 4.
SEC (MJ/kg) for thin-layer drying of rosemary at different air velocities and temperatures.
4. Discussion
In this study, rosemary foliage was dried under different temperature conditions, and energy and exergy indices were investigated. Thermodynamic calculations showed that the specific energy consumption decreased with higher input temperatures and velocities in the drying chamber. The effective moisture diffusivity (Deff) values of rosemary samples varied between 4.8 × 10−10 and 1.57 × 10−9 m2/s at a temperature range of 40–70 °C using Fick’s diffusion model, and the activation energy changed from 16.9 to 25.3 kJ/mol. The lowest and highest specific energy consumptions were 24.854 and 64.836 MJ/kg, respectively. The EUR ranged from 0.246 to 0.502, and was higher at lower temperatures and air velocities. With increasing air velocity and temperature, EUR increased. The lowest and highest EU rates were 0.017 and 0.060 kJ/s. Increasing the temperature and air velocity of drying led to an increase in the rate of input exergy, output exergy, and exergy loss. The average exergy efficiency values ranged from 35.08% for the temperature of 40 °C and air velocity of 1 m/s, to 78.50% for the temperature of 70 °C and air velocity of 2 m/s. Finally, due to higher exergy efficiency, at lower velocities and temperatures, the sustainability index increased, leading to fewer environmental impacts. Hence, as a measure of the quality of energy, exergy analysis can be used to assess the loss of heat and reflect the thermodynamic values of the operation of an HSD. Thus, exergy analysis should be applied to the design of convective HSD systems with the largest possible thermodynamic efficiencies.
Author Contributions
Conceptualization, H.K. and M.K.; methodology, H.K. and M.K.; software, M.K.; validation, H.K. and M.K.; formal analysis, M.K.; investigation, H.K.; resources, H.K.; data curation, H.K.; writing—original draft preparation, H.K.; writing—review and editing, R.R., I.G., E.K. and B.D.J.; visualization, M.G.; supervision, M.G.; project administration, H.K. and M.K.; funding acquisition, H.K. and M.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The datasets used and/or analyzed during the current study are available from the corresponding author on reasonable request.
Acknowledgments
Not applicable.
Conflicts of Interest
The authors declare that there is no conflict of interest regarding the publication of this paper.
References
- Karami, H.; Rasekh, M.; Darvishi, Y.; Khaledi, R. Effect of Drying Temperature and Air Velocity on the Essential Oil Content of Mentha aquatica L. J. Essent. Oil-Bear. Plants 2017, 20, 1131–1136. [Google Scholar] [CrossRef]
- de Macedo, L.M.; Santos, É.M.D.; Militão, L.; Tundisi, L.L.; Ataide, J.A.; Souto, E.B.; Mazzola, P.G. Rosemary (Rosmarinus officinalis L., syn Salvia rosmarinus Spenn.) and Its Topical Applications: A Review. Plants 2020, 9, 651. [Google Scholar] [CrossRef] [PubMed]
- Mohammed, H.A.; Al-Omar, M.S.; Mohammed, S.A.A.; Aly, M.S.A.; Alsuqub, A.N.A.; Khan, R.A. Drying Induced Impact on Composition and Oil Quality of Rosemary Herb, Rosmarinus Officinalis Linn. Molecules 2020, 25, 2830. [Google Scholar] [CrossRef]
- Kaveh, M.; Karami, H.; Jahanbakhshi, A. Investigation of mass transfer, thermodynamics, and greenhouse gases properties in pennyroyal drying. J. Food Process Eng. 2020, 43, e13446. [Google Scholar] [CrossRef]
- Karami, H.; Lorestani, A.N.; Tahvilian, R. Assessment of kinetics, effective moisture diffusivity, specific energy consumption, and percentage of thyme oil extracted in a hybrid solar-electric dryer. J. Food Process Eng. 2021, 44, e13588. [Google Scholar] [CrossRef]
- Karami, H.; Kaveh, M.; Mirzaee-Ghaleh, E.; Taghinezhad, E. Using PSO and GWO techniques for prediction some drying properties of tarragon (Artemisia dracunculus L.). J. Food Process Eng. 2018, 41, e12921. [Google Scholar] [CrossRef]
- Karami, H.; Rasekh, M.; Darvishi, Y. Effect of temperature and air velocity on drying kinetics and organo essential oil extraction efficiency in a hybrid dryer. Innov. Food Technol. 2017, 5, 65–75. [Google Scholar]
- Karami, H.; Rasekh, M. Kinetics mass transfer and modeling of tarragon drying (Artemisia dracunculus L.). Iran. J. Med. Arom. Plants Res. 2018, 34, 734–747. [Google Scholar]
- Suherman, S.; Susanto, E.E.; Zardani, A.W.; Dewi, N.H.R.; Hadiyanto, H. Energy–exergy analysis and mathematical modeling of cassava starch drying using a hybrid solar dryer. Cogent Eng. 2020, 7, 1771819. [Google Scholar] [CrossRef]
- Reyes, A.; Mahn, A.; Vásquez, F. Mushrooms dehydration in a hybrid-solar dryer, using a phase change material. Energy Convers. Manag. 2014, 83, 241–248. [Google Scholar] [CrossRef]
- Eltawil, M.A.; Azam, M.M.; Alghannam, A.O. Energy analysis of hybrid solar tunnel dryer with PV system and solar collector for drying mint (MenthaViridis). J. Clean. Prod. 2018, 181, 352–364. [Google Scholar] [CrossRef]
- Amer, B.M.A.; Gottschalk, K.; Hossain, M.A. Integrated hybrid solar drying system and its drying kinetics of chamomile. Renew. Energy 2018, 121, 539–547. [Google Scholar] [CrossRef]
- Bosomtwe, A.; Danso, J.K.; Osekre, E.A.; Opit, G.P.; Mbata, G.; Armstrong, P.; Arthur, F.H.; Campbell, J.; Manu, N.; McNeill, S.G.; et al. Effectiveness of the solar biomass hybrid dryer for drying and disinfestation of maize. J. Stored Prod. Res. 2019, 83, 66–72. [Google Scholar] [CrossRef]
- Aghbashlo, M.; Kianmehr, M.H.; Arabhosseini, A. Energy and Exergy Analyses of Thin-Layer Drying of Potato Slices in a Semi-Industrial Continuous Band Dryer. Dry. Technol. 2008, 26, 1501–1508. [Google Scholar] [CrossRef]
- Beigi, M.; Tohidi, M.; Torki-Harchegani, M. Exergetic analysis of deep-bed drying of rough rice in a convective dryer. Energy 2017, 140, 374–382. [Google Scholar] [CrossRef]
- Liu, Z.-L.; Bai, J.-W.; Wang, S.-X.; Meng, J.-S.; Wang, H.; Yu, X.-L.; Gao, Z.-J.; Xiao, H.-W. Prediction of energy and exergy of mushroom slices drying in hot air impingement dryer by artificial neural network. Dry. Technol. 2020, 38, 1959–1970. [Google Scholar] [CrossRef]
- Taskin, O.; Polat, A.; Etemoglu, A.B.; Izli, N. Energy and exergy analysis, drying kinetics, modeling, microstructure and thermal properties of convective-dried banana slices. J. Therm. Anal. Calorim. 2021. [Google Scholar] [CrossRef]
- Taheri-Garavand, A.; Karimi, F.; Karimi, M.; Lotfi, V.; Khoobbakht, G. Hybrid response surface methodology–artificial neural network optimization of drying process of banana slices in a forced convective dryer. Food Sci. Technol. Int. 2018, 24, 277–291. [Google Scholar] [CrossRef] [PubMed]
- Islam, M.A.; Mondal, M.H.T.; Akhtaruzzaman, M.; Sheikh, M.A.M.; Islam, M.M.; Haque, M.A.; Sarker, M.S.H. Energy, exergy, and milling performance of parboiled paddy: An industrial LSU dryer. Dry. Technol. 2021, 1–15. [Google Scholar] [CrossRef]
- Li, B.; Li, C.; Huang, J.; Li, C. Exergoeconomic Analysis of Corn Drying in a Novel Industrial Drying System. Entropy 2020, 22, 689. [Google Scholar] [CrossRef]
- Yu, X.-L.; Zielinska, M.; Ju, H.-Y.; Mujumdar, A.S.; Duan, X.; Gao, Z.-J.; Xiao, H.-W. Multistage relative humidity control strategy enhances energy and exergy efficiency of convective drying of carrot cubes. Int. J. Heat Mass Transf. 2020, 149, 119231. [Google Scholar] [CrossRef]
- Castro, M.; Román, C.; Echegaray, M.; Mazza, G.; Rodriguez, R. Exergy Analyses of Onion Drying by Convection: Influence of Dryer Parameters on Performance. Entropy 2018, 20, 310. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Karthikeyan, A.K.; Murugavelh, S. Thin layer drying kinetics and exergy analysis of turmeric (Curcuma longa) in a mixed mode forced convection solar tunnel dryer. Renew. Energy 2018, 128, 305–312. [Google Scholar] [CrossRef]
- Lakshmi, D.V.N.; Muthukumar, P.; Layek, A.; Nayak, P.K. Drying kinetics and quality analysis of black turmeric (Curcuma caesia) drying in a mixed mode forced convection solar dryer integrated with thermal energy storage. Renew. Energy 2018, 120, 23–34. [Google Scholar] [CrossRef]
- Tagnamas, Z.; Lamsyehe, H.; Moussaoui, H.; Bahammou, Y.; Kouhila, M.; Idlimam, A.; Lamharrar, A. Energy and exergy analyses of carob pulp drying system based on a solar collector. Renew. Energy 2021, 163, 495–503. [Google Scholar] [CrossRef]
- Kaveh, M.; Abbaspour-Gilandeh, Y.; Chen, G. Drying kinetic, quality, energy and exergy performance of hot air-rotary drum drying of green peas using adaptive neuro-fuzzy inference system. Food Bioprod. Process. 2020, 124, 168–183. [Google Scholar] [CrossRef]
- Vijayan, S.; Arjunan, T.V.; Kumar, A. Exergo-environmental analysis of an indirect forced convection solar dryer for drying bitter gourd slices. Renew. Energy 2020, 146, 2210–2223. [Google Scholar] [CrossRef]
- Suherman, S.; Hadiyanto, H.; Susanto, E.E.; Utami, I.A.P.; Ningrum, T. Hybrid solar dryer for sugar-palm vermicelli drying. J. Food Process Eng. 2020, 43, e13471. [Google Scholar] [CrossRef]
- Aghbashlo, M.; Mobli, H.; Rafiee, S.; Madadlou, A. Energy and exergy analyses of the spray drying process of fish oil microencapsulation. Biosyst. Eng. 2012, 111, 229–241. [Google Scholar] [CrossRef]
- Das, I.; Arora, A. Alternate microwave and convective hot air application for rapid mushroom drying. J. Food Eng. 2018, 223, 208–219. [Google Scholar] [CrossRef]
- Taghinezhad, E.; Kaveh, M.; Jahanbakhshi, A.; Golpour, I. Use of artificial intelligence for the estimation of effective moisture diffusivity, specific energy consumption, color and shrinkage in quince drying. J. Food Process Eng. 2020, 43, e13358. [Google Scholar] [CrossRef]
- Sehrawat, R.; Nema, P.K.; Kaur, B.P. Quality evaluation and drying characteristics of mango cubes dried using low-pressure superheated steam, vacuum and hot air drying methods. LWT 2018, 92, 548–555. [Google Scholar] [CrossRef]
- Kian-Pour, N.; Karatas, S. Impact of different geometric shapes on drying kinetics and textural characteristics of apples at temperatures above 100 °C. Heat Mass Transf. 2019, 55, 3721–3732. [Google Scholar] [CrossRef]
- Quispe-Fuentes, I.; Vega-Gálvez, A.; Vásquez, V.; Uribe, E.; Astudillo, S. Mathematical modeling and quality properties of a dehydrated native Chilean berry. J. Food Process Eng. 2017, 40, e12499. [Google Scholar] [CrossRef]
- Kaveh, M.; Chayjan, R.A.; Golpour, I.; Poncet, S.; Seirafi, F.; Khezri, B. Evaluation of exergy performance and onion drying properties in a multi-stage semi-industrial continuous dryer: Artificial neural networks (ANNs) and ANFIS models. Food Bioprod. Process. 2021, 127, 58–76. [Google Scholar] [CrossRef]
- Okunola, A.; Adekanye, T.; Idahosa, E. Energy and exergy analyses of okra drying process in a forced convection cabinet dryer. Res. Agric. Eng. 2021, 67, 8–16. [Google Scholar] [CrossRef]
- Liu, Z.-L.; Zielinska, M.; Yang, X.-H.; Yu, X.-L.; Chen, C.; Wang, H.; Wang, J.; Pan, Z.; Xiao, H.-W. Moisturizing strategy for enhanced convective drying of mushroom slices. Renew. Energy 2021, 172, 728–739. [Google Scholar] [CrossRef]
- Aviara, N.A.; Onuoha, L.N.; Falola, O.E.; Igbeka, J.C. Energy and exergy analyses of native cassava starch drying in a tray dryer. Energy 2014, 73, 809–817. [Google Scholar] [CrossRef]
- Mokhtarian, M.; Tavakolipour, H.; Kalbasi-Ashtari, A. Energy and exergy analysis in solar drying of pistachio with air recycling system. Dry. Technol. 2016, 34, 1484–1500. [Google Scholar] [CrossRef]
- Fudholi, A.; Sopian, K.; Yazdi, M.H.; Ruslan, M.H.; Gabbasa, M.; Kazem, H.A. Performance analysis of solar drying system for red chili. Sol. Energy 2014, 99, 47–54. [Google Scholar] [CrossRef]
- Prommas, R.; Keangin, P.; Rattanadecho, P. Energy and exergy analyses in convective drying process of multi-layered porous packed bed. Int. Commun. Heat Mass Transf. 2010, 37, 1106–1114. [Google Scholar] [CrossRef]
- Argo, B.D.; Ubaidillah, U. Thin-layer drying of cassava chips in multipurpose convective tray dryer: Energy and exergy analyses. J. Mech. Sci. Technol. 2020, 34, 435–442. [Google Scholar] [CrossRef]
- Yogendrasasidhar, D.; Pydi Setty, Y. Drying kinetics, exergy and energy analyses of Kodo millet grains and Fenugreek seeds using wall heated fluidized bed dryer. Energy 2018, 151, 799–811. [Google Scholar] [CrossRef]
- Ndukwu, M.C.; Bennamoun, L.; Abam, F.I.; Eke, A.B.; Ukoha, D. Energy and exergy analysis of a solar dryer integrated with sodium sulfate decahydrate and sodium chloride as thermal storage medium. Renew. Energy 2017, 113, 1182–1192. [Google Scholar] [CrossRef]
- Kavak Akpinar, E. The effects of some exergetic indicators on the performance of thin layer drying process of long green pepper in a solar dryer. Heat Mass Transf. 2019, 55, 299–308. [Google Scholar] [CrossRef]
- Mugi, V.R.; Chandramohan, V.P. Energy and exergy analysis of forced and natural convection indirect solar dryers: Estimation of exergy inflow, outflow, losses, exergy efficiencies and sustainability indicators from drying experiments. J. Clean. Prod. 2021, 282, 124421. [Google Scholar] [CrossRef]
- Erbay, Z.; Icier, F. Energy and exergy analyses on drying of olive leaves (olea europaea L.) In tray drier. J. Food Process Eng. 2011, 34, 2105–2123. [Google Scholar] [CrossRef]
- Amjad, W.; Ali Gilani, G.; Munir, A.; Asghar, F.; Ali, A.; Waseem, M. Energetic and exergetic thermal analysis of an inline-airflow solar hybrid dryer. Appl. Therm. Eng. 2020, 166, 114632. [Google Scholar] [CrossRef]
- Szeląg-Sikora, A.; Sikora, J.; Niemiec, M.; Gródek-Szostak, Z.; Suder, M.; Kuboń, M.; Borkowski, T.; Malik, G. Solar Power: Stellar Profit or Astronomic Cost? A Case Study of Photovoltaic Installations under Poland’s National Prosumer Policy in 2016–2020. Energies 2021, 14, 4233. [Google Scholar] [CrossRef]
- Kurpaska, S.; Knaga, J.; Latała, H.; Cupiał, M.; Konopacki, P.; Hołownicki, R. The Comparison of Different Types of Heat Accumulators and Benefits of Their Use in Horticulture. Sensors 2020, 20, 1417. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zadhossein, S.; Abbaspour-Gilandeh, Y.; Kaveh, M.; Szymanek, M.; Khalife, E.; D. Samuel, O.; Amiri, M.; Dziwulski, J. Exergy and Energy Analyses of Microwave Dryer for Cantaloupe Slice and Prediction of Thermodynamic Parameters Using ANN and ANFIS Algorithms. Energies 2021, 14, 4838. [Google Scholar] [CrossRef]
- Kaveh, M.; Abbaspour-Gilandeh, Y.; Nowacka, M. Optimisation of microwave-rotary drying process and quality parameters of terebinth. Biosyst. Eng. 2021, 208, 113–130. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).