1. Introduction
The balanced demand and supply of electrical energy is a key requirement for electrical energy systems. The impacts of climate change on human society have dramatically changed the structure of energy sources by developing a wide range of renewable production plants [
1]. Since the traditional concept of electrical power systems with massive fossil fuel-based power plants is changing towards systems with many small and distributed renewable energy production units, some new challenges have arisen in the fields of the planning, management and operation of electrical power systems [
2]. This new paradigm has fundamentally changed the role of existing fossil fuel-based power plants. Previously stated conditions (initially not considered in the design process) have mostly affected coal-fired power plants. The consequence of reducing their environmental impact is the increased cost of electricity production. Furthermore, the constantly increasing fee for CO
2 emissions has reduced profitability and pushed coal-fired power plants to the brink of profitability [
3]. Increasing plant efficiency may be a possible means to cope with this issue, but in coal-fired power plants, increasing efficiency implies numerous structural changes that in many cases are not justified because of their high cost. On the other hand, to cope with this challenge, many research activities have focused on finding new ways to increase the availability and reliability of a plant.
In this paper, a novel maintenance strategy is proposed for coal mills in a coal-fired power plant based on generalized stochastic Petri nets. In a case study of a coal mill, which is the critical subsystem in a coal-fired power plant, we demonstrated that, by introducing a remedial maintenance method, availability and reliability are significantly increased, and overall maintenance costs are reduced. The goal of this paper is to provide a scientific confirmation that by implementing the proposed remediation-based maintenance, plant reliability can be significantly improved. The work described in this paper differs from those in the relevant literature in several aspects. First, unlike the widespread risk-based maintenance strategies used in many power plants, we propose a simple and effective preventive remediation-based maintenance model. In the application scenario that we were dealing with, we focused on a plant’s the most critical subsystems and found that many faults do not affect process parameters, but cause plant breakdown. We introduced an experienced repair team, that was able, in an early stage of fault detection, to fix the cause of the faults and insure the regular operation of the subsystem. For the sake of clarity, in the rest of this paper, a fault that can be repaired during plant operation will be referred to as damage. Second, by applying the proposed classification of failures, statistical conclusions are drawn based on data gathered during a certain period of plant operation. The degradation process of damages and failures have been modeled using Weibull distributions. Finally, the distribution of times needed for repair damage and failure are described by lognormal distributions. Therefore, to the best of out knowledge, the maintenance strategy of the coal mill in a coal-fired power plant using a generalized stochastic Petri net has not been carried out to date. To summarize, the contributions of this paper are:
The categorization of coal mill faults into two categories;
The introduction of novel maintenance procedures that ensure the remedial of equipment during system operation;
Statistical classification of faults of the coal mill;
A maintenance model based on generalized stochastic Petri nets.
In the remainder of this paper, first we will describe in
Section 2 the coal mills in the observed coal-fired power plant, give a brief overview of the maintenance strategies implemented in thermal power plants, and provide an introduction of generalized stochastic Petri nets.
Section 2.4 introduces a remediation-based maintenance method modeled using GSPNs. The data collected during an extensive period of coal mill operation of the thermal power plant located in Plomin, Croatia, and the verification of the proposed maintenance method can be found in
Section 3. Finally, the results’ discussion, concluding remarks and future research directions are given in
Section 4.
Literature Overview
Maintenance is defined as all administrative and technical actions which ensure that a system is in its required functioning state [
4]. In a complex technical system, an adequate maintenance policy should be implemented in order to reduce unplanned system breakdowns and to increase the available operational time. Preventive maintenance is a proactive maintenance approach by which repair actions are scheduled during the system’s planned stops. Maintenance actions aimed at increasing the reliability of any complex system and reducing maintenance costs should be appropriately selected and performed after an adequate period of operation. To do so, many modeling techniques have been developed that analyze the system’s performance. In the field of electric energy production, the most commonly used evaluating models are based on discrete events with different statistical classification (such as Markov chain, probability reward networks and Petri nets.) [
5].
The earliest scientific approaches in maintenance optimization for thermal power plants were introduced in [
6,
7]. A similar approach was taken in the field of reliability-centered maintenance [
8,
9,
10,
11], where the objective of the proposed methods was to identify the most critical components of the system on which maintenance activities should be focused. Novel maintenance approaches have recently been investigated in the field of renewable energy sources such as hydroelectric and wind power plants. For instance, the authors in [
12], proposed a multi-criteria decision-making model for determining the maintenance periods of the most critical equipment in a hydroelectric power plant. On the other hand, the reliability of wind power farms was determined using artificial neural networks that dynamically estimated the impact of operational conditions on the failures of wind turbines, as has been presented in [
13]. Alternative approaches for increasing reliability and durability in enterprises in the energy sector based on digitization, digital twins, blockchain and Industry 4.0 can be found in [
14].
Promising results in terms of minimizing the costs of system failure were already obtained in the maintenance strategy optimization of the cooling towers of a coal-fired power plant [
15]. The authors increased the availability, reliability and performance of the plant’s subsystem by defining the proper size of a repair team. The simulations were carried out using generalized stochastic Petri nets, where each cooling tower was modeled with the same basic model with five operational states. However, for coal-fired power plants that are not equipped with cooling towers, such as the power plant introduced in this paper, where the advantage of the plant’s location at the sea coast is taken into account, and the cooling process is implemented using seawater, the described model is not applicable. On the other hand, in a coal-fired power plant, there are many other components that play a more crucial role for stable and continuous electricity production. For instance, the maintenance optimization of a turbo-generator of a thermal power plant using a particle swarm optimization algorithm was described in [
16]. The importance of the coal mill in coal-fired power plants was recognized as a critical component that ensures the performance, reliability and effectiveness of the plant [
17]. Thus, substantial research interest in the field of process monitoring and fault diagnosis of coal mills is not surprising. Remarkable examples of intelligent solutions for faults’ detection in coal mills are given in [
18,
19,
20], while methods for modeling a coal mill for fault monitoring and diagnosis are considered in [
21,
22]. Another interesting model capable of predicting power plant availability implemented using a generalized stochastic Petri net has been carried out in [
23]. The main drawback of this solution is the assumption that the degradation process of the equipment is linear, which, in general, is not the case for the coal mills subsystem.
The fault diagnosis of discrete event systems based on Petri nets has been extensively researched in the field of computer hardware and software [
24,
25,
26], communication networks [
27,
28], sensor networks [
29], and discrete event systems [
30,
31]. A further advantage of Petri nets is their ability to introduce timed transitions between states that can change over time.
2. Materials and Methods
In this section, we describe the operational principle of coal mills in a power plant, its importance in coal combustion process and frequently appearing faults. After that, we provide an overview of the maintenance polices used in power plants and address how the quality of the maintenance process can be quantified.
2.1. Coal Mills Description
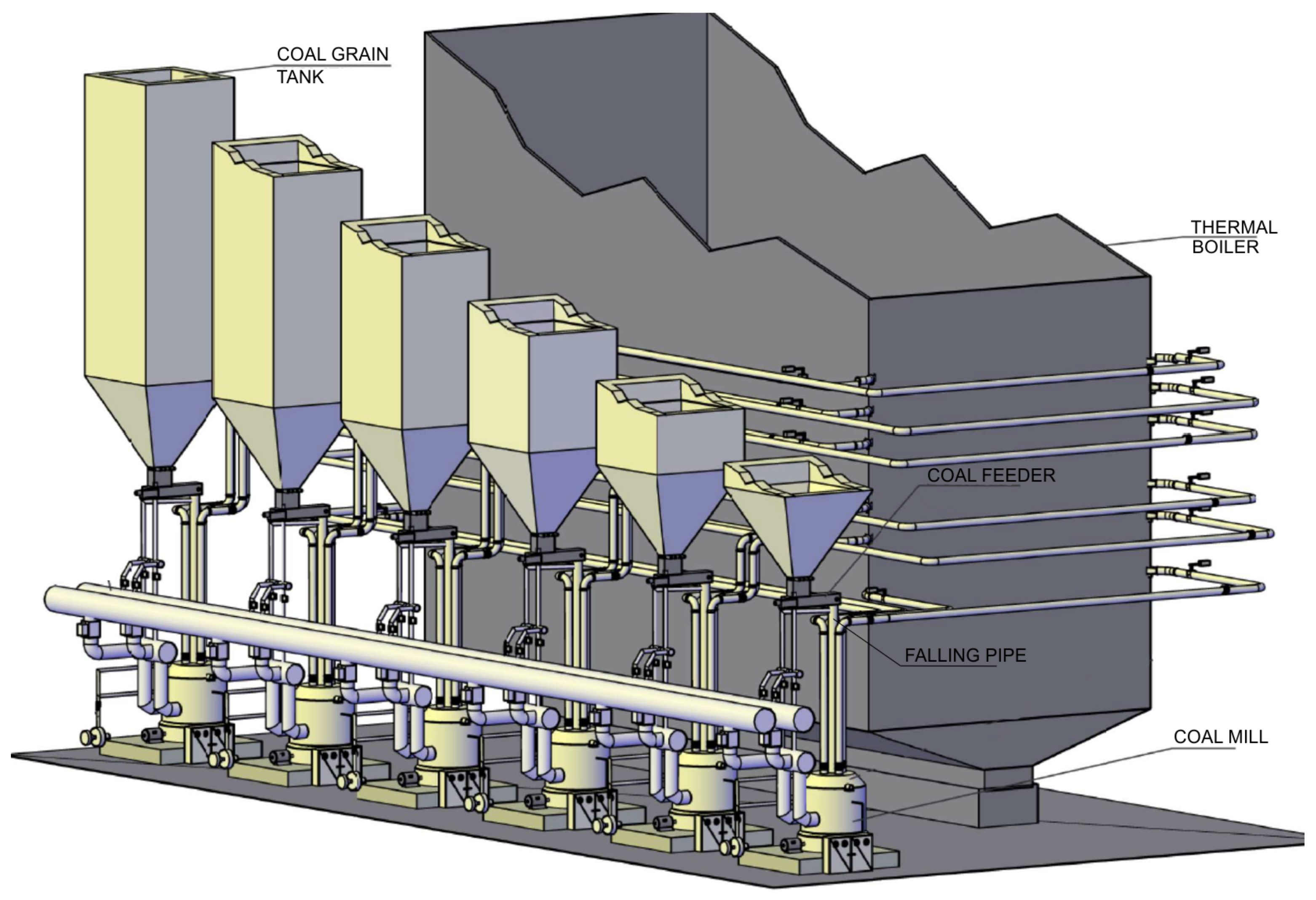
The basic process in a coal-based thermal plant, beyond the production of electrical power, is the transformation of chemical energy embodied in coal-to-thermal energy that is then transformed into mechanical energy used to spin the turbine. The mentioned ability of energy transformation is a result of coal combustion inside a thermal boiler. However, in order to achieve the required heat generation, coal combustion should be carried out under appropriate and time-constant conditions. Thus, the requested quantity and quality of coal powder entering the furnace of the boiler is provided by six coal mills, specifically positioned at certain locations of the boiler, as presented in
Figure 1. Each component of such a complex system should be in perfect operating condition to guarantee proper operation during the extensive time of exploitation. At the same time, the continued degradation of essential elements in the system could disrupt its functionality and cause breakdowns. During exploitation, we found that several critical faults responsible for production breakdown are often caused by components that are a part of the coal mill subsystem. Because of the complex nature of the power plant and the countless faults that could potentially cause plant breakdown, we optimized maintenance actions and costs by determining two crucial components, i.e., the coal feeder and falling pipe of the coal mill subsystem that are responsible for most faults. It is important to note that in the current maintenance strategy, any fault reported on one of these two components of the coal mill causes the automatic unavailability of the power plant. Frequent power outages, in addition to losses caused by undelivered electrical power to the distribution network, are also causing additional costs due to the complex and lengthy process of restarting the electricity production.
The raw coal is transported from the grain tank using the coal feeder, onto the falling pipe and then enters inside the coal mill where the coal particles are mixed with air and transferred into the furnace. The coal feeder, shown in
Figure 2a, consists of a belt conveyor driven by an AC motor with controllable rotational speed and various sensors. Its capacity is from 6 to 15 t/h. The falling pipe, shown in
Figure 2b, is a 6.5 m-long pipe that is shielded with another wall where hot air flows. This structure facilitates the continuous transportation of coal without clogging caused by variation in the moisture level of raw coal.
2.2. Maintenance Strategies Overview
Maintenance policy defines actions prior and during system failure in order to reduce breakdown time and maintenance costs, as well as increase the availability, reliability and efficiency of the observed plant [
32]. The preventive maintenance determines predefined actions that are based on the system’s measurable physical parameters and component lifetime [
33]. It can be implemented using two approaches: a time- and condition-based approach. A time-based approach includes overhauls and scheduled checks planned according to system’s operating hours depending on whether a failure occurred or not, and it is assumed that this approach brings the equipment to its initial operating state (as good as “new”). The advantage of this approach is that it reduces the repair costs, but it may increase loss of income due to production downtime and cold start costs. The second approach is based on process conditions where actions are taken according to data monitoring and fault diagnostic systems. The process data can include important system parameters or reliability functions.
In the observed 220 MW coal-fired power plant, the maintenance policy is based on prevention, where each crucial equipment of this complex system has a predefined set of actions that should be performed periodically. Additionally, in addition to a time-based maintenance approach, the maintenance strategy implemented in the described power plant defines activities that should be performed based on some crucial process parameters. The coal mill fault detection system is monitoring the values of those parameters and is taking actions according to their limits. Now, we outline two types of faults that commonly occur in coal mills: failure and damage. Failure is a fault where the values of process variables exceed permissible limits and cause the system’s breakdown. It can potentially cause the greater destruction of equipment and impact the environment and safety of operators, so it is very important to detect failure in its early stage. Damage is defined as the incompatibility of process variables from their reference values with an acceptable environmental impact (if some impact exists). Additionally, the overall system’s performance after the appearance of the damage is within allowed boundaries. Considering this, in large-scale plants, best practice in maintenance is often very useful, after an elementary analysis given in [
34], we noticed that the coal mill damage can be repaired during plant operation. Therefore, we introduced a remediation-based maintenance strategy, which defines a set of faults that do not have an implication on process performance (damages) and a set of actions that can be performed to repair those faults. It is important to notice that repair actions restore the component under fault to conditions which are as good as new, which means that the component has initial technical characteristics and effects of the repair work on its performance can be neglected.
From the maintenance perspective, the following indicators should be defined in order to quantify the effectiveness of a chosen maintenance approach applied on a certain technical system. The availability of a technical system is defined as the ability of a system to perform its required function over a certain period of time and it can be given by the following equation:
Additionally, a statistical analysis of the data gathered from the observed system during operation should be carried out. Among many probability density distributions, the Weibull distribution is the one commonly used for describing the lifetime of a system or its component. The Weibull probability density function over time
t is defined as
where
is the shape parameter and
is the scale parameter. On the other hand, to determine the time needed for repair, the longnormal distribution is commonly used. Its probability density function is defined as
where
t is time,
is the standard deviation of the natural logarithm and
the mean of the natural logarithms.
The reliability of a technical system is the probability that a system will properly perform its designed functions satisfactorily during a specified period of time and under a given set of operating conditions. The reliability of the Weibull distribution is given in the following form:
Further details on maintenance performance measurements and indicators can be found in [
35].
2.3. Generalized Stochastic Petri Nets
Herein, we introduce the Petri net (PN) notation and definitions. PN is an alternative representation of automata and is used for modeling discrete event systems, where states are associated with places and events are associated with transitions. A system can be described with a graph that defines the explicit conditions under which a transition between two nodes can occur [
36]. A PN is a weighted bipartite graph
, that consists of:
—a finite set of places;
—a finite set of transitions;
—a set of arcs representing connections between places and transitions;
—the initial marking of places.
The PN graphical representation includes two types of nodes (places and transitions), arcs and tokens. Each type of node is represented with a different symbol, places are represented with circles and transitions are represented with bars. The tokens are described by a black dot located inside the places representing a method that indicates when the conditions described by a certain state are satisfied. One or more tokens can be assigned to each place. The process of assigning tokens to the places of a PN graph is defined as marking. The initial marking
defines token positions at the beginning of the process. Additionally, we assume that
has no isolated places or transitions. A comprehensive overview of the PN can be found in [
37].
With the described concept of PN, it is possible to examine a sequence of events without any knowledge about time. Thus, the authors in [
38] presented the stochastic Petri nets where transitions are related with time-driven probabilistic models. In [
39], a complex system with multi-unit configuration is modeled by generalized stochastic Petri nets (GSPN) where the time to failure of degraded components follows a Weibull distribution.
2.4. Remediation-Based Maintenance Method
Our basic idea for the proposed maintenance principle is based on the observation that a certain equipment in complex production plants is causing the majority of breakdowns. In the coal-fired power plant introduced in the previous section, the experienced maintenance engineers noticed that the coal mill is often a cause of the system’s failure. A comprehensive analysis of the observed thermal plant showed that some types of failures (damages) do not affect the process. In other words, after the occurrence of such a failure, the system enters a stage of degradation, often called the degradation zone. During the degradation state, the condition of the system deteriorates and causes system breakdown. We assume that an experienced repair team is able to fix a damage after its occurrence before it progresses to the condition that has impact on a process variable and/or safety. The goal of the proposed approach is to verify whether the performance of the plant can be improved by introducing a novel remediation-based maintenance strategy for the coal mill. We consider a coal mill with two main components, i.e., the falling pipe and coal feeder. Each subsystem of the mill can be represented with a separate GSPN, where the firing time distributions of each subsystem were provided based on statistical analysis.
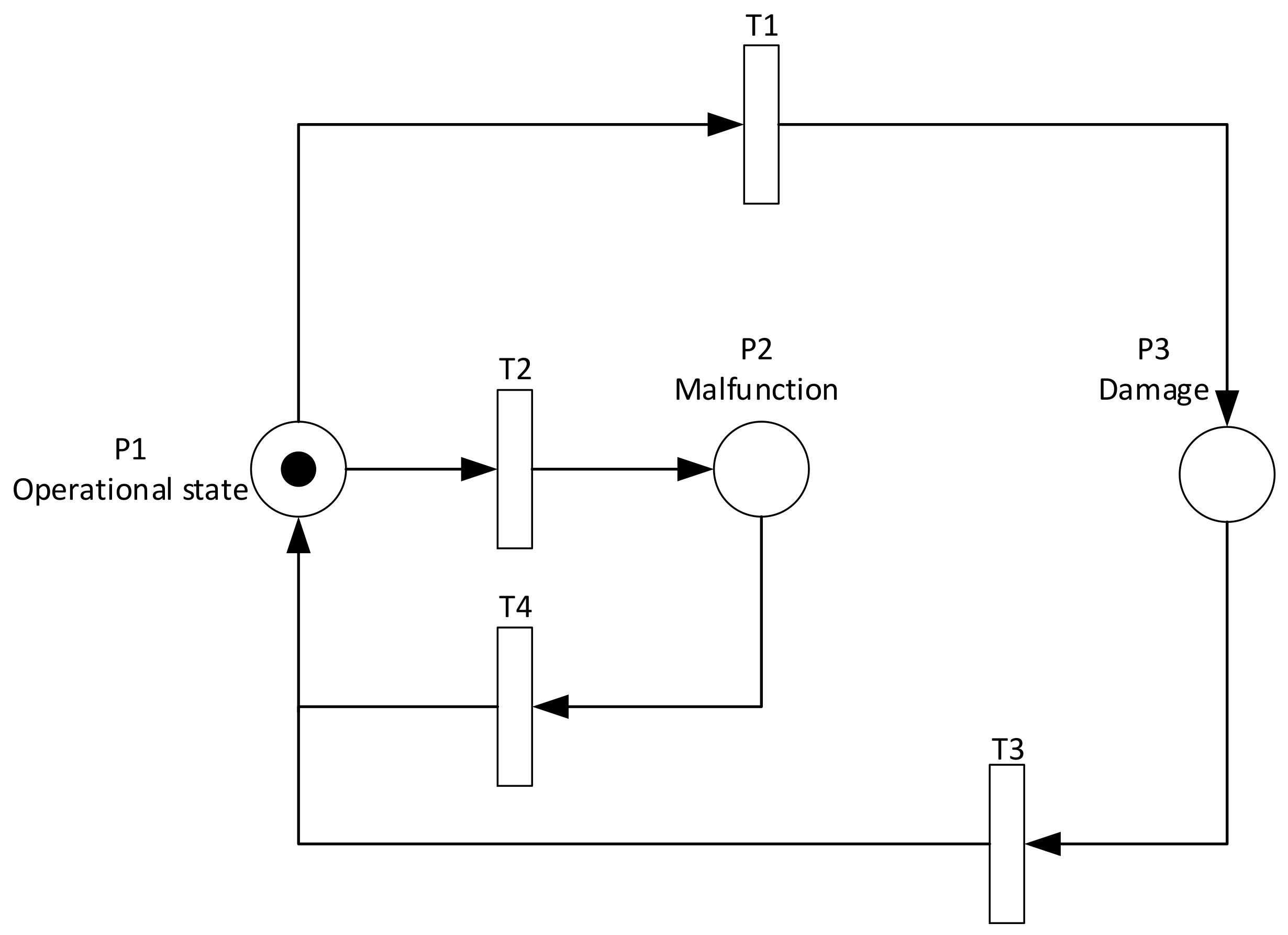
Now, we introduce a simple GSPN by which the single component of a coal mill can be described. The GSPN graph of a basic component of the coal mill is demonstrated in
Figure 3. It can be represented with three states:
P1—operational state;
P2—damage state;
P3—failure state.
We assume that the initial state of the Petri net is the operational state (P1). During the operation of the system, depending on the elapsed time and transition values, T1 and T2, failure or damage can occur. Time transition values are randomly generated (based on the Weibull distribution for failure and damage) when a token is placed into an operational state. The main assumption about the damage state (P2) and failure state (P3) is that maintenance operators are immediately available after the state is activated and starts the repair process. Additionally, we assume that actions conducted as part of the repair procedure will restore the regular operating conditions of the components, i.e., the work performed during maintenance will not affect the performance of the subsystem. The time necessary to repair a component is embodied by transitions T3 and T4, which are based on lognormal distribution for each type of repair.
By combining two basic components, where the first GSPN describes a falling pipe (PN1), and the second GSPN describes a coal feeder (PN2), we propose a simulation model of the coal mill (presented in
Figure 4). The purpose of the model was to evaluate the hypothesis that, by introducing a remediation-based maintenance strategy, the effectiveness of the whole system can be improved. Therefore, the status of the coal mill in the aforementioned model is described through a simple Petri net (PN3). The PN contains two states, i.e., P10 indicates whether the coal mill is operating properly, and P11 indicates a failure of its components. Immediate transitions T10 and T11 are triggered by falling pipe and coal feeder Petri nets in cases when any kind of failure happens or a component is repaired.
3. Results
Based on data collected from the actual power plant obtained over more than eight years of operation, a statistical analysis was carried out in
Minitab. The obtained parameters of the probabilistic distributions for each event were used in simulations performed in
Matlab. We decomposed the data derived from the coal feeder and falling pipe, and classified it into two types of failures.
Table 1 and
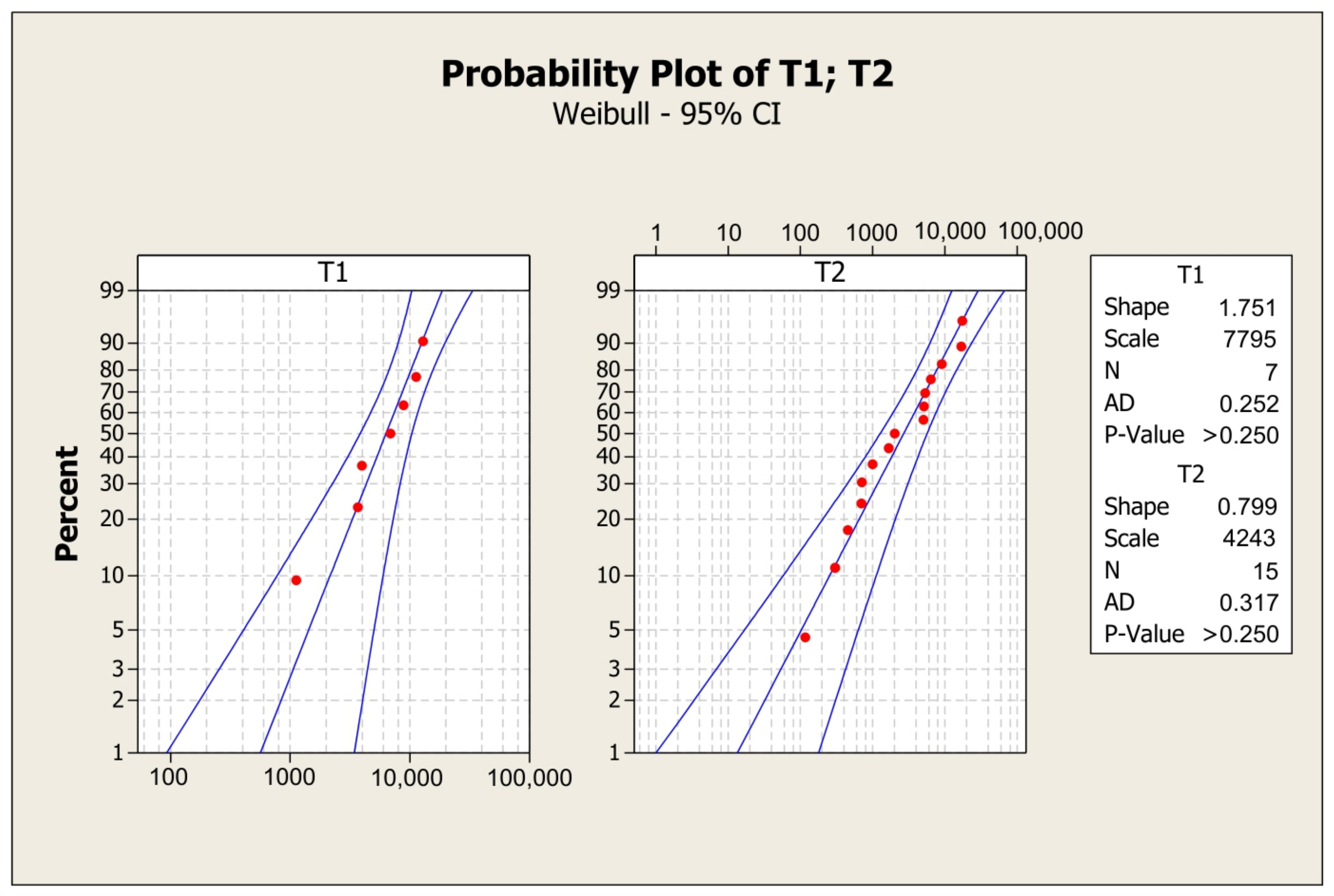
Table 2 represent the empirical data for coal feeder failures and damages, respectively. By applying the maximum likelihood estimation (MLE) method, parameters of the Weibull probabilistic distributions for time-to-failure and time-to-damage for the coal feeder were estimated. The probabilistic distribution of the time necessary for repairing a failure and damage was described by lognormal distributions. The significance level of estimated probabilistic distributions is 5%. A graphical representation of Weibull and lognormal distributions are presented in
Figure 5 and
Figure 6. As can be shown in
Figure 5, the shape and scale parameters of the Weibull probabilistic distribution of the coal feeder time-to-failure (T1) are
and
, while goodness of fit was calculated using the Anderson–Darling statistical test. The goodness-of-fit measure indicates how well the data follow a particular distribution. The Anderson–Darling test gives a smaller value for data that better fit certain distributions. An additional measure of the degree to which the data follow the specified distribution is provided by a
p-value of the Anderson–Darling test. If the
p-value is available, its value should be greater than the chosen significance level, which in our case is
p-value > 0.05. A more detailed description concerning the methodology for determining probabilistic distributions can be found in [
40].
Figure 6 graphically represents the goodness of fit of the coal feeder repair periods that are estimated by lognormal distributions for each event, where the variable
Loc describes the mean of the natural algorithm
and the variable
Scale indicates the standard deviation
according to Equation (
3). For instance, it can be seen that for time to repair from failure (T3), the parameters of the lognormal distribution are equal to
and
. According to Anderson–Darling test, the data of both events follow the calculated distributions with the significance level of 5%.
In a similar manner, statistical analysis was carried out for the falling pipe. The data gathered for the falling pipe during plant operation are shown in
Table 3 and
Table 4. However, due to space constraints, graphical representation and statistical tests for the falling pipe were omitted.
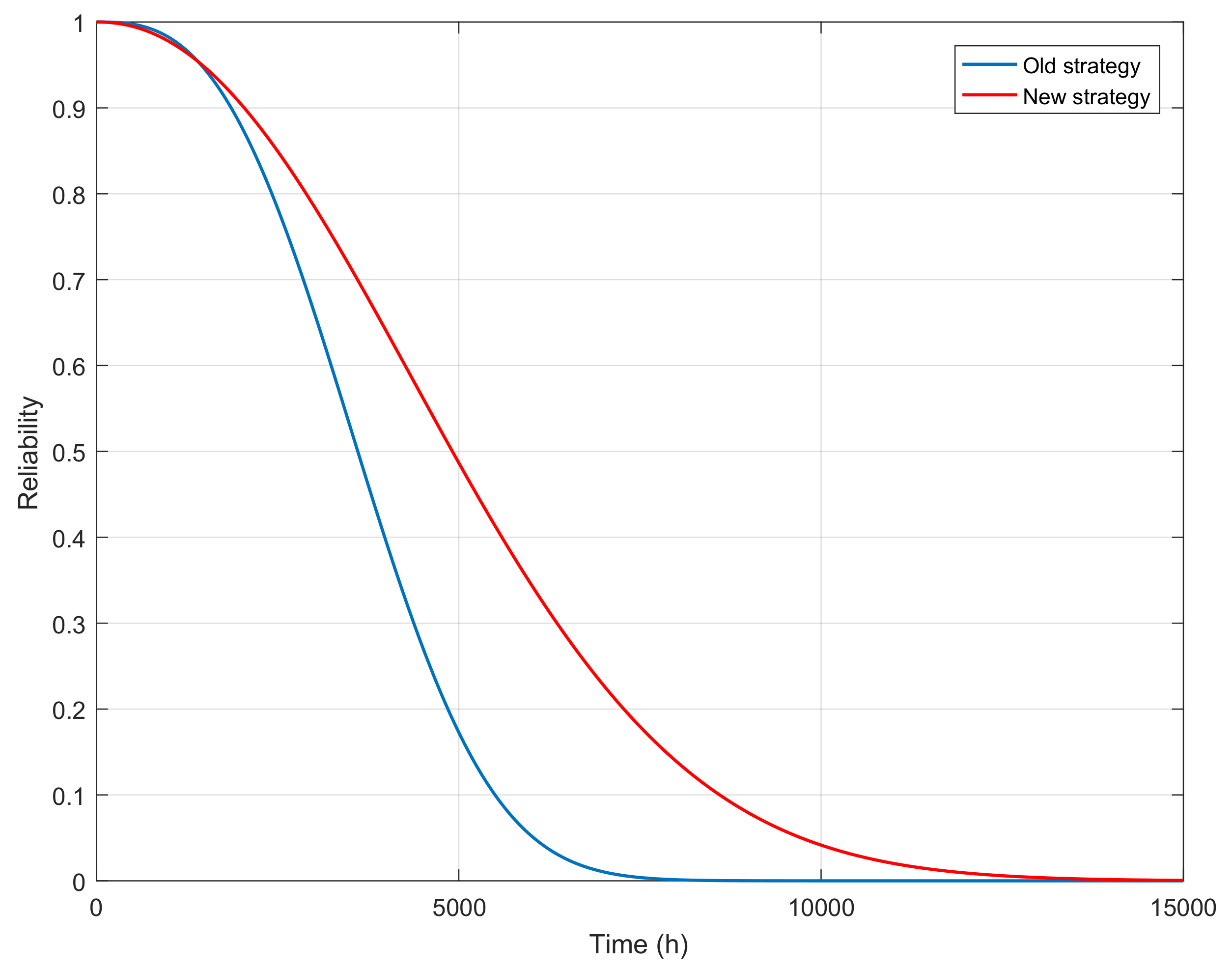
Simulation experiments were conducted by running the GSPN described in the previous section. The duration of the simulations performed was set to 50,000 h or approximately 2083 days, in order to present the benefits of the proposed remediation-based maintenance strategy in a single run. Obtained results were compared with the results of the actual maintenance strategy that does not have the possibility to repair a fault without stopping the delivery of the coal powder in the plant furnace, i.e., the unavailability of a thermal power plant. Comparison of the reliability value of coal mills with an existing (old) corrective maintenance and the proposed (new) remediation-based maintenance strategies is shown in
Figure 7. In general, the reliability value for a component asymptotically approaches o zero over time; however, the reliability value of the old strategy, presented with the blue line, is (except for a small amount of time at the beginning) lower than the reliability value of the new strategy.
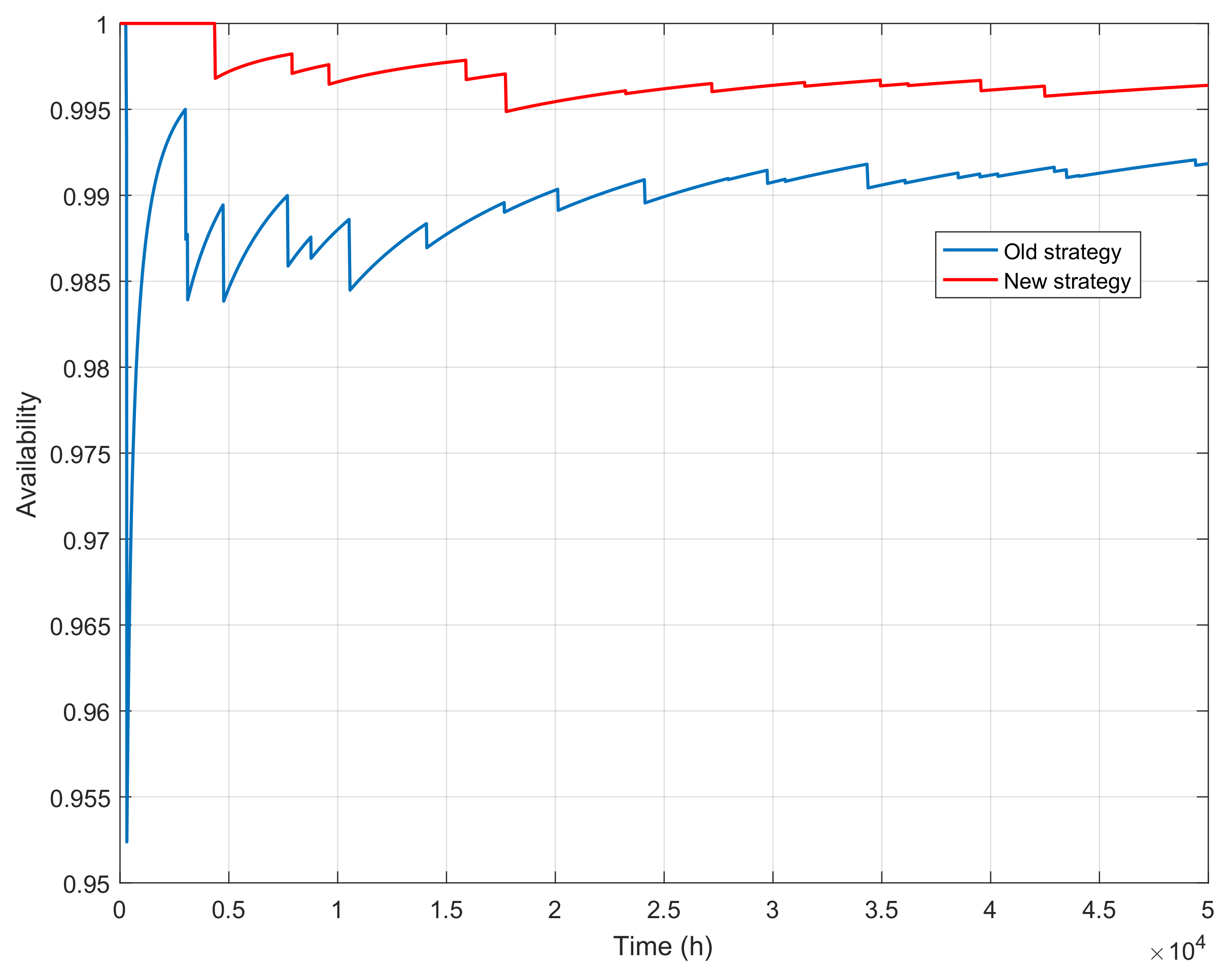
Figure 8 shows the availability of the simulated model, which is another important measurement of the system’s performance. As can been seen, the availability value of the proposed remediation-based maintenance is higher than the availability value of the old strategy during the entire period of simulation. After a year (8760 h) in operation, the availability of coal mills, when the new strategy is applied, is equal to
of the availability when the old maintenance strategy is applied—while during the same period, the availability of coal mills, when the proposed remediation-based maintenance is used, is equal to
. It can also be noticed that a minimal availability value for the old strategy (
) is much lower than the minimal availability value of the new strategy (
).
Finally,
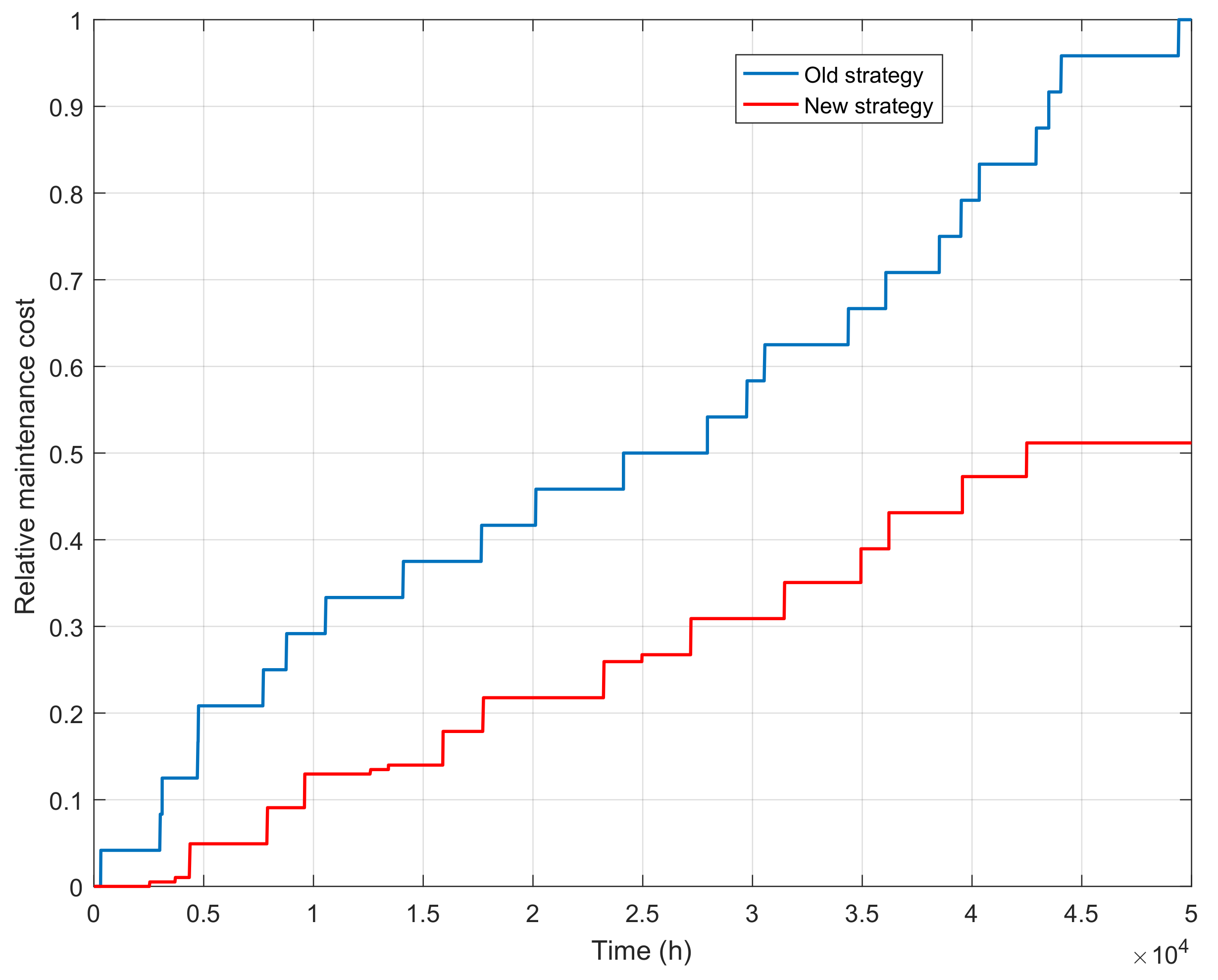
Figure 9 shows the maintenance costs of the coal mill obtained in the performed simulations. In order to emphasize the relative difference between the costs of two different strategies, the maintenance costs were scaled to values in the range from 0 to 1. We defined the cost of each maintenance action, i.e., the cost of failure and the cost of damage. The cost of failure includes the cost that reflects the time required to repair a certain component plus the cost incurred due to unrealized revenue. On the other hand, for the damage of a component, the repair cost is equal to the cost of the material consumed and the time spent during repair works. For the falling pipe, a failure repair cost is equal to 0.83, while the damage repair cost is equal to 0.17. Furthermore, failure and damage repair costs of the coal feeder are equal to 0.89 and 0.11, respectively. As can been seen in the plots, after the first year (8760 h) of operation, the cost of the old strategy is equal to 0.29, while the cost of the new strategy is equal to 0.09. Therefore, the proposed remediation strategy reduced the maintenance cost by
after one year of operation. After the second year of operation, the savings in maintenance costs are equal to
, while at the end of the simulation, the cost savings are
.
4. Discussion
Due to rapid changes in the structure of electricity production, increasing the efficiency of coal-fired power plants that are already in operation has become an important challenge for maintenance engineers. The question is how to determine adequate maintenance procedures and a decision-making process to maximize plant operation without unexpected breakdowns. It is obvious that this an optimization problem.
The main hypothesis tested in this paper is the possibility of increasing the reliability and availability of coal mills by introducing remediation procedures in the repair actions of certain failures. Firstly, data about failures during coal mill operation were collected, statistically analyzed and used for remediation-based maintenance strategy design using GSPNs. Obtained results show that the appropriate categorization of system failures and adequate maintenance activities in a production process are a fundamental prerequirement for reliable, efficient and profitable plant’s operation. An unplanned stop of the coal-fired power plant, in addition to unrealized revenue and penalties for undelivered electrical power, not only causes costs of maintenance actions and spare parts, but also extensive cost in terms of fuel and electrical power (consumed from the electrical network) required for the so-called cold start, i.e., as resuming production means that the system should be heated up by another and more expensive type of fuel before the steam can be produced by burning coal. From an environmental impact point of view, this means that each breakdown increases emissions per unit of produced energy.
Future work will include a comparison of the results obtained in the actual plant during an extensive period of exploitation with simulated results. Our ongoing work is focused on introducing a relation between the number of unplanned stops and costs caused due to increased maintenance costs and unrealized revenue during the period of system breakdown. Additionally, the proposed strategy will be extended to encompass other subsystems in the power plant where remediation can be applied.