Abstract
One of the main characteristics of power systems is keeping voltages within given limits, done by implementing fast automatic voltage regulators (AVR), which can raise generator voltage (i.e., excitation voltage) in a short time to ceiling voltage limits while simultaneously affecting the damping component of the synchronous generator electromagnetic torque. The efficient way to increase damping in the power system is to implement a power system stabilizer (PSS) in the excitation circuit of the synchronous generator. This paper proposes an enhanced algorithm for PSS tuning in the multimachine system. The algorithm is based on the analysis of system participation factors and the pole placement method while respecting the time domain behavior of the system after being subdued with a small disturbance. The observed time-domain outputs, namely active power, speed, and rotor angle of the synchronous generator, have been classified and validated with proposed weight functions based on the minimal square deviation between the initial values in a steady-state and all sampled values during the transitional process. The system weight function proposed in this algorithm comprises s-domain and time-domain indices and represents a novel approach for PSS tuning. The proposed algorithm performance is validated on IEEE 14-bus system with a detailed presentation of the results in a graphical and table form.
1. Introduction
Low-frequency oscillations, also known as electromechanical oscillations, were first noticed in the American West system. They can appear in large interconnected systems within the frequency range between 0.01 to 3 Hz [1], mainly caused by an imbalance between energy demand and generation. Electromechanical oscillations represent characteristic system responses (low-frequency modes) to a disturbance in the system and, if not properly damped, can lead to system instability [2]. PSSs are a practical solution for electromechanical oscillations damping and their implementation as an additional block in generator excitation systems is simple. PSS is the most efficient for local oscillatory modes with frequencies 6–12 rads−1 and can also be used to improve transient stability mostly combined with AVR [3,4] or flexible AC transmission system devices (FACTS) [5,6,7].
However, PSS tuning is a complex task. One of the most common methods for the PSS tuning is a pole placement method where the dominant pair of the poles of the observed power system is damped and shifted to the left side of the S-plane by selecting the proper PSS parameters. One of the challenges for PSS implementation in a multi-machine system is to find an optimal PSS location. Participation factor analysis shows the impact of each generator on the system state variables and thus indicates the location where PSS should be implemented [8]. Participation factors can be found for both monotone and oscillatory modes. In comparison with oscillatory modes, participation factors are very low for monotone modes [9]. In papers [10,11], the participation analysis is applied on a large multi-machine system to identify critical generators and modes in the system. Several papers combine both the participation factor analysis in the multi-machine system and advance methods for PSS tuning [12,13,14]. The author [15] presents global pole placement problems as the composition of separate global and local pole-placement problems used to solve local oscillatory modes, usually undamped. This solution was applicable for multiple operating conditions, which led to a robust design technique [16]. In paper [17], extensive research on system stability for various combinations of system parameters is performed. In a three-part paper [18,19,20], PSS application and a complete tuning process are overviewed. Over the years, application and tuning processes evolved into more sophisticated methods, mostly heuristic methods [21,22,23], like genetic algorithms [24], fuzzy logic [25,26], or other optimization techniques [27,28]. Paper [29] compares three different types of stabilizers, conventional PSS (CPSS), fuzzy, and adaptive neuro-fuzzy inference system (ANFIS) based PSS. All three types show appropriate responses to a system disturbance, giving a slight advantage in performance to ANFIS. Artificial intelligence methods are mainly applied on single machine infinite bus (SMIB) system models, as in [30,31,32,33,34]. Additionally, many novel approaches for PSS and AVR tuning are applied on SMIB, for example, nonlinear robust PSS-AVR controller [35]. However, PSS tuning in multi-machine systems is much more complex in comparison to SMIB since one generator can deteriorate the performance of other generators in the system.
In most papers, tuning of the PSS parameters is based on results in the S-domain [36,37,38], and, afterwards, results were verified in the time domain by comparing the system response to disturbances before and after PSS implementation. Due to the possible inertia decrease with high penetration of converter-interfaced renewable energy sources, the modern power system may become more vulnerable to disturbances that can initiate low-frequency oscillations. From the consumer side, the amplitude of active power low-frequency oscillations is particularly unfavorable since they can lead to load shedding. The PSS parameters obtained with the traditional pole-placement method show satisfactory results regarding s-domain system performance measures; however, this paper points to the improvement of damping of the low-frequency oscillations when the time-domain system performance measures are included in the PSS tuning too. Hence, the paper proposes the algorithm for the PSS1A tuning considering both the s-domain and time-domain system performance measures. The synthesis of these measures is achieved through the proposed weight functions that output comparable absolute values; the s-domain weight function is proposed as the damping ratio of the damping oscillatory mode since the damping ratio takes values between 0 and 1; the time domain weight functions are proposed as the distance between value 1 and the sum of the square differences from the initial steady-state value and the sampled values of the observed variable during the time-domain simulation of the disturbance in the system. The proposed time-domain weight functions are related to active power, speed, and the rotor angle of the generator where the PSS has been implemented according to the participation factor analysis and represents the generator with the most significant contribution to the dominant system mode. The output of the weight functions closer to value 1 indicates the higher function weight. The sum of the s-domain and time-domain weight functions constitutes a system performance weight function. The maximum of the system performance weight function is obtained with the PSS parameters variations in an ascending and a descending order in separate clusters. The PSS parameters that correspond to the maximum of the system weight function are classified as optimal.
This paper consists of six sections. The Introduction provides a literature overview of the PSS tuning techniques and briefly highlights the novelties proposed in the paper. The second section gives a brief description of the PSS1A structure. The proposed algorithm for PSS1A tuning, considering both the s-domain and time domain system performance measures, is the scope of Section 3. In the fourth section, the application of the proposed algorithm is examined on the performance of the IEEE 14-bus system model after initiation of the disturbances with a different duration within three case studies. The Discussion follows the Results, presented in figures and tables for all case studies. Final remarks and possible benefits from the application of the proposed algorithm are given in the Conclusion.
2. Materials and Methods
The authors conducted an extensive literature review on the topic of PSS tuning, covering both the fundamentals of tuning and modern optimization methods. Based on this research, it was found that commonly used PSS tuning procedures based solely on the s-domain system performance measures can be improved by involving the time-domain system performance measures. To address this deficiency, the authors proposed a method that includes both domain system performance measures to find the optimal PSS parameters. The results were verified on the IEEE 14–bus test system consisting of five generators with parameters publicly available. All generators are equipped with standard IEEE AVRs models with parameters available in the Appendix A.
3. PSS Structure
Power system stabilizer provides an additional damping torque in a phase with generator speed variation and it is simply implemented as a part of the synchronous generator excitation system [18]—Figure 1.
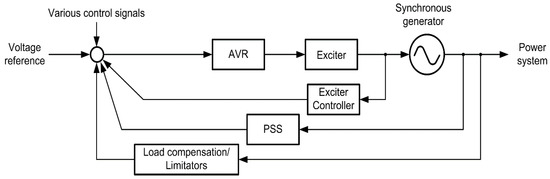
Figure 1.
Synchronous generator excitation system.
The main structure of the PSS presented in Figure 2 (also known in [39] as PSS1A), consists of the gain, wash-out filter, and phase compensation blocks (lead-lag filters). Some additional blocks, such as high-frequency torsional filters or transducer time constant compensation, may be implemented [39]. Torsional filter block can be implemented by defining constants A1 and A2. If the torsional filter is to be neglected, these constants are set to be 1 and this block is used to compensate torsional modes, which are the result of rotational movement. The first block is used to compensate transducer time constant and can be neglected by setting time constant T6 to 1.

Figure 2.
Type PSS1A single-input power system stabilizer. Reproduced from [39], Copyright 2016 IEEE.
Gain KS defines a circuit gain and damping torque. Gain increase leads to damping increase until it reaches a maximum point after which a further gain increase results in less damping torque [40]. Gain should be tuned following the maximum damping but also all the other limitations need to be taken into consideration. The second block is the wash-out filter (defined by its time constant T5). This is a high-pass filter which defines the operating margin for PSS. PSS should not respond to small and slow changes which are mostly caused by a change of the system operating point. Wash-out filter eliminates these disturbances and only reacts to transient disturbances [40]. The value of T5 must be in a range in which it does not change observed frequencies but also does not lead to unwanted voltage trips. The range for T5 is 1 to 20 s [41]; for local modes, it should be 1–2 s and 10–20 s for interarea modes [42]. Input in an excitation system and electrical torque as an output signal has a phase shift, which needs to be compensated. Phase compensation is achieved with cascade lead-lag filters, which are presented with constants T1–T4. To simplify the process, it is assumed to be T2 = T4 and T1 = T3. T2 and T4 usually have fixed values and the other two-time constants need to be tuned. PSS output voltage needs to be limited to restrict terminal voltage fluctuations [43]. The output voltage is limited between values VSTmin and VSTmax.
4. PSS Tuning Algorithm
The first step in PSS tuning in the proposed algorithm is the system modal analysis in order to identify a dominant oscillatory mode since it determines the dynamic system properties. Each oscillatory mode is the system eigenvalue represented as a complex pair with the real part—the damping constant, and the imaginary part—the oscillation (damping) frequency. The dominant system oscillatory mode is identified as the complex pair closest to the imaginary axis on the system S-plane. The pole placement method used in this algorithm aims to nullify the imaginary part of the dominant system mode and to significantly shift it left from the initial location on the S-plane integrating the PSS into the system [1]. The most efficient PSS application would be for the damping frequencies range of the dominant system mode within 1.5–12 rads−1, i.e., for the inter-area and local oscillatory modes [44]. Hence, the system oscillatory modes with damping frequencies outside this range will not be the subject for this paper’s analysis.
Once the appropriate dominant system mode is identified, the proposed algorithm tends to find an optimal location for the PSS implementation in the multi-machine system. Participation factors determine the contributions of each active component in the system oscillatory properties [41]. Since the PSS affects the system damping, the participation of the state variable speed for the dominant oscillatory mode is chosen as a criterion for the PSS allocation, which implies that the excitation system of the synchronous machine with the highest participation of the state variable speed in the dominant oscillatory mode is the most appropriate for the PSS implementation.
The PSS tuning optimization is based on the optimal selection of the PSS parameters: the washout filter time constant-T5, gain-K, and lead-lag time constants-T2 = T4 and T1 = T3. According to the suggestions in literature [18,19,20,39,45], the lead-lag-T2 = T4 constants should be set to fixed value T2 = T4 = 0.02 s. The washout filter time constant is set to T5 = 10 s according to the suggested values in [18,19,20,40]. The initial gain- is determined according to the damping of the dominant oscillatory mode- represented as [45]:
and should be at least equal to coefficient-:
While coefficient-H represents an inertia time constant of the synchronous machine with the highest participation in the dominant oscillatory mode.
As recommended in [18,19,20,39], the initial value for time constants T1 and T3 should be T1 = T3 = 0.2 s.
The PSS tuning procedure proposed in this paper is the optimization problem to find the PSS gain-K and the PSS time constant-T = T1 = T3 for the maximal left-shift and the maximal damping ratio ζdom of the dominant oscillatory mode in the S-plane considering the time-domain behavior of the rotor angle, speed, and active power of the synchronous machine with the highest participation in the dominant oscillatory mode after initiating a (small) disturbance in the system.
The time-domain indices presented in this paper are related to the time-domain measures of the system performance after initiating a small disturbance. The proposed measures are based on the sum of the square differences between the initial values of the rotor angle-δ (related to synchronizing torque); speed-ω (related to damping torque); active power-P in steady-state-, , ; and all of the simulated values , , during the time domain simulation period after a (small) disturbance has been subdued at the time instant :
The smaller outputs of the sum of the square differences (3)–(5) correspond to better time-domain measures of the system performance. Based on (3)–(5), the weight functions and are introduced:
Hence, the output of each weight function closer to 1 represents better time-domain system performance. Since the damping ratio of the dominant system mode falls into the interval (0, 1) and indicates better system dynamic properties when it tends to a value of 1, as the s-domain system performance measure, the damping ratio is comparable with the proposed weight functions (6)–(8). It follows that a new weight function based on the damping ratio- can be presented as:
Comprising both the time-domain and s-domain measures, the system performance function can be represented as the weight function-:
The optimal PSS time constant T is selected as value obtained for the maximal output of weight function which represents the system performance weight function-calculated in the iterative procedure for the j-th cluster composed of five PSS time constants- increasing the initial value-for the increment of 0.1 s in each subsequent i-th iteration:
Until , a new cluster, composed of five will be defined according to (12), where the initial PSS time constant value will be the last value from the previous cluster j−1:
After the PSS time constant T has been determined, the PSS gain K will be obtained in iterative procedures with invariant T.
The PSS gain K is chosen as one of the values obtained in the following procedure:
If
K = Ku
else
K = Kl
where - is the PSS gain obtained for the maximal output of weight function (i), which represents the system performance weight function-calculated in the iterative procedure for the u-th cluster composed of five PSS gain constants-increasing the initial PSS gain-for increment 1 in each subsequent i-th iteration:
Until , a new cluster composed of five PSS gain constants-, will be defined according to (16) where the initial PSS time constant value will be the last value from the previous cluster u−1:
is the PSS gain obtained for the maximal output of weight function (i) which represents the system performance weight function-calculated in the iterative procedure for the l-th cluster composed of five PSS gain constants- decreasing the initial PSS gain-for decrement 1 in each subsequent i-th iteration:
Until , a new cluster, composed of five PSS gain constants -, will be defined according to (19) where the initial PSS time constant value will be the last value from the previous cluster l−1:
More detailed insight into the proposed algorithm is presented in Figure 3. The proposed principle makes both the s-domain and time-domain measures of the system performance comparable and can be considered beneficial for the PSS fine-tuning.
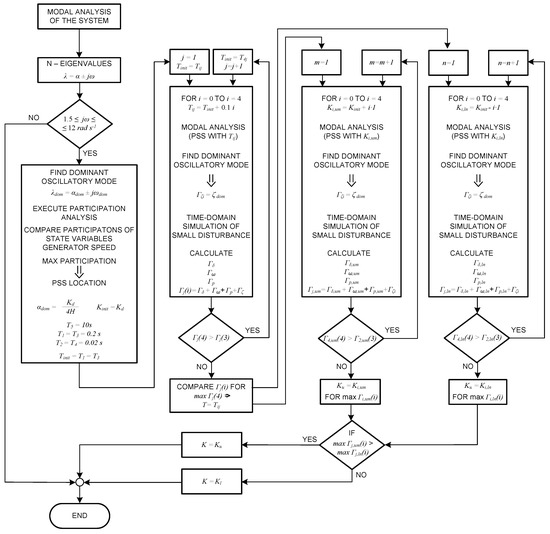
Figure 3.
PSS tuning algorithm.
5. PSS Tuning Algorithm Impact on the System Performance
The proposed algorithm’s impact on the system performance has been analyzed on the IEEE 14–bus multi-machine system in DIgSILENT PowerFactory simulation interface. The single line diagram system model is presented in Figure 4. All the generators in the model are equipped with AVRs (parameters are given in the Appendix A). Busbars 2, 4, and 5 are equipped with static compensation devices (parameters are given in the Appendix A).
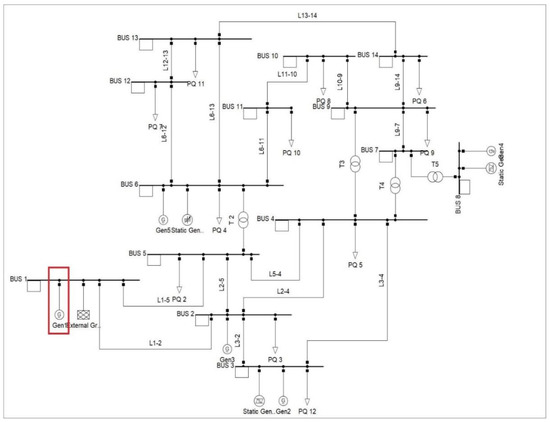
Figure 4.
IEEE 14 bus system model in DIgSILENT PowerFactory simulation interface.
Modal analysis of the system indicates, on 55 modes (eigenvalues), 22 modes are oscillatory while 33 modes are monotone. Damping frequencies of five oscillatory modes fall in the range of 8.6–13 rads−1 (1.3–2.1 Hz), which corresponds to local modes and will be further analyzed in Table 1. Other oscillatory modes correspond to low-frequency modes mainly caused by AVRs and are supposed to be well-damped after the PSS implementation.

Table 1.
Local oscillatory modes for the analyzed system without the PSS implementation.
The root-locus diagram of the analyzed system is presented in Figure 5; monotone modes are marked green, low-frequency oscillatory modes are marked red, while local oscillatory modes are marked blue.
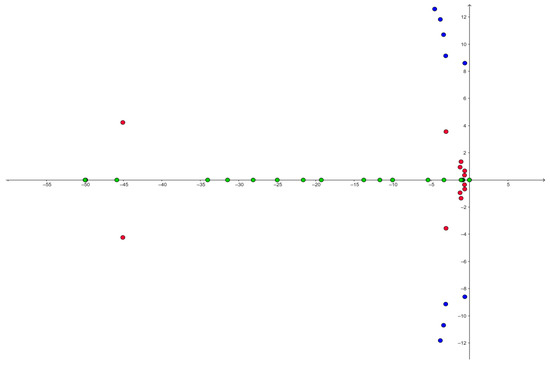
Figure 5.
Root locus diagram of the analyzed system without the PSS implementation.
The damping closest to the horizontal axis on the S-plane indicates Mode 1 as the dominant oscillatory mode. According to the algorithm proposed in the previous chapter, the PSS location will be determined considering the highest participation of the generator speed state variable in the dominant oscillatory mode. As can be seen in Table 2, the highest participation, the value of 0.954, belongs to synchronous generator 1 (Gen1, highlighted in Figure 4), which implies that the excitation system of this generator is the most suitable for the PSS implementation. The participation of other synchronous generators (Gen 2–Gen 5 and External Grid) in the dominant system mode can almost be neglected.

Table 2.
Participation of the generator speed state variable for the dominant oscillatory mode.
After the PSS location has been determined, the tuning process begins with washout filter time constant setting to T5 = 10 s according to the proposed algorithm, i.e., the suggested values in [18,19,20,39]. This value will not affect the regulation loop regarding the phase shift. According to (1) and (2), the initial PSS gain is set to == 10. The value for the time constants T1 and T3 is initially set to T1 = T3 = 0.2 s (recommended in [18,19,20,39]).
5.1. PSS Lead-Lag Tuning
According to (11) and (12) in the proposed algorithm, modal analyses and time-domain simulations are made in clusters containing five samples, changing T = T1 = T3 in each iteration while maintaining the PSS gain as a constant value. Table 3 shows the modal analyses results for time constants of cluster 1 − = T = 0.2–0.6 s for the dominant oscillatory mode. Increasing PSS time constants T shifts this pole further to the left side of the S-plane and at the same time increases the damping ratio. The maximum value of the damping ratio and the minimum value of the damping are fulfilled with the time constant(s) T = T3,1 = 0.5 s. A further increase of time constant(s) pushes the dominant oscillatory pole back in the right part of the S-plane while at the same time the damping ratio decreases (Figure 6). Mode T00 represents the dominant pole without implemented PSS.

Table 3.
Dominant oscillatory pole for PSS parameters K = 10, T = Ti,1 = 0.2–0.6 s (cluster 1).
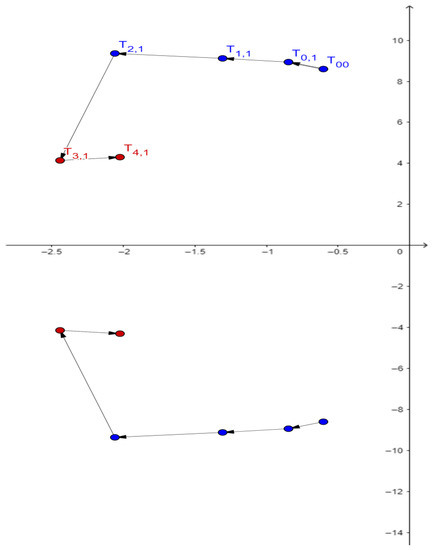
Figure 6.
Dominant oscillatory pole movement in the S-plane after the PSS implementation with K = 10 and the increasing time constants from T = 0.2 s to T = 0.6 s.
The observed variables in the time-domain simulations are rotor angle, speed, and active power of Gen 1 after initiating a (small) disturbance (3-phase short-circuit) on BUS 4 with the duration of 30 ms at the time instance tinit = 0.1 s from the simulation beginning. Figure 7 shows the rotor angle response with different PSS time constant(s)-T = Ti,1 setting. As can be seen from the figure, increasing the PSS time constant(s) results in a shorter settling time and decreased overshoot and undershoot of the rotor angle during the transitional process. Similar behavior is shown by the generator speed (Figure 8) and the active power (Figure 9).
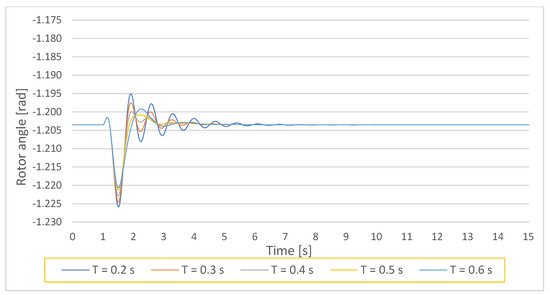
Figure 7.
Gen1 rotor angle response on a small disturbance with PSS parameters K = 10, and T = Ti,1 = 0.2–0.6 s.
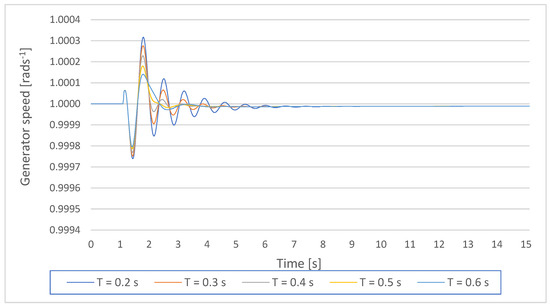
Figure 8.
Gen1 speed response on a small disturbance with PSS parameters K = 10, and T = Ti,1 = 0.2–0.6 s.
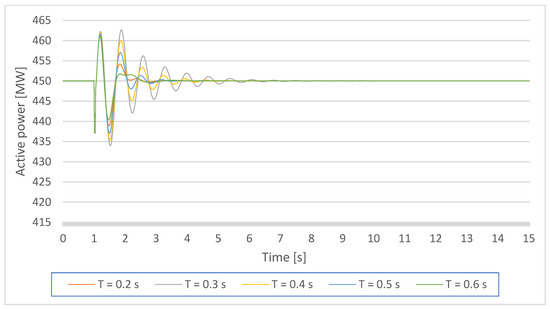
Figure 9.
Gen1 active power response on a small disturbance with PSS parameters K = 10, and T = Ti,1 = 0.2–0.6 s.
Visual observation of the mentioned figures implies the most favorable time-domain system performance measures with PSS gain-K = 10 and time constant(s)-T = T4,1 = 0.6 s.
Table 4 shows results of the weight functions calculated following the proposed algorithm for the first cluster.

Table 4.
Weight functions for K = 10, T = Ti,1 = 0.2–0.6 s (cluster 1).
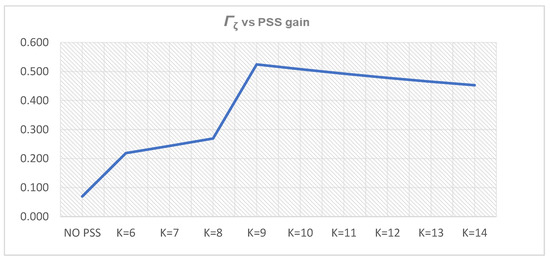
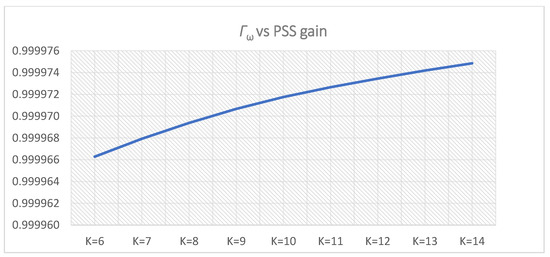
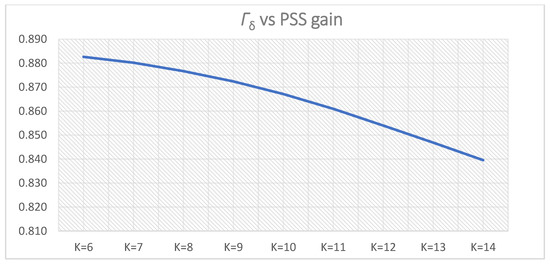
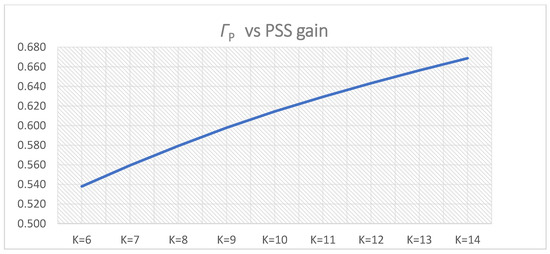
Except for Γδi, the time-domain weight functions-Γωi and ΓPi increase with increasing the PSS time constant(s)-Ti,1. However, the system performance weight function-Γ1(i) obtained maximum for Γ1(3), which corresponds to PSS parameters K = 10 and T = T3,1 = 0.5 s. Since Γ1(4) < Γ1(3), a new cluster (cluster 2) of five samples of PSS time constant(s)-Ti,2 will not be created, T3,1 will be selected for the PSS time constant(s)-T:
max Γ1(i) = Γ1(3) → T3,1 = T = 0.5 s
The weight functions from Table 1 are illustrated in Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14.
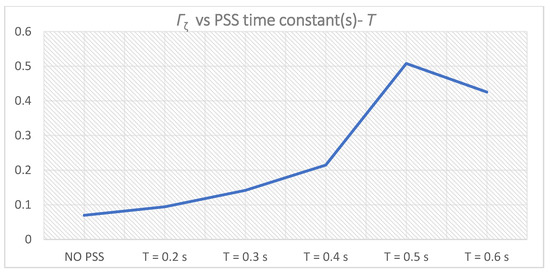
Figure 10.
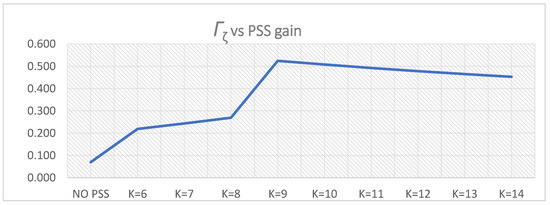
Γζi for PSS parameters K = 10, T = Ti,1 = 0.2–0.6 s.
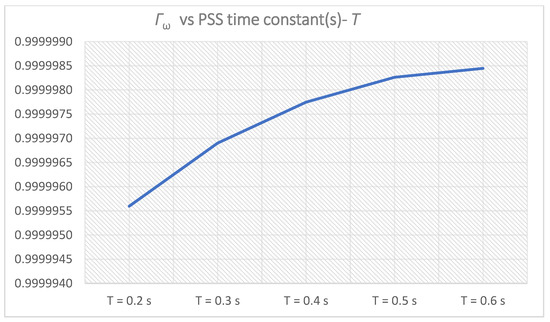
Figure 11.
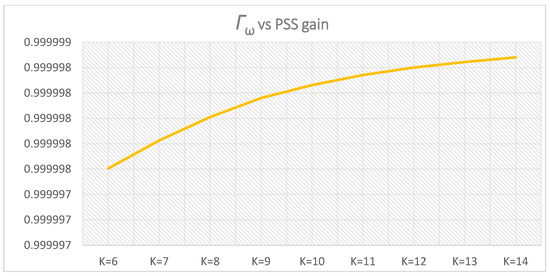
Γωi for PSS parameters K = 10, T = Ti,1 = 0.2–0.6 s.
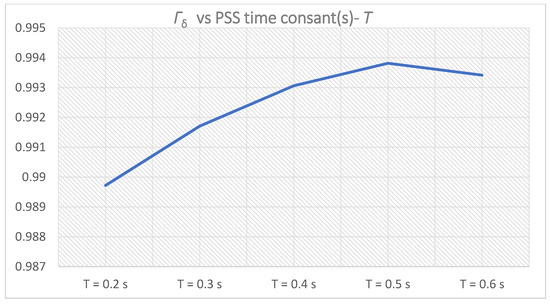
Figure 12.
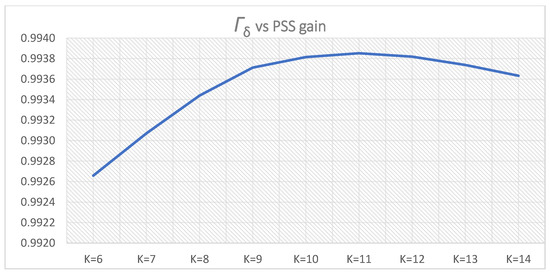
Γδi for PSS parameters K = 10, T = Ti,1 = 0.2–0.6 s.
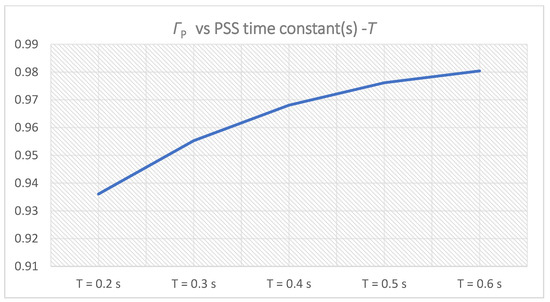
Figure 13.
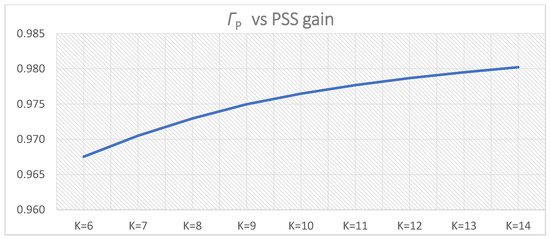
ΓPi for PSS parameters K = 10, T = Ti,1 = 0.2–0.6 s.
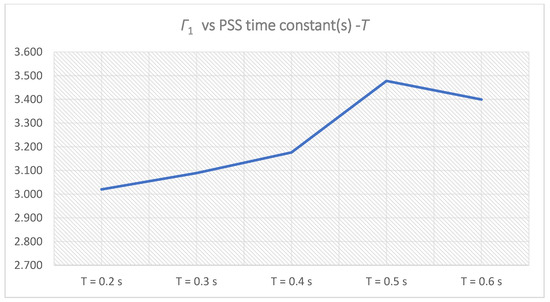
Figure 14.
Γ1 for PSS parameters K = 10, T = Ti,1 = 0.2–0.6 s.
5.2. PSS Gain Tuning
Performed time-domain simulations imply the insignificant influence of the (small) disturbance duration on the PSS time constant tuning. However, the PSS gain tuning will be studied for different durations of the same (small) disturbance (3-phase short-circuit) on BUS 4.
5.3. Case Study 1—Disturbance Duration 30 ms
Following the proposed algorithm, the PSS gain is varied from the initial value K == 10. Table 5 presents the dominant oscillatory pole s-domain measures for the cluster where the PSS initial value is decreased by 1 in each subsequent iteration (lower cluster).

Table 5.
Dominant oscillatory pole for PSS parameters T = T1 = T3 = 0.5 s, Ki,ln = 6–10, n = 1 (lower cluster 1).
Table 6 presents the dominant oscillatory pole s-domain measures for the cluster where the PSS initial value is increased by 1 in each subsequent iteration (upper cluster).

Table 6.
Dominant oscillatory pole for PSS parameters T = 0.5 s, Ki,um = 10–14, m = 1 (upper cluster 1).
Increasing the PSS gain in the lower cluster 1 resulted in the initial dominant system oscillatory pole (system without the PSS) better damping ratio and movement to the left side of the S-plane until a complex pair of the eigenvalues obtained for PSS gain K3,l1 = 9 became a new dominant oscillatory pole. However, the further increase of the PSS gain in lower cluster 1 resulted in the dominant system oscillatory pole decreased damping ratio and movement to right-side on the S-plane, which was continued in the first upper cluster 1 too (Figure 15).
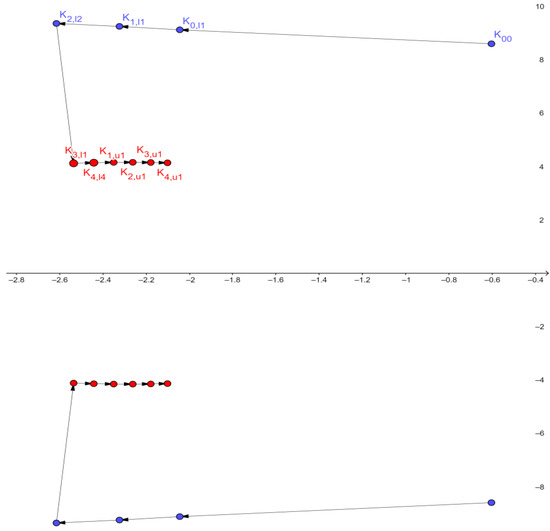
Figure 15.
Dominant oscillatory pole before the PSS implementation-K0,0 and after the PSS implementation with T = 0.5 s, PSS gain increase in the lower cluster 1-Ki,ln = 6–10 and the upper cluster 1 Ki,um = 10–14.
On the other hand, a continual increase of the PSS gain in both lower cluster 1 and upper cluster 1 resulted in better time-domain measures of the system performance (Figure 16, Figure 17 and Figure 18).
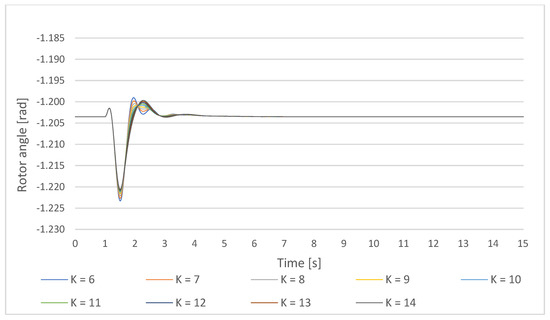
Figure 16.
Gen1 rotor angle response on a small disturbance with PSS parameters T = 0.5 s, the PSS gain increase in the lower cluster 1-Ki,ln = 6–10 and the upper cluster 1 Ki,um = 10–14.
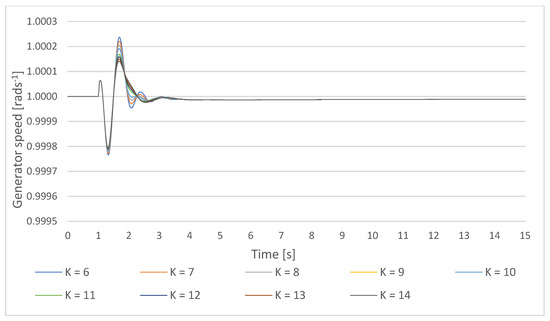
Figure 17.
Gen1 speed response on a small disturbance with PSS parameters T = 0.5 s, the PSS gain increase in the lower cluster 1-Ki,ln = 6–10, and the upper cluster 1 Ki,um = 10–14.
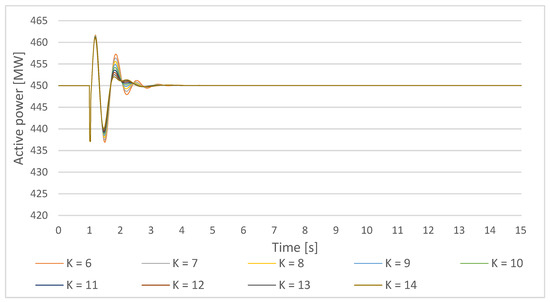
Figure 18.
Gen1 active power response on a small disturbance with PSS parameters T = 0,5 s, the PSS gain increase in the lower cluster 1-Ki,ln = 6–10 and the upper cluster 1 Ki,um = 10–14.
Table 7 and Table 8 give an overview of the proposed weight functions. The damping ratio of the dominant oscillatory mode reached the maximum in the lower cluster 1 for the PSS gain K3,l1 = 9. Weight functions representing the generator speed-Γωi and active power-ΓPi increase with the PSS gain increase. The weight function representing the rotor-angle-Γδi increases with the PSS gain increase before it reaches the maximum in upper cluster 1, for K1,u1 = 11.

Table 7.
Weight functions for PSS parameters T = 0.5 s, Ki,ln = 6–10, n = 1 (lower cluster 1), t = 30 ms.

Table 8.
Weight functions for PSS parameters T = 0.5 s, Ki,um = 10–14, m = 1 (upper cluster 1); t = 30 ms.
Since Γi,l1(i) reached the maximum for Γ1,l1(1) and Γ4,l1(4) < Γ3,l1(3), according to (18), it follows:
Further, Γi,u1(i) reached the maximum for Γ0,u1(0) and Γ4,u1(4) < Γ3,u1(3), according to (15), it follows:
Further, according to (14):
Which implies that the PSS gain K is chosen as:
It can be noticed that the overall weight functions and are mainly influenced by the s-domain system performance measures. However, the weight functions related to time-domain system performance measures increase with the PSS gain increase, resulting in better over-shoots and under-shoots of the simulated variable after initiating a (small) disturbance. High amplitudes of the active power oscillations can cause the loss of load and trigger the protection devices in the system. Decreased amplitude of the active power oscillations obtained with the PSS gain increase supports the idea of tuning PSS taking into consideration both the s-domain and time-domain system performance measures.
The weight functions from Table 7 and Table 8 are presented in Figure 19, Figure 20, Figure 21, Figure 22 and Figure 23. For the sake of better visibility, the results for both lower cluster 1 and upper cluster 1 are shown on a single diagram.
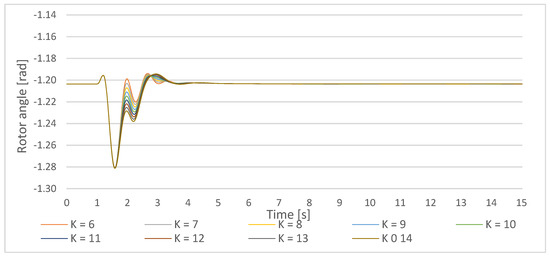
Figure 23.
Gen1 rotor angle response on a small disturbance with PSS parameters T = 0.5 s, the PSS gain increase in the lower cluster 1-Ki,ln = 6–10, and the upper cluster 1 Ki,um = 10–14.
Due to protection activation time and circuit-breaker opening time, in the real power system, disturbance duration lasts longer than the one simulated in this case study, hence the proposed algorithm performance will be examined for longer disturbance durations.
5.4. Case Study 2—Disturbance Duration 150 ms
The observations from the aforementioned case study will be supplemented with the new time-domain system performance measures for the disturbance duration of 150 ms. The simulation results for the lower cluster 1 and the upper cluster 1 are presented in Figure 23, Figure 24 and Figure 25.
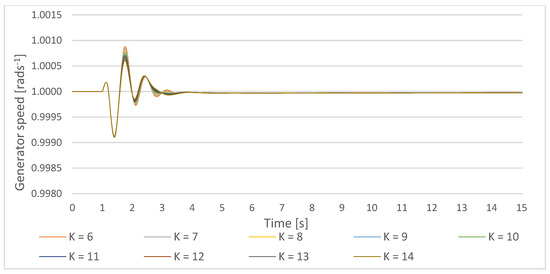
Figure 24.
Gen1 speed response on a small disturbance with PSS parameters T = 0.5 s, the PSS gain increase in the lower cluster 1-Ki,ln = 6–10, and the upper cluster 1 Ki,um = 10–14.
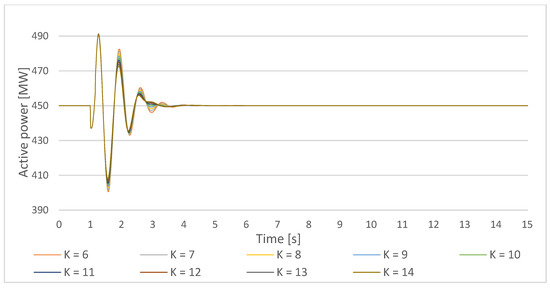
Figure 25.
Gen1 active power response on a small disturbance with PSS parameters T = 0.5 s, the PSS gain increase in the lower cluster 1-Ki,ln = 6–10, and the upper cluster 1 Ki,um = 10–14.
Gen1 rotor angle settling time and the maximal undershoot increase with the increase of the PSS gain in both upper cluster 1 and lower cluster 1 in this study case. The active power and the generator speed undershoot decrease with the PSS gain increase while the settling times remain almost the same. Table 9 and Table 10 give an overview of the proposed weight functions.

Table 9.
Weight functions for PSS parameters T = 0.5 s, Ki,ln = 6–10, n = 1 (lower cluster 1), t = 150 ms.

Table 10.
Weight functions for PSS parameters T = 0.5 s, Ki,um = 10–14, m = 1 (upper cluster 1); t = 150 ms.
Speed weight function Γω as well as active power weight function ΓP increase with the PSS gain increase. As in the previous study case:
Γi,l1(i) reached the maximum for Γ1,l1(1) and Γ4,l1(4) < Γ3,l1(3), and according to (18), it follows:
Γi,u1(i) reached the maximum for Γ0,u1(0) and Γ4,u1(4) < Γ3,u1(3), and according to (15), it follows:
Further, according to (14):
Which implies that the PSS gain K is:
The difference between the maximal outputs of the Γi,um(i) and Γi,ln(i) functions is smaller than in the previous case study, implying that the disturbance duration affects the weight functions related to the time-domain system performance measures and emphasize their significance in the PSS tuning process. As in the previous case study, the weight functions from Table 9 and Table 10 are illustrated in Figure 26, Figure 27, Figure 28 and Figure 29.
5.5. Case Study 3—Disturbance Duration-220 ms
New time-domain system performance measures for the (small) disturbance duration of 220 ms are obtained from the simulations presented in Figure 30, Figure 31 and Figure 32.
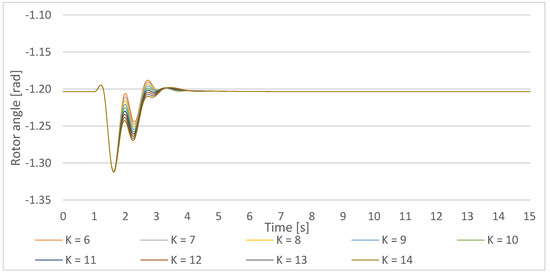
Figure 30.
Gen1 rotor angle response on a small disturbance with PSS parameters T = 0.5 s, the PSS gain increase in the lower cluster 1-Ki,ln = 6–10, and the upper cluster 1 Ki,um = 10–14.
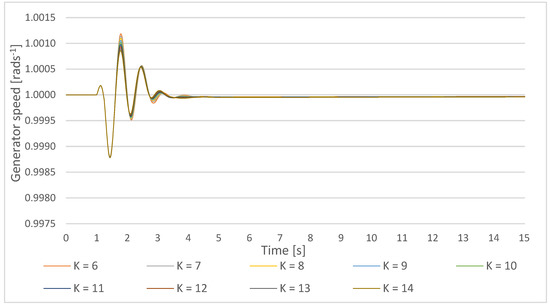
Figure 31.
Gen1 speed response on a small disturbance with PSS parameters T = 0.5 s, the PSS gain increase in the lower cluster 1-Ki,ln = 6–10, and the upper cluster 1 Ki,um = 10–14.
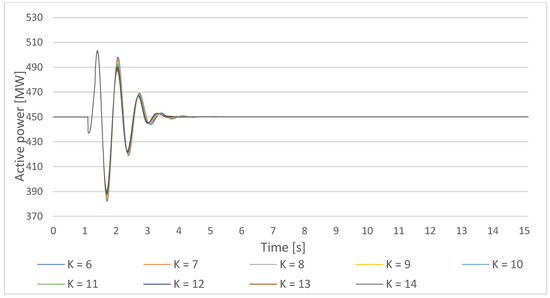
Figure 32.
Gen1 active power response on a small disturbance with PSS parameters T = 0.5 s, the PSS gain increase in the lower cluster 1-Ki,ln = 6–10, and the upper cluster 1 Ki,um = 10–14.
Table 11 and Table 12 give an overview of the weight functions. As in the previous case, the weight functions related to generator speed and active power increase with the PSS gain increase in both lower cluster 1 and upper cluster 1 while the rotor angle weight function decreases.

Table 11.
Weight functions for T = 0.5 s, Ki,ln = 6–10, n = 1 (lower cluster 1); t = 220 ms.

Table 12.
Weight functions for T = 0.5, Ki,um = 10–14, m = 1 (upper cluster 1); t = 220 ms.
The damping ratio of the dominant oscillatory mode reached the maximum in the lower cluster 1 for the PSS gain K1,l1 = 9.
reached the maximum for and and, according to (18), it follows:
Further, Γi,u1(i) reached the maximum for Γ0,u1(0) and Γ4,u1(4) < Γ3,u1(3) and, according to (15), it follows:
Further, according to (14):
Which implies that the PSS gain K is chosen as:
Here, it can also be noticed that difference between weight functions Γ1,l1(1) → K1,l1 = 9 and Γ0,u1(0) → K0,l1 = 10 becomes smaller as the fault duration increase. The weight functions from Table 11 and Table 12 are presented in Figure 33, Figure 34, Figure 35, Figure 36 and Figure 37.
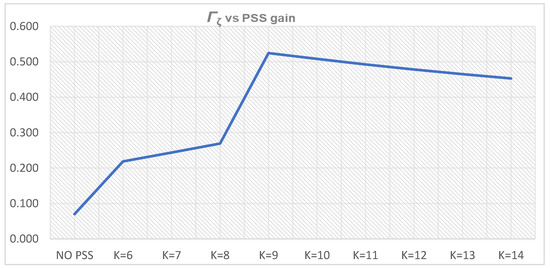
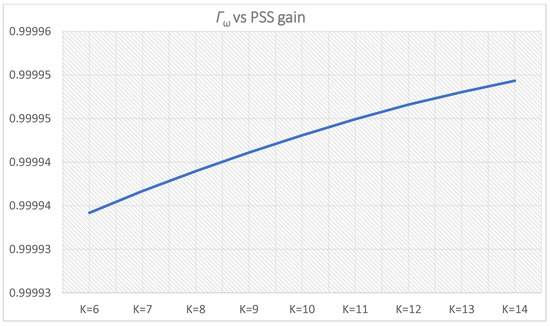
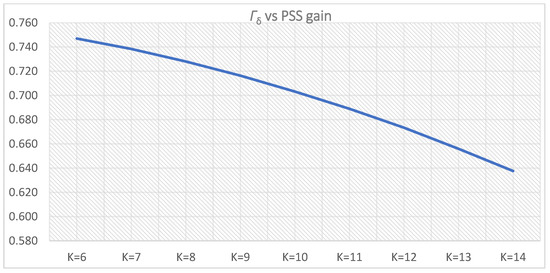
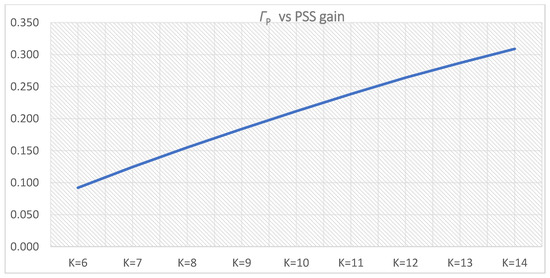
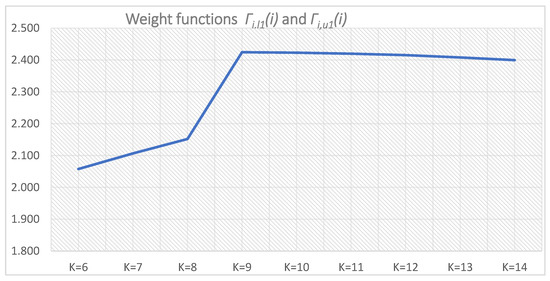
Figure 37.
Weight functions: Γi,l1(i)—(i = 0–4 for K = 6–10), Γi,u1(i) (i = 0–4 for K = 10–14), T = 0.5 s.
The difference between the outputs of the weight functions Γi,l1(i) and Γi,u1(i) becomes insignificant with further PSS gain increase after the maximum has been reached for K = 9 (Figure 37).
Hence, the weight functions representing the time-domain system performance measures have a more significant influence on the PSS parameters selection. The weight function associated with the generator active power oscillations is of particular importance since the active power oscillations can lead to the load loss. All the simulation results indicate the lower amplitude of active power oscillations if the PSS parameters are selected according to a higher value of this function. Therefore, the impact of the proposed weight function associated with the generator active power oscillations can be emphasized by multiplying it with the corrective factor. Even multiplied with value 1.1, the weight functions ΓPi,l1 and ΓPi,u1 will increase the PSS gain from K = 9 to K = 10. With the further increase of this corrective factor, the reduction of the active power oscillations amplitudes will be more emphasized. The decision of the most appropriate corrective factor value will be subjected to future works applying machine learning methods.
6. Conclusions
In this paper, an algorithm for the PSS1A tuning comprising both the s-domain and the time domain system performance measures was proposed and tested on multi-machine IEEE 14-bus system model. The location of the PSS implementation is determined by analyzing the participation of the generator speeds state variables in the dominant oscillatory mode of the analyzed system. The well-known phase compensation method for the PSS tuning based on the s-domain system performance measures has only been upgraded with the time-domain system performance measures incorporating the weight functions comparable with the damping ratio of the dominant system mode as the proposed weight function related with the s-domain system performance measures. For different system disturbance durations, three case studies were examined. As the duration of system disturbances increases, the impact of the time-domain system measures on PSS tuning increases as well. Besides the damping of the electromechanical oscillations in the power system, the implementation of the PSS, according to the proposed algorithm, can reduce the amplitudes of the active power oscillations to which the modern power systems with possible inertia reduction are particularly vulnerable. Hence, the PSS implementation and tuning, according to the proposed algorithm, can be beneficial for both small-signal and transient stability in the power system.
Author Contributions
Conceptualization, P.M. and R.K.; methodology, R.K.; software, P.M.; validation, P.M. and H.R.C.; formal analysis, H.R.C. and H.G.; investigation, R.K.; resources, R.K.; data curation, H.G.; writing—original draft preparation, R.K.; writing—review and editing, P.M.; visualization, H.G.; supervision, H.R.C.; project administration, P.M.; funding acquisition, P.M., R.K. and H.G. All authors have read and agreed to the published version of the manuscript.
Funding
The APC was funded by Faculty of Electrical Engineering, Computer Science, and Information Technology Osijek.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
IEEE 14-bus test system data are available online. AVR and PSS standard models are available online; AVRs parameters are given in Appendix A. All other data presented in this study are available on request.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
AVR parameters (AVR, IEEE URST5B):
AVR1, AVR2, AVR3: Tr = 0.01 s, Tb1 = 10 s, Tc1 = 2 s, Tb2 = 1 s, Tc2 = 1 s, Kr = 200 p.u., T1 = 0.01 s, Kc = 0.1 p.u., Vmin = −3 p.u., Vmax = 3.4 p.u.
AVR4, AVR5: Tr = 0.01 s, Tb1 = 10 s, Tc1 = 2 s, Tb2 = 1 s, Tc2 = 1 s, Kr = 150 p.u., T1 = 0.01 s, Kc = 0.1 p.u., Vmin = −3 p.u., Vmax = 3.4 p.u.
Static compensation devices parameters:
SC: SB = 100 MVA, UB = 13.8 kV, UN = 1.07 p.u., Qmax = 0.24 p.u., Qmin = −0.06 p.u., Vmax = 1.2 p.u., Vmin = 0.8 p.u.
SC1: SB = 100 MVA, UB = 69 kV, UN = 1.01 p.u., Qmax = 0.4 p.u., Qmin = 0.00 p.u., Vmax = 1.2 p.u., Vmin = 0.8 p.u.
SC2: SB = 100 MVA, UB = 18 kV, UN = 1.09 p.u., Qmax = 0.24 p.u., Qmin = −0.06 p.u., Vmax = 1.2 p.u., Vmin = 0.8 p.u.
References
- Peres, W.; Coelho, F.C.; Costa, J.N. A pole placement approach for multi-band power system stabilizer tuning. Int. Trans. Electr. Energy Syst. 2020, 30, e12548. [Google Scholar] [CrossRef]
- Prasertwong, K.; Mithulananthan, N.; Thakur, D. Understanding low-frequency oscillation in power systems. Int. J. Electr. Eng. Educ. 2010, 47, 248–262. [Google Scholar] [CrossRef]
- Falehi, A.D.; Rostami, M.; Mehrjadi, H. Transient Stability Analysis of Power System by Coordinated PSS-AVR Design Based on PSO Technique. Energy Power Eng. 2011, 3, 478–484. [Google Scholar] [CrossRef][Green Version]
- Dudgeon, G.J.; Leithead, W.E.; Dysko, A.; O’Reilly, J.; McDonald, J.R. The effective role of AVR and PSS in power systems: Frequency response analysis. IEEE Trans. Power Syst. 2007, 22, 1986–1994. [Google Scholar] [CrossRef]
- Benaissa, O.M.; Hadjeri, S.; Zidi, S.A. Impact of PSS and SVC on the power system transient stability. In Proceedings of the 8th International Conference on Modelling, Identification and Control (ICMIC), Algiers, Algeria, 15–17 November 2016; pp. 303–307. [Google Scholar] [CrossRef]
- Dysko, A.; Leithead, W.E.; O’Reilly, J. Enhanced power system stability by coordinated PSS design. IEEE Trans. Power Syst. 2009, 25, 413–422. [Google Scholar] [CrossRef]
- Sahare, S.B.; Bonde, U.G. Transient stability enhancement in multi-machine power system by using power system stabilizer (Pss) and static var compensator (Svc). Int. J. Eng. Res. 2020, 9. [Google Scholar] [CrossRef]
- Calderón-Guizar, J.G.; Ramírez-González, M.; Castellanos-Bustamante, R. Castellanos, identification of low frequency oscillation modes in large transmission systems. Rev. Fac. Ing. 2017, 82, 31–39. [Google Scholar]
- Pagola, F.L.; Perez-Arriaga, I.J.; Verghese, G.C. On sensitivities, residues and participations: Applications to oscillatory stability analysis and control. IEEE Trans. Power Syst. 1989, 4, 278–285. [Google Scholar] [CrossRef]
- Djalal, M.R.; Imran, A.; Robandi, I. Optimal placement and tuning power system stabilizer using participation factor and imperialist competitive algorithm in 150 kV South of Sulawesi system. In Proceedings of the International Seminar on Intelligent Technology and Its Applications (ISITIA), Surabaya, Indonesia, 20–22 May 2015; pp. 147–152. [Google Scholar] [CrossRef]
- Benasla, M.; Allaoui, T.; Brahami, M.; Hadji, B. Frequency response analysis to select the best PSS locations in power systems. In Proceedings of the 2016 8th International Conference on Modelling, Identification and Control (ICMIC), Algiers, Algeria, 15–17 November 2016; pp. 269–273. [Google Scholar] [CrossRef]
- Flores, H.B.; Cepeda, J.C.; Gallardo, C.F. Optimum location and tuning of PSS devices considering multi-machine criteria and a heuristic optimization algorithm. In Proceedings of the IEEE PES Innovative Smart Grid Technologies Conference—Latin America (ISGT Latin America), Quito, Ecuador, 20–22 September 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Khormizi, A.B.; Nia, A.S. Damping of power system oscillations in multi-machine power systems using coordinate design of PSS and TCSC. In Proceedings of the 10th International Conference on Environment and Electrical Engineering, Rome, Italy, 1–7 May 2011; pp. 1–4. [Google Scholar] [CrossRef]
- Sharma, A.; Kumar, R. Optimum location of PSS and its parameters by using particle swarm optimization. Int. J. Adv. Res. Eng. Technol. 2019, 10. [Google Scholar] [CrossRef]
- Chow, J.H. A pole-placement design approach for systems with multiple operating conditions. In Proceedings of the 27th IEEE Conference on Decision and Control, Austin, TX, USA, 7–9 December 1988; pp. 1272–1277. [Google Scholar] [CrossRef]
- Othman, H.; Sanchez-Gasca, J.J.; Kale, M.A.; Chow, J.H. On the design of robust power system stabilizers. In Proceedings of the 28th IEEE Conference on Decision and Control, Tampa, FL, USA, 13–15 December 1989; pp. 1853–1857. [Google Scholar] [CrossRef]
- Demello, F.P.; Concordia, C. Concepts of synchronous machine stability as affected by excitation control. IEEE Trans. Power Appar. Syst. 1969, 88, 316–329. [Google Scholar] [CrossRef]
- Larsen, E.V.; Swann, D.A. Applying power system stabilizers. Part I: General concepts. IEEE Power Eng. Rev. 1981, PER-1, 62–63. [Google Scholar] [CrossRef]
- Larsen, E.V.; Swann, D.A. Applying power system stabilizers part II: Performance objectives and tuning concepts. IEEE Trans. Power Appar. Syst. 1981, PAS-100, 3025–3033. [Google Scholar] [CrossRef]
- Larsen, E.V.; Swann, D.A. Applying power system stabilizers part III: Practical considerations. IEEE Trans. Power Appar. Syst. 1981, PAS-100, 3034–3046. [Google Scholar] [CrossRef]
- Sebaa, K.; Boudour, M. Robust power system stabilizers design using multi-objective genetic algorithm. In Proceedings of the IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–7. [Google Scholar] [CrossRef]
- Spoljaric, T.; Pavic, I. AVR and PSS coordination strategy by using multi-objective ant lion optimizer. In Proceedings of the 2020 43rd International Convention on Information, Communication and Electronic Technology (MIPRO), Opatija, Croatia, 28 September–2 October 2020; pp. 928–933. [Google Scholar] [CrossRef]
- Attia, A.-F. Online tuning based fuzzy logic controller for power system stabilizers. In Proceedings of the 2017 Nineteenth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 19–21 December 2017; pp. 952–957. [Google Scholar] [CrossRef]
- Shafiullah, M.; Rana, M.J.; Alam, M.S.; Abido, M.A. Online tuning of power system stabilizer employing genetic programming for stability enhancement. J. Electr. Syst. Inf. Technol. 2018, 5, 287–299. [Google Scholar] [CrossRef]
- Bakolia, V. Design and analysis of fuzzy logic based power system stabilizer. Int. J. Eng. Res. 2020, 9. [Google Scholar] [CrossRef]
- Douidi, B.; Mokrani, L.; Machmoum, M. A new cascade fuzzy power system stabilizer for multi-machine system stability enhancement. J. Control. Autom. Electr. Syst. 2019, 30, 765–779. [Google Scholar] [CrossRef]
- Verdejo, H.; Torres, R.; Pino, V.; Kliemann, W.; Becker, C.; Delpiano, J. Tuning of controllers in power systems using a heuristic-stochastic approach. Energies 2019, 12, 2325. [Google Scholar] [CrossRef]
- Kim, J.J.; Park, J.H. A novel structure of a power system stabilizer for microgrids. Energies 2021, 14, 905. [Google Scholar] [CrossRef]
- Ahmed, M.; Roy, N.K. A comparative analysis on different types of power system stabilizers. In Proceedings of the 2016 5th International Conference on Informatics, Electronics and Vision (ICIEV), Dhaka, Bangladesh, 13–14 May 2016; pp. 797–802. [Google Scholar] [CrossRef]
- Farah, A.; Guesmi, T.; Abdallah, H.H.; Ouali, A. Real-time stability enhancement based on neural fuzzy networks and genetic algorithms. In Proceedings of the 10th International Multi-Conferences on Systems, Signals & Devices 2013 (SSD13), Hammamet, Tunisia, 18–21 March 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Rafiee, Z.; Ganjefar, S.; Fattahi, A. A new PSS tuning technique using ICA and PSO methods with the fourier transform. Electr. Electron. Eng. 2012, 1, 17–23. [Google Scholar] [CrossRef]
- Li, X.; Wang, Z.; Xu, J.; Chen, B. Power system stabilizer parameters designing based on genetic simulated annealing algorithm. J. Clean Energy Technol. 2015, 4, 178–182. [Google Scholar] [CrossRef]
- Castrillon, N.J.; Sanchez, H.M.; Perez, J.A. A tool for optimal PSS tuning for the Colombian power system. In Proceedings of the 2014 IEEE PES T & D Conference and Exposition, Chicago, IL, USA, 14–17 April 2014; pp. 1–5. [Google Scholar] [CrossRef]
- Alhaj, A.K.; Hassan, M.O. Design and performance evaluation of TCSC and PSS to mitigate low frequency oscillations. In Proceedings of the 2018 International Conference on Computer, Control, Electrical, and Electronics Engineering (ICCCEEE), Khartoum, Sudan, 12–14 August 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Verrelli, C.M.; Marino, R.; Tomei, P.; Damm, G. Nonlinear robust coordinated PSS-AVR control for a synchronous generator connected to an Infinite Bus. IEEE Trans. Automat. Contr. 2021. [Google Scholar] [CrossRef]
- Zea, A.A. Power System Stabilizers for The Synchronous Generator: Tuning and Performance Evaluation. Master’s Thesis, Chalmers University of Technologyg, Gothenburg, Sweden, 2013. [Google Scholar]
- PPande, W.; Chakrabarti, S.; Srivastava, S.C. Online updating of synchronous generator linearised model parameters and PSS Tuning. In Proceedings of the 2018 20th National Power Systems Conference (NPSC), Tiruchirappalli, India, 14–16 December 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Lu, S.; Zhang, W.; Wang, T.; Cai, T.; Sui, X.; Li, H.; Zhu, T.; Gang, Y.; Yu, Y. Parameter tuning and simulation analysis of PSS function in excitation system with suppression of low frequency Oscillation. In Proceedings of the 2019 IEEE 8th International Conference on Advanced Power System Automation and Protection (APAP), Xi’an, China, 21–24 October 2019; pp. 474–479. [Google Scholar] [CrossRef]
- IEEE Power Engineering Society. IEEE Recommended practice for excitation system models for power system stability studies. In IEEE Standard 421.5-2016 (Revision of IEEE Standard 421.5-2005—Redline); IEEE: New York, NY, USA, 2016. [Google Scholar] [CrossRef]
- Dey, P.; Bhattacharya, A.; Das, P. Tuning of power system stabilizer for small signal stability improvement of interconnected power system. Appl. Comput. Inform. 2017, 16, 3–28. [Google Scholar] [CrossRef]
- Kundur, P. Power System Stability and Control; McGraw-Hilll: New York, NY, USA, 1993. [Google Scholar]
- Tharani P., A.S.; Jyothsna, T.R. Design of PSS for small signal stability improvement. Int. J. Eng. Sci. Technol. 2010, 3, 2–7. [Google Scholar]
- Kundur, P.; Klein, M.; Rogers, G.J.; Zywno, M.S. Application of power system stabilizers for enhancement of overall system stability. IEEE Trans. Power Syst. 1989, 4, 614–626. [Google Scholar] [CrossRef]
- JChow, H.; Sanchez-Gasca, J.J. Power System Modeling, Computation, and Control; Wiley-IEEE Press: New York, NY, USA, 2020. [Google Scholar]
- Pourbeik, P.; Vowles, D.J.; Gibbard, M.J. Small-Signal Stability, Control and Dynamic Performance of Power Systems; University of Adelaide Press: Adelaide, Australia, 2015. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).