Characterization of Partial Discharge Activities in WBG Power Converters under Low-Pressure Condition
Abstract
:1. Introduction
- -
- Extending the 2D axisymmetrical models of laboratory electrode geometries to the 3D modeling of real-world cases with multiple voids.
- -
- Tackling the computational cost and convergence issues associated with the 3D modeling of configurations with extremely nonuniform electric field distribution.
- -
- Incorporating the impact of air pressure variation into different characteristics of silicone gel and AlN, as well as the inception and extinction of the discharges.
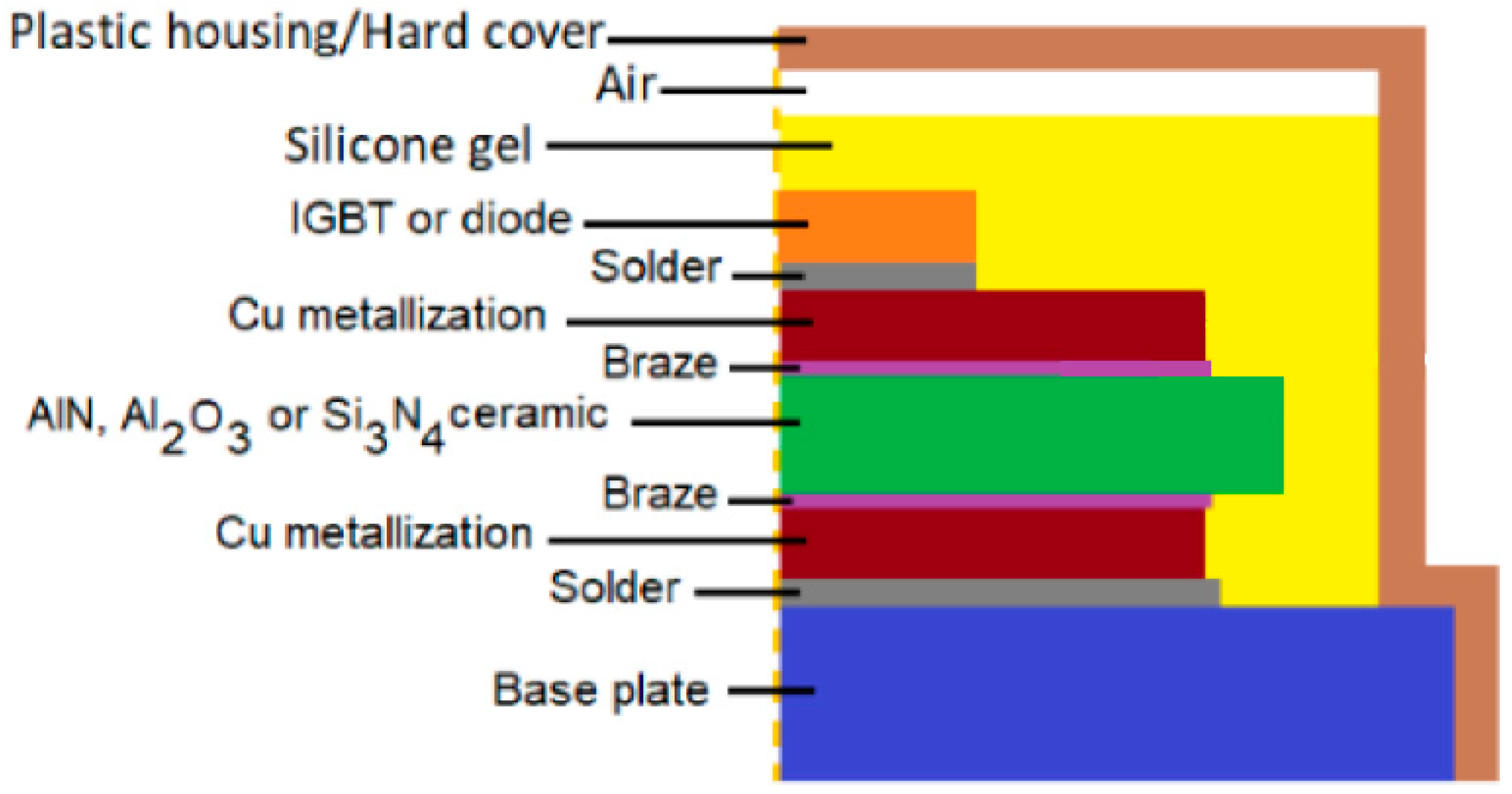
2. FEA Model for PD Analysis
2.1. Introduction to PD Numerical Modeling
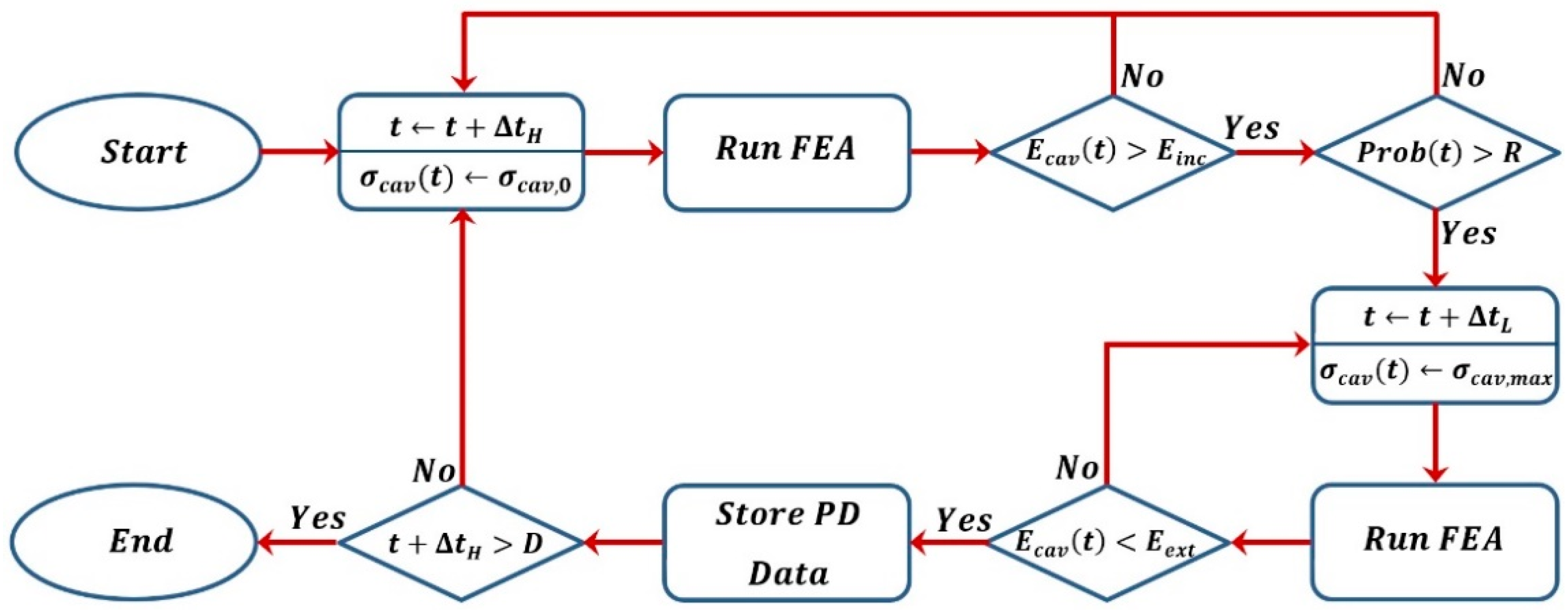
2.2. Algorithm
2.3. Initial Electron Generation
2.4. PD Inception/Extinction Criterion
3. Numerical Results
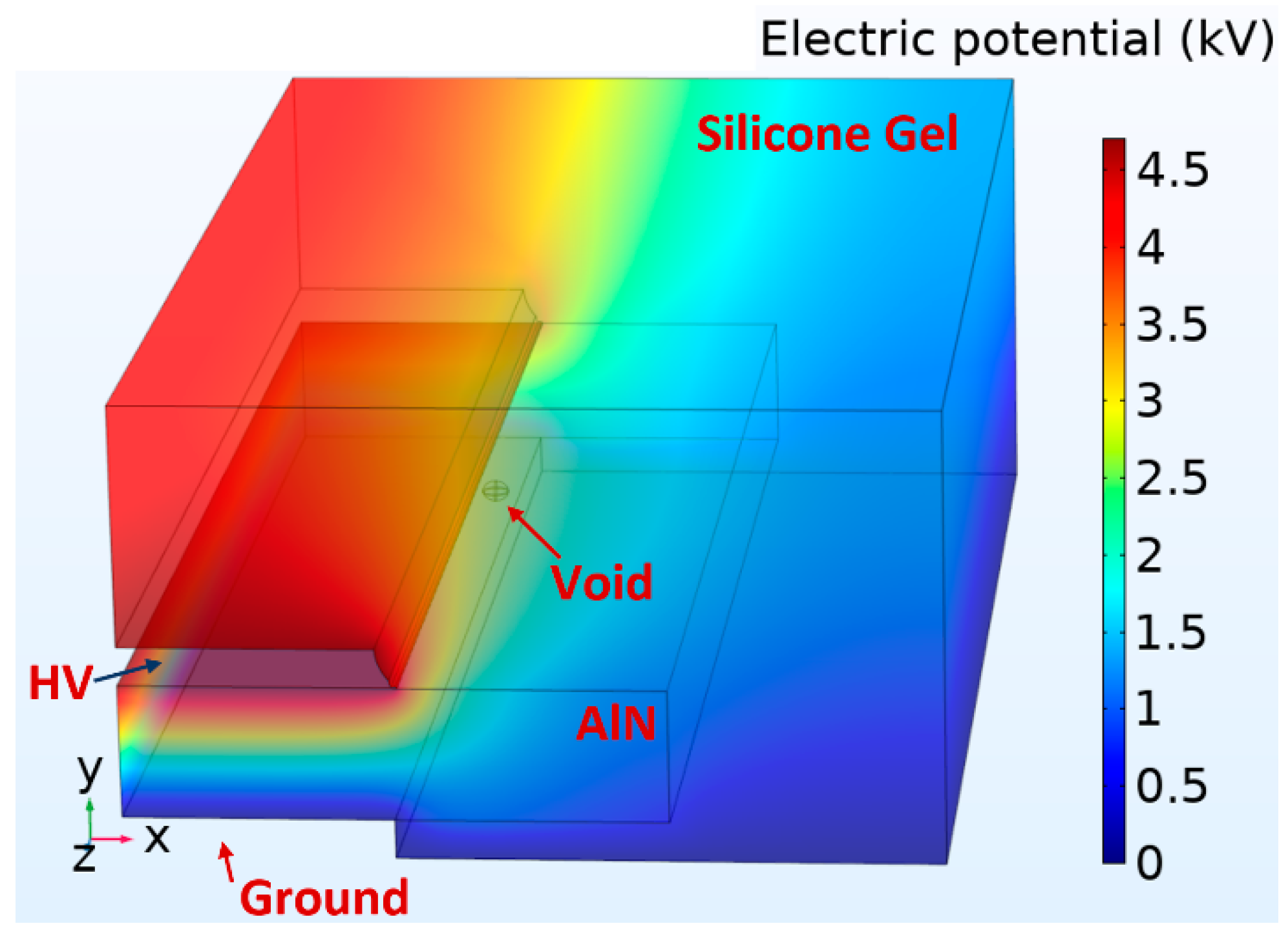
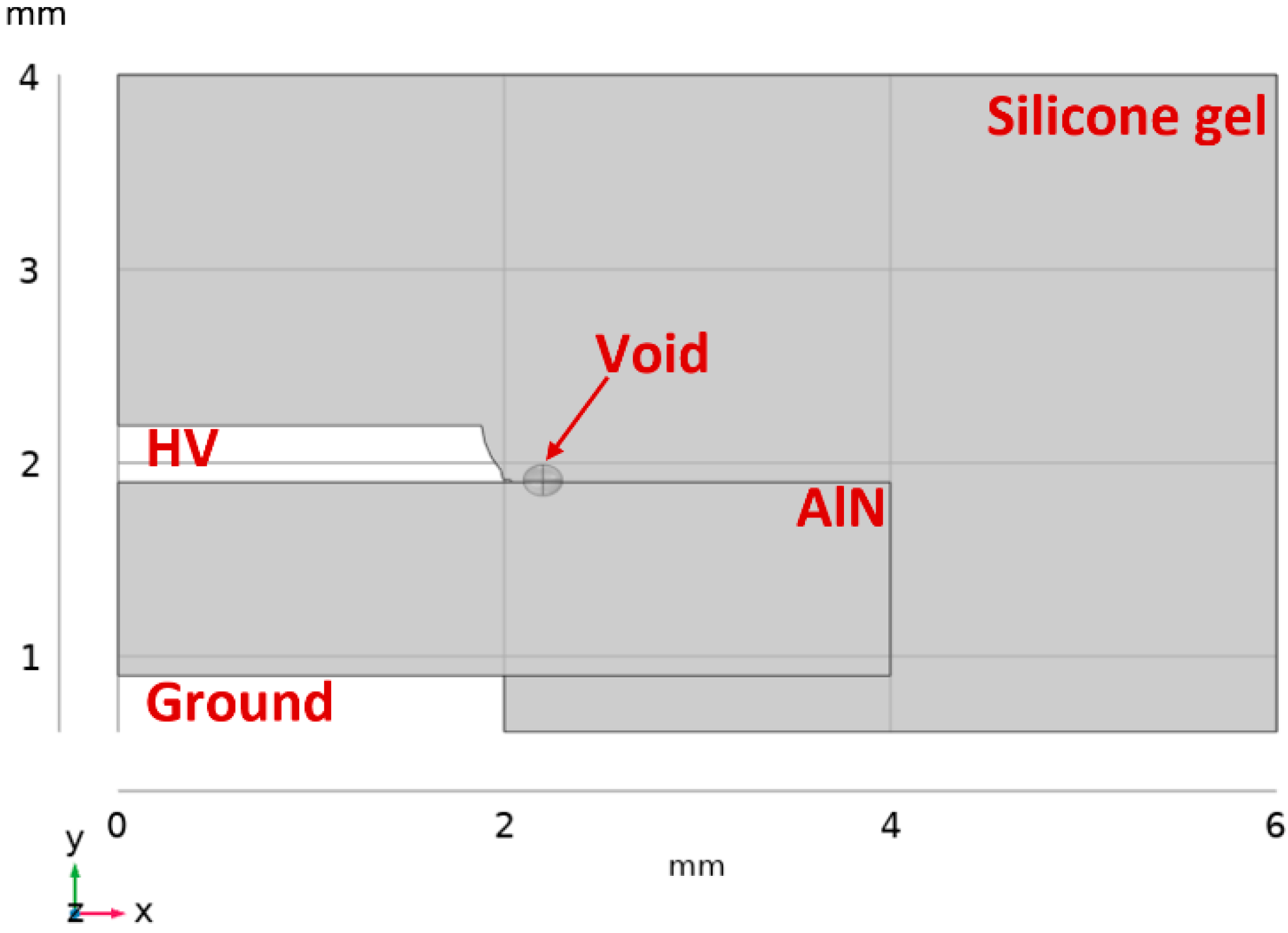
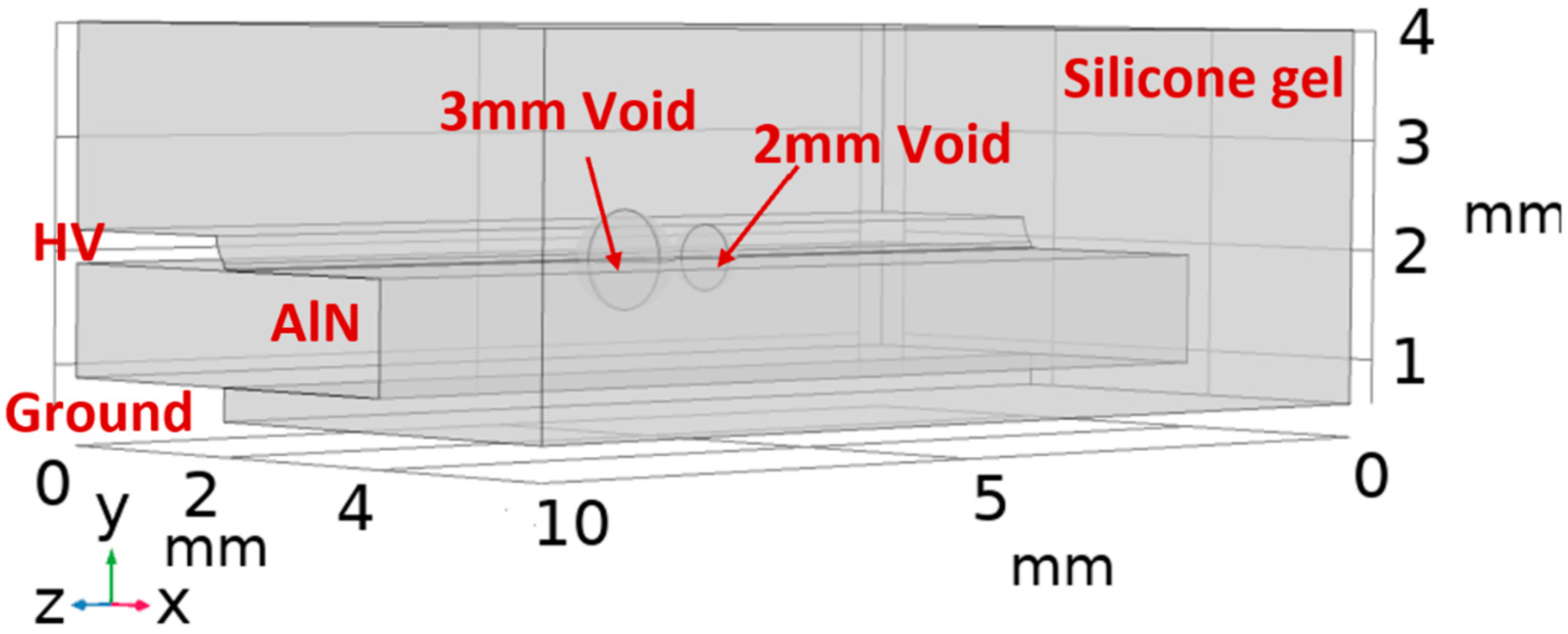
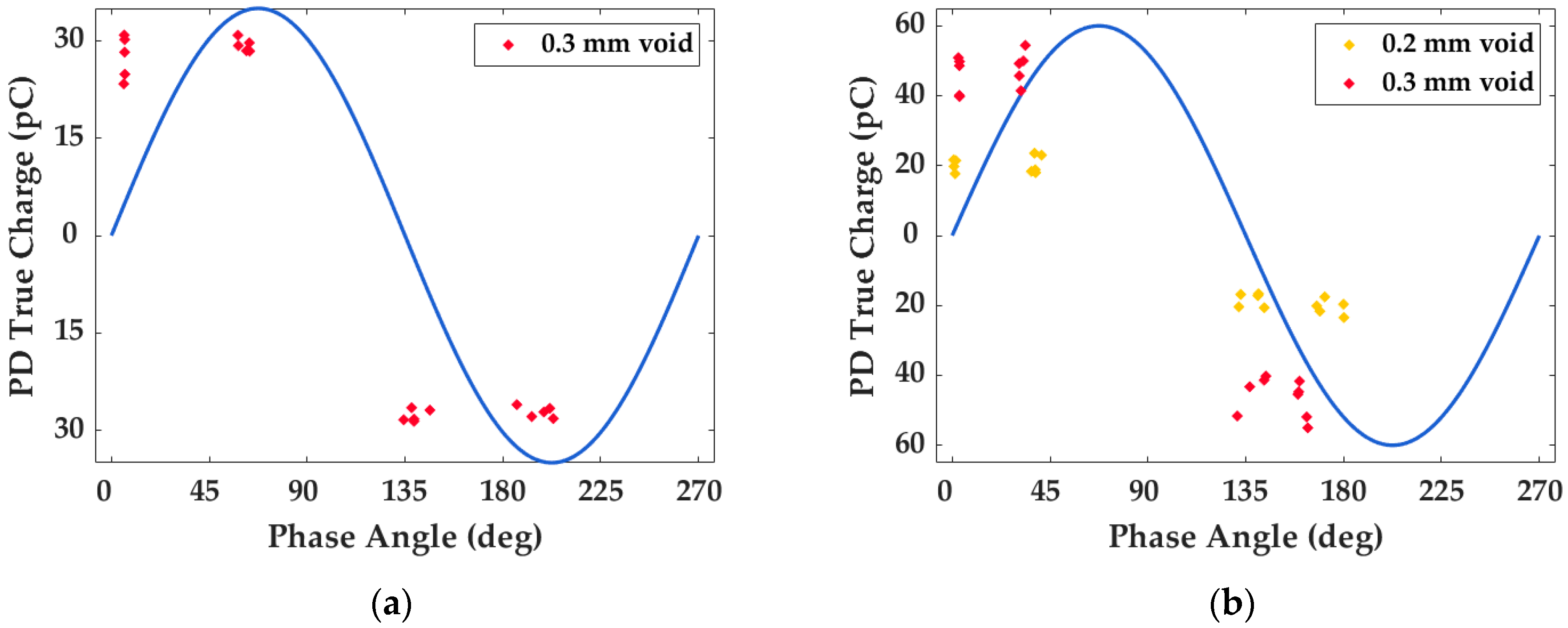
3.1. Single-Void Case Study
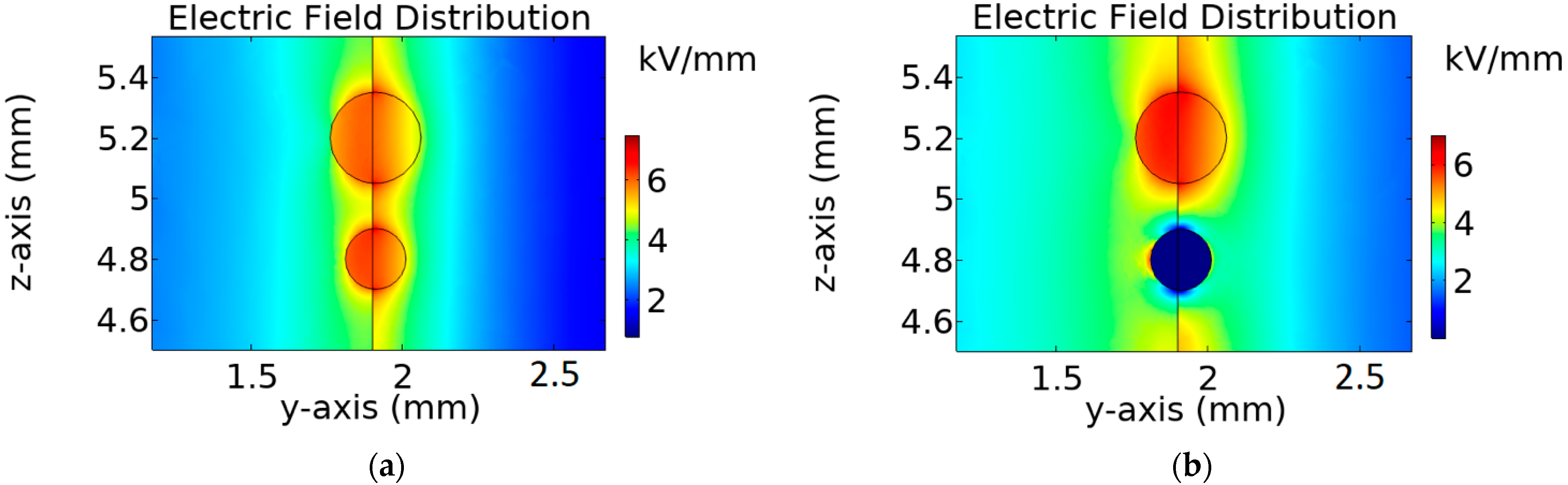
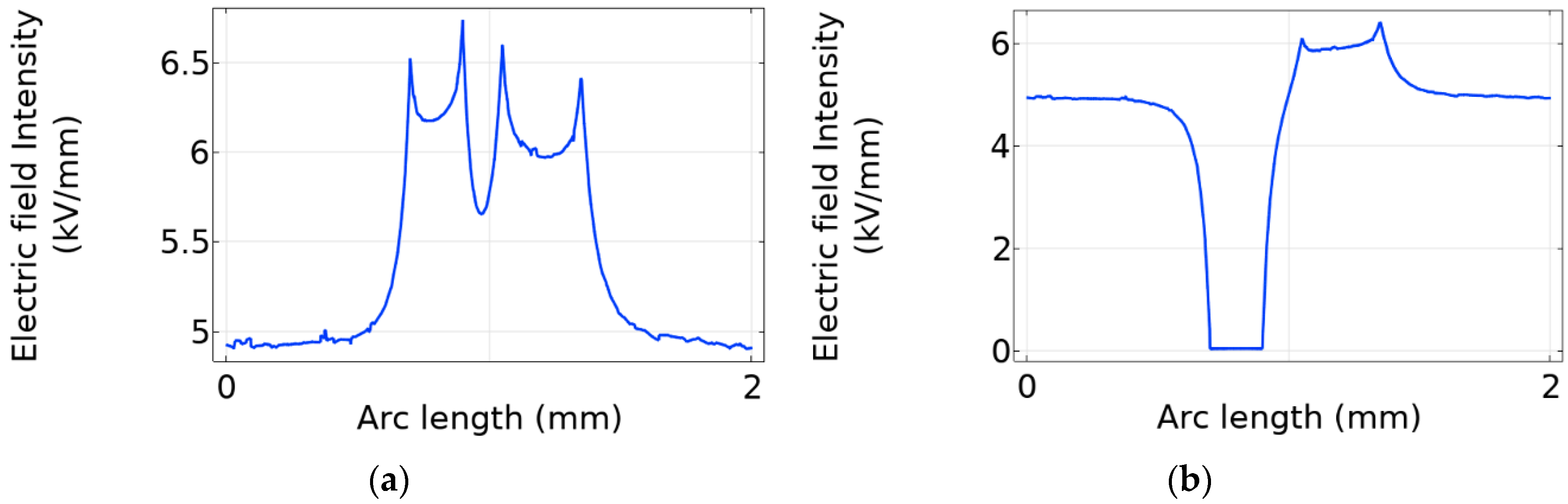
3.2. Double-Void Case Study
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AlN | Aluminum Nitride |
| CO2 | Carbon Dioxide |
| CSM | Charge Simulation Method |
| FDM | Finite Difference Method |
| FEA | Finite Element Analysis |
| FEM | Finite Element Method |
| GHG | Greenhouse Gases |
| HV | High Voltage |
| IGBT | Insulated Gate Bipolar Transistor |
| PCB | Printed Circuit Board |
| PI | Polyimide |
| PD | Partial Discharge |
| PDIV | Partial Discharge Inception Voltage |
| PRPD | Phase-Resolved Partial Discharge |
| WBG | Wide Bandgap |
References
- IPCC. Summary for Policymakers. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M.I., et al., Eds.; Cambridge University Press: Cambridge, UK, 2021; in press. [Google Scholar]
- Wolf, S.; Teitge, J.; Mielke, J.; Schütze, F.; Jaeger, C. The European Green Deal—More Than Climate Neutrality. Intereconomics 2021, 56, 99–107. [Google Scholar] [CrossRef] [PubMed]
- Traffic Data for U.S. Airlines and Foreign Airlines U.S. Flights. Bureau of Transportation Statistics, United States Department of Transportation. Available online: https://www.bts.gov/statistical-releases (accessed on 12 August 2020).
- Soloveichik, G. Electrified Future of Aviation: Batteries or Fuel Cells? The Advanced Research Projects Agency–Energy (ARPA-E): Washington, DC, USA, 2019. [Google Scholar]
- Barzkar, A.; Ghassemi, M. Electric Power Systems in More and All Electric Aircraft: A Review. IEEE Access 2020, 8, 169314–169332. [Google Scholar] [CrossRef]
- Liu, X.; Furrer, D.; Kosters, J.; Holmes, J. Vision 2040: A Roadmap for Integrated, Multiscale Modeling and Simulation of Materials and Systems; Tech. Rep. NASA/CR-2018-219771; NASA: Cleveland, OH, USA, March 2018. [Google Scholar]
- Borghei, M.; Ghassemi, M. Insulation Materials and Systems for More- and All-Electric Aircraft: A Review Identifying Challenges and Future Research Needs. IEEE Trans. Transp. Electrif. 2021, 7, 1930–1953. [Google Scholar] [CrossRef]
- Yongxing, W.; Enyuan, D.; Jiyuan, C.; Jiyan, Z.; Koenig, D. Arc Tracking Properties of the Aging Wires in Aircraft. In Proceedings of the 2008 2nd International Symposium on Systems and Control in Aerospace and Astronautics, Shenzhen, China, 10–12 December 2008; pp. 462–466. [Google Scholar] [CrossRef]
- Riba, J.-R.; Gómez-Pau, Á.; Moreno-Eguilaz, M.; Bogarra, S. Arc Tracking Control in Insulation Systems for Aeronautic Applications: Challenges, Opportunities, and Research Needs. Sensors 2020, 20, 1654. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hillard, G.B.; Kirkici, H. High Voltage Design Guidelines: A Timely Update. In Proceedings of the 2001 Annual Report Conference on Electrical Insulation and Dielectric Phenomena (Cat. No.01CH37225), Kitchener, ON, Canada, 14–17 October 2001; pp. 409–411. [Google Scholar] [CrossRef] [Green Version]
- Kaplar, R.J.; Neely, J.C.; Huber, D.L.; Rashkin, L.J. Generation-After-Next Power Electronics: Ultrawide-Bandgap Devices, High-Temperature Packaging, and Magnetic Nanocomposite Materials. IEEE Power Electron. Mag. 2017, 4, 36–42. [Google Scholar] [CrossRef]
- Wang, P.; Cavallini, A.; Montanari, G.C. The Influence of Repetitive Square Wave Voltage Parameters on Enameled Wire Endurance. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 1276–1284. [Google Scholar] [CrossRef]
- Wang, P.; Cavallini, A.; Montanari, G.C.; Wu, G. Effect of Rise Time on PD Pulse Features under Repetitive Square Wave Voltages. IEEE Trans. Dielectr. Electr. Insul. 2013, 20, 245–254. [Google Scholar] [CrossRef]
- Borghei, M.; Ghassemi, M. Partial discharge finite element analysis under fast, repetitive voltage pulses. In Proceedings of the 2019 IEEE Electric Ship Technologies Symposium (ESTS), Washington, DC, USA, 14–16 August 2019; pp. 324–328. [Google Scholar] [CrossRef]
- Ghassemi, M. Geometrical techniques for electric field control in (ultra) wide bandgap power electronics modules. In Proceedings of the 2018 IEEE Electrical Insulation Conference (EIC), San Antonio, TX, USA, 17–20 June 2018; pp. 589–592. [Google Scholar] [CrossRef]
- Tousi, M.M.; Ghassemi, M. Combined Geometrical Techniques and Applying Nonlinear Field Dependent Conductivity Layers to Address the High Electric Field Stress Issue in High Voltage High-Density Wide Bandgap Power Modules. IEEE Trans. Dielectr. Electr. Insul. 2020, 27, 305–313. [Google Scholar] [CrossRef]
- Tousi, M.M.; Ghassemi, M. Characterization of Nonlinear Field Dependent Conductivity Layer Coupled with Protruding Substrate to Address High Electric Field Issue within High Voltage High-Density Wide Bandgap Power Modules. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 343–350. [Google Scholar] [CrossRef]
- Wang, N.; Cotton, I.; Robertson, J.; Follmann, S.; Evans, K.; Newcombe, D. Partial Discharge Control in a Power Electronic Module Using High Permittivity Non-Linear Dielectrics. IEEE Trans. Dielectr. Electr. Insul. 2010, 17, 1319–1326. [Google Scholar] [CrossRef]
- Fang, L.; Cotton, I.; Wang, Z.J.; Freer, R. Insulation Performance Evaluation of High Temperature Wire Candidates for Aerospace Electrical Machine Winding Application. In Proceedings of the 2013 IEEE Electrical Insulation Conference (EIC), Ottawa, ON, Canada, 2–5 June 2013; pp. 253–256. [Google Scholar] [CrossRef]
- Gardner, R.; Cotton, I.; Emersic, C.; Rowland, S.; Freer, R. Thermal Stresses of Conformal Coating on Printed Circuit Boards. In Proceedings of the 2015 IEEE Electrical Insulation Conference (EIC), Seattle, WA, USA, 7–10 June 2015; pp. 106–109. [Google Scholar] [CrossRef]
- Meyer, D.R.; Cavallini, A.; Lusuardi, L.; Barater, D.; Pietrini, G.; Soldati, A. Influence of Impulse Voltage Repetition Frequency on RPDIV in Partial Vacuum. IEEE Trans. Dielectr. Electr. Insul. 2018, 25, 873–882. [Google Scholar] [CrossRef]
- Bayer, C.F.; Baer, E.; Waltrich, U.; Malipaard, D.; Schletz, A. Simulation of the electric field strength in the vicinity of metallization edges on dielectric substrates. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 257–265. [Google Scholar] [CrossRef]
- Bayer, C.F.; Waltrich, U.; Soueidan, A.; Baer, E.; Schletz, A. Partial discharges in ceramic substrates—Correlation of electric field strength simulations with phase resolved partial discharge measurements. In Proceedings of the 2016 International Conference on Electronics Packaging (ICEP), Hokkaido, Japan, 20–22 April 2016; pp. 530–535. [Google Scholar] [CrossRef]
- Borghei, M.; Ghassemi, M. Partial Discharge Analysis under High-Frequency, Fast-Rise Square Wave Voltages in Silicone Gel: A Modeling Approach. Energies 2019, 12, 4543. [Google Scholar] [CrossRef] [Green Version]
- Borghei, M.; Ghassemi, M. Finite element modeling of partial discharge activity within a spherical cavity in a solid dielectric material under fast, repetitive voltage pulses. In Proceedings of the 2019 IEEE Electrical Insulation Conference (EIC), Calgary, AB, Canada, 16–19 June 2019; pp. 34–37. [Google Scholar] [CrossRef]
- Borghei, M.; Ghassemi, M. A Finite Element Analysis Model for Partial Discharges in Silicone Gel under a High Slew Rate, High-Frequency Square Wave Voltage in Low-Pressure Conditions. Energies 2020, 13, 2152. [Google Scholar] [CrossRef]
- Whitehead, S. Dielectric Breakdown in Solids; Clarendon Press: Oxford, UK, 1951. [Google Scholar]
- Crichton, G.C.; Karlsson, P.W.; Pedersen, A. Partial Discharges in Ellipsoidal and Spheroidal Voids. IEEE Trans. Electr. Insul. 1989, 24, 335–342. [Google Scholar] [CrossRef] [Green Version]
- Pedersen, A.; Crichton, G.C.; McAllister, I.W. The Theory and Measurement of Partial Discharge Transients. IEEE Trans. Electr. Insul. 1991, 26, 487–497. [Google Scholar] [CrossRef] [Green Version]
- Pedersen, A.; Crichton, G.C.; McAllister, I.W. The Functional Relation between Partial Discharges and Induced Charge. IEEE Trans. Dielectr. Electr. Insul. 1995, 2, 535–543. [Google Scholar] [CrossRef] [Green Version]
- Niemeyer, L. A Generalized Approach to Partial Discharge Modeling. IEEE Trans. Dielectr. Electr. Insul. 1995, 2, 510–528. [Google Scholar] [CrossRef] [Green Version]
- Forssen, C.; Edin, H. Partial Discharges in a Cavity at Variable Applied Frequency Part 2: Measurements and Modeling. IEEE Trans. Dielectr. Electr. Insul. 2008, 15, 1610–1616. [Google Scholar] [CrossRef]
- Gutfleisch, F.; Niemeyer, L. Measurement and Simulation of PD in Epoxy Voids. IEEE Trans. Dielectr. Electr. Insul. 1995, 2, 729–743. [Google Scholar] [CrossRef]
- Ghassemi, M. PD Measurements, Failure Analysis, and Control in High-Power IGBT Modules. High Volt. 2018, 3, 170–178. [Google Scholar] [CrossRef]



| Quantity | ||
|---|---|---|
| Number of PDs per Cycle | ||
| Mean True Charge | ||
| Mean Apparent Charge | ||
| Maximum True Charge | ||
| Maximum Apparent Charge | ||
| Mean True Charge per Cycle | ||
| Mean Apparent Charge per Cycle |
| Quantity | ||||
|---|---|---|---|---|
| 0.2 mm Void | 0.3 mm Void | 0.2 mm Void | 0.3 mm Void | |
| Number of PDs per Cycle | 4.00 | 3.80 | 0 | 3.80 |
| Mean True Charge | 19.73 | 46.82 | - | 28.06 |
| Mean Apparent Charge | 3.15 | 8.68 | - | 3.93 |
| Maximum True Charge | 20.69 | 48.82 | - | 29.27 |
| Maximum Apparent Charge | 3.37 | 9.19 | - | 4.38 |
| Total True Charge per Cycle | 78.84 | 177.74 | - | 106.82 |
| Total Apparent Charge per Cycle | 12.60 | 32.96 | - | 14.85 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borghei, M.; Ghassemi, M. Characterization of Partial Discharge Activities in WBG Power Converters under Low-Pressure Condition. Energies 2021, 14, 5394. https://doi.org/10.3390/en14175394
Borghei M, Ghassemi M. Characterization of Partial Discharge Activities in WBG Power Converters under Low-Pressure Condition. Energies. 2021; 14(17):5394. https://doi.org/10.3390/en14175394
Chicago/Turabian StyleBorghei, Moein, and Mona Ghassemi. 2021. "Characterization of Partial Discharge Activities in WBG Power Converters under Low-Pressure Condition" Energies 14, no. 17: 5394. https://doi.org/10.3390/en14175394
APA StyleBorghei, M., & Ghassemi, M. (2021). Characterization of Partial Discharge Activities in WBG Power Converters under Low-Pressure Condition. Energies, 14(17), 5394. https://doi.org/10.3390/en14175394








